Management Zones Delineation, Correct and Incorrect Application Analysis in a Coriander Field Using Precision Agriculture, Soil Chemical, Granular and Hydraulic Analyses, Fuzzy k-Means Zoning, Factor Analysis and Geostatistics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area, Design of the Trial Plots, Management Zones, Irrigation and Variable Rate Application, Soil Sampling, Laboratory Soil and Hydraulic Analysis
2.2. Farm Machines, Irrigation Pipeline System, Soil-Crop Management
2.3. Climate Data Sensors’ Readings, Net Irrigation Requirements; Reference, Crop, and Actual Evapotranspiration; Soil–Water–Crop–Atmosphere (SWCA) Model, Soil Moisture Depletion Model and the Water Stress Coefficient Ks-Weighted Average
2.4. Statistical Data Analysis of Management Zones
2.5. Data Preparation, Exploratory Geostatistics Analysis and Modelling, Spatial Interpolation Methods and Models Validation Measures
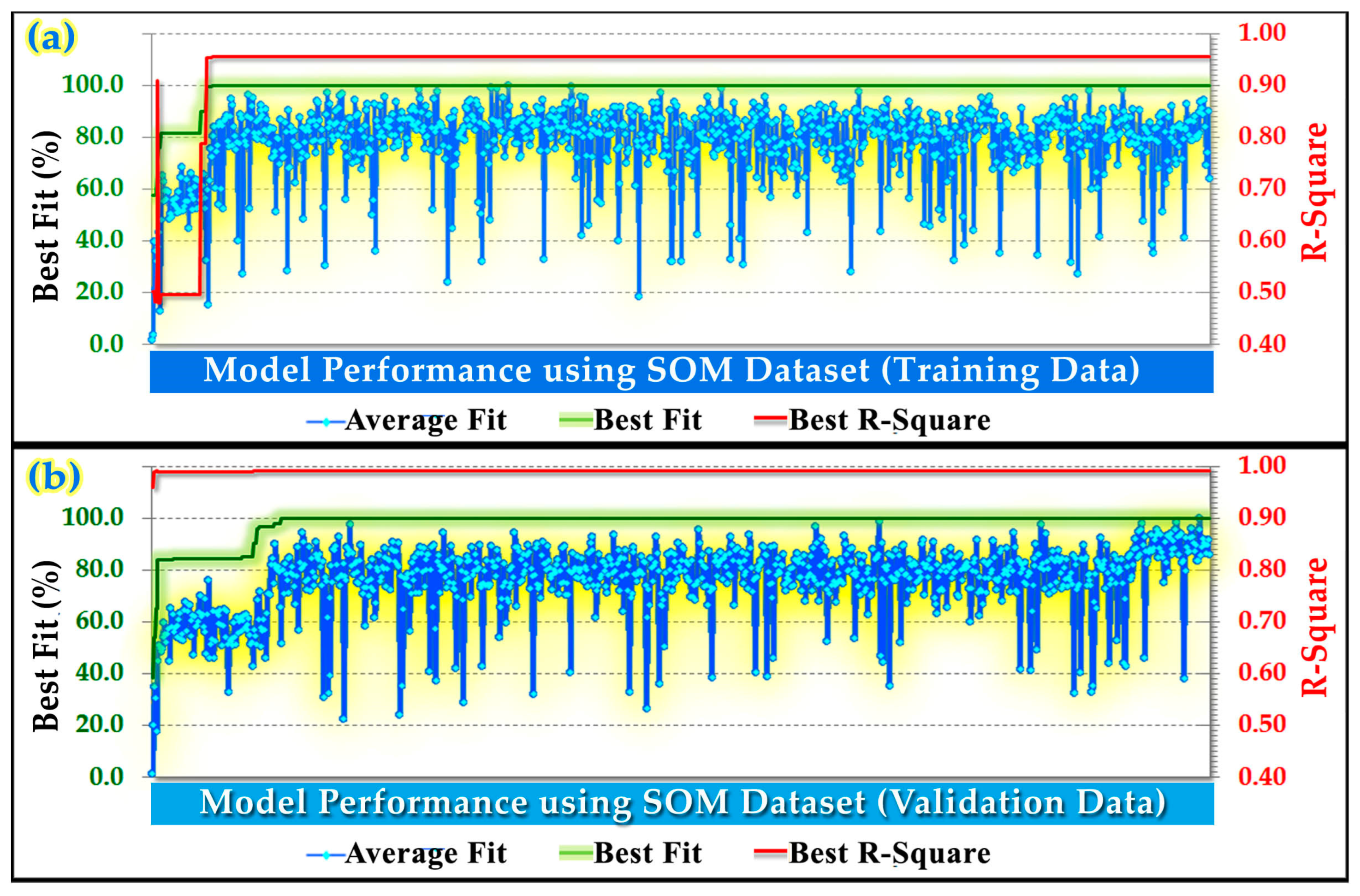
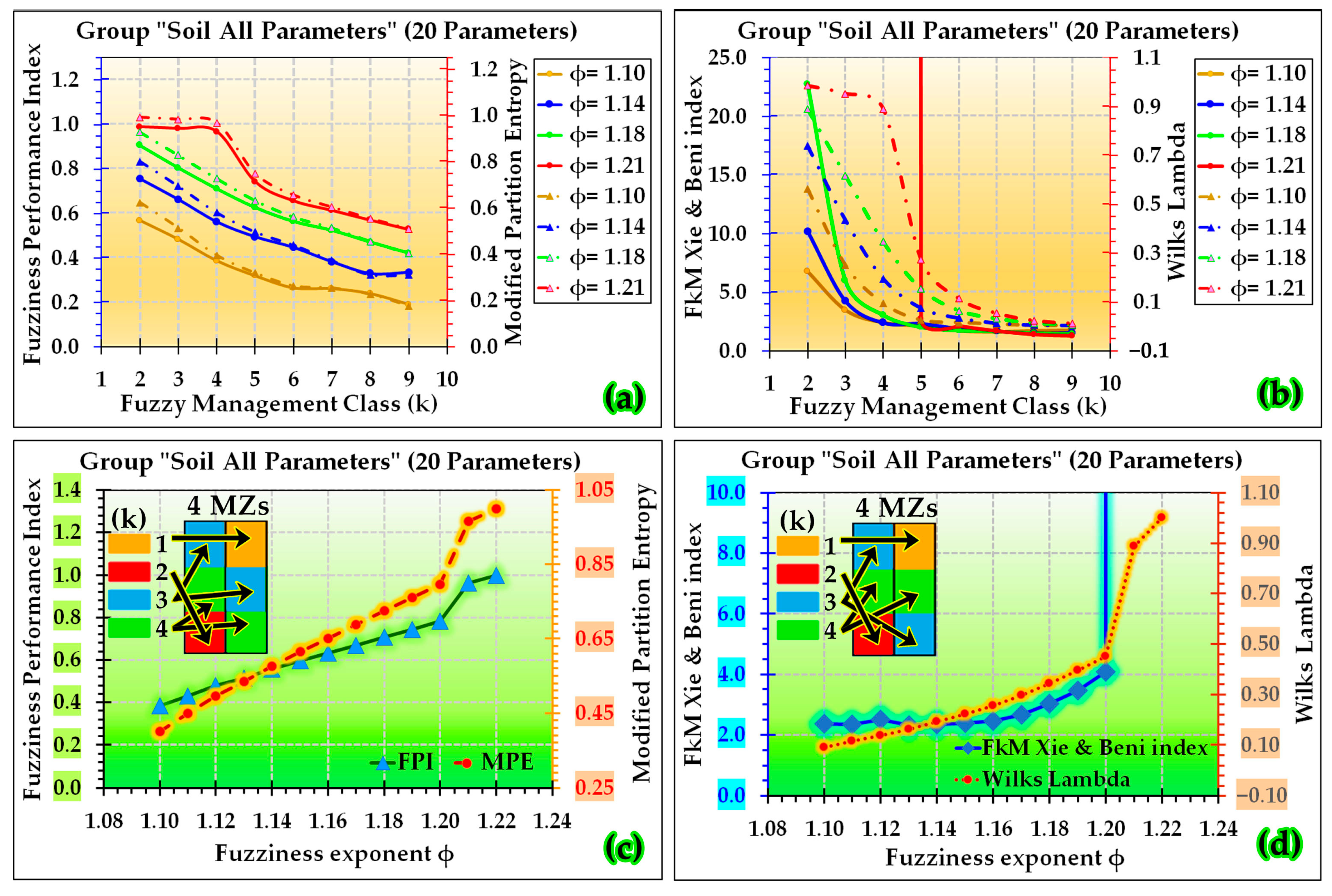
2.6. Factor Analysis, Principal Components Analysis, Delination of Management Zones Using Fuzzy k-Means Clustering and Validation Measures
3. Results and Discussion
3.1. Results of Climate Studied
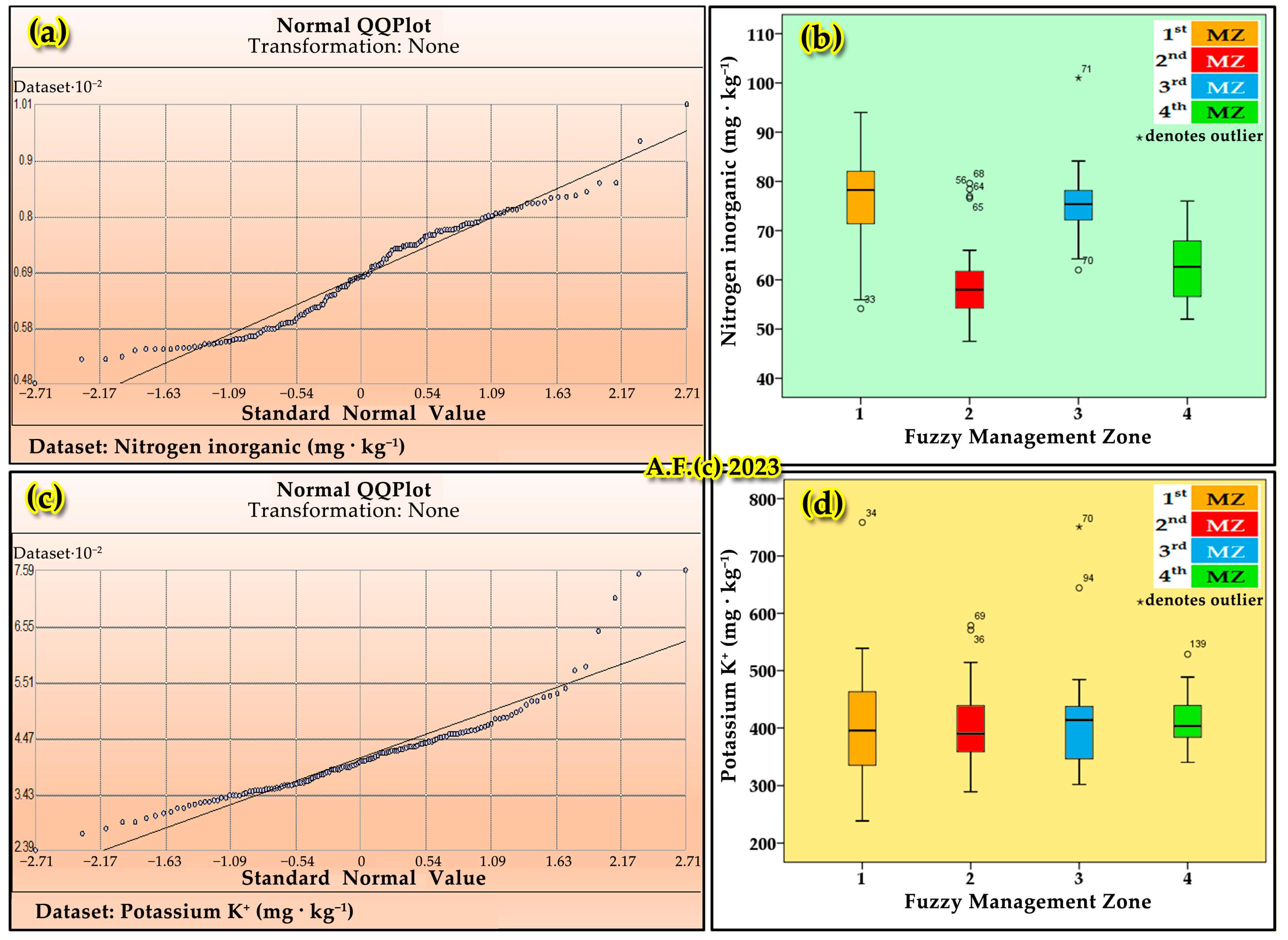
3.2. Results and Discussion of Soil’s Chemical, Granular and Hydraulic Analyses
- (a)
- Low coefficient of variation (CV < 15%);
- (b)
- Moderate coefficient of variation (CV = 15–35%);
- (c)
- High coefficient of variation (CV > 35%).
3.3. Results and Discussion of Exploratory Data and Correlations Analysis of Soil’s Chemical, Granular and Hydraulic Parameters
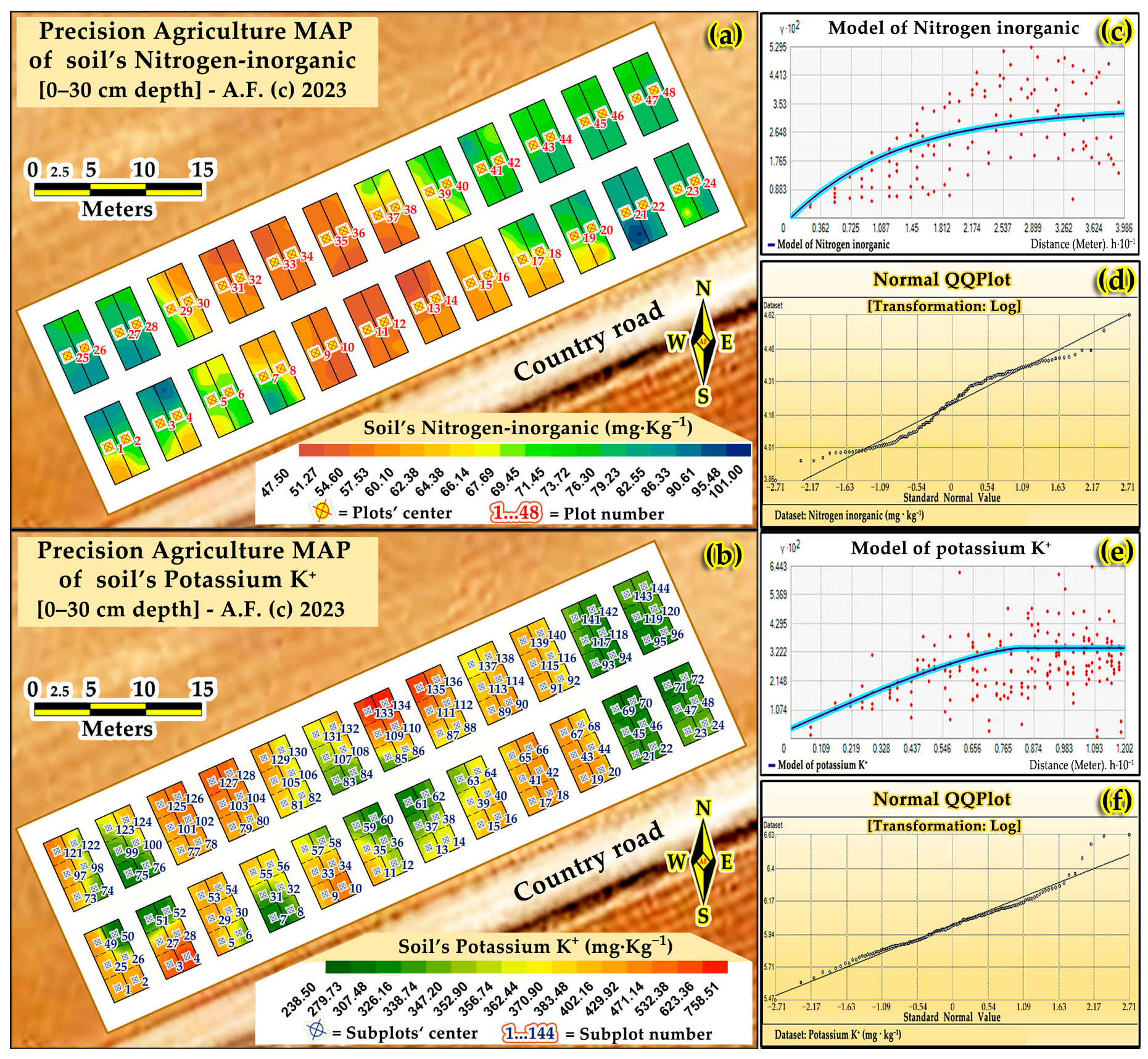
3.4. Results and Discussion of Precision Agriculture Geostatistical Modelling of Soil’s Chemical, Granular and Hydraulic Parameters
3.5. Results and Discussion of Best-Fitted Semivariogram Models, Spatial Dependence of Soil’s Chemical, Granular and Hydraulic Parameters, and Models Cross-Validation
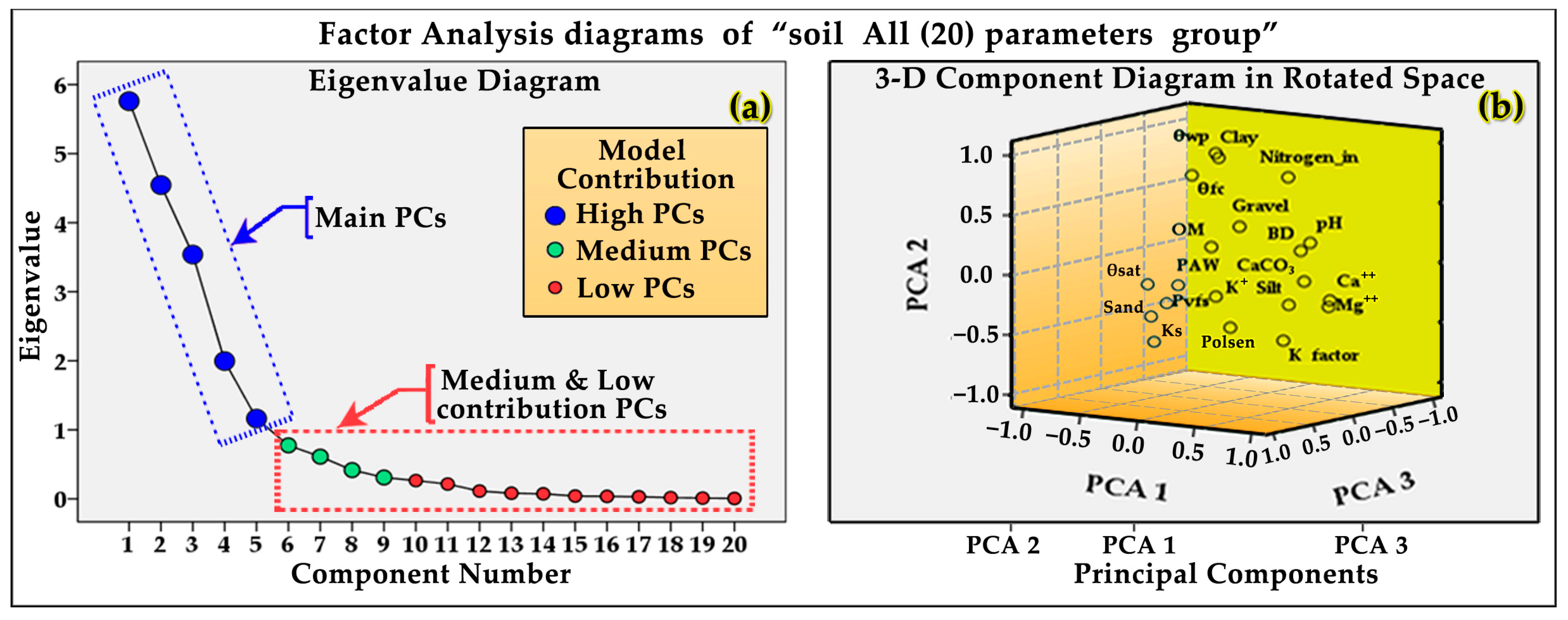
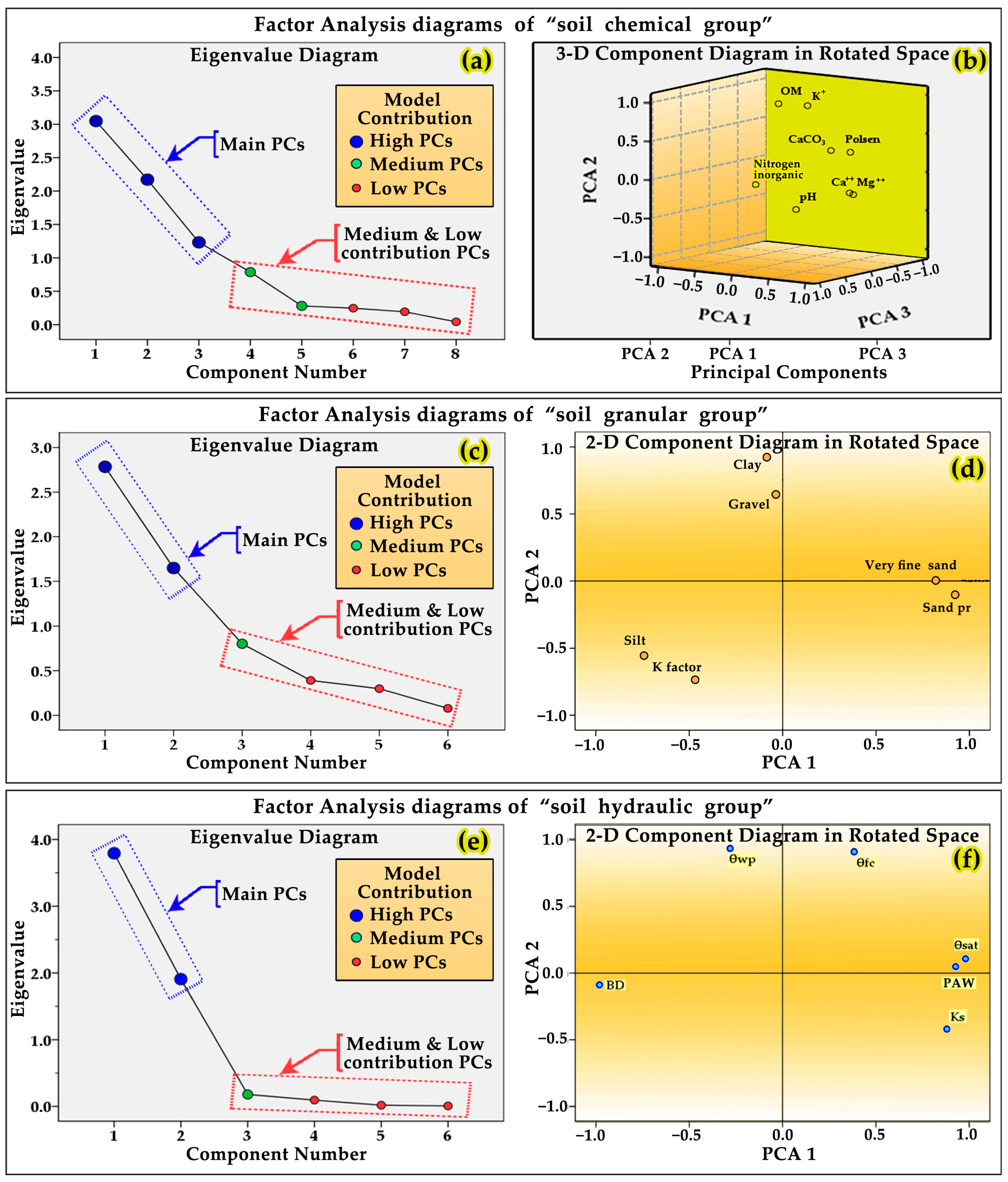
3.6. FactorAnalysis Results and Discussion of Soil’s Chemical, Granular and Hydraulic Groups
- Factor-1 contains significant loadings of eight parameters, which are magnesium Mg++, calcium Ca++, calcium carbonate CaCO3, sand pr (size: 0.2–2 mm), pH, soil erodibility [Kfactor], very fine sand (size: 0.02–0.2 mm) and clay (size: <0.002 mm). Factor-1 can be considered as an ‘Mg-Ca-CaCO3-Sand-pH-K factor-Vfs-Clay’ component that explains the synergistic soil chemistry interactions between the above-mentioned eight parameters as the dominating chemical processes in the field’s soil. Factor-1 stands for 28.798% of the data matrix’s variance. The presence of high levels of calcium Ca++ and magnesium Mg++ in the soil is associated with the intensive farming activities taking place in the area. The soil of the experimental plots was categorized as alkaline with pH values between 7.45 and 8.13;
- Factor-2 accounts for 22.725% of the variance and consists of five parameters, which are wilting point θwp, silt (size: 0.002–0.02 mm), field capacity θfc, nitrogen inorganic and phosphorus P-olsen. Factor-2 may be considered as a ‘θwp-silt-θfc-nitrogen inorganic-Polsen’ component that explains hydraulic and chemical interactions between the above-mentioned five parameters. This factor is mainly represented by positive high θfc and nitrogen inorganic loadings and shows negative loading of phosphorus P-olsen. Inorganic nitrogen of this factor does not have a significantly lithologic origin in the site and may be related to the agricultural activities of the region and the surface runoff of nitrogen fertilizers;
- Factor-4 accounts for 9.976% of the variance in the data matrix and is mainly represented by two parameters, and may be considered as an ‘organic matter and potassium K‘ component that exhibits high loadings of OM and potassium K+;
- Factor-5 is less significant and accounts for only 5.815% of the overall variance in the data matrix. This factor is considered as a ‘gravel‘ component that exhibits high loading of gravel content, indicating that this factor is rock weathering.
3.7. Delineating Field’s Management Zones Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Küppers, M.; O’Rourke, L.; Bockelée-Morvan, D.; Zakharov, V.; Lee, S.; Von Allmen, P.; Carry, B.; Teyssier, D.; Marston, A.; Müller, T.; et al. Localized sources of water vapour on the dwarf planet (1) Ceres. Nature 2014, 505, 525–527. [Google Scholar] [CrossRef] [PubMed]
- Siddique, K.H.M.; Bramley, H. Water Deficits: Development; CRC Press: Boca Raton, FL, USA, 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Filintas, A. Land Use Evaluation and Environmental Management of Biowastes, for Irrigation with Processed Wastewaters and Application of Bio-Sludge with Agricultural Machinery, for Improvement-Fertilization of Soils and Crops, with the Use of GIS-Remote Sensing, Precision Agriculture and Multicriteria Analysis. Ph.D. Thesis, University of the Aegean, Mitilini, Greece, 2011. [Google Scholar]
- Gleick, P.H.; Palaniappan, M. Peak water limits to freshwater withdrawal and use. Proc. Natl. Acad. Sci. USA 2010, 107, 11155–11162. [Google Scholar] [CrossRef] [PubMed]
- Shiklomanov, I.A. Appraisal and assessment of world water resources. Water Int. 2000, 25, 11–32. [Google Scholar] [CrossRef]
- Schiermeier, Q. The parched planet: Water on tap. Nature 2014, 510, 326–328. [Google Scholar] [CrossRef] [PubMed]
- Gan, Y.; Siddique, K.H.M.; Turner, N.C.; Li, X.-G.; Niu, J.-Y.; Yang, C.; Liu, L.; Chai, Q. Ridge-furrow mulching systems—An innovative technique for boosting crop productivity in semiarid rain-fed environments. Adv. Agron. 2013, 118, 429–476. [Google Scholar] [CrossRef]
- FAO. Coping with Water Scarcity: An Action Framework for Agriculture and Food Security; FAO: Rome, Italy, 2012; p. 100. [Google Scholar]
- Stamatis, G.; Parpodis, K.; Filintas, A.; Zagana, E. Groundwater quality, nitrate pollution and irrigation environmental management in the Neogene sediments of an agricultural region in central Thessaly (Greece). Environ. Earth Sci. 2011, 64, 1081–1105. [Google Scholar] [CrossRef]
- EEA. Use of Freshwater Resources in Europe, CSI 018; European Environment Agency (EEA): Copenhagen, Denmark, 2019.
- Koutseris, Ε.; Filintas, A.; Dioudis, P. Antiflooding prevention, protection, strategic environmental planning of aquatic resources and water purification: The case of Thessalian basin, in Greece. Desalination 2010, 250, 318–322. [Google Scholar] [CrossRef]
- Κoutseris, Ε.; Filintas, A.; Dioudis, P. Environmental control of torrents environment: One valorisation for prevention of water flood disasters. WIT Trans. Ecol. Environ. 2007, 104, 249–259. [Google Scholar] [CrossRef]
- Islam, S.M.F.; Karim, Z. World’s Demand for Food and Water: The Consequences of Climate Change. In Desalination-Challenges and Opportunities; Farahani, M.H.D.A., Vatanpour, V., Taheri, A.H., Eds.; IntechOpen: London, UK, 2019; Chapter 4; pp. 1–27. [Google Scholar] [CrossRef]
- Filintas, A.; Wogiatzi, E.; Gougoulias, N. Rainfed cultivation with supplemental irrigation modelling on seed yield and oil of Coriandrum sativum L. using Precision Agriculture and GIS moisture mapping. Water Supply 2021, 21, 2569–2582. [Google Scholar] [CrossRef]
- Siebert, S.; Kummu, M.; Porkka, M.; Döll, P.; Ramankutty, N.; Scanlon, B.R. A global data set of the extent of irrigated land from 1900 to 2005. Hydrol. Earth Syst. Sci. 2015, 19, 1521–1545. [Google Scholar] [CrossRef]
- Garrote, L.; Iglesias, A.; Granados, A.; Mediero, L.; Martin-Carrasco, F. Quantitative assessment of climate change vulnerability of irrigation demands in Mediterranean Europe. Water Resour. Manag. 2015, 29, 325–338. [Google Scholar] [CrossRef]
- Kreins, P.; Henseler, M.; Anter, J.; Herrmann, F.; Wendland, F. Quantification of climate change impact on regional agricultural irrigation and groundwater demand. Water Resour. Manag. 2015, 29, 3585–3600. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M. Crop Evapotranspiration; Drainage & Irrigation Paper No. 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Filintas, A.; Nteskou, A.; Kourgialas, N.; Gougoulias, N.; Hatzichristou, E. A Comparison between Variable Deficit Irrigation and Farmers’ Irrigation Practices under Three Fertilization Levels in Cotton Yield (Gossypium hirsutum L.) Using Precision Agriculture, Remote Sensing, Soil Analyses, and Crop Growth Modeling”. Water 2022, 14, 2654. [Google Scholar] [CrossRef]
- Kalavrouziotis, I.K.; Filintas, A.T.; Koukoulakis, P.H.; Hatzopoulos, J.N. Application of multicriteria analysis in the Management and Planning of Treated Municipal Wastewater and Sludge reuse in Agriculture and Land Development: The case of Sparti’s Wastewater Treatment Plant, Greece. Fresenious Environ. Bull. 2011, 20, 287–295. [Google Scholar]
- Dioudis, P.; Filintas, A.; Koutseris, E. GPS and GIS based N-mapping of agricultural fields’ spatial variability as a tool for non-polluting fertilization by drip irrigation. Int. J. Sustain. Dev. Plan. 2009, 4, 210–225. [Google Scholar] [CrossRef]
- Dioudis, P.; Filintas, A.; Papadopoulos, A. Corn yield response to irrigation interval and the resultant savings in water and other overheads. Irrig. Drain. 2009, 58, 96–104. [Google Scholar] [CrossRef]
- Filintas, A.; Dioudis, P.; Prochaska, C. GIS modeling of the impact of drip irrigation, of water quality and of soil’s available water capacity on Zea mays L, biomass yield and its biofuel potential. Desalination Water Treat. 2010, 13, 303–319. [Google Scholar] [CrossRef]
- FAO. New Quality Criteria to Be Developed for Booming Spice and Herb Sector; Food and Agriculture Organization of the United Nations: Rome, Italy, 2018; Available online: https://www.fao.org/news/story/en/item/213612/icode/ (accessed on 5 February 2021).
- Wan, S.; Norby, R.J.; Ledford, J.; Weltzin, J.F. Responses of soil respiration to elevated CO2, air warming, and changing soil water availability in a model oldfield grassland. Glob. Chang. Biol. 2007, 13, 2411–2424. [Google Scholar] [CrossRef]
- Filintas, A. Study and Mapping of Biomass Yield with the Use of Spatial Statistics and Geoinformation. Master’s Thesis, Dept. of Natural Resources Management and Agricultural Engineering, Agricultural University of Athens, Athens, Greece, 2008. (In Greek with English Abstract). [Google Scholar]
- Garten, C.T., Jr.; Classen, A.T.; Norby, R.J. Soil moisture surpasses elevated CO2 and temperature as a control on soil carbon dynamics in a multi-factor climate change experiment. Plant Soil 2009, 319, 85–94. [Google Scholar] [CrossRef]
- Falloon, P.; Jones, C.D.; Ades, M.; Paul, K. Direct soil moisture controls of future global soil carbon changes: An important source of uncertainty. Glob. Biogeochem. Cycles 2011, 25, GB3010. [Google Scholar] [CrossRef]
- Dioudis, P.; Filintas, A.; Papadopoulos, A.; Sakellariou-Makrantonaki, M. The influence of different drip irrigation layout designs on sugar beet yield and their contribution to environmental sustainability. Fresenious Environ. Bull. 2010, 19, 818–831. [Google Scholar]
- Page, A.L.; Miller, R.H.; Keeney, D.R. Methods of Soil Analysis Part 2: Chemical and Microbiological Properties; Agronomy, ASA and SSSA: Madison, WI, USA, 1982; p. 1159. [Google Scholar]
- Rodriguez, H.G.; Popp, J.; Gbur, E.; Chaubey, I. Environmental and economic impacts of reducing total phosphorous runoff in an agricultural watershed. Agric. Syst. 2011, 104, 623–633. [Google Scholar] [CrossRef]
- Filintas, A. Soil Moisture Depletion Modelling Using a TDR Multi-Sensor System, GIS, Soil Analyzes, Precision Agriculture and Remote Sensing on Maize for Improved Irrigation-Fertilization Decisions. Eng. Proc. 2021, 9, 36. [Google Scholar] [CrossRef]
- Geerts, S.; Raes, D. Deficit irrigation as an on-farm strategy to maximize crop water productivity in dry areas. Agric. Water Manag. 2009, 96, 1275–1284. [Google Scholar] [CrossRef]
- Fleming, K.L.; Westfall, D.G.; Collins, F. Evaluating management zone technology and grid soil sampling for variable rate nitrogen application. In Proceedings of the 5th International Conference on Precision Agriculture, Minneapolis, MN, USA, 16–19 July 2000; Robert, P.C., Rust, R.H., Larson, W.E., Eds.; ASA, CSSA, and SSSA: Madison, WI, USA, 2000. [Google Scholar]
- Haghverdi, A.; Leib, B.G.; Washington-Allen, R.A.; Ayers, P.D.; Buschermohle, M.J. Perspectives on delineating management zones for variable rate irrigation. Comput. Electron. Agric. 2015, 117, 154–167. [Google Scholar] [CrossRef]
- Vrindts, E.; Mouazen, A.M.; Reyniers, M.; Maertens, K.; Maleki, M.R.; Ramon, H.; De Baerdemaeker, J. Management zones based on correlation between soil compaction, yield and crop data. Biosyst. Eng. 2005, 92, 419–428. [Google Scholar] [CrossRef]
- Filintas, A.; Gougoulias, N.; Hatzichristou, E. Modeling Soil Erodibility by Water (Rainfall/Irrigation) on Tillage and No-Tillage Plots of a Helianthus Field Utilizing Soil Analysis, Precision Agriculture, GIS, and Kriging Geostatistics. Environ. Sci. Proc. 2023, 25, 54. [Google Scholar] [CrossRef]
- Bezdek, J.C. Cluster validity with fuzzy sets. J. Cybern. 1974, 3, 58–73. [Google Scholar] [CrossRef]
- Bezdek, J.C. A convergence theorem for the fuzzy ISODATA clustering algorithm. IEEE Trans. Pattern Anal. Mach. Intell. 1980, 2, 1–8. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Plenum Press: New York, NY, USA, 1981. [Google Scholar]
- Bezdek, J.C.; Trivedi, M.; Ehrlich, R.; Full, W. Fuzzy clustering: A new approach for geostatistical analysis. Int. J. Syst. Meas. Decis. 1981, 2, 13–23. [Google Scholar]
- Filintas, A.; Gougoulias, N.; Kourgialas, N.; Hatzichristou, E. Management Soil Zones, Irrigation, and Fertigation Effects on Yield and Oil Content of Coriandrum sativum L. Using Precision Agriculture with Fuzzy k-Means Clustering. Sustainability 2023, 15, 13524. [Google Scholar] [CrossRef]
- McBratney, A.B.; Moore, A.W. Application of fuzzy sets to climate classification. Agric. For. Meteorol. 1985, 35, 165–185. [Google Scholar] [CrossRef]
- De Gruijter, J.J.; McBratney, A.B. A modified fuzzy k-means method for predictive classification. In Classijkation and Related Methods of Data Analysis; Bock, H.H., Ed.; Elsevier: Amsterdam, The Netherlands, 1988; pp. 97–104. [Google Scholar]
- Odeh, I.O.A.; McBratney, A.B.; Chittleborough, D.J. Design of optimal sample spacings for mapping soil using fuzzy k-means and regionalized variable theory. Geoderma 1990, 47, 93–122. [Google Scholar] [CrossRef]
- Xie, X.L.; Beni, G. A validity measure for fuzzy clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 841–847. [Google Scholar] [CrossRef]
- McBratney, A.B.; de Gruijter, J.J. A continuum approach to soil classification by modified fuzzy k-means with extragrades. J. Soil Sci. 1992, 43, 159–175. [Google Scholar] [CrossRef]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. On clustering validation techniques. J. Intell. Inf. Syst. 2001, 17, 107–145. [Google Scholar] [CrossRef]
- Minasny, B.; McBratney, A.B. FuzME Version 3.0. Australian Centre for Precision Agriculture; The University of Sydney: Sydney, Australia, 2002; Available online: http://www.usyd.edu.au/sulagriclacpa (accessed on 16 May 2006).
- Fridgen, J.J.; Kitchen, N.R.; Sudduth, A.K.; Drummond, S.T. Management Zone Analyst (MZA): Software for subfeld management zone delineation. Agron. J. 2004, 96, 100–108. [Google Scholar] [CrossRef]
- Steinley, D. K-means clustering: A half-century synthesis. Br. J. Math. Stat. Psychol. 2006, 59, 1–34. [Google Scholar] [CrossRef]
- Luz López García, M.; García-Ródenas, R.; González Gómez, A. K-means algorithms for functional data. Neurocomputing 2015, 151, 231–245. [Google Scholar] [CrossRef]
- Taylor, J.A.; Dresser, J.; Hickey, C.C.; Nuske, S.T.; Bates, T.R. Considerations on spatial crop load mapping. Aust. J. Grape Wine Res. 2019, 25, 144–155. [Google Scholar] [CrossRef]
- Soil Survey Staff. Soil Taxonomy: A Basic System of Soil Classification for Making and Interpreting Soil Surveys; USDA Natural Resources Conservation Service: Washington, DC, USA, 1975.
- Bouyoucos, J.G. Hydrometer method improved for making particle size analysis of soils. Agron. J. 1962, 54, 464–465. [Google Scholar] [CrossRef]
- Beretta, N.A.; Silbermann, V.A.; Paladino, L.; Torres, D.; Bassahun, D.; Musselli, R.; García-Lamohte, A. Soil texture analyses using a hydrometer: Modification of the Bouyoucos method. Cien. Investig. Agr. 2014, 41, 263–271. [Google Scholar] [CrossRef]
- Filintas, A.; Nteskou, A.; Katsoulidi, P.; Paraskebioti, A.; Parasidou, M. Rainfed and Supplemental Irrigation Modelling 2D GIS Moisture Rootzone Mapping on Yield and Seed Oil of Cotton (Gossypium hirsutum) Using Precision Agriculture and Remote Sensing. Eng. Proc. 2021, 9, 37. [Google Scholar] [CrossRef]
- Varian “Flame Atomic Absorption Spectroscopy”, Analytical Methods; Publ. No: 85-100009-00; Varian Techtron Pty. Ltd.: Springvale, Australia, 1989; Available online: https://www.agilent.com/cs/library/usermanuals/Public/0009.pdf (accessed on 17 May 2018).
- Muller, G.; Gatsner, M. Chemical analysis. Neues Jahrb. Mineral. Monatshefte 1971, 10, 466–469. [Google Scholar]
- Lamas, F.; Irigaray, C.; Oteo, C.; Chacon, J. Selection of the most appropriate method to determine the carbonate content for engineering purposes with particular regard to marls. Eng. Geol. 2005, 81, 32–41. [Google Scholar] [CrossRef]
- Meena, S.S.; Singh, B.; Singh, D.; Ranjan, J.K.; Meena, R.D. Pre and post harvest factors effecting yield and quality of seed spices: A review. Int. J. Seed Spices 2013, 3, 1–11. [Google Scholar]
- USDA-SCS. Irrigation Water Requirements; Technical, R. No. 21; USDA Soil Conservation Service: Washington, DC, USA, 1970.
- Norusis, M.J. IBM SPSS Statistics 19 Advanced Statistical Procedures Companion; Pearson: London, UK, 2011. [Google Scholar]
- Hatzigiannakis, E.; Filintas, A.; Ilias, A.; Panagopoulos, A.; Arampatzis, G.; Hatzispiroglou, I. Hydrological and rating curve modelling of Pinios River water flows in Central Greece, for environmental and agricultural water resources management. Desalination Water Treat. 2016, 57, 11639–11659. [Google Scholar] [CrossRef]
- Davis, J.C. Statistics and Data Analysis in Geology; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Hatzopoulos, N.J. Topographic Mapping, Covering the Wider Field of Geospatial Information Science & Technology (GIS&T); Universal Publishers: Irvine, CA, USA, 2008. [Google Scholar]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientists, 2nd ed.; John Wiley & Sons: Chichester, UK, 2007; p. 271. Available online: https://onlinelibrary.wiley.com/doi/book/10.1002/9780470517277 (accessed on 5 February 2023).
- Bogunovic, I.; Mesic, M.; Zgorelec, Z.; Jurisic, A.; Bilandzija, D. Spatial variation of soil nutrients on sandy-loam soil. Soil Tillage Res. 2014, 144, 174–183. [Google Scholar] [CrossRef]
- Cass, A. Interpretation of some soil physical indicators for assessing soil physical fertility. In Soil Analysis: An Interpretation Manual, 2nd ed.; Peverill, K.I., Sparrow, L.A., Reuter, D.J., Eds.; CSIRO Publishing: Melbourne, Australia, 1999; pp. 95–102. [Google Scholar]
- Soropa, G.; Mbisva, O.M.; Nyamangara, J.; Nyakatawa, E.Z.; Nyapwere, N.; Lark, R.M. Spatial variability and mapping of soil fertility status in a high-potential smallholder farming area under sub-humid conditions in Zimbabwe. SN Appl. Sci. 2021, 3, 396. [Google Scholar] [CrossRef]
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Zhang, H.; Zhuang, S.; Qian, H.; Wang, F.; Ji, H. Spatial variability of the topsoil organic carbon in the Moso bamboo forests of southern China in association with soil properties. PLoS ONE 2015, 10, e0119175. [Google Scholar] [CrossRef]
- Yang, P.G.; Byrne, J.M.; Yang, M. Spatial variability of soil magnetic susceptibility, organic carbon and total nitrogen from farmland in northern China. Catena 2016, 145, 92–98. [Google Scholar] [CrossRef]
- Tang, X.L.; Xia, M.P.; Pérez-Cruzado, C.; Guan, F.Y.; Fan, S.H. Spatial distribution of soil organic carbon stock in Moso bamboo forests in subtropical China. Sci. Rep. 2017, 7, 42640. [Google Scholar] [CrossRef]
- John, K.; Abraham, I.I.; Kebonye, N.M.; Agyeman, P.C.; Ayito, E.O.; Kudjo, A.S. Soil organic carbon prediction with terrain derivatives using geostatistics and sequential Gaussian simulation. J. Saudi Soc. Agric. Sci. 2021, 20, 379–389. [Google Scholar] [CrossRef]
- Qu, M.K.; Li, W.D.; Zhang, C.R.; Wang, S.Q. Effect of land use types on the spatial prediction of soil nitrogen. GISci. Remote Sens. 2012, 49, 397–411. [Google Scholar] [CrossRef]
- Ferreiro, J.P.; Pereira De Almeida, V.; Cristina Alves, M.; Aparecida De Abreu, C.; Vieira, S.R.; Vidal Vázquez, E. Spatial variability of soil organic matter and cation exchange capacity in an Oxisol under different land uses. Commun. Soil Sci. Plant Anal. 2016, 47 (Suppl. 1), 75–89. [Google Scholar] [CrossRef]
- Loague, K.; Green, R.E. Statistical and graphical methods for evaluating solute transport models: Overview and application. J. Contam. Hydrol. 1991, 7, 51–73. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, R.M. Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Jolliffe, I.T. Principal Component Analysis; Springer: Berlin, Germany, 1986. [Google Scholar] [CrossRef]
- Kaiser, H.F. The Application of Electronic Computers to Factor Analysis. Educ. Psychol. Meas. 1960, 20, 141–151. [Google Scholar] [CrossRef]
- Manly, B.F.J.; Navarro Alberto, J.A. Multivariate Statistical Methods: A Primer, 4th ed.; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Friedrich, S.; Konietschke, F.; Pauly, M. Resampling-based analysis of multivariate data and repeated measures designs with the R Package MANOVA.RM. R J. 2019, 11, 380–400. [Google Scholar] [CrossRef]
- Johnson, G.V.; Raun, W.R.; Zhang, H.; Hattey, J.A. Oklahoma Soil Fertility Handbook; OK Agricultural Experiment Station and Oklahoma Cooperative Extension Service, Oklahoma State University: Stillwater, OK, USA, 2000. [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses–A Guide to Conservation Planning; Agriculture Handbook 537; U.S. Department of Agriculture (Science and Education Administration): Washington, DC, USA, 1978.
- Renard, K.; Foster, G.; Weesies, G.; McCool, D.; Yoder, D. Predicting soil erosion by water: A guide to conservation planning with the Revised Universal Soil Loss Equation (RUSLE). In Agricultural Handbook; United States Government Printing: Washington, DC, USA, 1997; pp. 65–100. [Google Scholar]
- USDA Department of Agriculture—Agricultural Research Service: Revised Universal Soil Loss Equation. 2002. Available online: http://www.sedlab.olemiss.edu/rusle (accessed on 22 April 2022).
- Panagos, P.; Meusburger, K.; Alewell, C.; Montarella, L. Soil erodibility estimation using LUCAS point survey data of Europe. Environ. Model. Softw. 2012, 30, 143–145. [Google Scholar] [CrossRef]
- Wilding, L.P. Spatial variability: Its documentation, accommodation and implication to soil survey. In Soil Spatial Variability; Nielsen, D.R., Bouma, J., Eds.; Pudoc: Wagenigen, The Netherlands, 1985; pp. 166–189. [Google Scholar]
- Yamamoto, J.K. Comparing ordinary kriging interpolation variance and indicator kriging conditional variance for assessing uncertainties at unsampled locations. In Application of Computers and Operations Research in the Mineral Industry; Gan, D., Guli, N.P., Dwyer, K., Eds.; Balkema: Kalamazoo, MI, USA, 2005. [Google Scholar]
- Goovaerts, P. Geostatistical tools for characterizing the spatial variability of microbiological and physico-chemical soil properties. Biol. Fertil. Soils 1998, 27, 315–334. [Google Scholar] [CrossRef]
- Cambardella, C.A.; Moorman, T.B.; Novak, J.M.; Parkin, T.B.; Turco, R.F.; Konopka, A.E. Field-scale variability of soil properties in central Iowa soils. Soil Sci. Soc. Am. J. 1994, 58, 1501–1511. [Google Scholar] [CrossRef]




| SN | Parameter | Range | Minimum | Maximum | Mean | Std. Deviation * | Variance | CV (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | Phosphorus P-olsen (mg·Kg−1) | 12.470 | 8.960 | 21.430 | 15.955 | 2.290 | 5.242 | 14.351 |
| 2 | Potassium K (mg·Kg−1) | 520.007 | 238.500 | 758.507 | 409.427 | 81.036 | 6566.865 | 19.793 |
| 3 | Calcium Ca (mg·Kg−1) | 2282.002 | 1190.841 | 3472.843 | 2236.163 | 427.379 | 182,653.088 | 19.112 |
| 4 | Magnesium Mg (mg·Kg−1) | 1775.510 | 1100.817 | 2876.327 | 1900.579 | 304.554 | 92,753.405 | 16.024 |
| 5 | pH [1:2 soil/water solution] | 0.680 | 7.450 | 8.130 | 7.820 | 0.095 | 0.009 | 1.220 |
| 6 | Nitrogen inorganic (mg·Kg−1) | 53.500 | 47.500 | 101.000 | 68.092 | 10.343 | 106.985 | 15.190 |
| 7 | Organic matter (%) | 2.743 | 1.327 | 4.070 | 1.790 | 0.331 | 0.109 | 18.489 |
| 8 | Calcium carbonate CaCO3 (%) | 3.853 | 0.366 | 4.219 | 1.572 | 0.827 | 0.684 | 52.581 |
| 9 | Clay (size: <0.002 mm) (%) | 6.540 | 22.180 | 28.720 | 24.832 | 1.131 | 1.279 | 4.553 |
| 10 | Silt (size: 0.002–0.02 mm) (%) | 8.700 | 13.610 | 22.310 | 19.664 | 1.694 | 2.870 | 8.615 |
| 11 | Very fine sand (size: 0.02–0.2 mm) (%) | 2.337 | 20.719 | 23.056 | 21.943 | 0.162 | 0.026 | 0.738 |
| 12 | Sand pr (size: 0.2–2 mm) (%) | 5.566 | 30.127 | 35.693 | 33.372 | 1.318 | 1.736 | 3.948 |
| 13 | Gravel (%) | 0.235 | 0.011 | 0.246 | 0.077 | 0.034 | 0.001 | 43.661 |
| 14 | Soil Erodibility [Kfactor] (Mg·ha·h·ha−1·MJ−1·mm−1) | 0.009 | 0.025 | 0.034 | 0.031 | 0.001 | 0.000 | 4.734 |
| 15 | Wilting point θwp (m3·m−3) | 4.607 | 13.365 | 17.972 | 15.981 | 0.672 | 0.451 | 4.204 |
| 16 | Field capacity θfc (m3·m−3) | 5.344 | 25.124 | 30.468 | 27.663 | 0.923 | 0.852 | 3.337 |
| 17 | Saturation θsat (m3·m−3) | 13.252 | 37.295 | 50.547 | 46.678 | 2.215 | 4.905 | 4.745 |
| 18 | Plant available water PAW (cm·cm−1) | 0.049 | 0.085 | 0.134 | 0.111 | 0.007 | 0.000 | 6.106 |
| 19 | Sat. Hydraulic conductivity Ks (mm·hr−1) | 18.283 | 4.656 | 22.939 | 16.275 | 4.226 | 17.855 | 25.964 |
| 20 | Bulk density (g·cm−1) | 0.351 | 1.311 | 1.662 | 1.415 | 0.055 | 0.003 | 3.904 |
| SN | Parameter | Phosphorus P-Olsen | Potassium K+ | Calcium Ca++ | Magnesium Mg++ | pH | Nitrogen Inorganic | Organic Matter | Calcium Carbonate CaCO3 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Phosphorus P-olsen | 1 | 0.281 ** | 0.145 | 0.202 * | 0.011 | −0.234 ** | 0.145 | 0.400 ** |
| 2 | Potassium K+ | 0.281 ** | 1 | −0.047 | −0.054 | −0.421 ** | −0.253 ** | 0.724 ** | 0.266 ** |
| 3 | Calcium Ca++ | 0.145 | −0.047 | 1 | 0.953 ** | 0.470 ** | 0.241 ** | −0.117 | 0.540 ** |
| 4 | Magnesium Mg++ | 0.202 * | −0.054 | 0.953 ** | 1 | 0.491 ** | 0.217 ** | −0.158 | 0.548 ** |
| 5 | pH [1:2 soil/water solution] | 0.011 | −0.421 ** | 0.470 ** | 0.491 ** | 1 | 0.613 ** | −0.269 ** | 0.428 ** |
| 6 | Nitrogen inorganic | −0.234 ** | −0.253 ** | 0.241 ** | 0.217 ** | 0.613 ** | 1 | 0.062 | 0.340 ** |
| 7 | Organic matter | 0.145 | 0.724 ** | −0.117 | −0.158 | −0.269 ** | 0.062 | 1 | 0.286 ** |
| 8 | Calcium carbonate CaCO3 | 0.400 ** | 0.266 ** | 0.540 ** | 0.548 ** | 0.428 ** | 0.340 ** | 0.286 ** | 1 |
| SN | Parameter | Clay | Silt | Sand pr | Very Fine Sand | Gravel | Soil Erodibility [Kfactor] |
|---|---|---|---|---|---|---|---|
| 1 | Clay | 1 | −0.508 ** | −0.650 ** | −0.493 ** | −0.203 * | 0.693 ** |
| 2 | Silt | −0.508 ** | 1 | −0.182 * | −0.079 | 0.400 ** | −0.594 ** |
| 3 | Sand pr | −0.650 ** | −0.182 * | 1 | 0.595 ** | −0.058 | −0.335 ** |
| 4 | Very fine sand | −0.493 ** | −0.079 | 0.595 ** | 1 | 0.137 | −0.318 ** |
| 5 | Gravel | −0.203 * | 0.400 ** | −0.058 | 0.137 | 1 | −0.301 ** |
| 6 | Soil Erodibility [Kfactor] | 0.693 ** | −0.594 ** | −0.335 ** | −0.318 ** | −0.301 ** | 1 |
| SN | Parameter | Wilting Point θwp | Field Capacity θfc | Saturation θsat | Plant Available Water PAW | Saturated Hydraulic Conductivity Ks | Bulk Density BD |
|---|---|---|---|---|---|---|---|
| 1 | Wilting point θwp | 1 | 0.720 ** | −0.174 * | −0.218 ** | −0.604 ** | 0.201 * |
| 2 | Field capacity θfc | 0.720 ** | 1 | 0.476 ** | 0.395 ** | −0.060 | −0.460 ** |
| 3 | Saturation θsat | −0.174 * | 0.476 ** | 1 | 0.867 ** | 0.825 ** | −0.991 ** |
| 4 | Plant available water PAW | −0.218 ** | 0.395 ** | 0.867 ** | 1 | 0.768 ** | −0.866 ** |
| 5 | Saturated Hydraulic conductivity Ks | −0.604 ** | −0.060 | 0.825 ** | 0.768 ** | 1 | −0.825 ** |
| 6 | Bulk density BD | 0.201 * | −0.460 ** | −0.991 ** | −0.866 ** | −0.825 ** | 1 |
| SN | Parameter | Model | Range (m) | Nugget (C0) | Partial Sill (C) | Sill (C0 + C) | N:S Ratio | Spatial Dependence |
|---|---|---|---|---|---|---|---|---|
| 1 | Phosphorus P-olsen | Gaussian | 19.1587 | 1.6796 | 4.4169 | 6.0965 | 0.2755 | Medium |
| 2 | Potassium K | Circular | 8.3288 | 0.0037 | 0.0301 | 0.0338 | 0.1096 | Strong |
| 3 | Calcium Ca | Exponential | 25.4364 | 0.0003 | 0.0384 | 0.0387 | 0.0069 | Strong |
| 4 | Magnesium Mg | Exponential | 61.7036 | 0.0030 | 0.0360 | 0.0390 | 0.0774 | Strong |
| 5 | pH [1:2 soil/water solution] | Exponential | 38.6096 | 0.0001 | 0.0110 | 0.0111 | 0.0090 | Strong |
| 6 | Nitrogen inorganic | Exponential | 39.8639 | 0.0001 | 0.0341 | 0.0342 | 0.0029 | Strong |
| 7 | Organic matter | Exponential | 25.1485 | 0.0005 | 0.0345 | 0.0350 | 0.0149 | Strong |
| 8 | Calcium carbonate CaCO3 | Gaussian | 16.5986 | 0.0745 | 0.7586 | 0.8332 | 0.0895 | Strong |
| 9 | Sand | Pentaspherical | 34.9317 | 0.3900 | 1.8638 | 2.2538 | 0.1730 | Strong |
| 10 | Silt | Exponential | 11.0822 | 0.7449 | 1.1814 | 1.9263 | 0.3867 | Medium |
| 11 | Clay | Pentaspherical | 61.7036 | 0.1000 | 1.9934 | 2.0934 | 0.0478 | Strong |
| 12 | Very fine sand | Exponential | 6.4629 | 0.0006 | 0.0262 | 0.0268 | 0.0235 | Strong |
| 13 | Gravel | Spherical | 20.6936 | 0.1267 | 0.1415 | 0.2682 | 0.4724 | Medium |
| 14 | Soil Erodibility (K factor) | Exponential | 4.8323 | 0.0008 | 0.0003 | 0.0011 | 0.7555 | Weak |
| 15 | Wilting point θwp | Gaussian | 41.6026 | 0.1340 | 0.6104 | 0.7444 | 0.1800 | Strong |
| 16 | Field capacity θfc | Circular | 25.7388 | 0.1799 | 0.9026 | 1.0825 | 0.1662 | Strong |
| 17 | Saturation θsat | Gaussian | 13.3309 | 1.0133 | 4.3668 | 5.3801 | 0.1883 | Strong |
| 18 | Plant available water PAW | Circular | 11.9197 | 0.00001 | 0.00004 | 0.00005 | 0.1323 | Strong |
| 19 | Sat. Hydraulic conductivity Ks | Circular | 17.8573 | 0.0075 | 0.1143 | 0.1217 | 0.0614 | Strong |
| 20 | Bulk density | Exponential | 18.9880 | 0.0001 | 0.0033 | 0.0034 | 0.0292 | Strong |
| SN | Parameter | Model | MPE | RMSE | MSPE | RMSSE | ASE |
|---|---|---|---|---|---|---|---|
| 1 | Phosphorus P-olsen | Gaussian | 0.00648 | 1.31122 | 0.00232 | 0.91665 | 1.42204 |
| 2 | Potassium K | Circular | −0.03741 | 51.16382 | 0.01199 | 0.98210 | 48.91566 |
| 3 | Calcium Ca | Exponential | 3.26177 | 134.16611 | 0.03086 | 0.67445 | 212.20118 |
| 4 | Magnesium Mg | Exponential | −0.59038 | 137.54021 | 0.00512 | 0.86182 | 161.58264 |
| 5 | pH [1:2 soil/water solution] | Exponential | 0.00014 | 0.02740 | 0.00242 | 0.67115 | 0.03993 |
| 6 | Nitrogen inorganic | Exponential | 0.06161 | 4.20908 | 0.01265 | 0.82269 | 4.76968 |
| 7 | Organic matter | Exponential | −0.00189 | 0.22948 | −0.01692 | 1.25388 | 0.16409 |
| 8 | Calcium carbonate CaCO3 | Gaussian | −0.00038 | 0.29917 | −0.00057 | 0.94818 | 0.31009 |
| 9 | Sand | Pentaspherical | −0.00223 | 0.87267 | −0.00224 | 1.06389 | 0.81605 |
| 10 | Silt | Exponential | −0.01460 | 1.16042 | −0.01170 | 0.95974 | 1.20448 |
| 11 | Clay | Pentaspherical | 0.00294 | 0.52318 | 0.00484 | 1.05010 | 0.49190 |
| 12 | Very fine sand | Exponential | −0.00114 | 0.15055 | −0.00802 | 1.07931 | 0.13837 |
| 13 | Gravel | Spherical | 0.00057 | 0.03041 | −0.01923 | 1.00337 | 0.03430 |
| 14 | Soil Erodibility (K factor) | Exponential | −0.00001 | 0.00106 | −0.01127 | 1.02658 | 0.00104 |
| 15 | Wilting point θwp | Gaussian | −0.00479 | 0.39571 | −0.01089 | 1.00732 | 0.39309 |
| 16 | Field capacity θfc | Circular | 0.00003 | 0.50707 | −0.00157 | 0.90904 | 0.55344 |
| 17 | Saturation θsat | Gaussian | 0.02077 | 1.03674 | 0.01423 | 0.88580 | 1.14763 |
| 18 | Plant available water PAW | Circular | 0.00011 | 0.00386 | 0.02377 | 0.93844 | 0.00408 |
| 19 | Sat. Hydraulic conductivity Ks | Circular | 0.08167 | 1.84392 | 0.01604 | 0.98314 | 2.67589 |
| 20 | Bulk density | Exponential | −0.00028 | 0.02808 | −0.00722 | 0.89908 | 0.03092 |
| R-Mode Factor (Component) Loading Matrix | ||||||
|---|---|---|---|---|---|---|
| SN | Parameter | Factor 1 | Factor 2 | Factor 3 | Factor 4 | Factor 5 |
| 1 | Phosphorus P-olsen | 0.249 | −0.419 | 0.303 | 0.297 | 0.325 |
| 2 | Potassium K | −0.042 | −0.222 | 0.069 | 0.891 | −0.014 |
| 3 | Calcium Ca | 0.838 | −0.192 | −0.103 | −0.055 | 0.070 |
| 4 | Magnesium Mg | 0.852 | −0.238 | −0.065 | −0.087 | 0.073 |
| 5 | pH [1:2 soil/water solution] | 0.726 | 0.292 | −0.015 | −0.374 | 0.015 |
| 6 | Nitrogen inorganic | 0.475 | 0.803 | −0.099 | −0.062 | −0.063 |
| 7 | Organic matter | −0.041 | 0.201 | 0.127 | 0.918 | −0.049 |
| 8 | Calcium carbonate CaCO3 | 0.776 | −0.005 | 0.130 | 0.380 | 0.126 |
| 9 | Sand | 0.772 | −0.175 | 0.317 | 0.122 | −0.258 |
| 10 | Silt | 0.239 | 0.872 | −0.249 | −0.205 | 0.149 |
| 11 | Clay | −0.753 | −0.491 | −0.136 | 0.004 | 0.154 |
| 12 | Very fine sand | −0.567 | −0.350 | −0.064 | −0.013 | 0.505 |
| 13 | Gravel | 0.017 | 0.337 | −0.143 | −0.054 | 0.784 |
| 14 | Soil Erodibility (K factor) | 0.644 | −0.502 | 0.203 | −0.363 | −0.232 |
| 15 | Wilting point θwp | −0.227 | 0.920 | −0.194 | 0.098 | 0.113 |
| 16 | Field capacity θfc | 0.022 | 0.855 | 0.460 | 0.075 | 0.130 |
| 17 | Saturation θsat | 0.003 | 0.016 | 0.985 | 0.071 | 0.038 |
| 18 | Plant available water PAW | 0.206 | 0.016 | 0.894 | 0.110 | −0.328 |
| 19 | Saturated hydraulic conductivity Ks | −0.044 | −0.490 | 0.838 | 0.036 | −0.107 |
| 20 | Bulk density | −0.034 | 0.007 | −0.984 | −0.062 | −0.049 |
| Variance (%) | 28.798 | 22.725 | 17.693 | 9.976 | 5.815 | |
| Cumulative variance (%) | 28.798 | 51.523 | 69.216 | 79.192 | 85.006 | |
| SN | Soil Parameters Group | Fuzzy Clustering Percentage of Management Zones Spatial Agreement (PoMZSA) (%) between Soil Groups | |||||
|---|---|---|---|---|---|---|---|
| Fuzziness Exponent φ | * MZ 1 | MZ 2 | MZ 3 | MZ 4 | All MZs | ||
| 1 | “soil All parameters group” (20 parameters), 4 MZs | 1.14 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 2 | “soil All parameters group” (20 parameters), 4 MZs | 1.30 | 35.29 | 11.43 | 8.82 | 0.00 | 13.19 |
| 3 | “soil All parameters group” (20 parameters), 4 MZs | 1.50 | 2.94 | 5.71 | 5.88 | 0.00 | 3.47 |
| 4 | “soil All parameters group” (20 PCAs), 4 MZs | 1.14 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| 5 | “soil All parameters group” (5 PCAs), 4 MZs | 1.56 | 40.00 | 60.00 | 20.59 | 2.44 | 29.86 |
| 6 | “soil chemical group” (8 parameters), 3 MZs | 1.14 | 100.00 | 100.00 | 100.00 | -- | 100.00 |
| 7 | “soil chemical group” (8 parameters), 3 MZs | 1.30 | 74.36 | 87.23 | 74.14 | -- | 78.47 |
| 8 | “soil chemical group” (8 parameters), 3 MZs | 1.50 | 82.05 | 93.62 | 77.59 | -- | 84.03 |
| 9 | “soil chemical group” (8 PCAs), 3 MZs | 1.12 | 100.00 | 100.00 | 100.00 | -- | 100.00 |
| 10 | “soil chemical group” (3 PCAs), 3 MZs | 1.69 | 35.90 | 25.53 | 70.69 | 46.53 | |
| 11 | “soil granular group” (6 parameters), 2 MZs | 1.16 | 100.00 | 100.00 | -- | -- | 100.00 |
| 12 | “soil granular group” (6 parameters), 2 MZs | 1.30 | 98.70 | 97.01 | -- | -- | 97.92 |
| 13 | “soil granular group” (6 parameters), 2 MZs | 1.50 | 97.40 | 95.52 | -- | -- | 96.53 |
| 14 | “soil granular group” (6 PCAs), 2 MZs | 1.16 | 100.00 | 100.00 | -- | -- | 100.00 |
| 15 | “soil granular group” (2 PCAs), 2 MZs | 1.61 | 80.52 | 95.52 | 87.50 | ||
| 16 | “soil hydraulic group” (6 parameters), 2 MZs | 1.16 | 100.00 | 100.00 | -- | -- | 100.00 |
| 17 | “soil hydraulic group” (6 parameters), 2 MZs | 1.30 | 98.51 | 98.70 | -- | -- | 98.61 |
| 18 | “soil hydraulic group” (6 parameters), 2 MZs | 1.50 | 98.51 | 96.10 | -- | -- | 97.22 |
| 19 | “soil hydraulic group” (6 PCAs), 2 MZs | 1.16 | 100.00 | 100.00 | -- | -- | 100.00 |
| 20 | “soil hydraulic group” (2 PCAs), 2 MZs | 1.15 | 85.07 | 81.82 | -- | -- | 83.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filintas, A.; Gougoulias, N.; Kourgialas, N.; Hatzichristou, E. Management Zones Delineation, Correct and Incorrect Application Analysis in a Coriander Field Using Precision Agriculture, Soil Chemical, Granular and Hydraulic Analyses, Fuzzy k-Means Zoning, Factor Analysis and Geostatistics. Water 2023, 15, 3278. https://doi.org/10.3390/w15183278
Filintas A, Gougoulias N, Kourgialas N, Hatzichristou E. Management Zones Delineation, Correct and Incorrect Application Analysis in a Coriander Field Using Precision Agriculture, Soil Chemical, Granular and Hydraulic Analyses, Fuzzy k-Means Zoning, Factor Analysis and Geostatistics. Water. 2023; 15(18):3278. https://doi.org/10.3390/w15183278
Chicago/Turabian StyleFilintas, Agathos, Nikolaos Gougoulias, Nektarios Kourgialas, and Eleni Hatzichristou. 2023. "Management Zones Delineation, Correct and Incorrect Application Analysis in a Coriander Field Using Precision Agriculture, Soil Chemical, Granular and Hydraulic Analyses, Fuzzy k-Means Zoning, Factor Analysis and Geostatistics" Water 15, no. 18: 3278. https://doi.org/10.3390/w15183278






