Study on the Constitutive Equation and Mechanical Properties of Natural Snow under Step Loading
Abstract
:1. Introduction
2. Sample Preparation and Experimental Procedure
2.1. Sample Preparation
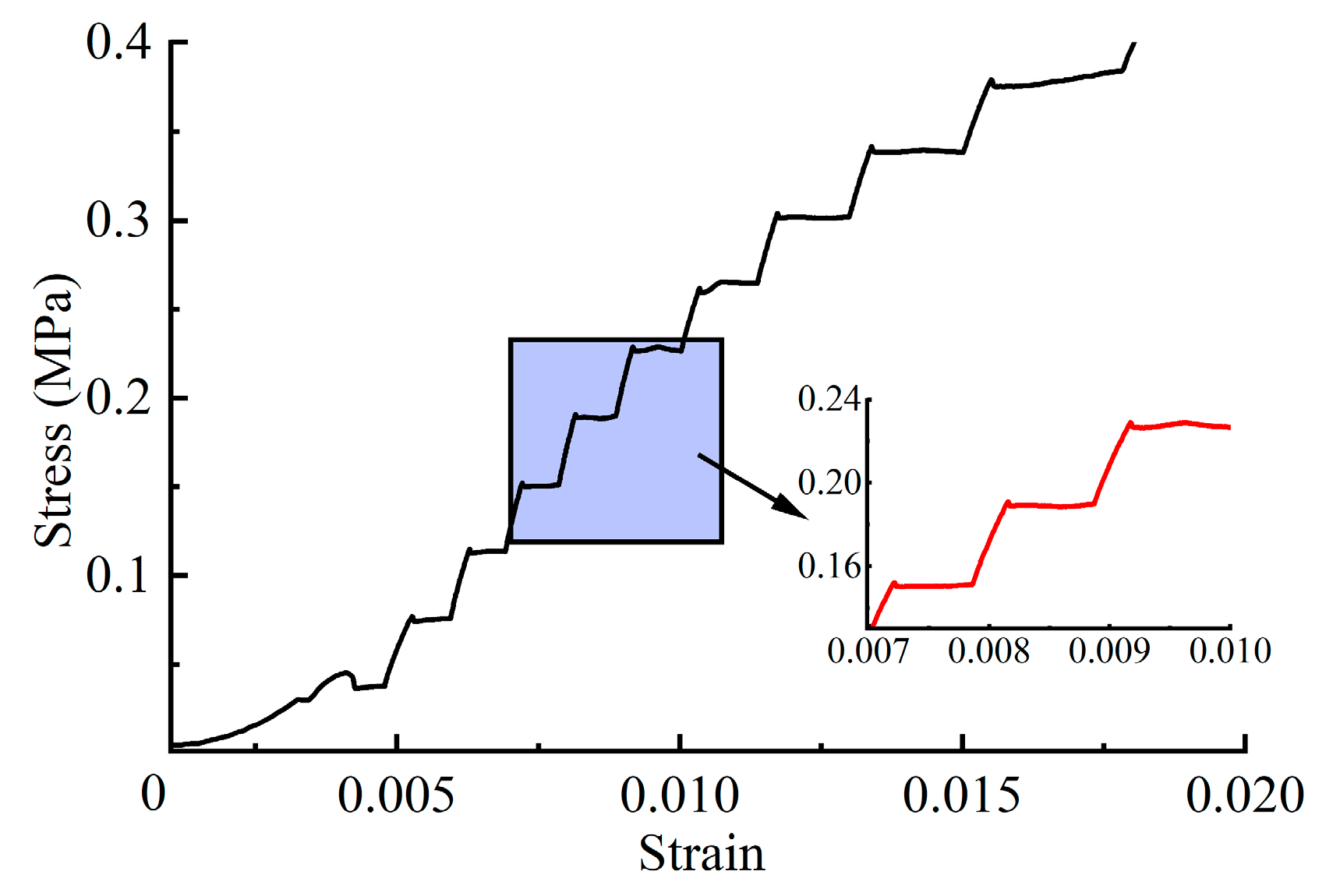
2.2. Test Procedure
3. Constitutive Model
3.1. Maxwell Model
3.2. Parameter Calculation
4. Results
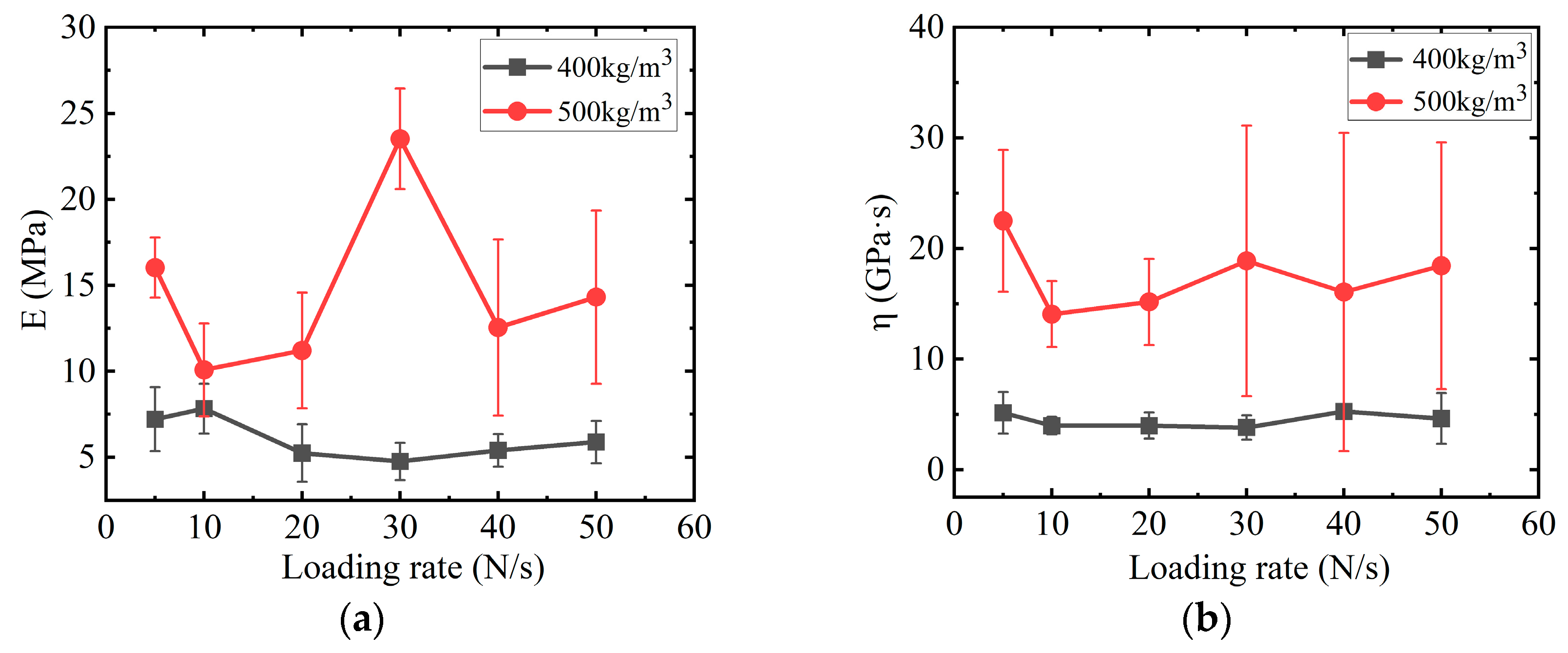
4.1. Effect of Loading Rate on Elastic Modulus and Viscosity Coefficient of Snow
4.2. Effect of Temperature on Elastic Modulus and Viscosity Coefficient of Snow
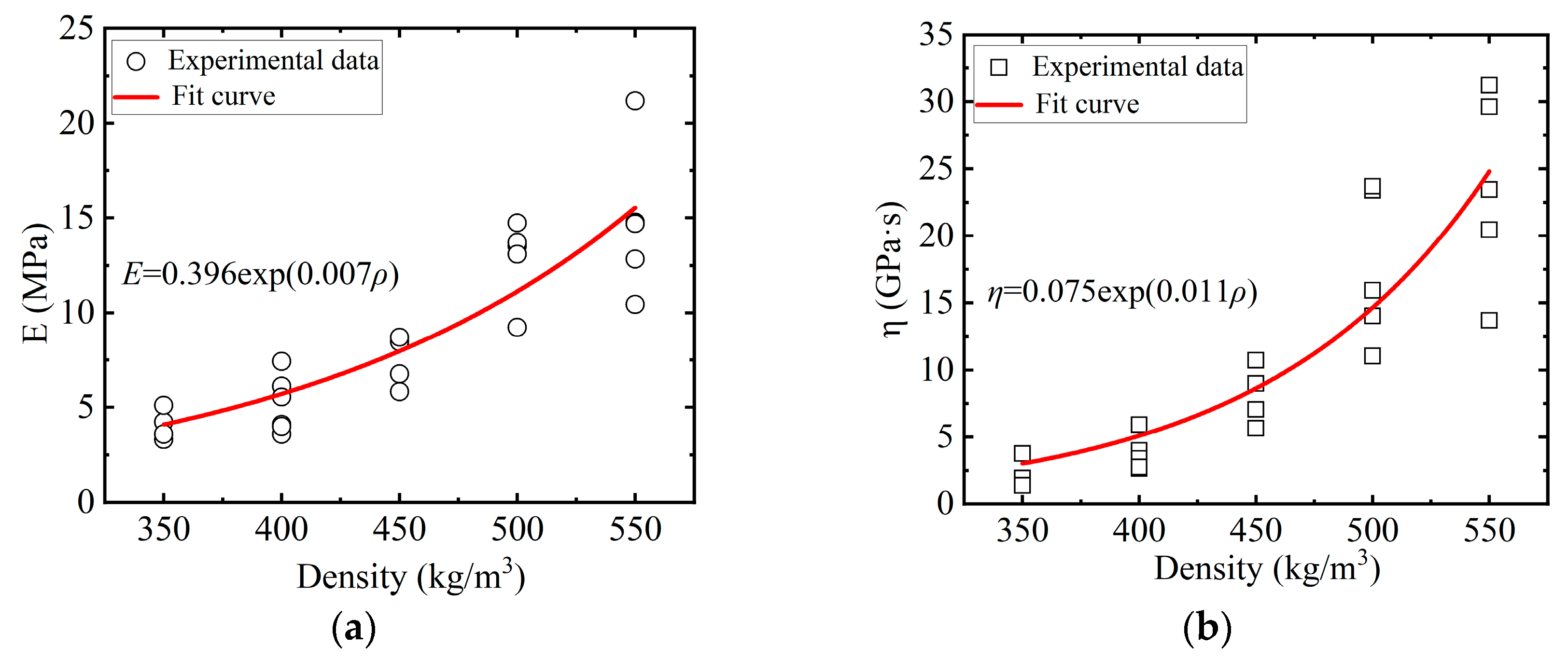
4.3. Effect of Density on Elastic Modulus and Viscosity Coefficient of Snow
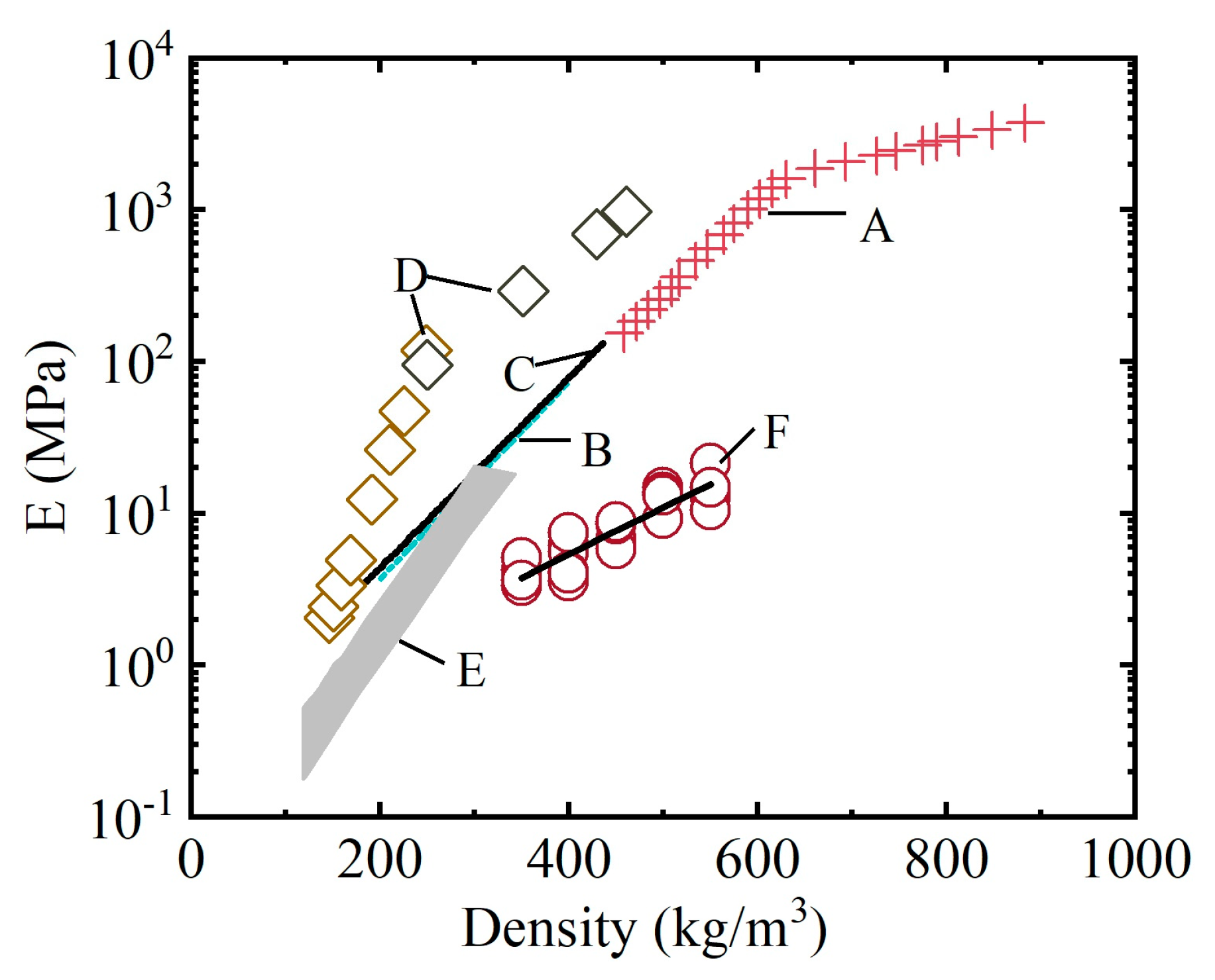
5. Discussion
5.1. Elastic Modulus
5.2. Viscosity Coefficient
6. Conclusions
- The elastic modulus of natural snow increases exponentially with increasing density. Temperature has a certain influence on the elastic modulus of snow. The elastic modulus first decreases and then increases with decreasing temperature, and this relationship is more obvious at high densities. There is no correlation between the elastic modulus and the loading rate.
- Density is an important factor in the change in the viscosity coefficient of snow. The viscosity coefficient increases exponentially as density increases. The snow viscosity coefficient is affected by temperature, that is, the viscosity coefficient first decreases and then increases as the temperature decreases. The loading rate is weakly correlated with the viscosity coefficient of snow.
- A new constitutive equation considering snow density is derived by introducing the functional relation between elastic modulus, viscosity coefficient, and the density of snow based on the Maxwell model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Křeček, J.; Šedivá, L.; Palán, L.; Stuchlík, E. Environmental role of snowmelt in headwaters affected by atmospheric acid deposition. Water 2023, 15, 2458. [Google Scholar] [CrossRef]
- Armstrong, R.L.; Brodzik, M.J. Recent northern hemisphere snow extent: A comparison of data derived from visible and microwave satellite sensors. Geophys. Res. Lett. 2001, 28, 3673–3676. [Google Scholar] [CrossRef]
- Parkinson, C.L. Earth’s cryosphere: Current state and recent changes. Annu. Rev. Environ. Resour. 2006, 31, 33–60. [Google Scholar] [CrossRef]
- Le Roux, E.; Evin, G.; Eckert, N.; Blanchet, J.; Morin, S. Elevation-dependent trends in extreme snowfall in the French Alps from 1959 to 2019. Cryosphere 2021, 15, 4335–4356. [Google Scholar] [CrossRef]
- Huning, L.S.; Margulis, S.A. Climatology of seasonal snowfall accumulation across the Sierra Nevada (USA): Accumulation rates, distributions, and variability. Water Resour. Res. 2017, 53, 6033–6049. [Google Scholar] [CrossRef]
- Nouri, M.; Homaee, M. Spatiotemporal changes of snow metrics in mountainous data-scarce areas using reanalyses. J. Hydrol. 2021, 603, 126858. [Google Scholar] [CrossRef]
- Wang, L.; Yang, H. Tibetan Plateau increases the snowfall in southern China. Sci. Rep. 2023, 13, 12796. [Google Scholar] [CrossRef]
- Markov, A.; Polyakov, S.; Sun, B.; Lukin, V.; Popov, S.; Yang, H.; Zhang, T.; Cui, X.; Guo, J.; Cui, P.; et al. The conditions of the formation and existence of “Blue Ice Areas” in the ice flow transition region from the Antarctic ice sheet to the Amery Ice Shelf in the Larsemann Hills area. Polar Sci. 2019, 22, 100478. [Google Scholar] [CrossRef]
- White, G.; McCallum, A. Review of ice and snow runway pavements. Int. J. Pavement Res. Technol. 2017, 11, 311–320. [Google Scholar] [CrossRef]
- Sun, B.; Tang, X.; Xiao, E.; Shi, X.; Cheng, X.; Li, L.; Wei, F.; Zhang, T. Ice and snow runway engineering in the Antarctica: Current status and prospect. Strateg. Study Chin. Acad. Eng. 2021, 23, 161–168. [Google Scholar] [CrossRef]
- Li, H.; Zhong, X.; Zheng, L.; Hao, X.; Wang, J.; Zhang, J. Classification of snow cover persistence across China. Water 2022, 14, 933. [Google Scholar] [CrossRef]
- Kabore, B.W.; Peters, B.; Michael, M.; Nicot, F. A discrete element framework for modeling the mechanical behaviour of snow—Part I: Mechanical behaviour and numerical model. Granul. Matter 2021, 23, 42. [Google Scholar] [CrossRef]
- Colbeck, S.; Parssinen, N. Regelation and the deformation of wet Snow. J. Glaciol. 1978, 21, 639–650. [Google Scholar] [CrossRef]
- Mishra, A.; Mahajan, P. A constitutive law for snow taking into account the compressibility. Ann. Glaciol. 2004, 38, 145–149. [Google Scholar] [CrossRef]
- Scapozza, C.; Bartelt, P. Triaxial tests on snow at low strain rate. Part II. Constitutive behaviour. J. Glaciol. 2003, 49, 91–101. [Google Scholar] [CrossRef]
- Birkeland, K.W.; van Herwijnen, A.; Reuter, B.; Bergfeld, B. Temporal changes in the mechanical properties of snow related to crack propagation after loading. Cold Reg. Sci. Technol. 2019, 159, 142–152. [Google Scholar] [CrossRef]
- Bobillier, G.; Bergfeld, B.; Dual, J.; Gaume, J.; van Herwijnen, A.; Schweizer, J. Micro-mechanical insights into the dynamics of crack propagation in snow fracture experiments. Sci. Rep. 2021, 11, 11711. [Google Scholar] [CrossRef]
- Nicot, F. Constitutive modelling of snow as a cohesive-granular material. Granul. Matter 2004, 6, 47–60. [Google Scholar] [CrossRef]
- Mahajan, P.; Brown, R.L. A microstructure-based constitutive law for snow. Ann. Glaciol. 1993, 18, 287–294. [Google Scholar] [CrossRef]
- Brown, R.L. A volumetric constitutive law for snow based on a neck growth model. J. Appl. Phys. 1980, 51, 161–165. [Google Scholar] [CrossRef]
- Bobillier, G.; Bergfeld, B.; Capelli, A.; Dual, J.; Gaume, J.; van Herwijnen, A.; Schweizer, J. Micromechanical modeling of snow failure. Cryosphere 2020, 14, 39–49. [Google Scholar] [CrossRef]
- Hagenmuller, P.; Chambon, G.; Naaim, M. Microstructure-based modeling of snow mechanics: A discrete element approach. Cryosphere 2015, 9, 1969–1982. [Google Scholar] [CrossRef]
- Herny, C.; Hagenmuller, P.; Chambon, G.; Peinke, I.; Roulle, J. Microstructure-based modelling of snow mechanics: Experimental evaluation on the cone penetration test. Cryosphere Discuss 2023. in review. [Google Scholar] [CrossRef]
- Mede, T.; Chambon, G.; Nicot, F.; Hagenmuller, P. Micromechanical investigation of snow failure under mixed-mode loading. Int. J. Solids Struct. 2020, 199, 95–108. [Google Scholar] [CrossRef]
- Singh, A.K.; Srivastava, P.K.; Kumar, N.; Mahajan, P. A fabric tensor based small strain constitutive law for the elastoplastic behavior of snow. Mech. Mater. 2022, 165, 104182. [Google Scholar] [CrossRef]
- Chandel, C.; Srivastava, P.K.; Mahajan, P. Micromechanical analysis of deformation of snow using X-ray tomography. Cold Reg. Sci. Technol. 2014, 101, 14–23. [Google Scholar] [CrossRef]
- Meyer, C.R.; Keegan, K.M.; Baker, I.; Hawley, R.L. A model for French-press experiments of dry snow compaction. Cryosphere 2020, 14, 1449–1458. [Google Scholar] [CrossRef]
- Shapiro, L.H.; Johnson, J.B.; Sturm, M.; Blaisdell, G.L. Snow mechanics review of the state of knowledge and applications. In US Army Cold Regions Research and Engineering Laboratory (CRREL) Report 97-3; Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1997. [Google Scholar]
- Masterson, D.; Løset, S. ISO 19906: Bearing capacity of ice and ice roads. In Proceedings of the 21st International Conference on Port and Ocean Engineering under Arctic Conditions, Montreal, QC, Canada, 10–14 July 2011. [Google Scholar]
- Wang, E.; Fu, X.; Han, H.; Liu, X.; Xiao, Y.; Leng, Y. Study on the mechanical properties of compacted snow under uniaxial compression and analysis of influencing factors. Cold Reg. Sci. Technol. 2021, 182, 103215. [Google Scholar] [CrossRef]
- Mellor, M. A review of basic snow mechanics. In Proceedings of the Snow Mechanics Symposium, Grindelwald, Switzerland, 1–5 April 1974; pp. 251–291. [Google Scholar]
- Reuter, B.; Proksch, M.; Löwe, H.; van Herwijnen, A.; Schweizer, J. Comparing measurements of snow mechanical properties relevant for slab avalanche release. J. Glaciol. 2018, 65, 55–67. [Google Scholar] [CrossRef]
- Gerling, B.; Löwe, H.; van Herwijnen, A. Measuring the elastic modulus of snow. Geophys. Res. Lett. 2017, 44, 11088–11096. [Google Scholar] [CrossRef]
- Johnson, J.B.; Schneebeli, M. Characterizing the microstructural and micromechanical properties of snow. Cold Reg. Sci. Technol. 1999, 30, 91–100. [Google Scholar] [CrossRef]
- Kry, P.R. The relationship between the visco-elastic and structural properties of fine-grained snow. J. Glaciol. 1975, 14, 479–500. [Google Scholar] [CrossRef]
- Lintzén, N.; Edeskär, T. Uniaxial strength and deformation properties of machine-made snow. J. Cold Reg. Eng. 2015, 29, 04014020. [Google Scholar] [CrossRef]
- Kovacs, A.; Weeks, W.F.; Michitti, F. Variation of some mechanical properties of polar snow, Camp Century, Greenland. In US Army Cold Regions Research and Engineering Laboratory (CRREL) Report 276; Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1969. [Google Scholar]
- Scapozza, C. Entwicklung eines dichte- und temperaturabhängigen Stoffgesetzes zur Beschreibung des visko-elastischen verhaltens von Schnee. Ph.D. Thesis, Eidgenössische Technische Hochschule ETH Zürich, Zürich, Switzerland, 2004. (In German). [Google Scholar] [CrossRef]
- von Moos, M.; Bartelt, P.; Zweidler, A.; Bleiker, E. Triaxial tests on snow at low strain rate. Part I. Experimental device. J. Glaciol. 2003, 49, 81–90. [Google Scholar] [CrossRef]
- Stoffel, M.; Bartelt, P. Modelling snow slab release using a temperature-dependent viscoelastic finite element model with weak layers. Surv. Geophys. 2003, 24, 417–430. [Google Scholar] [CrossRef]
- Köchle, B.; Schneebeli, M. Three-dimensional microstructure and numerical calculation of elastic properties of alpine snow with a focus on weak layers. J. Glaciol. 2014, 60, 705–713. [Google Scholar] [CrossRef]
- Kojima, K. Visco-elastic property of snow. Low Temp. Sci. 1954, 12, 1–15. (In Japanese) [Google Scholar]
- Zhao, Q.; Li, Z.; Lu, P.; Wang, Q.; Wei, J.; Hu, S.; Yang, H. An investigation of the influence on compacted snow hardness by density, temperature and punch head velocity. Water 2023, 15, 2897. [Google Scholar] [CrossRef]
- Zhuang, F.; Lu, P.; Li, Z.J.; Han, H.W.; Li, W. Modified Rammsonde tests in layered compacted snow. Adv. Polar Sci. 2019, 30, 118–131. [Google Scholar] [CrossRef]
- Sinha, N.K. Elasticity of natural types of polycrystalline ice. Cold Reg. Sci. Technol. 1989, 17, 127–135. [Google Scholar] [CrossRef]
- Shenvi, M.N.; Sandu, C.; Untaroiu, C. Review of compressed snow mechanics: Testing methods. J. Terramech. 2022, 100, 25–37. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Yang, M.; Liu, X.; Li, Y.; Gao, G.; Wang, E. Study on the Constitutive Equation and Mechanical Properties of Natural Snow under Step Loading. Water 2023, 15, 3271. https://doi.org/10.3390/w15183271
Han H, Yang M, Liu X, Li Y, Gao G, Wang E. Study on the Constitutive Equation and Mechanical Properties of Natural Snow under Step Loading. Water. 2023; 15(18):3271. https://doi.org/10.3390/w15183271
Chicago/Turabian StyleHan, Hongwei, Meiying Yang, Xingchao Liu, Yu Li, Gongwen Gao, and Enliang Wang. 2023. "Study on the Constitutive Equation and Mechanical Properties of Natural Snow under Step Loading" Water 15, no. 18: 3271. https://doi.org/10.3390/w15183271





