Optimal Design of Intermittent Water Distribution Network Considering Network Resilience and Equity in Water Supply
Abstract
:1. Introduction
2. Methodology
2.1. Pressure-Driven Analysis
- (1)
- Network modeling: Using EPANET, a hydraulic model of the WDN is created. The model contains data on the boundary conditions, nodal demands, pipe characteristics, and network topology. The network’s hydraulic behavior can be simulated using this model as a starting point.
- (2)
- Demand allocation: For realistic simulations, it is essential to accurately estimate demands at each node. Based on past trends, demographic estimates, and specific consumer data, the demands may be determined. To capture genuine demand profiles, seasonal fluctuations and nocturnal patterns are taken into account.
- (3)
- Pressure simulation: Various scenarios for the network’s behavior are simulated using the hydraulic model. The operating conditions, such as pump operation, valve settings, and tank levels, are taken into account during the simulation. Based on the water conservation and energy calculations, the simulation determines pressure heads and flow rates across the network.
- (4)
- Performance assessment: The network’s performance is then assessed using the simulation findings. It is possible to evaluate key performance indicators such as minimum and maximum pressures, pressure deficits, network resilience, uniformity coefficient, or equity and flow rates. These indicators aid in locating trouble spots, such as low-pressure locations, high-pressure areas, and probable water quality problems.
2.2. Source Head Method
- 1.
- Run hydraulic analysis in EPANET (RunH) to determine the pressure head at the source ().
- 2.
- For each node in the network:
- a.
- Get the pressure head at the node.
- b.
- Calculate the head loss between the source and the node as: = − .
- c.
- Calculate the desired pressure head at the source for this node as:End of loop.
- 3.
- To calculate the minimum source pressure head at which discharge at each node is zero, for each node in the network:
- i.
- Set Qj (discharge) to 0.
- ii.
- Run hydraulic analysis (RunH) to get the pressure head at the node.
- iii.
- Calculate the head loss between the source and the node when only Qj is zero, as: = − .
- iv.
- Reset Qj to its actual value.
- v.
- Calculate the minimum pressure head at the source when only Qj is zero, as:End of loop.
- 4.
- Sort the nodes in ascending order of .
- 5.
- For each node in the sorted order:Set Qj (discharge) to 0.
- a.
- Run hydraulic analysis (RunH) to get the pressure head at the node.
- b.
- Calculate the head loss between the source and the node when discharge at this node and also the nodes above this in the sorted list are zero, as: = − .
- c.
- Calculate the minimum pressure head at the source when all discharge at this node and also the nodes above this are zero, as: = elj + + .
End of loop. - 6.
- After getting and , for each node, calculate the corrected discharge and check the head (if − > Limit, go for previous steps, otherwise, continue with step 6), calculate average supply ratio (SR), uniformity coefficient (CU).
2.3. Performance Indicators
2.4. Multi-Objective Evolutionary Optimization (MOEA)
2.5. Analysis of Networks
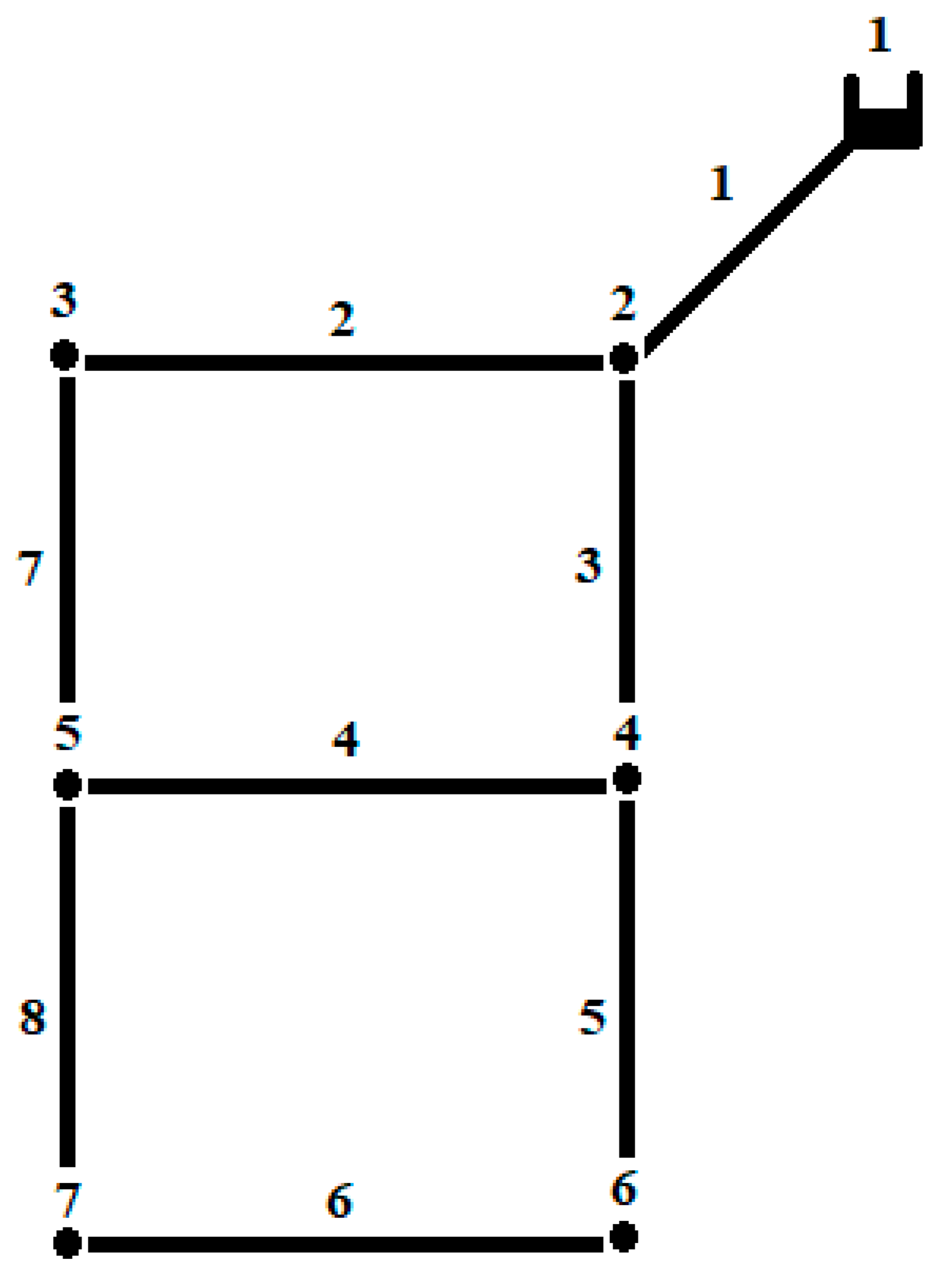
2.5.1. Network-1
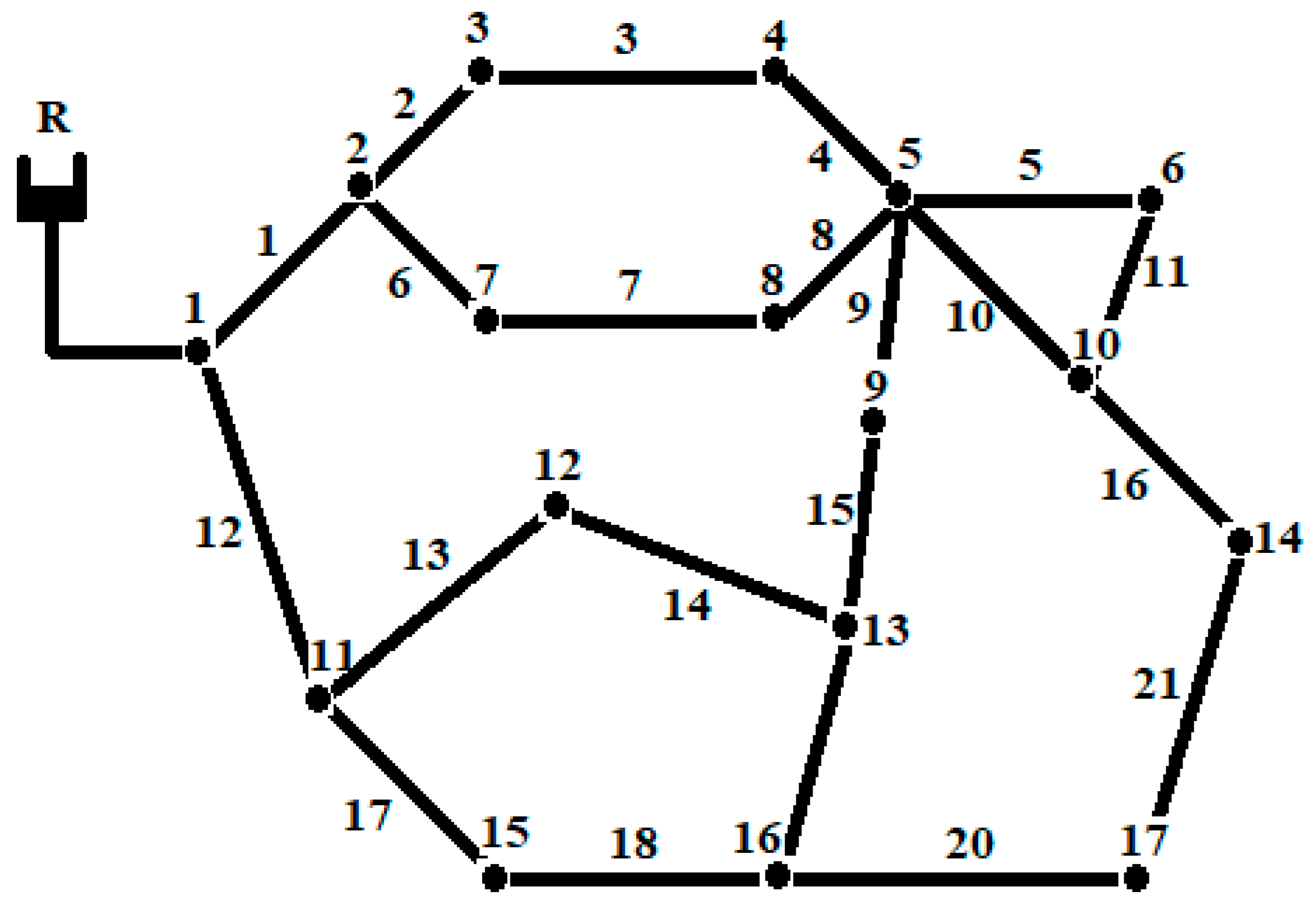
2.5.2. Network-2
2.6. Multidimensional Pareto Analysis
- (a)
- Dominance matrix: The code constructs a dominance matrix where each element (i, j) represents whether solution i dominates solution j. This matrix captures the dominant relationships among solutions for multiple objectives.
- (b)
- Identifying Pareto solutions: By analyzing the dominance matrix, the code identifies solutions that are Pareto optimal, meaning they are not dominated by any other solutions for all the objectives.
- (c)
- Extracting Pareto front: The code extracts the Pareto front solutions from the original dataset based on the identified Pareto optimal solutions.
3. Results and Discussions
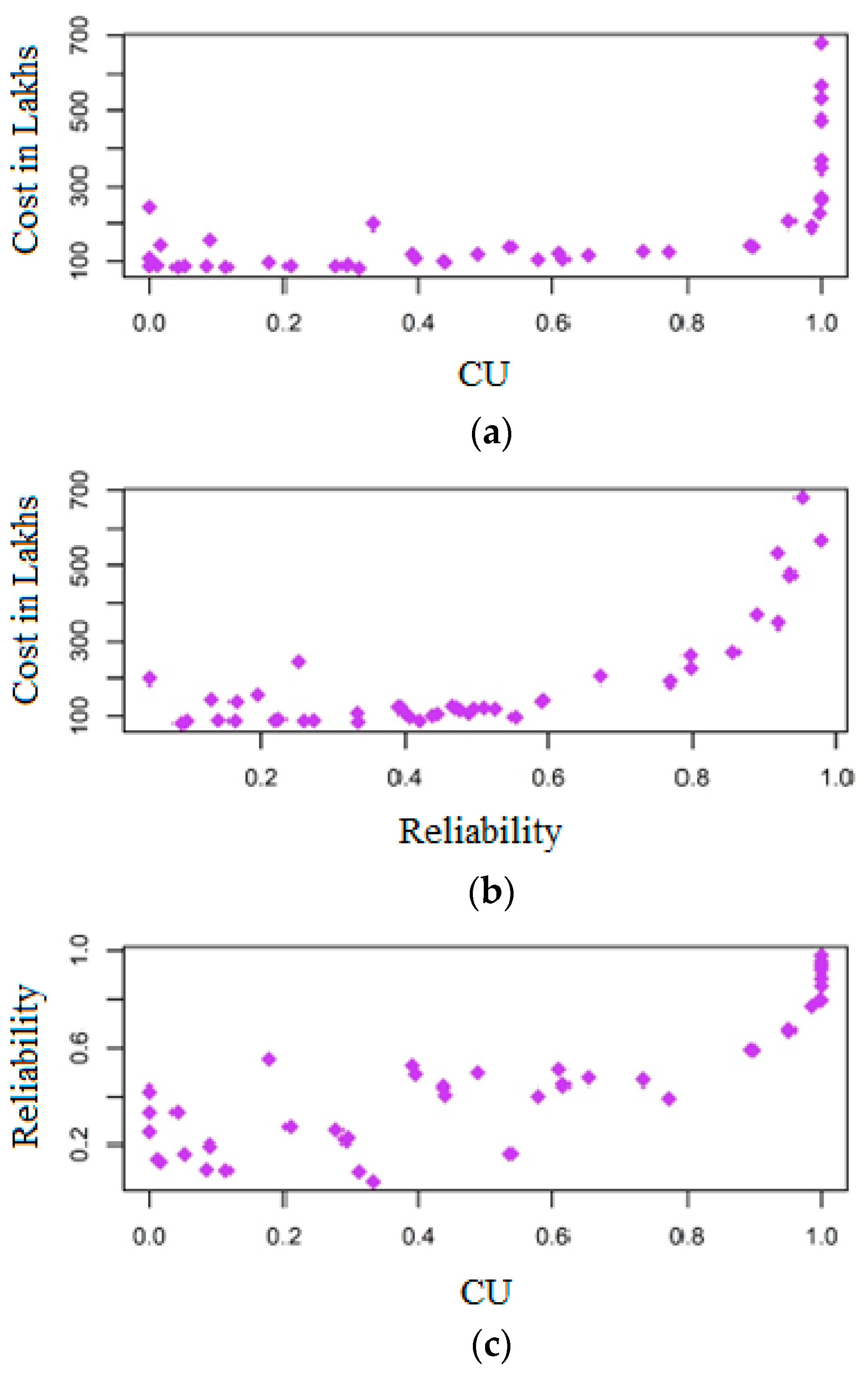
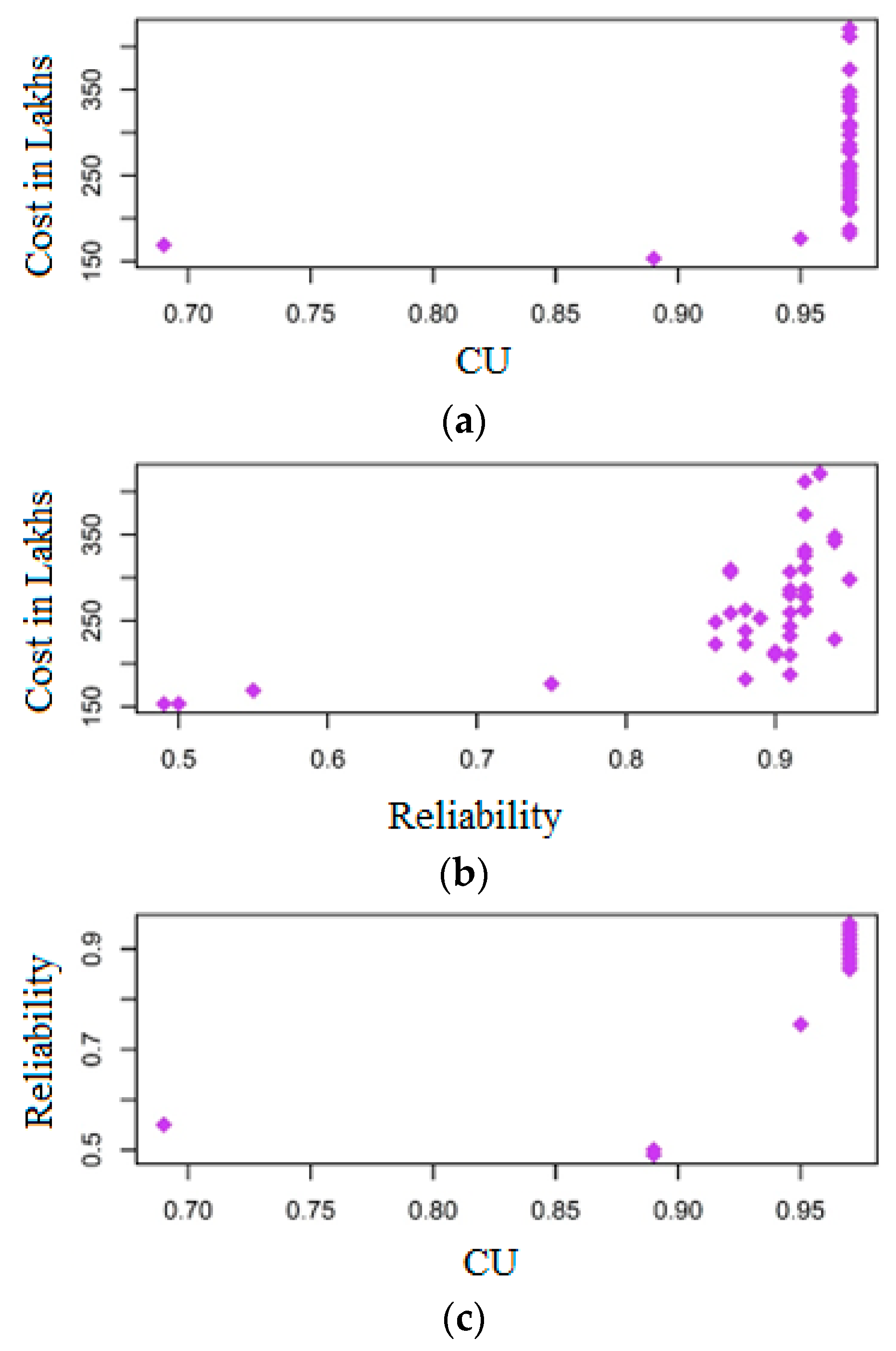
3.1. Trade-off between the Objective Functions
3.2. Multidimensional Pareto Analysis
4. Conclusions
- The approach accelerates the optimization of intermittent water distribution networks, considering into account factors such as equity, reliability, and cost. Enhancing equity has a significant influence on the overall reliability of the networks. Hence, conducting a comprehensive analysis that considers both aspects are crucial to understanding the mutual impact they have on each other.
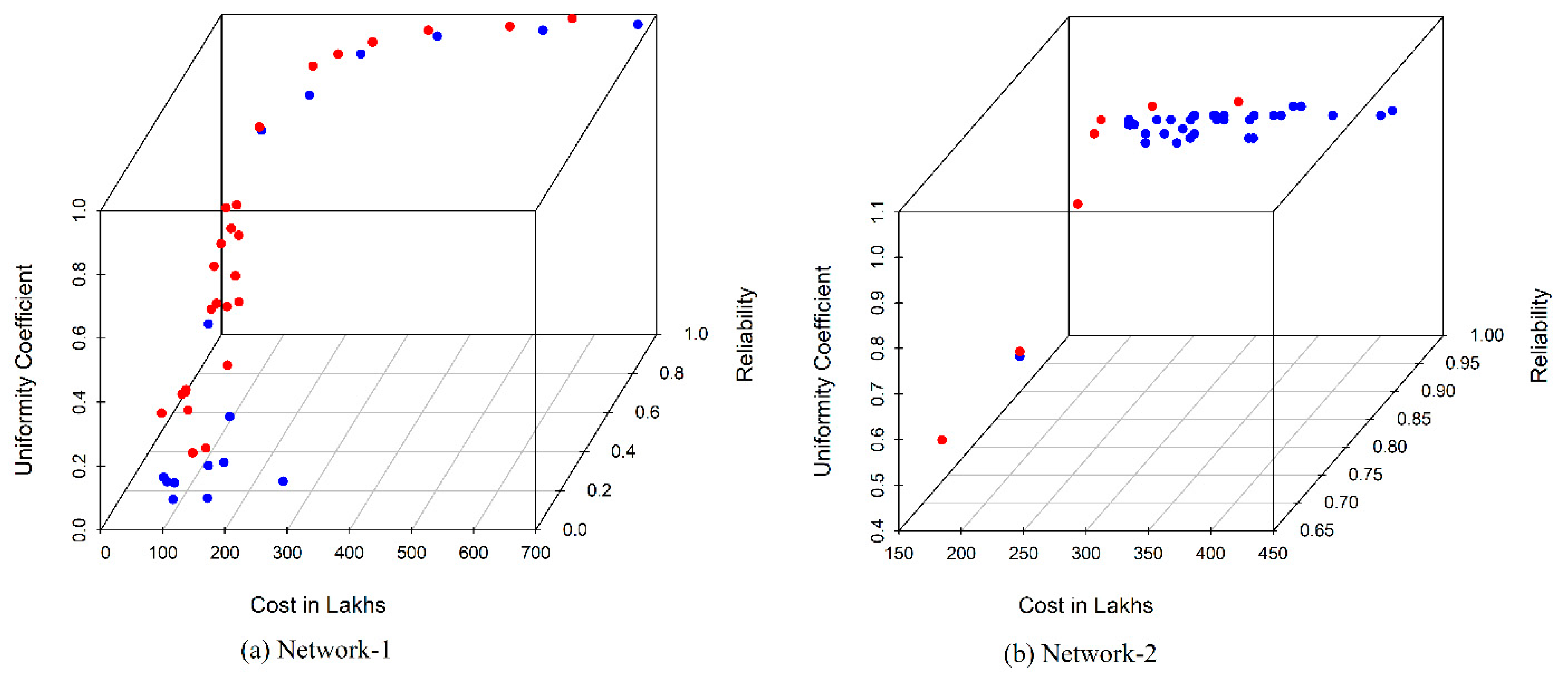
- Two indices, network resilience () and uniformity coefficient (), are taken as the performance indicators that improve the network reliability and equity in the distribution networks considered in the study. The results from the two networks show that increasing network resilience can also increase water supply equity. Optimizing the layout of the networks, especially in the case of large networks, may improve the equity in the water supply, without increasing the cost of the network.
- The application of NSGA-II to the benchmark networks from the literature to optimize the design of WDN is analyzed in the present study. Results show that network resilience can be increased up to 0.9 with minimal cost. As reliability approaches 1, cost of the network increases significantly with a marginal increment of reliability, which is uneconomical for the design.
- It is observed that the CU solution set obtained for the networks indicates increasing equity can be achieved to a certain extent (up to 0.85) with lesser increment in cost. Beyond the CU value of 0.85, the cost of networks increases, which indicates the effort needed in the selection of pipe, pump, and source tank to enhance the equity in supply with minimal cost.
- Overall, the present study considered equity and reliability as major factors for the design of WDNs along with cost, and results obtained from the application of NSGA-II conclude that equity and reliability of the networks are enhanced simultaneously to a reasonable extent with minimal cost.
- A multidimensional Pareto analysis carried out in the present study benefits the decision-makers to identify non-dominated solutions out of the Pareto front.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Atkinson, S.; Farmani, R.; Memon, F.A.; Butler, D. Reliability Indicators for Water Distribution System Design: Comparison. J. Water Resour. Plan. Manag. 2014, 140, 160–168. [Google Scholar] [CrossRef]
- Rudraswamy, G.K.; Manikanta, V.; Umamahesh, N. Hydrological Assessment of Tungabhadra River Basin 1 Based on CMIP6 GCMs and Multiple Hydrological models. J. Water Clim. Chang. 2023, 14, 1371–1394. [Google Scholar] [CrossRef]
- UN DESA. 2018 Revision of World Urbanization Prospects; United Nations News; United Nations: Geneva, Switzerland, 2018; pp. 1–5. [Google Scholar]
- Suribabu, C.R. Differential Evolution Algorithm for Optimal Design of Water Distribution Networks. J. Hydroinform. 2010, 12, 66–82. [Google Scholar] [CrossRef]
- Sheikholeslami, R.; Zecchin, A.C.; Zheng, F.; Talatahari, S. A Hybrid Cuckoo-Harmony Search Algorithm for Optimal Design of Water Distribution Systems. J. Hydroinform. 2016, 18, 544–563. [Google Scholar] [CrossRef]
- Aragones, D.G.; Calvo, G.F.; Galan, A. A Heuristic Algorithm for Optimal Cost Design of Gravity-Fed Water Distribution Networks. A Real Case Study. Appl. Math. Model. 2021, 95, 379–395. [Google Scholar] [CrossRef]
- Ezzeldin, R.M.; Djebedjian, B. Optimal Design of Water Distribution Networks Using Whale Optimization Algorithm. Urban Water J. 2020, 17, 14–22. [Google Scholar] [CrossRef]
- Moghaddam, A.; Alizadeh, A.; Faridhosseini, A.; Ziaei, A.N.; Heravi, D.F. Optimal Design of Water Distribution Networks Using Simple Modified Particle Swarm Optimization Approach. Desalin. Water Treat. 2018, 104, 99–110. [Google Scholar] [CrossRef]
- Patil, M.B.; Naidu, M.N.; Vasan, A.; Varma, M.R.R. Water Distribution System Design Using Multi-Objective Particle Swarm Optimisation. Sadhana Acad. Proc. Eng. Sci. 2020, 45, 21. [Google Scholar] [CrossRef]
- Khedr, A.; Tolson, B. Comparing Optimization Techniques with an Engineering Judgment Approach to WDN Design. J. Water Resour. Plan. Manag. 2016, 142, 1–8. [Google Scholar] [CrossRef]
- Boindala, S.P.; Ostfeld, A. Robust Multi-Objective Design Optimization of Water Distribution System under Uncertainty. Water 2022, 14, 2199. [Google Scholar] [CrossRef]
- Farmani, R.; Savic, D.A.; Walters, G.A. Evolutionary Multi-Objective Optimization in Water Distribution Network Design. Eng. Optim. 2005, 37, 167–183. [Google Scholar] [CrossRef]
- Muranho, J.; Ferreira, A.; Sousa, J.; Gomes, A.; Marques, A.S. Pressure-Driven Simulation of Water Distribution Networks: Search. Numer. Stab. 2020, 2, 48. [Google Scholar] [CrossRef]
- Tao, Y.; Yan, D.; Yang, H.; Ma, L.; Kou, C. Multi-Objective Optimization of Water Distribution Networks Based on Non-Dominated Sequencing Genetic Algorithm. PLoS ONE 2022, 17, e0277954. [Google Scholar] [CrossRef]
- Wang, Q.; Guidolin, M.; Savic, D.; Kapelan, Z. Two-Objective Design of Benchmark Problems of a Water Distribution System via MOEAs: Towards the Best-Known Approximation of the True Pareto Front. J. Water Resour. Plan. Manag. 2015, 141, 04014060. [Google Scholar] [CrossRef]
- Montalvo, I.; Izquierdo, J.; Schwarze, S.; Pérez-García, R. Multi-Objective Particle Swarm Optimization Applied to Water Distribution Systems Design: An Approach with Human Interaction. Math. Comput. Model. 2010, 52, 1219–1227. [Google Scholar] [CrossRef]
- Savić, D.; Mala-Jetmarova, H.; Sultanova, N. History of Optimization in Water Distribution System Analysis. In Proceedings of the 1st International WDSA/CCWI 2018 Joint Conference, Kingston, ON, Canada, 23–25 July 2018. [Google Scholar]
- Monsef, H.; Naghashzadegan, M.; Jamali, A.; Farmani, R. Comparison of Evolutionary Multi Objective Optimization Algorithms in Optimum Design of Water Distribution Network. Ain Shams Eng. J. 2019, 10, 103–111. [Google Scholar] [CrossRef]
- Liu, W.; Song, Z.; Wan, Z.; Li, J. Lifecycle Operational Reliability Assessment of Water Distribution Networks Based on the Probability Density Evolution Method. Probabilistic Eng. Mech. 2020, 59, 103037. [Google Scholar] [CrossRef]
- Mu, T.; Li, Y.; Li, Z.; Wang, L.; Tan, H.; Zheng, C. Improved Network Reliability Optimization Model with Head Loss for Water Distribution System. Water Resour. Manag. 2021, 35, 2101–2114. [Google Scholar] [CrossRef]
- Paez, D.; Filion, Y. Water Distribution Systems Reliability under Extended-Period Simulations. J. Water Resour. Plan. Manag. 2020, 146, 1–10. [Google Scholar] [CrossRef]
- Mazumder, R.K.; Salman, A.M.; Li, Y.; Yu, X. Reliability Analysis of Water Distribution Systems Using Physical Probabilistic Pipe Failure Method. J. Water Resour. Plan. Manag. 2019, 145, 1–14. [Google Scholar] [CrossRef]
- Gheisi, A.; Forsyth, M.; Naser, G. Water Distribution Systems Reliability: A Review of Research Literature. J. Water Resour. Plan. Manag. 2016, 142, 04016047. [Google Scholar] [CrossRef]
- Todini, E. Looped Water Distribution Networks Design Using a Resilience Index Based Heuristic Approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Prasad, T.D.; Park, N.-S. Multiobjective Genetic Algorithms for Design of Water Distribution Networks. J. Water Resour. Plan. Manag. 2004, 130, 73–82. [Google Scholar] [CrossRef]
- Ilaya-Ayza, A.E.; Martins, C.; Campbell, E.; Izquierdo, J. Implementation of DMAs in Intermittentwater Supply Networks Based on Equity Criteria. Water 2017, 9, 851. [Google Scholar] [CrossRef]
- Gottipati, P.V.K.S.V.; Nanduri, U.V. Equity in Water Supply in Intermittent Water Distribution Networks. Water Environ. J. 2014, 28, 509–515. [Google Scholar] [CrossRef]
- Vairavamoorthy, K.; Gorantiwar, S.D.; Mohan, S. Intermittent Water Supply under Water Scarcity Situations. Water Int. 2007, 32, 121–132. [Google Scholar] [CrossRef]
- Erickson, J.J.; Quintero, Y.C.; Nelson, K.L. Characterizing Supply Variability and Operational Challenges in an Intermittentwater Distribution Network. Water 2020, 12, 2143. [Google Scholar] [CrossRef]
- Raad, D.; Sinske, A.; Van Vuuren, J. Robust Multi-Objective Optimization for Water Distribution System Design Using a Meta-Metaheuristic. Int. Trans. Oper. Res. 2009, 16, 595–626. [Google Scholar] [CrossRef]
- Wang, Q.; Savić, D.A.; Kapelan, Z. GALAXY: A New Hybrid MOEA for the Optimal Design of Water Distribution Systems. Water Resour. Res. 2017, 53, 1997–2015. [Google Scholar] [CrossRef]
- Moosavian, N.; Lence, B.J. Fittest Individual Referenced Differential Evolution Algorithms for Optimization of Water Distribution Networks. J. Comput. Civ. Eng. 2019, 33. [Google Scholar] [CrossRef]
- Sirsant, S.; Reddy, M.J. Improved MOSADE Algorithm Incorporating Sobol Sequences for Multi-Objective Design of Water Distribution Networks. Appl. Soft Comput. 2022, 120, 108682. [Google Scholar] [CrossRef]
- Tanyimboh, T.T.; Tabesh, M.; Burrows, R. Appraisal of Source Head Methods for Calculating Reliability of Water Distribution Networks. J. Water Resour. Plan. Manag. 2001, 127, 206–213. [Google Scholar] [CrossRef]
- Mahmoud, H.A.; Savić, D.; Kapelan, Z. New Pressure-Driven Approach for Modeling Water Distribution Networks. J. Water Resour. Plan. Manag. 2017, 143, 04017031. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Improved Hardy Cross Method for Pipe Networks. Civ. Eng. 2018, 1–13. [Google Scholar] [CrossRef]
- Vita, V. Development of a Decision-Making Algorithm for the Optimum Size and Placement of Distributed Generation Units in Distribution Networks. Energies 2017, 10, 1433. [Google Scholar] [CrossRef]
- Nayak, M.A.; Turnquist, M.A. Optimal Recovery from Disruptions in Water Distribution Networks. Comput. Civ. Infrastruct. Eng. 2016, 31, 566–579. [Google Scholar] [CrossRef]
- Abdy Sayyed, M.A.H.; Gupta, R.; Tanyimboh, T.T. Modelling Pressure Deficient Water Distribution Networks in EPANET. Procedia Eng. 2014, 89, 626–631. [Google Scholar] [CrossRef]
- Baek, C.W.; Jun, H.D.; Kim, J.H. Development of a PDA Model for Water Distribution Systems Using Harmony Search Algorithm. KSCE J. Civ. Eng. 2010, 14, 613–625. [Google Scholar] [CrossRef]
- Martin-candilejo, A.; Santill, D.; Iglesias, A.; Garrote, L. Optimization of the Design of Water Distribution Systems for Variable Pumping Flow Rates. Water 2020, 12, 359. [Google Scholar] [CrossRef]
- Tanyimboh, T.T.; Tabesh, M. The Basis of the Source Head Method of Calculating Distribution Network Reliability; Mechanical Engineering Publications Ltd.: London, UK, 1997; pp. 211–220. [Google Scholar]
- Rossman, L.A. EPANET 2 Users Manual EPA/600/R-00/57; Water Supply Water Resour. Div. U.S. Agency, Environ. Prot.: Washington, DC, USA, 2000. [Google Scholar]
- Reddy, L.S.; Elango, K. Analysis of Water Distribution Networks with Head-Dependent Outlets. Civ. Eng. Syst. 1989, 6, 102–110. [Google Scholar] [CrossRef]
- Gupta, R.; Bhave, P.R. Comparison of Methods for Predicting Deficient-Network Performance. J. Water Resour. Plan. Manag. 1996, 122, 214–217. [Google Scholar] [CrossRef]
- Chandapillai, J. Realistic Simulation of Water Distribution System. J. Transp. Eng. 1991, 117, 258–263. [Google Scholar] [CrossRef]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water Distribution Reliability: Analytical Methods. J. Water Resour. Plan. Manag. 1988, 114, 253–275. [Google Scholar] [CrossRef]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms: An Introduction; Wiley: Chichester, UK, 2001; ISBN 978-0-471-87339-6. [Google Scholar]
- Ercan, M.B.; Goodall, J.L. A Python Tool for Multi-Gage Calibration of SWAT Models Using the NSGA-II Algorithm. In Proceedings of the 7th International Congress on Environmental Modelling and Software, San Diego, CA, USA, 15–19 June 2014; Volume 4, pp. 2325–2331. [Google Scholar] [CrossRef]
- Reed, P.M.; Hadka, D.; Herman, J.D.; Kasprzyk, J.R.; Kollat, J.B. Evolutionary Multiobjective Optimization in Water Resources: The Past, Present, and Future. Adv. Water Resour. 2013, 51, 438–456. [Google Scholar] [CrossRef]
- Savic, D. Single-Objective vs Multiobjective Optimisation for Integrated Decision Support. Int. Congr. Environ. Model. Softw. 2002, 119, 7–12. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Kansal, M.L.; Kumar, A.; Sharma, P.B. Reliability Analysis of Water Distribution Systems under Uncertainty. Reliab. Eng. Syst. Saf. 1995, 50, 51–59. [Google Scholar] [CrossRef]
- Demir, I.; Ergin, F.C.; Kiraz, B. A New Model for the Multi-Objective Multiple Allocation Hub Network Design and Routing Problem. IEEE Access 2019, 7, 90678–90689. [Google Scholar] [CrossRef]
| S. No | Pipe Diameter (in mm) | Total Cost of Pipe (in INR per meter) |
|---|---|---|
| 1 | 100 | 560 |
| 2 | 150 | 900 |
| 3 | 200 | 1303 |
| 4 | 250 | 1757 |
| 5 | 300 | 2267 |
| 6 | 350 | 2848 |
| 7 | 400 | 3485 |
| 8 | 450 | 4220 |
| 9 | 500 | 4820 |
| 10 | 550 | 5795 |
| 11 | 600 | 6794 |
| 12 | 650 | 7352 |
| 13 | 700 | 8050 |
| 14 | 750 | 9280 |
| 15 | 800 | 10,692 |
| Parameter | Value |
|---|---|
| Size of population | 200 |
| Probability of crossover | 0.6 |
| Probability of mutation | 1/(number of real variables) |
| Mutation distribution index | 15 |
| Crossover distribution index | 25 |
| Node ID | Elevation, m | Demand in Meter Cube per Hour (m3/h) |
|---|---|---|
| 1 | 210 | Tank |
| 2 | 180 | 100 |
| 3 | 190 | 100 |
| 4 | 185 | 120 |
| -5 | 180 | 270 |
| 6 | 195 | 330 |
| 7 | 190 | 200 |
| Link ID | Start Node | End Node | Length, m | Roughness Coefficient |
|---|---|---|---|---|
| 1 | 1 | 2 | 1000 | 100 |
| 2 | 2 | 3 | 1000 | 100 |
| 3 | 2 | 4 | 1000 | 100 |
| 4 | 4 | 5 | 1000 | 100 |
| 5 | 4 | 6 | 1000 | 100 |
| 6 | 6 | 7 | 1000 | 100 |
| 7 | 3 | 5 | 1000 | 100 |
| 8 | 5 | 7 | 1000 | 100 |
| Node ID | Elevation (In m) | Demand in Meter Cube per Day (m3/day) |
|---|---|---|
| 1 | 180 | Tank |
| 2 | 178 | 600 |
| 3 | 179 | 1000 |
| 4 | 180 | 900 |
| 5 | 181 | 1200 |
| 6 | 183 | 900 |
| 7 | 182 | 800 |
| 8 | 181 | 800 |
| 9 | 180 | 1200 |
| 10 | 182 | 1200 |
| 11 | 181 | 600 |
| 12 | 181 | 800 |
| 13 | 183 | 1200 |
| 14 | 184 | 800 |
| 15 | 179 | 800 |
| 16 | 180 | 600 |
| 17 | 181 | 900 |
| Link ID | Start Node | End Node | Length, m | Roughness Coefficient |
|---|---|---|---|---|
| 1 | 1 | 2 | 1400 | 100 |
| 2 | 2 | 3 | 1700 | 100 |
| 3 | 3 | 4 | 1000 | 100 |
| 4 | 4 | 5 | 900 | 100 |
| 5 | 5 | 6 | 1350 | 100 |
| 6 | 2 | 7 | 900 | 100 |
| 7 | 7 | 8 | 1100 | 100 |
| 8 | 8 | 5 | 1400 | 100 |
| 9 | 5 | 9 | 900 | 100 |
| 10 | 5 | 10 | 1000 | 100 |
| 11 | 6 | 10 | 1200 | 100 |
| 12 | 1 | 11 | 1100 | 100 |
| 13 | 11 | 12 | 800 | 100 |
| 14 | 12 | 13 | 1400 | 100 |
| 15 | 13 | 9 | 800 | 100 |
| 16 | 10 | 14 | 1100 | 100 |
| 17 | 11 | 15 | 1200 | 100 |
| 18 | 15 | 16 | 800 | 100 |
| 19 | 16 | 13 | 900 | 100 |
| 20 | 16 | 17 | 1400 | 100 |
| 21 | 17 | 14 | 1200 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramani, K.; Rudraswamy, G.K.; Umamahesh, N.V. Optimal Design of Intermittent Water Distribution Network Considering Network Resilience and Equity in Water Supply. Water 2023, 15, 3265. https://doi.org/10.3390/w15183265
Ramani K, Rudraswamy GK, Umamahesh NV. Optimal Design of Intermittent Water Distribution Network Considering Network Resilience and Equity in Water Supply. Water. 2023; 15(18):3265. https://doi.org/10.3390/w15183265
Chicago/Turabian StyleRamani, Katineni, G. K. Rudraswamy, and Nanduri V. Umamahesh. 2023. "Optimal Design of Intermittent Water Distribution Network Considering Network Resilience and Equity in Water Supply" Water 15, no. 18: 3265. https://doi.org/10.3390/w15183265





