Optimal Design of Intermittent Water Distribution Network Considering Network Resilience and Equity in Water Supply

Abstract

In urban areas of developing countries, due to industrialization and population growth, water demand has been increasing significantly, thereby increasing stress on the existing water distribution systems (WDSs). Under these circumstances, maintaining equity in the allocation of water becomes a significant challenge. When building an intermittent water distribution system, it is important to provide a minimum level of supply that is acceptable as well as water supply equity. A non-dominated sorting genetic algorithm (NSGA-II) is employed for the optimal design of an intermittent water distribution network (WDN). Network resilience is taken as a measure of reliability (In), while the uniformity coefficient (CU) is taken as a measure of equity in the water supply. Maximizing network resilience, uniformity coefficient, and minimization of cost of the network are considered as the objectives in the multi-objective optimization model. Pressure-driven analysis (PDA) is used for the hydraulic simulation of the network. The NSGA-II model is applied and demonstrated over two water distribution networks taken from the literature. The results indicate that reliability and equity in WDNs can be accomplished to a reasonable extent with minimal cost.

1. Introduction

Water distribution network (WDN) is a critical and complex infrastructure in urban water supply systems that needs significant investment. WDNs have to provide a minimum acceptable level of supply, in terms of pressure, availability, and water quality, to the consumers under all ranges of operating conditions [1]. The increasing population and rapid urbanization, especially in developing countries, have put additional stress on the existing systems [2]. Hence, developing the optimal design of WDN has been a challenge to the design engineers. More than half of the world’s population now resides in towns and cities, marking the biggest wave of urban expansion in history. This figure is anticipated to rise to almost 5 billion by 2030, with a large portion of this urbanization occurring in Africa and Asia. According to projections, the number of people living in urban areas worldwide could increase by 2.5 billion by the year 2050, with about 90% of this expansion occurring in Asia and Africa [3]. The optimal design of WDNs is a complex, combinatorial optimization problem due to the nonlinear relation between the flow, head, and the discrete nature of the decision variables, such as the diameters of the pipes [4,5,6,7]. The typical approach to designing a WDN involves finding the most efficient pipe diameters that minimize network cost while ensuring sufficient pressure at all nodes. In addition to the cost, factors such as reliability, water quality, fluctuations, and uncertainties in demands also play a significant role in the design of WDNs. Many studies in the literature have considered minimization of the cost as the objective function and used different techniques such as linear programming, nonlinear programming, enumeration techniques, heuristic methods, and evolutionary techniques for finding the optimal design [7,8,9].

Since the design of WDN is complex, the design includes solving a set of non-linear equations. The continuity equation, minimum pressure at nodal sites, and commercially available pipe sizes are the factors to be taken into account. The least costly design of WDNs is a complex nonlinear problem, involving a large number of decision variables [10]. Usually, the optimal design of WDN involves determining the diameters of the pipes to minimize the cost of the network, while maintaining the required pressure at all the nodes. Hence, designing WDNs by considering minimizing the cost as the only objective may not be suitable for systems operating under varying operating conditions. Multi-objective optimization of WDNs, considering cost and performance as objectives, has received considerable attention during the last two decades [9,11,12,13,14]. Multi-objective evolutionary algorithms (MOEAs) were widely used for this purpose. Many studies on benchmarking networks have demonstrated the strength of MOEAs in designing WDNs [15,16]. Savić et al. (2018) discussed the history of optimization techniques in the design of WDNs and provided a detailed review on the application of optimization techniques in the design of WDNs [17]. Monsef et al. (2019) compared different evolutionary algorithms used for multi-objective optimization of WDNs [18].

Water system designers and operators are becoming increasingly concerned about the reliability and equity of water distribution systems. Reliability may be defined as the degree to which a system can achieve a minimum acceptable level of supply under both normal and abnormal conditions [1]. Several measures for reliability have been proposed in the literature [15,19,20,21,22]. Gheisi et al. (2016) provided a comprehensive review on the different types of reliability measures [23]. Atkinson et al. (2014) presented a comparative analysis of various reliability indicators used in the analysis of WDNs [1].

Todini [24] introduced the concept of resilience to define a new index for reliability. The concept of resilience is based on the premise that the availability of surplus power at the nodes of the system will improve reliability, as the available surplus power can meet the increased internal head losses that take place during a failure. Prasad and Park [25] formulated a multi-objective genetic algorithm model for the optimal design of WDN, considering the minimization of cost and the maximization of resilience as the objectives. Several studies have indicated that the WDN systems that were optimized using the resilience index were more reliable in hydraulic failure conditions compared to mechanical failure conditions [23].

Equity refers to delivering unbiased shares across the system [26]. Gottipati and Nanduri [27] proposed an index called the ‘Uniformity Index’ to quantify the equity in the distribution of water in an intermittent system, as spatial and temporal distribution of water were affected by low pressure in the system. Vairavamoorthy et al. (2007) proposed the improvement of equity as one of the design guidelines for intermittent water supply systems [28]. In intermittent supply, the flows in the pipes are greater than the anticipated discharge for which they are designed [28]. This results in excessive pressure losses and will lead to inequities between users upstream and downstream [29].

Various studies have applied evolutionary multi-objective algorithms such as NSGA-II, particle swarm optimization [16], genetically adaptive multi-objective (AMALGAM) [30], multi-objective genetic algorithms [11], and many more to design WDNs. Wang et al. (2015) compared five multi-objective evolutionary algorithms to obtain the best Pareto optimal front by eliminating dominated solutions [15]. Non-dominated sorting differential evolution (NSDE) is used for designing optimal WDS to get a Pareto front between cost and resilience [15]. A new evolutionary algorithm GALAXY is developed for optimizing WDN design [31]. Various mutation tactics and hybrid forms were developed to enhance the exploitation capacities [32,33]. Nevertheless, there is no standard algorithm that is accepted as an optimization tool in the design of WDN as superior results can be still produced by improvements in the existing algorithms.

The objective of the proposed study is to assess the optimal design of a WDN considering equity in the water supply as a criterion in addition to cost and reliability. Pressure-driven analysis based on the approach is used for the hydraulic simulation of the network [27,34]. NSGA-II, which is a multi-objective genetic algorithm (MOGA), is demonstrated over two benchmark networks taken from the literature. Pareto optimal solutions indicating the trade-offs between the three objectives considered are presented.

2. Methodology

2.1. Pressure-Driven Analysis

Pressure-driven analysis is a fundamental approach used to model and analyze water distribution networks (WDNs). It is a critical aspect of hydraulic engineering and plays a crucial role in designing, optimizing, and evaluating the performance of water supply networks. To evaluate the system performance and optimize system operation, it primarily focuses on modeling and analyzing the hydraulic behavior of the network under various operating situations. The PDA approach evaluates pressure changes, flow rates, and other pertinent hydraulic parameters by taking into account the link between pressure and flow in the network [27,34,35].

The following steps are included in the implementation of the PDA method:

(1)

Network modeling: Using EPANET, a hydraulic model of the WDN is created. The model contains data on the boundary conditions, nodal demands, pipe characteristics, and network topology. The network’s hydraulic behavior can be simulated using this model as a starting point.

(2)

Demand allocation: For realistic simulations, it is essential to accurately estimate demands at each node. Based on past trends, demographic estimates, and specific consumer data, the demands may be determined. To capture genuine demand profiles, seasonal fluctuations and nocturnal patterns are taken into account.

(3)

Pressure simulation: Various scenarios for the network’s behavior are simulated using the hydraulic model. The operating conditions, such as pump operation, valve settings, and tank levels, are taken into account during the simulation. Based on the water conservation and energy calculations, the simulation determines pressure heads and flow rates across the network.

(4)

Performance assessment: The network’s performance is then assessed using the simulation findings. It is possible to evaluate key performance indicators such as minimum and maximum pressures, pressure deficits, network resilience, uniformity coefficient, or equity and flow rates. These indicators aid in locating trouble spots, such as low-pressure locations, high-pressure areas, and probable water quality problems.

The PDA approach is used to optimize the network’s functioning and design. The network’s effectiveness and dependability can be improved by analyzing various operating tactics, such as pump scheduling, pressure management, and valve modifications. To meet the desired performance goals, it may entail sizing and placing additional infrastructure components, such as pipelines, pumps, tanks, and pressure-reducing valves. In the demand driven analysis (DDA), the nodal discharges are fixed (equal to the nodal demands) and the set of nonlinear equations, consisting of continuity equation at nodes and the energy conservation equation around each loop in the network, are solved to determine the pressure heads at the nodes and the pipe flows. This set of nonlinear equations can be solved using any iterative techniques such as the Hardy–Cross method [36], Newton–Raphson method [37], linear theory method, or gradient method [38]. EPANET [39,40,41] is one of the most popularly used hydraulic simulators for WDNs based on DDA.

In PDA, the discharge at the nodes is assumed to depend on the nodal pressure heads [27,34]. Hence, the set of nonlinear equations needs to be solved simultaneously for both nodal heads and discharges. One of the major obstacles to the easy application of PDA in analyzing WDNs is the development of a methodology for simultaneous estimation of unknown nodal heads and nodal discharges [40]. Several iterative techniques are proposed in the literature for PDA [13,41].

An Iterative procedure using source head approach was suggested by Tanyimboh and Tabesh [34,42], and Tanyimboh et al. (2001) used it for calculating the nodal discharges $Q_j$ at all nodes [34]. A demand driven analysis using EPANET [43] is performed using the demands $Q_j^{req}$ at all nodes in the network. An iterative method is used for calculating the minimum source head required $H_{sj}^{min}$ and the required source head $H_{sj}^{des}$ at all the nodes. These values are used to calculate the actual nodal discharges $Q_j$. The source head method is applicable only to networks with a single source.

2.2. Source Head Method

In the conventional DDA, the head and flow available at a node are considered independent entities. This is possible only when there exists a controlled mechanism that can be manipulated to ensure that only the required quantity of water is drawn at each node irrespective of the head available at that node [44]. This may be true in continuous supply systems operating under normal conditions. However, in intermittent supply systems and continuous supply systems operating under abnormal conditions (such as excessive fire demand), the outflow and the head at the node cannot be assumed to be independent. The discharge available at the node is proportional to the head available at the node, and the unknown nodal head and nodal discharges should be solved simultaneously [40]. Many researchers have proposed different theoretical relationships between the nodal head and discharge. Gupta and Bhave compared different head–discharge relationships suggested in the literature [45] and concluded that the parabolic head–discharge relationship is the most suitable for designing WDNs [46,47]. Tanyimboh et al. (2001) used a modified parabolic relationship and related the nodal discharge as a function of the head at the source [34]. A modified version of this relationship is used in the present study. The parabolic head–discharge relationship is given by [34]:

$$Q_j=Q_j^{req}{\left(\frac{H_s-H_{sj}^{min}}{H_{sj}^{des}-H_{sj}^{min}}\right)}^{1/n}\mathrm{if}{H}_s>H_{sj}^{min}$$

(1)

$$Q_j=0\hspace{1em}\hspace{1em}\mathrm{if}{H}_s\le H_{sj}^{min}$$

(2)

where $H_s$ is the source head; $H_{sj}^{min}$ is the minimum head required at the source to initiate flow at node $j$; $Q_j$ is the discharge at node $j$; $H_{sj}^{des}$ is the desired head at the source that will satisfy the demand at node $j$; and $Q_j^{req}$ is the required discharge (demand) at node $j$. In the original head–discharge relationship proposed by Tanyimboh et al. (2001) [34], it is assumed that $Q_j$ is equal to $Q_j^{req}$ when $H_{sj}$ is more than $H_{sj}^{des}$, and also in the present study, it is assumed that $Q_j$ will increase with $H_{sj}$ beyond $Q_j^{req}$. In an intermittent system, there is a tendency by the consumers to draw as much water as possible, and hence, the discharge at nodes can exceed the demand if sufficient head is available. The value of the exponent in Equation (1) is taken as 2 for the analysis purpose.

Algorithm to run calculation of $H_{sj}^{des}$ and $H_{sj}^{minf}$ is:

1.

Run hydraulic analysis in EPANET (RunH) to determine the pressure head at the source ($H_s$).

2.

For each node in the network:

a.

Get the pressure head at the node.

b.

Calculate the head loss between the source and the node as: ${HL}_j$ = $H_s$ − $H_j$.

c.

Calculate the desired pressure head at the source for this node as:

$$H_{sj}^{des}=\mathit{elj}+H_{jmin}+{HL}_j+H_j^{des}s\left(\mathrm{where}\mathit{elj}\mathrm{is}\mathrm{the}\mathrm{elevation}\mathrm{at}\mathrm{node}j\right).$$

End of loop.

3.

To calculate the minimum source pressure head at which discharge at each node is zero, for each node in the network:

i.

Set Q_j (discharge) to 0.

ii.

Run hydraulic analysis (RunH) to get the pressure head at the node.

iii.

Calculate the head loss between the source and the node when only Q_j is zero, as: ${HL}_{j1}$ = $H_s$ − $H_j$.

iv.

Reset Q_j to its actual value.

v.

Calculate the minimum pressure head at the source when only Q_j is zero, as:

$$H_{sj}^{min1}=\mathit{elj}+H_{jmin}+{HL}_{j1}.$$

End of loop.

4.

Sort the nodes in ascending order of $H_{sj}^{min1}$.

5.

For each node in the sorted order:

Set Q_j (discharge) to 0.

a.

Run hydraulic analysis (RunH) to get the pressure head at the node.

b.

Calculate the head loss between the source and the node when discharge at this node and also the nodes above this in the sorted list are zero, as: ${HL}_{j2}$ = $H_s$ − $H_j$.

c.

Calculate the minimum pressure head at the source when all discharge at this node and also the nodes above this are zero, as: $H_{sj}^{min1}$ = elj +$H_{jmin}$ + ${HL}_{j2}$.

End of loop.

6.

After getting $H_{sj}^{min}$ and $H_{sj}^{des}$, for each node, calculate the corrected discharge and check the head (if $H_{ji}$ − $h_{ji}$> Limit, go for previous steps, otherwise, continue with step 6), calculate average supply ratio (SR), uniformity coefficient (CU).

2.3. Performance Indicators

In the present study, two performance indicators, namely, network resilience and uniformity coefficient, are used to evaluate the performance of the WDN. Network resilience ($I_n$) is popularly used as a surrogate measure of the reliability of the network [24,25], while uniformity coefficient is a measure of the equity in supply under pressure-deficient conditions.

Network resilience measures the combined impact of surplus power and nodal uniformity, taking into account the effects of dependable loops and extra power, and is given by Equation (3):

$$I_n=\frac{\sum _{j=1}^{nn}{C}_j{Q}_j\left(H_j-H_j^l\right)}{\left[\sum _{k=1}^{nr}{Q}_k{H}_k+\sum _{i=1}^{np}\left(\raisebox{1ex}{$P_i$}\!\left/ \!\raisebox{-1ex}{$\gamma $}\right.\right)\right]-\sum _{j=1}^{nn}{Q}_j{H}_j^l}$$

(3)

where$nn$ is the number of junction nodes; $H_j$ is the head at node $j$; $H_j^l$ is the minimum head required at node $j$; $Q_j$ is the discharge at node $j$; $nr$ is the number of reservoirs in the network; $Q_k$ and $H_k$ are the discharge and head, respectively, at reservoir node $k$; $np$ is the number of pumping units; $P_i$ is power supplied by pump $i$; and $\gamma$ is the specific weight of water. The term $C_j$ is a measure of the uniformity of the pipes connected to node $j$ and is given as:

$$C_j=\frac{\sum _{i=1}^{npj}{D}_i}{npj\times \underset{}{\max }\left\{D_i\right\}}$$

(4)

where $npj$ is the number of pipes connected to the node $j$ and $D_i$ is the diameter of the pipe $i$.

The value of $I_n$ may vary between 0 and 1. Maximizing network resilience improves the reliability of the WDN under failure conditions [25]. Gottipati and Nanduri [27] introduced an index called uniformity coefficient (CU) as a measure of equity in water distribution in an intermittent water distribution system. CU is given as:

$$CU=1-\left(\frac{DEV}{SR}\right)$$

(5)

where $SR$ is the average supply ratio. The supply ratio of the node is defined as the proportion of the actual water supplied at a node to the node’s demand. The average of the supply ratios of all the nodes is known as $SR$. The average of the deviations of the nodal supply ratio from $SR$ over all nodes is the average deviation ($DEV$). The value of CU ranges between 0 and 1. If the CU value is 1, it indicates that there is perfect equity in water distribution even under water scarcity conditions.

2.4. Multi-Objective Evolutionary Optimization (MOEA)

Non-dominated sorting genetic algorithm II (NSGA-II) [37,48], which is an MOEA, is based on the concept of non-dominated solutions, and it has been used widely in various water resources optimization problems [49,50]. It is a population-based, fast, and efficient optimization technique and can be parallelized. The multi-objective optimization algorithm simultaneously optimizes the various objectives considered and provides solutions that are often referred to as trade-off, non-dominated, non-inferior, or Pareto optimal solutions [51]. NSGA-II is well suited for handling constraints. The multi-objective optimization for the optimal design of WDN is implemented using the MATLAB platform.

A multi-objective optimization model is formulated for the optimal design of the WDN. Three objective functions, namely, minimization of cost, maximization of network resilience ($I_n$), and maximization of uniformity coefficient ($CU$), are used for the design of the network. The optimization model is given as:

$$\min f_1={\sum }_{i=1}^{np}{C}_i\left(D_i,L_i\right)$$

(6)

$$\max f_2=I_n$$

(7)

$$\max f_3=CU$$

(8)

where $np$ is the number of pipes; and $C_i\left(D_i,L_i\right)$ is the cost of pipe $i$ with a diameter $D_i$ and length $L_i$. The nodal mass balance equations and energy conservation equations are the constraints for the above optimization problems. These constraints are externally satisfied by using a hydraulic network solver [25]. The PDA explained in the below section is used for the hydraulic simulation of the network. The diameters of the pipes are selected from a set of commercially available sizes. The non-dominated sorting genetic algorithm (NSGA-II) [52] is used to solve this multi-objective optimization model and develop Pareto optimal solutions. The applicability of the NSGA-II is demonstrated on two standard WDNs taken from the literature. The details of these two networks and the results obtained are discussed in the following sections.

2.5. Analysis of Networks

The multi-objective optimization model discussed in the previous sections is applied to two networks. The networks considered in the present study are taken from the literature [25,53]. It is assumed that all the pipes are made of cast iron. The list of commercially available pipe diameters and their costs are given in

Table 1. Commercially available standard pipe diameters and their respective costs.

S. No	Pipe Diameter (in mm)	Total Cost of Pipe (in INR per meter)
1	100	560
2	150	900
3	200	1303
4	250	1757
5	300	2267
6	350	2848
7	400	3485
8	450	4220
9	500	4820
10	550	5795
11	600	6794
12	650	7352
13	700	8050
14	750	9280
15	800	10,692

. The NSGA-II tool in MATLAB 1.8.0.0 is used for solving the multi-objective optimization for the optimal design of the WDN. The parameters of the NSGA-II are fixed based on several trial runs, and the values of the parameters used in this study are given in

Table 2. Parameters of NSGA-II.

Parameter	Value
Size of population	200
Probability of crossover	0.6
Probability of mutation	1/(number of real variables)
Mutation distribution index	15
Crossover distribution index	25

. The details of the two networks used in the study and the corresponding results are presented in the following sections.

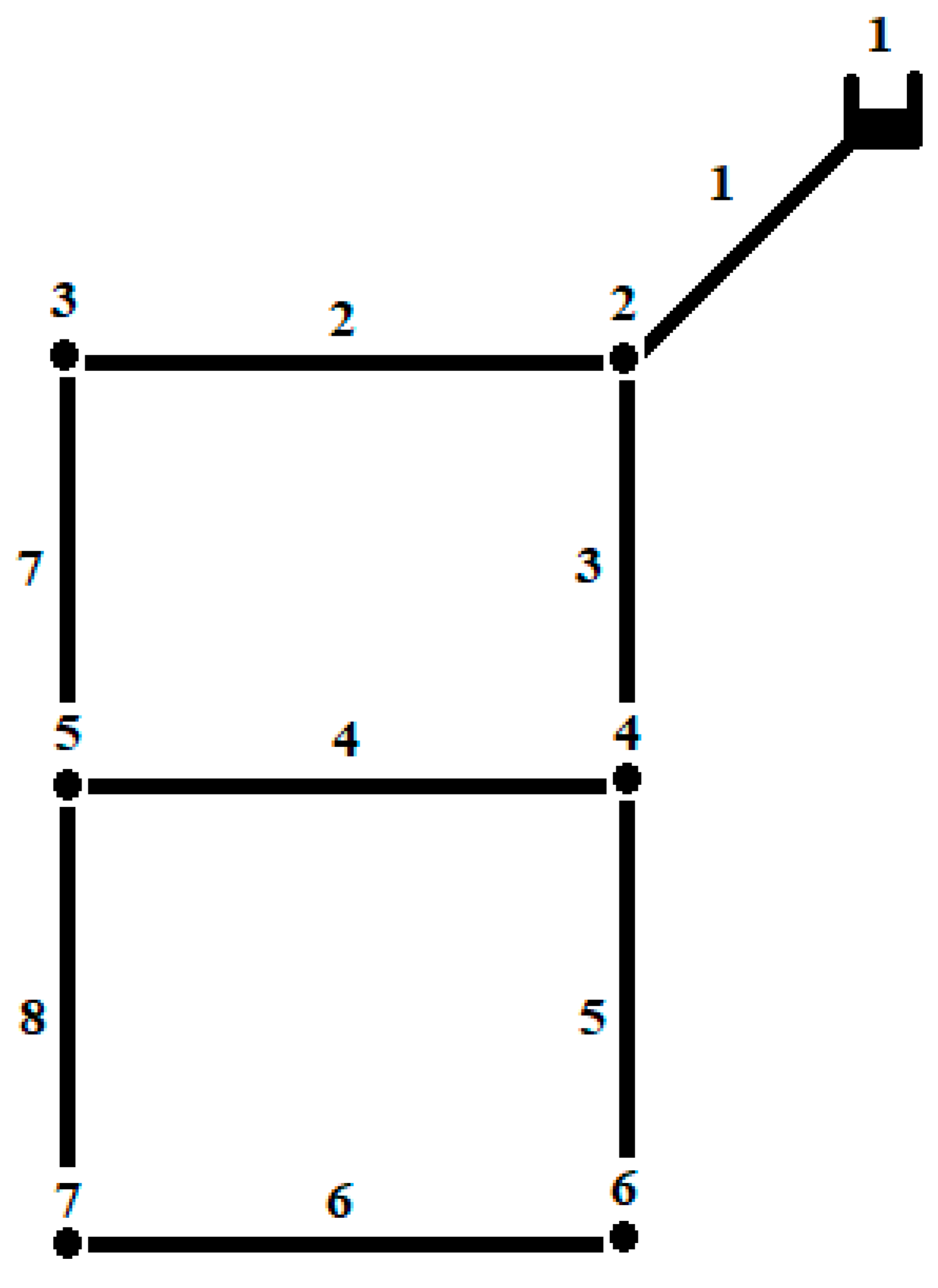
2.5.1. Network-1

Network-1 considered in the study and shown in Figure 1 is a simple network consisting of eight pipes with two loops fed by gravity from a constant head reservoir [25]. This network consists of 8 links, 6 demand nodes, and 1 source node. The minimum head required at all demand nodes is taken as 30 m. The node and link data are given in

Table 3. Node data for two-loop Network-1.

Node ID	Elevation, m	Demand in Meter Cube per Hour (m3/h)
1	210	Tank
2	180	100
3	190	100
4	185	120
-5	180	270
6	195	330
7	190	200

and

Table 4. Link data for two-loop Network-1.

Link ID	Start Node	End Node	Length, m	Roughness Coefficient
1	1	2	1000	100
2	2	3	1000	100
3	2	4	1000	100
4	4	5	1000	100
5	4	6	1000	100
6	6	7	1000	100
7	3	5	1000	100
8	5	7	1000	100

, respectively. Hazen–Williams equation is used as the head loss equation, and the roughness coefficient for all the pipes is taken as 100.

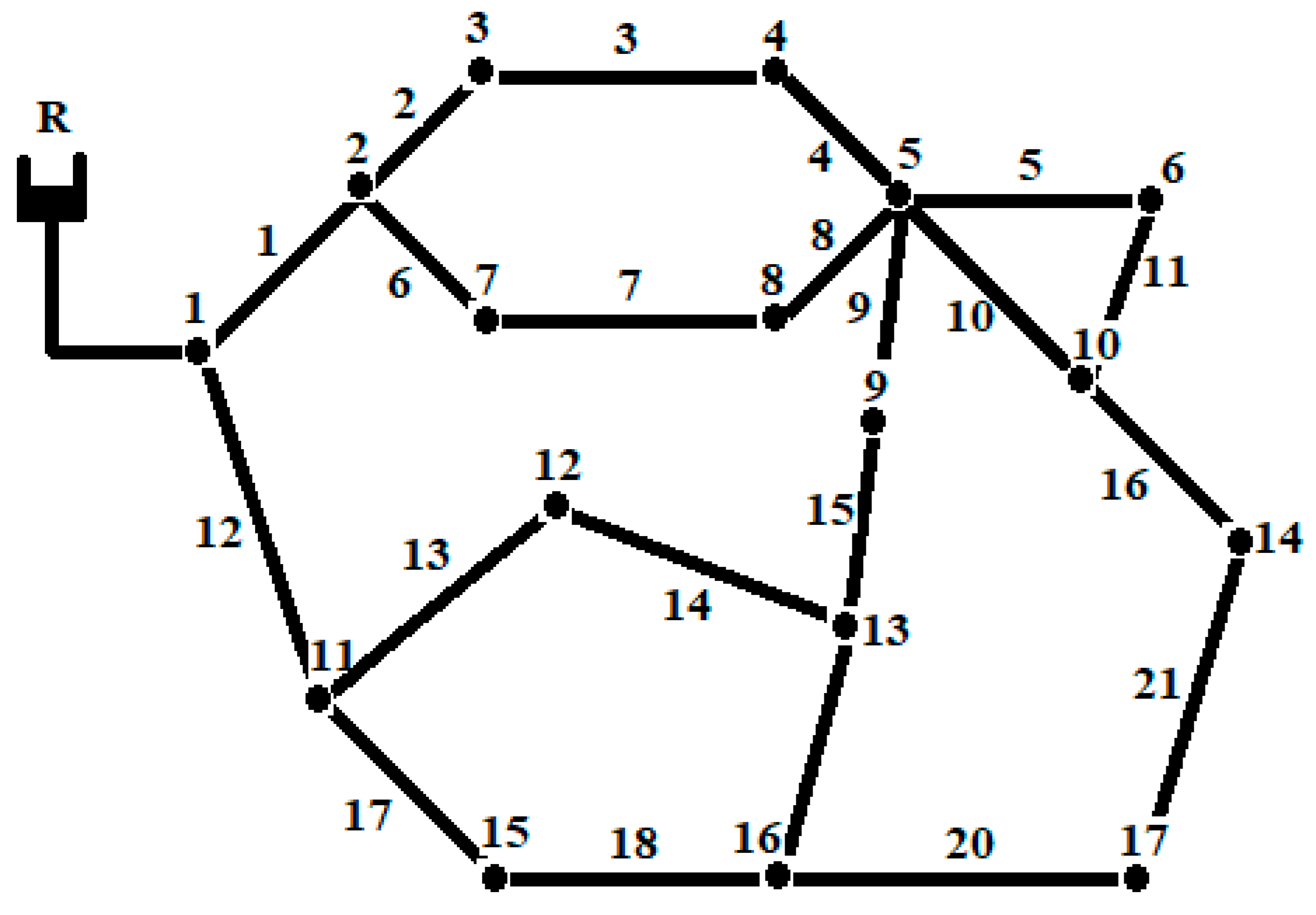
2.5.2. Network-2

Network-2 considered in the present study is shown in Figure 2 and was selected from the literature [53]. The network consists of Single source (Reservoir), 17 demand nodes and 21 links. The minimum head required at all the nodes is assumed as 30 m. The elevation and demand at each node are given in

Table 5. Node data for Network-2.

Node ID	Elevation (In m)	Demand in Meter Cube per Day (m3/day)
1	180	Tank
2	178	600
3	179	1000
4	180	900
5	181	1200
6	183	900
7	182	800
8	181	800
9	180	1200
10	182	1200
11	181	600
12	181	800
13	183	1200
14	184	800
15	179	800
16	180	600
17	181	900

, and the length of each link is given in

Table 6. Link data for Network-2.

Link ID	Start Node	End Node	Length, m	Roughness Coefficient
1	1	2	1400	100
2	2	3	1700	100
3	3	4	1000	100
4	4	5	900	100
5	5	6	1350	100
6	2	7	900	100
7	7	8	1100	100
8	8	5	1400	100
9	5	9	900	100
10	5	10	1000	100
11	6	10	1200	100
12	1	11	1100	100
13	11	12	800	100
14	12	13	1400	100
15	13	9	800	100
16	10	14	1100	100
17	11	15	1200	100
18	15	16	800	100
19	16	13	900	100
20	16	17	1400	100
21	17	14	1200	100

. The Hazen–Williams roughness coefficient is taken as 100 for all the pipes.

2.6. Multidimensional Pareto Analysis

The method used in the Pareto analysis is often referred to as brute force dominance check. It involves systematically comparing each solution in a dataset with every other solution to determine dominance relationships based on multiple objectives [54]. This method is straightforward but may become computationally expensive as the dataset size increases. More efficient algorithms, such as the fast non-dominated sorting algorithm (NSGA-II) or the strength Pareto evolutionary algorithm (SPEA2), are commonly used for large-scale multi-objective optimization problems to reduce computation time. The method identifies and extracts the Pareto front solutions from a dataset that contain multiple objective function values. The code iterates through all pairs of solutions and checks for dominance relationships based on the Pareto principle, which is the essence of multi-objective Pareto analysis.

The key steps in the code that contribute to multi-objective Pareto analysis are:

(a)

Dominance matrix: The code constructs a dominance matrix where each element (i, j) represents whether solution i dominates solution j. This matrix captures the dominant relationships among solutions for multiple objectives.

(b)

Identifying Pareto solutions: By analyzing the dominance matrix, the code identifies solutions that are Pareto optimal, meaning they are not dominated by any other solutions for all the objectives.

(c)

Extracting Pareto front: The code extracts the Pareto front solutions from the original dataset based on the identified Pareto optimal solutions.

3. Results and Discussions

A multi-objective genetic algorithm (MOGA) model is formulated for the optimal design of a water distribution network. The hydraulic simulation of the network is performed using a PDA. Three objectives, namely, minimization of network cost, maximization of network reliability (network resilience, $I_n$), and maximization of the uniformity coefficient $CU$, are considered in the MOGA model. Both reliability and equity play vital roles in an intermittent system, as they directly influence each other. In this context, customers consider the service unfair and unreliable. To address this, it is essential to incorporate the availability of excess energy into the resilience index. This is particularly important in cases where changes in the flow regime might lead to service failures. By combining equity and reliability, we can effectively assess whether the nodal demand is met, aiming for a level of equity equal to one. However, achieving higher reliability may necessitate the addition of a new pressure head to the system.

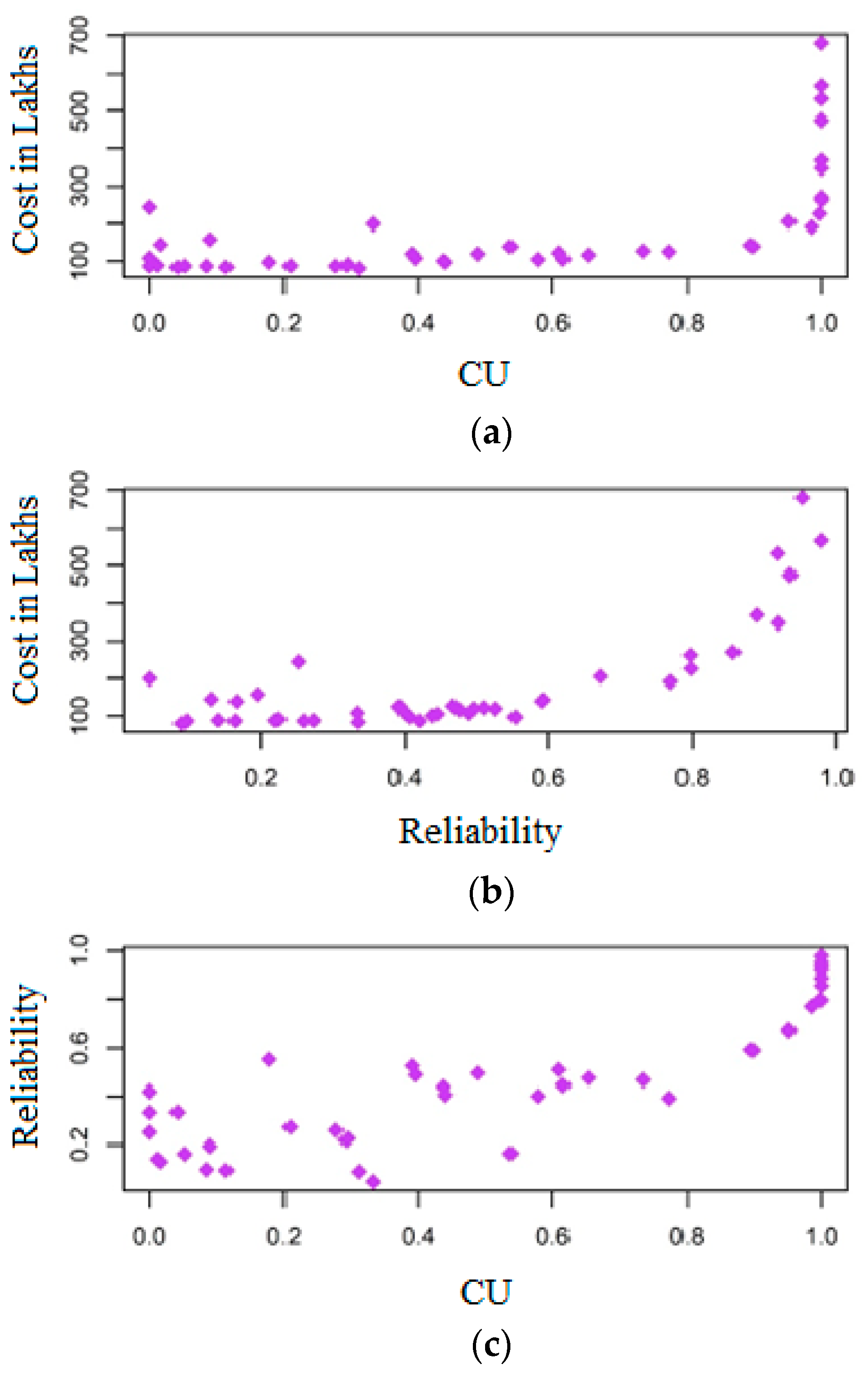
3.1. Trade-off between the Objective Functions

The multi-objective optimization model was successfully applied to the two previously described networks, leading to the identification of Pareto optimal solutions. In Figure 3a, we can observe the graphical representation illustrating the trade-off between the network’s cost and the $CU$. Additionally, Figure 3b displays the trade-off between the cost and the network resilience index$I_n$.

From a careful examination of Figure 3a,b, a clear pattern emerges; as the values of $CU$ and $I_n$ approach 1, the cost of the network experiences an increase. Interestingly, beyond a certain point, specifically when $I_n$exceeds 0.8 and $CU$ surpasses 0.85, the cost exhibits a sharp and significant rise. To gain further insights into the behavior of the network, Figure 3c illustrates the trade-off between network resilience $I_n$ and the $CU$. As depicted in the graph, network resilience demonstrates a positive correlation with the $CU$. However, upon closer examination, it becomes evident that when both $I_n$ and the $CU$ approach 1, the cost experiences a substantial increase. In conclusion, the graphical representations provide valuable information about the trade-offs between cost, uniformity, and network resilience. These insights can aid decision-makers in striking an optimal balance between these factors while designing and managing the water distribution networks.

For Network-2, the Pareto optimal fronts obtained by applying the multi-objective optimization model shown in Figure 4a–c are the trade-offs between cost and $CU$, cost and $I_n$, and $I_n$ and $CU$, respectively. As observed in the other network, the cost increases sharply as $CU$ increases beyond 0.85. Figure 4a,b indicates that the cost of the network is not affected significantly by a reliability less than 0.7. However, the cost of the network increases sharply when attaining a reliability beyond 0.7. The behaviors of the objective function $I_n$ and $CU$ aare similar to that of Case 1. As observed in Figure 4c, high reliability in the network also indicates a high equity in the water supply.

For Network-2, the application of the multi-objective optimization model resulted in the identification of the trade-offs, illustrated in Figure 4a–c. These figures represent the trade-off between various parameters: Figure 4a displays the relationship between the network’s cost and the uniformity coefficient ($CU$), Figure 4b illustrates the relationship between the cost and network resilience index $I_n$, and Figure 4c shows the relationship between $I_n$and the $CU$.

Similar to the findings in the other network, we observe that the cost experiences a sharp increase as $CU$ surpasses 0.85, as depicted in Figure 4a. In Figure 4b, an interesting pattern emerges, revealing that the cost of the network is not significantly affected by reliability values below 0.7. However, the cost increases sharply when aiming for reliability levels beyond 0.7. Analyzing the graphical representation in Figure 4c, we observe a behavior similar to that of Case 1. Specifically, the relationship between $I_n$and the $CU$ follows a similar trend as in the previous network. Moreover, it is worth noting that high levels of reliability in the network, as depicted in Figure 4c, correspond to a high degree of equity in the water supply. These findings provide valuable insights into the trade-offs between cost, uniformity, and network resilience for Network-2. Decision-makers can utilize this information to make informed choices when optimizing and managing water distribution networks, ensuring an optimal balance between the different objectives.

Equity is one of the major issues in intermittent water supply systems. To measure the equity in water supply systems, the uniformity coefficient ($CU)$ is used. It is observed from Figure 3a and Figure 4a that the network cost is not very sensitive to $CU$ up to a certain level. The cost of the network increases sharply at high values of$CU$. High equity in the water supply ($CU$ close to 1) can be achieved only at a very high cost. According to Gottipati and Nanduri (2014), the location of the source within the network and the layout of the network have a significant impact on $CU$ [27]. In the present study, the layout of the network and the location of the source are considered fixed. Higher equity in the supply without a significant increase in the cost may be achieved by optimizing the layout while designing the water distribution network.

Network resilience is considered the surrogate measure of network reliability. As observed from Figure 3b and Figure 4b, the cost of the network does not vary significantly for low values of $I_n$. However, an $I_n$ above 0.9 can be achieved in a network with an increase in cost. A similar kind of relationship between cost and $I_n$ was reported in the literature [15,25]

As observed from Figure 3c and Figure 4c, high equity in the water supply can be achieved by increasing the network resilience. It can be observed that a reasonably high equity ($CU$ value up to 0.85) can be achieved with relatively high resilience. However, high equity ($CU$ beyond 0.85) can be achieved only for high network resilience. In larger networks, the layout of the network plays a significant role in improving $CU$[27,53].

The results indicate that both tank structure and its placement significantly contribute to improving distribution equity in water supply within a network. Therefore, when designing a new network, careful attention must be given to these factors. The research findings demonstrate that the performance indicators uniformity coefficient and resilience index enhance the design of intermittent water distribution networks (WDNs) along with the cost.

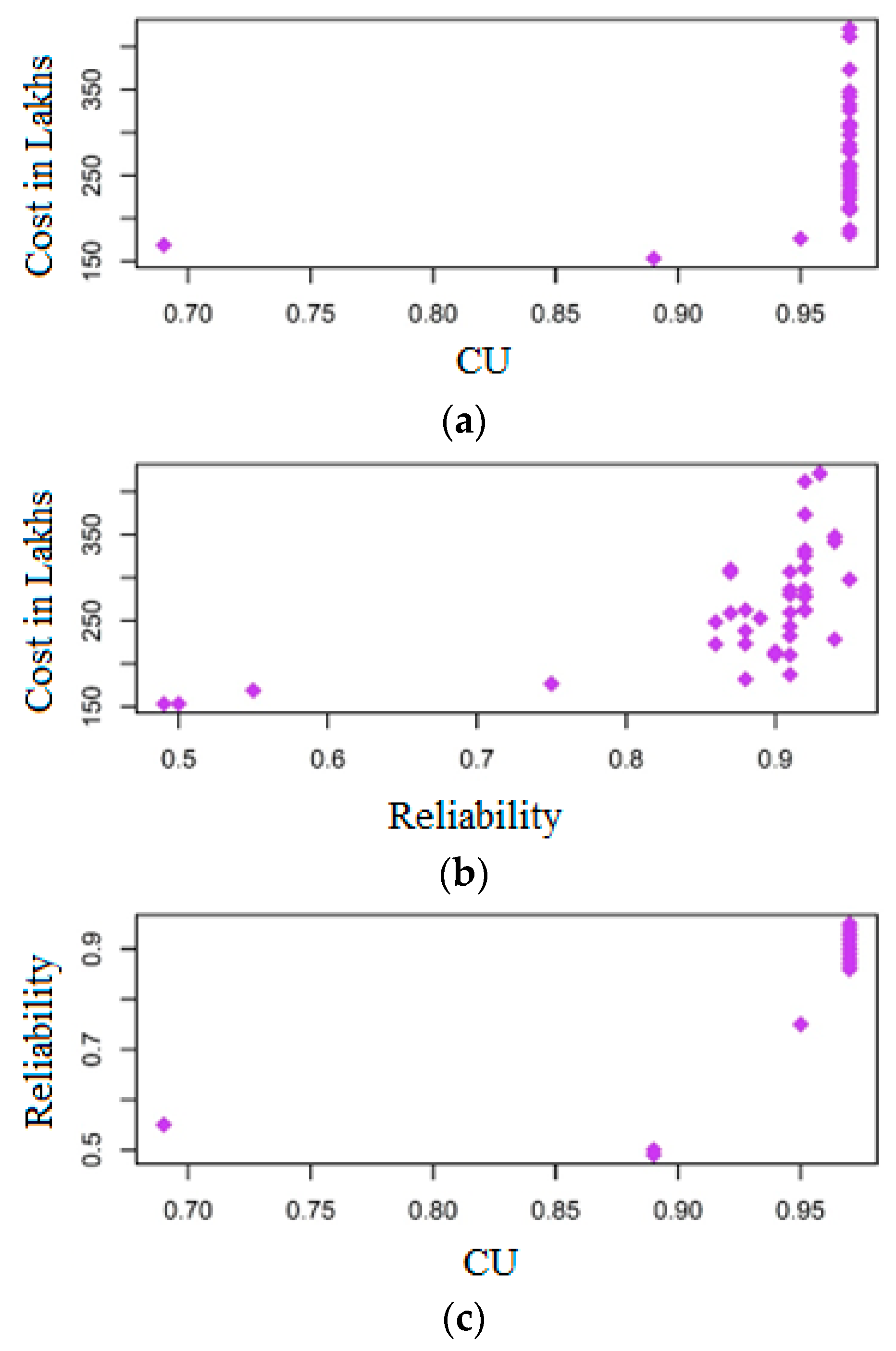
3.2. Multidimensional Pareto Analysis

The results obtained from the multidimensional Pareto analysis using the naive Pareto dominance algorithm are given in Figure 5. The blue and red dots represent the non-dominated solutions, whereas the red dots only represent the final selected solutions which are obtained using the above-mentioned algorithm. The analysis will help decision-makers choose a suitable solution set among the feasible solutions obtained with the multi-objective optimization. The Pareto front list obtained after the analysis includes all the non-dominated solutions, representing the optimal trade-offs between the conflicting objectives.

4. Conclusions

• The approach accelerates the optimization of intermittent water distribution networks, considering into account factors such as equity, reliability, and cost. Enhancing equity has a significant influence on the overall reliability of the networks. Hence, conducting a comprehensive analysis that considers both aspects are crucial to understanding the mutual impact they have on each other.
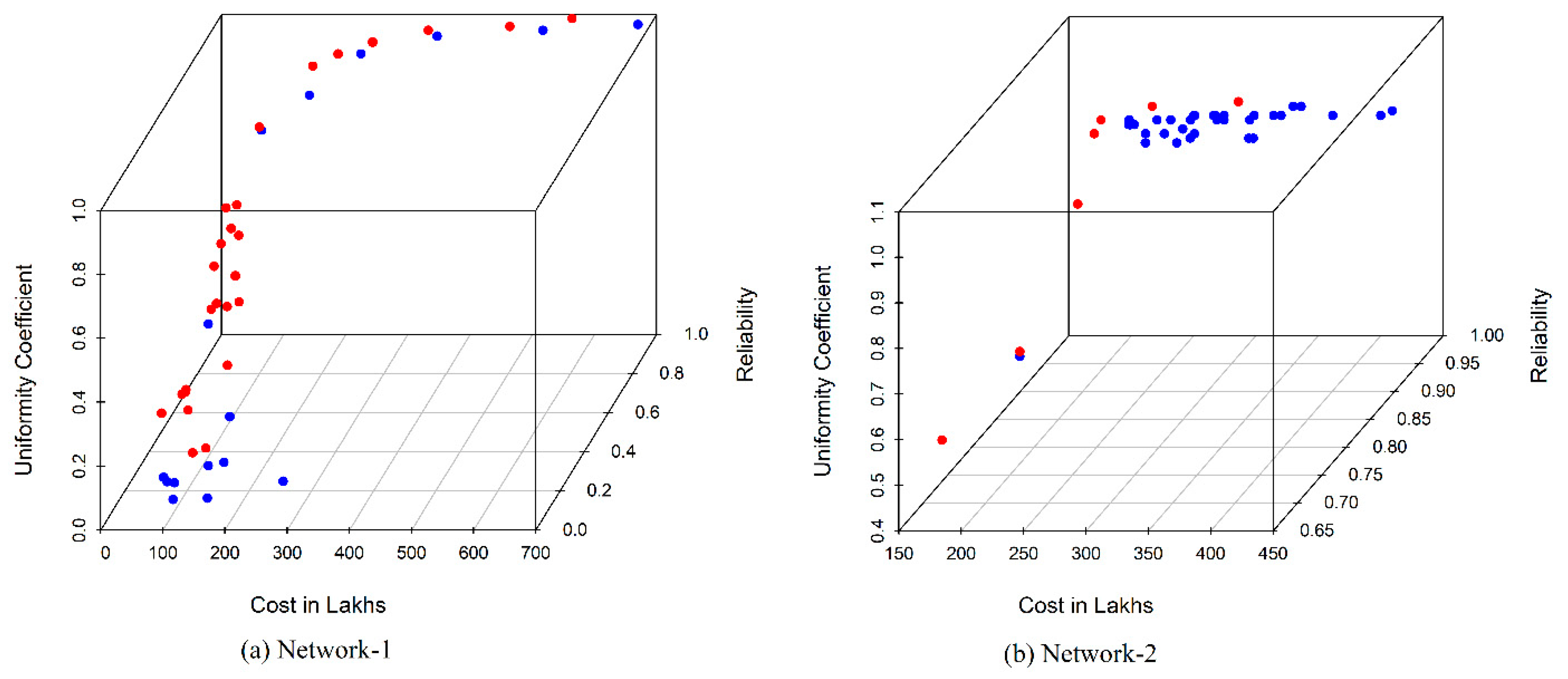
• Two indices, network resilience ($I_n$) and uniformity coefficient ($CU$), are taken as the performance indicators that improve the network reliability and equity in the distribution networks considered in the study. The results from the two networks show that increasing network resilience can also increase water supply equity. Optimizing the layout of the networks, especially in the case of large networks, may improve the equity in the water supply, without increasing the cost of the network.
• The application of NSGA-II to the benchmark networks from the literature to optimize the design of WDN is analyzed in the present study. Results show that network resilience can be increased up to 0.9 with minimal cost. As reliability approaches 1, cost of the network increases significantly with a marginal increment of reliability, which is uneconomical for the design.
• It is observed that the CU solution set obtained for the networks indicates increasing equity can be achieved to a certain extent (up to 0.85) with lesser increment in cost. Beyond the CU value of 0.85, the cost of networks increases, which indicates the effort needed in the selection of pipe, pump, and source tank to enhance the equity in supply with minimal cost.
• Overall, the present study considered equity and reliability as major factors for the design of WDNs along with cost, and results obtained from the application of NSGA-II conclude that equity and reliability of the networks are enhanced simultaneously to a reasonable extent with minimal cost.
• A multidimensional Pareto analysis carried out in the present study benefits the decision-makers to identify non-dominated solutions out of the Pareto front.