Application of Simple Crested Weirs to Control Outflows from Tiles Drainage
Abstract
:1. Introduction
1.1. Instrumental Methods to Measure Flow from Controlled Tile Drainages
1.2. Commonly Used V-Notch Weir Equations
- Qideal is the discharge (m3∙s−1);
- is the angle of the notch (°);
- is the gravitational acceleration (m∙s−2);
- is the height of water above the crest (m).
- QVnotch is the flow discharge (m3∙s−1);
- Cd is the discharge coefficient (-).
- QVnotch is the flow discharge (m3∙s−1);
- C is the discharge coefficient (-);
- h is the depth of water (head) behind the weir (m);
- k is the head correction factor (m).
- QVnotch is the flow discharge (m3∙s−1);
- h1e = h1 + kh (m);
- h1 is the high of water above the crest (m);
- kh is the head correction factor (0.001 m).
- QVnotch is the flow rate (m3∙s−1);
- is the height of water above the crest (m).
- QVnotch is the flow rate (m3∙s−1);
- is the height of water above the crest (m).
- H is the head over the weir measured [m];
- a and b are coefficients determined experimentally.
- (a)
- with a 90° notch (also known as Thomson weir) and flow formula:
- (b)
- with a half 90° notch (53°8’) and flow formula:
- (c)
- with a quarter 90° notch (9 = 28°4’) and flow formula:
2. Materials and Methods
2.1. Experimental Setup and Flow Measurement
- H is the water table level (m3∙s−1);
- ph is the hydrostatic pressure (kPa);
- patm is the atmospheric pressure (kPa);
- is the gravitational acceleration (m∙s−2);
- is the height of water above the crest (m);
- ρ is the liquid density (kg∙m−3);
- ×100 is the conversion factor resulting from the conversion of units;
- +2 is the correction for the logger, determining its position relative to the bottom of the well (cm).
2.2. Developing the Empirical Flow Equation
2.3. Comparison between Actual and Theoretical Discharges
- QVnotch is the flow rate (L∙s−1);
- is the height of water above the crest (cm).
- QVnotch is the flow rate (dm3∙min−1);
- is the high of water above the crest (cm).
- QVnotch is the flow rate (dm3∙min−1);
- is the height of water above the crest (cm).
3. Results and Discussion
3.1. Empirical Flow Equations with Regression Analysis
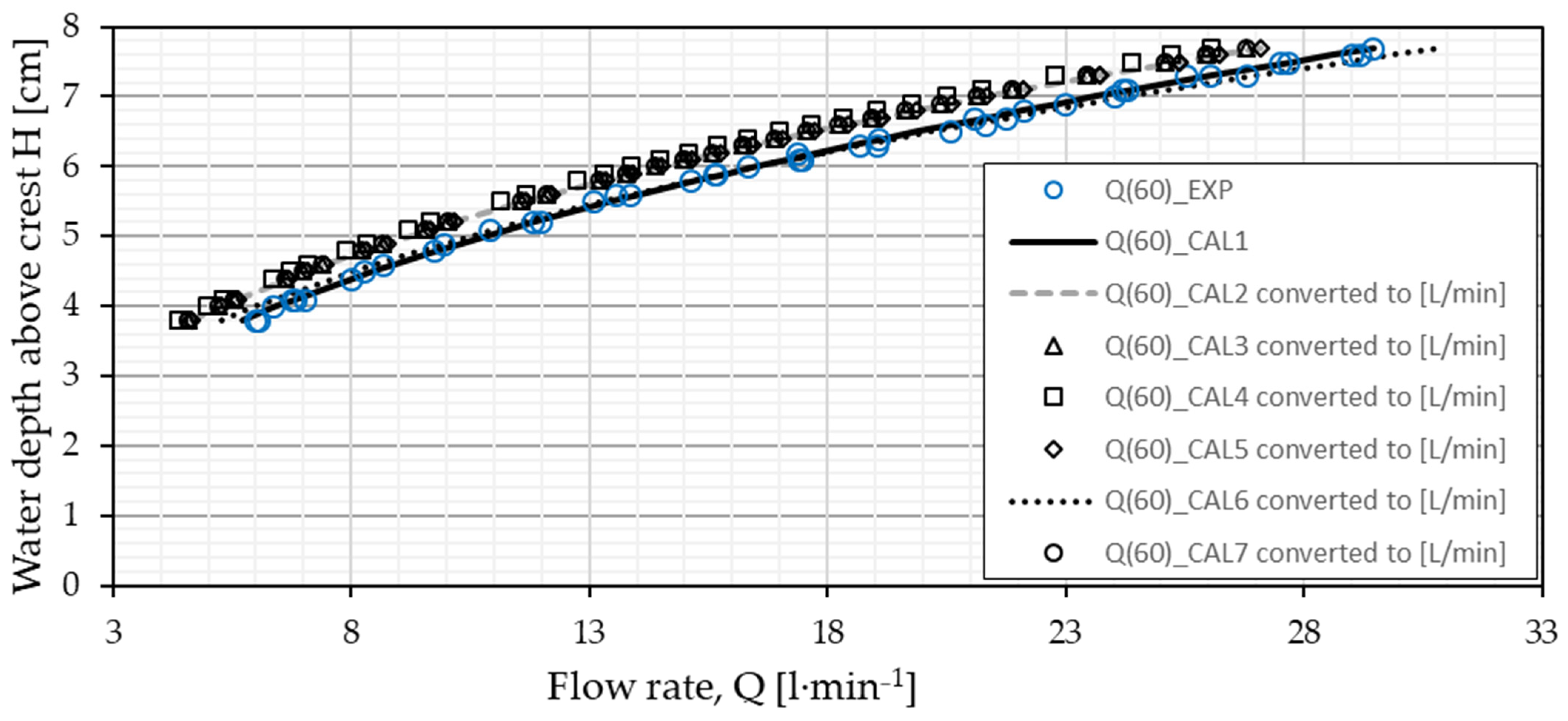
3.2. Comparison with Previously Reported V-Notch Weirs
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fowler, D.; Coyle, M.; Skiba, U.; Sutton, M.A.; Cape, J.N.; Reis, S.; Voss, M. The global nitrogen cycle in the twenty-first century. Philos. Trans. R. Soc. B Biol. Sci. 2013, 368, 20130164. [Google Scholar] [CrossRef] [PubMed]
- Galloway, J.N.; Townsend, A.R.; Erisman, J.W.; Bekunda, M.; Cai, Z.; Freney, J.R.; Sutton, M.A. Transformation of the nitrogen cycle: Recent trends, questions, and potential solutions. Science 2008, 320, 889–892. [Google Scholar] [CrossRef]
- Smith, V.H.; Tilman, G.D.; Nekola, J.C. Eutrophication: Impacts of excess nutrient inputs on freshwater, marine, and terrestrial ecosystems. Environ. Pollut. 1999, 100, 179–196. [Google Scholar] [CrossRef] [PubMed]
- Bissoli, R. Water Framework Directive 2000/60/EC. La Qual. Delle Acque Di Superf. 2008, 9–12. [Google Scholar]
- Carstensen, M.V.; Hashemi, F.; Hoffmann, C.C.; Zak, D.; Audet, J.; Kronvang, B. Efficiency of mitigation measures targeting nutrient losses from agricultural drainage systems: A review. AMBIO 2020, 49, 1820–1837. [Google Scholar] [CrossRef]
- Tournebize, J.; Chaumont, C.; Mander, Ü. Implications for constructed wetlands to mitigate nitrate and pesticide pollution in agricultural drained watersheds. Ecol. Eng. 2017, 103, 415–425. [Google Scholar] [CrossRef]
- Frankenberger, J.; Kladivko, E.; Sands, G.; Jaynes, D.; Fausey, N.; Helmers, M.; Cooke, R.; Strock, J.; Nelson, K.; Brown, L. Questions and Answers about the Drainage Water Management in the Midwest; Purdue Extension Publication (WQ–44): West Lafayette, IN, USA, 2006. [Google Scholar]
- Ale, S.; Bowling, L.C.; Owens, P.R.; Brouder, S.M.; Frankenberger, J.R. Development and application of a distributed modeling approach to assess the watershed-scale impact of drainage water management. Agric. Water Manag. 2012, 107, 23–33. [Google Scholar] [CrossRef]
- King, K.W.; Fausey, N.R.; Williams, M.R. Effect of subsurface drainage on streamflow in an agricultural headwater watershed. J. Hydrol. 2014, 519, 438–445. [Google Scholar] [CrossRef]
- Macrae, M.L.; English, M.C.; Schiff, S.L.; Stone, M. Intra-annual variability in the contribution of tile drains to basin discharge and phosphorus export in a first-order agricultural catchment. Agric. Water Manag. 2007, 92, 171–182. [Google Scholar] [CrossRef]
- Culley, J.L.B.; Bolton, E.F. Suspended Solids and Phosphorus Loads from a Clay Soil: II. Watershed Study; American Society of Agronomy, Crop Science Society of America, and Soil Science Society of America: Madison, WI, USA, 1983; Volume 12, pp. 498–503. [Google Scholar] [CrossRef]
- Xue, Y.; David, M.B.; Gentry, L.E.; Kovacic, D.A. Kinetics and Modeling of Dissolved Phosphorus Export from a Tile-Drained Agricultural Watershed; American Society of Agronomy, Crop Science Society of America, and Soil Science Society of America: Madison, WI, USA, 1998; Volume 27, pp. 917–922. [Google Scholar] [CrossRef]
- Edwards, I.J.; Jackon, W.D.; Fleming, P.M. Tipping bucket gauges for measuring run-off from experimental plots. Agric. Meteorol. 1974, 13, 189–201. [Google Scholar] [CrossRef]
- Lalonde, V.; Madramootoo, C.A.; Trenholm, L.; Broughton, R.S. Effects of controlled drainage on nitrate concentrations in subsurface drain discharge. Agric. Water Manag. 1996, 29, 187–199. [Google Scholar] [CrossRef]
- Wesström, I.; Messing, I.; Linner, H.; Lindström, J. Controlled drainage—Effects on drain outflow and water quality. Agric. Water Manag. 2001, 47, 85–100. [Google Scholar] [CrossRef]
- Wesström, I.; Joel, A.; Messing, I. Controlled drainage and subirrigation–A water management option to reduce non-point source pollution from agricultural land. Agric. Ecosyst. Environ. 2014, 198, 74–82. [Google Scholar] [CrossRef]
- Tait, R.; Madramootoo, C.A.; Enright, P. An instrumented, field-scale research facility for drainage and water quality studies. Comput. Electron. Agric. 1995, 12, 131–145. [Google Scholar] [CrossRef]
- Williams, M.R.; King, K.W.; Fausey, N.R. Drainage water management effects on tile discharge and water quality. Agric. Water Manag. 2015, 148, 43–51. [Google Scholar] [CrossRef]
- Ford, W.; King, K.; Williams, M.; Williams, J.; Fausey, N. Sensitivity analysis of the Agricultural Policy/Environmental eXtender (APEX) for phosphorus loads in tile-drained landscapes. J. Environ. Qual. 2015, 44, 1099–1110. [Google Scholar] [CrossRef]
- Nazari, S.; Ford, W.I.; King, K.W. Impact of flow pathway and source water connectivity on subsurface sediment and particulate phosphorus dynamics in tile-drained agroecosystems. Agric. Water Manag. 2022, 269, 107641. [Google Scholar] [CrossRef]
- Walkowiak, D.K. ISCO Open Channel Flow Measurement Handbook, 6th ed.; Teledyne ISCO, Incl.: Lincoln, NE, USA, 2008; pp. 132–142. ISBN 0-9622757-3-5. [Google Scholar]
- Szejba, D.; Bajkowski, S. Determination of tile drain discharge under variable hydraulic conditions. Water 2019, 11, 120. [Google Scholar] [CrossRef]
- Bajkowski, S.; Szejba, D. Adapter for Measuring Water Flow in Pipes. Patent Number PL396437-A1, 21 April 2015. [Google Scholar]
- Saadat, S.; Bowling, L.; Frankenberger, J.; Brooks, K. Effects of controlled drainage on water table recession rate. Trans. ASABE 2017, 60, 813. [Google Scholar] [CrossRef]
- Kolavani, F.L.; Bijankhan, M.; Di Stefano, C.; Ferro, V.; Mazdeh, A.M. Flow measurement using circular portable flume. Flow Meas. Instrum. 2018, 62, 76–83. [Google Scholar] [CrossRef]
- Bosch, D.D.; Potter, T.L.; Truman, C.C.; Bednarz, C.W.; Strickland, T.C. Surface runoff and lateral subsurface flow as a response to conservation tillage and soil-water conditions. Trans. ASAE 2005, 48, 2137–2144. [Google Scholar] [CrossRef]
- Allred, B.J.; Brown, L.C.; Fausey, N.R.; Cooper, R.L.; Clevenger, W.B.; Prill, G.L.; Czartoski, B.J. Water table management to enhance crop yields in a wetland reservoir subirrigation system. Appl. Eng. Agric. 2003, 19, 407. [Google Scholar] [CrossRef]
- Bos, M.G.; Repogle, J.; Clemmens, A.J. Flow Measuring Flumes for Open Channel Systems; Wiley-Interscience: New York, NY, USA, 1984; ISBN 0-471-80637-4. [Google Scholar]
- Bahceci, I.; Çakir, R.; Nacar, A.; Bahceci, P. Estimating the effect of controlled drainage on soil salinity and irrigation efficiency in the Harran Plain using SaltMod. Turk. J. Agric. For. 2008, 32, 101–109. [Google Scholar]
- Brooks, K. Measurement of Drain Flow, Soil Moisture, and Water Table to Assess Drainage Water Management. Master’s Thesis, Purdue University, Agricultural and Biological Engineering Department, West Lafayette, IN, USA, 2003. [Google Scholar]
- Sojka, M.; Kozłowski, M.; Kęsicka, B.; Wróżyński, R.; Stasik, R.; Napierała, M.; Jaskuła, J.; Liberacki, D. The Effect of Climate Change on Controlled Drainage Effectiveness in the Context of Groundwater Dynamics, Surface, and Drainage Outflows. Central-Western Poland Case Study. Agronomy 2020, 10, 625. [Google Scholar] [CrossRef]
- Liu, W.; Maxwell, B.; Birgand, F.; Youssef, M.; Chescheir, G.; Tian, S. Multipoint high-frequency sampling system to gain deeper insights on the fate of nitrate in artificially drained fields. J. Irrig. Drain. Eng. 2020, 146, 06019012. [Google Scholar] [CrossRef]
- Sunohara, M.D.; Gottschall, N.; Craiovan, E.; Wilkes, G.; Topp, E.; Frey, S.K.; Lapen, D.R. Controlling tile drainage during the growing season in Eastern Canada to reduce nitrogen, phosphorus, and bacteria loading to surface water. Agric. Water Manag. 2016, 178, 159–170. [Google Scholar] [CrossRef]
- Liu, Y.; Youssef, M.A.; Chescheir, G.M.; Appelboom, T.W.; Poole, C.A.; Arellano, C.; Skaggs, R.W. Effect of controlled drainage on nitrogen fate and transport for a subsurface drained grass field receiving liquid swine lagoon effluent. Agric. Water Manag. 2019, 217, 440–451. [Google Scholar] [CrossRef]
- Satchithanantham, S.; Ranjan, R.S.; Bullock, P. Protecting water quality using controlled drainage as an agricultural BMP for potato production. Trans. Asabe 2014, 57, 815–826. [Google Scholar] [CrossRef]
- Satchithanantham, S.; Ranjan, R.S.; Shewfelt, B. Effect of water table management and irrigation on potato yield. Trans. ASABE 2012, 55, 2175–2184. [Google Scholar] [CrossRef]
- Povilaitis, A.; Rudzianskaite, A.; Miseviciene, S.; Gasiunas, V.; Miseckaite, O.; Živatkauskiene, I. Efficiency of drainage practices for improving water quality in Lithuania. Trans. ASABE 2018, 61, 179–196. [Google Scholar] [CrossRef]
- Christianson, L.E.; Christianson, R.D.; Lipka, A.E.; Bailey, S.; Chandrasoma, J.; McCoy, C.; Cooke, R.A. Calibration of stainless steel-edged V-notch weir stop logs for water level control structures. Appl. Eng. Agric. 2019, 35, 745–749. [Google Scholar] [CrossRef]
- Shokrana, M.S.B.; Ghane, E. An empirical V-notch weir equation and standard procedure to accurately estimate drainage discharge. Appl. Eng. Agric. 2021, 37, 1097–1105. [Google Scholar] [CrossRef]
- Helmers, M.; Christianson, R.; Brenneman, G.; Lockett, D.; Pederson, C. Water table, drainage, and yield response to drainage water management in southeast Iowa. J. Soil Water Conserv. 2012, 67, 495–501. [Google Scholar] [CrossRef]
- Herschy, R. General purpose flow measurement equations for flumes and thin plate weirs. Flow Meas. Instrum. 1995, 6, 283–293. [Google Scholar] [CrossRef]
- Popek, Z.; Bajkowski, S.; Siwicki, P.; Urbański, J. Laboratory Tests of New Groundwater Table Level Regulators in Subsurface Drainage Systems. Water 2021, 13, 631. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics, 7th ed.; McGraw-Hill Companies, Inc.: New York, NY, USA, 2011; Available online: http://ftp.demec.ufpr.br/disciplinas/TM240/Marchi/Bibliografia/White_2011_7ed_Fluid-Mechanics.pdf (accessed on 3 August 2023)ISBN 978-0-07-352934-9.
- El Hattab, M.H.; Mijic, A.; Vernon, D. Optimised Triangular Weir Design for Assessing the Full-Scale Performance of Green Infrastructure. Water 2019, 11, 773. [Google Scholar] [CrossRef]
- Cording, A.; Hurley, S.; Whitney, D. Monitoring methods and designs for evaluating bioretention performance. J. Environ. Eng. 2017, 143, 05017006. [Google Scholar] [CrossRef]
- Kulin, G.; Compton, P.R. A Guide to Methods and Standards for the Measurement of Water Flow; US Department of Commerce, National Bureau of Standards: Washington, DC, USA, 1975; Volume 13. [Google Scholar]
- El-Ansary, M.Y.; Awad, M.A.; Nassar, A.A.; Farag, A.A. Calibration of three common flow measurement devices for open channels. Misr J. Agric. Eng. 2010, 27, 151–169. [Google Scholar] [CrossRef]
- USGS. Measurement and computation of streamflow. In Computation of Discharge (Geological Survey Water-Supply Paper 2175); USGS: Washington, DC, USA, 1982; Volume 2. [Google Scholar]
- ISO 1438:2017; Hydrometry—Open Channel Flow Measurement Using Thin-Plate Weirs. International Organization for Standardization (ISO): London, UK, 2017.
- Jaynes, D.B.; Isenhart, T.M. Reconnecting tile drainage to riparian buffer hydrology for enhanced nitrate removal. J. Environ. Qual. 2014, 43, 631–638. [Google Scholar] [CrossRef]
- Shen, J. Discharge Characteristics of Triangular-Notch Thin-Plate Weirs; (No. 1617); United States Department of the Interior, Geological Survey: Reston, VI, USA, 1981. [Google Scholar]
- Prakash, M.S.; Shivapur, A.V. Generalized head-discharge equation for flow over sharp-crested inclined inverted V-notch weir. J. Irrig. Drain. Eng. 2004, 130, 325–330. [Google Scholar] [CrossRef]
- Herschy, R.W. Flow through weirs, flumes, orifices, sluices and pipes. In Hydrology and Lakes. Encyclopedia of Earth Science; Springer: Dordrecht, The Netherlands, 1998. [Google Scholar] [CrossRef]
- Bos, M.G. (Ed.) Discharge Measurement Structures, 3rd ed.; ILRI Publication 20: Wageningen, The Netherlands, 1989; p. 320. [Google Scholar]
- Brassington, R. Field Hydrogeology; John Wiley & Sons: Hoboken, NJ, USA, 2023. [Google Scholar]
- Eli, R.N. V-notch weir calibration using new parameters. J. Hydraul. Eng. 1986, 112, 321–325. [Google Scholar] [CrossRef]
- Lenz, A.T. Viscosity and surface tension effects on V-notch weir coefficients. Trans. Am. Soc. Civ. Eng. 1943, 108, 759–782. [Google Scholar] [CrossRef]


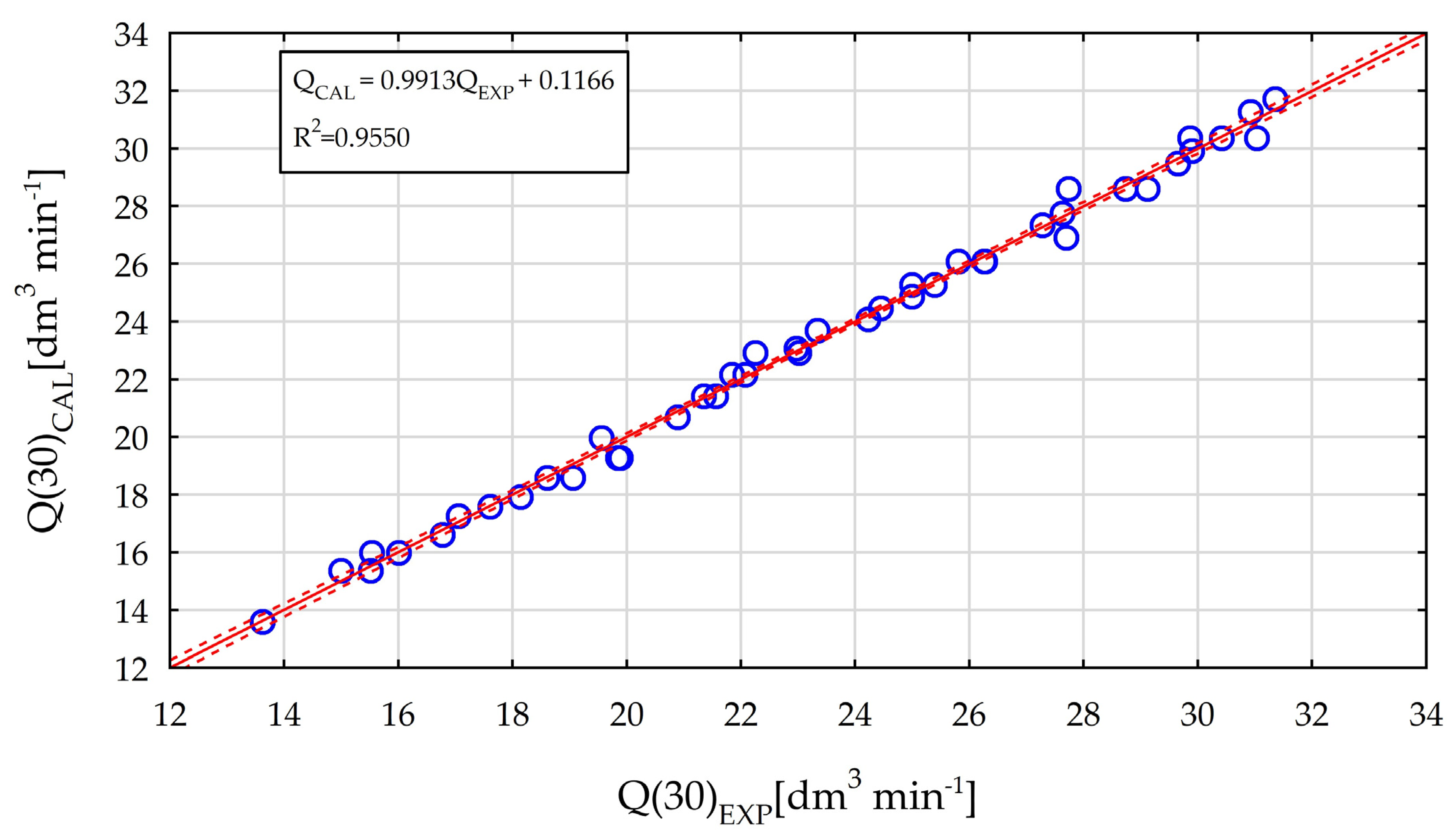
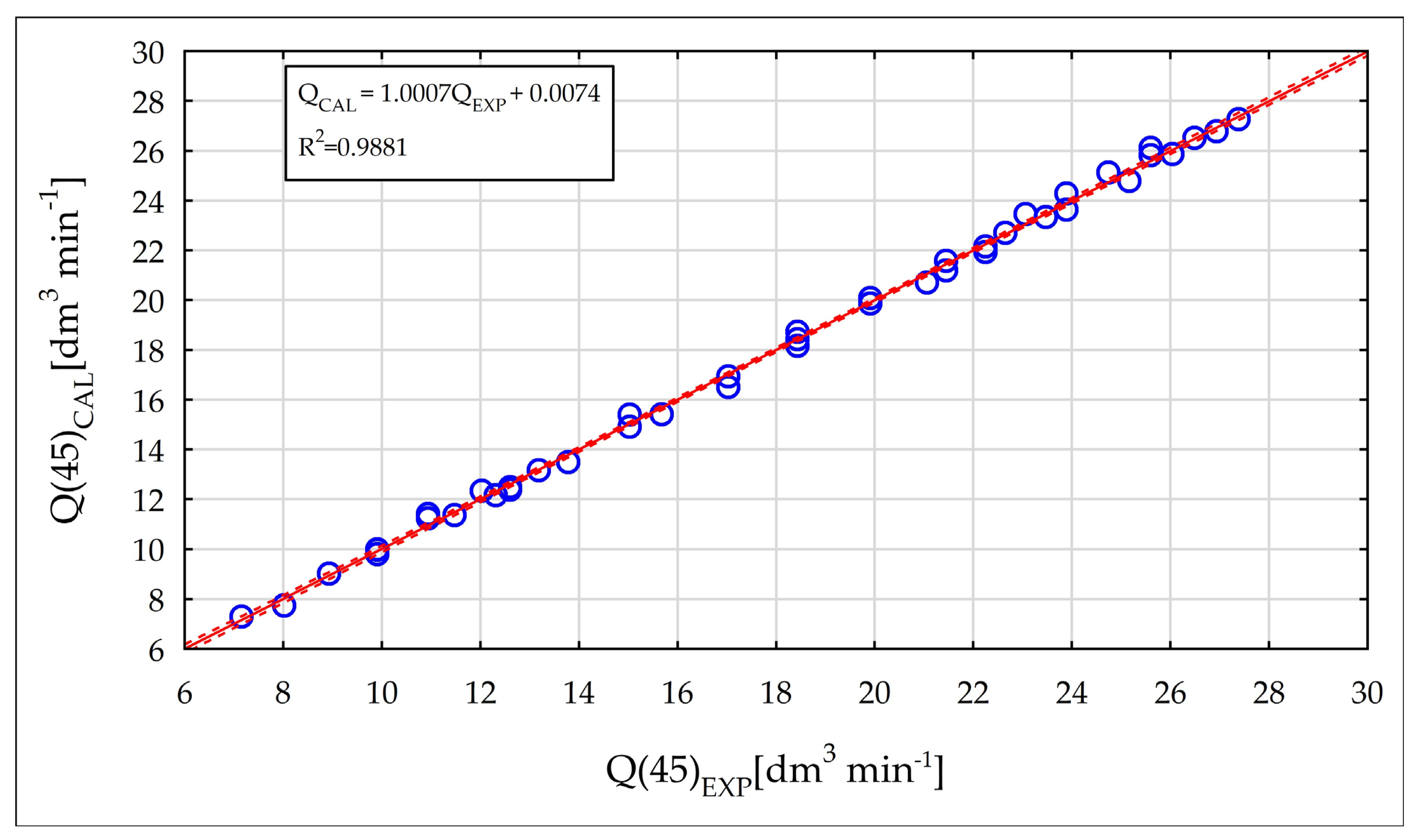

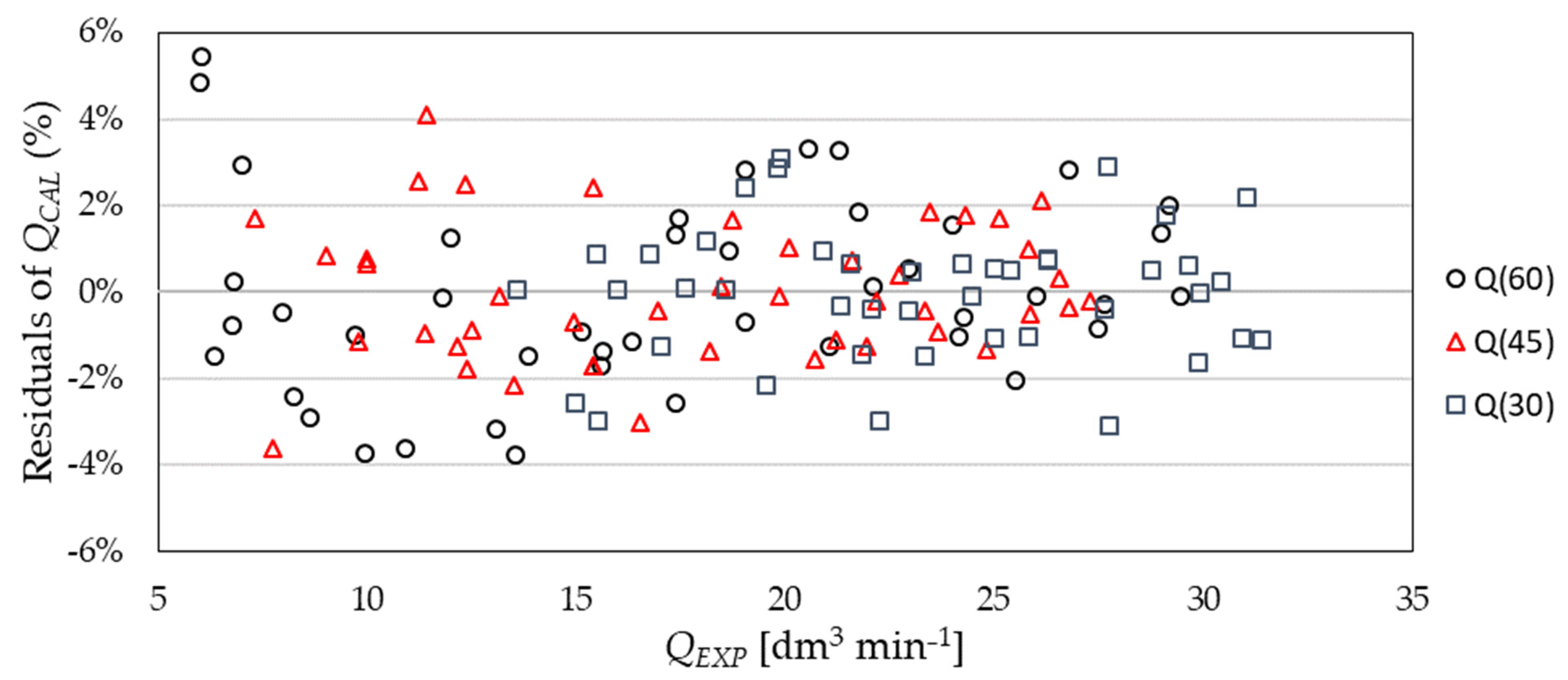

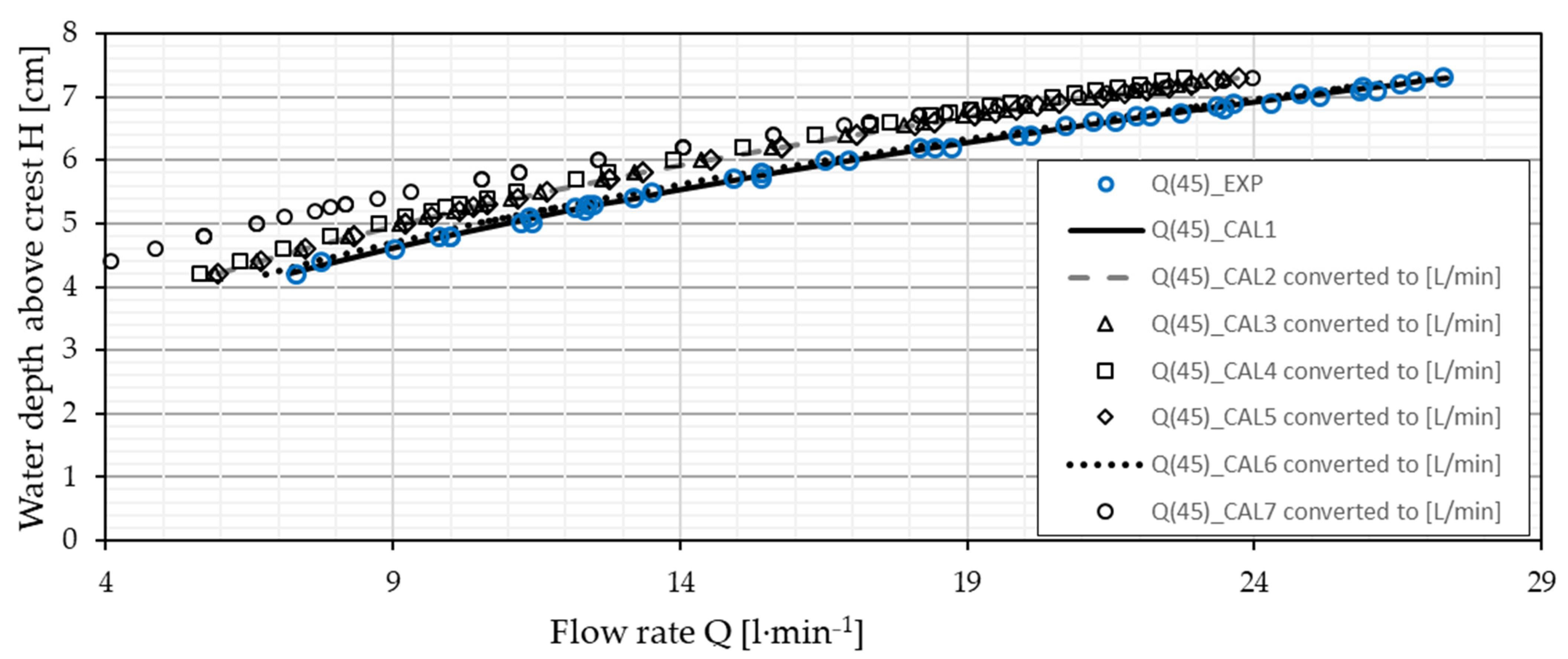
| Angle of slope | Calculated Equation (QCAL1) | R-Squared (R2) | Root Mean Square Error (RMSE) | Height of Water above the Crest H (cm) (Range) | Range of Flow Measurement Q (L∙min−1) |
|---|---|---|---|---|---|
| 30° | Q = 0.298H2.266 | 0.9955 | 0.346 | 5.4–7.8 (2.45) | 13.60–31.38 |
| 45° | Q = 0.224H2.418 | 0.9981 | 0.255 | 4.2–7.3 (3.10) | 7.31–27.29 |
| 60° | Q = 0.256H2.325 | 0.9980 | 0.332 | 3.8–7.7 (3.90) | 6.00–29.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Napierała, M. Application of Simple Crested Weirs to Control Outflows from Tiles Drainage. Water 2023, 15, 3248. https://doi.org/10.3390/w15183248
Napierała M. Application of Simple Crested Weirs to Control Outflows from Tiles Drainage. Water. 2023; 15(18):3248. https://doi.org/10.3390/w15183248
Chicago/Turabian StyleNapierała, Michał. 2023. "Application of Simple Crested Weirs to Control Outflows from Tiles Drainage" Water 15, no. 18: 3248. https://doi.org/10.3390/w15183248
APA StyleNapierała, M. (2023). Application of Simple Crested Weirs to Control Outflows from Tiles Drainage. Water, 15(18), 3248. https://doi.org/10.3390/w15183248






