Multi-Objective Optimal Scheduling of Generalized Water Resources Based on an Inter-Basin Water Transfer Project
Abstract
:1. Introduction
2. Methods
2.1. Optimal Allocation Model of Generalized Water Resources
2.1.1. Objective Functions
- (1)
- Minimizing total water shortage
- (2)
- Minimizing water loss in water resources systems
2.1.2. Constraints
- (1)
- Water balance constraint
- (2)
- Soil water depth constraint
- (3)
- Lake storage constraint
- (4)
- Pumping capacity constraint
- (5)
- Sluice capacity constraint
- (6)
- Minimizing water transfer level
- (7)
- Non-negative constraint
2.2. Improved Multi-Objective Optimization Algorithm
2.2.1. Dynamic Discovery Probability
2.2.2. Mechanisms of Population Variation
2.3. Evaluation of Non-Inferior Solutions for Scheduling of Water Resources
2.3.1. Index System for Evaluating Water Resources Optimization Allocation
2.3.2. Index Weight Quantification and Evaluation Methods
2.3.3. Determination of the Optimal Allocation Schemes of Water Resources
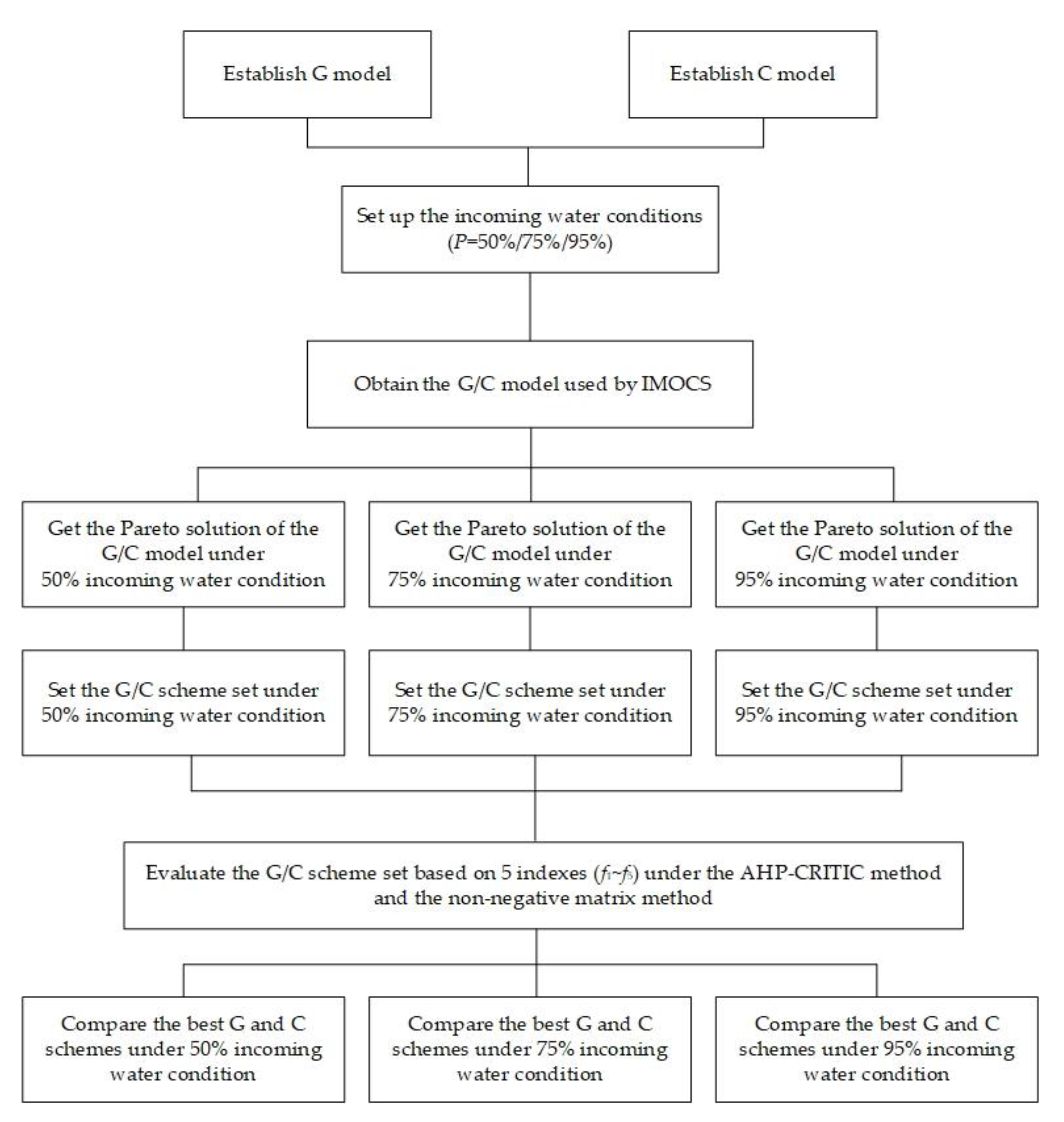
2.3.4. Evaluation of the Optimal Allocation Schemes and Technology Road Map of the Study
3. Study Area and Data
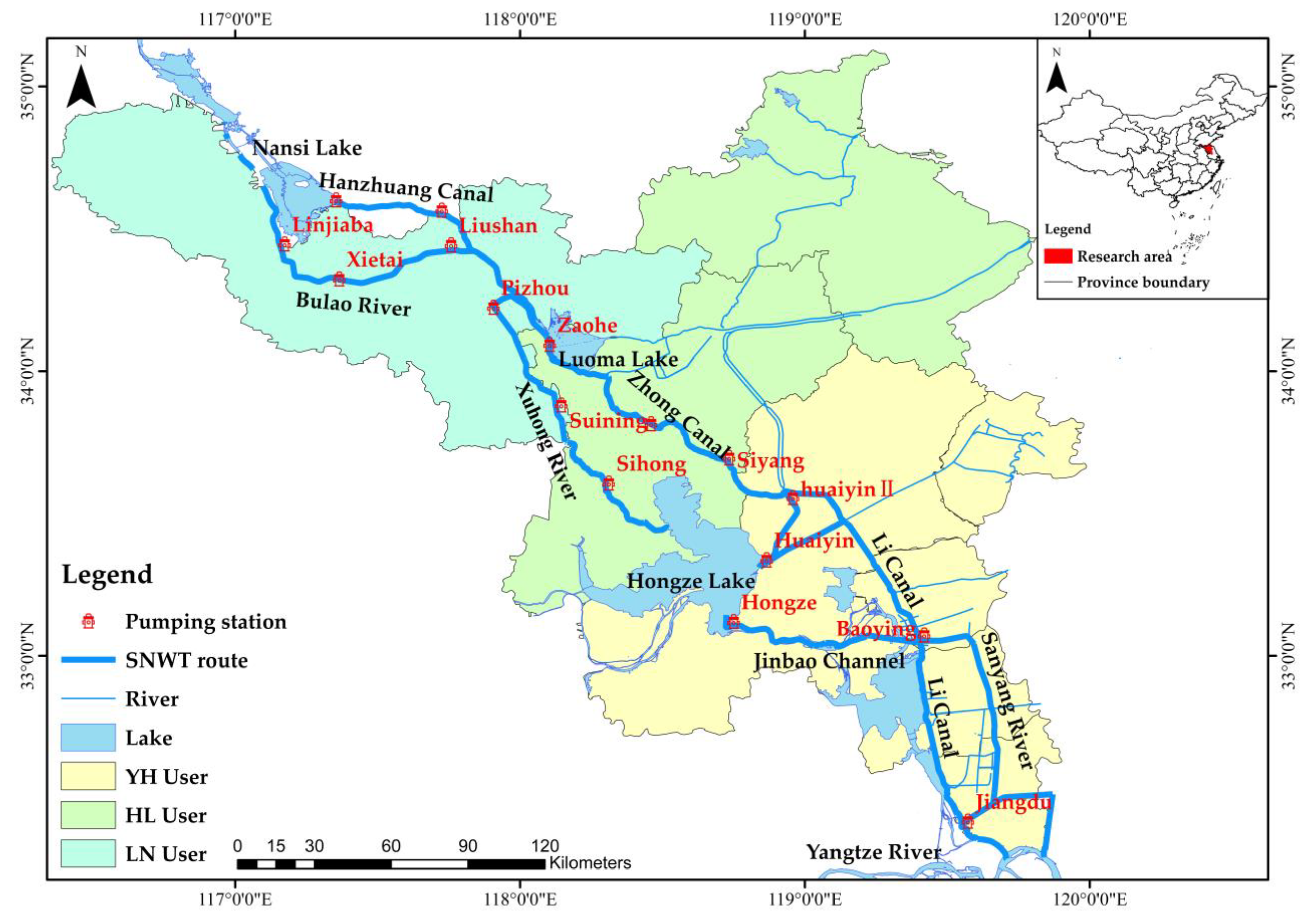
3.1. Study Area
3.2. Data
3.2.1. Surface Water
3.2.2. Soil Water
4. Results
4.1. Multi-Objective Optimal Allocation of Water Resources Based on the J-SNWT Project
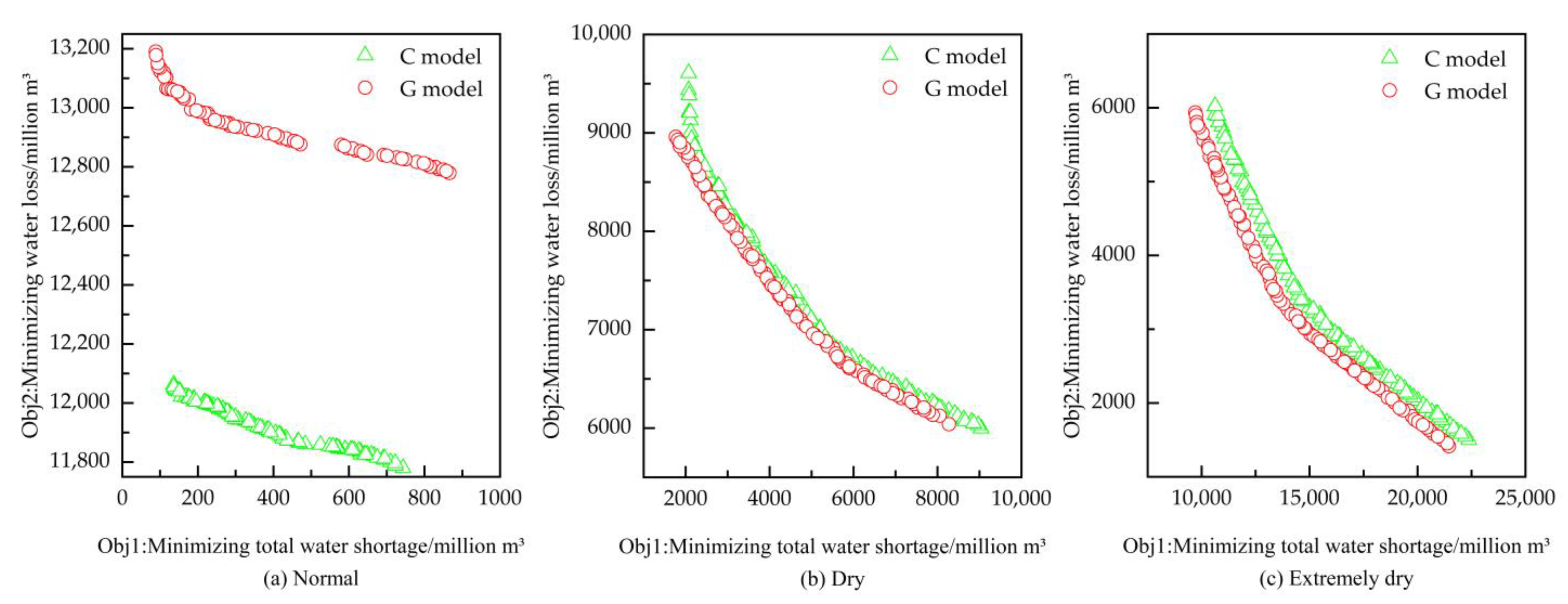
4.1.1. Pareto Frontiers of the G and C Models
4.1.2. Pareto Optimal Solutions Box Diagram of G and C Models
4.2. Optimal Allocation Scheme Set of Water Resources Based on the J-SNWT Project
4.2.1. Filtering Pareto Optimal Solutions of G (C) Model
4.2.2. Quantification of the Index Weights for the G (C) Scheme Set
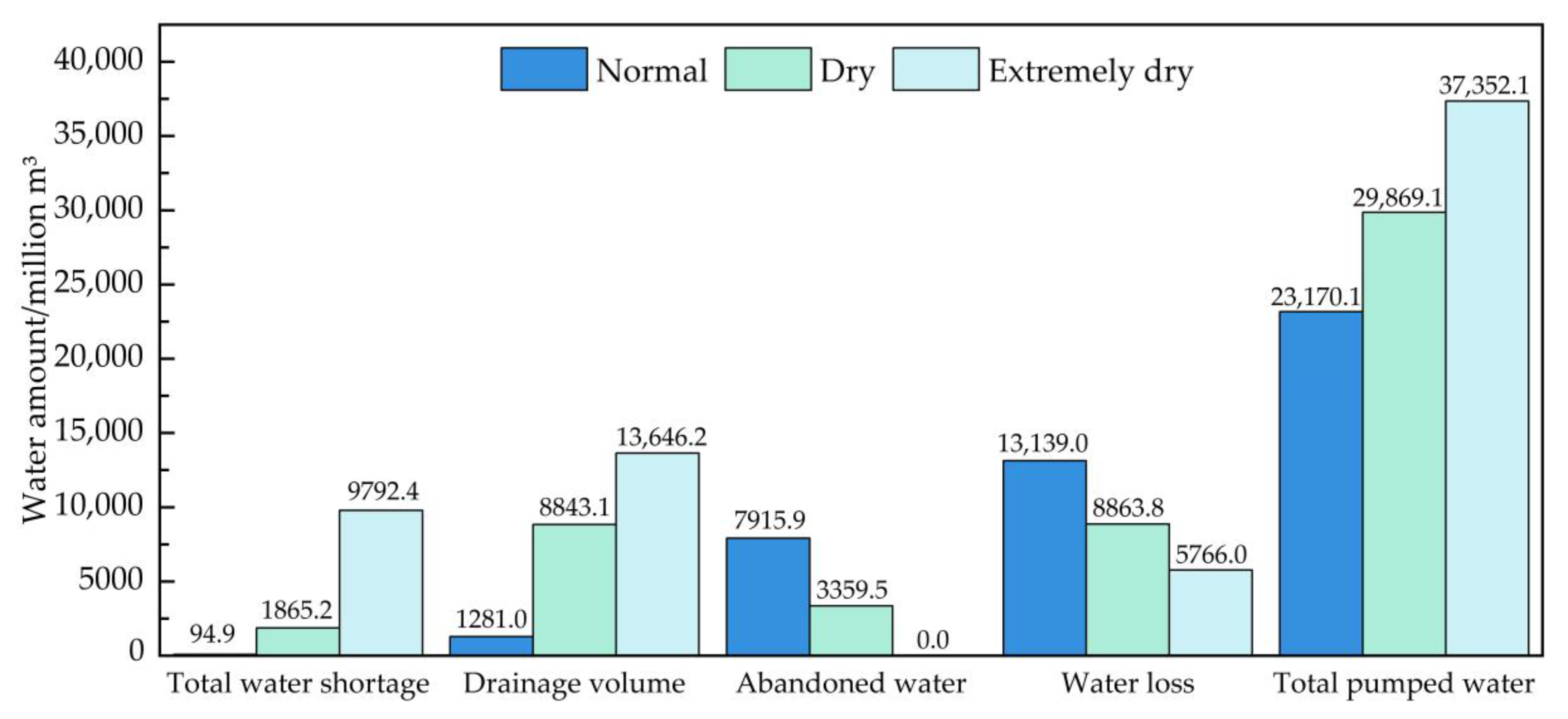
4.3. The Best Scheme of Water Resources Based on the J-SNWT Project
4.3.1. Evaluation of the Best G Scheme
4.3.2. Evaluation of the Best C Scheme
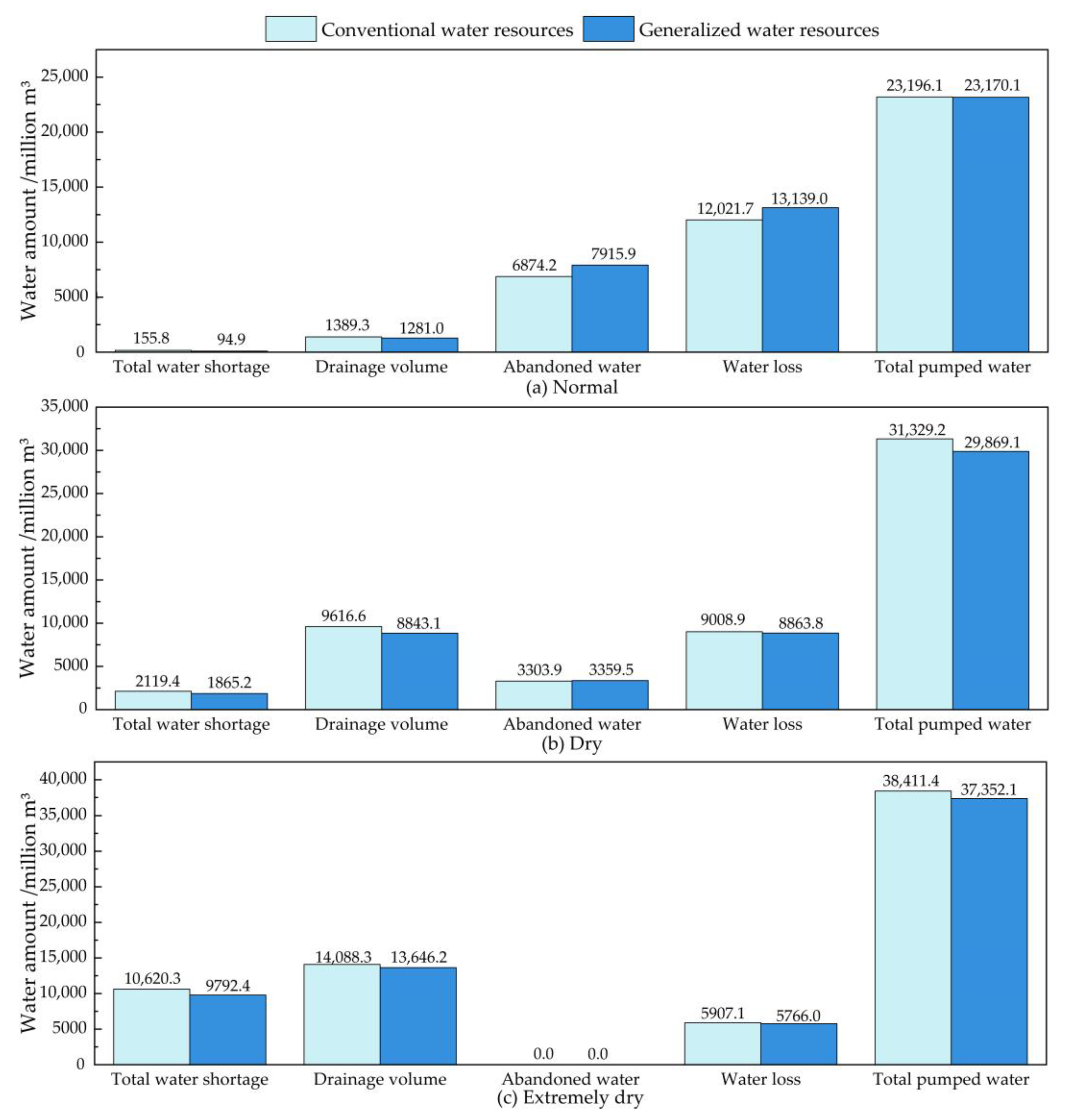
4.3.3. Comparison of the Best G Scheme and the Best C Scheme
5. Discussion
5.1. Effectiveness and Excellence of the G Model
5.2. Optimized Allocation Scheme of J-SNWT
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| IBWT | Inter-basin water transfer projects. |
| SNWT | The South–North Water Transfer project. |
| J-SNWT | The Jiangsu section of the South-to-North Water Transfer. |
| G model | Optimal allocation model of generalized water resources. |
| C model | Optimal allocation model of conventional water resources. |
| IMOCS | Improved multi-objective cuckoo optimization algorithm. |
| AHP | Analytic hierarchy process. |
| CRITIC | Criteria importance through inter-criteria correlation. |
| G scheme | The optimal allocation scheme of generalized water resources. |
| C scheme | The optimal allocation scheme of conventional water resources. |
References
- Cosgrove, W.J.; Loucks, D.P. Water management: Current and future challenges and research directions. Water Resour. Res. 2015, 51, 4823–4839. [Google Scholar] [CrossRef]
- Dong, C.; Schoups, G.; Giesen, N.V.D. Scenario development for water resource planning and management: A review. Technol. Forecast. Soc. Chang. 2013, 80, 749–761. [Google Scholar] [CrossRef]
- Li, Y.; Cui, Q.; Li, C.; Wang, X.; Cai, Y.; Cui, G.; Yang, Z. An improved multi-objective optimization model for supporting reservoir operation of China’s South-to-North Water Diversion Project. Sci. Total Environ. 2017, 575, 970–981. [Google Scholar] [CrossRef]
- Akron, A.; Ghermandi, A.; Dayan, T.; Hershkovitz, Y. Interbasin water transfer for the rehabilitation of a transboundary Mediterranean stream: An economic analysis. J. Environ. Manag. 2017, 202, 276–286. [Google Scholar] [CrossRef]
- Dou, X. China’s inter-basin water management in the context of regional water shortage. Sustain. Water Resour. Manag. 2018, 4, 519–526. [Google Scholar] [CrossRef]
- Yan, B.; Chen, L. Coincidence probability of precipitation for the middle route of South-to-North water transfer project in China. J. Hydrol. 2013, 499, 19–26. [Google Scholar] [CrossRef]
- Lopez, J.C. Interbasin water transfers and the size of regions: An economic geography example. Water Resour. Econ. 2018, 21, 40–54. [Google Scholar] [CrossRef]
- Pohlner, H. Institutional change and the political economy of water megaprojects: China’s south-north water transfer. Glob. Environ. Chang. 2016, 38, 205–216. [Google Scholar] [CrossRef]
- Davijani, M.H.; Banihabib, M.E.; Anvar, A.N.; Hashemi, S.R. Optimization model for the allocation of water resources based on the maximization of employment in the agriculture and industry sectors. J. Hydrol. 2016, 533, 430–438. [Google Scholar] [CrossRef]
- Tian, J.; Guo, S.; Deng, L.; Yin, J.; Pan, Z.; He, S.; Li, Q. Adaptive optimal allocation of water resources response to future water availability and water demand in the Han River basin, China. Sci. Rep. 2021, 11, 7879. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, G.; Peng, Y.; Tang, G.; Liang, G. A Negotiation-Based Multi-Objective, Multi-Party Decision-Making Model for Inter-Basin Water Transfer Scheme Optimization. Water Resour. Manag. 2012, 26, 4029–4038. [Google Scholar] [CrossRef]
- Guan, H.; Chen, L.; Huang, S.; Yan, C.; Wang, Y. Multi-objective optimal allocation of water resources based on ‘three red lines’ in Qinzhou, China. Water Policy 2020, 22, 541–560. [Google Scholar] [CrossRef]
- Zhuang, X.; Li, Y.; Huang, G.; Zeng, X. An inexact joint-probabilistic programming method for risk assessment in water resources allocation. Stoch. Environ. Res. Risk Assess. 2015, 29, 1287–1301. [Google Scholar] [CrossRef]
- Jafarzadegan, K.; Abed-Elmdoust, A.; Kerachian, R. A stochastic model for optimal operation of inter-basin water allocation systems: A case study. Stoch. Environ. Res. Risk Assess. 2014, 28, 1343–1358. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S.; Hong, X.; Chang, F. Systematic impact assessment on inter-basin water transfer projects of the Hanjiang River Basin in China. J. Hydrol. 2017, 553, 584–595. [Google Scholar] [CrossRef]
- Zeng, C.; Ma, J.; Cao, M.; Xu, C.; Qi, W.; Wang, L. Modeling Water Allocation under Extreme Drought of South-to-North Water Diversion Project in Jiangsu Province, Eastern China. Front. Earth Sci. 2020, 8, 541664. [Google Scholar] [CrossRef]
- Gonzalez, J.F.; Decker, C.A.; Hall, J.W. A Linear Programming Approach to Water Allocation during a Drought. Water 2018, 10, 363. [Google Scholar] [CrossRef]
- Ahmad, A.; El-Shafie, A.; Razali, S.F.M.; Mohamad, Z.S. Reservoir optimization in water resources: A review. Water Resour. Manag. 2014, 28, 3391–3405. [Google Scholar] [CrossRef]
- Eum, H.; Kim, Y.; Palmer, N.R. Optimal Drought Management Using Sampling Stochastic Dynamic Programming with a Hedging Rule. J. Water Resour. Plan. Manag. 2011, 137, 113–122. [Google Scholar] [CrossRef]
- Tian, J.; Liu, D.; Guo, S.; Pan, Z.; Hong, X. Impacts of Inter-Basin Water Transfer Projects on Optimal Water Resources Allocation in the Hanjiang River Basin, China. Sustainability 2019, 11, 2044. [Google Scholar] [CrossRef]
- Wu, X.; Wang, Z. Multi-objective optimal allocation of regional water resources based on slime mould algorithm. J. Supercomput. 2022, 78, 18288–18317. [Google Scholar] [CrossRef]
- Wang, Z.; Tian, J.; Feng, K. Optimal allocation of regional water resources based on simulated annealing particle swarm optimization algorithm. Energy Rep. 2022, 8, 9119–9126. [Google Scholar] [CrossRef]
- Li, Y.; Han, Y.; Liu, B.; Li, B.; Li, H.; Du, X.; Wang, Q.; Wang, X.; Zhu, X. Construction and application of a refined model for the optimal allocation of water resources-Taking Guantao County, China as an example. Ecol. Indic. 2023, 146, 109929. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Engineering optimization by cuckoo search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar]
- Yang, X.; Deb, S. Multi-objective cuckoo search for design optimization. Comput. Oper. Res. 2013, 40, 1616–1624. [Google Scholar] [CrossRef]
- Sun, S.; Fu, G.; Bao, C.; Fang, C. Identifying hydro-climatic and socioeconomic forces of water scarcity through structural decomposition analysis: A case study of Beijing city. Sci. Total Environ. 2019, 687, 590–600. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, S.; Qin, H.; Shao, J.; Lu, J.; Bing, J.; Wang, X.; Zhang, R. Multi-objective optimal water supply scheduling model for an inter-basin water transfer system: The South-to-North Water Diversion Middle Route Project, China. Water Supply 2020, 20, 550–564. [Google Scholar] [CrossRef]
- Fang, G.; Guo, Y.; Wen, X.; Fu, X.; Lei, X.; Tian, Y.; Wang, T. Multi-Objective Differential Evolution-Chaos Shuffled Frog Leaping Algorithm for Water Resources System Optimization. Water Resour. Manag. 2018, 32, 3835–3852. [Google Scholar] [CrossRef]
- Guo, Y.; Tian, X.; Fang, G.; Xu, Y. Many-objective optimization with improved shuffled frog leaping algorithm for inter-basin water transfers. Adv. Water Resour. 2020, 138, 103531. [Google Scholar] [CrossRef]
- Yan, B.; Jiang, H.; Zou, Y.; Liu, Y.; Mu, R.; Wang, H. An integrated model for optimal water resources allocation under “3 Redlines” water policy of the upper Hanjiang river basin. J. Hydrol. Reg. Stud. 2022, 42, 101167. [Google Scholar] [CrossRef]
- Jing, S.; Xiao, W.; Wang, J.; Zhen, Y.; Wang, W.; Liu, Q.; Zhang, Z.; Hu, C. Evaporation variability and its control factors of Lake Taihu from 1958 to 2017. J. Lake Sci. 2022, 34, 1697–1711, (Chinese with English Abstract). [Google Scholar]
- Ma, Y.; Li, X.; Wilson, M.; Wu, X.; Smith, A.; Wu, J. Water loss by evaporation from China’s South-North Water Transfer Project. Ecol. Eng. 2016, 95, 206–215. [Google Scholar] [CrossRef]
- Pei, Y.; Zhang, J. The Conceptual Framework for Rational Allocation of Water Resources. Resour. Sci. 2006, 4, 166–171, (Chinese with English Abstract). [Google Scholar]
- Veettil, A.V.; Mishra, A.K. Water security assessment using blue and green water footprint concepts. J. Hydrol. 2016, 542, 589–602. [Google Scholar] [CrossRef]
- Wang, H.; You, J. Progress of water resource allocation during the past 30 years in China. J. Hydraul. Eng. 2016, 47, 265–271, (Chinese with English Abstract). [Google Scholar]
- Parhi, P.K.; Mishra, S.K.; Singh, R. A Modification to Kostiakov and Modified Kostiakov Infiltration Models. Water Resour. Manag. 2007, 21, 1973–1989. [Google Scholar] [CrossRef]
- Ming, B.; Huang, Q.; Wang, Y.; Liu, D.; Bai, T. Cascade reservoir operation optimization based-on improved Cuckoo Search. J. Hydraul. Eng. 2015, 46, 341–349, (Chinese with English Abstract). [Google Scholar]
- Mosadeghi, R.; Warnken, J.; Tomlinson, R.; Mirfenderesk, H. Comparison of Fuzzy-AHP and AHP in a spatial multi-criteria decision-making model for urban land-use planning. Comput. Environ. Urban Syst. 2015, 49, 54–65. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R. A novel plithogenic TOPSIS-CRITIC model for sustainable supply chain risk management. J. Clean. Prod. 2020, 247, 119586. [Google Scholar] [CrossRef]
- Li, Y.; Li, Q.; Jiao, S. River health evaluation based on improved analytic hierarchy process, CRITIC method and compound fuzzy matter-element VIKOR model. Chin. J. Ecol. 2022, 41, 822–832. [Google Scholar]
- Xie, Y.; Huang, Q.; Li, X.; Liu, S.; Wang, Y. Method for optimal selection of schemes based on the non-negative matrix factorization principle and its applications. J. Xi’an Univ. Technol. 2017, 33, 138–144, (Chinese with English Abstract). [Google Scholar]
- Tangdamrongsub, N.; Ditmar, P.G.; Steele-Dunne, S.C.; Gunter, B.C.; Sutanudjaja, E.H. Assessing total water storage and identifying flood events over Tonlé Sap basin in Cambodia using GRACE and MODIS satellite observations combined with hydrological models. Remote Sens. Environ. 2016, 181, 162–173. [Google Scholar] [CrossRef]
- GB/T 51051-2014; Code for Water Resources Planning. Planning Publishing House: Beijing, China, 2014.
- Yan, Z.; Sha, J.; Liu, B.; Tian, W.; Lu, J. An Ameliorative Whale Optimization Algorithm for Multi-Objective Optimal Allocation of Water Resources in Handan, China. Water 2020, 10, 87. [Google Scholar] [CrossRef]
- Yu, F.; Fang, G.; Wang, W.; Wu, X.; Wen, X. Optimized dispatching of the lake group system along the South-to-North Water Diversion Route based on the multi-objective genetic algorithm. J. Irrig. Drain. 2016, 35, 78–85, (Chinese with English Abstract). [Google Scholar]
- Wen, X.; Wang, Z.; Fang, G.; Guo, Y.; Zhou, L. Study on optimal operation of Jiangsu section of eastern route of South-to-North Water Diversion Project based on improved multi-objective particle swarm optimization algorithm. J. Water Resour. Water Eng. 2017, 28, 110–116, (Chinese with English Abstract). [Google Scholar]




| Evaluation Criteria | Index |
|---|---|
| Water use efficiency (million m3) | total water shortage (f1) |
| drainage volume (f2) | |
| abandoned water (f3) | |
| water loss (f4) | |
| Water system costs (million m3) | total pumped water (f5) |
| Lake | Dead Water Level (m) | Normal Water Level (m) | July–August | September–November | November–March | April–June | |
|---|---|---|---|---|---|---|---|
| Flood Season | Non-Flood Season | ||||||
| Hongze Lake | 11.3 | 12.5 | 13.5 | 12.0 | 12.0~11.9 | 12.0~12.5 | 12.5~12.0 |
| Luoma Lake | 20.5 | 22.5 | 23 | 22.2~22.1 | 22.1~22.2 | 22.1~23.0 | 23.0~22.5 |
| Nansi Lake | 31.5 | 32.5 | 33 | 31.8 | 31.5~31.9 | 31.9~32.8 | 32.3~31.8 |
| Section | Pumping Station Group | Pumping Station | Capacity (m3/s) |
|---|---|---|---|
| YR-HZ | Drainage volume | Baoying | 100 |
| Jiangdu | 400 | ||
| Into Hongze lake | Hongze | 150 | |
| Huaiyin | 300 | ||
| HZ-LM | Out of Hongze lake | Sihong | 120 |
| Siyang | 230 | ||
| Into Luoma lake | Pizhou | 100 | |
| Zaohe | 175 | ||
| LM-NS | Out of Luoma lake | Taierzhuang | 125 |
| Liushan | 125 | ||
| Into Nansi lake | Hanzhuang | 125 | |
| Linjiaba | 75 |
| Water Source | Conditions | Water Users | |||||
|---|---|---|---|---|---|---|---|
| Hongze Lake | Luoma Lke | Nansi Lake | |||||
| Surface water | Normal | 1971.7~1972.6 | 1975.7~1976.6 | 1988.7~1989.6 | 1971.7~1972.6 | 1975.7~1976.6 | 1988.7~1989.6 |
| Dry | 1958.7~1959.6 | 1969.7~1970.6 | 1967.7~1968.6 | 1958.7~1959.6 | 1969.7~1970.6 | 1967.7~1968.6 | |
| Extremely dry | 1959.7~1960.7 | 1959.7~1960.6 | 1966.7~1967.6 | 1959.7~1960.7 | 1959.7~1960.6 | 1966.7~1967.6 | |
| YR-HZ User | HZ User | HZ-LM User | LM User | LM-NS User | NS User | ||
| Soil water | Normal | 2007.7~2008.6 | 2012.7~2013.6 | 2006.7~2007.6 | 2006.7~2007.6 | 2016.7~2017.6 | 2016.7~2017.7 |
| Dry | 2014.7~2015.6 | 2014.7~2015.6 | 2012.7~2013.6 | 2012.7~2013.6 | 2015.7~2016.6 | 2015.7~2016.6 | |
| Extremely dry | 2004.7~2005.6 | 2019.7~2020.6 | 2011.7~2012.6 | 2011.7~2012.6 | 2011.7~2012.6 | 2011.7~2012.6 | |
| Model | Weights | Normal | Dry | Extremely Dry | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f1 | f2 | f3 | f4 | f5 | f1 | f2 | f3 | f4 | f5 | f1 | f2 | f3 | f4 | f5 | ||
| G model | W1 | 0.18 | 0.15 | 0.15 | 0.36 | 0.16 | 0.21 | 0.10 | 0.21 | 0.34 | 0.14 | 0.24 | 0.16 | 0.18 | 0.30 | 0.12 |
| W2 | 0.52 | 0.14 | 0.11 | 0.11 | 0.11 | 0.45 | 0.15 | 0.14 | 0.12 | 0.15 | 0.47 | 0.13 | 0.13 | 0.13 | 0.13 | |
| W | 0.35 | 0.15 | 0.13 | 0.23 | 0.14 | 0.33 | 0.12 | 0.17 | 0.23 | 0.14 | 0.36 | 0.15 | 0.15 | 0.21 | 0.13 | |
| C model | W1 | 0.18 | 0.15 | 0.15 | 0.36 | 0.16 | 0.21 | 0.10 | 0.21 | 0.34 | 0.14 | 0.24 | 0.16 | 0.18 | 0.30 | 0.12 |
| W2 | 0.40 | 0.17 | 0.14 | 0.16 | 0.13 | 0.51 | 0.13 | 0.13 | 0.11 | 0.12 | 0.50 | 0.12 | 0.13 | 0.13 | 0.12 | |
| W | 0.29 | 0.16 | 0.15 | 0.26 | 0.14 | 0.36 | 0.11 | 0.17 | 0.23 | 0.13 | 0.34 | 0.14 | 0.19 | 0.21 | 0.12 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, H.; Xie, Y.; Liu, S.; Mao, Q.; Shen, T.; Zhang, Q. Multi-Objective Optimal Scheduling of Generalized Water Resources Based on an Inter-Basin Water Transfer Project. Water 2023, 15, 3195. https://doi.org/10.3390/w15183195
Xi H, Xie Y, Liu S, Mao Q, Shen T, Zhang Q. Multi-Objective Optimal Scheduling of Generalized Water Resources Based on an Inter-Basin Water Transfer Project. Water. 2023; 15(18):3195. https://doi.org/10.3390/w15183195
Chicago/Turabian StyleXi, Haichao, Yangyang Xie, Saiyan Liu, Qing Mao, Teng Shen, and Qin Zhang. 2023. "Multi-Objective Optimal Scheduling of Generalized Water Resources Based on an Inter-Basin Water Transfer Project" Water 15, no. 18: 3195. https://doi.org/10.3390/w15183195
APA StyleXi, H., Xie, Y., Liu, S., Mao, Q., Shen, T., & Zhang, Q. (2023). Multi-Objective Optimal Scheduling of Generalized Water Resources Based on an Inter-Basin Water Transfer Project. Water, 15(18), 3195. https://doi.org/10.3390/w15183195








