Combined Physical Process and Deep Learning for Daily Water Level Simulations across Multiple Sites in the Three Gorges Reservoir, China
Abstract
:1. Introduction
2. Materials and Methods
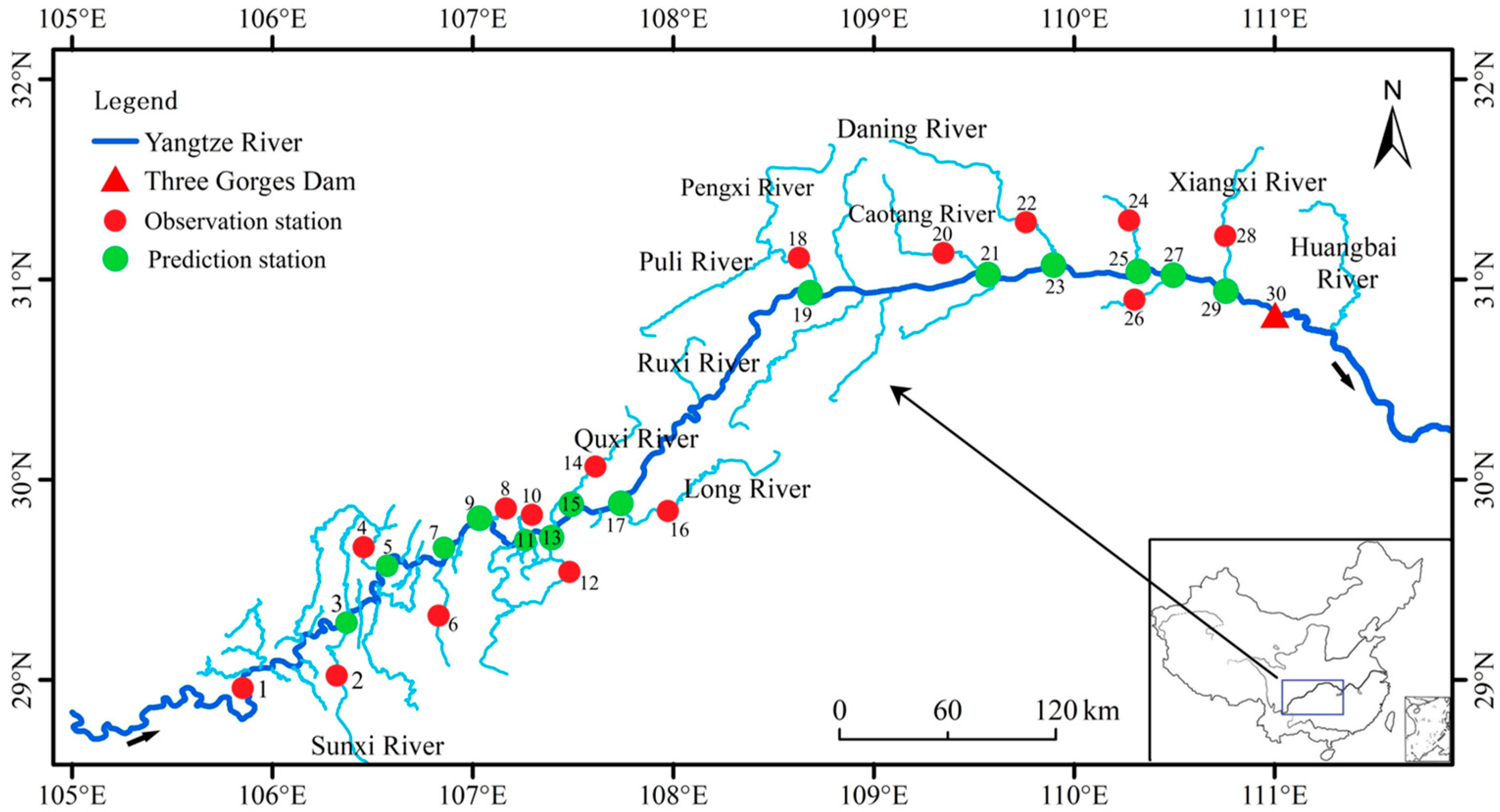
2.1. Study Sites
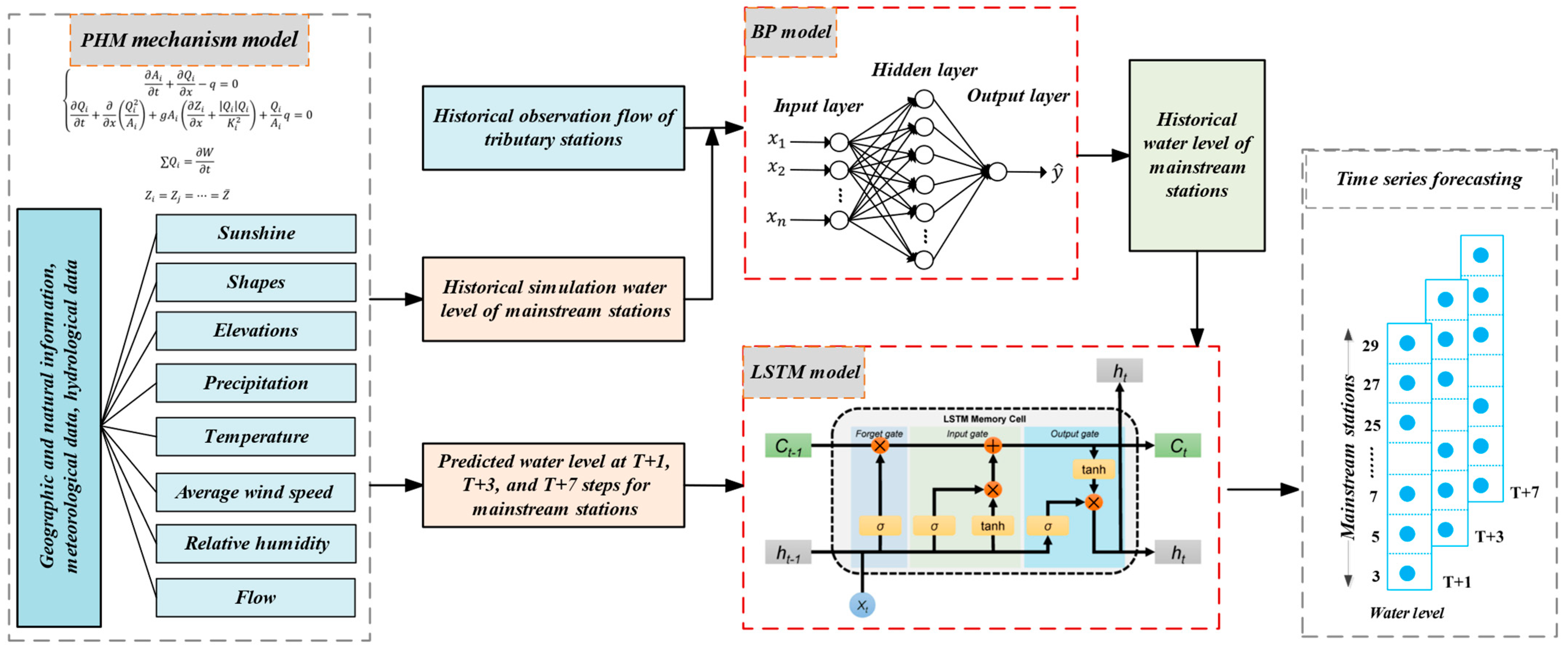
2.2. Physical-Based Hydrological Model
2.3. Deep Learning Model
2.3.1. Back Propagation Neural Network
2.3.2. Long Short-Term Memory
2.4. Comparative Modes
2.4.1. Support Vector Regression
2.4.2. Classification and Regression Tree
2.5. Model Evaluation Index
3. Results and Discussion
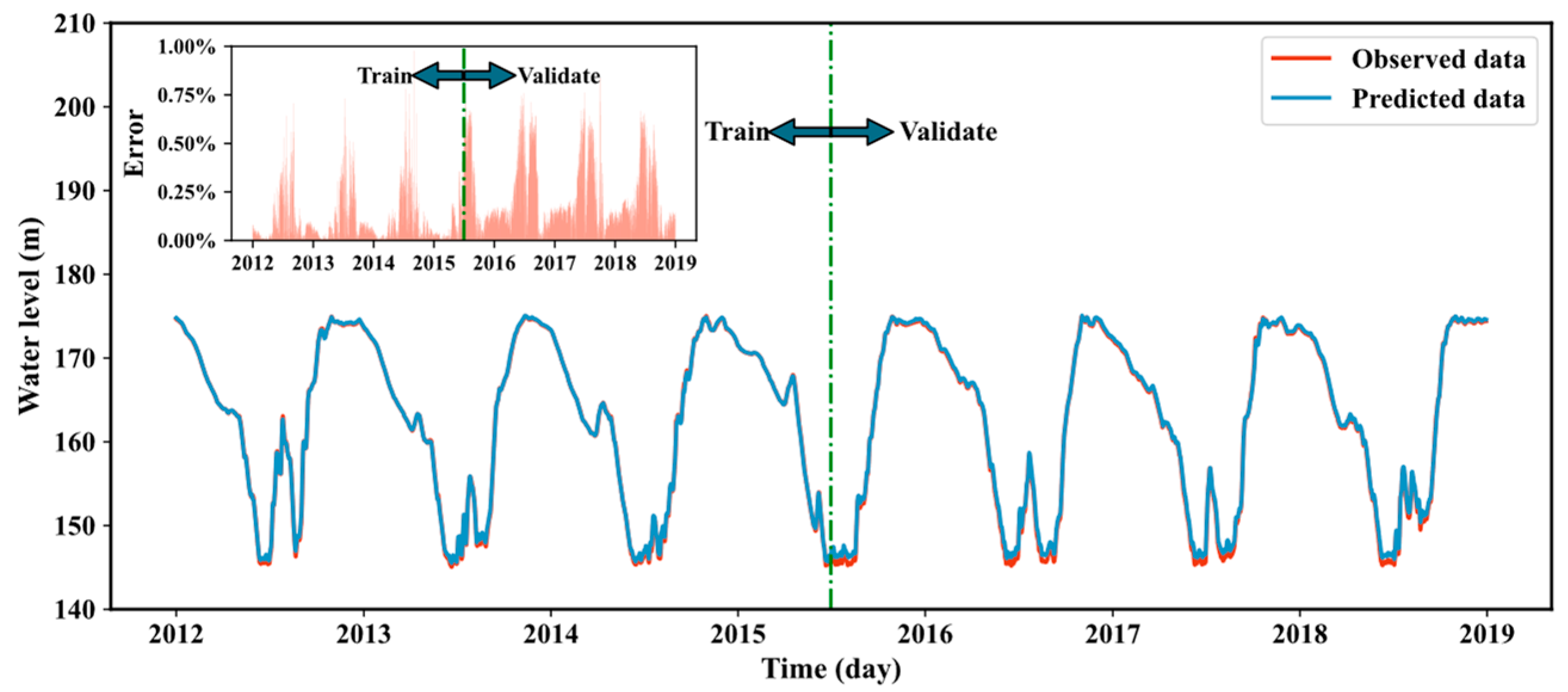
3.1. Building the Connections between Mainstream and Its Tributaries in TGR
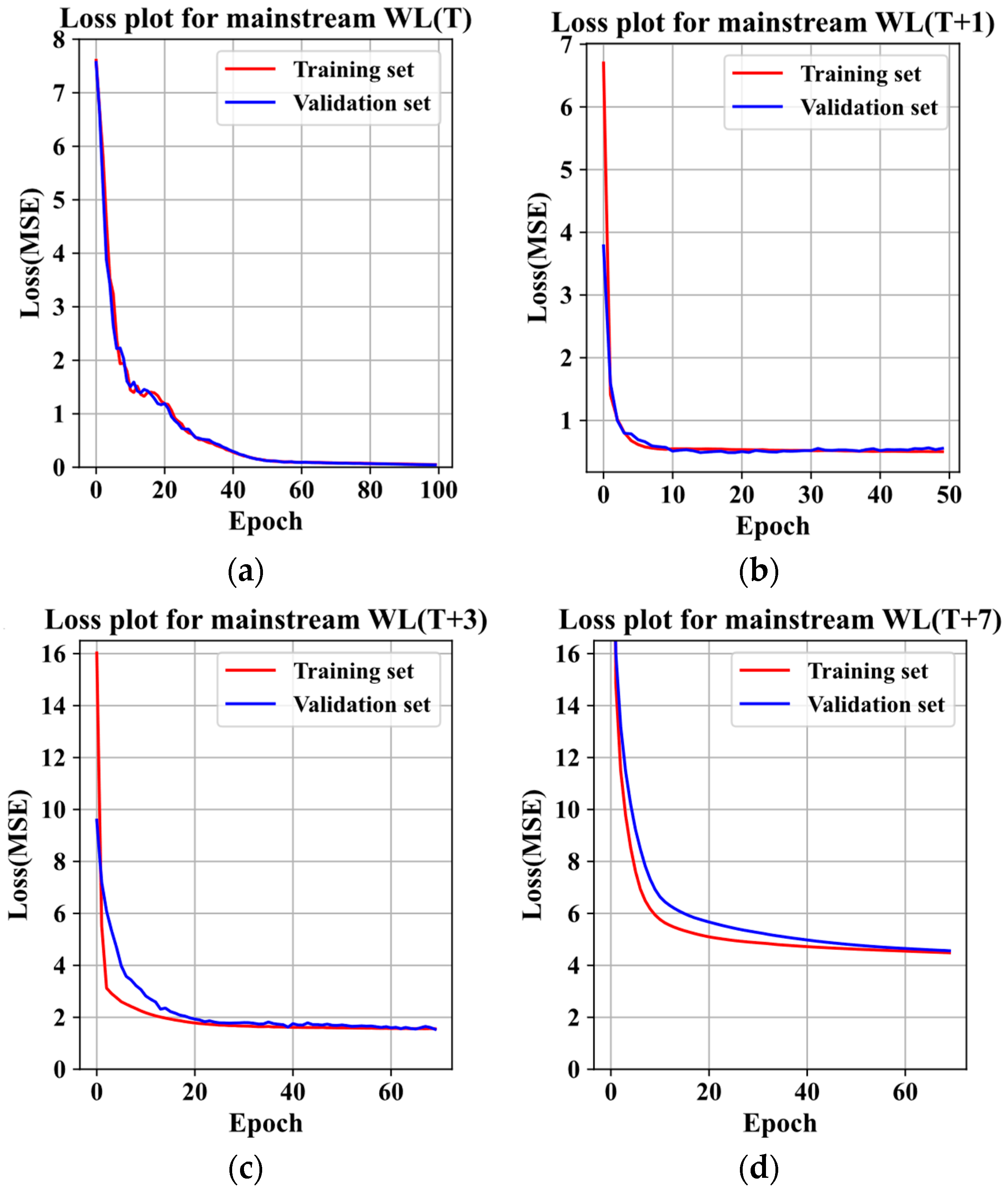
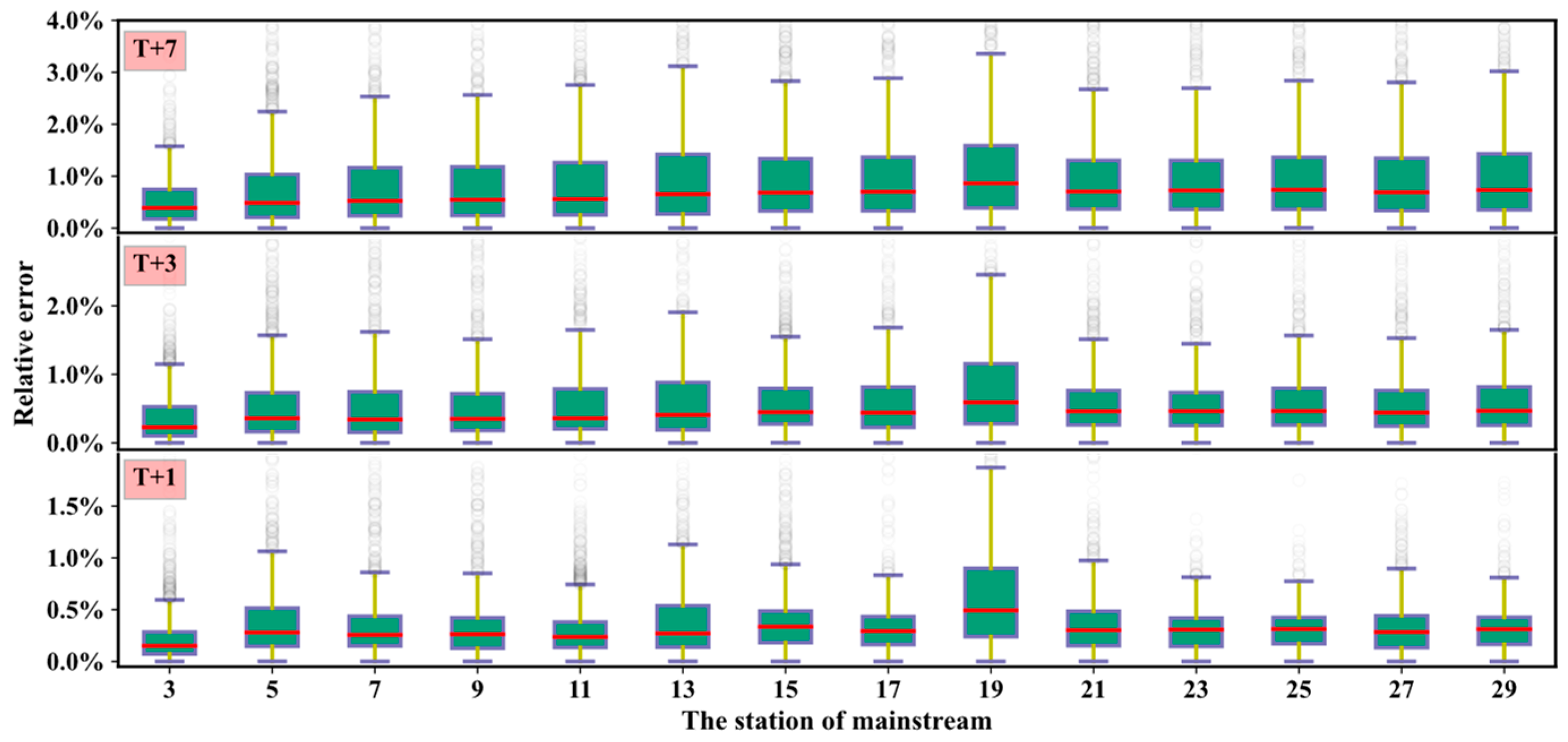
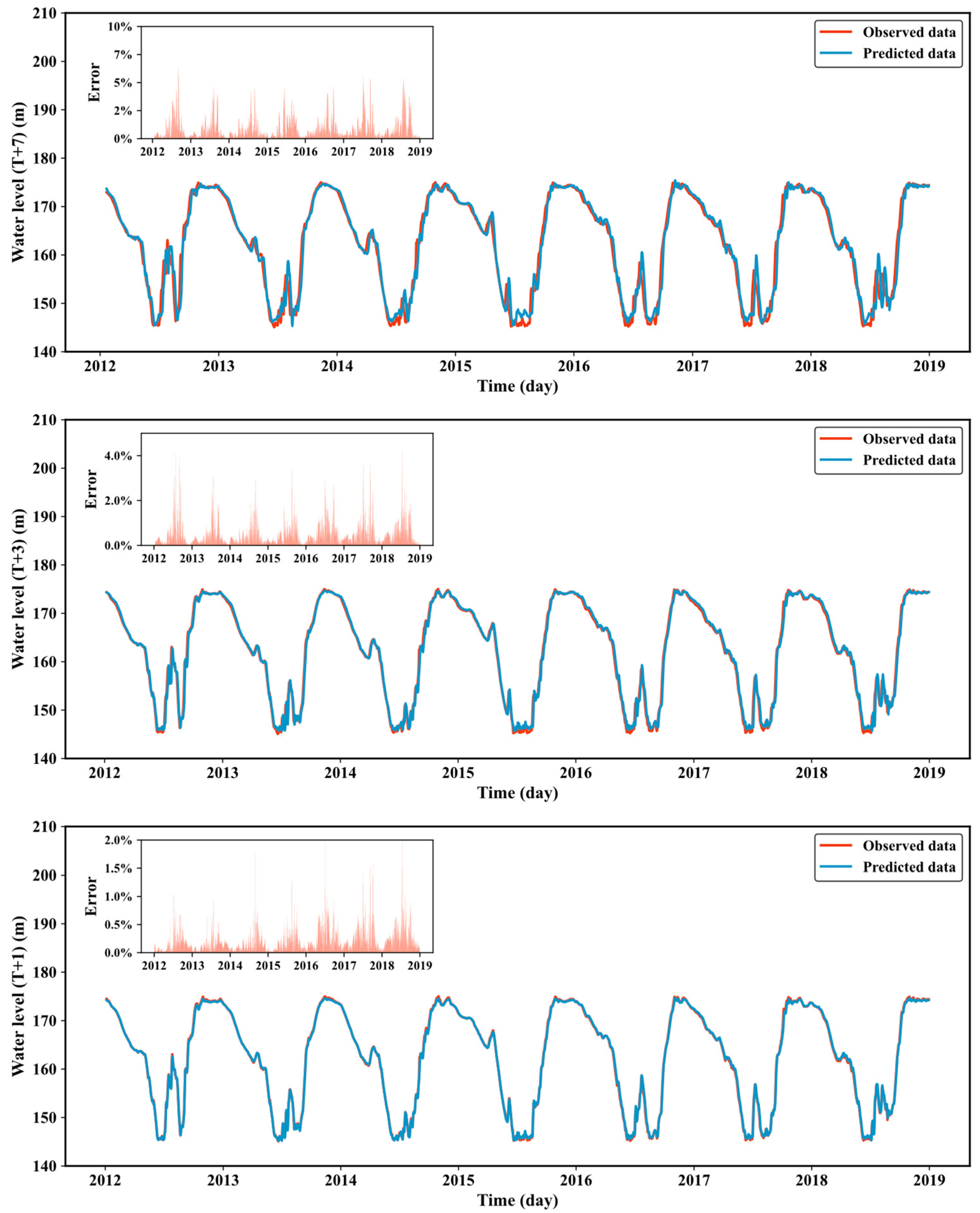
3.2. Water Level Forecasting Based on the Proposed Model at Different Time Tasks
3.3. Model Comparisons with Conventional Machine Learning Approaches
- (1)
- Introduce multi-feature data and construct water level prediction models based on multi-input multi-output or multi-task learning techniques;
- (2)
- Compare different deep learning techniques for water level prediction tasks, and design more suitable deep learning structures for hydrological data characteristics and patterns.
- (3)
- Investigate the interpretability issues of hybrid models in predicting water level fluctuations in order to reveal underlying causal relationships more effectively.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, J.G.; Zang, C.F.; Tian, S.Y.; Liu, J.G.; Yang, H.; Jia, S.F.; You, L.Z.; Liu, B.; Zhang, M. Water conservancy projects in China: Achievements, challenges and way forward. Glob. Environ. Chang. Hum. Policy Dimens. 2013, 23, 633–643. [Google Scholar] [CrossRef]
- Lopez-Pujol, J.; Ren, M.X. Biodiversity and the Three Gorges Reservoir: A troubled marriage. J. Nat. Hist. 2009, 43, 2765–2786. [Google Scholar] [CrossRef]
- Yang, S.L.; Milliman, J.D.; Li, P.; Xu, K. 50,000 dams later: Erosion of the Yangtze River and its delta. Glob. Planet. Chang. 2011, 75, 14–20. [Google Scholar] [CrossRef]
- Ahmed, S.S.; Bali, R.; Khan, H.; Mohamed, H.I.; Sharma, S.K. Improved water resource management framework for water sustainability and security. Environ. Res. 2021, 201, 111527. [Google Scholar] [CrossRef] [PubMed]
- Moisello, U.; Todeschini, S.; Vullo, F. The effects of water management on annual maximum floods of Lake Como and River Adda at Lecco (Italy). Civ. Eng. Environ. Syst. 2013, 30, 56–71. [Google Scholar] [CrossRef]
- Bengtsson, L.; Malm, J. Using rainfall-runoff modeling to interpret lake level data. J. Paleolimnol. 1997, 18, 235–248. [Google Scholar] [CrossRef]
- Kadioglu, M.; Sen, Z.; Batur, E. Cumulative Departures Model for Lake-Water Fluctuations. J. Hydrol. Eng. 1999, 4, 245–250. [Google Scholar] [CrossRef]
- Izady, A.; Davary, K.; Alizadeh, A.; Ziaei, A.N.; Alipoor, A.; Joodavi, A.; Brusseau, M.L. A framework toward developing a groundwater conceptual model. Arab. J. Geosci. 2014, 7, 3611–3631. [Google Scholar] [CrossRef]
- Irvine, K.N.; Eberhardt, A.J. Multiplicative, Seasonal Arima Models for Lake Erie and Lake-Ontario Water Levels. Water Resour. Bull. 1992, 28, 385–396. [Google Scholar] [CrossRef]
- Kasiviswanathan, K.; Saravanan, S.; Balamurugan, M.; Saravanan, K. Genetic programming based monthly groundwater level forecast models with uncertainty quantification. Model. Earth Syst. Environ. 2016, 2, 27. [Google Scholar] [CrossRef]
- Wang, K.; Hu, T.F.; Zhang, P.P.; Huang, W.Q.; Mao, J.Q.; Xu, Y.F.; Shi, Y. Improving Lake Level Prediction by Embedding Support Vector Regression in a Data Assimilation Framework. Water 2022, 14, 3718. [Google Scholar] [CrossRef]
- Moghaddam, D.D.; Rahmati, O.; Haghizadeh, A.; Kalantari, Z. A Modeling Comparison of Groundwater Potential Mapping in a Mountain Bedrock Aquifer: QUEST, GARP, and RF Models. Water 2020, 12, 679. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Kisi, O.; Yaseen, Z.M.; Shahid, S.; Zounemat-Kermani, M. Improving streamflow prediction using a new hybrid ELM model combined with hybrid particle swarm optimization and grey wolf optimization. Knowl. Based Syst. 2021, 230, 107379. [Google Scholar] [CrossRef]
- Adnan, R.M.; Kisi, O.; Mostafa, R.R.; Ahmed, A.N.; El-Shafie, A. The potential of a novel support vector machine trained with modified mayfly optimization algorithm for streamflow prediction. Hydrol. Sci. J. 2022, 67, 161–174. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Ewees, A.A.; Parmar, K.S.; Yaseen, Z.M.; Shahid, S.; Kisi, O. The viability of extended marine predators algorithm-based artificial neural networks for streamflow prediction. Appl. Soft Comput. 2022, 131, 109739. [Google Scholar] [CrossRef]
- Rogers, L.L.; Dowla, F.U. Optimization of Groundwater Remediation Using Artificial Neural Networks with Parallel Solute Transport Modeling. Water Resour. Res. 1994, 30, 457–481. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Le, J.; Liao, X.B.; Zheng, F.; Li, Y.H. A novel combination forecasting model for wind power integrating least square support vector machine, deep belief network, singular spectrum analysis and locality-sensitive hashing. Energy 2019, 168, 558–572. [Google Scholar] [CrossRef]
- Smys, S.; Basar, A.; Wang, H. CNN based flood management system with IoT sensors and cloud data. J. Artif. Intell. 2020, 2, 194–200. [Google Scholar]
- Kimura, N.; Yoshinaga, I.; Sekijima, K.; Azechi, I.; Baba, D. Convolutional Neural Network Coupled with a Transfer-Learning Approach for Time-Series Flood Predictions. Water 2020, 12, 96. [Google Scholar] [CrossRef]
- Palmitessa, R.; Mikkelsen, P.S.; Borup, M.; Law, A.W.K. Soft sensing of water depth in combined sewers using LSTM neural networks with missing observations. J. Hydro-Environ. Res. 2021, 38, 106–116. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Mostafa, R.R.; Chen, Z.; Parmar, K.S.; Kisi, O.; Zounemat-Kermani, M. Water temperature prediction using improved deep learning methods through reptile search algorithm and weighted mean of vectors optimizer. J. Mar. Sci. Eng. 2023, 11, 259. [Google Scholar] [CrossRef]
- Yang, X.Y.; Zhang, Z.R. A CNN-LSTM Model Based on a Meta-Learning Algorithm to Predict Groundwater Level in the Middle and Lower Reaches of the Heihe River, China. Water 2022, 14, 2377. [Google Scholar] [CrossRef]
- Baek, S.S.; Pyo, J.; Chun, J.A. Prediction of Water Level and Water Quality Using a CNN-LSTM Combined Deep Learning Approach. Water 2020, 12, 3399. [Google Scholar] [CrossRef]
- Yang, S.; Yang, D.; Chen, J.; Santisirisomboon, J.; Lu, W.; Zhao, B. A physical process and machine learning combined hydrological model for daily streamflow simulations of large watersheds with limited observation data. J. Hydrol. 2020, 590, 125206. [Google Scholar] [CrossRef]
- Li, G.; Zhu, H.; Jian, H.; Zha, W.; Wang, J.; Shu, Z.; Yao, S.; Han, H. A combined hydrodynamic model and deep learning method to predict water level in ungauged rivers. J. Hydrol. 2023, 625, 130025. [Google Scholar] [CrossRef]
- Yuan, Z.; Liu, J.; Liu, Y.; Zhang, Q.; Li, Y.; Li, Z. A two-stage modelling method for multi-station daily water level prediction. Environ. Model. Softw. 2022, 156, 105468. [Google Scholar] [CrossRef]
- Lafaysse, M.; Hingray, B.; Etchevers, P.; Martin, E.; Obled, C. Influence of spatial discretization, underground water storage and glacier melt on a physically-based hydrological model of the Upper Durance River basin. J. Hydrol. 2011, 403, 116–129. [Google Scholar] [CrossRef]
- Saber, M.; Hamaguchi, T.; Kojiri, T.; Tanaka, K.; Sumi, T. A physically based distributed hydrological model of wadi system to simulate flash floods in arid regions. Arab. J. Geosci. 2015, 8, 143–160. [Google Scholar] [CrossRef]
- Li, B.; Yang, G.S.; Wan, R.R.; Dai, X.; Zhang, Y.H. Comparison of random forests and other statistical methods for the prediction of lake water level: A case study of the Poyang Lake in China. Hydrol. Res. 2016, 47, 69–83. [Google Scholar] [CrossRef]
- Pan, M.Y.; Zhou, H.N.; Cao, J.Y.; Liu, Y.S.; Hao, J.L.; Li, S.X.; Chen, C.H. Water Level Prediction Model Based on GRU and CNN. IEEE Access 2020, 8, 60090–60100. [Google Scholar] [CrossRef]
- Gao, Q.F.; He, G.J.; Fang, H.W.; Bai, S.; Huang, L. Numerical simulation of water age and its potential effects on the water quality in Xiangxi Bay of Three Gorges Reservoir. J. Hydrol. 2018, 566, 484–499. [Google Scholar] [CrossRef]
- Li, X.; Sha, J.; Wang, Z.L. Influence of the Three Gorges Reservoir on climate drought in the Yangtze River Basin. Environ. Sci. Pollut. Res. 2021, 28, 29755–29772. [Google Scholar] [CrossRef] [PubMed]
- Peel, M.C.; Blöschl, G. Hydrological modelling in a changing world. Prog. Phys. Geogr. 2011, 35, 249–261. [Google Scholar] [CrossRef]
- Yang, L.; Zeng, S.; Xia, J.; Wang, Y.; Huang, R.; Chen, M. Effects of the Three Gorges Dam on the downstream streamflow based on a large-scale hydrological and hydrodynamics coupled model. J. Hydrol. Reg. Stud. 2022, 40, 101039. [Google Scholar] [CrossRef]
- Zeng, S.; Liu, X.; Xia, J.; Du, H.; Chen, M.; Huang, R. Evaluating the hydrological effects of the Three Gorges Reservoir based on a large-scale coupled hydrological-hydrodynamic-dam operation model. J. Geogr. Sci. 2023, 33, 999–1022. [Google Scholar] [CrossRef]
- Singarimbun, R.N. Adaptive Moment Estimation To Minimize Square Error In Backpropagation Algorithm. Data Sci. J. Comput. Appl. Inform. 2020, 4, 27–46. [Google Scholar] [CrossRef]
- Robert, H.-N. Theory of the backpropagation neural network. IEEE Xplore 1989, 1, 593–605. [Google Scholar]
- Buscema, M. Back propagation neural networks. Subst. Use Misuse 1998, 33, 233–270. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Feng, X.a.; Zhou, S.; Jiang, J.; Chen, H.; Li, Y.; Li, C. A new fruit fly optimization algorithm enhanced support vector machine for diagnosis of breast cancer based on high-level features. BMC Bioinform. 2019, 20, 290. [Google Scholar] [CrossRef]
- Lin, J.-Y.; Cheng, C.-T.; Chau, K.-W. Using support vector machines for long-term discharge prediction. Hydrol. Sci. J. 2006, 51, 599–612. [Google Scholar] [CrossRef]
- Timofeev, R. Classification and Regression Trees (CART) Theory and Applications; Humboldt University: Berlin, Germany, 2004; p. 54. [Google Scholar]
- Morgan, J. Classification and Regression Tree Analysis; Boston University: Boston, MA, USA, 2014; p. 298. [Google Scholar]
- Ahmadisharaf, E.; Camacho, R.A.; Zhang, H.X.; Hantush, M.M.; Mohamoud, Y.M. Calibration and validation of watershed models and advances in uncertainty analysis in TMDL studies. J. Hydrol. Eng. 2019, 24, 03119001. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Ramkar, P.; Yadav, S. Identification of critical watershed using hydrological model and drought indices: A case study of upper Girna, Maharashtra, India. ISH J. Hydraul. Eng. 2021, 27, 471–482. [Google Scholar] [CrossRef]
- Tang, J.; Yin, X.-A.; Yang, P.; Yang, Z. Assessment of contributions of climatic variation and human activities to streamflow changes in the Lancang River, China. Water Resour. Manag. 2014, 28, 2953–2966. [Google Scholar] [CrossRef]
- Lallahem, S.; Mania, J.; Hani, A.; Najjar, Y. On the use of neural networks to evaluate groundwater levels in fractured media. J. Hydrol. 2005, 307, 92–111. [Google Scholar] [CrossRef]
- Aminikhanghahi, S.; Cook, D.J. A survey of methods for time series change point detection. Knowl. Inf. Syst. 2017, 51, 339–367. [Google Scholar] [CrossRef]
- Montanez, G.; Amizadeh, S.; Laptev, N. Inertial hidden markov models: Modeling change in multivariate time series. In Proceedings of the AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; Volume 29. [Google Scholar]
- Liu, Y.; Wang, H.; Feng, W.W.; Huang, H.C. Short Term Real-Time Rolling Forecast of Urban River Water Levels Based on LSTM: A Case Study in Fuzhou City, China. Int. J. Environ. Res. Public Health 2021, 18, 9287. [Google Scholar] [CrossRef]
- Hutter, F.; Hoos, H.; Leyton-Brown, K. An efficient approach for assessing hyperparameter importance. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 754–762. [Google Scholar]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Shan, K.; Song, L.; Chen, W.; Li, L.; Liu, L.; Wu, Y.; Jia, Y.; Zhou, Q.; Peng, L. Analysis of environmental drivers influencing interspecific variations and associations among bloom-forming cyanobacteria in large, shallow eutrophic lakes. Harmful Algae 2019, 84, 84–94. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Allawi, M.F.; Yousif, A.A.; Jaafar, O.; Hamzah, F.M.; El-Shafie, A. Non-tuned machine learning approach for hydrological time series forecasting. Neural Comput. Appl. 2018, 30, 1479–1491. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Short-term water quality variable prediction using a hybrid CNN–LSTM deep learning model. Stoch. Environ. Res. Risk Assess. 2020, 34, 415–433. [Google Scholar] [CrossRef]
- Mohammed, S.J.; Zubaidi, S.L.; Ortega-Martorell, S.; Al-Ansari, N.; Ethaib, S.; Hashim, K. Application of hybrid machine learning models and data pre-processing to predict water level of watersheds: Recent trends and future perspective. Cogent Eng. 2022, 9, 2143051. [Google Scholar] [CrossRef]
- Morovati, K.; Nakhaei, P.; Tian, F.; Tudaji, M.; Hou, S. A Machine learning framework to predict reverse flow and water level: A case study of Tonle Sap Lake. J. Hydrol. 2021, 603, 127168. [Google Scholar] [CrossRef]
| Location Index | Training Set | Validation Set | ||||
|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | RMSE | MAE | R2 | |
| 3 | 0.883 | 0.414 | 0.918 | 0.661 | 0.363 | 0.939 |
| 5 | 0.818 | 0.526 | 0.966 | 0.684 | 0.453 | 0.969 |
| 7 | 0.355 | 0.239 | 0.995 | 0.311 | 0.218 | 0.996 |
| 9 | 0.361 | 0.271 | 0.996 | 0.321 | 0.246 | 0.997 |
| 11 | 0.648 | 0.504 | 0.992 | 0.613 | 0.492 | 0.994 |
| 13 | 0.751 | 0.459 | 0.992 | 0.763 | 0.497 | 0.993 |
| 15 | 1.025 | 0.686 | 0.985 | 0.883 | 0.591 | 0.991 |
| 17 | 0.446 | 0.296 | 0.997 | 0.487 | 0.321 | 0.997 |
| 19 | 1.453 | 0.939 | 0.974 | 1.275 | 0.845 | 0.984 |
| 21 | 0.773 | 0.48 | 0.993 | 0.664 | 0.409 | 0.995 |
| 23 | 0.412 | 0.272 | 0.998 | 0.381 | 0.268 | 0.998 |
| 25 | 0.232 | 0.142 | 0.999 | 0.256 | 0.163 | 0.999 |
| 27 | 0.639 | 0.392 | 0.995 | 0.561 | 0.347 | 0.997 |
| 29 | 0.241 | 0.153 | 0.999 | 0.259 | 0.174 | 0.999 |
| Step | Time Lag | Hidden Size | Learning Rate | Num Layers | Batch Size | Activation Function |
|---|---|---|---|---|---|---|
| T + 1 | 4 | 32 | 0.001 | 1 | 32 | relu |
| T + 3 | 18 | 32 | 0.001 | 1 | 32 | relu |
| T + 7 | 30 | 32 | 0.0005 | 1 | 32 | relu |
| Step | Model | Training Set | Validation Set | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | ||||||
| T + 1 | LSTM | 0.717 | - | 0.412 | 0.793 | 0.489 | |||
| SVR | 0.783 | (−Δ9.2%) | 0.524 | (−Δ27.2%) | 0.858 | (−Δ8.1%) | 0.598 | (−Δ22.3%) | |
| CART | 0.764 | (−Δ6.6%) | 0.503 | (−Δ22.1%) | 0.89 | (−Δ12.2%) | 0.619 | (−Δ26.6%) | |
| T + 3 | LSTM | 1.23 | - | 0.71 | 1.282 | 0.833 | |||
| SVR | 1.377 | (−Δ11.9%) | 0.923 | (−Δ30%) | 1.39 | (−Δ8.4%) | 0.981 | (−Δ17.8%) | |
| CART | 1.237 | (−Δ0.6%) | 0.781 | (−Δ10%) | 1.379 | (−Δ7.6%) | 0.94 | (−Δ12.8%) | |
| T + 7 | LSTM | 1.909 | - | 1.168 | 1.981 | - | 1.321 | - | |
| SVR | 2.132 | (−Δ11.7%) | 1.443 | (−Δ23.5%) | 2.136 | (−Δ7.8%) | 1.53 | (−Δ15.8%) | |
| CART | 2.008 | (−Δ5.2%) | 1.333 | (−Δ14.1%) | 2.118 | (−Δ6.9%) | 1.437 | (−Δ8.8%) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, M.; Shan, K.; Zeng, S.; Wang, L.; Gong, Z.; Wu, X.; Yang, B.; Shang, M. Combined Physical Process and Deep Learning for Daily Water Level Simulations across Multiple Sites in the Three Gorges Reservoir, China. Water 2023, 15, 3191. https://doi.org/10.3390/w15183191
Xie M, Shan K, Zeng S, Wang L, Gong Z, Wu X, Yang B, Shang M. Combined Physical Process and Deep Learning for Daily Water Level Simulations across Multiple Sites in the Three Gorges Reservoir, China. Water. 2023; 15(18):3191. https://doi.org/10.3390/w15183191
Chicago/Turabian StyleXie, Mingjiang, Kun Shan, Sidong Zeng, Lan Wang, Zhigang Gong, Xuke Wu, Bing Yang, and Mingsheng Shang. 2023. "Combined Physical Process and Deep Learning for Daily Water Level Simulations across Multiple Sites in the Three Gorges Reservoir, China" Water 15, no. 18: 3191. https://doi.org/10.3390/w15183191





