Exploring the Effect of Meteorological Factors on Predicting Hourly Water Levels Based on CEEMDAN and LSTM
Abstract
:1. Introduction
2. Materials and Methods
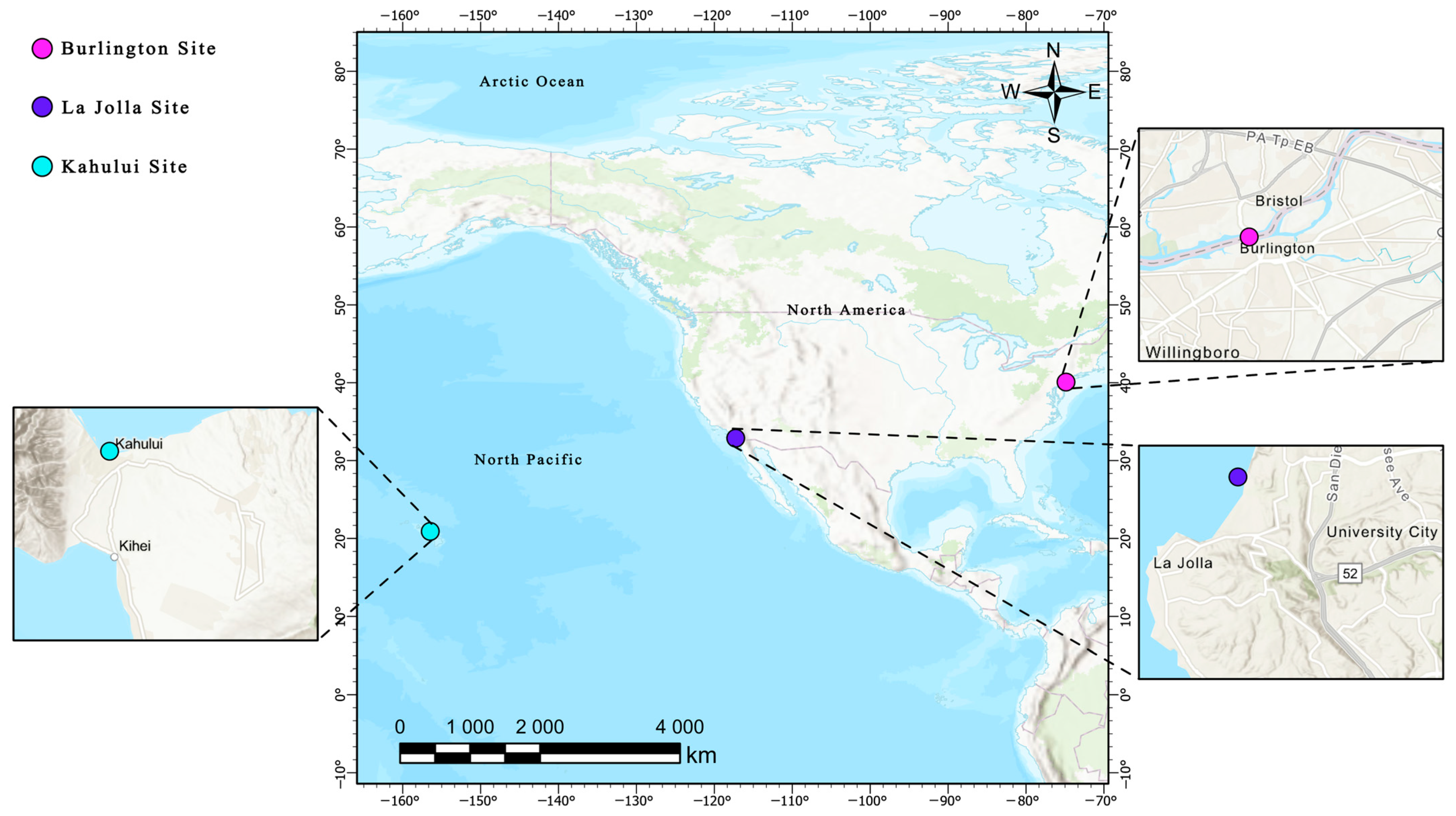
2.1. Study Area Description
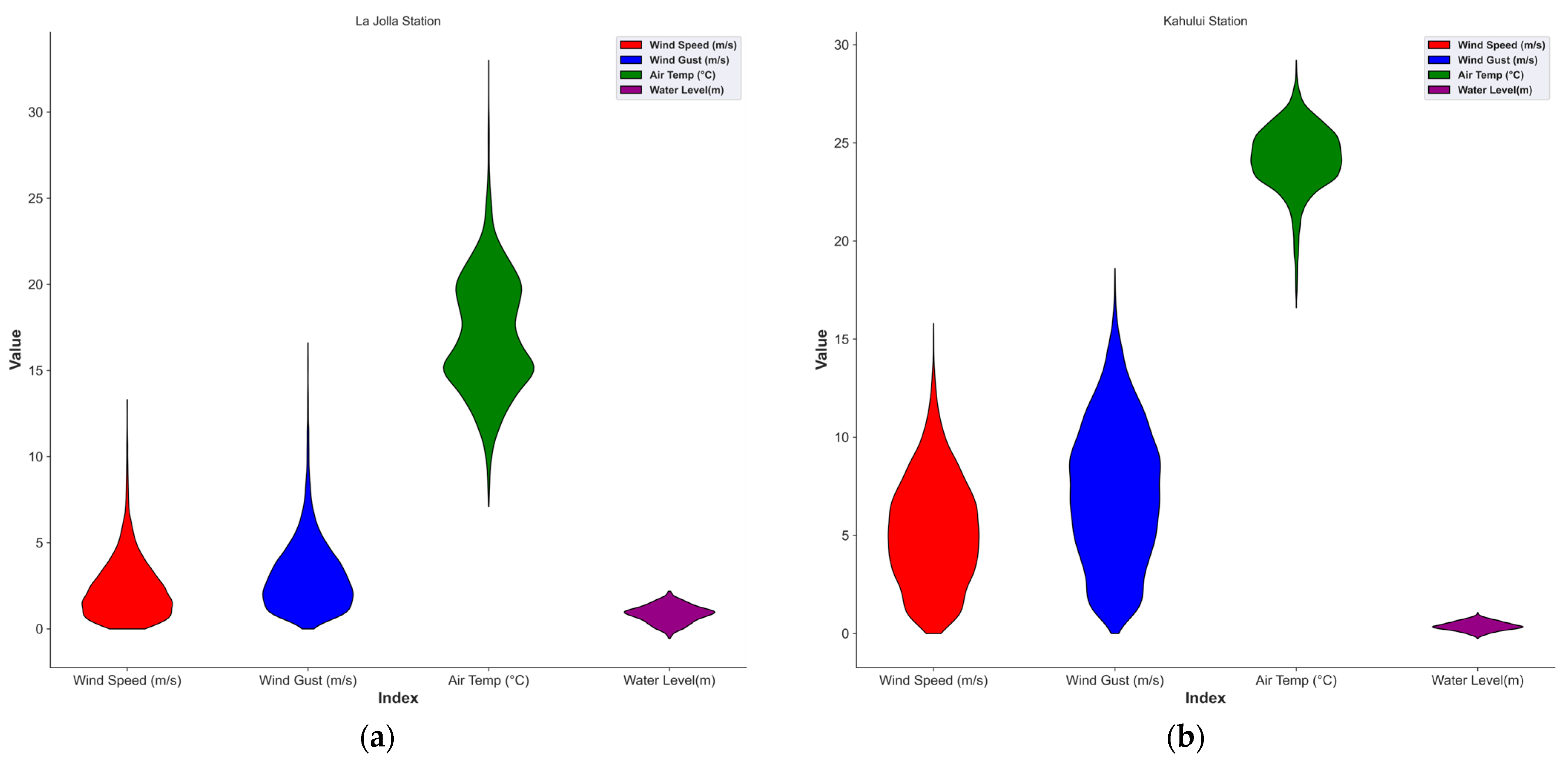
2.2. Data Collection and Analysis
2.3. Machine Learning Algorithms for Predicting Water Level References
2.3.1. Support Vector Machine (SVM)
2.3.2. Random Forest (RF)
2.3.3. Extreme Gradient Boosting (XGBoost)
2.3.4. Light Gradient Boosting Machine (LightGBM)
2.4. Deep Learning Algorithms for Predicting Water Level Reference
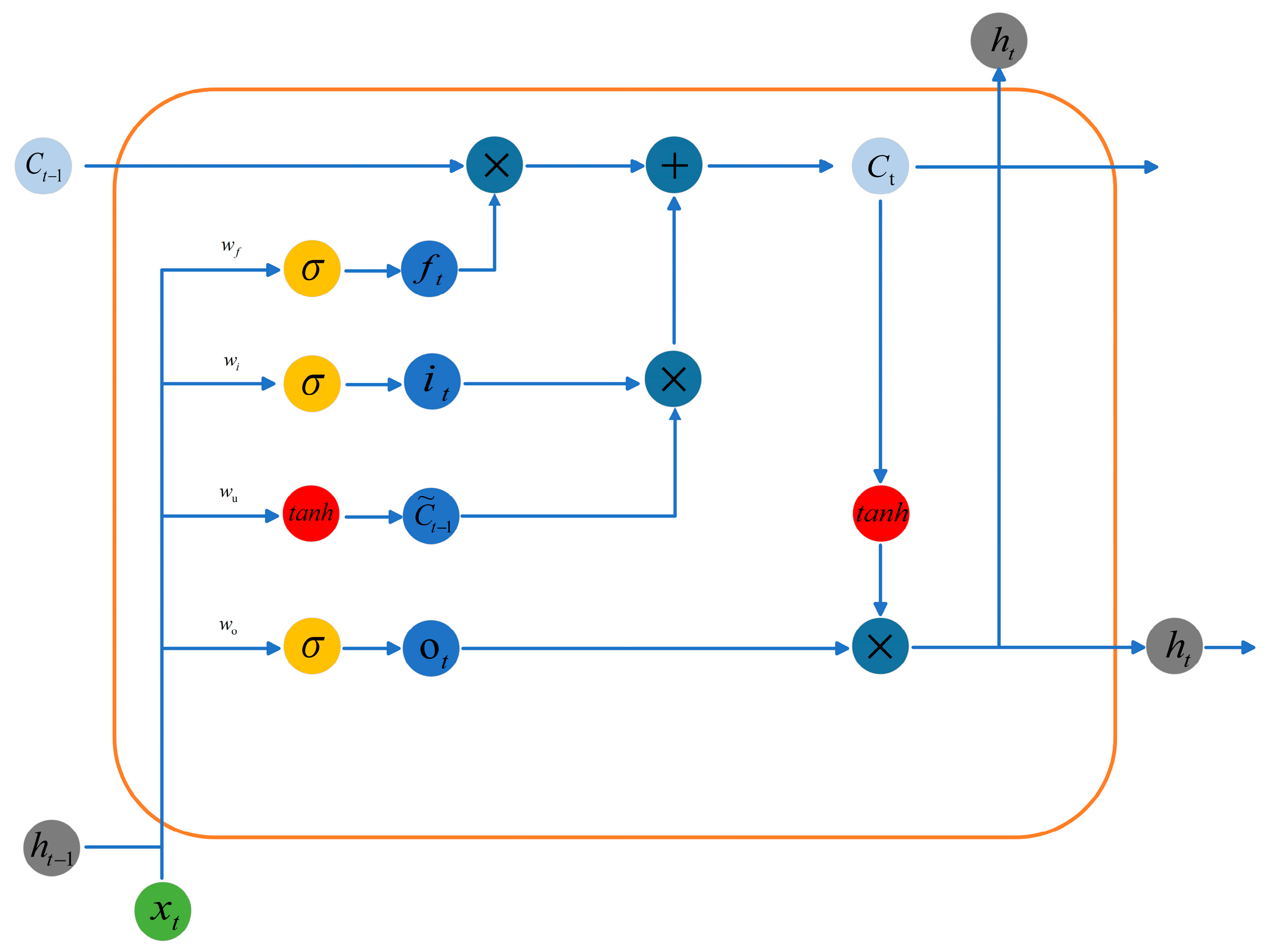
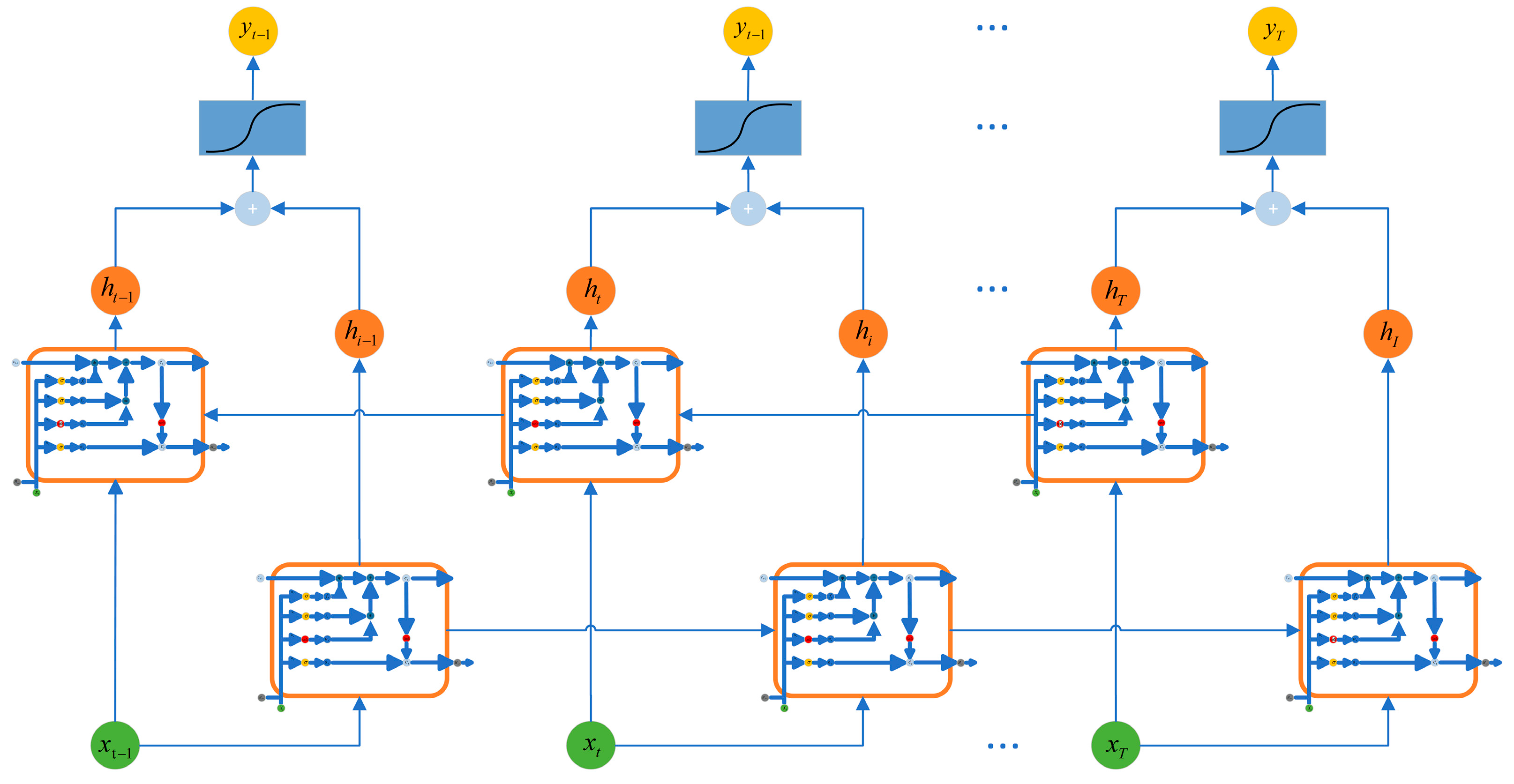
2.4.1. Long Short-Term Memory (LSTM)
2.4.2. Stack Long Short-Term Memory (StackLSTM)
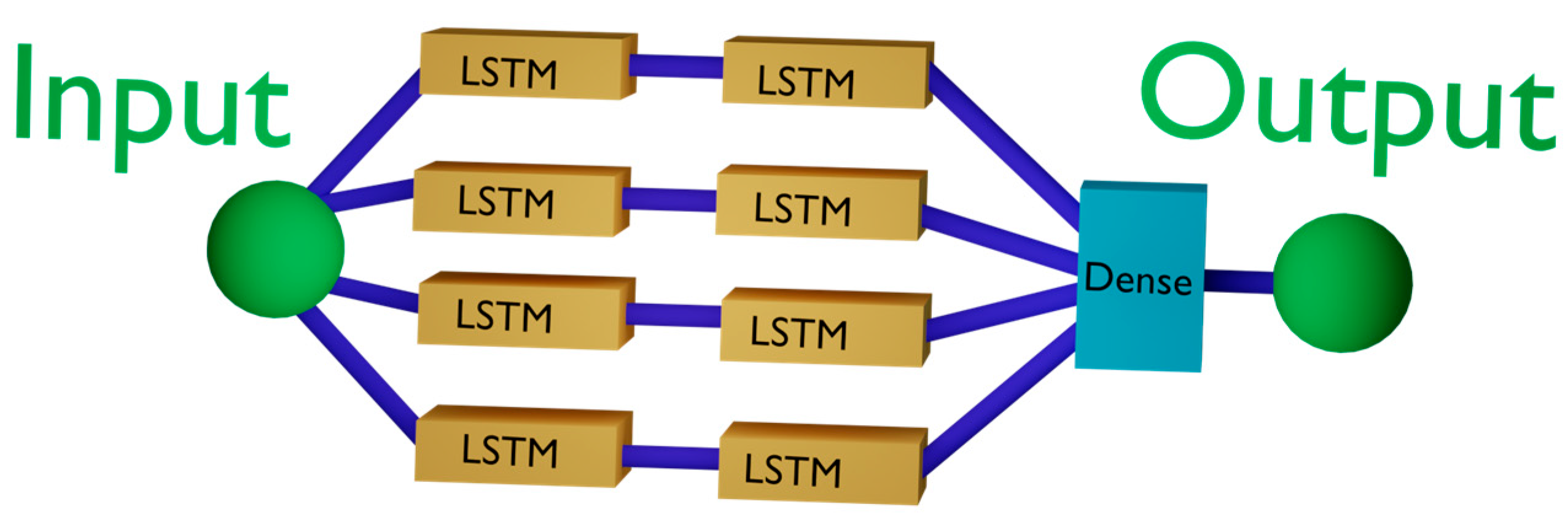
2.4.3. Bi-Directional Long Short-Term Memory (BiLSTM)
2.5. Input Portfolio Strategy
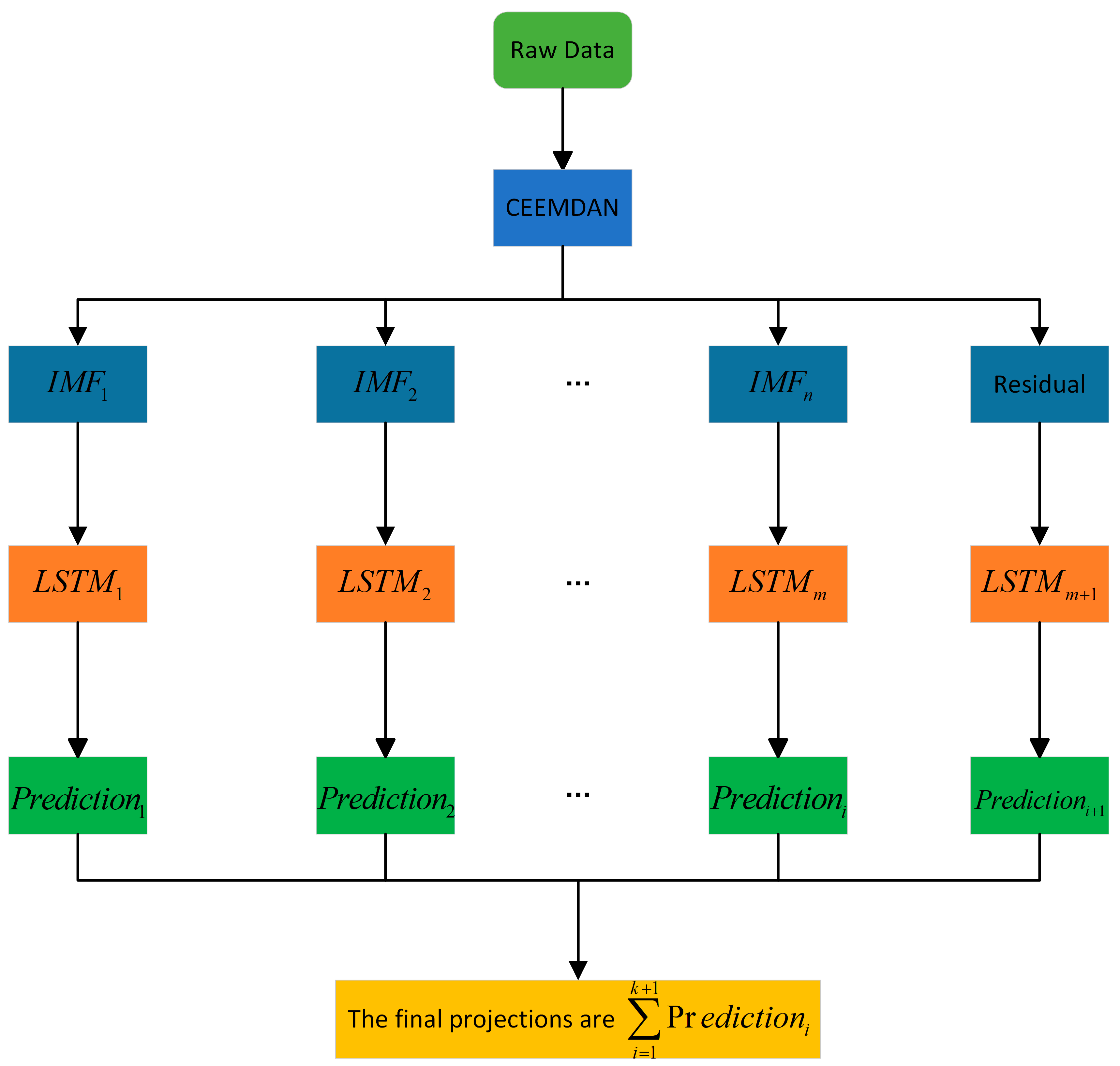
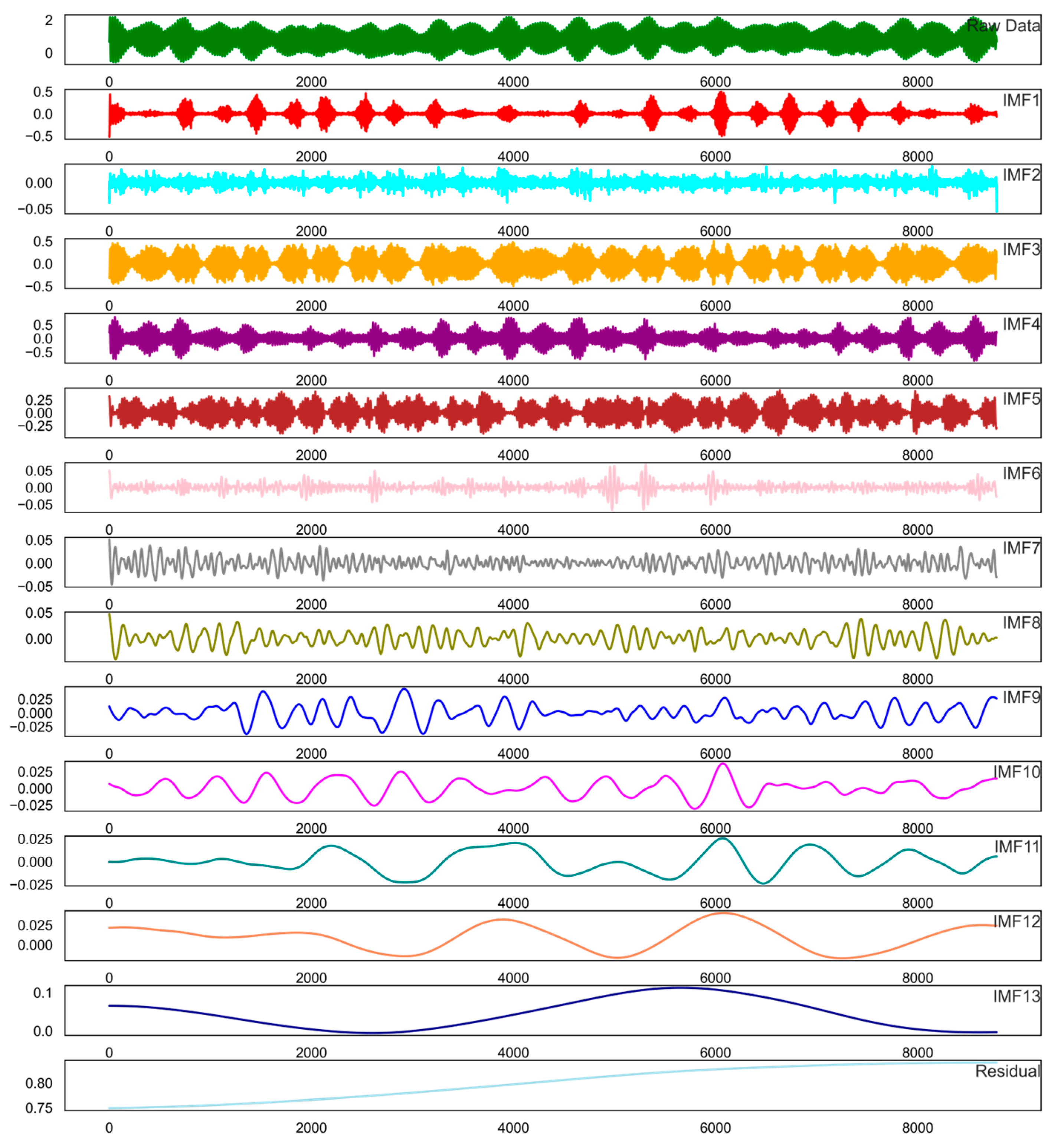
2.6. Complete Ensemble Empirical Mode Decomposition Adaptive Noise (CEEMDAN)
2.7. Model Comparison Statistical Analysis
2.8. Hyperparameter Tuning
3. Results
3.1. Compare the Accuracy of Each Model Prediction for Different Combinations of Inputs
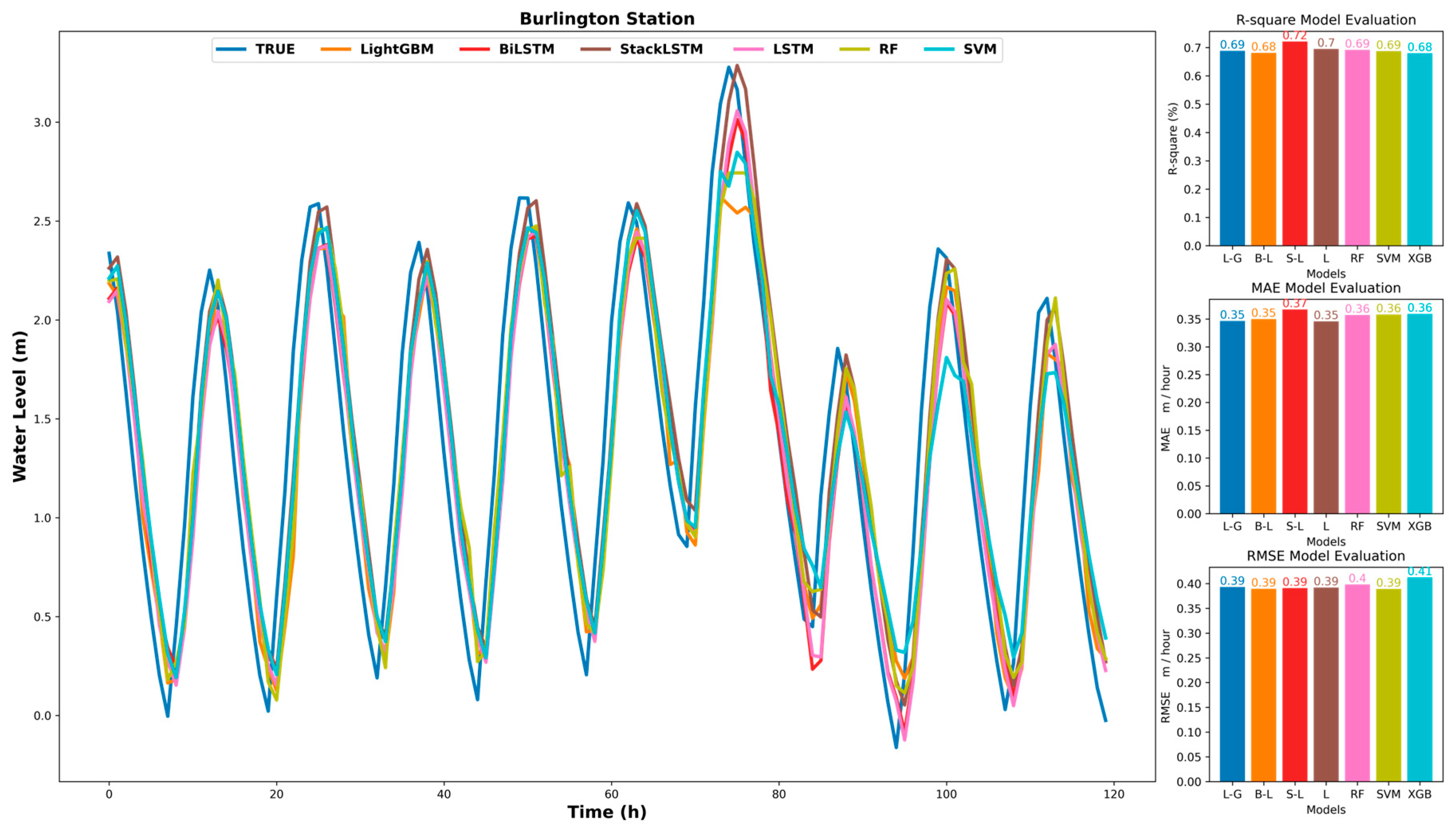
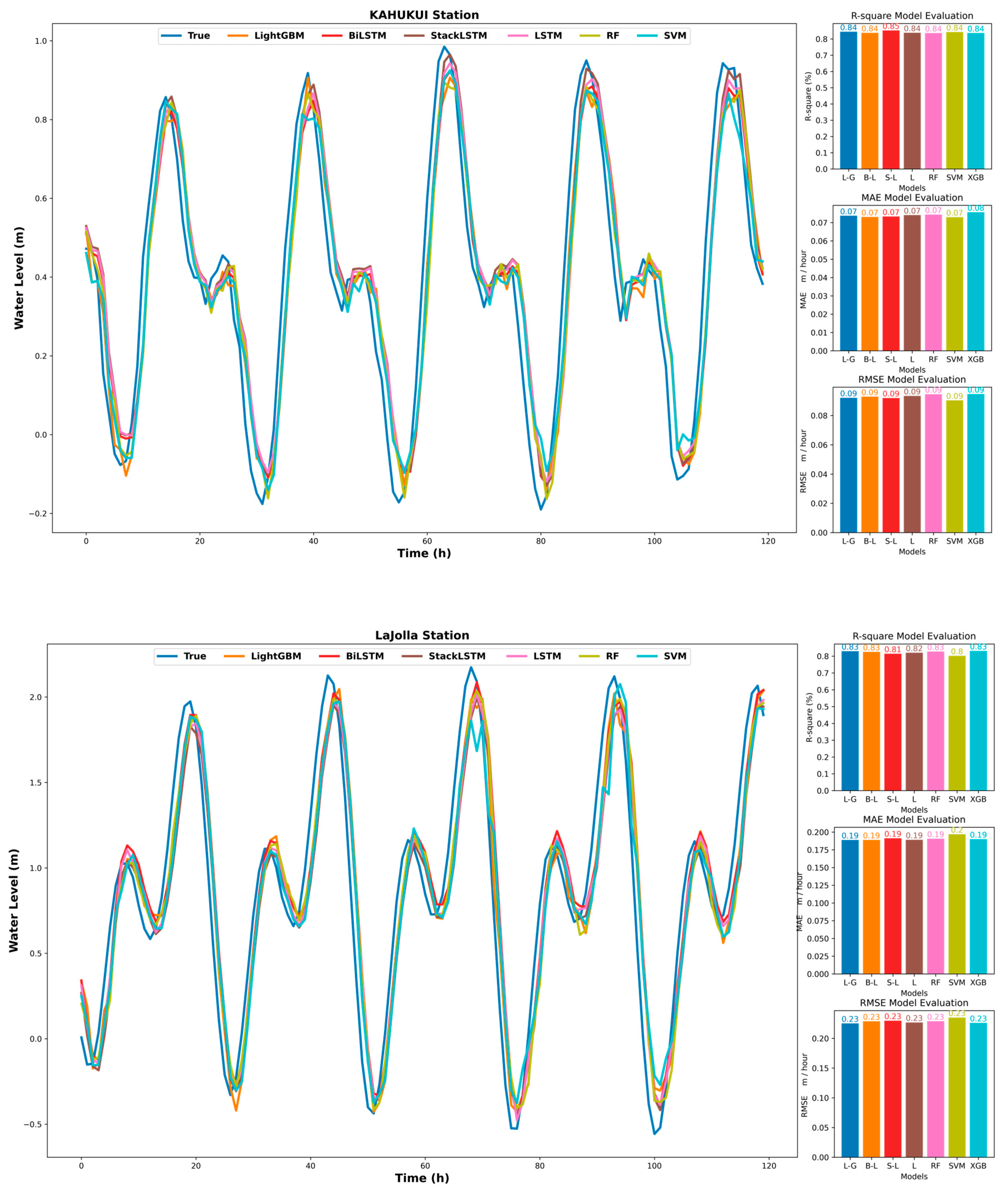
3.2. Compare the Stability of Each Model
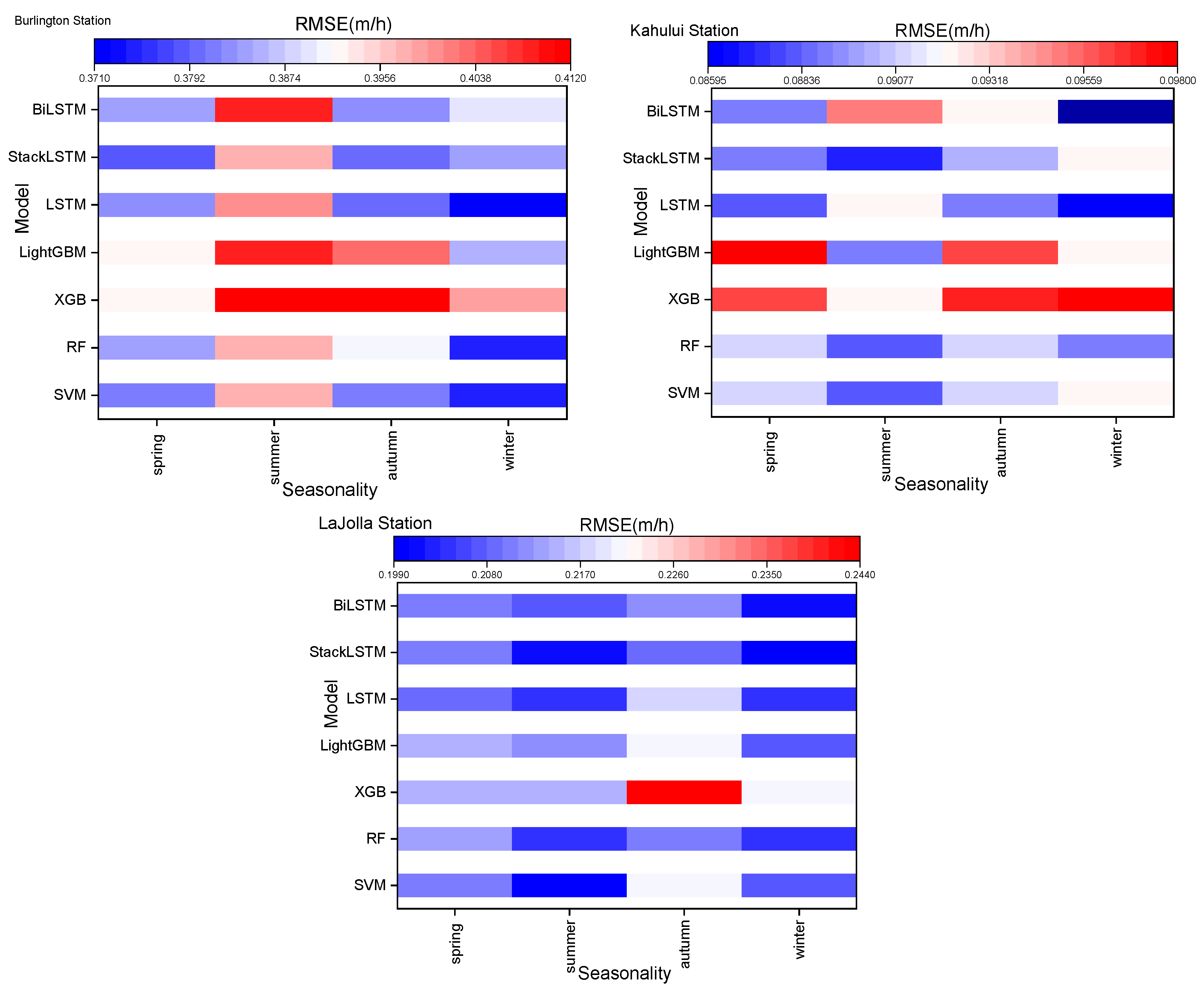
3.3. Seasonal Analysis of Predicted Water Levels
3.4. Application of CEEMDAN to the Prediction Accuracy of Individual Models Based on All Meteorological Combinations
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
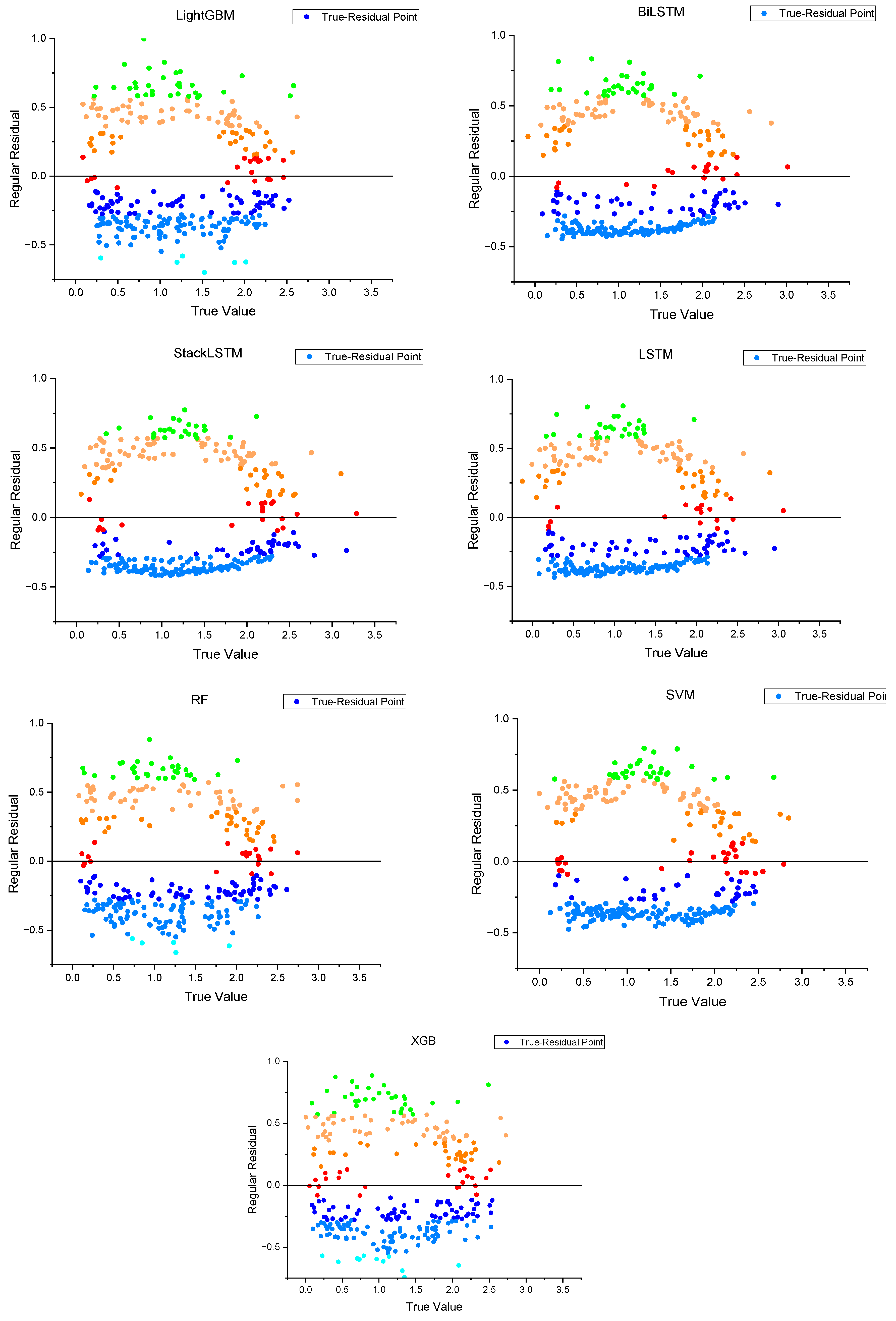
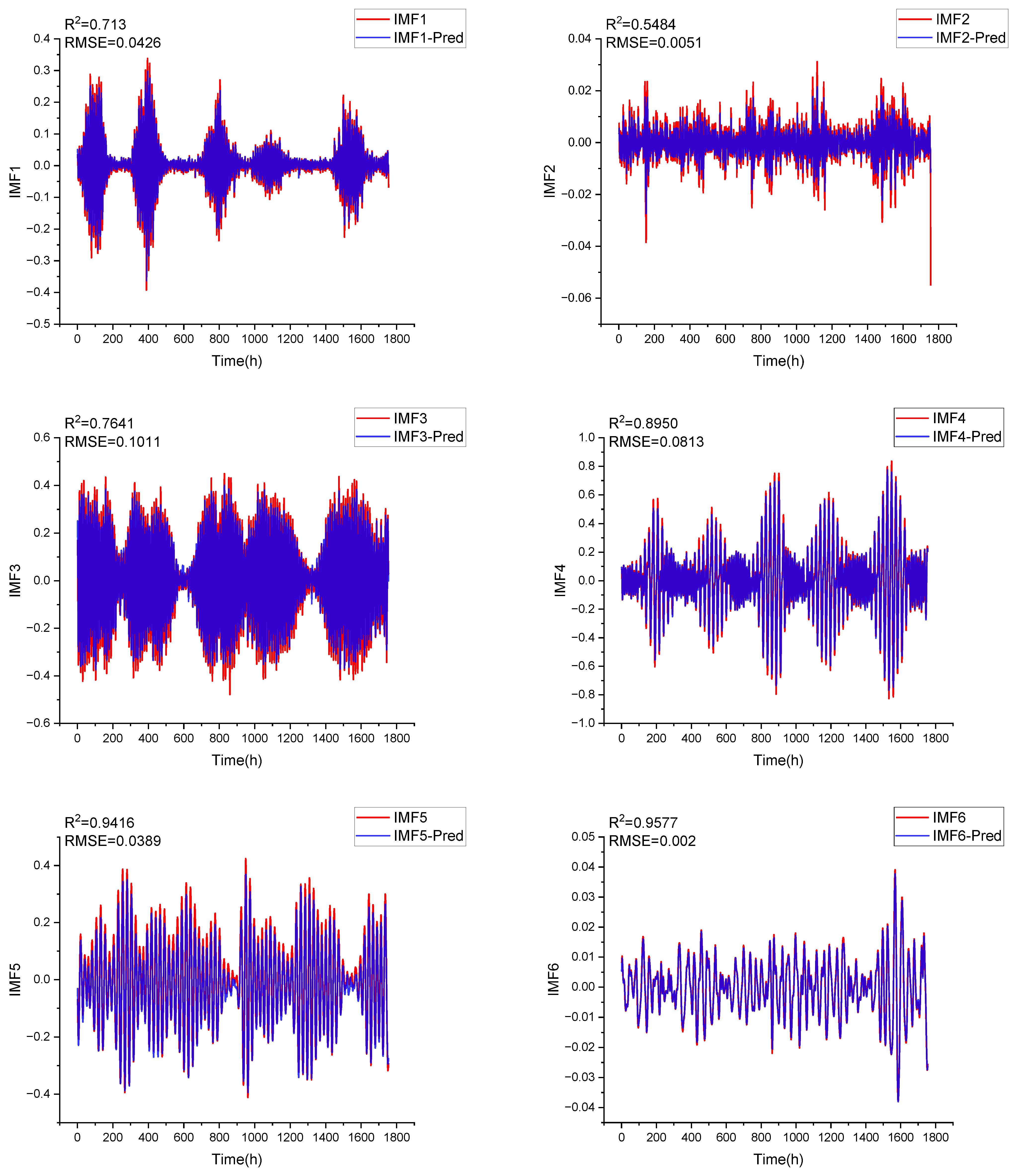
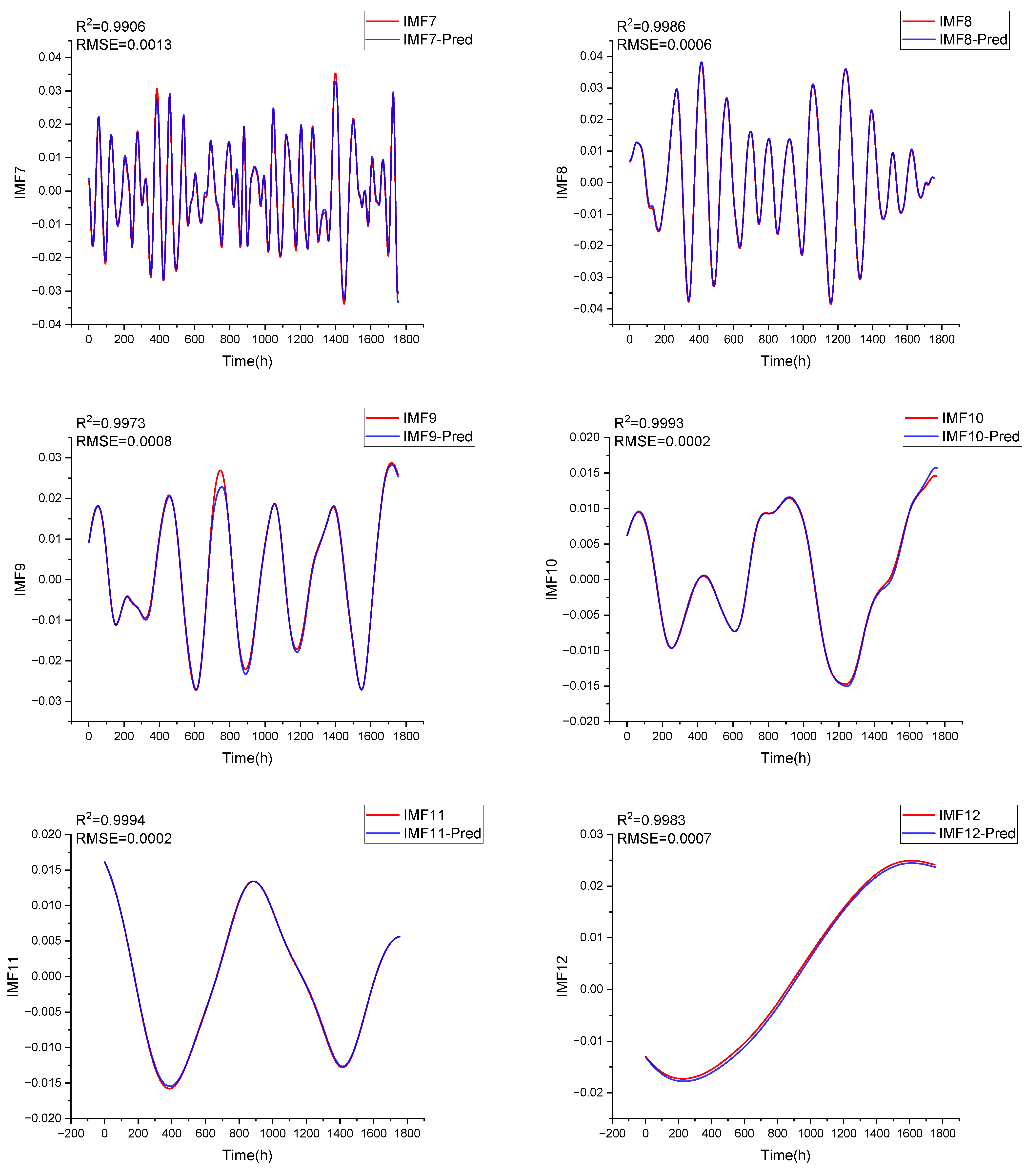
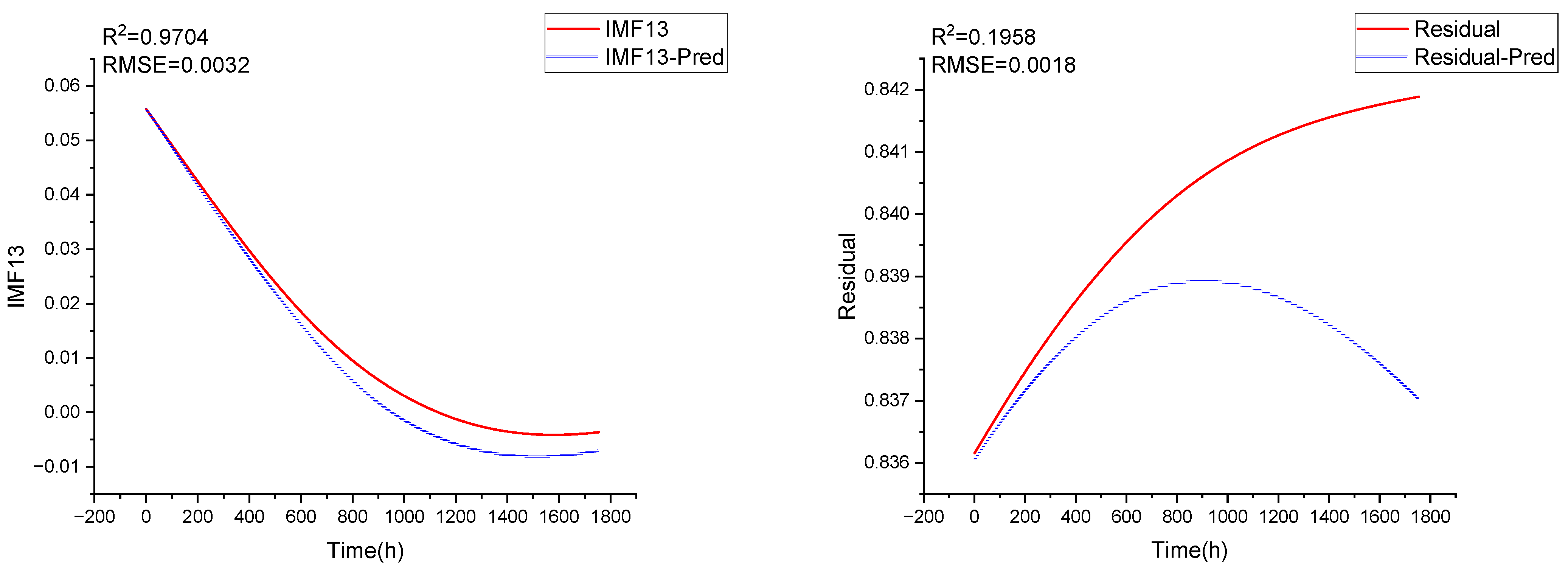
Appendix B
References
- Wang, Z.; Wang, Z. A review on tidal power utilization and operation optimization. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; p. 052015. [Google Scholar]
- Roberts, A.; Thomas, B.; Sewell, P.; Khan, Z.; Balmain, S.; Gillman, J. Current tidal power technologies and their suitability for applications in coastal and marine areas. J. Ocean. Eng. Mar. Energy 2016, 2, 227–245. [Google Scholar] [CrossRef]
- Khan, M.S.; Coulibaly, P. Application of Support Vector Machine in Lake Water Level Prediction. J. Hydrol. Eng. 2006, 11, 199–205. [Google Scholar] [CrossRef]
- Shiri, J.; Shamshirband, S.; Kisi, O.; Karimi, S.; Bateni, S.M.; Hosseini Nezhad, S.H.; Hashemi, A. Prediction of Water-Level in the Urmia Lake Using the Extreme Learning Machine Approach. Water Resour. Manag. 2016, 30, 5217–5229. [Google Scholar] [CrossRef]
- Azad, A.S.; Sokkalingam, R.; Daud, H.; Adhikary, S.K.; Khurshid, H.; Mazlan, S.N.A.; Rabbani, M.B.A. Water level prediction through hybrid SARIMA and ANN models based on time series analysis: Red hills reservoir case study. Sustainability 2022, 14, 1843. [Google Scholar] [CrossRef]
- Panyadee, P.; Champrasert, P.; Aryupong, C. Water level prediction using artificial neural network with particle swarm optimization model. In Proceedings of the 2017 5th International Conference on Information and Communication Technology (ICoIC7), Melaka, Malaysia, 17–19 May 2017; pp. 1–6. [Google Scholar]
- Wang, B.; Wang, B.; Wu, W.; Xi, C.; Wang, J. Sea-water-level prediction via combined wavelet decomposition, neuro-fuzzy and neural networks using SLA and wind information. Acta Oceanol. Sin. 2020, 39, 157–167. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Noor, F.; Haq, S.; Rakib, M.; Ahmed, T.; Jamal, Z.; Siam, Z.S.; Hasan, R.T.; Adnan, M.S.G.; Dewan, A.; Rahman, R.M. Water level forecasting using spatiotemporal attention-based long short-term memory network. Water 2022, 14, 612. [Google Scholar] [CrossRef]
- Assem, H.; Ghariba, S.; Makrai, G.; Johnston, P.; Gill, L.; Pilla, F. Urban water flow and water level prediction based on deep learning. In Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2017, Skopje, Macedonia, 18–22 September 2017, Proceedings, Part III 10, 2017; Springer International Publishing: Cham, Switzerland, 2017; pp. 317–329. [Google Scholar]
- Zhang, Z.; Qin, H.; Yao, L.; Liu, Y.; Jiang, Z.; Feng, Z.; Ouyang, S.; Pei, S.; Zhou, J. Downstream water level prediction of reservoir based on convolutional neural network and long short-term memory network. J. Water Resour. Plan. Manag. 2021, 147, 04021060. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Pan, M.; Zhou, H.; Cao, J.; Liu, Y.; Hao, J.; Li, S.; Chen, C.-H. Water level prediction model based on GRU and CNN. IEEE Access 2020, 8, 60090–60100. [Google Scholar] [CrossRef]
- Baek, S.-S.; Pyo, J.; Chun, J.A. Prediction of Water Level and Water Quality Using a CNN-LSTM Combined Deep Learning Approach. Water 2020, 12, 3399. [Google Scholar] [CrossRef]
- Zan, Y.; Gao, Y.; Jiang, Y.; Pan, Y.; Li, X.; Su, P. The Effects of Lake Level and Area Changes of Poyang Lake on the Local Weather. Atmosphere 2022, 13, 1490. [Google Scholar] [CrossRef]
- Behzad, M.; Asghari, K.; Coppola, E.A., Jr. Comparative study of SVMs and ANNs in aquifer water level prediction. J. Comput. Civ. Eng. 2010, 24, 408–413. [Google Scholar] [CrossRef]
- Choi, C.; Kim, J.; Han, H.; Han, D.; Kim, H.S. Development of water level prediction models using machine learning in wetlands: A case study of Upo wetland in South Korea. Water 2019, 12, 93. [Google Scholar] [CrossRef]
- Arkian, F.; Nicholson, S.E.; Ziaie, B. Meteorological factors affecting the sudden decline in Lake Urmia’s water level. Theor. Appl. Climatol. 2018, 131, 641–651. [Google Scholar] [CrossRef]
- Cox, D.T.; Tissot, P.; Michaud, P. Water Level Observations and Short-Term Predictions Including Meteorological Events for Entrance of Galveston Bay, Texas. J. Waterw. Port Coast. Ocean. Eng. 2002, 128, 21–29. [Google Scholar] [CrossRef]
- Yadav, B.; Eliza, K. A hybrid wavelet-support vector machine model for prediction of Lake water level fluctuations using hydro-meteorological data. Measurement 2017, 103, 294–301. [Google Scholar] [CrossRef]
- Lu, H.; Ma, X. Hybrid decision tree-based machine learning models for short-term water quality prediction. Chemosphere 2020, 249, 126169. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Gruber, A.; Krueger, A.F. The Status of the NOAA Outgoing Longwave Radiation Data Set. Bull. Am. Meteorol. Soc. 1984, 65, 958–962. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Noble, W.S. What is a support vector machine? Nat. Biotechnol. 2006, 24, 1565–1567. [Google Scholar] [CrossRef]
- Pai, P.-F.; Lin, C.-S. A hybrid ARIMA and support vector machines model in stock price forecasting. Omega 2005, 33, 497–505. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Qi, Y. Random forest for bioinformatics. In Ensemble Machine Learning: Methods and Applications; Springer: New York, NY, USA, 2012; pp. 307–323. [Google Scholar]
- Janitza, S.; Tutz, G.; Boulesteix, A.-L. Random forest for ordinal responses: Prediction and variable selection. Comput. Stat. Data Anal. 2016, 96, 57–73. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Wang, C.; Deng, C.; Wang, S. Imbalance-XGBoost: Leveraging weighted and focal losses for binary label-imbalanced classification with XGBoost. Pattern Recognit. Lett. 2020, 136, 190–197. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Chen, C.; Zhang, Q.; Ma, Q.; Yu, B. LightGBM-PPI: Predicting protein-protein interactions through LightGBM with multi-information fusion. Chemom. Intell. Lab. Syst. 2019, 191, 54–64. [Google Scholar] [CrossRef]
- Janiesch, C.; Zschech, P.; Heinrich, K. Machine learning and deep learning. Electron. Mark. 2021, 31, 685–695. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Bai, K.; Zhan, C.; Tu, B. Parameter prediction of coiled tubing drilling based on GAN–LSTM. Sci. Rep. 2023, 13, 10875. [Google Scholar] [CrossRef] [PubMed]
- Dyer, C.; Ballesteros, M.; Ling, W.; Matthews, A.; Smith, N.A. Transition-based dependency parsing with stack long short-term memory. arXiv 2015, arXiv:1505.08075. [Google Scholar]
- Pattana-Anake, V.; Joseph, F.J.J. Hyper parameter optimization of stack LSTM based regression for PM 2.5 data in Bangkok. In Proceedings of the 2022 7th International Conference on Business and Industrial Research (ICBIR), Bangkok, Thailan, 19–20 May 2022; pp. 13–17. [Google Scholar]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Ma, X.; Hovy, E. End-to-end sequence labeling via bi-directional lstm-cnns-crf. arXiv 2016, arXiv:1603.01354. [Google Scholar]
- Joseph, R.V.; Mohanty, A.; Tyagi, S.; Mishra, S.; Satapathy, S.K.; Mohanty, S.N. A hybrid deep learning framework with CNN and Bi-directional LSTM for store item demand forecasting. Comput. Electr. Eng. 2022, 103, 108358. [Google Scholar] [CrossRef]
- Cui, Y.; Jia, L.; Fan, W. Estimation of actual evapotranspiration and its components in an irrigated area by integrating the Shuttleworth-Wallace and surface temperature-vegetation index schemes using the particle swarm optimization algorithm. Agric. For. Meteorol. 2021, 307, 108488. [Google Scholar] [CrossRef]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and four tree-based ensemble models for predicting daily reference evapotranspiration using limited meteorological data in different climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]
- Chang, K.-M. Ensemble empirical mode decomposition for high frequency ECG noise reduction. Biomed. Technol. 2010, 55, 193–201. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Fernandez, G.C. Residual analysis and data transformations: Important tools in statistical analysis. HortScience 1992, 27, 297–300. [Google Scholar] [CrossRef]
- Atashi, V.; Gorji, H.T.; Shahabi, S.M.; Kardan, R.; Lim, Y.H. Water level forecasting using deep learning time-series analysis: A case study of red river of the north. Water 2022, 14, 1971. [Google Scholar] [CrossRef]
- Hsu, K.l.; Gupta, H.V.; Sorooshian, S. Artificial neural network modeling of the rainfall-runoff process. Water Resour. Res. 1995, 31, 2517–2530. [Google Scholar] [CrossRef]
- Xin, Y.; Kong, L.; Liu, Z.; Chen, Y.; Li, Y.; Zhu, H.; Gao, M.; Hou, H.; Wang, C. Machine learning and deep learning methods for cybersecurity. IEEE Access 2018, 6, 35365–35381. [Google Scholar] [CrossRef]
- Li, L.; Jamieson, K.; Rostamizadeh, A.; Gonina, E.; Hardt, M.; Recht, B.; Talwalkar, A. Massively parallel hyperparameter tuning. arXiv 2018, arXiv:1810.05934. [Google Scholar]
| Burlington | ||||||
|---|---|---|---|---|---|---|
| Variable | Wind Speed (m/s) | Wind Dir (deg) | Wind Gust (m/s) | Air Temp (°C) | Baro (mb) | Water Level (m) |
| 2.674 | 197.173 | 4.212 | 13.279 | 1017.397 | 1.316 | |
| 1.954 | 103.032 | 2.895 | 10.174 | 7.619376 | 0.793 | |
| 0.000 | 0.000 | 0.000 | −13.400 | 985.000 | −0.595 | |
| 1.200 | 93.000 | 1.900 | 5.3000 | 1012.700 | 0.621 | |
| 2.300 | 229.000 | 3.700 | 13.600 | 1016.900 | 1.307 | |
| 3.800 | 283.000 | 5.800 | 21.800 | 1022.300 | 2.028 | |
| 13.100 | 360.000 | 21.300 | 35.000 | 1040.600 | 3.278 | |
| Site | Kahului | La Jolla | ||
|---|---|---|---|---|
| Variable | Wind Dir (deg) | Baro (mb) | Wind Dir (deg) | Baro (mb) |
| 94.608 | 1016.683 | 198.091 | 1015.177 | |
| 90.115 | 2.348 | 102.664 | 3.867 | |
| 0.000 | 997.700 | 0.000 | 998.600 | |
| 45.000 | 1015.400 | 114.000 | 1012.500 | |
| 66.000 | 1016.800 | 213.500 | 1014.700 | |
| 82.000 | 1018.200 | 286.000 | 1017.700 | |
| 360.000 | 1023.100 | 360.000 | 1027.600 | |
| Input Combinations | SVM | RF | XGB | LightGBM | LSTM | StackLSTM | BiLSTM |
|---|---|---|---|---|---|---|---|
| WS, WD, WG, AT, Baro, WL | SVM1 | RF1 | XGB1 | LightGBM1 | LSTM1 | StackLSTM1 | BiLSTM1 |
| WS, WD, WG, WL | SVM2 | RF2 | XGB2 | LightGBM2 | LSTM2 | StackLSTM2 | BiLSTM2 |
| AT, Baro, WL | SVM3 | RF3 | XGB3 | LightGBM3 | LSTM3 | StackLSTM3 | BiLSTM3 |
| WL, WS, AT | SVM4 | RF4 | XGB4 | LightGBM4 | LSTM4 | StackLSTM4 | BiLSTM4 |
| Site | Models | Parameters |
|---|---|---|
| Burlington, Kahului, La Jolla | SVM | Kernel: RBF |
| RF | N_Estimators: 50, Oob_Score: True, N_Jobs: −1, Random_State: 50, Max_Features: 1.0, Min_Samples_leaf: 10 | |
| XGB | Objective: reg:squarederror, N_Estimatorsl: 50 | |
| LightGBM | Boosting Type: Gbdt, Objective: Regression, Num_Leaves: 29, Learning_Rate: 0.09, Feature_Fraction: 0.9, Bagging_Fraction: 0.8, Bagging_Freq: 6 | |
| LSTM | Layers: 1, Number of Neurons: 200, Dense: 1, Activation: ReLU, Optimizer: Adam, Loss Function: MSE, Epochs: 40, Batch Size: 1 | |
| StackLSTM | Layers: 2, Number of Neurons: 200 (2×100), Dense: 1, Activation: ReLU, Optimizer: Adam, Loss Function: MSE, Epochs: 40, Batch Size: 1 | |
| BiLSTM | Layers: 2, Number of Neurons: 200 (2×100), Dense: 1, Activation: ReLU, Optimizer: Adam, Loss Function: MSE, Epochs: 40, Batch Size: 1 |
| Model | Statistical Indicators | Model | Statistical Indicators | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Input | MAE mh−1 | RMSE mh−1 | nRMSE | MAE mh−1 | RMSE mh−1 | nRMSE | |||
| WS, WD, WG, AT, Baro, WL | WS, WD, WG, WL | ||||||||
| SVM1 | 0.688 | 0.358 | 0.389 | 0.111 | SVM2 | 0.696 | 0.361 | 0.387 | 0.110 |
| RF1 | 0.692 | 0.357 | 0.398 | 0.110 | RF2 | 0.686 | 0.356 | 0.395 | 0.112 |
| XGB1 | 0.680 | 0.359 | 0.412 | 0.110 | XGB2 | 0.658 | 0.363 | 0.409 | 0.116 |
| LightGBM1 | 0.689 | 0.347 | 0.393 | 0.110 | LightGBM2 | 0.682 | 0.351 | 0.390 | 0.110 |
| LSTM1 | 0.695 | 0.346 | 0.392 | 0.112 | LSTM2 | 0.686 | 0.350 | 0.387 | 0.110 |
| StackLSTM1 | 0.721 | 0.367 | 0.391 | 0.110 | StackLSTM2 | 0.719 | 0.356 | 0.384 | 0.109 |
| BiLSTM1 | 0.681 | 0.350 | 0.390 | 0.116 | BiLSTM2 | 0.699 | 0.357 | 0.386 | 0.109 |
| WS, AT, WL | AT, Baro, WL | ||||||||
| SVM3 | 0.682 | 0.364 | 0.391 | 0.111 | SVM4 | 0.698 | 0.362 | 0.390 | 0.110 |
| RF3 | 0.689 | 0.362 | 0.401 | 0.113 | RF4 | 0.678 | 0.368 | 0.409 | 0.116 |
| XGB3 | 0.674 | 0.366 | 0.419 | 0.119 | XGB4 | 0.662 | 0.371 | 0.428 | 0.121 |
| LightGBM3 | 0.698 | 0.353 | 0.399 | 0.113 | LightGBM4 | 0.691 | 0.360 | 0.402 | 0.114 |
| LSTM3 | 0.698 | 0.353 | 0.388 | 0.110 | LSTM4 | 0.704 | 0.357 | 0.386 | 0.109 |
| StackLSTM3 | 0.695 | 0.346 | 0.392 | 0.111 | StackLSTM4 | 0.689 | 0.347 | 0.391 | 0.110 |
| BiLSTM3 | 0.702 | 0.353 | 0.389 | 0.110 | BiLSTM4 | 0.704 | 0.358 | 0.385 | 0.109 |
| Model | Statistical Indicators | Model | Statistical Indicators | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Input | MAE mh−1 | RMSE mh−1 | nRMSE | MAE mh−1 | RMSE mh−1 | nRMSE | |||
| WS, WD, WG, AT, Baro, WL | WS, WD, WG, WL | ||||||||
| SVM1 | 0.843 | 0.073 | 0.090 | 0.077 | SVM2 | 0.838 | 0.075 | 0.093 | 0.079 |
| RF1 | 0.837 | 0.074 | 0.095 | 0.081 | RF2 | 0.831 | 0.076 | 0.096 | 0.082 |
| XGB1 | 0.836 | 0.076 | 0.095 | 0.081 | XGB2 | 0.815 | 0.080 | 0.100 | 0.085 |
| LightGBM1 | 0.845 | 0.074 | 0.092 | 0.078 | LightGBM2 | 0.840 | 0.075 | 0.093 | 0.079 |
| LSTM1 | 0.838 | 0.074 | 0.093 | 0.080 | LSTM2 | 0.835 | 0.074 | 0.094 | 0.080 |
| StackLSTM1 | 0.852 | 0.073 | 0.092 | 0.078 | StackLSTM2 | 0.847 | 0.074 | 0.093 | 0.079 |
| BiLSTM1 | 0.838 | 0.073 | 0.093 | 0.079 | BiLSTM2 | 0.842 | 0.074 | 0.094 | 0.080 |
| WS, AT, WL | AT, Baro, WL | ||||||||
| SVM3 | 0.839 | 0.074 | 0.093 | 0.079 | SVM4 | 0.831 | 0.076 | 0.095 | 0.081 |
| RF3 | 0.834 | 0.075 | 0.096 | 0.082 | RF4 | 0.839 | 0.075 | 0.095 | 0.081 |
| XGB3 | 0.830 | 0.077 | 0.098 | 0.083 | XGB4 | 0.831 | 0.078 | 0.097 | 0.083 |
| LightGBM3 | 0.840 | 0.074 | 0.094 | 0.080 | LightGBM4 | 0.832 | 0.076 | 0.096 | 0.082 |
| LSTM3 | 0.850 | 0.072 | 0.091 | 0.077 | LSTM4 | 0.836 | 0.074 | 0.094 | 0.08 |
| StackLSTM3 | 0.831 | 0.074 | 0.095 | 0.081 | StackLSTM4 | 0.838 | 0.074 | 0.094 | 0.08 |
| BiLSTM3 | 0.839 | 0.073 | 0.093 | 0.080 | BiLSTM4 | 0.837 | 0.075 | 0.095 | 0.081 |
| Model | Statistical Indicators | Model | Statistical Indicators | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Input | MAE mh−1 | RMSE mh−1 | nRMSE | MAE mh−1 | RMSE mh−1 | nRMSE | |||
| WS, WD, WG, AT, Baro, WL | WS, WD, WG, WL | ||||||||
| SVM1 | 0.802 | 0.197 | 0.235 | 0.086 | SVM2 | 0.805 | 0.192 | 0.232 | 0.085 |
| RF1 | 0.828 | 0.191 | 0.229 | 0.084 | RF2 | 0.818 | 0.194 | 0.234 | 0.086 |
| XGB1 | 0.831 | 0.190 | 0.226 | 0.083 | XGB2 | 0.810 | 0.197 | 0.239 | 0.088 |
| LightGBM1 | 0.830 | 0.189 | 0.225 | 0.082 | LightGBM2 | 0.821 | 0.193 | 0.232 | 0.085 |
| LSTM1 | 0.820 | 0.189 | 0.227 | 0.083 | LSTM2 | 0.817 | 0.193 | 0.233 | 0.085 |
| StackLSTM1 | 0.815 | 0.191 | 0.230 | 0.084 | StackLSTM2 | 0.815 | 0.190 | 0.231 | 0.085 |
| BiLSTM1 | 0.826 | 0.189 | 0.229 | 0.084 | BiLSTM2 | 0.808 | 0.193 | 0.235 | 0.086 |
| WS, AT, WL | AT, Baro, WL | ||||||||
| SVM3 | 0.820 | 0.191 | 0.229 | 0.084 | SVM4 | 0.813 | 0.193 | 0.230 | 0.084 |
| RF3 | 0.826 | 0.193 | 0.231 | 0.085 | RF4 | 0.821 | 0.194 | 0.232 | 0.085 |
| XGB3 | 0.831 | 0.191 | 0.232 | 0.085 | XGB4 | 0.833 | 0.189 | 0.228 | 0.083 |
| LightGBM3 | 0.833 | 0.191 | 0.228 | 0.084 | LightGBM4 | 0.837 | 0.188 | 0.223 | 0.082 |
| LSTM3 | 0.824 | 0.191 | 0.229 | 0.084 | LSTM4 | 0.828 | 0.188 | 0.227 | 0.083 |
| StackLSTM3 | 0.830 | 0.191 | 0.228 | 0.084 | StackLSTM4 | 0.827 | 0.189 | 0.226 | 0.083 |
| BiLSTM3 | 0.830 | 0.190 | 0.227 | 0.083 | BiLSTM4 | 0.835 | 0.188 | 0.225 | 0.082 |
| Site | Model | Statistical Indicators | |||
|---|---|---|---|---|---|
| Input | MAE mh−1 | RMSE mh−1 | |||
| WS, WD, WG, AT, Baro, WL | |||||
| Burlington | CEEMDAN-SVM | 0.9652 | 0.1131 | 0.1448 | 0.0397 |
| CEEMDAN-RF | 0.9742 | 0.1015 | 0.1245 | 0.0342 | |
| CEEMDAN-XGB | 0.9738 | 0.0996 | 0.1255 | 0.0344 | |
| CEEMDAN-LightGBM | 0.9755 | 0.0982 | 0.1213 | 0.0333 | |
| CEEMDAN-LSTM | 0.9803 | 0.0864 | 0.1088 | 0.0299 | |
| CEEMDAN-StackLSTM | 0.9803 | 0.0881 | 0.1089 | 0.0299 | |
| CEEMDAN-BiLSTM | 0.9820 | 0.0790 | 0.1040 | 0.0285 | |
| Kahului | CEEMDAN-SVM | 0.9317 | 0.0475 | 0.0596 | 0.0474 |
| CEEMDAN-RF | 0.9695 | 0.0317 | 0.0399 | 0.0317 | |
| CEEMDAN-XGB | 0.9667 | 0.0330 | 0.0416 | 0.0331 | |
| CEEMDAN-LightGBM | 0.9676 | 0.0325 | 0.0410 | 0.0326 | |
| CEEMDAN-LSTM | 0.9800 | 0.0254 | 0.0322 | 0.0256 | |
| CEEMDAN-StackLSTM | 0.9794 | 0.0258 | 0.0327 | 0.0260 | |
| CEEMDAN-BiLSTM | 0.9799 | 0.0254 | 0.0323 | 0.0257 | |
| La Jolla | CEEMDAN-SVM | 0.9493 | 0.0851 | 0.1164 | 0.0426 |
| CEEMDAN-RF | 0.9754 | 0.0630 | 0.0811 | 0.0297 | |
| CEEMDAN-XGB | 0.9694 | 0.0683 | 0.0904 | 0.0331 | |
| CEEMDAN-LightGBM | 0.9742 | 0.0635 | 0.0831 | 0.0304 | |
| CEEMDAN-LSTM | 0.9833 | 0.0514 | 0.0669 | 0.0245 | |
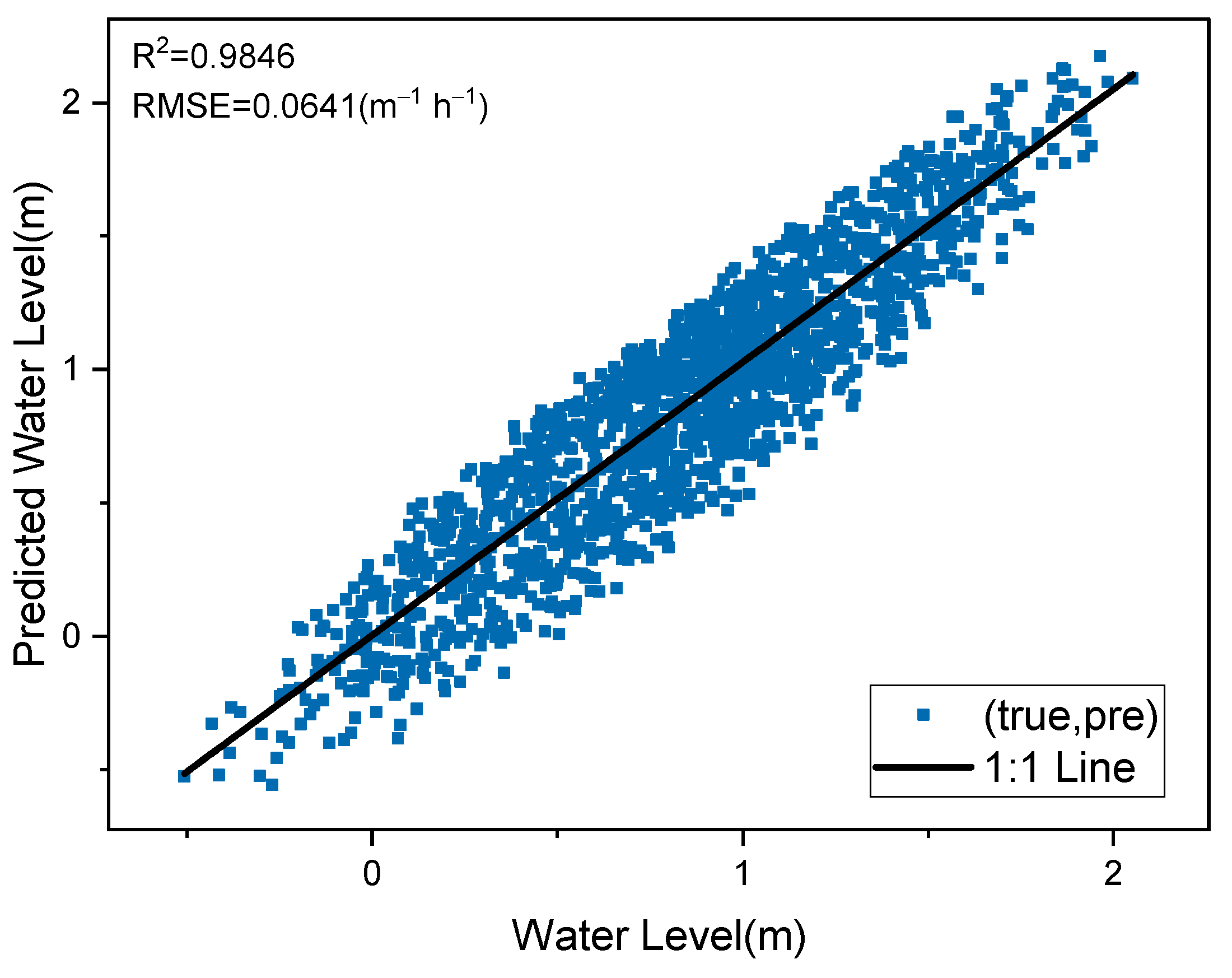
| CEEMDAN-StackLSTM | 0.9844 | 0.0503 | 0.0646 | 0.0237 | |
| CEEMDAN-BiLSTM | 0.9846 | 0.0501 | 0.0641 | 0.0235 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Z.; Lu, X.; Wu, L. Exploring the Effect of Meteorological Factors on Predicting Hourly Water Levels Based on CEEMDAN and LSTM. Water 2023, 15, 3190. https://doi.org/10.3390/w15183190
Yan Z, Lu X, Wu L. Exploring the Effect of Meteorological Factors on Predicting Hourly Water Levels Based on CEEMDAN and LSTM. Water. 2023; 15(18):3190. https://doi.org/10.3390/w15183190
Chicago/Turabian StyleYan, Zihuang, Xianghui Lu, and Lifeng Wu. 2023. "Exploring the Effect of Meteorological Factors on Predicting Hourly Water Levels Based on CEEMDAN and LSTM" Water 15, no. 18: 3190. https://doi.org/10.3390/w15183190






