1. Introduction
The increasing demand for water resources in recent times is directly associated with excessive pumping of water from aquifers [
1,
2,
3]. The increase in water resources demand is caused by human activities and may be intensified due to climate change effects causing prolonged drought periods without rainfall. This effect in combination with excessive pumping, failure to recharge the water aquifers, and with excessive fluid withdrawal, results in notable ground subsidence, which can become a problem of major importance to environmental poro-geomechanics [
4,
5].
In general, subsidence can be classified according to anthropogenic or geological processes. This work investigates the anthropogenic processes focusing on water withdrawal from an aquifer. Water in an aquifer is usually pressurized owing to the weight of the overburden strata. The weight of the overburden is partly transferred onto the solid framework of the rock formation and into the fluid according to the Biot effective stress principle. When water is withdrawn from the aquifer, the fluid pressure reduces but the pressure caused by the weight of the overburden layer remains constant thereby increasing the vertical effective stress undertaken by the solid skeleton of the aquifer formation. This phenomenon has the effect that the grains can take new locations in the solid matrix responsible for volume change in the aquifer, eventually resulting in ground subsidence [
6,
7].
There are only a few mathematical formulations to model or describe the behavior of the rock formation after altering the pressure distribution in the aquifer by production (i.e., water withdrawal). However, to the authors’ knowledge there is no single formulation that has benefits over others. Many of these models are based on different theories (e.g., elastic, plastic, or poroelastic) by considering weak or strong rock formations under partial or fully saturated conditions with time dependency. The analysis is usually performed by deriving analytical or semi-analytical solutions and by numerical modeling. Although the physical problem can be considered understood, there is always room for improvement [
8,
9].
The problem of ground subsidence is by no means a trivial process to model as it involves a certain geomechanical complexity owing to the different formations overlaying the aquifer formation and to a hydrodynamic complexity due to the transport properties of the permeating fluid through the aquifer. Upon assuming homogeneity, the mathematical problem at hand processes radial symmetry around a groundwater production well. Among the earliest contributions, models were based on the uniaxial strain assumption or the incremental vertical total stress [
10,
11]. However, the solutions of such models have proved to overestimate subsidence [
12,
13]. The widely used analytical model for predicting compaction and subsidence, based on the theory of poroelasticity it the classic model of [
14]. With this model, the compaction of a flat aquifer under radial symmetry about its center axis is calculated under a uniform pressure drawdown. Also, the aquifer is included in a semi-infinite homogeneous elastic rock formation. Since then, many models have been proposed in the literature to improve the geometric complexities (layered stratigraphy) and to incorporate non-uniform pressure distributions simulating the actual pressure drawdown distribution. The author of [
15] obtained the necessary Greens function to calculate the stress and deformation fields for an arbitrary radial distribution of pressure. Quite some time later, the authors of [
5] dealt with the more complicated problem of calculating ground subsidence due to fluid extraction from a poroelastic medium coupling the fluid flow process and the skeletal deformations in the context of the Biot poroelasticity model, leading to somewhat complicated solutions. Recently, the authors of [
9] utilized Geertsma’s surface subsidence expression at the location of the well to derive a simple closed-form expression for surface subsidence due to pumping at a constant rate, using the solution of [
15] and the principle of superposition [
16]. The issue of geometric complexities was also investigated by [
17] by attempting to apply poroelastic principles to reservoirs with arbitrary shapes by utilizing rectangular prismatic blocks. Lately, a poroelastic model to deal with the inhomogeneities in layered formations with separate elastic properties between the aquifer and the surrounding rocks was proposed by [
18]. Case studies involving surface subsidence include [
19,
20,
21,
22,
23]. Recent attempts to analyze models and predict subsidence using artificial intelligence methods in real case scenarios combined also with decision making and risk management methodologies can be found in [
24,
25,
26,
27].
In this work, the main objective of this work is the simplification of the mathematical derivation of the radial distribution of subsidence in the problem of fluid withdrawal from a disk-shaped confined aquifer. This new formulation facilitates the deduction of new results, e.g., the closed-form asymptotic solutions for the case of a deep aquifer. We suitably modify the theory presented in [
28] and later in [
29] that deals with surface deformations caused by a pressurized region inside an elastic half-space, applied to uniform and non-uniform radial pressure distributions around an injector, respectively, in order to deduce the radial subsidence by fluid withdrawal from a confined aquifer. Through this method we first re-derive the closed form solutions for the subsidence at the well location obtained by [
9] utilizing the initial theory of [
14] and we simplify the calculation of the radial distribution of the subsidence field and as a result we obtain a (asymptotic) closed form solution for the subsidence field for deep aquifer, which holds well for a depth greater or equal to the aquifer radius. This asymptotic solution verifies explicitly the observation made by [
9] that aquifer permeability and fluid viscosity have a negligible effect on subsidence at the well location, showing that this holds also at the level of the radial distribution. Such models present a plausible approach that conveniently calculates surface subsidence in fluid-saturated aquifers. Also, results from such solutions present the benefit of a first approximation to the estimation and calibration of numerical studies for predicting subsidence in more complex conditions.
This paper is organized as follows: In
Section 2, we present the mathematical modeling of the problem, derive, and analyze the new mathematical expressions for the radial distribution of surface subsidence and discuss in detail the method presented in [
9]. In
Section 3, we apply these results to four suitable test cases (corresponding to shallow/deep aquifer and weak/strong formations) and analyze the physical dependencies of the subsidence field. Finally,
Section 4 summarizes and discusses the findings of this work.
2. Mathematical Formulation
Subsidence or uplift due to pumping from or injection into a confined aquifer is calculated using the theory of deformations in an elastic layer due to pumping/injection of fluids at depth, as described in [
28] for uniform pressure distributions and modified later by [
29] for non-uniform cases, suitably applied for our purposes. The analysis of [
9], which was based on the theory of [
14], for calculating surface subsidence using the superposition principle is revisited and discussed in detail. It is worth noting that the researcher in [
15] derived Green’s functions related to this problem.
The physical model and the associated assumptions can be described as follows. Fluid is withdrawn by volumetric rate
Q through a vertical production well with negligible radius from a confined (horizontal and disk-shaped) aquifer at a mean depth
D, radius
R, and thickness
H, as shown in
Figure 1. The formation is semi-infinite, assuming uniform elastic properties (shear modulus
G and Poisson ratio
ν). The permeable disk-shaped region (i.e., the confined aquifer) is also assumed to have uniform hydraulic properties, permeability
k, porosity
φ. The fluid properties in the aquifer are also assumed to be uniform, in particular its viscosity
μ, is constant. Due to the cylindrical symmetry of the problem the pressure
p and vertical deformations
w are fields depend only on the radial distance
r and pumping time
t.
The pressure distribution within the aquifer is given by the classic solution of [
16], see also [
30,
31], using also the series expansion of [
32]. This approximation makes use the so-called radius of influence
re of the production well within the aquifer formation given by:
where
γ = 0.577216 is the Euler–Masceroni constant,
μ is the dynamic viscosity of the fluid and
S is the specific storage coefficient of the aquifer which may be expressed as [
9]:
with
Kf being the fluid bulk modulus,
K the rock bulk modulus,
α is the Biot coefficient, and
Cm is the coefficient of uniaxial compaction:
Then, the pressure distribution can be expressed as:
Case re >
R
while
p(
r) is zero elsewhere in each case. The two forms of the pressure field (4) and (5), hold at times such that the (time-dependent) radius of influence lies within the aquifer, and outside the aquifer, respectively.
Pi is the initial value of the pressure in the aquifer before production starts.
2.1. Subsidence Derived from the Theory of Selvadurai, 2009 [28] and Li et al., 2015 [29]
In the present problem, the result for the deflection field of [
29] that considers a storage formation, a cap rock, and an elastic half-space overburden layer, is reduced to the result of interest by taking the thickness of the caprock to zero and setting the shear modulus of the overburden layer to zero. One easily finds:
where
is the Hankel transform of the pressure difference
p(
r) −
Pi caused by pumping:
J0 is the zeroth order Bessel function of the first kind, and
ξ is a radial wavenumber.
The calculation of the deflection profile in Equation (6) may proceed straightforwardly because the required Hankel transforms of the pressure field in (4) and (5) can be calculated exactly. Utilizing the following identities for the Bessel functions of the first kind (see e.g., [
33]):
one finds that the transforms of the profiles (4) and (5) can be calculated by the identity:
where
f is an arbitrary function that includes logarithmic and quadratic terms in the variable
r. A similar methodology for the evaluation of the subsidence formula has been used in [
34].
Using these results, one finds straightforwardly the following solutions for the subsidence radial distribution for the cases respective to Equations (4) and (5).
Case re >
R
using suitable rescaling of the radial wavenumber
ξ to render it dimensionless in each case. (These results for the radial distribution of subsidence are much simpler than the previously obtained solutions discussed in
Section 2.2 below). We observe that in both cases the subsidence field, which depends also on time through
re, is of the general form:
Hence the behavior of the subsidence field can be analyzed solely in terms of the two ratios re/R and D/R, that is, in terms of the radius of influence and aquifer depth scaled by the aquifer radial extent.
The first explicit results one may deduce from Formulas (10) and (11) is the subsidence at r = 0 (the well location).
Formulas (13) and (14) are precisely the ones derived in [
9] using a different method as discussed in the next subsection.
Let us consider now the subsidence profile for the case of the deep aquifer, i.e., D >> R. The exponential factor in the integrals in Equations (10) and (11) implies that the main contribution to the asymptotic result comes from the small wavenumbers. Hence, we may approximate the quantities in the brackets by their approximate form for small ξ, which both turn out to be linear in ξ, to find:
We observe that the results differ only by a constant factor
eγ = 1.78, and both Equations (15) and (16) are linear in time owing to Equation (1). That is, they are linear in the produced fluid volume
Qt. We may also note that the scaled subsidence
w/
w0 is given by a single formula in both cases:
Equation (17) is the same for all times. As we shall see below, it turns out that this result holds well for
D ≳ 2
R. One should note that Equations (15) and (16) make explicit the observation of [
9] that subsidence becomes insensitive to fluid viscosity and aquifer permeability when its depth is greater than its radial extent, deduced here also at the level of the subsidence radial distribution.
2.2. Subsidence from the Theory of Geertsma, 1973 [14]
In the work of [
9], the authors start off with the subsidence formula at the location of the well for the case of uniform pressure difference, obtained by [
14]. Setting
r = 0 in Equation (6) and utilizing Equation (7) for a uniform (unit) pressure difference up to a distance R′, one finds by Equation (8) [
14]:
Clearly, [
W] = (length)/(pressure). Because of the linearity of (18) with respect to the pressure difference, a non-uniform profile can be obtained by superposing constant infinitesimal profiles of variable radial extent [
9]:
where the integration with respect to
R′ extends over the interval where
p(
r) −
Pi is not zero. In particular, for the profiles of interest we have:
The last term of Equation (21) accounts for the fact that the pressure profile in Equation (5) does not vanish at the outer boundary of the aquifer and hence the contribution from a uniform profile of ‘thickness’ −(p(R) − Pi) should also be added. Upon integrating Equations (20) and (21) one arrives at Equations (13) and (14).
The author of [
14] also derived the stress and deformation fields for this problem, which are quoted in the works of [
35]. The subsidence field (at the surface) for a unit uniform pressure profile with radial extent R′ can be written as (using the notation of [
35])
where the function
I3 is defined by
where
U(
x) is the unit step function,
U(
x) = 1 for
x > 0, and
U(
x) = 0 for
x < 0. The quantities
m and
β are given by
while the function Λ
0 takes the form
expressed in the terms of the incomplete elliptic integrals:
and their complete versions,
K(
m) =
F(
π/2|
m) and E(m) =
E(π/2|
m). Upon replacing
W(0,
R′) with
W(
r,
R′) in Equations (20) and (21), we obtain
Equations (22)–(28) provide the surface subsidence field
w(
r) for the pressure distributions (4) and (5). The subsidence profiles of [
9] were deduced by this method.
One may note that the difference in the derivations of the subsidence field obtained in the work of [
9] and in this work, where we arrived at the relatively compact Equations (10) and (11), essentially corresponds to a change in the order of integration between the radial wavenumber and the radial coordinate. Hence, the results are expected to be mathematically and hence numerically equivalent, but they are different in form and hence different with respect to the ease of manipulating and analyzing them. This is indeed shown in the derivation of the deep aquifer asymptotic solutions in Equations (15) and (16).
3. Results
We now turn to the application and further analysis of the mathematical results presented in the previous section. For part of the analysis, we shall adopt the four different cases that describe two relatively shallow and two relatively deep aquifers (for weak and strong sandstones), which were used in [
9]. The input data for the four cases are given in
Table 1.
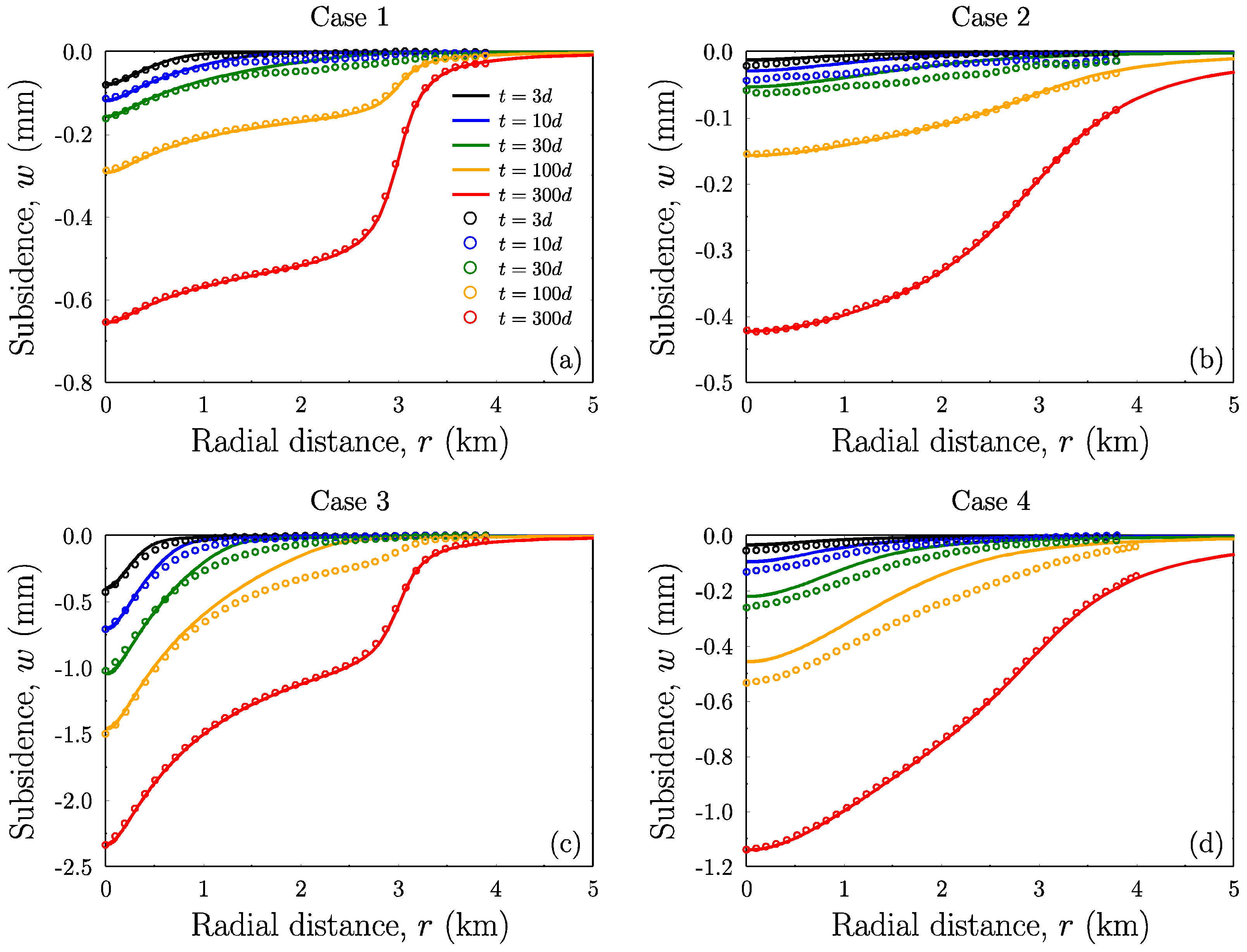
Figure 2 shows the subsidence profiles (in continuous lines) for the four cases of
Table 1, obtained by the proposed method given by Formulas (10) and (11), and from the [
9] method contained in Equations (22)–(28), for production times
t = {3, 10, 30, 100, 300} days.
Only a single curve is given in each case as the results agree exactly in all decimal figures (using the default integration algorithms of Mathematica to perform the integrations). The circles correspond to the numerical simulations given in [
9].
Figure 2a,c corresponds to the case of shallow aquifers while
Figure 2b,d to relatively deep aquifers. Furthermore,
Figure 2a,b corresponds to the strong sandstone while
Figure 2c,d to the weak sandstone.
In
Figure 2a the curves for
t = {100, 300} days and in
Figure 2c the curve for
t = {300} days exhibit a qualitative difference with respect to the other curves, that is the presence of the aquifer outer boundary at 3 km is quite pronounced on the shape of these profiles for which
re >
R. When the rock is strong (case 1), the radius of influence reaches the boundary earlier. For
Figure 2b,d the radius of influence affects the solution in the same way but the larger depth smooths out the influence of the aquifer size on the subsidence profiles.
We observe a certain discrepancy between our results and those of the numerical simulations of [
9] although they appear—in that paper—to be in good agreement with the theoretical calculations of the authors, which we repeat also in this work. Given that there appear certain inconsistencies in the numerics of the semi-analytical calculations of [
9], e.g., the subsidence at the location of the well, which follows from the closed-form solution given here by Equations (13) and (14), does not agree with the presented semi-analytical subsidence profiles (but it does appear to agree with our profiles). We attribute these discrepancies to the numerical precision of the calculations of the authors of [
9].
The influence of the various physical parameters on the subsidence radial distribution is summarized in
Figure 3. Equation (12), stemming from Equations (10) and (11), states that the subsidence radial distribution depends essentially on two dimensionless ratios:
D/
R and
re/
R. The ratio
D/
R, depth over aquifer size, is formed purely by geometry. The second ratio
re/
R involves the dynamics of fluid withdrawal, as the radius of influence depends on time, and also depends on the elastic moduli of the aquifer rock.
The stage of evolution is given in terms of this ratio, and all curves correspond to ratios re/R = {1/7, 3/7, 5/7, 1, 9/7, 11/7} in the indicated colors. Given that re encodes also the influence of elastic moduli, porosity, permeability of the aquifer rock, and the viscosity of the fluid, the ratio re/R quantifies the ‘stage’ of evolution with respect to all these parameters. E.g., for a given production time, a more permeable or strong formation, will be in a more advanced stage, i.e., it will have a larger ratio re/R, than a less permeable or weak formation.
Figure 3 illustrates explicitly the qualitative behavior of the subsidence field in dimensionless form. The scaled subsidence
w/|
w0|, where
w0 is the subsidence at
r = 0 (well location) for each case, is given as function of the scaled radial distance
r/
R. We observe that when the aquifer is shallow, i.e.,
D/
R << 1, the subsidence distribution is essentially negligible outside the radial extent of the aquifer (
Figure 3a,b). One the other hand, for the case of deep aquifer, i.e.,
D/
R near or larger than 1, the effect of the aquifer size on the subsidence distribution is virtually insignificant (
Figure 3c,d). Equations (15)–(17) state the asymptotic solutions that illustrate mathematically such observations. In
Figure 3d, we also include the solution (17) with crossed circle marks, which shows that the asymptotic solutions are in fact an excellent approximation already for
D/
R ~ 2. An implication of this fact is that the subsidence radial distribution is insensitive to variations in the permeability of the rock and the viscosity of the fluid.
4. Conclusions
In this work we study the problem of surface subsidence as a result of fluid withdrawal from a confined aquifer at depth, under assumptions of cylindrical symmetry and formation homogeneity. Disk-shaped homogeneous confined aquifers typically form in geological settings characterized by specific conditions that allow for the development of relatively flat, horizontally extensive aquifer systems. These settings are influenced by various factors such as sedimentary deposition, tectonics, and lithology. In homogeneous formations, where the subsurface materials have consistent properties, such aquifers can occur in the following geological settings: sedimentary basins, lacustrine environments, or fluvial systems. One the other hand, the assumed geometry cannot be accommodated in geological settings like mountainous and hilly terrains, in highly tectonically active areas, or Karstic landscapes.
This idealized problem has been revisited many times in the past due to its importance in both hydrology and petroleum-related applications.
The main findings and results can be summarized as follows:
We deduce novel mathematical expressions for the radial distribution of subsidence utilizing methods by [
28,
29];
We re-derive the subsidence at the well locations deduced by [
9] through a different approach based on [
14]; this method is also discussed in detail;
We derive the analytical asymptotic solutions for the radial distribution of subsidence, w(r), for the case of deep aquifer, showing that these solutions amount to an excellent approximation even when the aquifer depth is larger than the aquifer diameter, and that w(r) is independent of the formation permeability and the fluid viscosity;
Finally, we express and analyze the influence of the physical parameters on the subsidence field through two similarity ratios, namely, the well radius of influence over aquifer radius and aquifer depth over aquifer radius.
The new method and the obtained analytical results present an efficient and robust first approximation for estimating the magnitude of the subsidence field for actual case studies.
These analytical solutions and their properties are essential tools for understanding, managing, and mitigating subsidence resulting from fluid withdrawal. In particular, the results from this work can prove to be beneficial in: (i) predictive modelling, for example in time varying pumping schedules; (ii) environmental impact assessment; (iii) infrastructure planning and design; (iv) resource management; but also (v) for calibrating benchmark solutions in numerical studies in the context of higher complexity.