A Probabilistic Analysis of Drought Areal Extent Using SPEI-Based Severity-Area-Frequency Curves and Reanalysis Data
Abstract
:1. Introduction
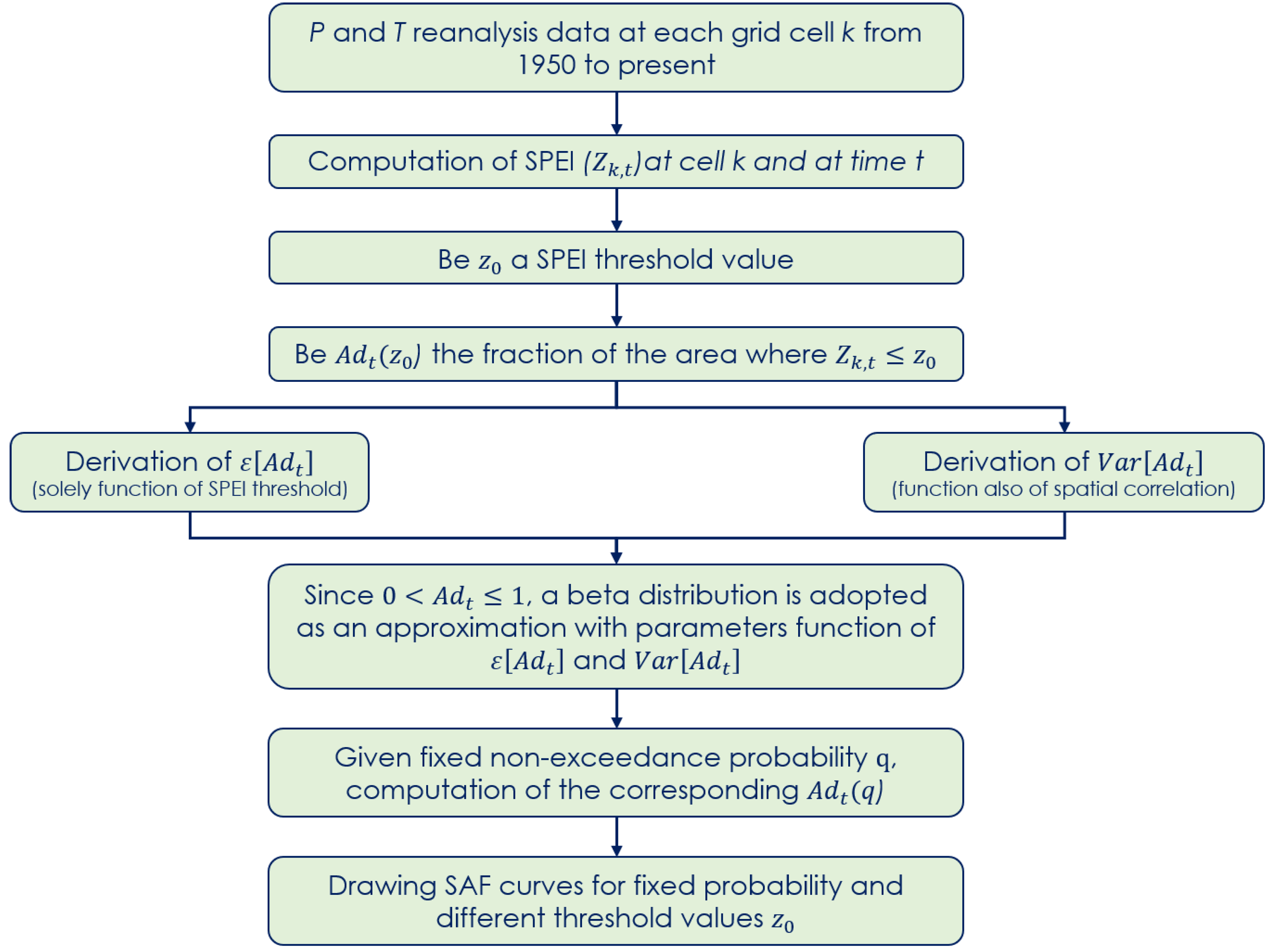
2. Methodology
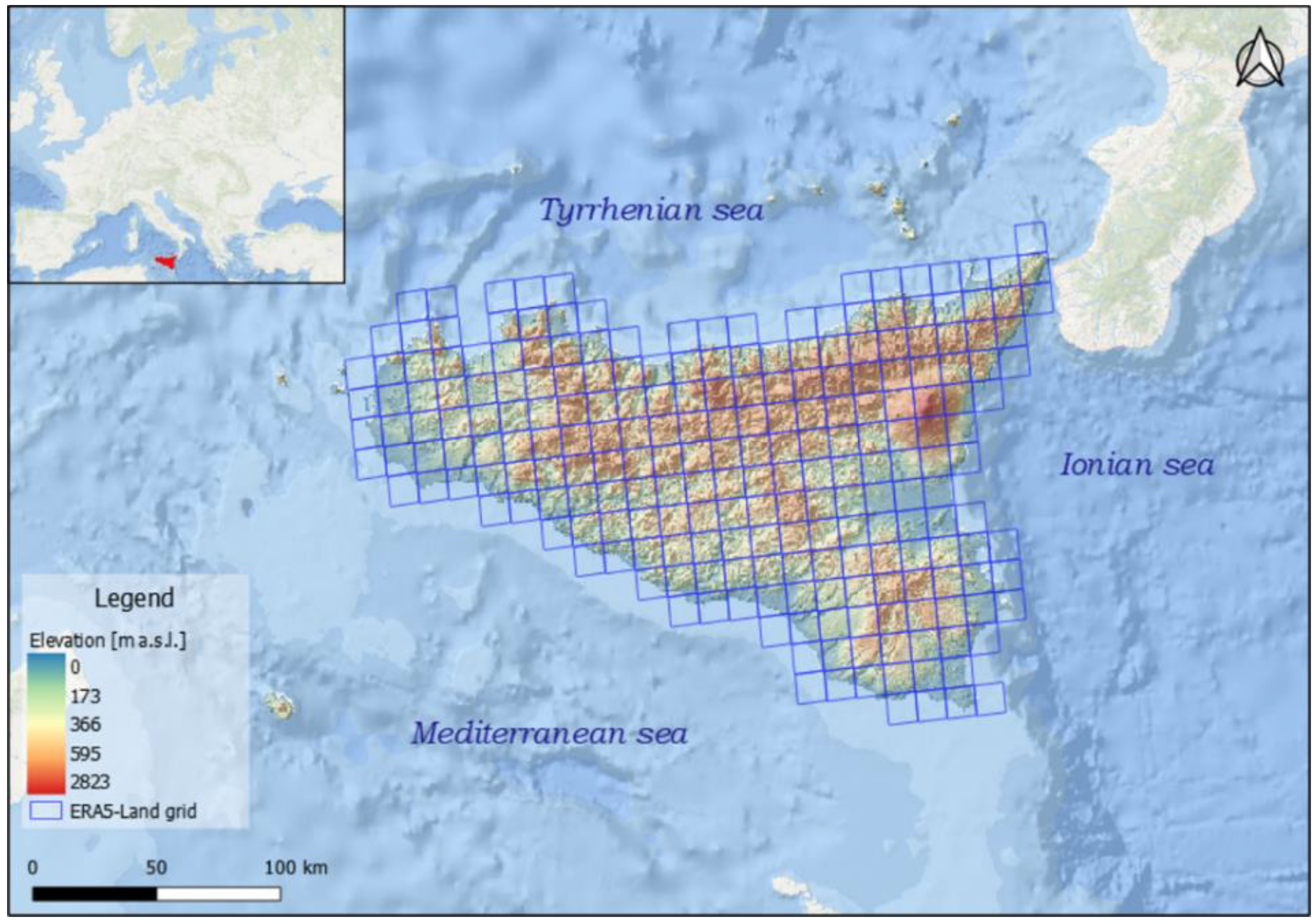
3. Study Area and Data
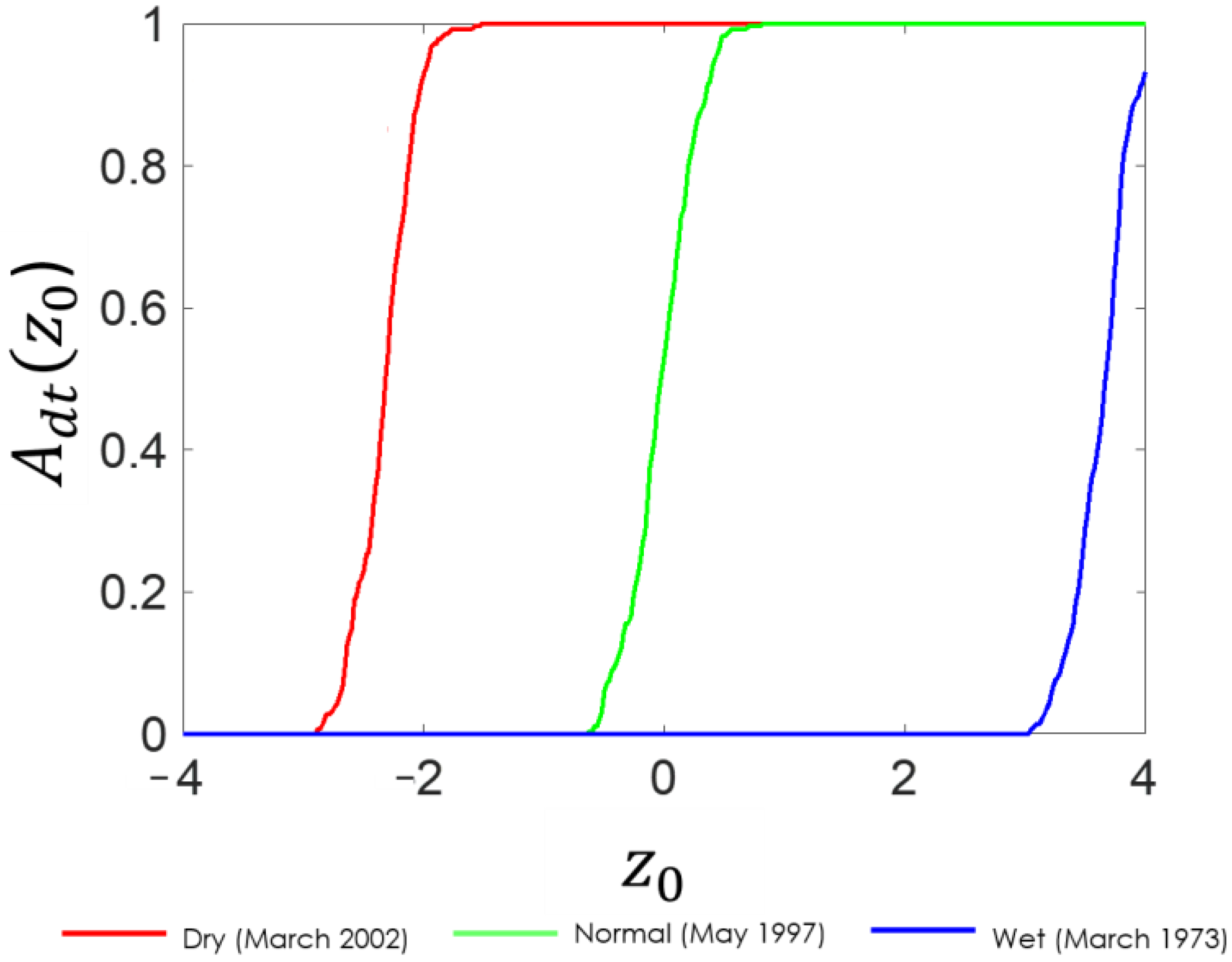
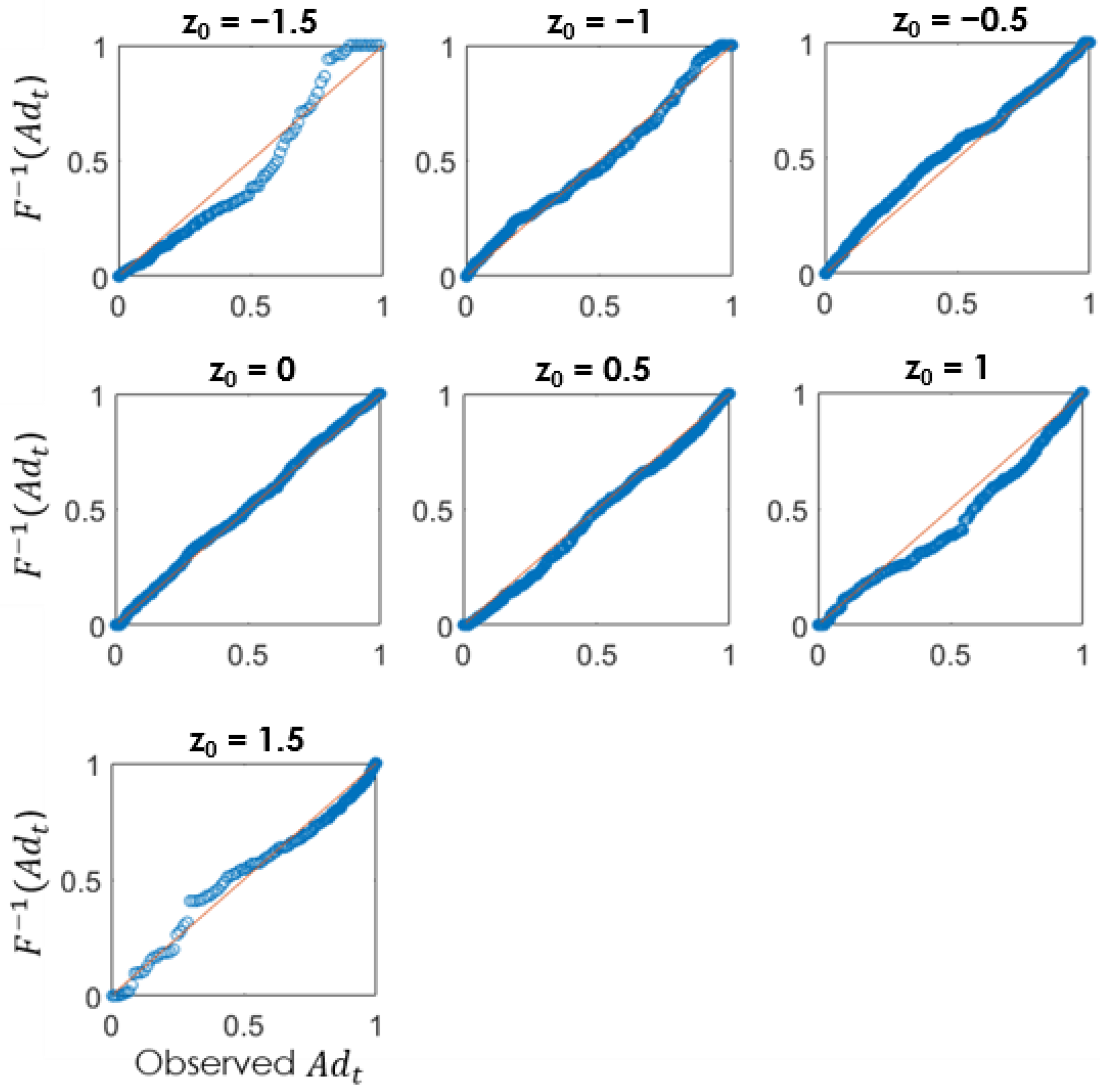
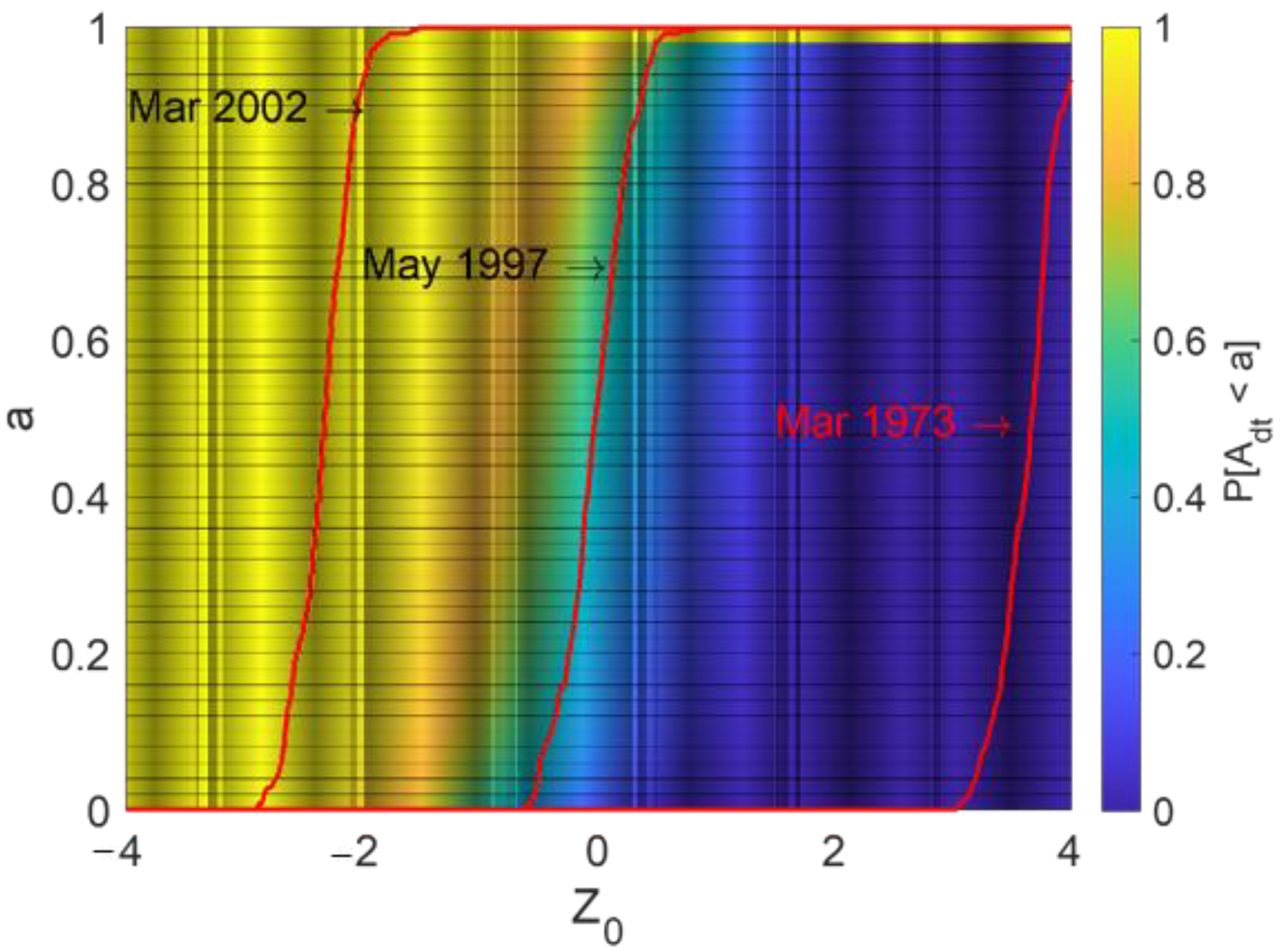
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Orimoloye, I.R.; Belle, J.A.; Orimoloye, Y.M.; Olusola, A.O.; Ololade, O.O. Drought: A Common Environmental Disaster. Atmosphere 2022, 13, 111. [Google Scholar] [CrossRef]
- Bandyopadhyay, N.; Bhuiyan, C.; Saha, A.K. Drought mitigation: Critical analysis and proposal for a new drought policy with special reference to Gujarat (India). Prog. Disaster Sci. 2020, 5, 100049. [Google Scholar] [CrossRef]
- Raziei, T.; Saghafian, B.; Paulo, A.A.; Pereira, L.S.; Bordi, I. Spatial patterns and temporal variability of drought in Western Iran. Water Resour. Manag. 2009, 23, 439–455. [Google Scholar] [CrossRef]
- Martins, D.S.; Raziei, T.; Paulo, A.A.; Pereira, L.S. Spatial and temporal variability of precipitation and drought in Portugal. Nat. Hazards Earth Syst. Sci. 2012, 12, 1493–1501. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Pan, Y.; Li, W. Spatial and temporal variability of drought in the arid region of China and its relationships to teleconnection indices. J. Hydrol. 2015, 523, 283–296. [Google Scholar] [CrossRef]
- Santos, J.F.; Pulido-Calvo, I.; Portela, M.M. Spatial and temporal variability of droughts in Portugal. Water Resour. Res. 2010, 46, W03503. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Rojas, L.P.T.; Díaz-Granados, M. The Construction and Comparison of Regional Drought Severity-Duration-Frequency Curves in Two Colombian River Basins—Study of the Sumapaz and Lebrija Basins. Water 2018, 10, 1453. [Google Scholar] [CrossRef]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- Zelenhasić, E.; Salvai, A. A method of streamflow drought analysis. Water Resour. Res. 1987, 23, 156–168. [Google Scholar] [CrossRef]
- Kendall, D.R.; Dracup, J.A. On the generation of drought events using an alternating renewal-reward model. Stoch. Hydrol. Hydraul. 1992, 6, 55–68. [Google Scholar] [CrossRef]
- Mohan, S.; Sahoo, P.K. Stochastic simulation of droughts. Part 1: Point droughts. Hydrol. Process. 2008, 22, 854–862. [Google Scholar] [CrossRef]
- Cancelliere, A.; Salas, J.D. Drought probabilities and return period for annual streamflows series. J. Hydrol. 2010, 391, 77–89. [Google Scholar] [CrossRef]
- Shah, D.; Mishra, V. Drought Onset and Termination in India. J. Geophys. Res. Atmos. 2020, 125, e2020JD032871. [Google Scholar] [CrossRef]
- Li, Z.; Shao, Q.; Tian, Q.; Zhang, L. Copula-based drought severity-area-frequency curve and its uncertainty, a case study of Heihe River basin, China. Hydrol. Res. 2020, 51, 867–881. [Google Scholar] [CrossRef]
- Dai, A. Characteristics and trends in various forms of the Palmer Drought Severity Index during 1900-2008. J. Geophys. Res. Atmos. 2011, 116, D12115. [Google Scholar] [CrossRef]
- An, Q.; He, H.; Gao, J.; Nie, Q.; Cui, Y.; Wei, C.; Xie, X. Analysis of Temporal-Spatial Variation Characteristics of Drought: A Case Study from Xinjiang, China. Water 2020, 12, 741. [Google Scholar] [CrossRef]
- Das, S.; Das, J.; Umamahesh, N.V. Investigating seasonal drought severity-area-frequency (SAF) curve over Indian region: Incorporating GCM and scenario uncertainties. Stoch. Environ. Res. Risk Assess. 2022, 36, 1597–1614. [Google Scholar] [CrossRef]
- Patil, R.; Polisgowdar, B.S.; Rathod, S.; Bandumula, N.; Mustac, I.; Srinivasa Reddy, G.V.; Wali, V.; Satishkumar, U.; Rao, S.; Kumar, A.; et al. Spatiotemporal Characterization of Drought Magnitude, Severity, and Return Period at Various Time Scales in the Hyderabad Karnataka Region of India. Water 2023, 15, 2483. [Google Scholar] [CrossRef]
- Kumar, P.; Ma, M.; Zang, H.; Wang, W.; Cui, H.; Sun, Y.; Cheng, Y. Copula-Based Severity–Duration–Frequency (SDF) Analysis of Streamflow Drought in the Source Area of the Yellow River, China. Water 2023, 15, 2741. [Google Scholar] [CrossRef]
- Reddy, M.J.; Ganguli, P. Spatio-temporal analysis and derivation of copula-based intensity-area-frequency curves for droughts in western Rajasthan (India). Stoch. Environ. Res. Risk Assess. 2013, 27, 1975–1989. [Google Scholar] [CrossRef]
- Amirataee, B.; Montaseri, M.; Rezaie, H. Regional analysis and derivation of copula-based drought Severity-Area-Frequency curve in Lake Urmia basin, Iran. J. Environ. Manag. 2018, 206, 134–144. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.W.; Valdés, J.B.; Aparicio, J. Frequency and spatial characteristics of droughts in the Conchos River Basin, Mexico. Water Int. 2002, 27, 420–430. [Google Scholar] [CrossRef]
- Loukas, A.; Vasiliades, L. Probabilistic analysis of drought spatiotemporal characteristics inThessaly region, Greece. Nat. Hazards Earth Syst. Sci. 2004, 4, 719–731. [Google Scholar] [CrossRef]
- Mishra, A.K.; Desai, V.R. Spatial and temporal drought analysis in the Kansabati river basin, India. Int. J. River Basin Manag. 2005, 3, 43–52. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Analysis of drought severity-area-frequency curves using a general circulation model and scenario uncertainty. J. Geophys. Res. Atmos. 2009, 114, D06120. [Google Scholar] [CrossRef]
- Sordo-Ward, A.; Bejarano, M.D.; Iglesias, A.; Asenjo, V.; Garrote, L. Analysis of Current and Future SPEI Droughts in the La Plata Basin Based on Results from the Regional Eta Climate Model. Water 2017, 9, 857. [Google Scholar] [CrossRef]
- Santos, M.A. Regional droughts: A stochastic characterization. J. Hydrol. 1983, 66, 183–211. [Google Scholar] [CrossRef]
- Cancelliere, A. Stochastic Characterization of Droughts in Stationary and Periodic Series; ProQuest Dissertations Publishing, Colorado State University: Fort Collins, CO, USA, 2011. [Google Scholar]
- Bonaccorso, B.; Peres, D.J.; Castano, A.; Cancelliere, A. SPI-Based Probabilistic Analysis of Drought Areal Extent in Sicily. Water Resour. Manag. 2015, 29, 459–470. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Achite, M.; Bazrafshan, O.; Katipoğlu, O.M.; Azhdari, Z. Evaluation of hydro-meteorological drought indices for characterizing historical droughts in the Mediterranean climate of Algeria. Nat. Hazards 2023, 118, 427–453. [Google Scholar] [CrossRef]
- Peres, D.J.; Bonaccorso, B.; Palazzolo, N.; Cancelliere, A.; Mendicino, G.; Senatore, A. A dynamic approach for assessing climate change impacts on drought: An analysis in Southern Italy. Hydrol. Sci. J. 2023, 68, 1213–1228. [Google Scholar] [CrossRef]
- Muñoz Sabater, J. ERA5-Land monthly averaged data from 1950 to present. Copernic. Clim. Chang. Serv. Clim. Data Store 2019. [Google Scholar] [CrossRef]
- Vanella, D.; Longo-Minnolo, G.; Belfiore, O.R.; Ramírez-Cuesta, J.M.; Pappalardo, S.; Consoli, S.; D’Urso, G.; Chirico, G.B.; Coppola, A.; Comegna, A.; et al. Comparing the use of ERA5 reanalysis dataset and ground-based agrometeorological data under different climates and topography in Italy. J. Hydrol. Reg. Stud. 2022, 42, 101182. [Google Scholar] [CrossRef]
- Li, M.; Wu, P.; Ma, Z. A comprehensive evaluation of soil moisture and soil temperature from third-generation atmospheric and land reanalysis data sets. Int. J. Climatol. 2020, 40, 5744–5766. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An Approach toward a Rational Classification of Climate. Geogr. Rev. 1948, 38, 55. [Google Scholar] [CrossRef]
- Norman, L.; Johnson, S.; Kotz, N.B. “14: Lognormal Distributions”, Continuous univariate distributions. Wiley Ser. Probab. Math. Stat. Appl. Probab. Stat. 1994, 1, 119. [Google Scholar]
- Sheffield, J.; Goteti, G.; Wen, F.; Wood, E.F. A simulated soil moisture based drought analysis for the United States. J. Geophys. Res. D Atmos. 2004, 109, 1–19. [Google Scholar] [CrossRef]
- Mendicino, G.; Senatore, A.; Versace, P. A Groundwater Resource Index (GRI) for drought monitoring and forecasting in a mediterranean climate. J. Hydrol. 2008, 357, 282–302. [Google Scholar] [CrossRef]
- Rossi, G.; Benedini, M. Water Resources of Italy; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Peres, D.J.; Senatore, A.; Nanni, P.; Cancelliere, A.; Mendicino, G.; Bonaccorso, B. Evaluation of EURO-CORDEX (Coordinated Regional Climate Downscaling Experiment for the Euro-Mediterranean area) historical simulations by high-quality observational datasets in southern Italy: Insights on drought assessment. Nat. Hazards Earth Syst. Sci. 2020, 20, 3057–3082. [Google Scholar] [CrossRef]
- Di Mauro, G.; Bonaccorso, B.; Cancelliere, A.; Rossi, G. Use of NAO index to improve drought forecasting in the Mediterranean area: Application to Sicily region. In Drought Management: Scientific and Technological Innovations; López-Francos, A., Ed.; CIHEAM: Zaragoza, Spain, 2008; pp. 311–319. [Google Scholar]
- Hurrell, J.W. Decadal Trends in the North Atlantic Oscillation: Regional Temperatures and Precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef] [PubMed]

| Categories | SPEI Values |
|---|---|
| Extremely drought | Less than −2 |
| Severe drought | −1.99 to −1.50 |
| Moderately drought | −1.49 to −1.00 |
| Near normal | −0.99 to 0.99 |
| Moderately wet | 1.00 to 1.49 |
| Severely wet | 1.50 to 1.99 |
| Extremely wet | More than 2.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palazzolo, N.; Peres, D.J.; Bonaccorso, B.; Cancelliere, A. A Probabilistic Analysis of Drought Areal Extent Using SPEI-Based Severity-Area-Frequency Curves and Reanalysis Data. Water 2023, 15, 3141. https://doi.org/10.3390/w15173141
Palazzolo N, Peres DJ, Bonaccorso B, Cancelliere A. A Probabilistic Analysis of Drought Areal Extent Using SPEI-Based Severity-Area-Frequency Curves and Reanalysis Data. Water. 2023; 15(17):3141. https://doi.org/10.3390/w15173141
Chicago/Turabian StylePalazzolo, Nunziarita, David J. Peres, Brunella Bonaccorso, and Antonino Cancelliere. 2023. "A Probabilistic Analysis of Drought Areal Extent Using SPEI-Based Severity-Area-Frequency Curves and Reanalysis Data" Water 15, no. 17: 3141. https://doi.org/10.3390/w15173141






