A Special Ordered Set of Type 2 Modeling for a Monthly Hydropower Scheduling of Cascaded Reservoirs with Spillage Controllable
Abstract
:1. Introduction
2. Problem Formulation
3. Solution Techniques
3.1. Spillage as a Nonlinear Function
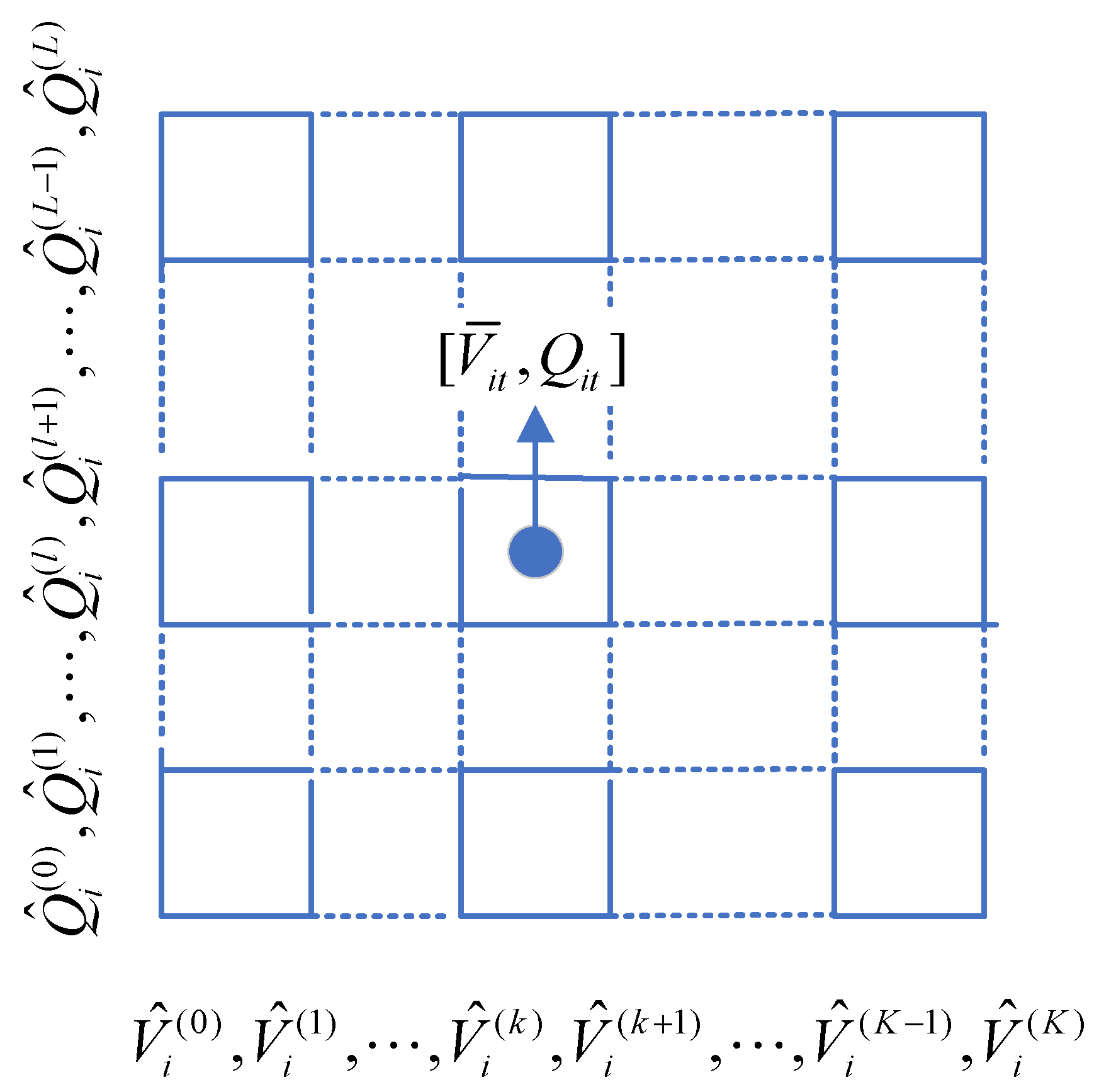
3.2. SOS2 Formulation
4. Case Studies
4.1. Engineering Background
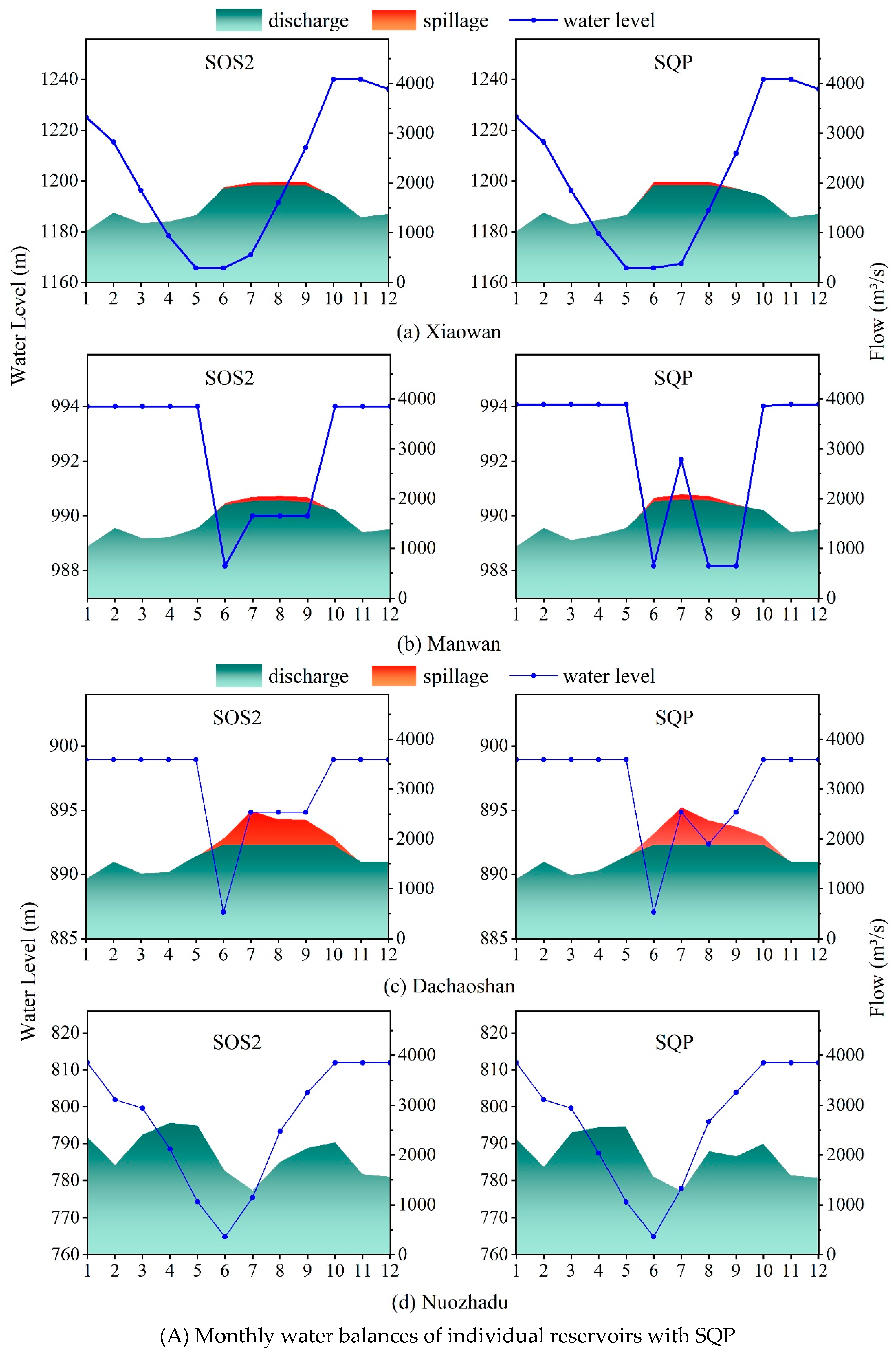
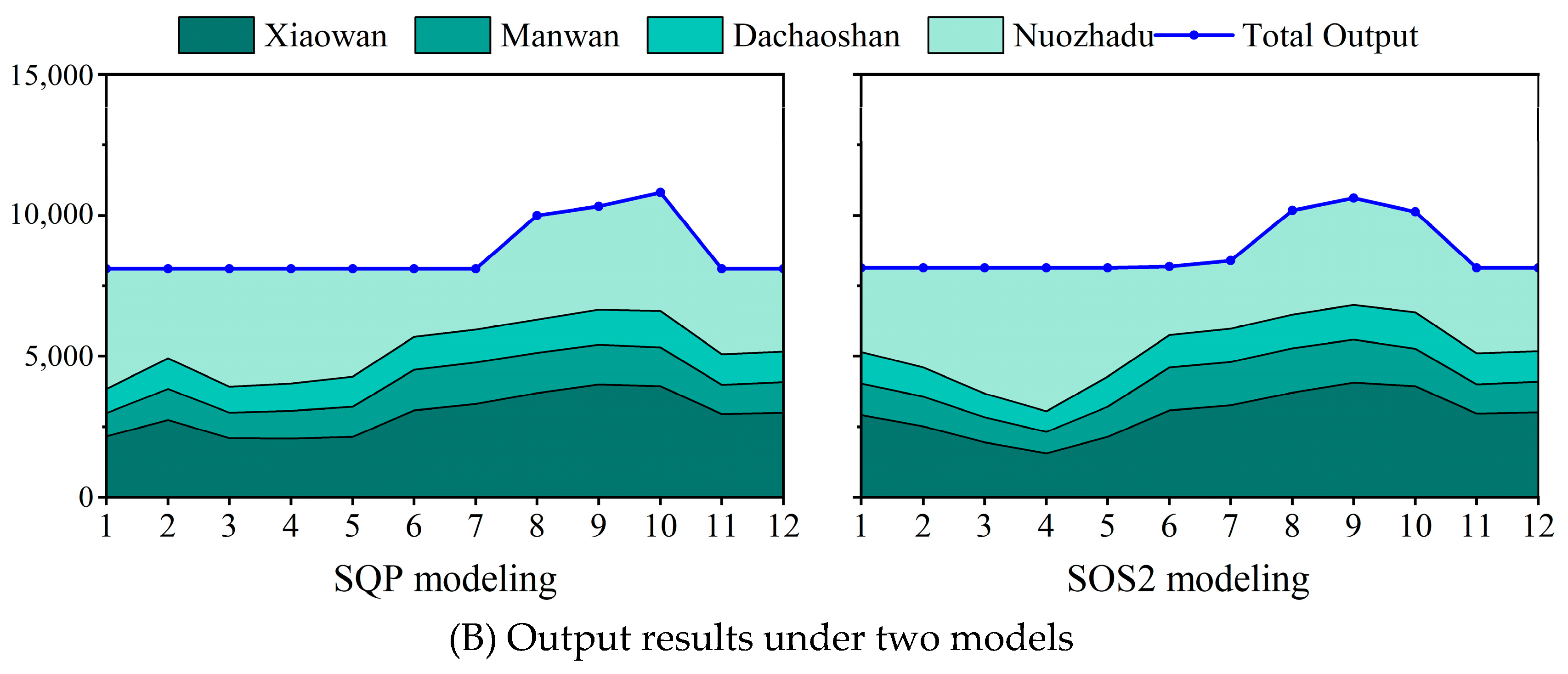
4.2. Detailed Results of Four Cascaded Hydropower Plants
4.3. Solution Efficiency of SOS2 Modeling
4.4. Comparisons with SQP
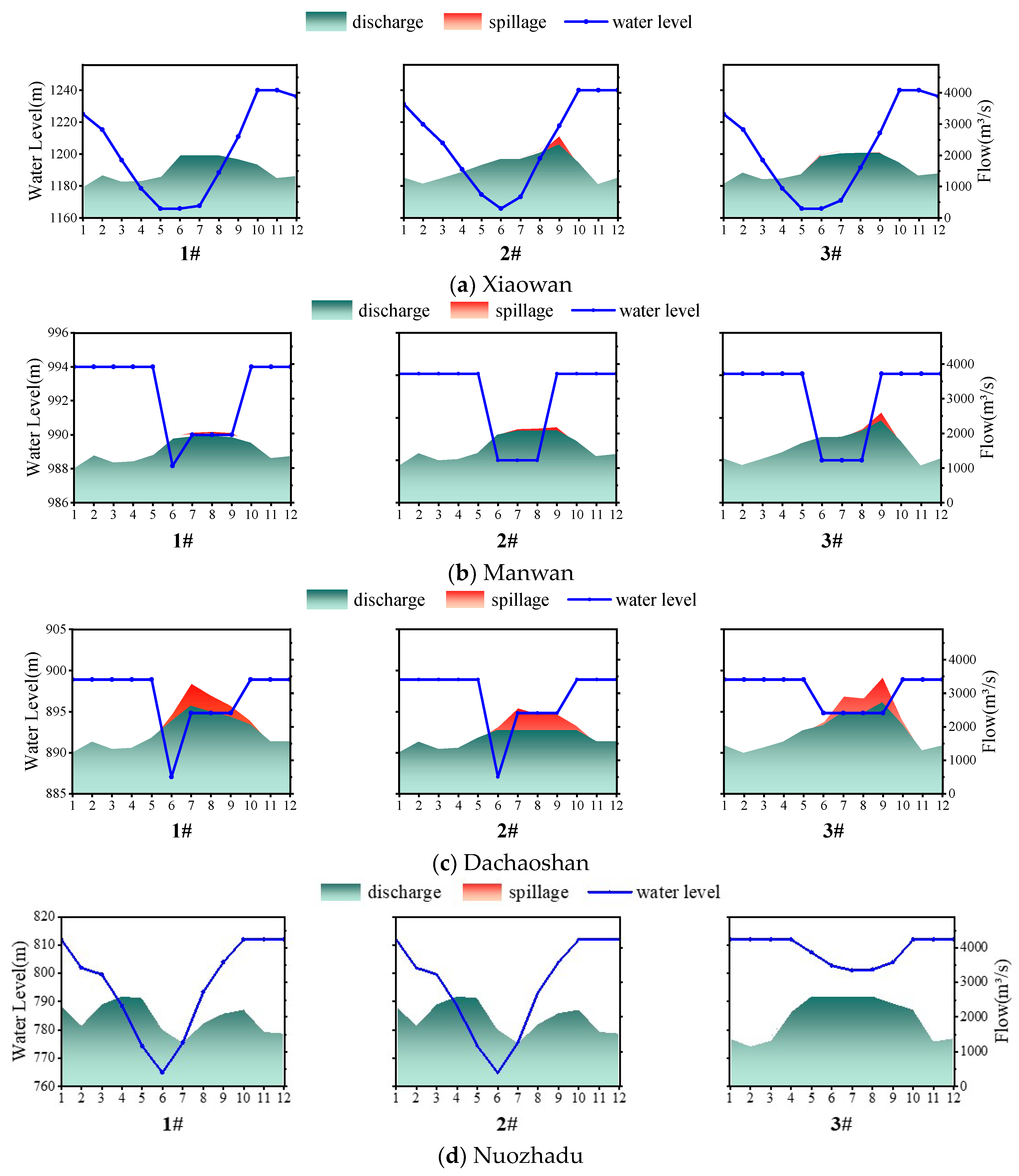
4.5. Impacts on Results by Prioritizing the Objectives in Different Ways
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Wang, X.; Lei, X.; Liao, W.; Wang, C.; Wang, J. The development and prospect of key techniques in the cascade reservoir operation. J. Hydraul. Eng. 2019, 50, 25–37. [Google Scholar]
- Ming, B.; Huang, Q.; Wang, Y.; Wei, J.; Tian, T. Search space reduction method and its application to hydroelectric operation of multi-reservoir systems. J. Hydroelectr. Eng. 2015, 34, 51–59. [Google Scholar]
- Zheng, H.; Feng, S.; Chen, C.; Wang, J. A new three-triangle based method to linearly concave hydropower output in long-term reservoir operation. Energy 2022, 250, 123784. [Google Scholar] [CrossRef]
- Zhuang-zhi, G.U.O.; Jie-kang, W.U.; Fan-nie, K.; Yu-nan, Z.H.U. Long-Term Optimization Scheduling Based on Maximal Storage Energy Exploitation of Cascaded Hydro-plant Reservoirs. Proc. Chin. Soc. Electr. Eng. 2010, 30, 20–26. [Google Scholar]
- Little, J.D.C. The Use of Storage Water in a Hydroelectric System. J. Oper. Res. Soc. Am. 1955, 3, 187–197. [Google Scholar] [CrossRef]
- Ahmed, J.A.; Sarma, A.K. Genetic Algorithm for Optimal Operating Policy of a Multipurpose Reservoir. Water Resour. Manag. 2005, 19, 145–161. [Google Scholar] [CrossRef]
- Guo, X.; Qin, T.; Lei, X.; Jiang, Y.; Wang, H. Advances in derivation method for multi-reservoir joint operation policy. J. Hydroelectr. Eng. 2016, 35, 19–27. [Google Scholar]
- Denham, W. Differential dynamic programming. IEEE Trans. Autom. Control 1971, 16, 389–390. [Google Scholar] [CrossRef]
- Shi, Y.; Peng, Y.; Xu, W. Optimal operation model of cascade reservoirs based on grey discrete differential dynamic programming. J. Hydroelectr. Eng. 2016, 35, 35–44. [Google Scholar]
- Liu, S.; Luo, J.; Chen, H.; Wang, Y.; Li, X.; Zhang, J.; Wang, J. Third-Monthly Hydropower Scheduling of Cascaded Reservoirs Using Successive Quadratic Programming in Trust Corridor. Water 2023, 15, 716. [Google Scholar] [CrossRef]
- Jothiprakash, V.; Arunkumar, R. Optimization of Hydropower Reservoir Using Evolutionary Algorithms Coupled with Chaos. Water Resour. Manag. 2013, 27, 1963–1979. [Google Scholar] [CrossRef]
- Wardlaw, R.; Sharif, M. Evaluation of Genetic Algorithms for Optimal Reservoir System Operation. J. Water Resour. Plan. Manag. 1999, 125, 25–33. [Google Scholar] [CrossRef]
- Ma, J.; Teng, G. Study on the feature construction method based on genetic programming. J. Agric. Univ. Hebei 2018, 41, 130–136. [Google Scholar]
- Wei, Z.Y.Z.; Zhiwu, L.; Pan, L.; Mengjie, L. Deep learning model guided by physical mechanism for reservoir operation. J. Hydroelectr. Eng. 2023, 42, 13–25. [Google Scholar] [CrossRef]
- Zhou, J.; Peng, T.; Zhang, C.; Sun, N. Data Pre-Analysis and Ensemble of Various Artificial Neural Networks for Monthly Streamflow Forecasting. Water 2018, 10, 628. [Google Scholar] [CrossRef]
- Baltar, A.M.; Fontane, D.G. Use of Multiobjective Particle Swarm Optimization in Water Resources Management. J. Water Resour. Plan. Manag. 2008, 134, 257–265. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, X.; Qin, H. Optimal operation of multi-reservoir hydropower systems using enhanced comprehensive learning particle swarm optimization. J. Hydro-Environ. Res. 2016, 10, 50–63. [Google Scholar] [CrossRef]
- Diao, Y.; Ma, H.; Wang, H.; Wang, J.; Li, S.; Li, X.; Pan, J.; Qiu, Q. Optimal Flood-Control Operation of Cascade Reservoirs Using an Improved Particle Swarm Optimization Algorithm. Water 2022, 14, 1239. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, J.; Lu, P.; Yuan, L. Long-term scheduling of large cascade hydropower stations in Jinsha River, China. Energy Convers. Manag. 2015, 90, 476–487. [Google Scholar] [CrossRef]
- Zhou, B.; Feng, S.; Xu, Z.; Jiang, Y.; Wang, Y.; Chen, K.; Wang, J. A Monthly Hydropower Scheduling Model of Cascaded Reservoirs with the Zoutendijk Method. Water 2022, 14, 3978. [Google Scholar] [CrossRef]
- Feng, S.Z.; Zheng, H.; Qiao, Y.F.; Yang, Z.T.; Wang, J.W.; Liu, S.Q. Weekly hydropower scheduling of cascaded reservoirs with hourly power and capacity balances. Appl. Energy 2022, 311, 118620. [Google Scholar] [CrossRef]
- Wang, C.; Guo, S.; Liu, P.; Zhou, F.; Xiong, L. Risk criteria and comprehensive evaluation model for the operation of Three Gorges reservoir under dynamic flood limit water level. Adv. Water Sci. 2004, 15, 376–381. [Google Scholar]
- Ai, X.; Fan, W. On Reservoir Ecological Operation Model. Resour. Environ. Yangtze Basin 2008, 17, 451–455. [Google Scholar]
- Zhang, W.; Wang, X.; Lei, X.; Liu, P.; Wang, H. Adaptive reservoir operating rules based on the Dempster-Shafer evidence theory. Adv. Water Sci. 2018, 29, 685–695. [Google Scholar]
- Zhong, J.; Dong, Z.; Yao, H.; Ni, X.; Chen, M.; Jia, W.; Ye, H. Multi-objective operation rules for cascade reservoirs. Case study of Xiluodu-Xiangjiaba cascade. J. Hydroelectr. Eng. 2021, 40, 46–54. [Google Scholar]
- Chen, C.; Kang, C.; Wang, J. Stochastic Linear Programming for Reservoir Operation with Constraints on Reliability and Vulnerability. Water 2018, 10, 175. [Google Scholar] [CrossRef]
- Beale, E.; Tomlin, J. Special facilities in a general mathematical programming system for nonconvex problems using ordered sets of variables. Oper. Res. 1969, 69, 447–454. [Google Scholar]
- Beale, E. Branch and Bound Methods for Mathematical Programming Systems. Ann. Discret. Math. 1979, 5, 201–219. [Google Scholar] [CrossRef]
- Kang, C.; Guo, M.; Wang, J. Short-Term Hydrothermal Scheduling Using a Two-Stage Linear Programming with Special Ordered Sets Method. Water Resour. Manag. 2017, 31, 3329–3341. [Google Scholar] [CrossRef]
- Yu, H.J.X.; Shen, J.J.; Cheng, C.T.; Lu, J.; Cai, H.X. Multi-Objective Optimal Long-Term Operation of Cascade Hydropower for Multi-Market Portfolio and Energy Stored at End of Year. Energies 2023, 16, 604. [Google Scholar] [CrossRef]
- Ilich, N. WEB.BM-a web-based river basin management model with multiple time-step optimization and the SSARR channel routing options. Hydrol. Sci. J. J. DES Sci. Hydrol. 2022, 67, 175–190. [Google Scholar] [CrossRef]


| V | Q | ||||||
|---|---|---|---|---|---|---|---|
| … | … | ||||||
| … | … | ||||||
| … | … | ||||||
| … | … | ||||||
| … | … | ||||||
| … | … | ||||||
| Name | Installed Capacity (MW) | Storage Capacity (108 m3) | Dam Height (m) | Water Level (m) | Operability | ||
|---|---|---|---|---|---|---|---|
| Flood | Normal | Dead | |||||
| Xiaowan | 4200 | 149.14 | 294.5 | 1232 | 1240 | 1166 | Annual |
| Manwan | 1670 | 5.02 | 132 | 994 | 994 | 988 | Seasonal |
| Dachaoshan | 1350 | 9.40 | 111 | 899 | 899 | 887 | Seasonal |
| Nuozhadu | 5850 | 126.70 | 261.5 | 804 | 812 | 765 | Over-year |
| Station | Starting Conditions | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sept | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Xiaowan | Local Inflow (m3/s) | 433 | 394 | 434 | 780 | 1350 | 2098 | 2844 | 3147 | 3781 | 1747 | 1037 | 642 | |
| Storage (mcm) | 11,937.09 | 10,380.27 | 7761.05 | 5785.14 | 4642 | 4642 | 5073.75 | 7194.42 | 10,054.05 | 14,557 | 14,557 | 13,841.62 | 11,937.09 | |
| Qspl (m3/s) | 0 | 0 | 0 | 0 | 0 | 36.02 | 76.14 | 83.75 | 89.67 | 0 | 0 | 0 | ||
| Qhp (m3/s) | 1033.63 | 1404.5 | 1196.31 | 1221.02 | 1350 | 1895.41 | 1949.70 | 1960 | 1954.08 | 1747 | 1313.00 | 1376.77 | ||
| Power (MW) | 2160.69 | 2742.34 | 2137.16 | 2007.89 | 2133.77 | 3018.06 | 3342.26 | 3739.61 | 4168.22 | 3939.98 | 2950.53 | 2999.469 | ||
| Energy (GWh) | 1607.55 | 1908.67 | 1590.05 | 1445.68 | 1587.53 | 2173.01 | 2486.64 | 2782.27 | 3001.12 | 2931.34 | 2124.381 | 2231.61 | ||
| Manwan | Local Inflow (m3/s) | 1038.63 | 1408.5 | 1201.31 | 1229.02 | 1364 | 1953.43 | 2055.84 | 2076.75 | 2083.75 | 1765 | 1324.00 | 1383.77 | |
| Storage (mcm) | 372 | 372 | 372 | 372 | 372 | 249 | 284.1 | 284.1 | 284.1 | 372 | 372 | 372 | 372 | |
| Qspl (m3/s) | 0 | 0 | 0 | 0 | 0 | 56.40 | 102.61 | 110.94 | 120.02 | 0 | 0 | 0 | ||
| Qhp (m3/s) | 1038.63 | 1408.5 | 1201.31 | 1229.02 | 1411.45 | 1883.48 | 1953.23 | 1965.81 | 1929.82 | 1765 | 1324 | 1383.77 | ||
| Power (MW) | 821.59 | 1103.93 | 945.78 | 966.94 | 1073.60 | 1385.82 | 1448.42 | 1457.18 | 1465.22 | 1376.05 | 1039.43 | 1085.05 | ||
| Energy (GWh) | 611.27 | 768.34 | 703.66 | 696.19 | 798.76 | 997.79 | 1077.62 | 1084.14 | 1054.96 | 1023.78 | 748.39 | 807.28 | ||
| Dachaoshan | Local Inflow (m3/s) | 1200.63 | 1537.5 | 1309.31 | 1338.02 | 1547.45 | 2099.87 | 2591.84 | 2416.75 | 2448.84 | 2060 | 1546 | 1540.77 | |
| Storage (mcm) | 740 | 740 | 740 | 740 | 740 | 465 | 637 | 637 | 637 | 740 | 740 | 740 | 740 | |
| Qspl (m3/s) | 0 | 0 | 0 | 0 | 0 | 150.53 | 708.84 | 533.75 | 526.1 | 177 | 0 | 0 | ||
| Qhp (m3/s) | 1200.63 | 1537.5 | 1309.31 | 1338.02 | 1653.55 | 1883 | 1883 | 1883 | 1883 | 1883 | 1546 | 1540.77 | ||
| Power (MW) | 859.72 | 1076.78 | 929.52 | 947.95 | 1073.61 | 1169.65 | 1195.14 | 1206.40 | 1241.09 | 1294.89 | 1082.35 | 1078.92 | ||
| Energy (GWh) | 639.63 | 749.44 | 691.57 | 682.53 | 798.76 | 842.15 | 889.19 | 897.56 | 893.59 | 963.40 | 779.29 | 802.72 | ||
| Nuozhadu | Local Inflow (m3/s) | 1200.63 | 1537.5 | 1323.31 | 1447.02 | 1895.549 | 2461.53 | 2852.84 | 2957.75 | 3069.1 | 2254 | 1614 | 1563.77 | |
| Storage (mcm) | 21,749 | 18,776.28 | 18,109.63 | 15,296.7 | 12,203.22 | 10,414 | 12,441.58 | 16,500.31 | 19,337 | 21,749 | 21,749 | 21,749 | 21,749 | |
| Qspl (m3/s) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| Qhp (m3/s) | 2347.51 | 1794.7 | 2408.55 | 2640.5 | 2585.83 | 1679.28 | 1286.97 | 1863.35 | 2138.54 | 2254 | 1614 | 1563.77 | ||
| Power (MW) | 4257.04 | 3175.99 | 4086.57 | 4176.26 | 3818.06 | 2525.50 | 2113.22 | 3262.11 | 3906.89 | 4187.95 | 3026.73 | 2935.59 | ||
| Energy (GWh) | 3167.24 | 2210.49 | 3040.41 | 3006.91 | 2840.64 | 1818.36 | 1572.23 | 2427.01 | 2812.96 | 3115.84 | 2179.24 | 2184.08 |
| 4 × 4 | 8 × 8 | 15 × 15 | 20 × 20 | 25 × 25 | |
|---|---|---|---|---|---|
| Spillage (m3/s) | 30,731.2 | 13,799.8 | 2431.4 | 2128.3 | 1951.4 |
| F (MW) | 5,511,737.2 | 7,067,768.6 | 8,042,369.1 | 8,097,267.3 | 8,093,758.3 |
| P (MW) | 72,789,359.6 | 90,731,379.7 | 103,268,755.2 | 103,975,851.6 | 104,052,755.0 |
| Obj | 25,146,663.1 | 6,641,342.9 | −5,714,286.2 | −6,072,947.9 | −6,246,391.5 |
| Number of variables | 1495 | 4183 | 12,583 | 21,181 | 32,462 |
| CPU time (s) | 0.14 | 0.68 | 4.70 | 10.00 | 31.59 |
| ∑Spillage (m3/s) | F (GW) | ∑P (GW) | Obj (MW) | Number of Variables | CPU Time (s) | |
|---|---|---|---|---|---|---|
| SOS2 | 2734.58 | 8.09 | 104.05 | −6246.39 | 32,462 | 31.59 |
| SQP | 2750.66 | 8.04 | 104.00 | −6074.57 | 725 | 100.19 |
| 0.58% ↓ | 0.62% ↑ | 0.05 ↑ | 2.83% ↓ | - | 0.68% ↓ |
| Experiments | Weights | Spillage | Firm Output | Total Output | ||
|---|---|---|---|---|---|---|
| W1 | W2 | W3 | (hm3) | (MW) | (GW) | |
| 1# | 1000 | 1 | 0.001 | 6318.709 | 7914.266 | 104.053 |
| 2# | 0.001 | 1000 | 1 | 6355.715 | 8138.426 | 104.237 |
| 3# | 0.001 | 1 | 1000 | 6601.307 | 6917.175 | 107.122 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Qian, G.; Xu, Z.; Wang, H.; Chen, K.; Wang, J.; Feng, S. A Special Ordered Set of Type 2 Modeling for a Monthly Hydropower Scheduling of Cascaded Reservoirs with Spillage Controllable. Water 2023, 15, 3128. https://doi.org/10.3390/w15173128
Liu S, Qian G, Xu Z, Wang H, Chen K, Wang J, Feng S. A Special Ordered Set of Type 2 Modeling for a Monthly Hydropower Scheduling of Cascaded Reservoirs with Spillage Controllable. Water. 2023; 15(17):3128. https://doi.org/10.3390/w15173128
Chicago/Turabian StyleLiu, Shuangquan, Guoyuan Qian, Zifan Xu, Hua Wang, Kai Chen, Jinwen Wang, and Suzhen Feng. 2023. "A Special Ordered Set of Type 2 Modeling for a Monthly Hydropower Scheduling of Cascaded Reservoirs with Spillage Controllable" Water 15, no. 17: 3128. https://doi.org/10.3390/w15173128






