Development of Simple Formula for Transverse Dispersion Coefficient in Meandering Rivers
Abstract
:1. Introduction
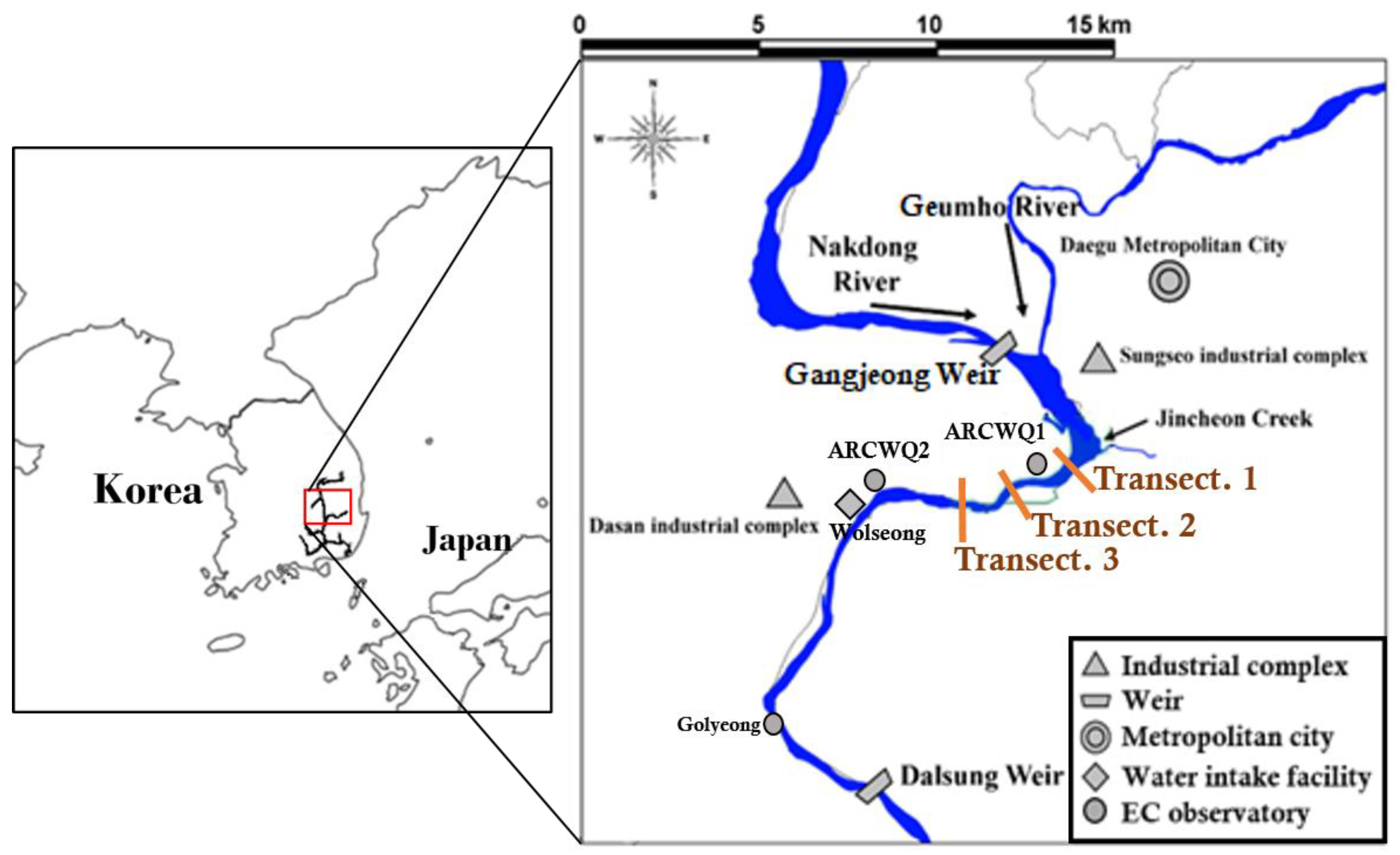
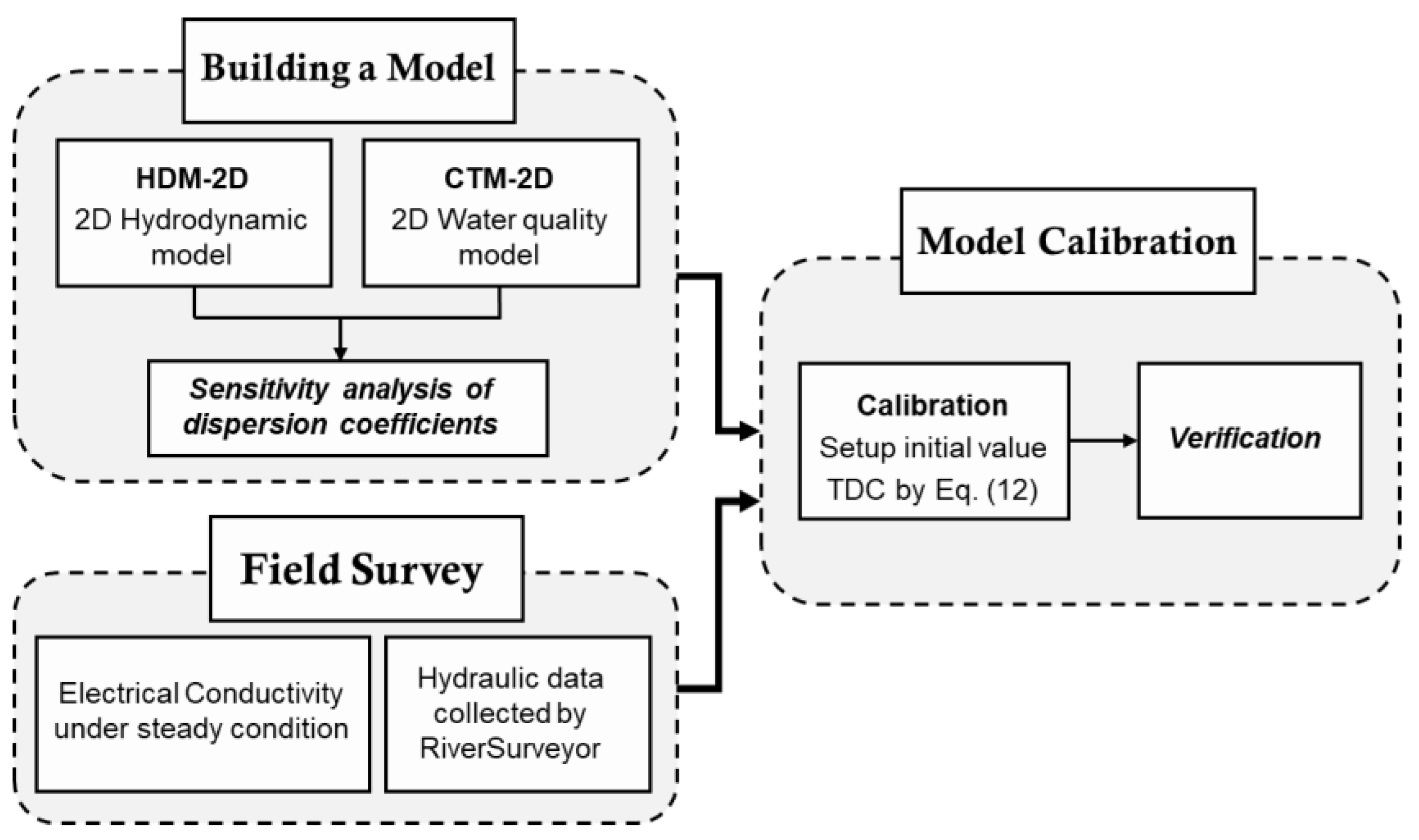
2. Methods
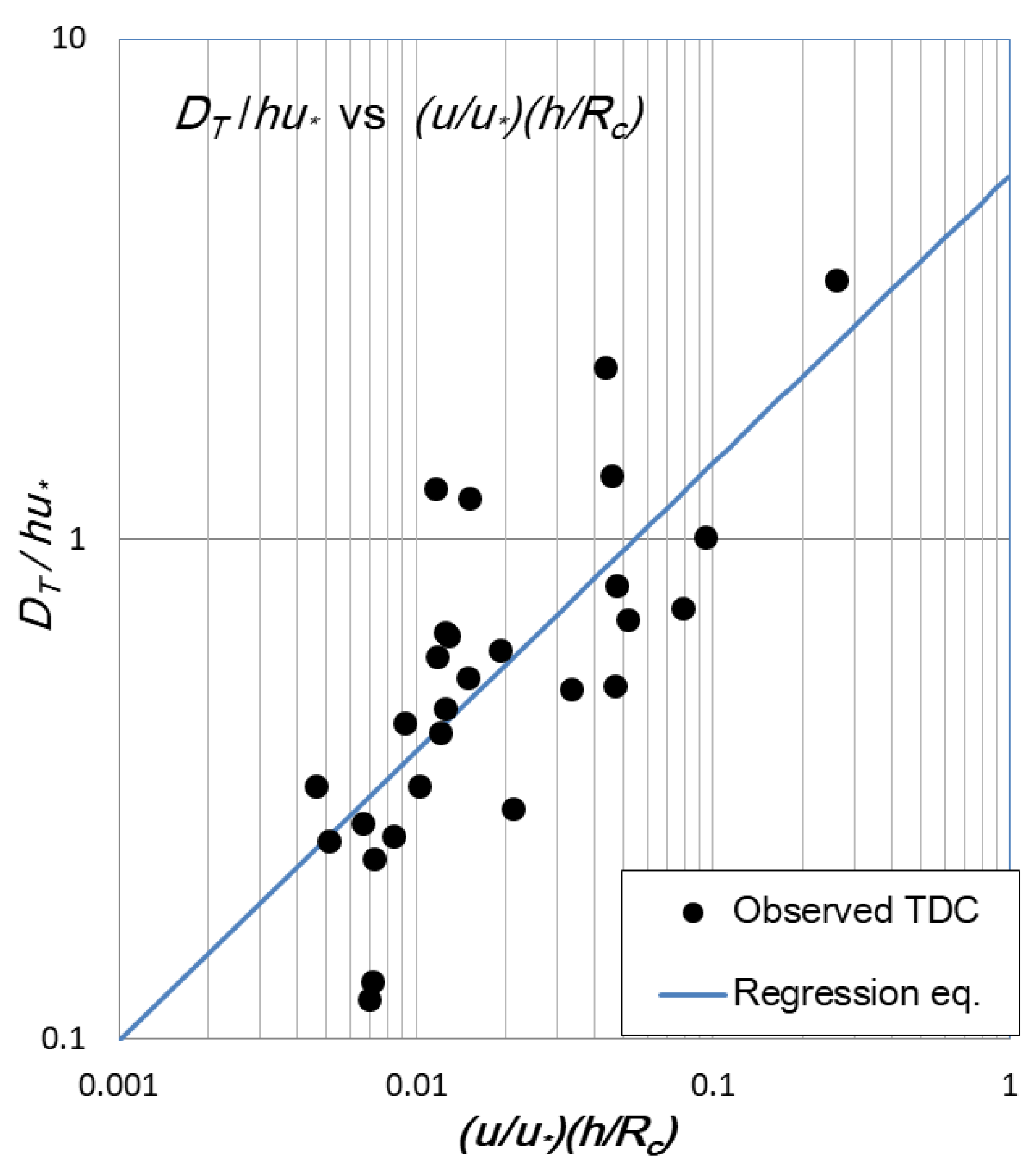
3. Results
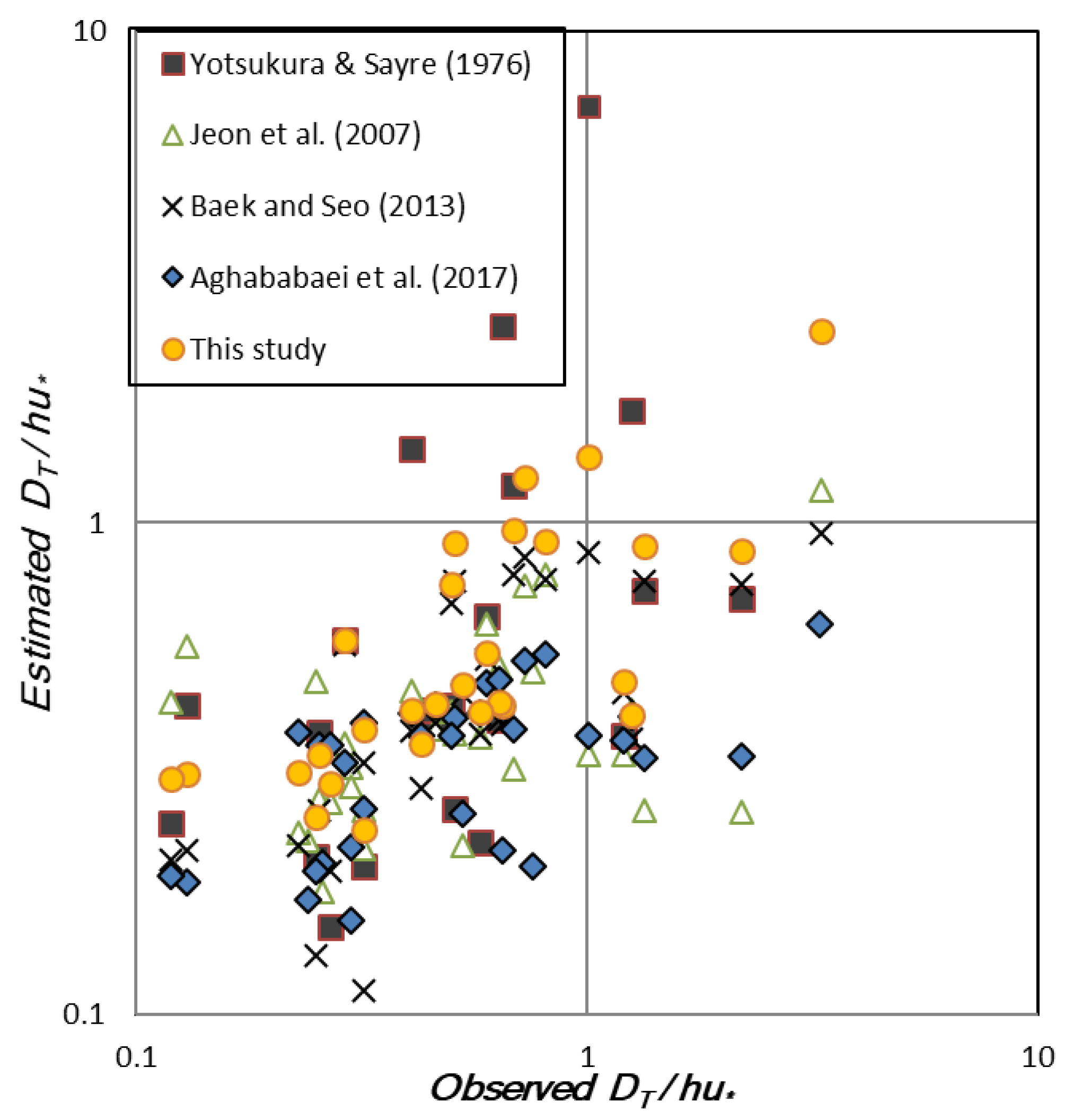
4. Application and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notation List
| , | regression coefficients |
| the transverse dispersion coefficient | |
| g | the gravitational acceleration |
| the water depth | |
| the radius of curvature | |
| the bed slope | |
| Sn | the sinuosity |
| the mean velocity | |
| the frictional velocity and defined as in an open channel here | |
| the channel width |
References
- Baek, K.O.; Seo, I.W. Empirical equation for transverse dispersion coefficient based on theoretical background in river bends. Environ. Fluid Mech. 2013, 13, 465–477. [Google Scholar] [CrossRef]
- Fischer, H.B. Transverse mixing in a sand-bed channel. US Geol. Surv. Prof. Pap. 1967, 575-D, 267–272. [Google Scholar]
- Fischer, H.B.; List, J.E.; Koh, C.R.; Imberger, J.; Brooks, N.H. Mixing in Inland and Coastal Waters; Academic Press: San Diego, CA, USA, 1979. [Google Scholar]
- Rutherford, J.C. River Mixing; Wiley: Chichester, UK, 1994. [Google Scholar]
- Fischer, H.B. The effect of bends on dispersion in streams. Water Resour. Res. 1969, 5, 496–506. [Google Scholar] [CrossRef]
- Yotsukura, N.; Sayre, W.W. Transverse mixing in natural channels. Water Resour. Res. 1976, 12, 695–704. [Google Scholar] [CrossRef]
- Sayre, W.W. Shore-attached thermal plumes in rivers. In Modelling in Rivers; Shen, H.W., Ed.; Wiley-Interscience: London, UK, 1979. [Google Scholar]
- Jeon, T.M.; Baek, K.O.; Seo, I.W. Development of an empirical equation for the transverse dispersion coefficient in natural streams. Environ. Fluid Mech. 2007, 7, 317–329. [Google Scholar] [CrossRef]
- Aghababaei, M.; Etemad-Shahidi, A.; Jabbari, E.; Taghipour, M. Estimation of transverse mixing coefficient in straight and meandering streams. Water Resour. Manag. 2017, 31, 3809–3827. [Google Scholar] [CrossRef]
- Boxall, J.B.; Guymer, I. Analysis and prediction of transverse mixing coefficients in natural channels. J. Hydraul. Eng. 2003, 129, 129–139. [Google Scholar] [CrossRef]
- Baek, K.O.; Seo, I.W. Transverse dispersion caused by secondary flow in curved channels. J. Hydraul. Eng. 2011, 137, 1126–1134. [Google Scholar] [CrossRef]
- Bansal, M.K. Dispersion in natural streams. J. Hydraul. Div. 1971, 97, 1867–1886. [Google Scholar] [CrossRef]
- Deng, Z.; Singh, V.P.; Bengtsson, L. Longitudinal dispersion coefficient in straight rivers. J. Hydraul. Eng. 2001, 127, 919–927. [Google Scholar] [CrossRef]
- Almquist, C.W.; Holley, E.R. Transverse Mixing in Meandering Laboratory Channels with Rectangular and Naturally Varying Cross Sections; Technical Report CRWR-205; University of Texas: Austin, TX, USA, 1985. [Google Scholar]
- Yotsukura, N.; Fischer, H.B.; Sayre, W.W. Measurement of Mixing Characteristics of the Missouri River between Sioux City, Iowa and Plattsmouth, Nebraska; USGS Water, Supply Paper No. 1899-G; USGPO: Washington, DC, USA, 1970. [Google Scholar] [CrossRef]
- Yotsukura, N.; Cobb, E.D. Transverse Diffusion of Solutes in Natural Streams; USGS Water, Supply Paper No. 582-C; US Government Printing Office: Washington, DC, USA, 1972. [Google Scholar]
- Fischer, H.B. Longitudinal dispersion and turbulent mixing in open channel flow. Annu. Rev. Fluid Mech. 1973, 5, 59–78. [Google Scholar] [CrossRef]
- Holley, E.R.; Abraham, G. Field Tests on Transverse Mixing in Rivers. J. Hydraul. Div. 1973, 99, 2313–2331. [Google Scholar] [CrossRef]
- Sayre, W.W.; Yeh, T. Transverse Mixing Characteristics of the Missouri River Downstream from the Cooper Nuclear Station; Rep. No. 145; University of Iowa: Iowa City, IA, USA, 1973. [Google Scholar]
- Jackman, A.P.; Yotsukura, N. Thermal Loading of Natural Streams; USGS Professional Paper No. 991; US Government Printing Office: Washington, DC, USA, 1977. [Google Scholar]
- Beltaos, S. Transverse mixing tests in natural streams. J. Hydraul. Div. 1980, 106, 1607–1625. [Google Scholar] [CrossRef]
- Lau, Y.L.; Krishnappan, B.G. Modelling transverse mixing in natural streams. J. Hydraul. Div. 1981, 107, 209–226. [Google Scholar] [CrossRef]
- Somlyody, L. An approach to the study of transverse mixing in stream. J. Hydraul. Res. 1982, 20, 203–220. [Google Scholar] [CrossRef]
- Holly, F.M.; Nerat, G. Field calibration of stream-tube dispersion model. J. Hydraul. Eng. 1983, 109, 1455–1470. [Google Scholar] [CrossRef]
- Demetracopoulos, A.C.; Stefan, H.G. Transverse mixing in wide and shallow river: Case study. J. Hydraul. Eng. 1983, 109, 685–699. [Google Scholar] [CrossRef]
- Seo, I.W.; Baek, K.O.; Jeon, T.M. Analysis of transverse mixing in natural streams under slug tests. J. Hydraul. Res. 2006, 44, 350–362. [Google Scholar] [CrossRef]
- Seo, I.W.; Choi, H.J.; Kim, Y.D.; Han, E.J. Analysis of Two-Dimensional Mixing in Natural Streams Based on Transient Tracer Tests. J. Hydraul. Eng. 2016, 142, 4016020. [Google Scholar] [CrossRef]
- Pouchoulin, S.; Le Coz, J.; Mignot, E.; Gond, L.; Riviere, N. Predicting transverse mixing efficiency downstream of a river confluence. Water Resour. Res. 2020, 56, e2019WR026367. [Google Scholar] [CrossRef]
- Song, C.G.; Seo, I.W.; Kim, Y.D. Analysis of secondary current effect in the modeling of shallow flow in open channels. Adv. Water Res. 2012, 41, 29–48. [Google Scholar] [CrossRef]
- Seo, I.W.; Lee, M.E.; Baek, K.O. 2D modeling of heterogeneous dispersion in meandering channels. J. Hydraul. Eng. 2008, 134, 196–204. [Google Scholar] [CrossRef]
- Baek, K.O.; Seo, I.W. Estimation of transverse dispersion coefficient for two-dimensional models of mixing in natural streams. J. Hydraul. Res. 2017, 15, 67–74. [Google Scholar] [CrossRef]
- Baek, K.O. Flowchart on choosing optimal method of observing transverse dispersion coefficient for solute transport in open channel flow. Sustainability 2018, 10, 1332. [Google Scholar] [CrossRef]
- Sayre, W.W.; Chang, F.M. A Laboratory Investigation of Open Channel Dispersion Processes for Dissolved, Suspended, and Floating Dispersants; Professional Paper No. 433-E.; U.S. Geological Survey: Reston, WV, USA, 1968. [Google Scholar]
- Holley, E.R.; Siemons, J.; Abraham, G. Some aspects of analyzing transverse diffusion in rivers. J. Hydraul. Res. 1972, 10, 27–57. [Google Scholar] [CrossRef]
- Beltaos, S. Evaluation of transverse mixing coefficients from slug tests. J. Hydraul. Res. 1975, 13, 351–360. [Google Scholar] [CrossRef]
- Baek, K.O.; Seo, I.W. Routing procedures for observed dispersion coefficients in two-dimensional river mixing. Adv. Water Res. 2010, 33, 1551–1559. [Google Scholar] [CrossRef]
- Baek, K.O.; Seo, W. On the methods for determining the transverse dispersion coefficient in river mixing. Adv. Water Res. 2016, 90, 1–9. [Google Scholar] [CrossRef]



| Research | River | (m) | (m/s) | (m/s) | (m) | (m) | |||
|---|---|---|---|---|---|---|---|---|---|
| Yotsukura et al. (1970) [15] | Missouri | 2.74 | 1.75 | 0.074 | 3400 | 183 | 1.6 | 0.019 | 0.60 |
| Yotsukura and Cobb (1972) [16] | Athabasca | 2.20 | 0.95 | 0.056 | - | 373 | 1.0 | - | 0.76 |
| Fischer (1973) [17] | Atrisco | 0.68 | 0.63 | 0.063 | - | 18.3 | 1.0 | - | 0.24 |
| Bernardo | 0.70 | 1.25 | 0.062 | - | 20 | 1.0 | - | 0.30 | |
| South | 0.44 | 0.18 | 0.040 | - | 18.3 | 1.0 | - | 0.26 | |
| Holley and Abraham (1973) [18] | Waal | 4.70 | 0.82 | 0.056 | 3238 | 266 | 1.08 | 0.021 | 0.29 |
| Ijssel | 4.00 | 0.97 | 0.075 | 1111 | 69.5 | 2.01 | 0.047 | 0.51 | |
| Sayre and Yeh (1973) [19] | Missouri | 3.96 | 5.40 | 0.085 | 968 | 240 | 2.10 | 0.260 | 3.30 |
| Jackman and Yotsukura (1977) [20] | Potomac | 1.74 | 0.58 | 0.051 | 1586 | 350 | 1.0 | 0.012 | 0.65 |
| Sayre (1979) [7] | Missouri | 2.94 | 1.58 | 0.074 | 792 | 214 | 2.1 | 0.079 | 0.73 |
| 1.99 | 1.39 | 0.074 | 792 | 214 | 2.1 | 0.047 | 0.81 | ||
| Beltaos (1980) [21] | Athabasca | 2.05 | 0.86 | 0.078 | 1875 | 320 | 1.2 | 0.012 | 0.41 |
| Beaver | 0.96 | 0.50 | 0.044 | 116 | 42.7 | 1.3 | 0.094 | 1.01 | |
| Lau and Krisnappan (1981) [22] | Grand | 0.51 | 0.35 | 0.069 | 310 | 59.2 | 1.1 | 0.008 | 0.26 |
| Somlyody (1982) [23] | Danube | 2.90 | 0.87 | 0.051 | 9778 | 415 | 1.0 | 0.005 | 0.25 |
| 2.90 | 0.87 | 0.036 | 9778 | 418 | 1.0 | 0.007 | 0.13 | ||
| 4.20 | 0.95 | 0.059 | 9778 | 475 | 1.0 | 0.007 | 0.12 | ||
| Holly and Nerat (1983) [24] | Isere | 2.25 | 1.40 | 0.059 | 1612 | 70 | 1.25 | 0.033 | 0.50 |
| Demetracopoulos and Stefan (1983) [25] | Mississippi | 1.00 | 0.67 | 0.079 | 733 | 178 | 1.18 | 0.012 | 1.26 |
| Seo et al. (2006) [26] | Sum | 0.69 | 0.34 | 0.049 | 381 | 54 | 1.66 | 0.013 | 0.46 |
| 1.02 | 0.58 | 0.056 | 700 | 65 | 1.19 | 0.015 | 1.21 | ||
| 0.68 | 0.31 | 0.046 | - | 80.1 | 1.0 | - | 0.30 | ||
| Cheongmi | 0.48 | 0.34 | 0.062 | 397 | 44.5 | 1.13 | 0.007 | 0.27 | |
| Hongcheon | 0.75 | 0.35 | 0.047 | 437.5 | 58.6 | 2.38 | 0.013 | 0.64 | |
| 1.10 | 0.21 | 0.057 | 559 | 69.9 | 1.4 | 0.007 | 0.23 | ||
| 0.97 | 0.20 | 0.053 | 355 | 67 | 1.54 | 0.010 | 0.32 | ||
| Seo et al. (2016) [27] | Daegok | 0.45 | 0.17 | 0.019 | 880.3 | 12 | 1.03 | 0.005 | 0.32 |
| Daepo | 0.43 | 0.65 | 0.061 | 308.4 | 9.2 | 1.03 | 0.015 | 0.53 | |
| Gam | 0.3 | 0.53 | 0.055 | 316.7 | 33.5 | 1.13 | 0.009 | 0.43 | |
| Miho | 1.27 | 0.27 | 0.030 | 221.3 | 42.5 | 1.55 | 0.052 | 0.69 | |
| 0.49 | 0.40 | 0.048 | 345.6 | 31 | 1.54 | 0.012 | 0.58 | ||
| Pouchoulin et al. (2020) [28] | Rhone | 9.23 | 0.60 | 0.065 | 1864 | 274 | 1.23 | 0.045 | 1.34 |
| 9.01 | 0.63 | 0.070 | 1864 | 275 | 1.23 | 0.043 | 2.21 |
| Correlation Coefficient | RMS Error | |
|---|---|---|
| Yotsukura and Sayer (1976) [6] | 0.76 | 19.49 |
| Jeon et al. (2007) [8] | 0.53 | 0.49 |
| Baek and Seo (2013) [1] | 0.63 | 0.54 |
| Aghababaei et al. (2017) [9] | 0.50 | 0.59 |
| This study | 0.79 | 0.34 |
| Date | River | Q (m3/s) | h (m) | W (m) | (m/s) | Rc (m) |
|---|---|---|---|---|---|---|
| 27 August 2014 | Nakdong | 312.3 | 5.47 | 436.6 | 0.154 | 1480 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baek, K.O.; Lee, D.Y. Development of Simple Formula for Transverse Dispersion Coefficient in Meandering Rivers. Water 2023, 15, 3120. https://doi.org/10.3390/w15173120
Baek KO, Lee DY. Development of Simple Formula for Transverse Dispersion Coefficient in Meandering Rivers. Water. 2023; 15(17):3120. https://doi.org/10.3390/w15173120
Chicago/Turabian StyleBaek, Kyong Oh, and Dong Yeol Lee. 2023. "Development of Simple Formula for Transverse Dispersion Coefficient in Meandering Rivers" Water 15, no. 17: 3120. https://doi.org/10.3390/w15173120
APA StyleBaek, K. O., & Lee, D. Y. (2023). Development of Simple Formula for Transverse Dispersion Coefficient in Meandering Rivers. Water, 15(17), 3120. https://doi.org/10.3390/w15173120








