Enhancing Water Temperature Prediction in Stratified Reservoirs: A Process-Guided Deep Learning Approach
Abstract
:1. Introduction
2. Materials and Methods
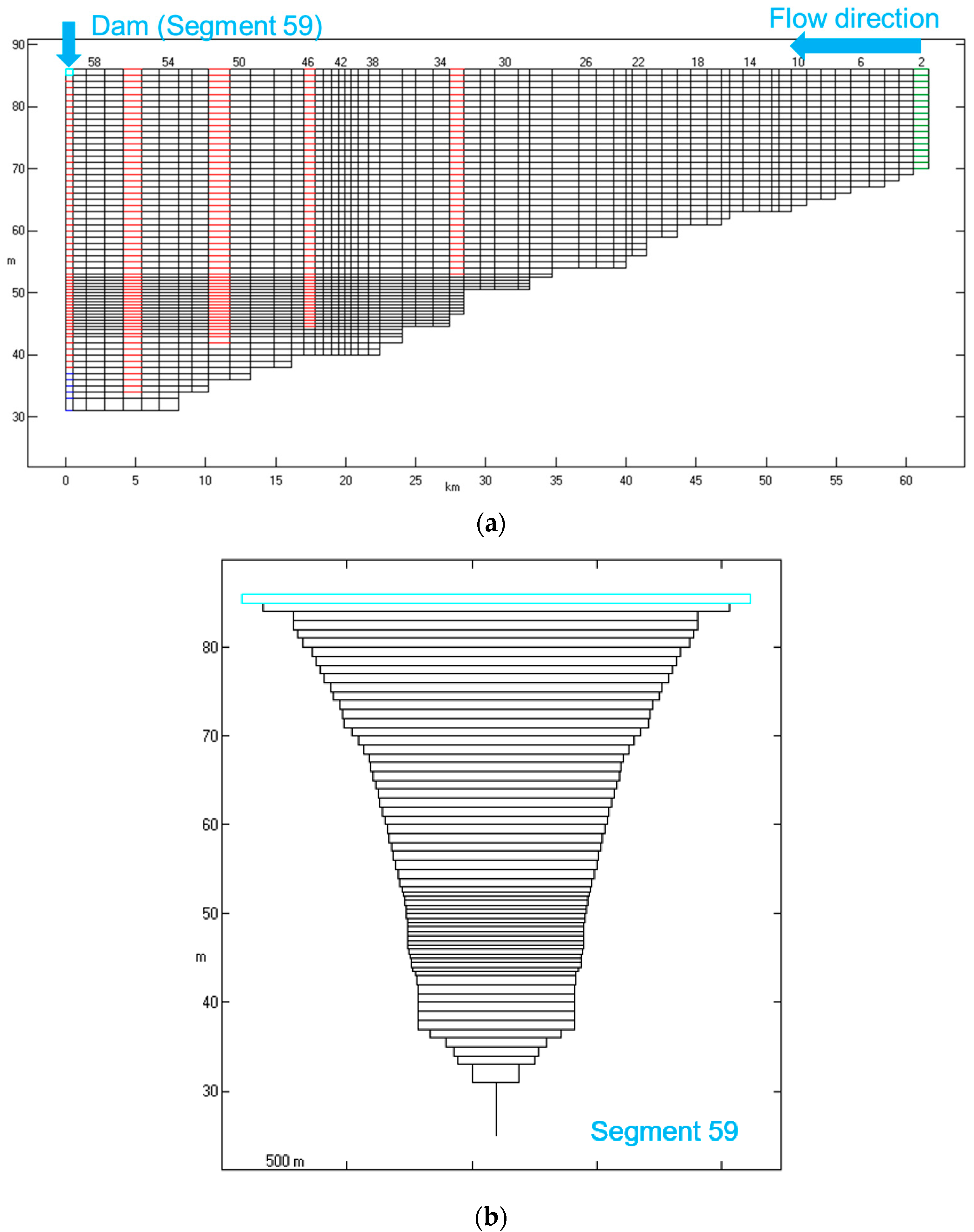
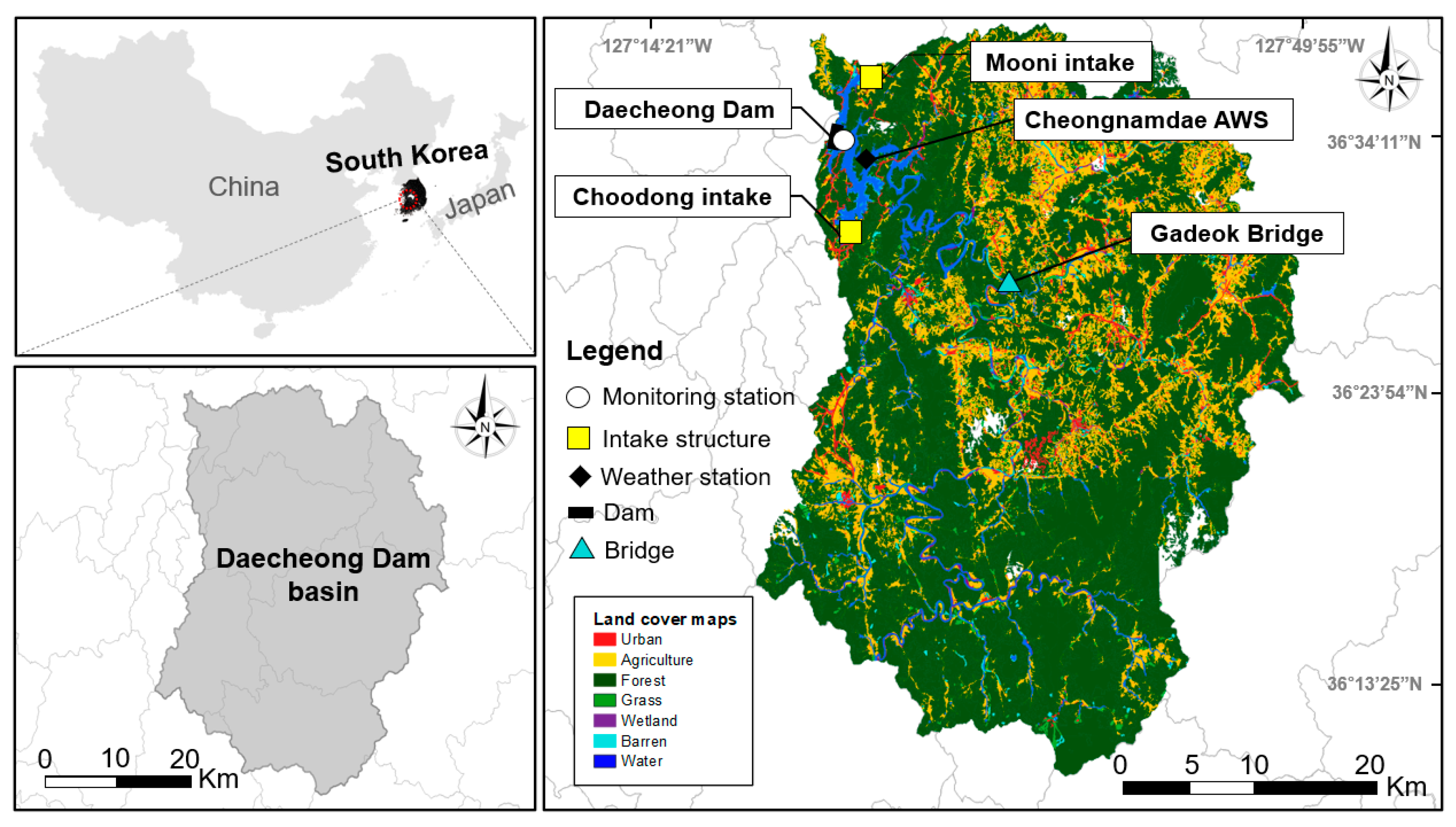
2.1. Description of the Site
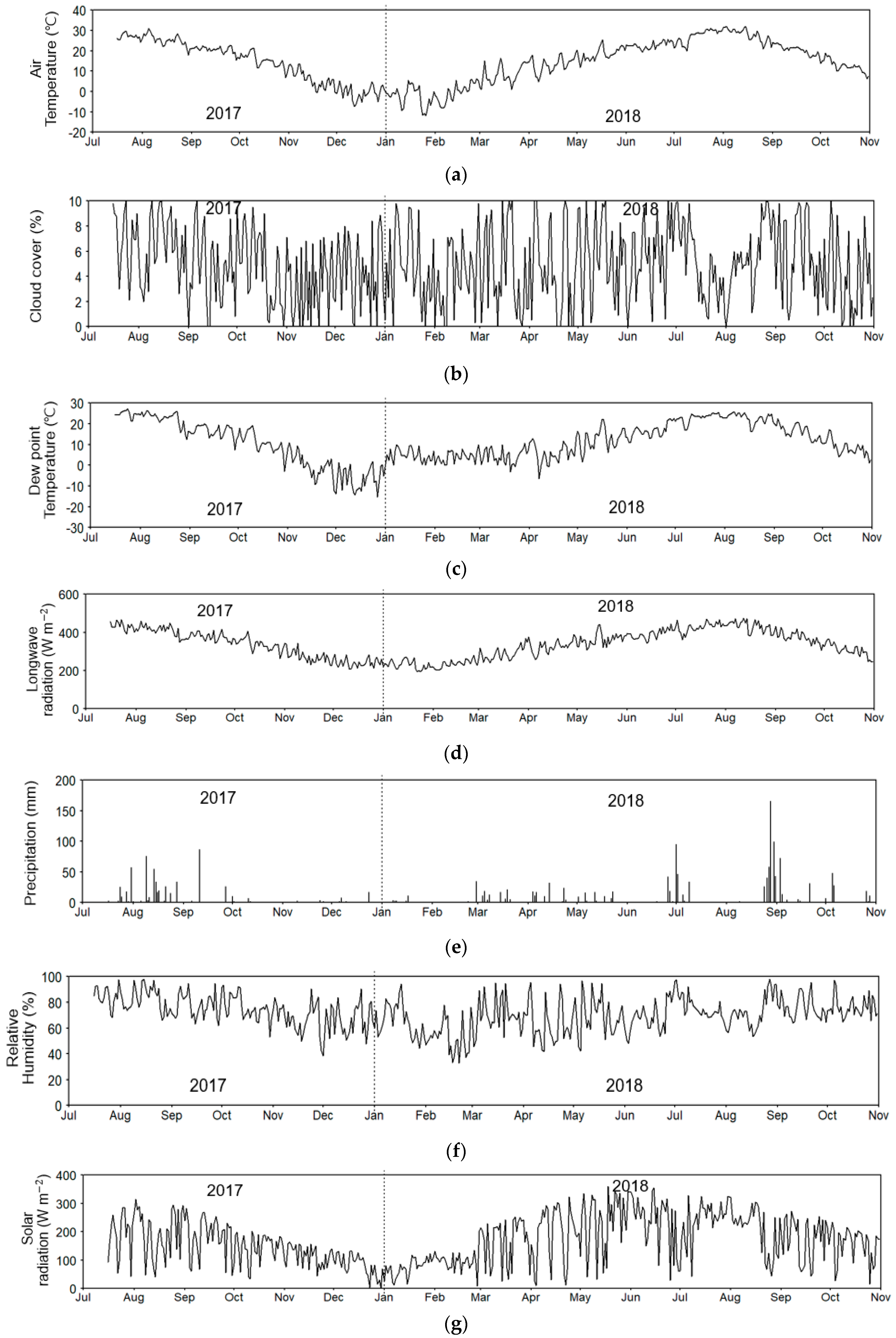
2.2. Field Monitoring and Data Collection
2.3. Process-Based Model (CE-QUAL-W2 (W2))
2.4. Deep Learning Model (Long Short-Term Memory (LSTM))
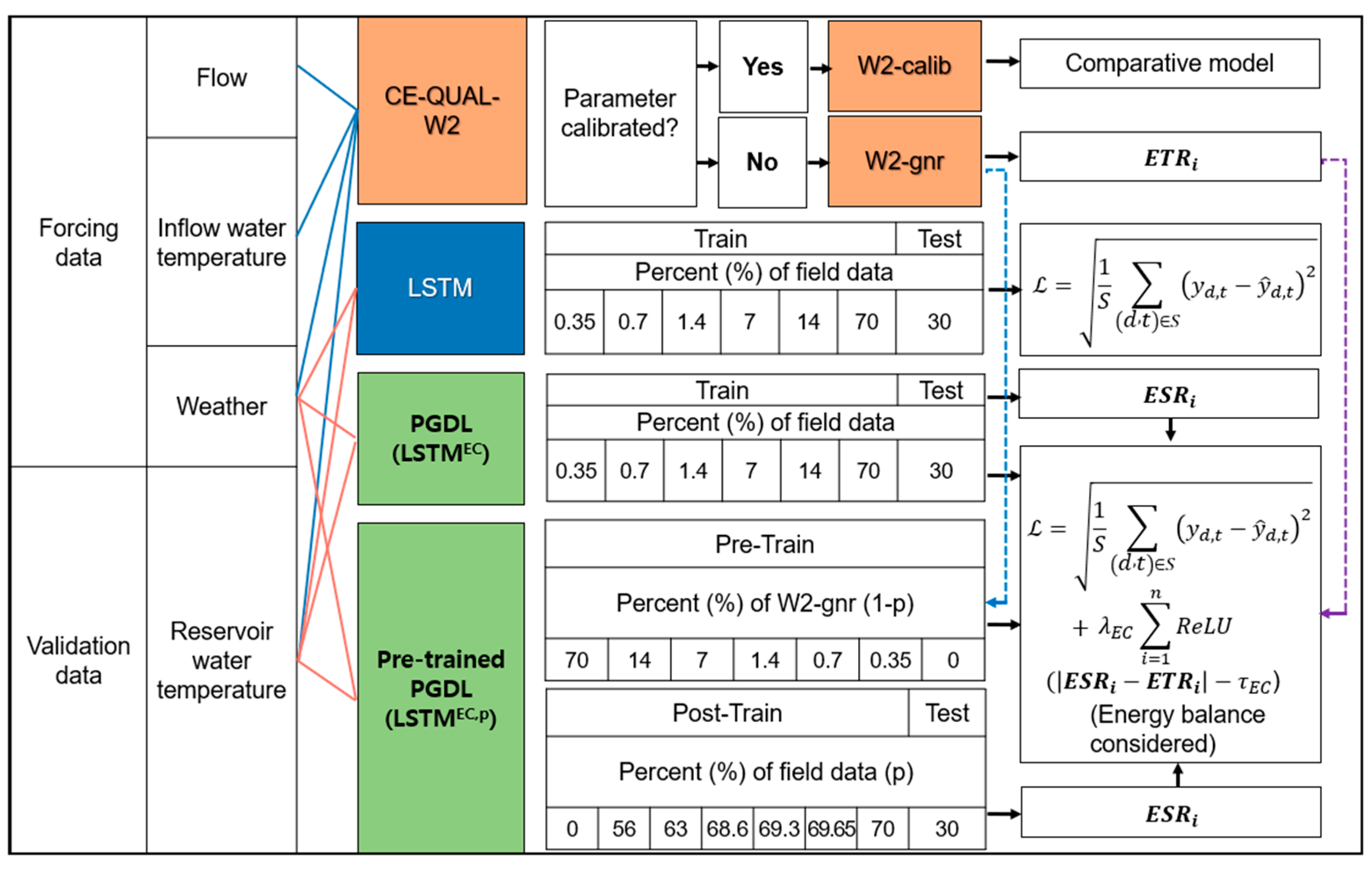
2.5. Development of the PGDL Model
2.6. Validation of Energy Conservation in the PGDL Model
2.7. Pre-Training of LSTM Using an Uncalibrated W2 (W2-gnr) Model
2.8. Evaluation of Model Performance
3. Results
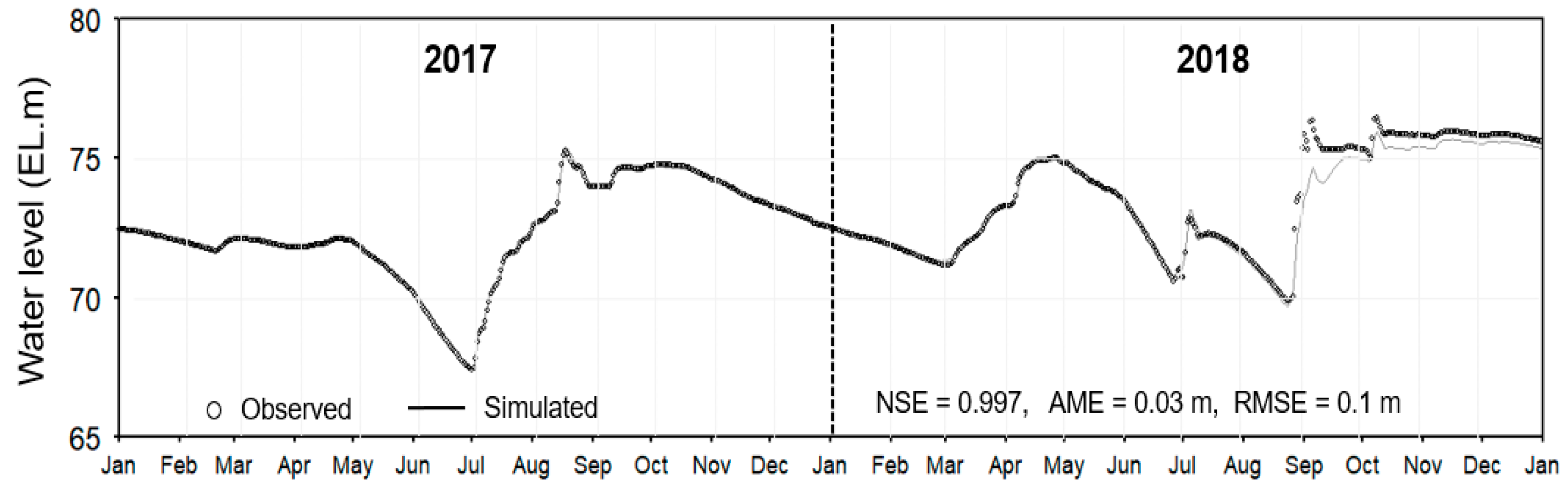
3.1. Validation of the CE-QUAL-W2 Model
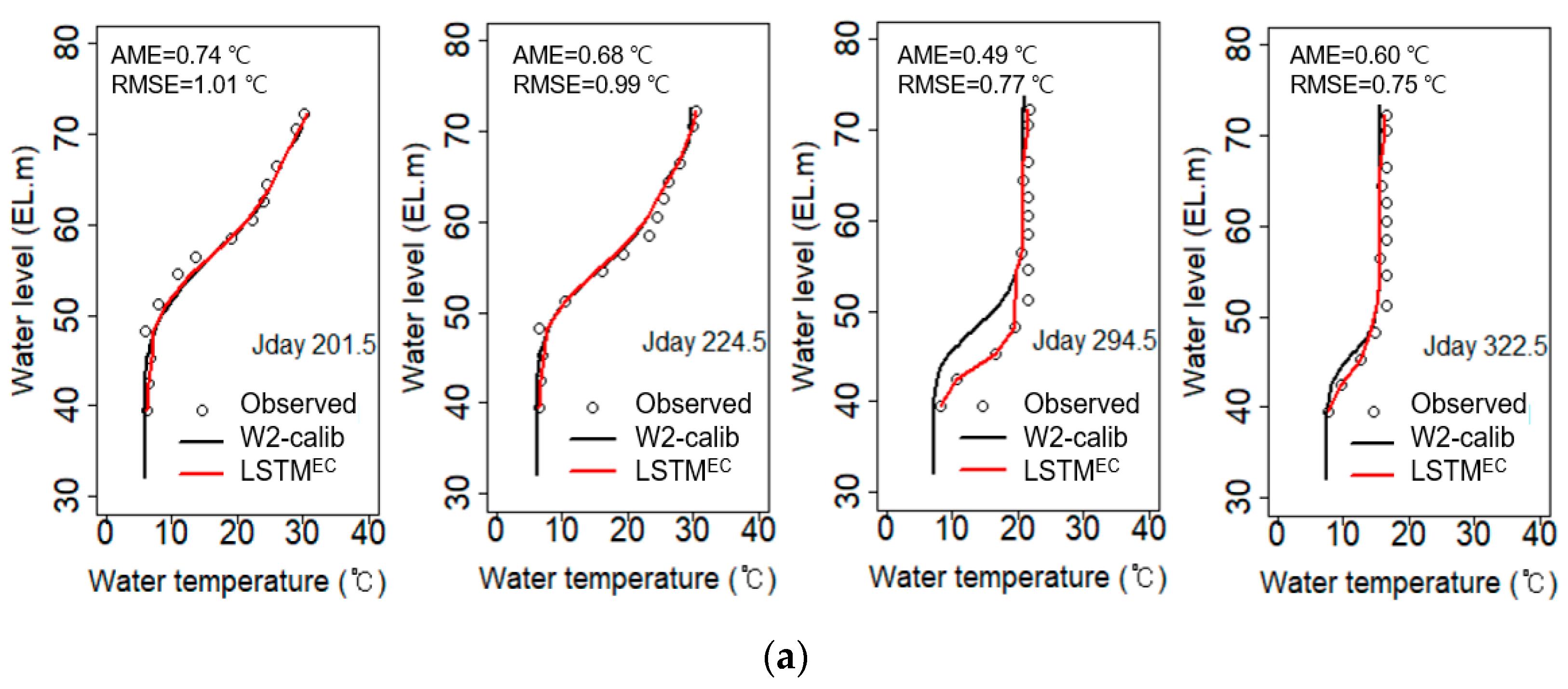
3.2. Prediction Performance of the PGDL Model
3.3. Prediction Performance of the Pre-Trained PGDL Model
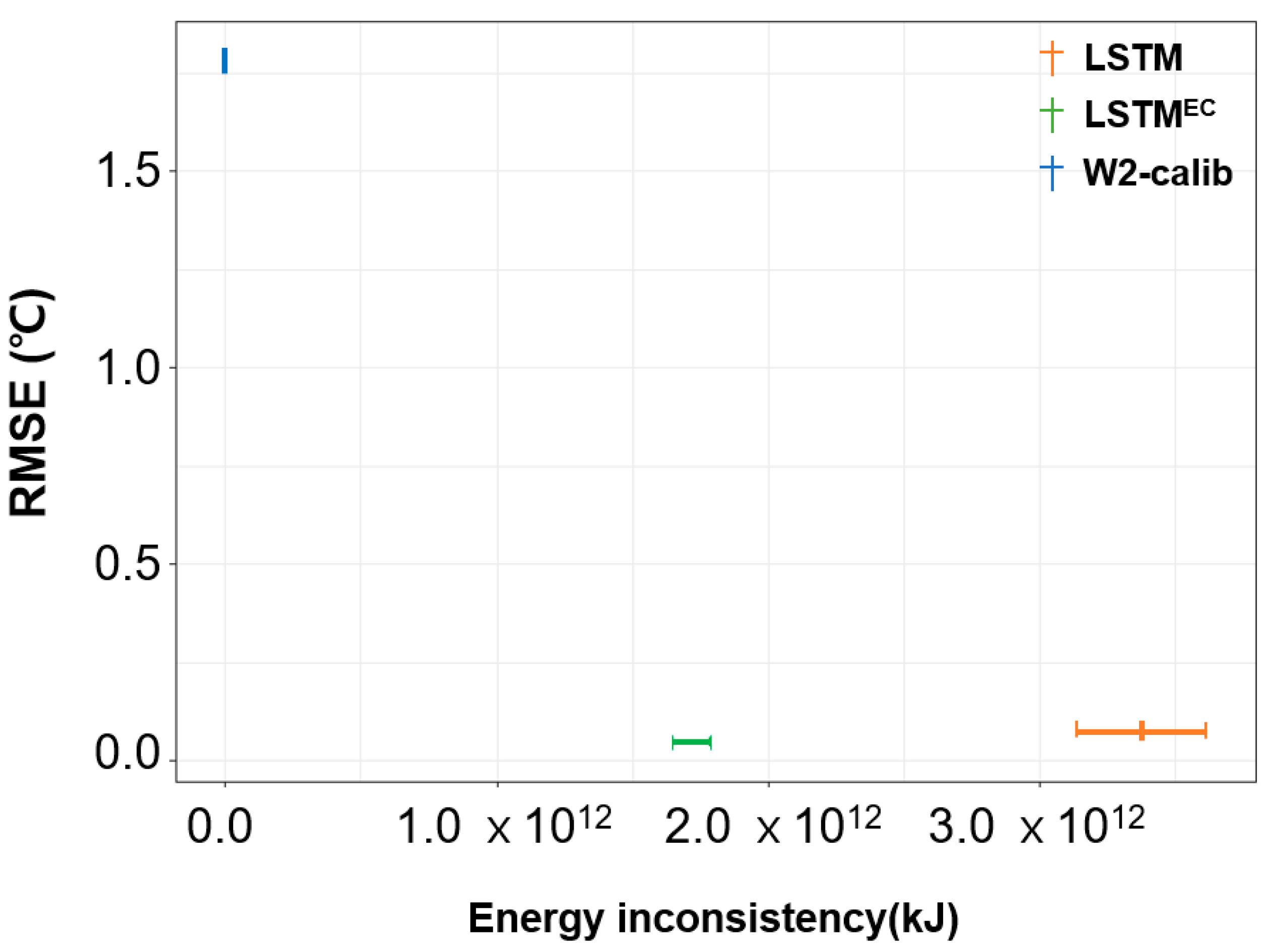
3.4. Evaluating the Energy Consistency of the PGDL Model
4. Discussion
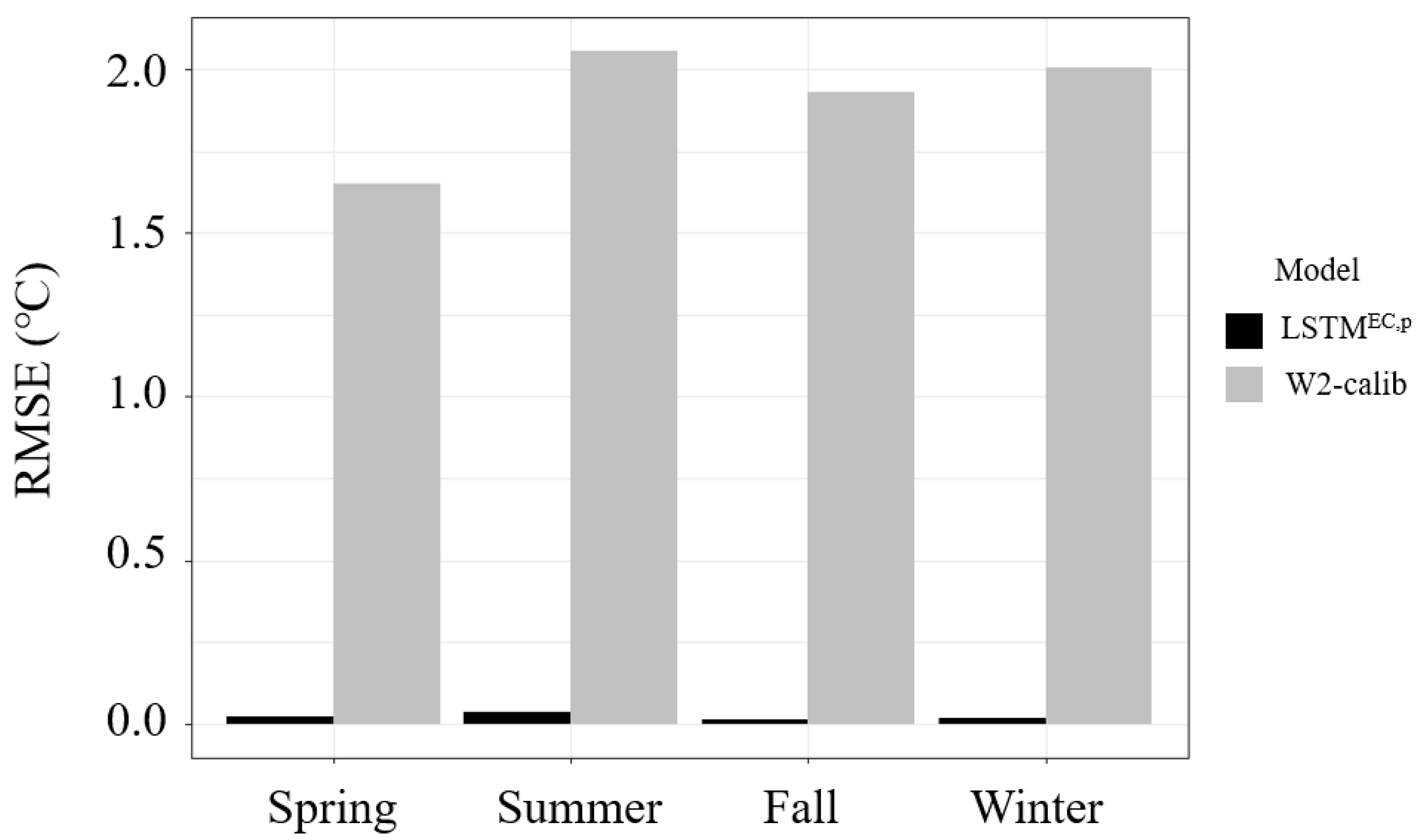
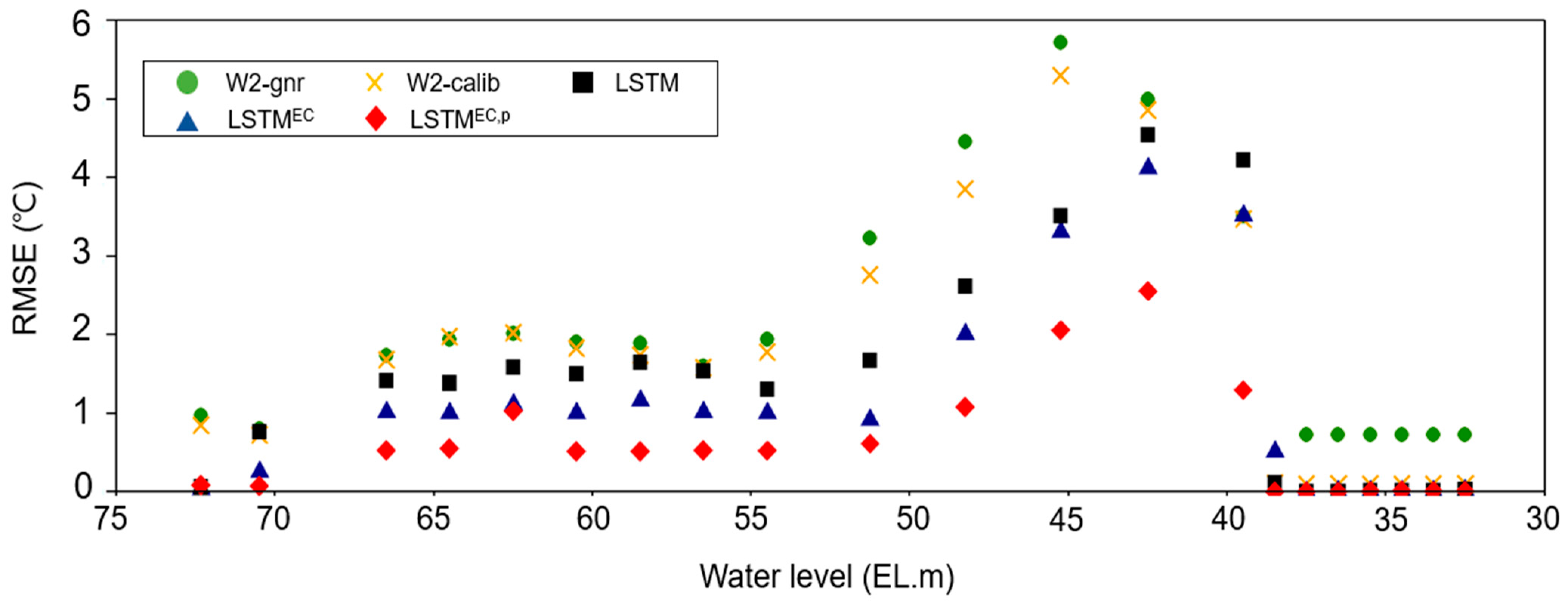
4.1. Comparative Analysis of Water Temperature Prediction Errors
4.2. Applicability of the PGDL Model for Water Quality Modeling
4.3. Strengths of the PGDL Model in the Lack of Data
4.4. Limitations of the PGDL Model and Scope for Future Studies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Variables | Unit | Value |
|---|---|---|
| Sample size | n | 399 |
| Air temperature | °C | 17.5 (8.9) * |
| Cloud cover | % | 5.0 (.0) |
| Dew point temperature | °C | 12.6 (9.8) |
| Long-wave radiation | W m−2 | 356.1 (64.8) |
| Precipitation | mm | 4.4 (15.2) |
| Relative humidity | % | 73.0 (12.2) |
| Solar radiation | W/m−2 | 168.8 (86.8) |
| Wind speed | m s−1 | 1.3 (.5) |
| Parameters | Units | Description | The Values of Model Parameters | |
|---|---|---|---|---|
| W2-gnr | W2-calib | |||
| AX | m2 s−1 | Horizontal eddy viscosity | 1.0 | 1.0 |
| DX | m2 s−1 | Horizontal eddy diffusivity | 1.0 | 1.0 |
| WSC | - | Wind sheltering coefficient | 0.85 | 1.0–1.5 |
| FRICT | m1/2 s−1 | Chezy coefficient | 70 | 70 |
| EXH2O | m−1 | Extinction coefficient for pure water | 0.25 | 0.45 |
| BETA | - | Solar radiation absorbed in the surface layer | 0.45 | 0.45 |
| CBHE | W m−2 s−1 | Coefficient of bottom heat exchange | 0.3 | 0.45 |
| Model | Hyperparameters | Definition | Hyperparameter Range | Defined Hyperparameters |
|---|---|---|---|---|
| LSTM | Learning rate | Amount of change in weight that is updated during learning. | [0.0001, 0.1] | [0.0001, 0.01] |
| Batch size | Group size to divide training data into several groups. | [32, 64] | [32, 64] | |
| Epochs | Number of learning iterations. | [1000, 50,000] | [40,000, 50,000] | |
| Optimizer | Optimization algorithm used for training. | [SGD, RMSprop, Adam] | Adam | |
| Dropout rate | Dropout setting applied to layers. | [0, 1] | [0.1, 0.2] | |
| LSTMEC | Learning rate | Amount of change in weight that is updated during learning. | [0.0001, 0.1] | [0.0001, 0.01] |
| Batch size | Group size to divide training data into several groups. | [32, 64] | [32, 64] | |
| Epochs | Number of learning iterations. | [1000, 50,000] | [40,000, 50,000] | |
| Optimizer | Optimization algorithm used for training. | [SGD, RMSprop, Adam] | Adam | |
| Dropout rate | Dropout setting applied to layers. | [0, 1] | [0.1, 0.2] | |
| LSTMEC,p | Learning rate | Amount of change in weight that is updated during learning. | [0.0001, 0.1] | [0.0001, 0.01] |
| Batch size | Group size to divide training data into several groups. | [32, 64] | [32, 64] | |
| Epochs | Number of learning iterations. | [1000, 50,000] | [40,000, 50,000] | |
| Optimizer | Optimization algorithm used for training. | [SGD, RMSprop, Adam] | Adam | |
| Dropout rate | Dropout setting applied to layers. | [0, 1] | [0.1, 0.2] |




References
- Cole, T.M.; Buchak, E.M. CE-QUAL-W2: A Two-Dimensional, Laterally Averaged, Hydrodynamic and Water Quality Model, Version 2.0 User Manual; US Army Corps of Engineers: Washington, DC, USA, 1995; pp. 1–357. [Google Scholar]
- Hamrick, J.M. A Three-Dimensional Environmental Fluid Dynamics Computer Code: Theoretical and Computational Aspects; Virginia Institute of Marine Science, William and Mary University: Williamsburg, VA, USA, 1992; pp. 1–317. [Google Scholar]
- Hodges, B.; Dallimore, C. Aquatic Ecosystem Model: AEM3D v1.0 User Manual; HydroNumerics: Victoria, Australia, 2019; pp. 1–167. [Google Scholar]
- Bouchard, D.; Knightes, C.; Chang, X.; Avant, B. Simulating multiwalled carbon nanotube transport in surface water systems using the water quality analysis simulation program (WASP). Environ. Sci. Technol. 2017, 51, 11174–11184. [Google Scholar] [CrossRef] [PubMed]
- Arhonditsis, G.B.; Neumann, A.; Shimoda, Y.; Kim, D.K.; Dong, F.; Onandia, G.; Yang, C.; Javed, A.; Brady, M.; Visha, A.; et al. Castles built on sand or predictive limnology in action? Part A: Evaluation of an integrated modelling framework to guide adaptive management implementation in Lake Erie. Ecol. Inform. 2019, 53, 100968. [Google Scholar] [CrossRef]
- Schuwirth, N.; Borgwardt, F.; Domisch, S.; Friedrichs, M.; Kattwinkel, M.; Kneis, D.; Kuemmerlen, M.; Langhans, S.D.; Martínez-López, J.; Vermeiren, P. How to make ecological models useful for environmental management. Ecol. Modell. 2019, 411, 108784. [Google Scholar] [CrossRef]
- Liu, X.; Lu, D.; Zhang, A.; Liu, Q.; Jiang, G. Data-driven machine learning in environmental pollution: Gains and problems. Environ. Sci. Technol. 2022, 56, 2124–2133. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Wang, R.; Qi, Y.; Wen, F. A watershed water quality prediction model based on attention mechanism and bi-LSTM. Environ. Sci. Pollut. Res. Int. 2022, 3, 75664–75680. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Ostfeld, A. Data-driven modelling: Some past experiences and new approaches. J. Hydroinform. 2008, 10, 3–22. [Google Scholar] [CrossRef]
- Kesavaraj, G.; Sukumaran, S. A study on classification techniques in data mining. In Proceedings of the 2013 Fourth International Conference on Computing, Communications and Networking Technologies (ICCCNT), Tiruchengode, India, 4–6 July 2013; IEEE: New York, NY, USA, 2003; pp. 1–7. [Google Scholar] [CrossRef]
- Ghavidel, S.Z.Z.; Montaseri, M. Application of different data-driven methods for the prediction of total dissolved solids in the Zarinehroud basin. Stoch. Environ. Res. Risk Assess. 2014, 28, 2101–2118. [Google Scholar] [CrossRef]
- Sanikhani, H.; Kisi, O.; Kiafar, H.; Ghavidel, S.Z.Z. Comparison of different data-driven approaches for modeling Lake Level fluctuations: The case of Manyas and Tuz Lakes (Turkey). Water Resour. Manag. 2015, 29, 1557–1574. [Google Scholar] [CrossRef]
- Amaranto, A.; Mazzoleni, M. B-AMA: A python-coded protocol to enhance the application of data-driven models in hydrology. Environ. Modell. Softw. 2023, 160, 105609. [Google Scholar] [CrossRef]
- Granata, F.; Nunno, F.D. Neuroforecasting of daily streamflows in the UK for short- and medium-term horizons: A novel insight. J. Hydrol. 2023, 624, 129888. [Google Scholar] [CrossRef]
- Nunno, F.D.; Zhu, S.; Ptak, M.; Sojka, M.; Granata, F. A stacked machine learning model for multi-step ahead prediction of lake surface water temperature. Sci. Total Environ. 2023, 890, 164323. [Google Scholar] [CrossRef] [PubMed]
- Cha, Y.K.; Shin, J.H.; Kim, Y.W. Data-driven modeling of freshwater aquatic systems: Status and prospects. J. Korean Soc. Water Environ. 2020, 36, 611–620. [Google Scholar] [CrossRef]
- Liu, Z.; Cheng, L.; Lin, K.; Cai, H. A hybrid bayesian vine model for water level prediction. Environ. Modell. Softw. 2021, 142, 105075. [Google Scholar] [CrossRef]
- Majeske, N.; Zhang, X.; Sabaj, M.; Gong, L.; Zhu, C.; Azad, A. Inductive predictions of hydrologic events using a Long Short-Term memory network and the Soil and water Assessment Tool. Environ. Modell. Softw. 2022, 152, 105400. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Hutchinson, L.; Steiert, B.; Soubret, A.; Wagg, J.; Phipps, A.; Peck, R.; Charoin, J.E.; Ribba, B. Models and machines: How deep learning will take clinical pharmacology to the next level. CPT Pharmacomet. Syst. Pharmacol. 2019, 8, 131–134. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Toward improved predictions in ungauged basins: Exploiting the power of machine learning. Water Resour. Res. 2019, 55, 11344–11354. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.L.; Chang, S. Hierarchical neural networks. Comput. Chem. Eng. 1992, 16, 347–369. [Google Scholar] [CrossRef]
- Antonetti, M.; Zappa, M. How can expert knowledge increase the realism of conceptual hydrological models? A case study based on the concept of dominant runoff process in the Swiss Pre-Alps. Hydrol. Earth Syst. Sci. 2018, 22, 4425–4447. [Google Scholar] [CrossRef]
- Read, J.S.; Jia, X.; Willard, J.; Appling, A.P.; Zwart, J.A.; Oliver, S.K.; Karpatne, A.; Hansen, G.J.A.; Hanson, P.C.; Watkins, W.; et al. Process-guided deep learning predictions of Lake water temperature. Water Resour. Res. 2019, 55, 9173–9190. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat, P. Deep learning and process understanding for data-driven earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Karpatne, A.; Atluri, G.; Faghmous, J.H.; Steinbach, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-guided data science: A new paradigm for scientific discovery from data. IEEE Trans. Knowl. Data Eng. 2017, 29, 2318–2331. [Google Scholar] [CrossRef]
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 1999, 10, 988–999. [Google Scholar] [CrossRef] [PubMed]
- Franklin, J. The elements of statistical learning: Data mining, inference and prediction. Math. Intell. 2005, 27, 83–85. [Google Scholar] [CrossRef]
- Wong, K.C.L.; Wang, L.; Shi, P. Active model with orthotropic hyperelastic material for cardiac image analysis. Lect. Notes Comput. Sci. 2009, 5528, 229–238. [Google Scholar] [CrossRef]
- Xu, J.; Sapp, J.L.; Dehaghani, A.R.; Gao, F.; Horacek, M.; Wang, L. Robust transmural electrophysiological imaging: Integrating sparse and dynamic physiological models into ECG-based inference. Med. Image Comput. Comput. Assist. Interv. 2015, 9350, 519–527. [Google Scholar] [CrossRef]
- Khandelwal, A.; Karpatne, A.; Marlier, M.E.; Kim, J.Y.; Lettenmaier, D.P.; Kumar, V. An approach for global monitoring of surface water extent variations in reservoirs using MODIS data. Remote Sens. Environ. 2017, 202, 113–128. [Google Scholar] [CrossRef]
- Khandelwal, A.; Mithal, V.; Kumar, V. Post classification label refinement using implicit ordering constraint among data instances. In Proceedings of the IEEE International Conference Data Mining, Atlantic City, NJ, USA, 14–17 November 2015; pp. 799–804. [Google Scholar] [CrossRef]
- Kawale, J.; Liess, S.; Kumar, A.; Steinbach, M.; Snyder, P.; Kumar, V.; Ganguly, A.R.; Samatova, N.F.; Semazzi, F. A graph-based approach to find teleconnections in climate data. Stat. Analy. Data Min. 2013, 6, 158–179. [Google Scholar] [CrossRef]
- Li, L.; Snyder, J.C.; Pelaschier, I.M.; Huang, J.; Niranjan, U.N.; Duncan, P.; Rupp, M.; Müller, K.R.; Burke, K. Understanding machine-learned density functionals. Int. J. Quantum Chem. 2016, 116, 819–833. [Google Scholar] [CrossRef]
- Faghmous, J.H.; Frenger, I.; Yao, Y.; Warmka, R.; Lindell, A.; Kumar, V. A daily global mesoscale ocean eddy dataset from satellite altimetry. Sci. Data 2015, 2, 150028. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, C. Structural damage identification via physics-guided machine learning: A methodology integrating pattern recognition with finite element model updating. Struct. Health Monit. 2021, 20, 1675–1688. [Google Scholar] [CrossRef]
- Pawar, S.; Ahmed, S.E.; San, O.; Rasheed, A. Data-driven recovery of hidden physics in reduced order modeling of fluid flows. Phys. Fluids 2020, 32, 36602. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, D.; Chang, H.; Li, H. Deep learning of subsurface flow via theory-guided neural network. J. Hydrol. 2020, 584, 124700. [Google Scholar] [CrossRef]
- Hunter, J.M.; Maier, H.R.; Gibbs, M.S.; Foale, E.R.; Grosvenor, N.A.; Harders, N.P.; Kikuchi-Miller, T.C. Framework for developing hybrid process-driven, artificial neural network and regression models for salinity prediction in River systems. Hydrol. Earth Syst. Sci. 2018, 22, 2987–3006. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Karimpouli, S.; Tahmasebi, P. Physics informed machine learning: Seismic wave equation. Geosci. Front. 2020, 11, 1993–2001. [Google Scholar] [CrossRef]
- Noori, R.; Asadi, N.; Deng, Z. A simple model for simulation of reservoir stratification. J. Hydraul. Res. 2018, 57, 561–572. [Google Scholar] [CrossRef]
- Noori, R.; Tian, F.; Ni, G.; Bhattarai, R.; Hooshyaripor, F.; Klöve, B. ThSSim: A novel tool for simulation of reservoir thermal stratification. Sci. Rep. 2019, 9, 18524. [Google Scholar] [CrossRef]
- Hanson, P.C.; Stillman, A.B.; Jia, X.; Karpatne, A.; Dugan, H.A.; Carey, C.C.; Stachelek, J.; Ward, N.K.; Zhang, Y.; Read, J.S.; et al. Predicting lake surface water phosphorus dynamics using process-guided machine learning. Ecol. Modell. 2020, 430, 109136. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Tavoosi, N.; Hooshyaripor, F.; Noori, R.; Farokhnia, A.; Maghrebi, M.; Kløve, B.; Haghighi, A.T. Experimental-numerical simulation of soluble formations in reservoirs. Adv. Water Resour. 2022, 160, 104109. [Google Scholar] [CrossRef]
- Noori, R.; Yeh, H.D.; Ashrafi, K.; Rezazadeh, N.; Bateni, S.M.; Karbassi, A.; Kachoosangi, F.T.; Moazami, S. A reduced order based CE-QUAL-W2 model for simulation of nitrate concentration in dam reservoirs. J. Hydrol. 2015, 530, 645–656. [Google Scholar] [CrossRef]
- Han, J.S.; Kim, S.J.; Kim, D.M.; Lee, S.W.; Hwang, S.C.; Kim, J.W.; Chung, S.W. Development of high-frequency data-based inflow water temperature prediction model and prediction of changes in stratification strength of Daecheong Reservoir due to climate change. J. Environ. Impact Assess 2021, 30, 271–296. [Google Scholar] [CrossRef]
- Noori, R.; Woolway, R.I.; Saari, M.; Pulkkanen, M.; Kløve, B. Six decades of thermal change in a pristine lake situated north of the Arcitic circle. Water Resour. Res. 2022, 58, e2021WR031543. [Google Scholar] [CrossRef]
- Korea Meteorological Administration (KMA). Available online: http://data.kma.go.kr/ (accessed on 22 January 2023).
- Wells, S.A. CE-QUAL-W2: A Two-Dimensional, Laterally Averaged, Hydrodynamic and Water Quality Model, Version 4.5 User Manual, User Manual: Part 1. Introduction, Model Download Package, How to Run the Model; Department of Civil and Environmental Engineering, Potland University: Portland, OR, USA, 2022; pp. 1–797. [Google Scholar]
- Water Resources Management Information System. Available online: http://www.wamis.go.kr/ (accessed on 22 January 2023).
- Water Environment Information System. Available online: http://water.nier.go.kr/ (accessed on 22 January 2023).
- Chung, S.W.; Oh, J.K. Calibration of CE-QUAL-W2 for a monomictic reservoir in a monsoon climate area. Water Sci. Technol. 2006, 54, 29–37. [Google Scholar] [CrossRef]
- Chollet, F.; Allaire, J.J. Deep Learning with R, 1st ed.; Manning: Shelter Island, NY, USA, 2018; pp. 1–360. ISBN 9781617295546. [Google Scholar]
- Jia, X.; Willard, J.; Karpatne, A.; Read, J.S.; Zwart, J.A.; Steinbach, M.; Kumar, V. Physics-guided machine learning for scientific discovery: An application in simulating lake temperature profiles. ACM/IMS Trans. Data Sci. 2021, 2, 1–26. [Google Scholar] [CrossRef]
- Chung, S.W.; Lee, H.S.; Jung, Y.R. The effect of hydrodynamic flow regimes on the algal bloom in a monomictic reservoir. Water Sci. Technol. 2008, 58, 1291–1298. [Google Scholar] [CrossRef]
- Lee, H.S.; Chung, S.W.; Choi, J.K.; Min, B.H. Feasibility of curtain weir installation for water quality management in Daecheong Reservoir. Desalin. Water Treat. 2010, 19, 164–172. [Google Scholar] [CrossRef]
- Chung, S.W.; Hipsey, M.R.; Imberger, J. Modelling the propagation of turbid density inflows into a stratified lake: Daecheong Reservoir, Korea. Environ. Modell. Softw. 2009, 24, 1467–1482. [Google Scholar] [CrossRef]
- Kim, S.J.; Seo, D.I.; Ahn, K.H. Estimation of proper EFDC parameters to improve the reproductability of thermal stratification in Korea Reservoir. J. Korea Water Resour. Assoc. 2011, 44, 741–751. [Google Scholar] [CrossRef]
- Hong, J.Y.; Jeong, S.I.; Kim, B.H. Prediction model suitable for long-term high turbidity events in a reservoir. J. Korean Soc. Hazard Mitig. 2021, 21, 203–213. [Google Scholar] [CrossRef]
- Cloern, J.E.; Jassby, A.D. Patterns and scales of phytoplankton variability in estuarine–coastal ecosystems. Estuaries Coast 2009, 33, 230–241. [Google Scholar] [CrossRef]
- Altunkaynak, A.; Wang, K.H. A comparative study of hydrodynamic model and expert system related models for prediction of total suspended solids concentrations in Apalachicola Bay. J. Hydrol. 2011, 400, 353–363. [Google Scholar] [CrossRef]
- Shen, C.; Laloy, E.; Elshorbagy, A.; Albert, A.; Bales, J.; Chang, F.; Ganguly, S.; Hsu, K.L.; Kifer, D.; Fang, Z.; et al. HESS opinions: Incubating deep-learning powered hydrologic science advances as a community. Hydrol. Earth Syst. Sci. 2018, 22, 5639–5656. [Google Scholar] [CrossRef]
- Chung, S.W.; Imberger, J.; Hipsey, M.R.; Lee, H.S. The Influence of physical and physiological processes on the spatial heterogeneity of a Microcystis bloom in a stratified Reservoir. Ecol. Modell. 2014, 289, 133–149. [Google Scholar] [CrossRef]
- Olden, J.D.; Lawler, J.J.; Poff, N.L. Machine learning methods without tears: A primer for ecologists. Q. Rev. Biol. 2008, 83, 171–193. [Google Scholar] [CrossRef] [PubMed]
- Hampton, S.E.; Strasser, C.A.; Tewksbury, J.J.; Gram, W.K.; Budden, A.E.; Batcheller, A.L.; Duke, C.S.; Porter, J.H. Big data and the future of ecology. Front. Ecol. Environ. 2013, 11, 156–162. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Kaushal, S.S.; Likens, G.E.; Jaworski, N.A.; Pace, M.L.; Sides, A.M.; Seekell, D.; Belt, K.T.; Secor, D.H.; Wingate, R.L. Rising stream and river temperatures in the United States. Front. Ecol. Environ. 2010, 8, 461–466. [Google Scholar] [CrossRef]
- Rahmani, F.; Lawson, K.; Ouyang, W.; Appling, A.; Oliver, S.; Shen, C. Exploring the exceptional performance of a deep learning stream temperature model and the value of streamflow data. Environ. Res. Lett. 2020, 16, 24025. [Google Scholar] [CrossRef]
- Nürnberg, G.K. Prediction of phosphorus release rates from total and reductant soluble phosphorus in anoxic Lake-sediments. Can. J. Fish. Aquat. Sci. 1988, 45, 453–462. [Google Scholar] [CrossRef]
- Nunn, A.D.; Cowx, I.G.; Frear, P.A.; Harvey, J.P. Is water temperature an adequate predictor of recruitment success in cyprinid fish populations in lowland river? Freshw. Biol. 2003, 48, 579–588. [Google Scholar] [CrossRef]
- Dokulil, M.T. Predicting summer surface water temperatures for large Austrian Lakes in 2050 under climate change scenarios. Hydrobiologia 2014, 731, 19–29. [Google Scholar] [CrossRef]
- Yang, K.; Yu, Z.; Luo, Y.; Zhou, X.; Shang, C. Spatial-temporal variation of lakesurface water temperature and its driving factors in yunnan-Guizhou Plateau. Water Resour. Res. 2019, 55, 4688–4703. [Google Scholar] [CrossRef]
- Yajima, H.; Kikkawa, S.; Ishiguro, J. Effect of selective withdrawal system operation on the longand short-term water conservation in a reservoir. J. Hydraul. Eng. 2006, 50, 1375–1380. [Google Scholar] [CrossRef]
- Gelda, R.K.; Effler, S.W. Modeling turbidity in a water supply reservoir: Advancements and issues. J. Environ. Eng. 2007, 133, 139–148. [Google Scholar] [CrossRef]
- Liu, W.; Guan, H.; Gutiérrez-Jurado, H.A.; Banks, E.W.; He, X.; Zhang, X. Modelling quasi-three-dimensional distribution of solar irradiance on complex terrain. Environ. Modell. Softw. 2022, 149, 105293. [Google Scholar] [CrossRef]
- Hawkins, C.P.; Hogue, J.N.; Decker, L.M.; Feminella, J.W. Channel morphology, water temperature, and assemblage structure of stream insects. Freshw. Sci. 1997, 16, 728–749. [Google Scholar] [CrossRef]
- Poff, N.L.; Richter, B.D.; Arthington, A.H.; Bunn, S.E.; Naiman, R.J.; Kendy, E.; Acreman, M.; Apse, C.; Bledsoe, B.P.; Freeman, M.C.; et al. The ecological limits of hydrologic alteration (ELOHA): A new framework for developing regional environmental flow standards. Freshw. Biol. 2010, 55, 147–170. [Google Scholar] [CrossRef]
- Noori, R.; Bateni, S.M.; Saari, M.; Almazroui, M.; Torabi Haghighi, A. Strong warming rates in the surface and bottom layers of a boreal lake: Results from approximately six decades of measurements (1964–2020). Earth Space Sci. 2022, 9, e2021EA001973. [Google Scholar] [CrossRef]
- Chen, C.; He, W.; Zhou, H.; Xue, Y.; Zhu, M. A comparative study machine learning and numerical models for simulating groundwater dynamics in the Heihe River Basin, northwestern China. Sci. Rep. 2020, 10, 3904. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Xu, B.; Zhang, C.; Fu, G.; Chen, X.; Zheng, Y.; Zhang, J. Surface water temperature prediction in large-deep reservoirs using a long short-term memory model. Ecol. Indic. 2022, 134, 108491. [Google Scholar] [CrossRef]
- Zhao, W.L.; Gentine, P.; Reichstein, M.; Zhang, Y.; Zhou, S.; Wen, Y.; Lin, C.; Li, X.; Qiu, G.Y. Physics-constrained machine learning of evapotranspiration. Geophys. Res. Lett. 2019, 46, 14496–14507. [Google Scholar] [CrossRef]
- Downing, J.A.; Prairie, Y.T.; Cole, J.J.; Duarte, C.M.; Tranvik, L.J.; Striegl, R.G.; McDowell, W.H.; Kortelainen, P.; Caraco, N.F.; Melack, J.M.; et al. The global abundance and size distribution of lakes, ponds and impoundments. Limnol. Oceanogr. 2006, 51, 2388–2397. [Google Scholar] [CrossRef]
- Paltan, H.; Dash, J.; Edwards, M. A refined mapping of Arctic lakes using landsat imagery. Int. J. Remote Sens. 2015, 36, 5970–5982. [Google Scholar] [CrossRef]
- Hipsey, M.R.; Bruce, L.C.; Boon, C.; Busch, B.; Carey, C.C.; Hamilton, D.P.; Hanson, P.C.; Read, J.S.; de Sousa, E.; Weber, M.; et al. A general lake model (GLM 3.0) for linking with high-frequency sensor data from the global lake ecological observatory network (GLEON). Geosci. Model Dev. 2019, 12, 473–523. [Google Scholar] [CrossRef]
- Gao, P.; Pasternack, G.B.; Bali, K.M.; Wallender, W.W. Suspended-sediment transport in an intensively cultivated watershed in southeastern California. Catena 2007, 69, 239–252. [Google Scholar] [CrossRef]
- Nardi, F.; Cudennec, C.; Abrate, T.; Allouch, C.; Annis, A.; Assumpção, T.; Aubert, A.H.; Bérod, D.; Braccini, A.M.; Buytaert, W.; et al. Citizens and HYdrology (CANDHY): Conceptualizing a transdisciplinary framwork for citizen science addressing hydrological challenges. Hydrol. Sci. J. 2021, 1, 2534–2551. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Kim, J.Y.; Seo, D.I.; Jang, M.Y.; Kim, J.Y. Augmentation of limited input data using an artificial neural network method to improve the accuracy of water quality modeling in a large lake. J. Hydrol. 2021, 602, 126817. [Google Scholar] [CrossRef]
- Mahlathi, C.D.; Wilms, J.; Brink, I. Investigation of scarce input data augmentation for modelling nitrogenous compounds in South African rivers. Water Pract. Technol. 2022, 17, 2499–2515. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A brief review of random forests for water scientists and practitioners and their recent history in water resources. Water 2019, 11, 910. [Google Scholar] [CrossRef]
- Caughlan, L.; Oakley, K.L. Cost considerations for long-term ecological monitoring. Ecol. Indic. 2001, 1, 123–134. [Google Scholar] [CrossRef]
- Willard, J.D.; Read, J.S.; Appling, A.P.; Oliver, S.K.; Jia, X.; Kumar, V. Predicting water temperature dynamics of unmonitored Lakes with meta transfer learning. Water Resour. Res. 2021, 57, e2021WR029579. [Google Scholar] [CrossRef]
- Erhan, D.; Bengio, Y.; Courville, A.; Manzagol, P.A.; Vincent, P.; Bengio, S. Why does unsupervised pretraining help deep learning? J. Mach. Learn. Res. 2011, 11, 625–660. Available online: http://www.jmlr.org/papers/volume11/erhan10a/erhan10a.pdf (accessed on 22 January 2023).
- Fang, K.; Shen, C.; Kifer, D.; Yang, X. Prolongation of SMAP to spatiotemporally seamless coverage of continental U.S. using a deep learning neural network. Geophys. Res. Lett. 2017, 44, 11030–11039. [Google Scholar] [CrossRef]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, H.; Jiang, P.; Yu, S.; Lin, G.; Bychkov, I.; Hmelnov, A.; Ruzhnikov, G.; Zhu, N.; Liu, Z. A transfer learning-based LSTM strategy for imputing large-scale consecutive missing data and its application in a water quality prediction system. J. Hydrol. 2021, 602, 126573. [Google Scholar] [CrossRef]
- Kumar, R.; Samaniego, L.; Attinger, S. Implications of distributed hydrologic model parameterization on water fluxes at multiple scales and locations. Water Resour. Res. 2013, 49, 360–379. [Google Scholar] [CrossRef]
- Roth, V.; Nigussie, T.K.; Lemann, T. Model parameter transfer for streamflow and sediment loss prediction with swat in a tropical watershed. Environ. Earth Sci. 2016, 75, 1321. [Google Scholar] [CrossRef]
- Koch, J.; Schneider, R. Long short-term memory networks enhance rainfall-runoff modelling at the national scale of Denmark. GEUS Bull. 2022, 49, 1–7. [Google Scholar] [CrossRef]




| Model | RMSE (°C) | ||||||
|---|---|---|---|---|---|---|---|
| Proportion of Field Data Used in the Model Training Phase (%) | |||||||
| 0 | 0.5 | 1 | 2 | 10 | 20 | 100 | |
| W2-gnr | - | - | - | - | - | - | 1.930 |
| W2-calib | - | - | - | - | - | - | 1.781 |
| LSTM | - | 15.978 0.380) | 9.403 0.284) | 2.432 0.257) | 0.289 0.113) | 0.131 0.089) | 0.062 0.010) |
| LSTMEC | - | 15.007 0.319) | 8.915 0.256) | 2.229 0.212) | 0.243 0.100) | 0.092 0.033) | 0.042 0.007) |
| LSTMEC,p | 7.214 0.327) | 3.007 0.301) | 2.015 0.156) | 1.160 0.115) | 0.230 0.088) | 0.078 0.012) | 0.018 0.001) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Chung, S. Enhancing Water Temperature Prediction in Stratified Reservoirs: A Process-Guided Deep Learning Approach. Water 2023, 15, 3096. https://doi.org/10.3390/w15173096
Kim S, Chung S. Enhancing Water Temperature Prediction in Stratified Reservoirs: A Process-Guided Deep Learning Approach. Water. 2023; 15(17):3096. https://doi.org/10.3390/w15173096
Chicago/Turabian StyleKim, Sungjin, and Sewoong Chung. 2023. "Enhancing Water Temperature Prediction in Stratified Reservoirs: A Process-Guided Deep Learning Approach" Water 15, no. 17: 3096. https://doi.org/10.3390/w15173096





