Experimental and DEM-CFD Coupling Investigations on the Characteristics and Mechanism of Seepage Erosion for Cohesionless Soil
Abstract
:1. Introduction
2. Model Test on Seepage Erosion of Cohesionless Soils
2.1. Material
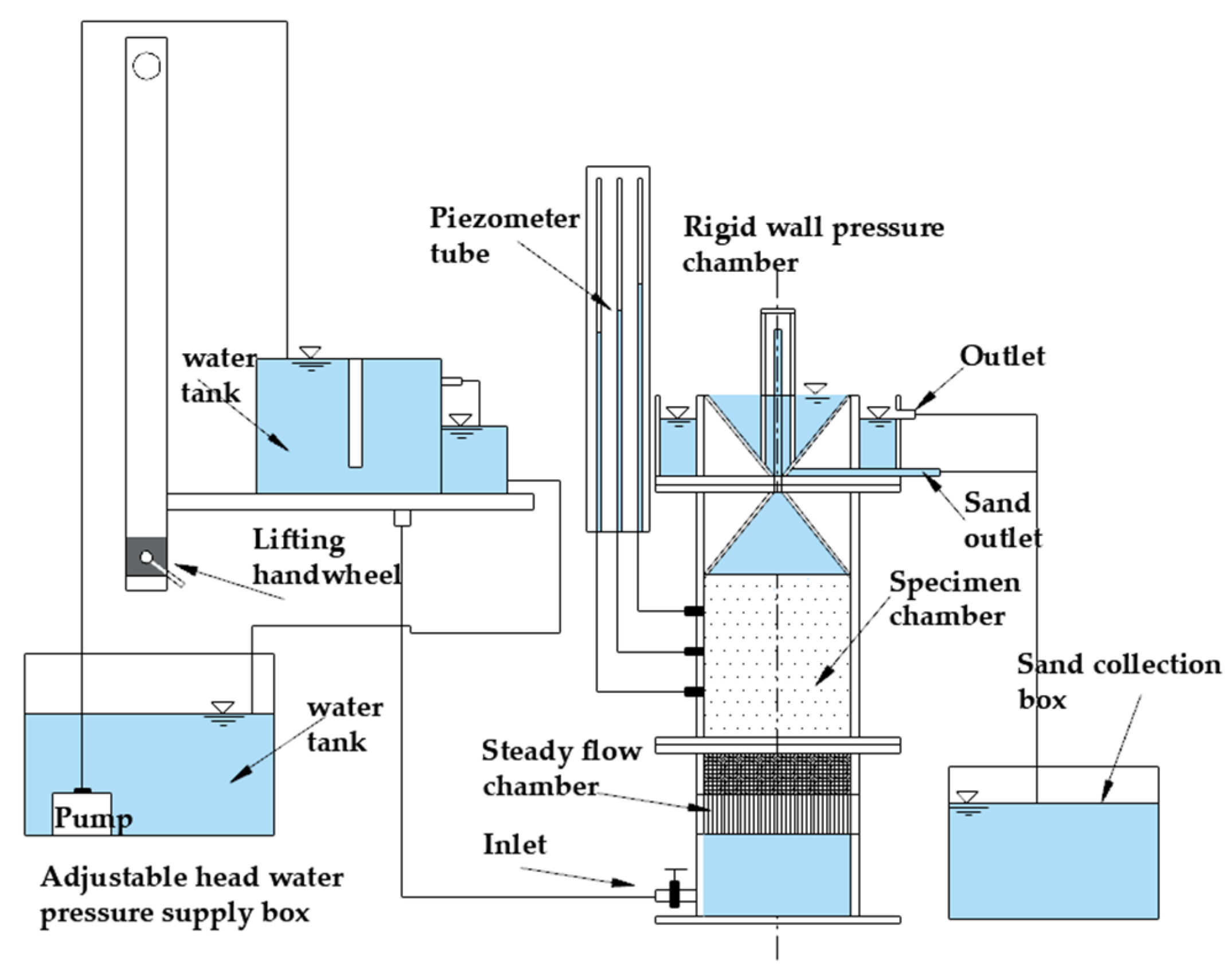
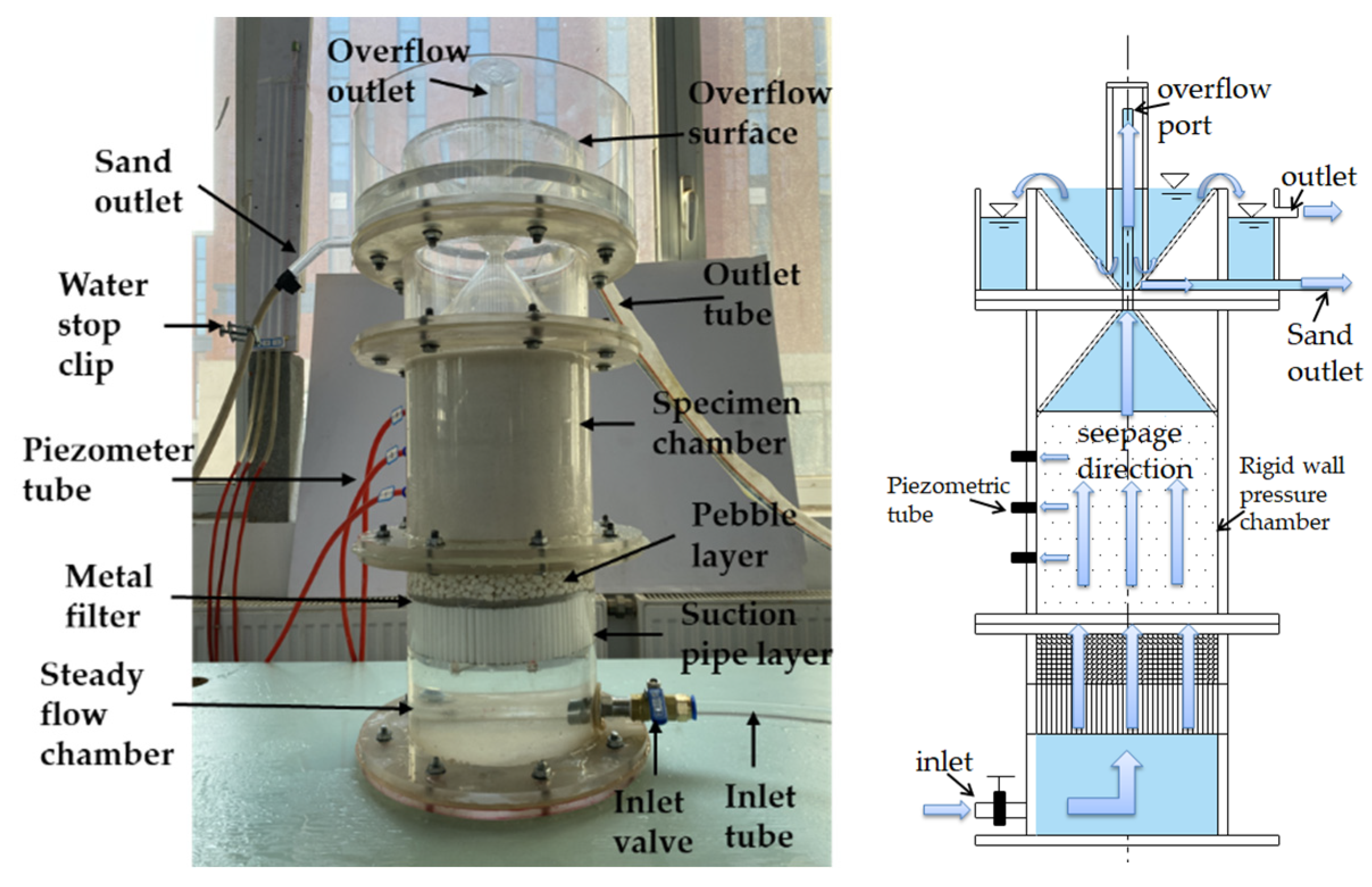
2.2. The Seepage Erosion Device
3. DEM-CFD Coupling Analysis of Seepage Erosion of Cohesionless Soils
3.1. DEM-CFD Coupling Method
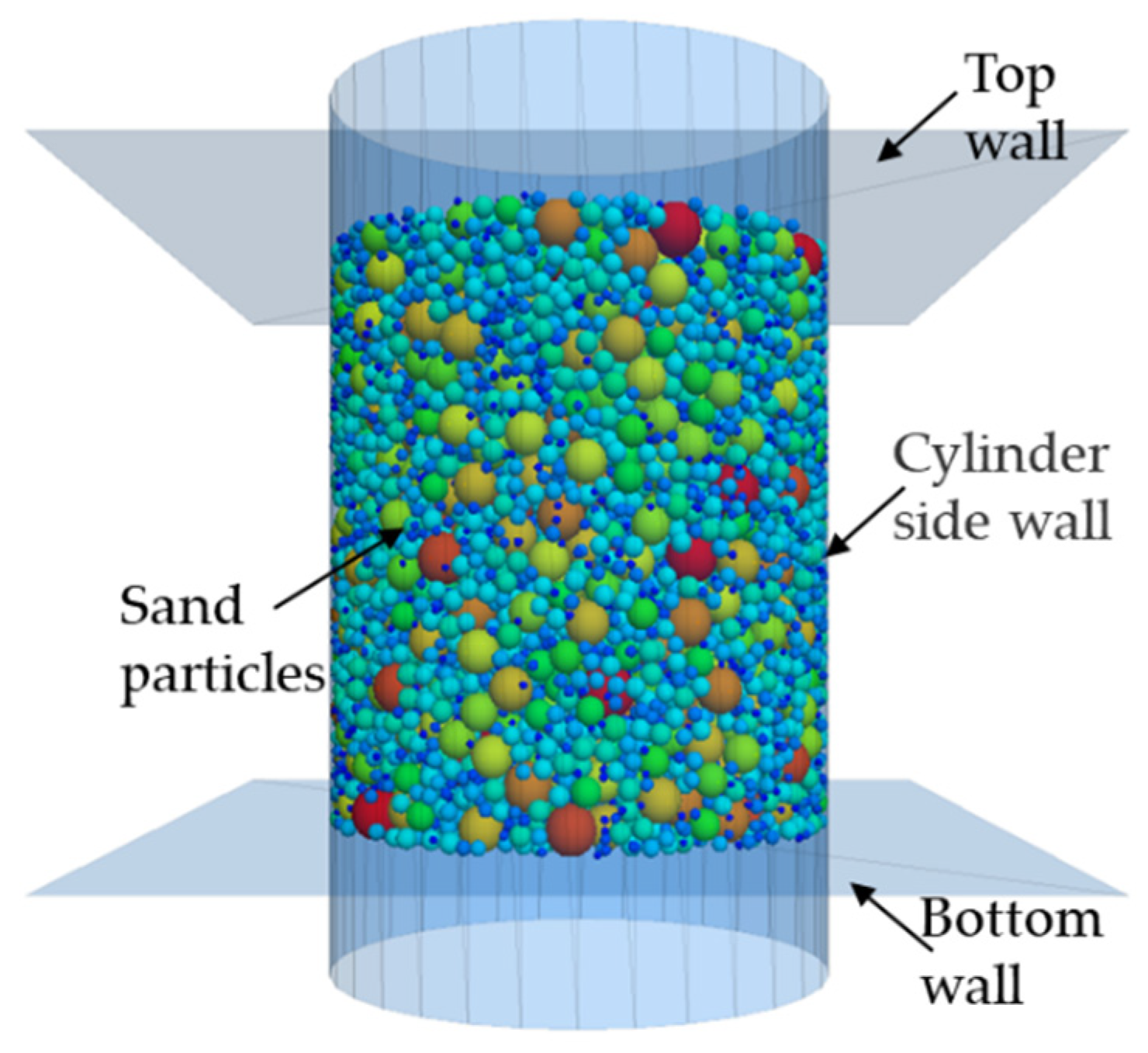
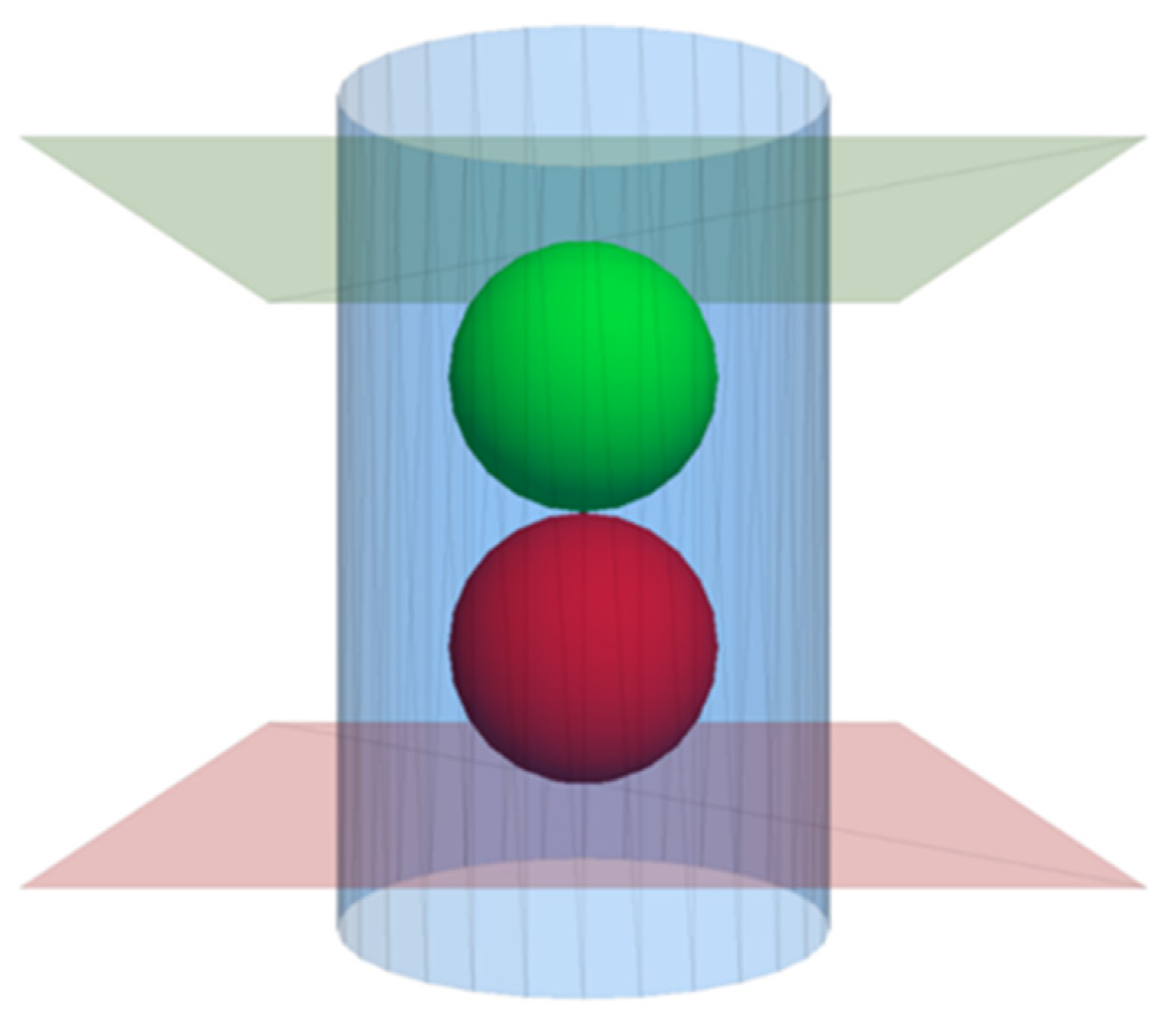
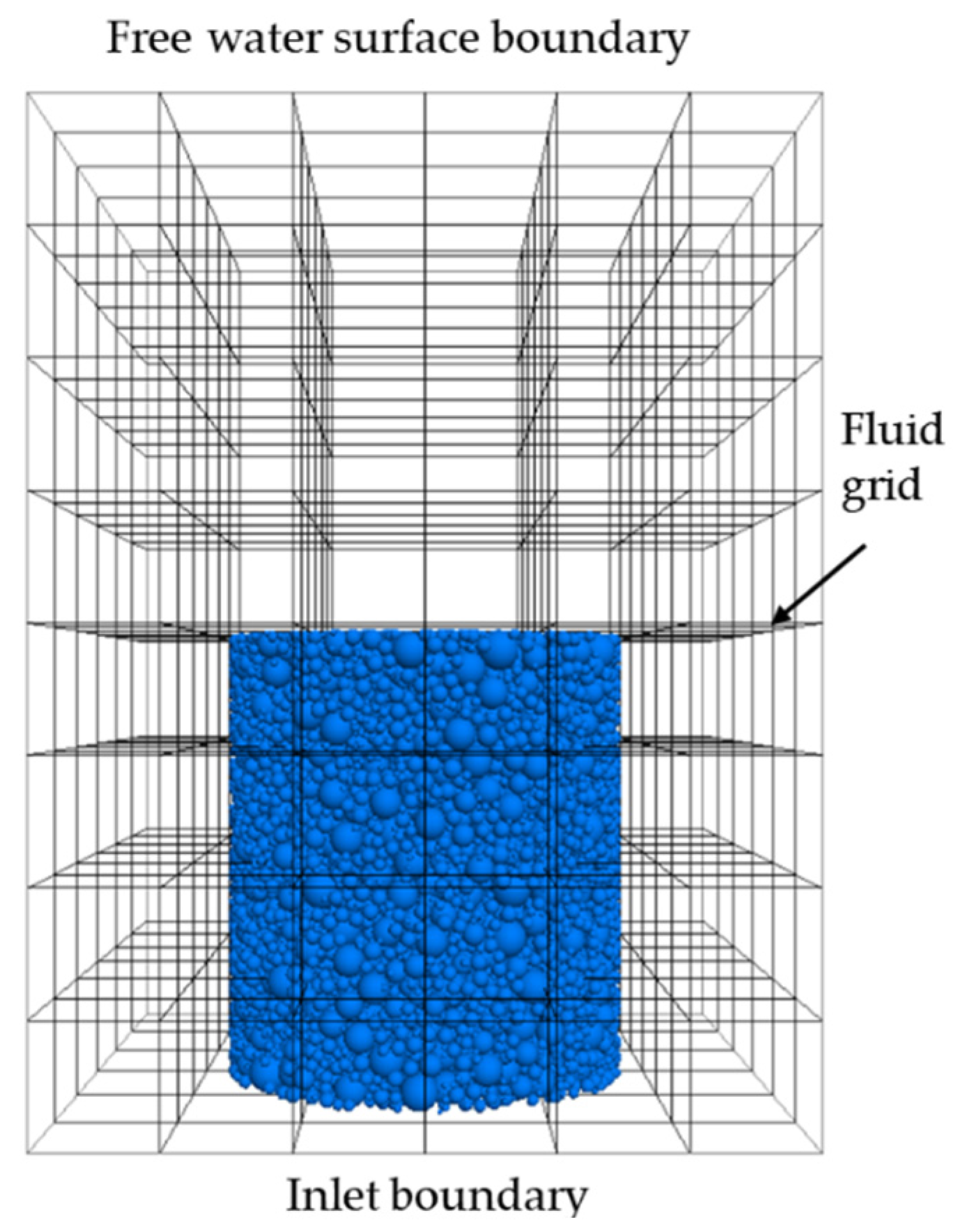
3.2. DEM-CFD Model of Seepage Erosion for Cohesionless Soils
4. Results and Discussion
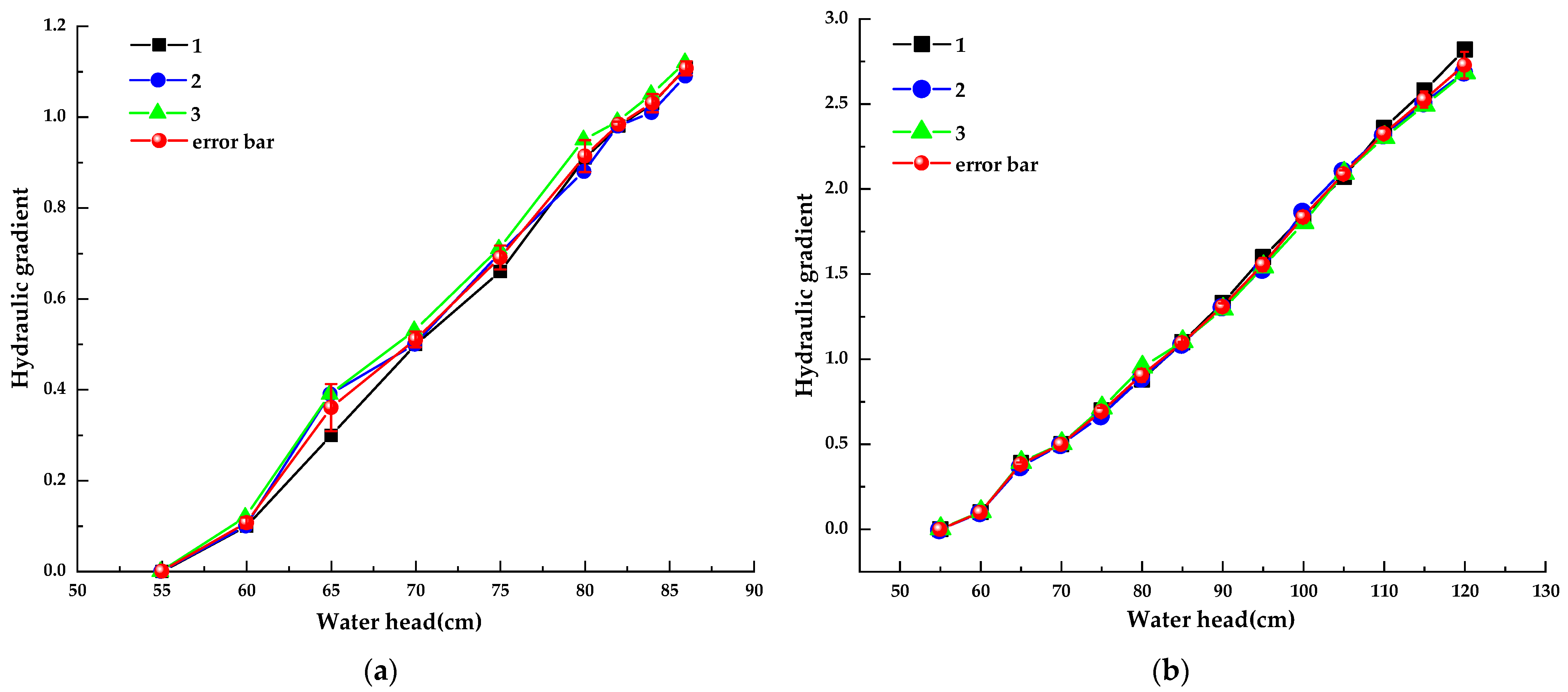
4.1. Experimental Phenomenon and Critical Hydraulic Gradient Analysis
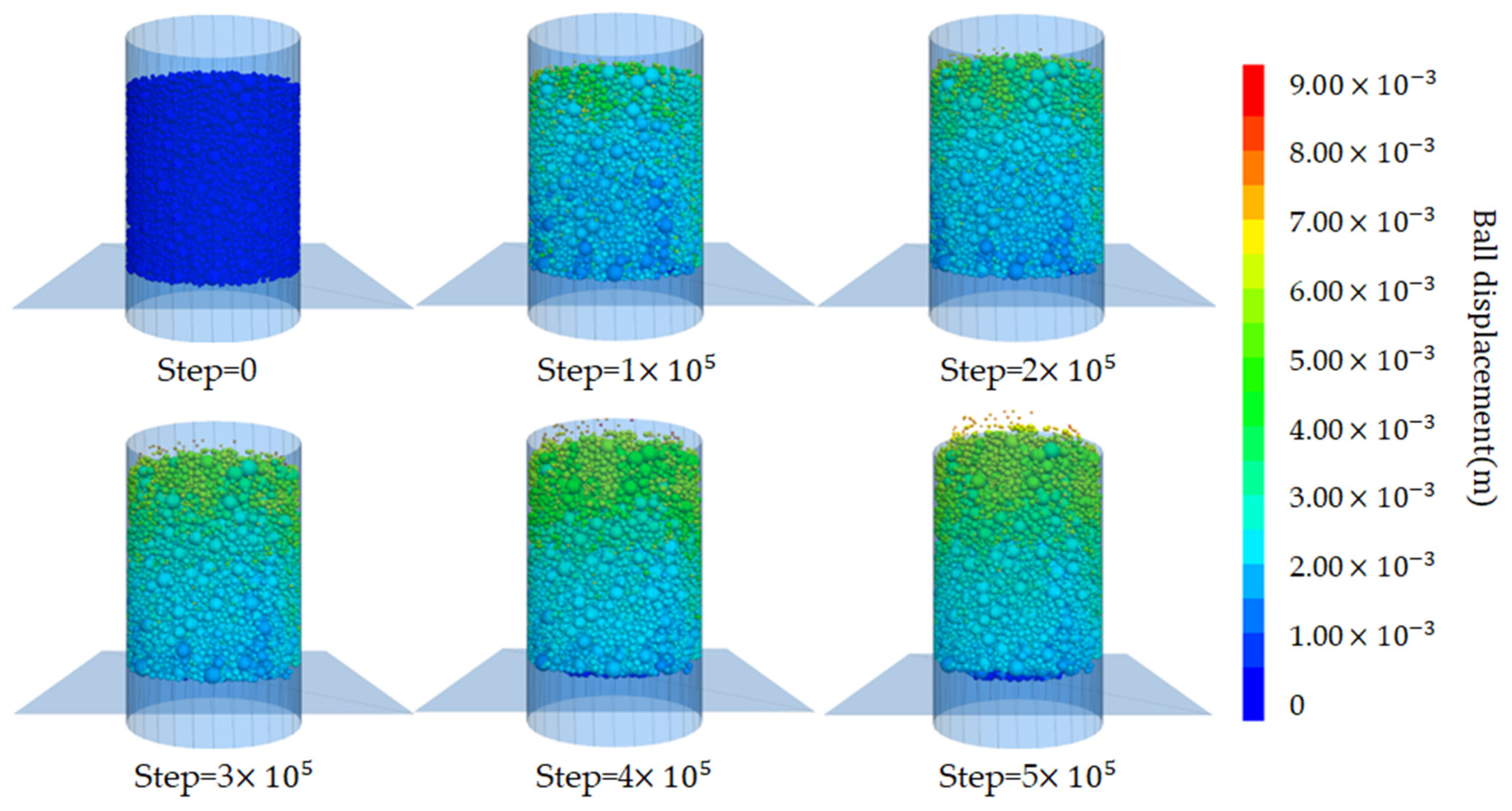
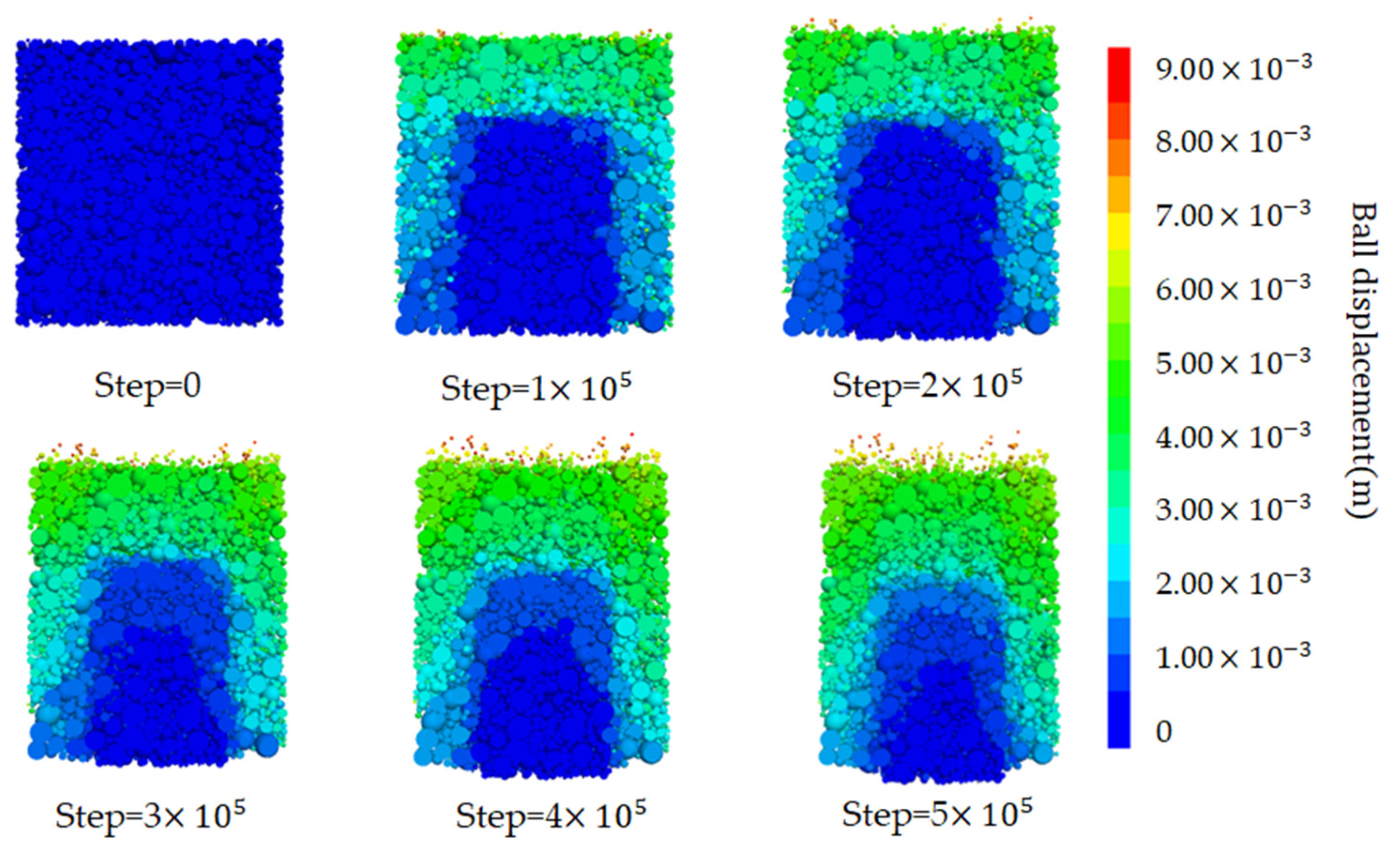
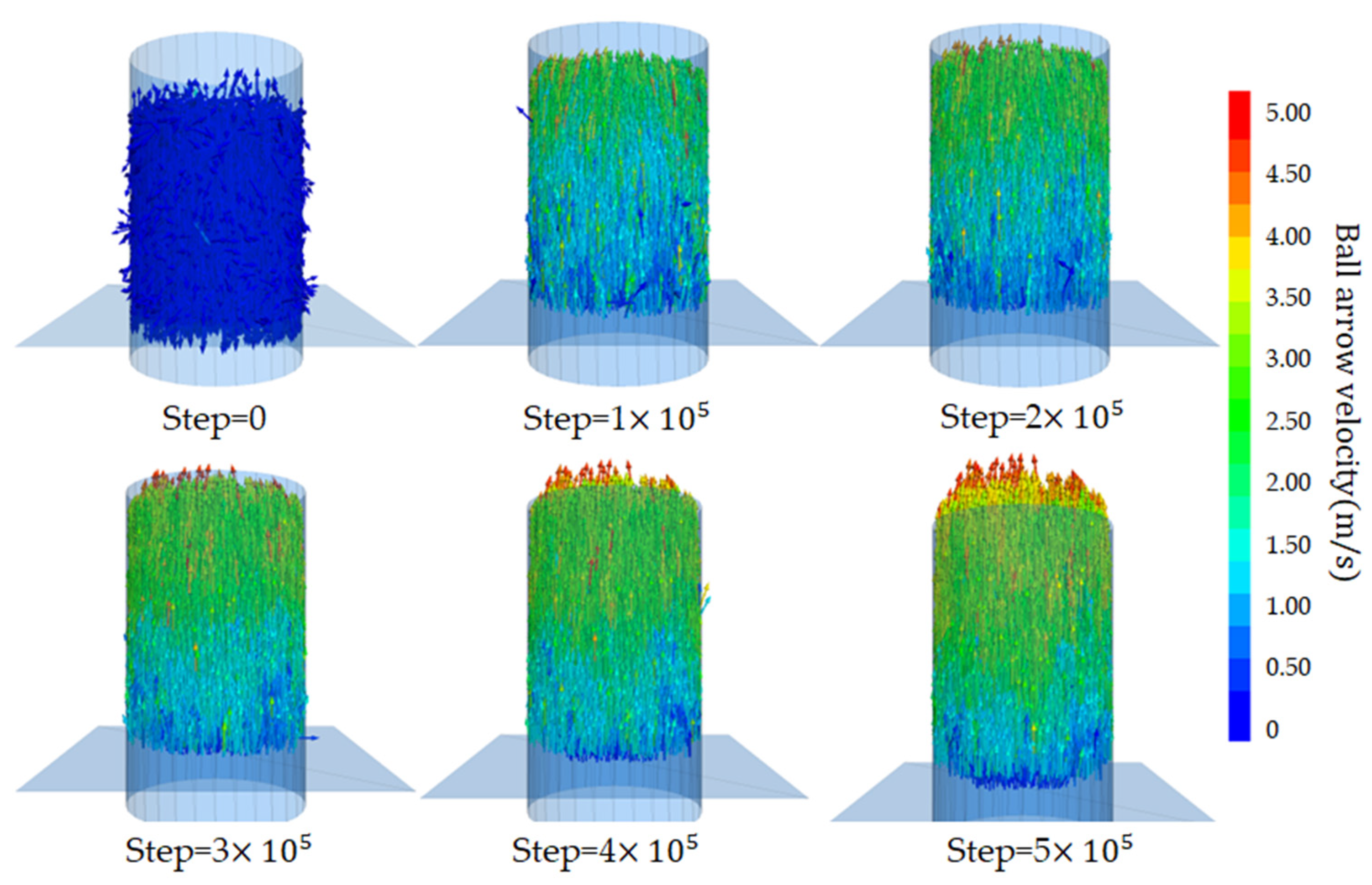
4.2. Mesoscopic Analysis of Seepage Erosion Process and Particle Migration Law
- (1)
- Stable seepage stage
- (2)
- Fine particle upward migration stage
- (3)
- Skeleton particle-loosening stage
- (4)
- Complete failure stage
4.3. Microstructural Characteristics of Soil Particles during the Seepage Erosion Process
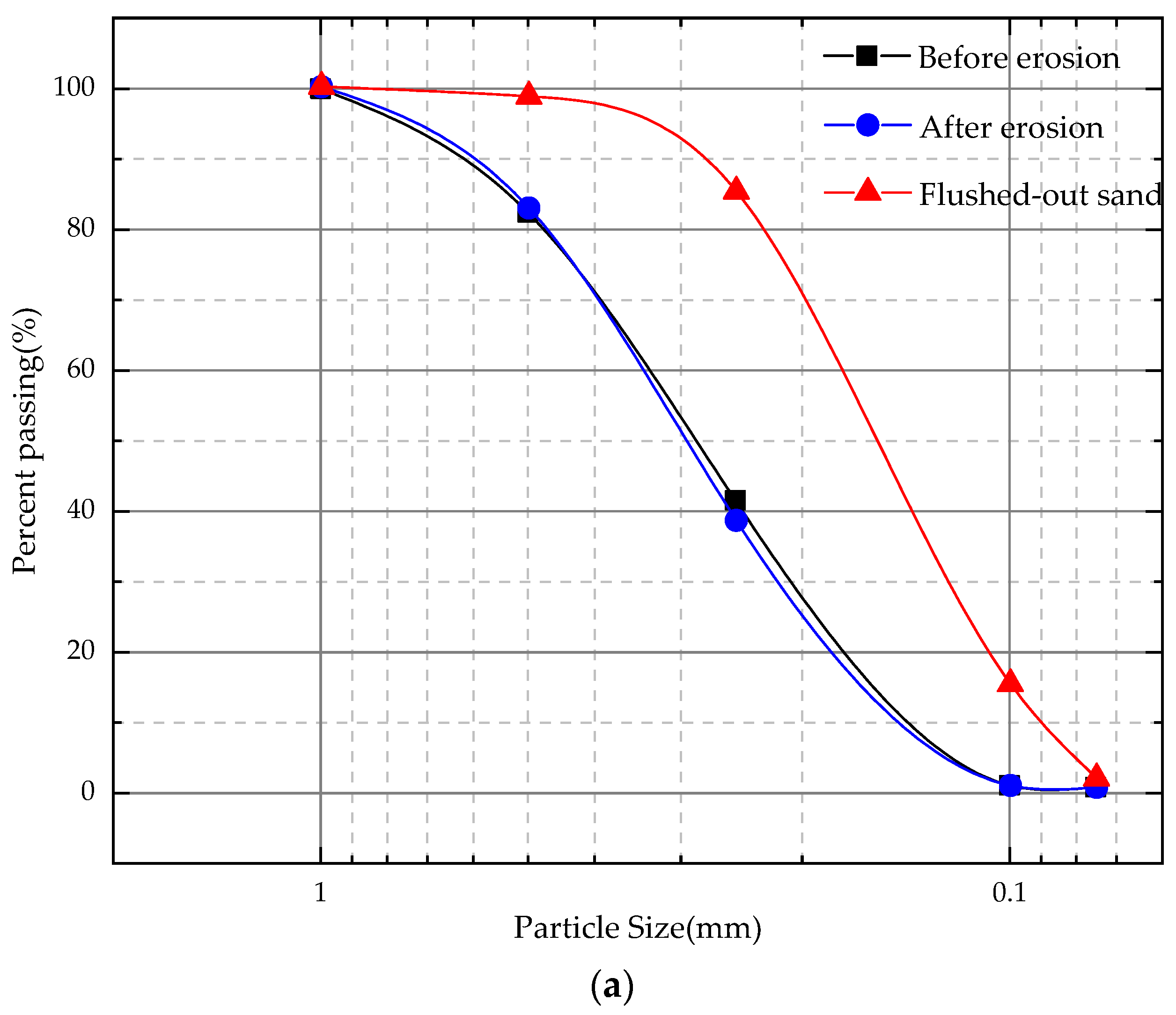
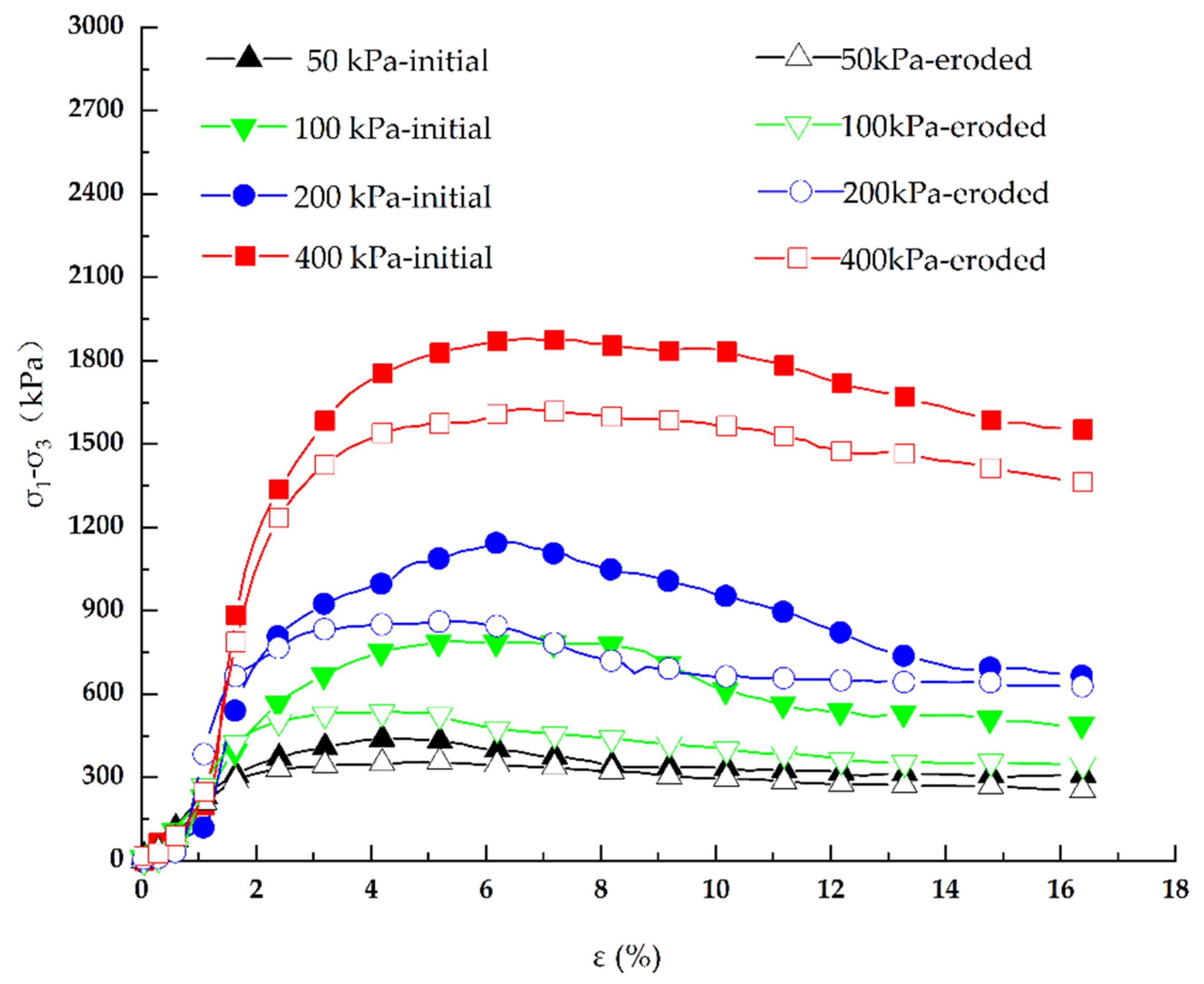
4.4. Influence and Mechanism Analysis of Seepage Erosion on the Mechanical Properties of Soil
5. Conclusions
- (1)
- A self-made seepage erosion device for cohesionless soil was developed, which could be used to observe the seepage erosion process, measure the critical hydraulic gradient of seepage erosion, and investigate the escaping particles during the seepage erosion process.
- (2)
- The seepage erosion process of cohesionless soil could be divided into four stages: stable seepage, fine particle upward migration, sand sample boiling, and erosion damage.
- (3)
- Mixing with coarse-grain sand could increase the critical hydraulic gradient of the fine-grain quartz sand sample because the coarse-grain sand could improve the soil structure and force chain of the fine-grain sand sample.
- (4)
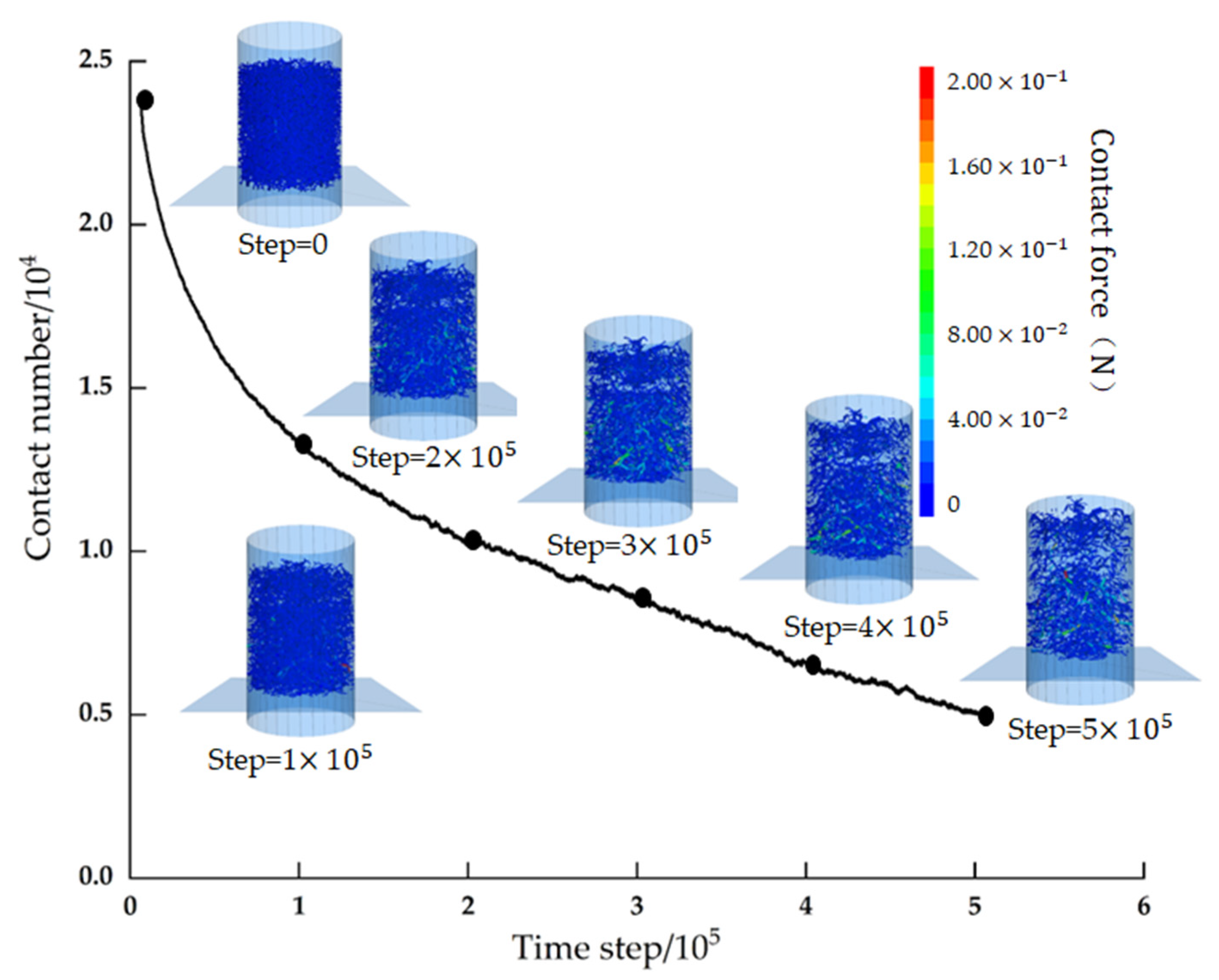
- Increasing erosion ratio meant more loss of fine sand particles and an increase in pore structure between soil skeleton particles. These changes could result in the rearrangement of soil particles, i.e., a decrease in contact number and the weakening of contact force, which led to strength decrease.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiao, Q.; Wang, J.-P. CFD–DEM Simulations of Seepage-Induced Erosion. Water 2020, 12, 678. [Google Scholar] [CrossRef]
- Li, W.; Qian, J.; Yin, Z. Simulation of seepage erosion in gap graded sand soil using CFD-DEM. Chin. Rock Soil Mech. 2021, 42, 1–11. [Google Scholar]
- Chen, C.; Zhang, L. Hydro-mechanical behaviour of soil experiencing seepage erosion under cyclic hydraulic gradient. Géotechnique 2021, 73, 115–127. [Google Scholar] [CrossRef]
- Richards, K.S.; Reddy, K.R. Critical appraisal of piping phenomena in earth dams. Bull. Eng. Geol. Environ. 2007, 66, 381–402. [Google Scholar] [CrossRef]
- Yang, J.; Yin, Z.-Y.; Laouafa, F.; Hicher, P.-Y. Analysis of suffusion in cohesionless soils with randomly distributed porosity and fines content. Comput. Geotech. 2019, 111, 157–171. [Google Scholar] [CrossRef]
- Wang, X.; Tang, Y.; Huang, B.; Hu, T.; Ling, D. Review on Numerical Simulation of the Internal Soil Erosion Mechanisms Using the Discrete Element Method. Water 2021, 13, 169. [Google Scholar] [CrossRef]
- Dassanayake, S.M.; Mousa, A.A.; Ilankoon, S.; Fowmes, G.J. Internal Instability in Soils: A Critical Review of the Fundamentals and Ramifications. Transp. Res. Rec. 2022, 2676, 1–26. [Google Scholar] [CrossRef]
- Fell, R.; Wan, C.F.; Cyganiewicz, J.; Foster, M. Time for Development of Internal Erosion and Piping in Embankment Dams. J. Geotech. Geoenviron. Eng. 2003, 129, 307–341. [Google Scholar] [CrossRef]
- Chen, F.; Xiong, H.; Wang, X.; Yin, Z.Y. Transmission effect of eroded particles in suffusion using the CFD-DEM coupling method. Acta Geotech. 2022, 18, 335–354. [Google Scholar] [CrossRef]
- Gong, J.; Liu, J. Mechanical transitional behavior of binary mixtures via DEM: Effect of differences in contact-type friction coefficients. Comput. Geotech. 2017, 85, 1–14. [Google Scholar] [CrossRef]
- Li, W.C.; Deng, G.; Liang, X.Q.; Sun, X.X.; Wang, S.W.; Lee, M.L. Effects of stress state and fine fraction on stress transmission in internally unstable granular mixtures investigated via discrete element method. Powder Technol. 2020, 367, 659–670. [Google Scholar] [CrossRef]
- Wang, Y.; Chai, J.; Xu, Z.; Qin, Y.; Wang, X. Numerical Simulation of the Fluid–Solid Coupling Mechanism of Internal Erosion in Granular Soil. Water 2020, 12, 137. [Google Scholar] [CrossRef]
- Guidoux, C.; Faure, Y.H.; Beguin, R.; Ho, C.C. Contact Erosion at the Interface between Granular Coarse Soil and Various Base Soils under Tangential Flow Condition. J. Geotech. Geoenviron. Eng. 2010, 136, 741–750. [Google Scholar]
- Liang, Y.; Yeh TC, J.; Zha, Y.; Wang, J.; Liu, M.; Hao, Y. Onset of suffusion in gap-graded soils under upward seepage. Soils Found. 2017, 57, 849–860. [Google Scholar] [CrossRef]
- Ming, P.; Lu, J.; Cai, X.; Liu, M.; Hu, S. Experimental study on internal erosion and seepage in the foundation of a dike under variable water head. Eur. J. Environ. Civ. Eng. 2021, 26, 5073–5087. [Google Scholar] [CrossRef]
- Wen, F.; Li, X.A.; Yang, W.; Li, J.; Zhou, B.; Gao, R.; Lei, J. Mechanism of loess planar erosion and numerical simulation based on CFD–DEM coupling model. Environ. Earth Sci. 2023, 82, 197. [Google Scholar] [CrossRef]
- Li, L.; Gu, Z.; Xu, W.; Tan, Y.; Fan, X.; Tan, D. Mixing mass transfer mechanism and dynamic control of gas-liquid-solid multiphase flow based on VOF-DEM coupling. Energy 2023, 272, 127015. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, T.; Liu, F.; Peng, M.; Furtney, J.; Zhang, L. Modeling of fluid-particle interaction by coupling the discrete element method with a dynamic fluid mesh: Implications to suffusion in gap-graded soils. Comput. Geotech. 2020, 124, 103617. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, F.; Furtney, J.; Damjanac, B. A review of methods, applications and limitations for incorporating fluid flow in the discrete element method. J. Rock Mech. Geotech. Eng. 2022, 14, 1005–1024. [Google Scholar] [CrossRef]
- Mu, L.; Zhang, P.; Shi, Z.; Huang, M. Coupled CFD–DEM Investigation of Erosion Accompanied by Clogging Mechanism under Different Hydraulic Gradients. Comput. Geotech. 2023, 153, 105058. [Google Scholar] [CrossRef]
- Wang, X.; Huang, B.; Tang, Y.; Hu, T.; Ling, D. Microscopic mechanism and analytical modeling of seepage-induced erosion in bimodal soils. Comput. Geotech. 2022, 141, 104527. [Google Scholar] [CrossRef]
- Li, L.; Lu, B.; Xu, W.X.; Gu, Z.H.; Yang, Y.S.; Tan, D.P. Mechanism of multiphase coupling transport evolution of free sink vortex. Acta Phys. Sin. 2023, 72, 182–195. [Google Scholar] [CrossRef]
- Wang, F.; Wang, F.; Gong, X.; Zhang, Y.; Li, G. Water Erosion and Extension of Ground Fissures in Weihe Basin Based on DEM-CFD Coupled Modeling. Water 2023, 15, 2321. [Google Scholar] [CrossRef]
- Li, B.-L.; Wang, C.-M.; Li, Y.-Y. Study on Dynamic Response of Blocking Structure and Debris Flow Impulsive Force considering Material Source Erosion. Lithosphere 2022, 2022, 1252637. [Google Scholar] [CrossRef]
- Zhou, W.; Ma, Q.; Ma, G.; Cao, X.; Cheng, Y. Microscopic investigation of internal erosion in binary mixtures via the coupled LBM-DEM method. Powder Technol. 2020, 376, 31–41. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, Y.; Yang, Z. Suffusion-induced deformation and microstructural change of granular soils: A coupled CFD–DEM study. Acta Geotech. 2019, 14, 795–814. [Google Scholar] [CrossRef]
- Wang, P.; Ge, Y.; Wang, T.; Liu, Q.W.; Song, S.X. CFD-DEM modelling of suffusion in multi-layer soils with different fines contents and impermeable zones. J. Zhejiang Univ.-Sci. A 2022, 24, 6–19. [Google Scholar] [CrossRef]
- Zhang, P.; Mu, L.; Huang, M. A coupled CFD-DEM investigation into hydro-mechanical behaviour of gap-graded soil experiencing seepage erosion considering cyclic hydraulic loading. J. Hydrol. 2023, 624, 129908. [Google Scholar] [CrossRef]
- Scholtès, L.; Hicher, P.Y.; Sibille, L. A Micromechanical Approach to Describe Internal Erosion Effects in Soils. In Geomechanics and Geotechnics: From Micro to Macro; IS-Shanghai: Shanghai, China, 2011; Available online: https://hal.science/hal-01007757 (accessed on 18 August 2023).
- Zhou, C.; Qian, J.G.; Yin, Z.Y. Microscopic investigation of the influence of complex stress states on internal erosion and its impacts on critical hydraulic gradients. Int. J. Numer. Anal. Methods Geomech. 2022, 46, 3377–3401. [Google Scholar] [CrossRef]
- Hu, Z.; Guo, N.; Yang, Z.X. Effect of fines loss on the microstructure and shear behaviors of gap-graded soils: A multiscale perspective. Comput. Geotech. 2023, 162, 105711. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, G.; Jia, C.; Li, C. A Novel, Coupled CFD-DEM Model for the Flow Characteristics of Particles Inside a Pipe. Water 2019, 11, 2381. [Google Scholar] [CrossRef]
- Tsuji, Y.; Tanaka, T.; Ishida, T. Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe-ScienceDirect. Powder Technol. 1992, 71, 239–250. [Google Scholar] [CrossRef]
- Tsuji, Y.; Kawaguchi, T.; Tanaka, T. Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 1993, 77, 79–87. [Google Scholar] [CrossRef]
- Anderson, T.B.; Jackson, R. Fluid Mechanical Description of Fluidized Beds. Stability of State of Uniform Fluidization. Ind. Eng. Chem. Fundam. 1968, 7, 12–21. [Google Scholar] [CrossRef]
- Zhao, J.; Shan, T. Coupled CFD–DEM simulation of fluid–particle interaction in geomechanics. Powder Technol. 2013, 239, 248–258. [Google Scholar] [CrossRef]
- Di Felice, R. The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 1994, 20, 153–159. [Google Scholar] [CrossRef]
- Ergun, S. Fluid Flow through Packed Columns. Engineering 1952, 48, 89–94. [Google Scholar]
- Hill, R.J.; Koch, D.L.; Ladd, A.J. Moderate-Reynolds-number flows in ordered and random arrays of spheres. J. Fluid Mech. 2001, 448, 243–278. [Google Scholar] [CrossRef]
- Xu, B.; Yu, A. Numerical simulation of the gas-solid flow in a fluidized bed by combining discrete particle method with computational fluid dynamics. Chem. Eng. Sci. 1997, 52, 2785–2809. [Google Scholar] [CrossRef]
- Fleshman, M.S.; Rice, J.D. Laboratory Modeling of the Mechanisms of Piping Erosion Initiation. J. Geotech. Geoenviron. Eng. 2014, 140, 04014017. [Google Scholar] [CrossRef]
- Cai, G.D.; Chen, L.; Teng, Y.Z.; Yin, Z.X.; Zhang, Z. Investigation on Drained Mechanical Properties of Sandy Soil after Internal Erosion with an Erosion-Stress Coupling Apparatus. KSCE J. Civ. Eng. 2022, 27, 480–494. [Google Scholar] [CrossRef]

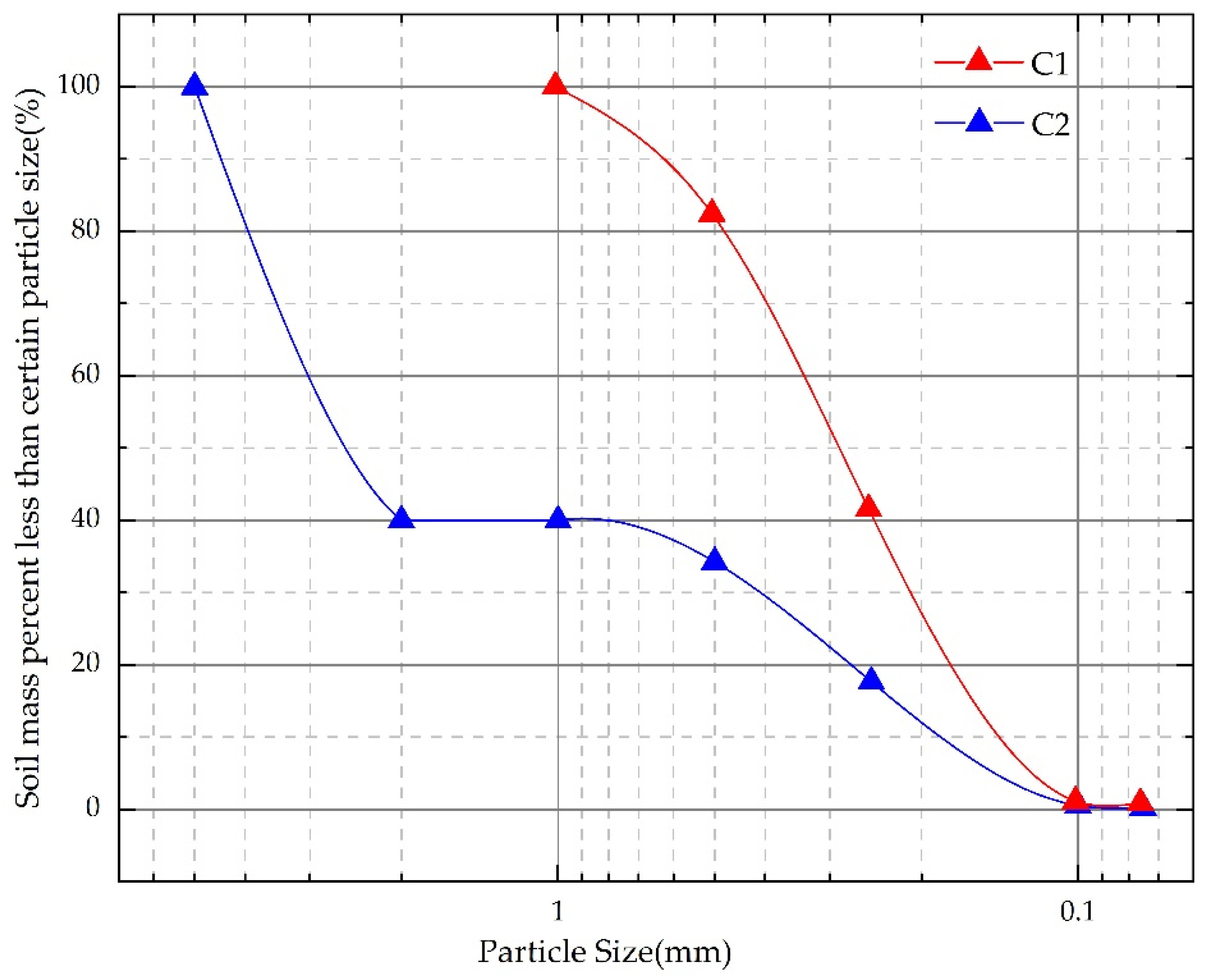



| Sand Sample | Particle Composition | Characteristic Particle Size (mm) | Grading Curve Coefficient | |||||
|---|---|---|---|---|---|---|---|---|
| 0.075–0.5 mm | 2–4 mm | |||||||
| C1 | 10 | 0 | 0.13 | 0.21 | 0.30 | 0.36 | 2.73 | 0.89 |
| C2 | 4 | 6 | 0.18 | 0.44 | 2.08 | 2.67 | 14.57 | 0.39 |
| Computation Modules | Parameter Types (Units) | Values |
|---|---|---|
| Particle model | Particle density, /(kg·m−3) | 2650 |
| Normal stiffness, /(N·m−1) | 3.0 × 106 | |
| Shear stiffness, /(N·m−1) | 2.0 × 106 | |
| Bond stiffness ratio, k1 | 1.5 | |
| Friction coefficient, | 0.5 | |
| Initial porosity | 0.48 | |
| Wall model | Bond stiffness ratio, k2 | 1.5 |
| Friction coefficient, | 0.3 | |
| Fluid model | Fluid density, /(kg·m−3) | 1000 |
| Fluid viscosity, /(Pa·s) | 0.001 | |
| Grid size, (m) | 0.03 × 0.03 × 0.04 | |
| Fluid grid cells, (m) | 0.005 × 0.005 × 0.005 | |
| Number of grid cells | 288 |
| Erosion Rate | State | Average Particle Size /mm | Fineness Modulus | Inhomogeneity Coefficient | Curvature Coefficient |
|---|---|---|---|---|---|
| C1 sample | Before erosion | 0.302 | 2.74 | 2.729 | 0.888 |
| = 0.014 | After erosion | 0.315 | 2.78 | 2.715 | 0.915 |
| Exudate particles | 0.175 | 1.99 | 2.178 | 0.988 | |
| = 0.020 | After erosion | 0.320 | 2.78 | 2.737 | 0.934 |
| Exudate particles | 0.178 | 2.04 | 1.849 | 0.971 | |
| = 0.043 | After erosion | 0.332 | 2.82 | 2.757 | 0.979 |
| Exudate particles | 0.202 | 2.26 | 2.093 | 0.984 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, H.; Dai, D.; Zhang, T.; Yang, J.; Mu, Z. Experimental and DEM-CFD Coupling Investigations on the Characteristics and Mechanism of Seepage Erosion for Cohesionless Soil. Water 2023, 15, 3085. https://doi.org/10.3390/w15173085
Su H, Dai D, Zhang T, Yang J, Mu Z. Experimental and DEM-CFD Coupling Investigations on the Characteristics and Mechanism of Seepage Erosion for Cohesionless Soil. Water. 2023; 15(17):3085. https://doi.org/10.3390/w15173085
Chicago/Turabian StyleSu, Hui, Da Dai, Ting Zhang, Jiaqi Yang, and Zhiyong Mu. 2023. "Experimental and DEM-CFD Coupling Investigations on the Characteristics and Mechanism of Seepage Erosion for Cohesionless Soil" Water 15, no. 17: 3085. https://doi.org/10.3390/w15173085






