Operation and Maintenance Cost of Water Management Systems: Analysis and Optimization
Abstract
:1. Introduction and Literature Review
2. Methodology
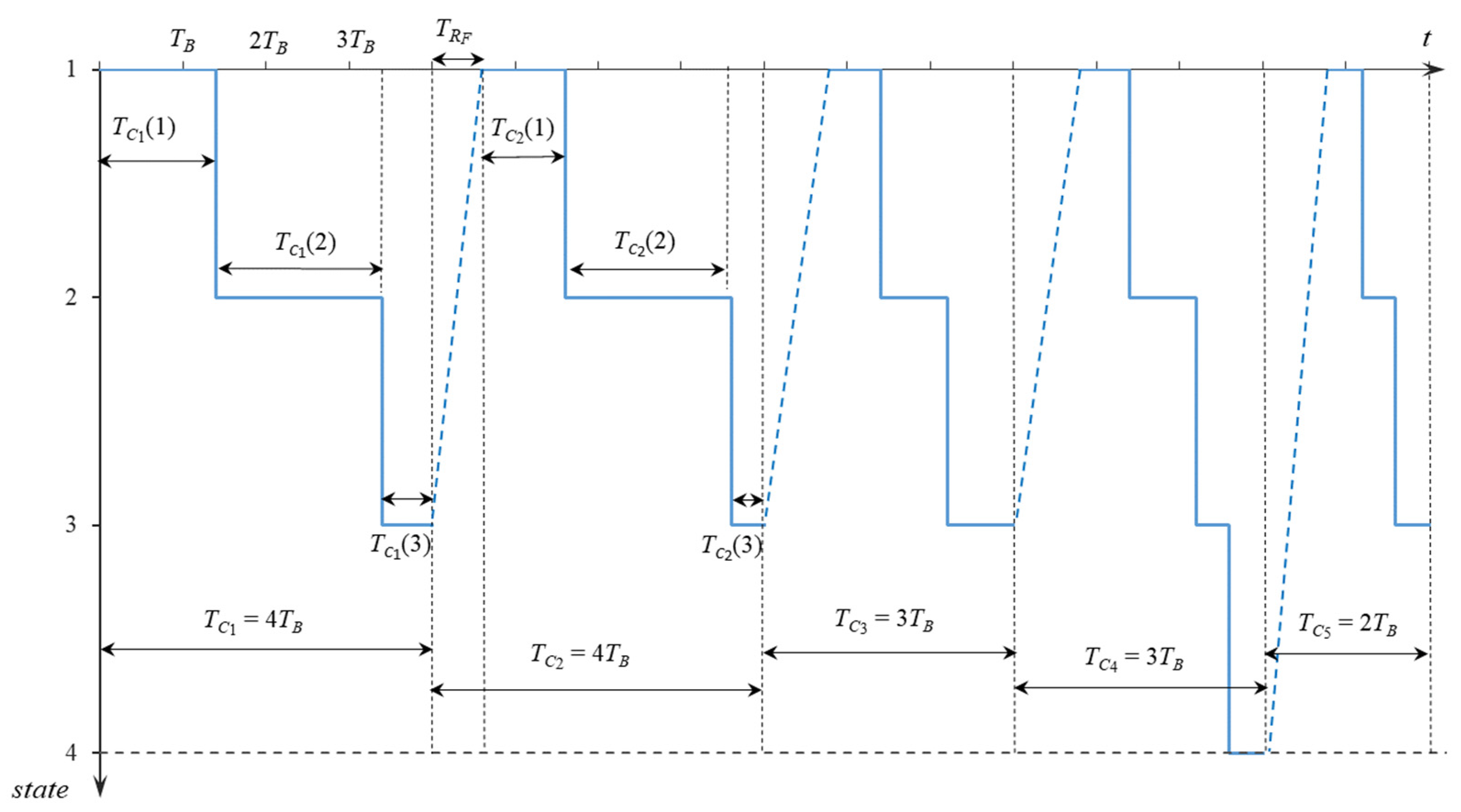
2.1. Description of Multistate Approach Model
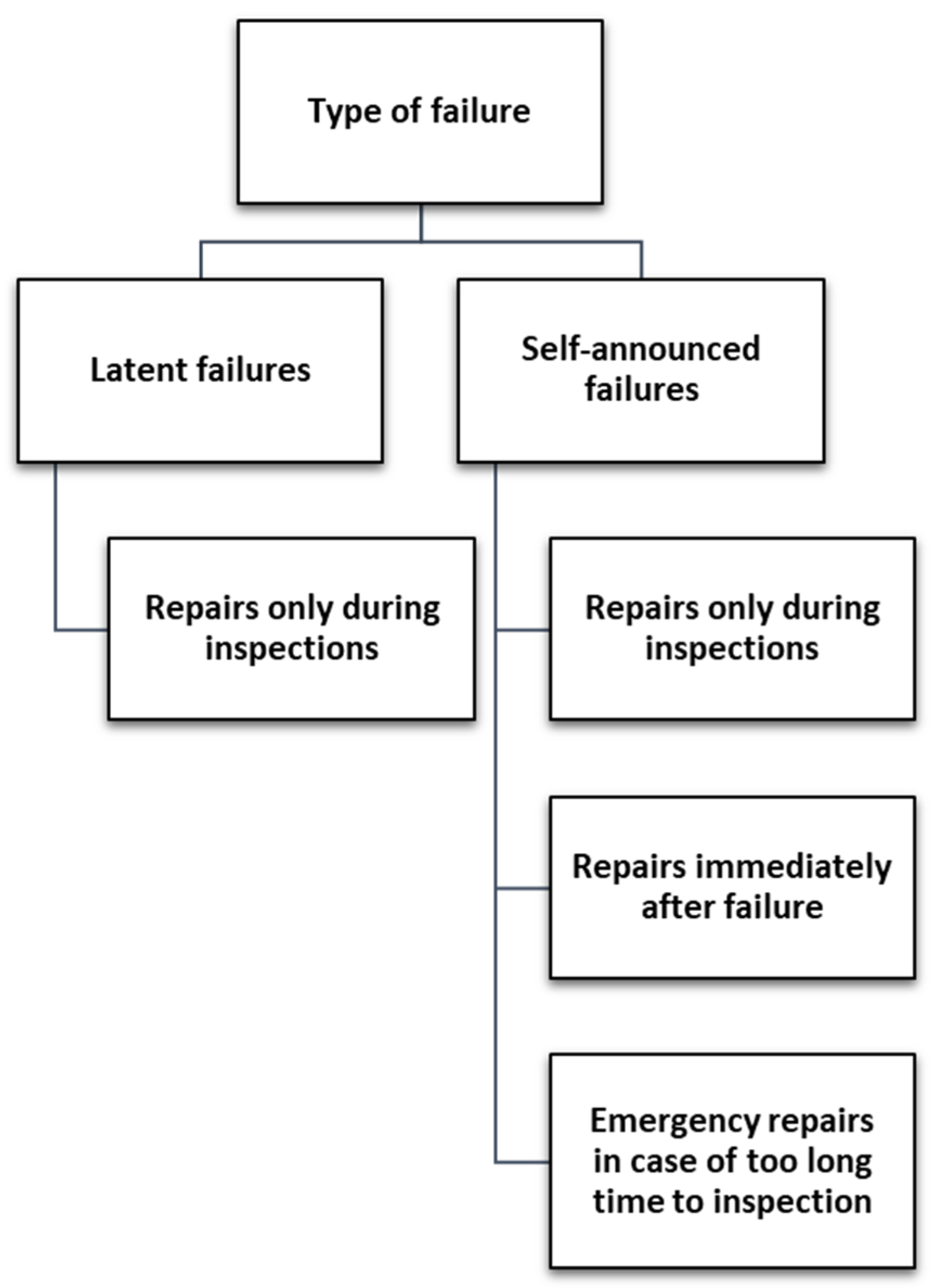
- Perfect/imperfect repairs: every repair leaves the system in the state of full reliability/it is possible to carry out a partial repair (leaving the system in a better state, but not necessarily “as good as new”).
- Always repair/custom repair objectives: every inspection finding the system in a state worse than State 1 results in a repair/for certain states; it is allowed to wait for further deterioration instead of implementing repair actions right away.
- Repairs only during inspections/possibility of emergency repairs: the state of the system is assessed only during scheduled inspections/after certain conditions are met; it is possible to request unscheduled emergency repair.
2.2. System Maintenance Cost and Its Optimization
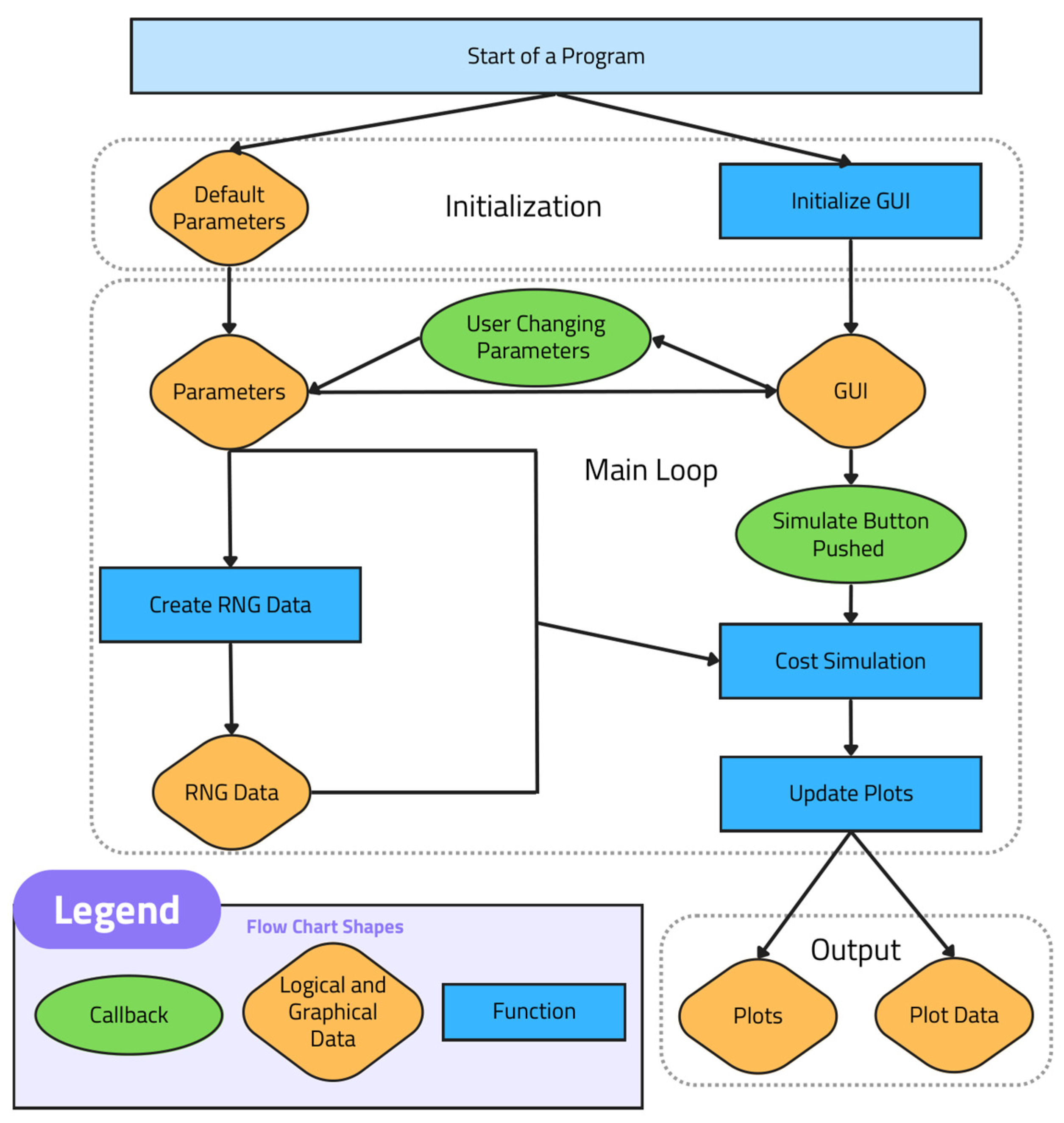
2.3. Simulation of System Maintenance Cost
- First, the user enters data in the presentation layer and the communication layer of the application. Section 3 provides a detailed description of the parameters required to perform the simulation.
- Determine the number of system reliability states and parameters of each of these states.
- Define the maintenance and repair strategy and set the repair objectives for a system, i.e., decide whether repair actions are carried out in a given state and, if so, to what state the system is repaired, taking into account the possibility of perfect and imperfect repairs.
- Determine the cost and the duration of repairs for the system to reach individual reliability states from other, worse states.
- Determine the remaining necessary parameters for the operation and repair of the system. Such parameters include the operational costs of running and servicing the system in individual reliability states and the costs of inspections.
- Decide whether emergency repairs are possible and input the related parameters such as delay, additional cost, and trigger conditions.
- The entered data related to the application is stored and managed in the data layer. These data are then processed by the application to estimate costs through a simulation. An illustration of cost simulation function is shown in the flowchart (Figure 4). Further description of the application is provided in Section 3.2 and Section 3.3. Again, for the sake of clarity, we do not include the steps related to emergency repair.
- The cost simulation application allows for the estimation of total costs of system maintenance and repair as well as comparison of different inspection and repair objectives. The results are graphically illustrated in the presentation layer with the possibility of analyzing the cost structure. To standardize the results of simulations, costs are normalized and provided per time unit. The simulation results for a water management system are described in Section 3 and discussed in Section 4.
3. Simulation Model and Its Application to a Water Management System
3.1. Water Management System Reliability States
- State 1: state of entire ability—representing a situation when the water management system is fully processing its operational tasks at minimal state cost.
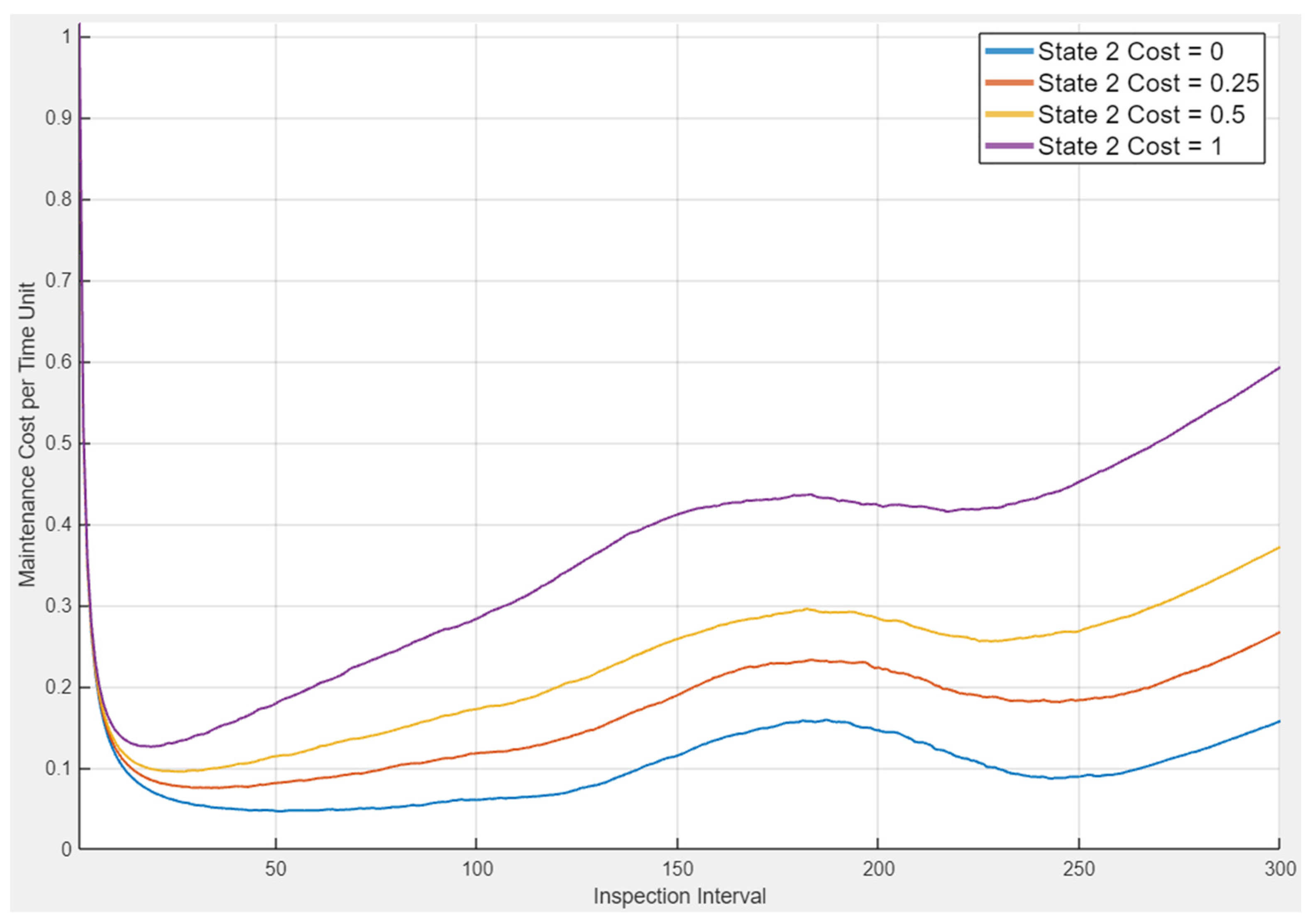
- State 2: state of restricted ability—appearing when disruptions of unintentional events interfere with system functionality. The system is still able to process its operational tasks and is fully able to maintain its functional capabilities; however, this state is associated with a rise in operational costs.
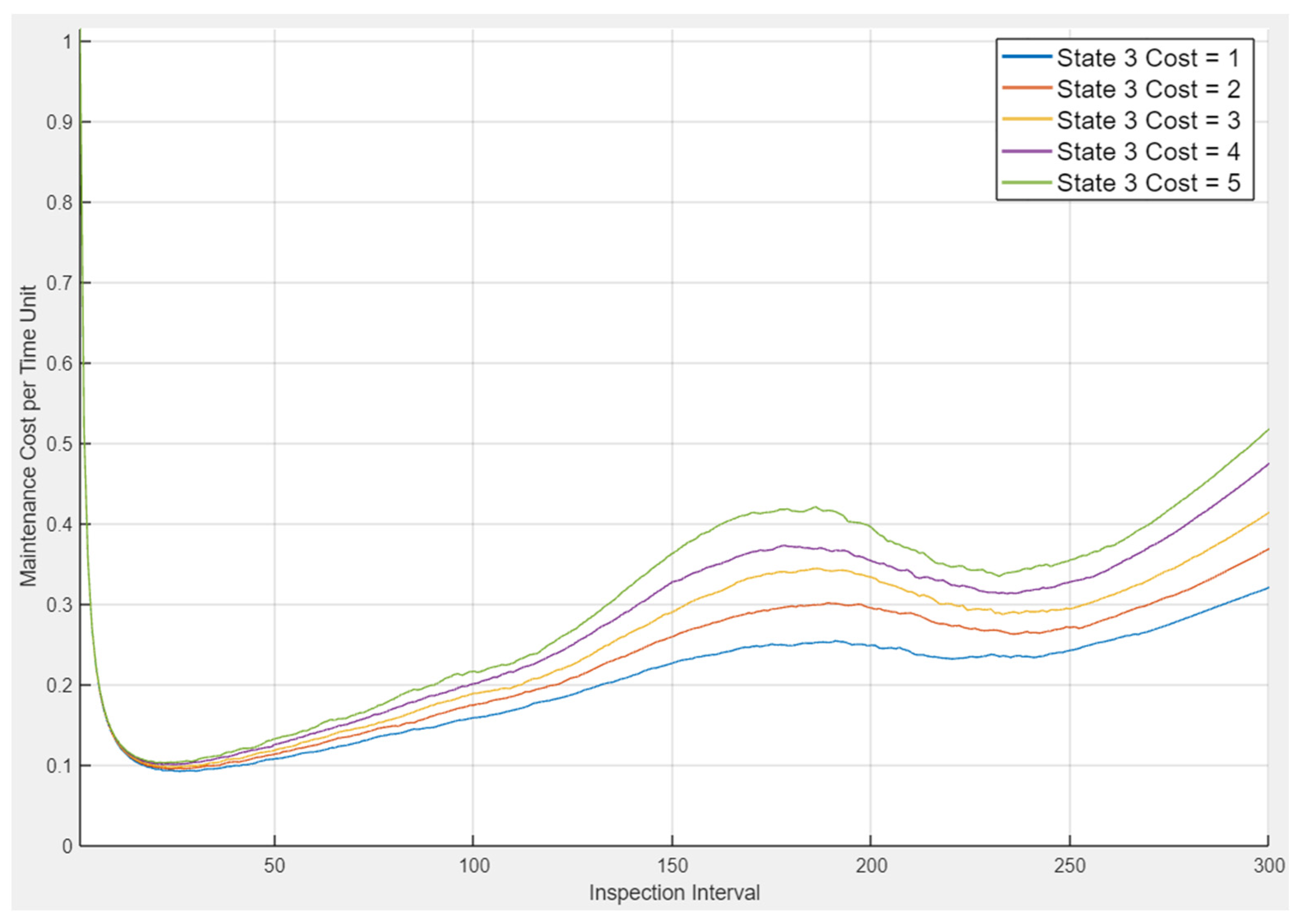
- State 3: state of emergency—disruptions within the system result in its restricted ability to process operational tasks; the system’s functional capabilities are also decreased. Simultaneously, state cost is significantly higher.
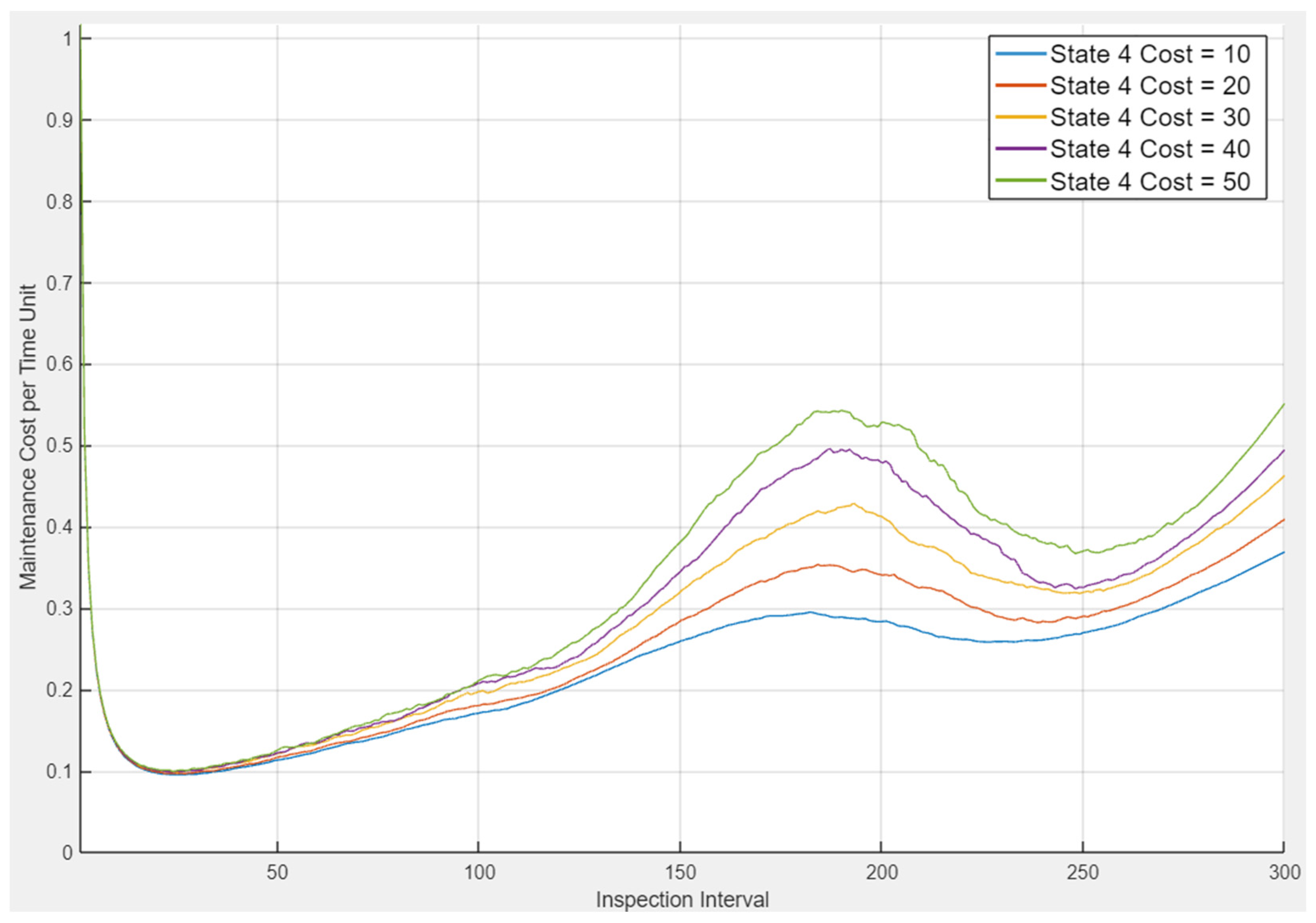
- State 4: state of total inability—emerging when the system stops operating and is unable to maintain its functional capabilities.
3.2. Application Parameters and Assumptions
3.2.1. System Parameters and Assumptions
- Inspection Objectives—the objectives of the inspection have to be defined in the case of a multistate system; for each imperfect state of the system, we declare whether it should be repaired to a perfect state, to some improved imperfect state, or not repaired at all; for the water management system, we assume that only perfect repairs (to the state of entire ability) are carried out (perfect repair can also mean replacing a system component with a new one). However, since State 2, of restricted ability, allows the operation of the system, we consider and compare two cases: “always repair” (repair when either of States 2, 3, or 4 is detected) and “repair from State 3” (that is, repair if a state of emergency or system failure is detected, and leave State 2 unrepaired);
- Emergency Repair Option—additional option of conducting repairs between scheduled inspections at extra cost. In the case study, we assume the emergency crew can be called immediately if the system reaches State 4 (the system operation stops) and no inspection is scheduled within the next 5 days. They arrive 2 days later (assumed delay), carry out the inspection and repair at usual costs, and charge an additional five units of cost for the unplanned repair. We also consider the possibility of calling them in State 3 (assuming that deterioration to the state of threat is self-announced);
- Repair Cost—direct costs related to the repair, such as the cost of repairs or replacement of components/subassemblies and the costs of labor of the servicing crew. For a multistate system, these costs may differ depending on the desired repair effect. For the case study, we assume the perfect repair costs two units of cost from State 2, three units from State 3, and ten units from State 4;
- Repair Time—the time required to perform a given variant of repair during which the system becomes shut down, resulting in additional operational costs. For the case study, we assume that repair from State 4 takes 4 days. As the repair from State 2 and State 3 in the considered system does not require a shutdown, we consider zero to be their Repair Time value;
- State Cost—all additional reliability associated costs per time unit; these costs are provided for each reliability state of the system as they are generated by the system operating in that state; apart from regular costs related to operation, it may also include the loss of profit (for example, due to the hydroelectric plant working at reduced efficiency). In the case study, the state cost (daily cost of the system being in imperfect state) is 0.5 of cost unit for State 2, 2 units for State 3, and 10 for State 4;
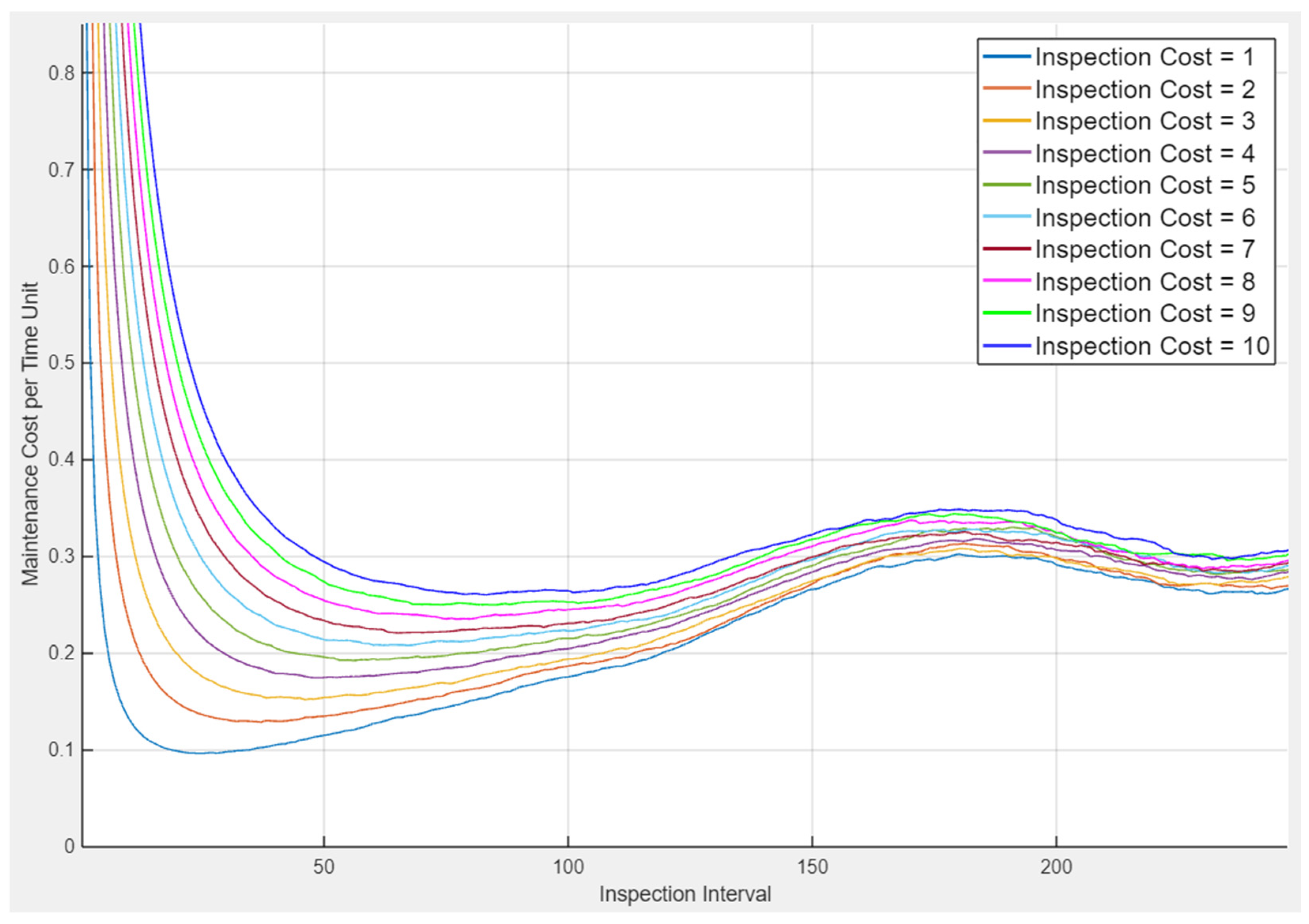
- Inspection Cost—a fixed cost of each inspection performed, regardless of whether it results in performing a repair or not; inspections occur periodically and are called off only when they happen during an ongoing repair. We assume that an inspection either does not require the shutdown of the system or that the time of such shutdown is negligible and, in that case, the cost of the shutdown should be included as a part of the Inspection Cost parameter. For the case study, we assume it equals one unit of cost.
3.2.2. Simulation Parameters
- Production Cycles—this parameter determines the supposed duration of the run of the simulation. In general, the higher the number of production cycles, the more stable the results of the simulation. Each production cycle ends exactly at the beginning of a new repair, which happens at the start of the next cycle. If the system reaches the state of total loss of function and the inspection objective for that state is “do not repair”, it cannot be repaired ever again. In that unordinary case, the production cycle is terminated at the time of the nearest inspection.
- Min/Max Interval—these values identify the minimal/maximal inspection interval considered in the simulation.
- Step—the fixed difference between two consecutive inspection intervals considered in the simulation. For example, if our intention is to generate the plot for intervals 10, 15, 20, …, 100, we set Min Interval = 10, Max Interval = 100, and Step = 5.
- Run … Times—if this box is checked, the simulation runs the chosen number of times. Then, in the Cost Plot tab, three curves are displayed, depicting the maximal, minimal, and average values obtained for each inspection interval. In the current version of the application, this checkbox does not alter the way other plots are generated.
- Hold The Data—if the box is checked, a new Cost Plot is added on top of previously drawn plots without removing them. This is useful for comparisons.
3.3. Application Description and Results
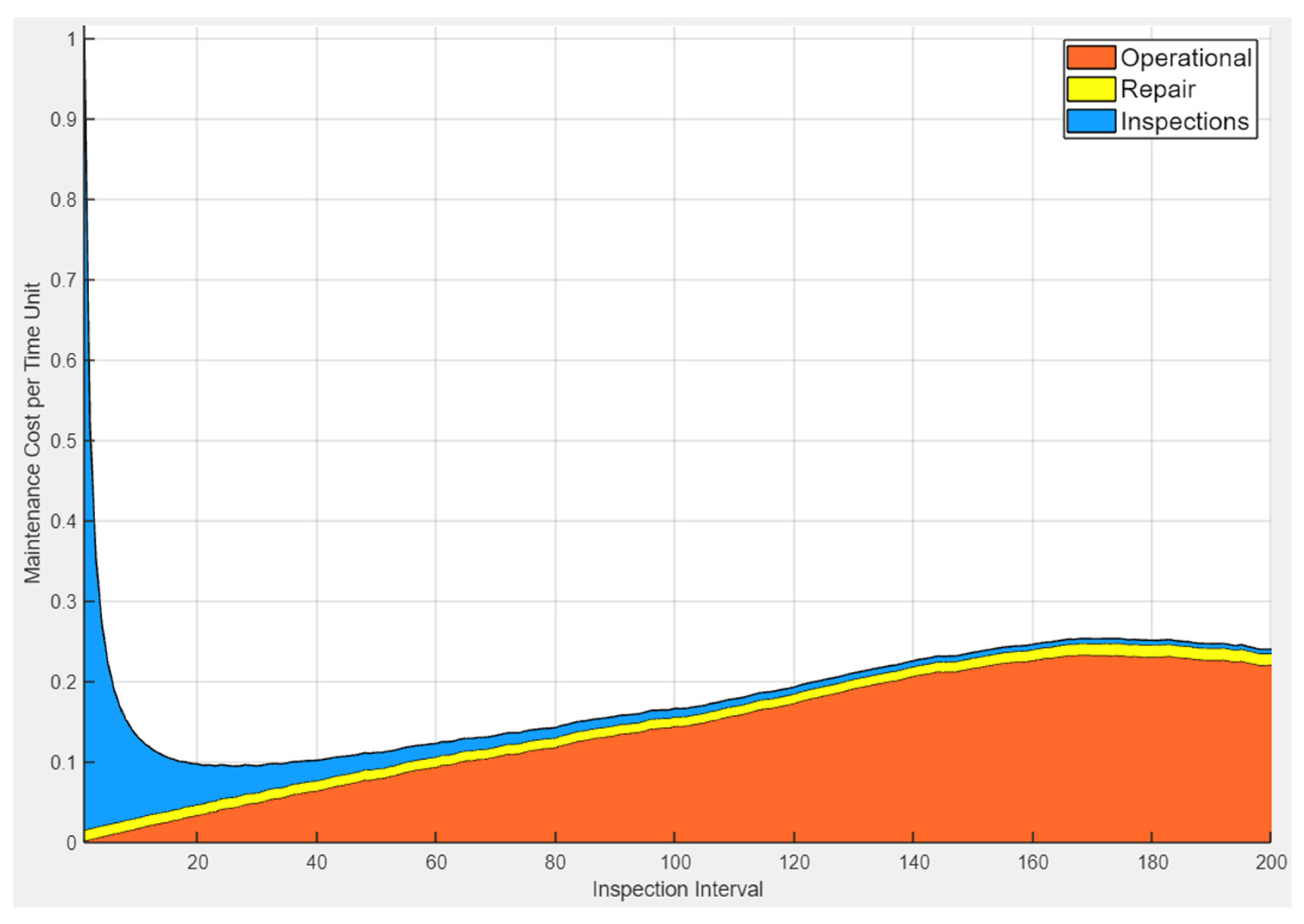
3.4. Case Study Results
4. Sensitivity Analysis of Cost Parameters and Discussion of Maintenance Strategies
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cole, J.; Sharvelle, S.; Grigg, N.; Pivo, G.; Haukaas, J. Collaborative, Risk-Informed, Triple Bottom Line, Multi-Criteria Decision Analysis Planning Framework for Integrated Urban Water Management. Water 2018, 10, 1722. [Google Scholar] [CrossRef]
- Larsen, T.; Gujer, W. The concept of sustainable urban water management. Water Sci. Technol. 1997, 35, 3–10. [Google Scholar] [CrossRef]
- Masia, O.A.; Erasmus, L.D. Smart metering implementation for enabling Water Conservation and water demand management: An investigation in Gauteng, South Africa. In Proceedings of the 2013 Africon, Pointe aux Piments, Mauritius, 9–12 September 2013. [Google Scholar] [CrossRef]
- Stewart, R.A.; Willis, R.; Giurco, D.; Panuwatwanich, K.; Capati, G. We-based knowledge management system: Linking smart metering to the future of urban water planning. Aust. Plan. 2010, 47, 66–74. [Google Scholar] [CrossRef]
- Marques, J.; Cunha, M.; Savi´c, D.A. Multi-objective optimization of water distribution systems based on a real options approach. Environ. Model. Softw. 2015, 63, 1–13. [Google Scholar] [CrossRef]
- Bithas, K. The sustainable residential water use: Sustainability, efficiency and social equity. The European experience. Ecol. Econ. 2008, 68, 221–229. [Google Scholar] [CrossRef]
- Esmail, B.A.; Suleiman, L. Analyzing Evidence of Sustainable Urban Water Management Systems: A Review through the Lenses of Sociotechnical Transitions. Sustainability 2020, 12, 4481. [Google Scholar] [CrossRef]
- Marlow, D.R.; Moglia, M.; Cook, S.; Beale, D.J. Towards sustainable urban water management: A critical reassessment. Water Res. 2013, 47, 7150–7161. [Google Scholar] [CrossRef]
- Cettner, A.; Söderholm, K.; Viklander, M. An adaptive stormwater culture? Historical perspectives on the status of stormwater within the Swedish Urban Water System. J. Urban Technol. 2012, 19, 25–40. [Google Scholar] [CrossRef]
- Quezada, G.; Walton, A.; Sharma, A. Risks and tensions in water industry innovation: Understanding adoption of decentralised water systems from a socio-technical transitions perspective. J. Clean. Prod. 2016, 113, 263–273. [Google Scholar] [CrossRef]
- Bagirov, A.M.; Barton, A.F.; Mala-Jetmarova, H.; Al Nuaimat, A.; Ahmed, S.T.; Sultanova, N.; Yearwood, J. An algorithm for minimization of pumping costs in water distribution systems using a novel approach to pump scheduling. Math. Comput. Model. 2013, 57, 873–886. [Google Scholar] [CrossRef]
- Van Dijk, M.; van Vuuren, S.J.; van Zyl, J.E. Optimising water distribution systems using a weighted penalty in a genetic algorithm. Water SA 2008, 34, 537–548. [Google Scholar] [CrossRef]
- Lopez-Ibanez, M.; Devi Prasad, T.; Paechter, B. Ant colony optimization for optimal control of pumps in water distribution networks. J. Water Resour. Plan. Manag. 2008, 134, 337–346. [Google Scholar] [CrossRef]
- van Zyl, J.E.; Savic, D.A.; Walters, G.A. Operational optimization of water distribution systems using a hybrid genetic algorithm. J. Water Resour. Plan. Manag. 2004, 130, 160–170. [Google Scholar] [CrossRef]
- Pamidimukkala, A.; Kermanshachi, S.; Adepu, N.; Safapour, E. Resilience in Water Infrastructures: A Review of Challenges and Adoption Strategies. Sustainability 2021, 13, 12986. [Google Scholar] [CrossRef]
- Mwendera, E.J.; Hazelton, D.; Nkhuwa, D.; Robinson, P.; Tjijenda, K.; Chavula, G. Overcoming constraints to the implementation of water demand management in southern Africa. Phys. Chem. Earth 2003, 28, 761–778. [Google Scholar] [CrossRef]
- Gupta, A.D.; Pandey, P.; Feijóo, A.; Yaseen, Z.M.; Bokde, N.D. Smart Water Technology for Efficient Water Resource Management: A Review. Energies 2020, 13, 6268. [Google Scholar] [CrossRef]
- Xiang, N.; Sha, J.; Yan, J.; Xu, F. Dynamic Modeling and Simulation of Water Environment Management with a Focus on Water Recycling. Water 2014, 6, 17–31. [Google Scholar] [CrossRef]
- Xuan, X.J.; Xu, H. Use of Reclaimed Water in China: Management issues and strategies. Manag. Sci. Eng. 2009, 3, 17–25. [Google Scholar] [CrossRef]
- Angelakis, A.N.; Bonoux, L.; Lazarova, V. Challenges and prospective for water recycling and reuse in EU countries. Water Sci. Technol. 2003, 3, 59–68. [Google Scholar] [CrossRef]
- Asano, T.; Cotruvo, J.A. Groundwater recharge with reclaimed municipal wastewater: Health and regulatory considerations. Water Res. 2004, 38, 1941–1951. [Google Scholar] [CrossRef]
- Global Water Partnership–Technical Advisory Committee (GWP-TAC). Integrated Water Resources Management; Background Paper No. 4; Global Water Partnership, Technical Advisory Committee: Stockholm, Sweden, 2000. [Google Scholar]
- Beck, M.B. Water quality modeling: A review of the analysis of uncertainty. Water Resour. Res. 1987, 23, 1393–1442. [Google Scholar] [CrossRef]
- Young, P. Data-based mechanistic modelling of environmental, ecological, economic and engineering systems. Environ. Model. Softw. 1998, 13, 105–122. [Google Scholar] [CrossRef]
- D’Ambrosio, C.; Lodi, A.; Wiese, S.; Bragalli, C. Mathematical programming techniques in water network optimization. Eur. J. Oper. Res. 2015, 243, 774–788. [Google Scholar] [CrossRef]
- Dennison, F.J.; Azapagic, A.; Clift, R.; Colbourne, J.S. Life cycle assessment: Comparing strategic options for the mains infrastructure d part I. Water Sci. Technol. 1999, 39, 315–319. [Google Scholar] [CrossRef]
- Cohen, D.; Shamir, U.; Sinai, G. Optimal operation of multi-quality water supply systems-II: The Q-H model. Eng. Optim. 2000, 32, 687–720. [Google Scholar] [CrossRef]
- Ostfeld, A.; Shamir, U. Optimal operation of multiquality networks. I: Steady-state conditions. J. Water Resour. Plan. Manag. 1993, 119, 645–662. [Google Scholar] [CrossRef]
- Ostfeld, A.; Shamir, U. Optimal operation of multiquality networks. II: Unsteady conditions. J. Water Resour. Plan. Manag. 1993, 119, 663–684. [Google Scholar] [CrossRef]
- Deak, J.; Bucht, E. Planning for climate change: The role of indigenous blue infrastructure, with a case study in Sweden. Town Plan. Rev. 2011, 82, 669–685. [Google Scholar] [CrossRef]
- Cettner, A.; Ashley, R.; Viklander, M.; Nilsson, K. Stormwater management and urban planning: Lessons from 40 years of innovation. J. Environ. Plan. Manag. 2013, 56, 786–801. [Google Scholar] [CrossRef]
- Echols, S. Artful rainwater design in the urban landscape. J. Green Build. 2007, 2, 101–122. [Google Scholar] [CrossRef]
- Brown, R.R.; Farrelly, M.A.; Loorbach, D.A. Actors working the institutions in sustainability transitions: The case of Melbourne’s stormwater management. Glob. Environ. Chang. 2013, 23, 701–718. [Google Scholar] [CrossRef]
- Rathnayaka, K.; Malano, H.; Arora, M. Assessment of Sustainability of Urban Water Supply and Demand Management Options: A Comprehensive Approach. Water 2016, 8, 595. [Google Scholar] [CrossRef]
- Hering, J.G.; Waite, T.D.; Luthy, R.G.; Drewes, J.E.; Sedlak, D.L. A changing framework for urban water systems. Environ. Sci. Technol. 2013, 47, 10721–10726. [Google Scholar] [CrossRef]
- Brown, R. Local institutional development and organizational change for advancing sustainable urban water futures. Environ. Manag. 2008, 41, 221–233. [Google Scholar] [CrossRef]
- Lebel, L.; Grothmann, T.; Siebenhuner, B. The role of social learning in adaptiveness: Insights from water management. Int. Environ. Agreem. 2010, 10, 333–353. [Google Scholar] [CrossRef]
- Liuzzo, L.; Notaro, V.; Freni, G. A Reliability Analysis of a Rainfall Harvesting System in Southern Italy. Water 2016, 8, 18. [Google Scholar] [CrossRef]
- Campisano, A.; Modica, C. Optimal sizing of storage tanks for domestic rainwater harvesting in Sicily. Resour. Conserv. Recycl. 2012, 63, 9–16. [Google Scholar] [CrossRef]
- Rahman, A.; Keane, J.; Imteaz, M.A. Rainwater harvesting in Greater Sydney: Water savings, reliability and economic benefits. Resour. Conserv. Recycl. 2012, 61, 16–21. [Google Scholar] [CrossRef]
- Hajani, E.; Rahman, A. Reliability and Cost Analysis of a Rainwater Harvesting System in Peri-Urban Regions of Greater Sydney, Australia. Water 2014, 6, 945–960. [Google Scholar] [CrossRef]
- Ahopelto, S.; Vahala, R. Cost–Benefit Analysis of Leakage Reduction Methods in Water Supply Networks. Water 2020, 12, 195. [Google Scholar] [CrossRef]
- Farmani, R.; Walters, G.; Savic, D. Evolutionary multi-objective optimization of the design and operation of water distribution network: Total cost vs. reliability vs. water quality. J. Hydroinform. 2006, 8, 165–179. [Google Scholar] [CrossRef]
- Lim, S.-R.; Suh, S.; Kim, J.-H.; Park, H.S. Urban water infrastructure optimization to reduce environmental impacts and costs. J. Environ. Manag. 2010, 91, 630–637. [Google Scholar] [CrossRef]
- Hutton, G.; Haller, L.; Bartram, J. Global cost-benefit analysis of water supply and sanitation interventions. J. Water Health 2007, 5, 481–502. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zhao, X.; Tian, Z.; Zuo, M.J. Optimum component reassignment for balanced systems with multi-state components operating in a shock environment. Reliab. Eng. Syst. Saf. 2021, 210, 107514. [Google Scholar] [CrossRef]
- Hu, J.; Xu, A.; Li, B.; Liao, H. Condition-based maintenance planning for multi-state systems under time-varying environmental conditions. Comput. Ind. Eng. 2021, 158, 107380. [Google Scholar] [CrossRef]
- Zhao, X.; Lv, Z.; He, Z.; Wang, W. Reliability and opportunistic maintenance for a series system with multi-stage accelerated damage in shock environments. Comput. Ind. Eng. 2019, 137, 106029. [Google Scholar] [CrossRef]
- Peng, S.; Feng, Q. Reinforcement learning with Gaussian processes for condition-based maintenance. Comput. Ind. Eng. 2021, 158, 107321. [Google Scholar] [CrossRef]
- Lisnianski, A.; Frenkel, I.; Ding, Y. Multi-State System Reliability Analysis and Optimization for Engineers and Industrial Managers, 1st ed.; Springer: London, UK, 2010; pp. 237–272. [Google Scholar] [CrossRef]
- Dhillon, B.S. Design Reliability: Fundamentals and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar] [CrossRef]
- Babiarz, B. Aspects of Heat Supply Security Management Using Elements of Decision Theory. Energies 2018, 11, 2764. [Google Scholar] [CrossRef]
- Guze, S.; Neumann, T.; Wilczyński, P. Multi-Criteria Optimisation of Liquid Cargo Transport According to Linguistic Approach to the Route Selection Task. Pol. Marit. Res. 2017, 24, 89–96. [Google Scholar] [CrossRef]
- Zonta, T.; da Costa, C.A.; da Rosa Righi, R.; de Lima, M.J.; da Trindade, E.S.; Li, G.P. Predictive maintenance in the Industry 4.0: A systematic literature review. Comput. Ind. Eng. 2020, 150, 106889. [Google Scholar] [CrossRef]
- Blokus, A. Multistate System Reliability with Dependencies, 1st ed.; Elsevier Academic Press: London, UK, 2020. [Google Scholar]
- Blokus, A.; Dziula, P. Relations of Imperfect Repairs to Critical Infrastructure Maintenance Costs. Sustainability 2021, 13, 4917. [Google Scholar] [CrossRef]
- Neumann, T. Automotive and telematics transportation systems. In Proceedings of the 2017 International Siberian Conference on Control and Communications (SIBCON), Astana, Kazakhstan, 29–30 June 2017. [Google Scholar] [CrossRef]
- De Jonge, B.; Teunter, R.; Tinga, T. The influence of practical factors on the benefits of condition-based maintenance over time-based maintenance. Reliab. Eng. Syst. Saf. 2017, 158, 21–30. [Google Scholar] [CrossRef]
- Van der Weide, J.A.M.; Pandey, M.D. Stochastic analysis of shock process and modelling of condition-based maintenance. Reliab. Eng. Syst. Saf. 2011, 96, 619–626. [Google Scholar] [CrossRef]
- Tchórzewska-Cieślak, B.; Pietrucha-Urbanik, K. Water System Safety Analysis Model. Energies 2023, 16, 2809. [Google Scholar] [CrossRef]
- Cox, D.R.; Miller, H.D. The Theory of Stochastic Processes; Chapman& Hall/CRC: Boca Raton, FL, USA, 1996. [Google Scholar]
- Grabski, F. Reliability and maintainability characteristics in semi-Markov model. J. Pol. Saf. Reliab. Assoc. 2016, 7, 79–85. [Google Scholar]
- Blokus, A.; Dziula, P. Safety analysis of interdependent critical infrastructure networks. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2019, 13, 781–787. [Google Scholar] [CrossRef]
- Valis, D.; Forbelská, M.; Vintr, Z. Forecasting study of mains reliability based on sparse field data and perspective models. Maint. Reliab. 2020, 22, 179–191. [Google Scholar] [CrossRef]
- AL-Washali, T.; Sharma, S.; AL-Nozaily, F.; Haidera, M.; Kennedy, M. Modelling the Leakage Rate and Reduction Using Minimum Night Flow Analysis in an Intermittent Supply System. Water 2019, 11, 48. [Google Scholar] [CrossRef]
- Młyński, D.; Bergel, T.; Młyńska, A.; Kudlik, K. A study of the water supply system failure in terms of the seasonality: Analysis by statistical approaches. AQUA Water Infrastruct. Ecosyst. Soc. 2021, 70, 289–302. [Google Scholar] [CrossRef]
- Tchórzewska-Cieślak, B. Methods for Analyzing and Assessing the Risk of Failure of the Water Distribution Subsystem; Rzeszów University of Technology Publishing House: Rzeszow, Poland, 2011. [Google Scholar]
- Grabski, F. Stochastic Systems Availabity Models. In Materials of the XXXVI Winter School of Reliability; Warsaw University of Technology, Polish Academy of Sciences: Warsaw, Poland, 2008; pp. 112–128. [Google Scholar]
- Stark, M.R. Mathematical Foundations for Design; McGraw-Hill Book Company: New York, NY, USA, 1972. [Google Scholar]
- Papciak, D.; Domoń, A.; Zdeb, M.; Skwarczyńska-Wojsa, A.; Konkol, J. Optimization of Quantitative Analysis of Biofilm Cell from Pipe Materials. Coatings 2021, 11, 1286. [Google Scholar] [CrossRef]
- Tchórzewska-Cieślak, B.; Pietrucha-Urbanik, K.; Kuliczkowska, E. An Approach to Analysing Water Consumers’ Acceptance of Risk-Reduction Costs. Resources 2020, 9, 132. [Google Scholar] [CrossRef]
- Waghmode, L.Y.; Sahasrabudhe, A.D. Modelling maintenance and repair costs using stochastic point processes for life cycle costing of repairable systems. Int. J. Comput. Integr. Manuf. 2012, 25, 353–367. [Google Scholar] [CrossRef]
- Blokus-Dziula, A.; Soszyńska-Budny, J. Condition-based maintenance and availability analysis of wind farm infrastructure. J. Infrastruct. Syst. 2022, 28, 05022001. [Google Scholar] [CrossRef]
- Debón, A.; Carrión, A.; Cabrera, E.; Solano, H. Comparing risk of failure models in water supply networks using ROC curves. Reliab. Eng. Syst. Saf. 2010, 95, 43–48. [Google Scholar] [CrossRef]
- Kossieris, P.; Makropoulos, C. Exploring the Statistical and Distributional Properties of Residential Water Demand at Fine Time Scales. Water 2018, 10, 1481. [Google Scholar] [CrossRef]
- Labhasetwar, P.K.; Yadav, A. Membrane Based Point-of-Use Drinking Water Treatment Systems, 1st ed.; IWA Publishing: London, UK, 2023. [Google Scholar] [CrossRef]

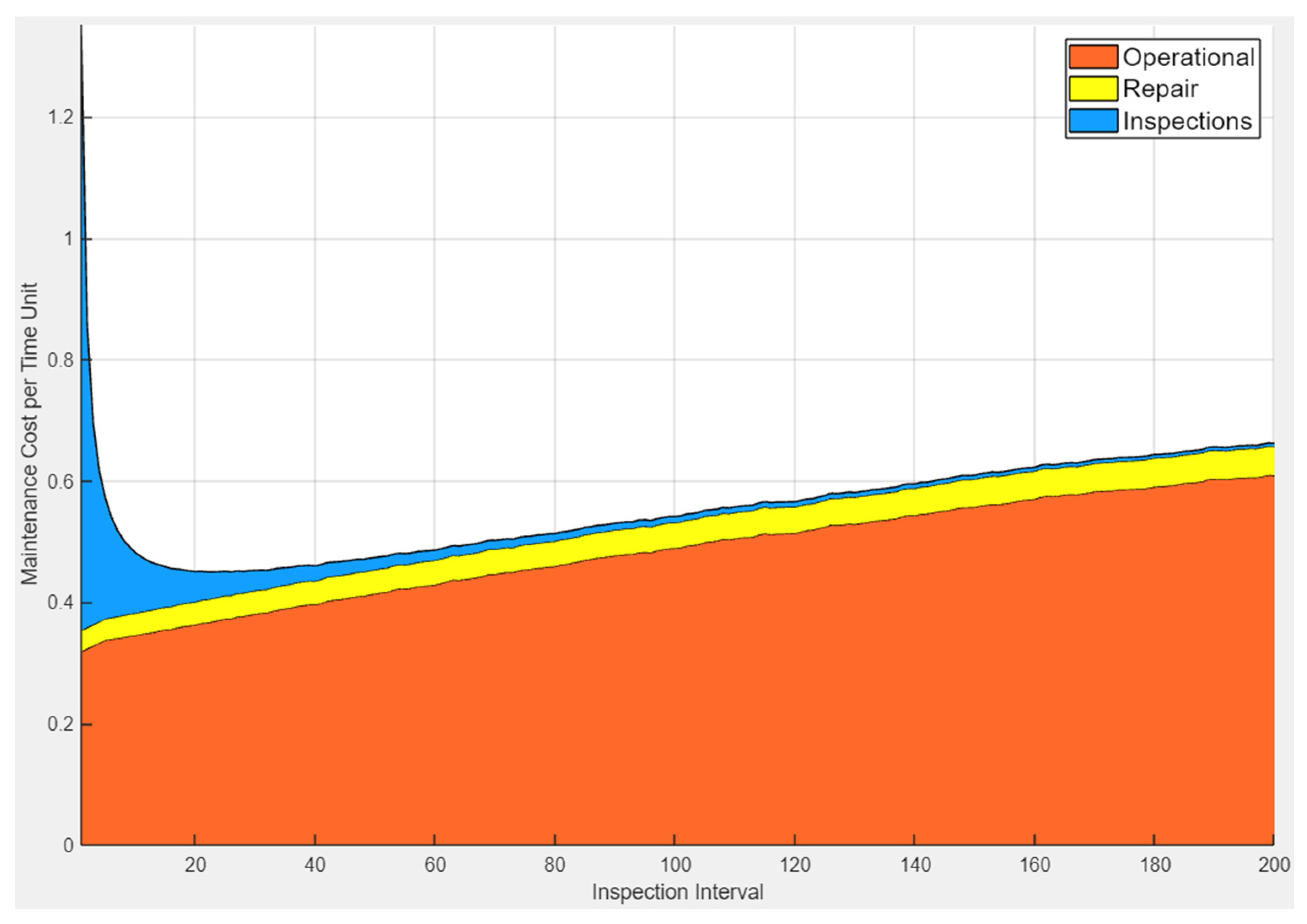

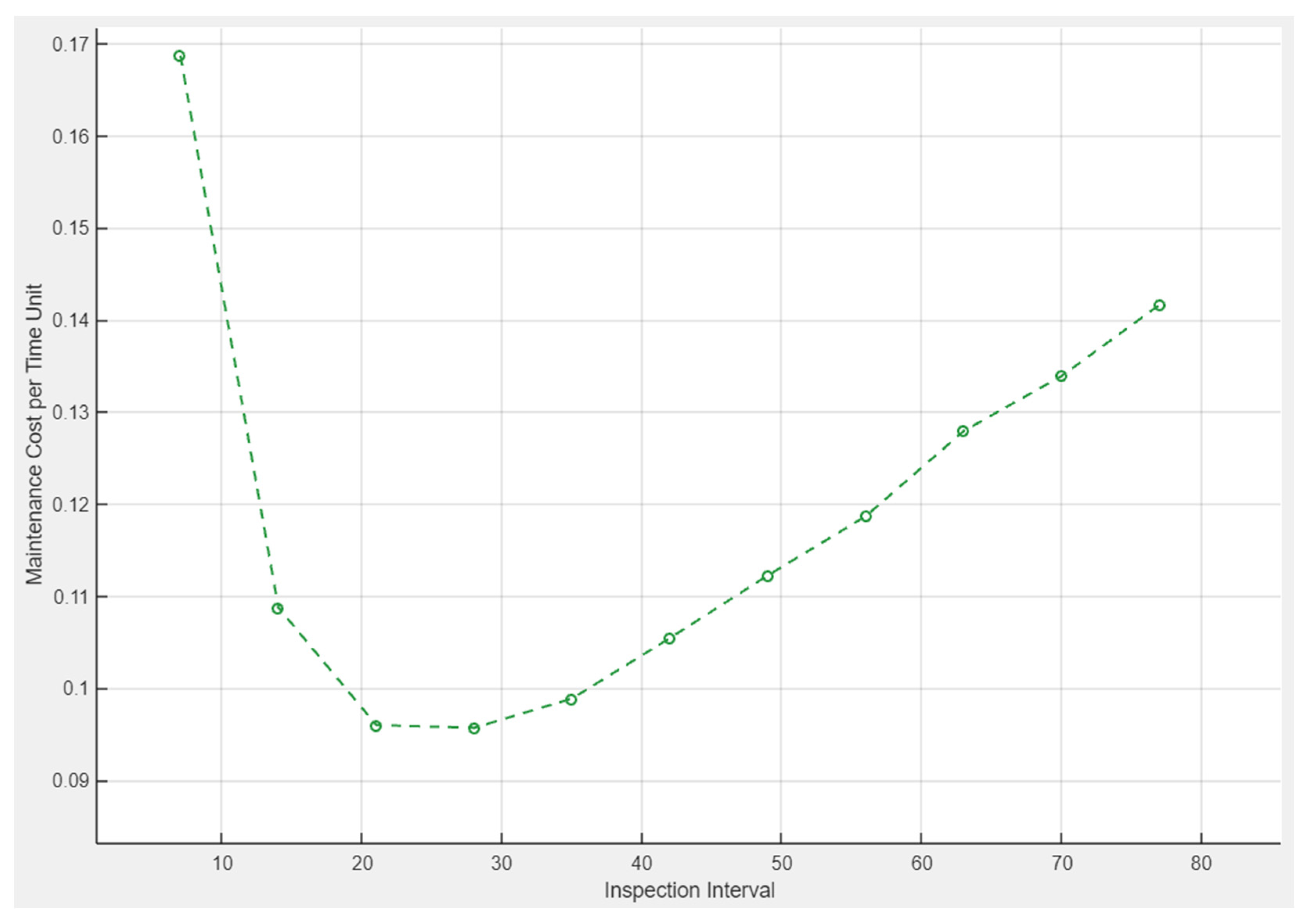
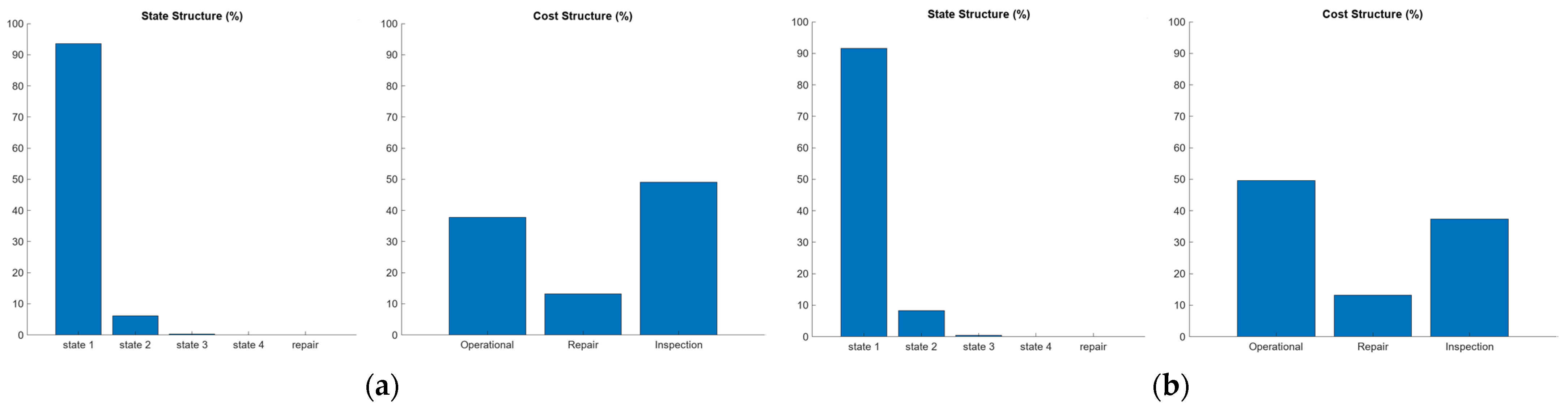
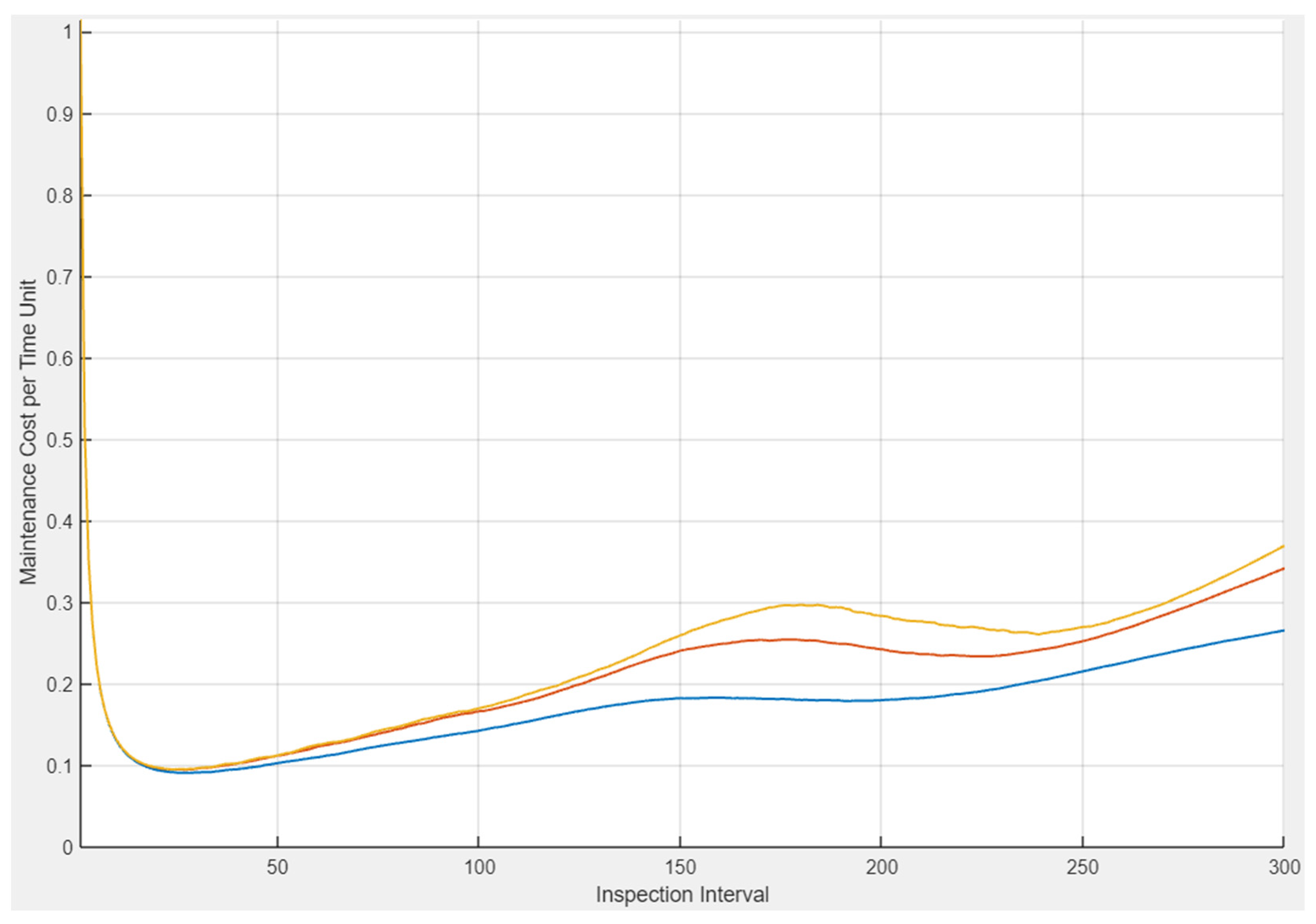
| Inspection Interval | Average Yearly Costs (Structure) | Total Yearly Costs | ||
|---|---|---|---|---|
| Operational | Repair | Inspection | ||
| 10 | 6.54 (14%) | 4.86 (10%) | 36.70 (76%) | 48.09 |
| 15 | 9.68 (25%) | 4.82 (12%) | 24.39 (63%) | 38.89 |
| 20 | 12.92 (36%) | 4.70 (13%) | 18.26 (51%) | 35.88 |
| 25 1 | 15.67 (45%) | 4.69 (13%) | 14.63 (42%) | 34.99 |
| 30 | 18.89 (53%) | 4.64 (13%) | 12.17 (34%) | 35.70 |
| 35 | 21.94 (59%) | 4.54 (12%) | 10.45 (28%) | 36.93 |
| 40 | 24.65 (64%) | 4.52 (12%) | 9.16 (24%) | 38.34 |
| Inspection Interval | Total Yearly Costs | Possible Savings | |
|---|---|---|---|
| “No Emergency Opt.” | “Emergency in State 3” | ||
| 10 | 48.09 | 47.66 | 0.44 (0.9%) |
| 15 | 38.89 | 38.15 | 0.74 (1.9%) |
| 20 | 35.88 | 34.75 | 1.13 (3.2%) |
| 25 | 34.99 1 | 33.55 | 1.44 (4.1%) |
| 30 | 35.70 | 33.35 1 | 2.35 (6.6%) |
| 35 | 36.93 | 33.99 | 2.94 (8.0%) |
| 40 | 38.34 | 35.18 | 3.16 (8.2%) |
| Inspection Cost 1 | Optimal Inspection Interval (in Days) |
|---|---|
| 1 | 25 |
| 2 | 37 |
| 3 | 46 |
| 4 | 49 |
| 5 | 56 |
| 6 | 67 |
| 7 | 65 |
| 8 | 77 |
| 9 | 84 |
| 10 | 83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blokus-Dziula, A.; Dziula, P.; Kamedulski, B.; Michalak, P. Operation and Maintenance Cost of Water Management Systems: Analysis and Optimization. Water 2023, 15, 3053. https://doi.org/10.3390/w15173053
Blokus-Dziula A, Dziula P, Kamedulski B, Michalak P. Operation and Maintenance Cost of Water Management Systems: Analysis and Optimization. Water. 2023; 15(17):3053. https://doi.org/10.3390/w15173053
Chicago/Turabian StyleBlokus-Dziula, Agnieszka, Przemysław Dziula, Bartosz Kamedulski, and Piotr Michalak. 2023. "Operation and Maintenance Cost of Water Management Systems: Analysis and Optimization" Water 15, no. 17: 3053. https://doi.org/10.3390/w15173053





