1. Introduction
The soaring trend in universal energy consumption, as indicated by the World Energy Council, forecasts a significant surge of over 100% in consumed energy over 40 years [
1,
2]. Fossil fuels dominate global energy production [
3]. Despite improvements in harnessing qualified energies, non-renewable sources will play a pivotal role in meeting humanity’s energy needs. Considering the difficulties of the grass-roots design of power plants, including financial restriction, land annihilation, and global warming problems, launching a new power plant may seem a challenging decision. To tackle the issue, retrofitting and finding the optimum site conditions of existing power plants to exploit more energy while simultaneously protecting budgets and the environment has become a topical subject. Thermodynamic analyses are the fundamental aspect of each energy sector. Energy analysis and energy loss are not proper rubrics to justify a system since they do not differentiate between the quality and quantity of energy [
4,
5]. Exergy is a measure to obtain the maximum amount of producible work of a system. Exergy analysis not only addresses the simple explanation of a system from the energy point of view but further provides additional notions such as exergoeconomic and exergoenvironmental analyses to characterize an energy sector more deeply [
6].
In 2011, Kaushik et al. [
7] reviewed in detail energy and exergy analyses in coal- and gas-fired combined power plants. They show that the primary exergy loss occurs in the combustion chamber for gas-fired and the boiler for coal-based power plants. Chen et al. [
8] investigated the thermodynamic performance of a hybrid system consisting of a gas turbine, a tubular solid oxide fuel cell, and hydrogen fuel. Their obtained results indicated that an increase in the turbine’s inlet temperature leads to a decrease in the system efficiency, yet the power generation of the system increases. Furthermore, raising the turbine’s inlet temperature and increasing the pressure ratio result in higher entropy and system instability. At the design point, the efficiency of the hybrid system was 9.81%, whereas the efficiency of the system without a fuel cell was 33.4%. Amiralipour and Kouhikamali [
9] simulated the retrofitting procedure of a combined steam power plant in Guilan by integrating a cooling water pump (CWP) accompanied with membrane and thermal distillation units. The power plant has a nominal electricity output of 450 MW. They presented two distinct scenarios, including the high-pressure line (HP) and low-pressure line (LP) of the heat recovery steam generator (HRSG) for water production, where the former produces about 25,000
, while the latter leads to 7000
. Considering their economic analysis, the price of the produced fresh water is from 2.5
to 3
. Lin et al. [
10] analyzed the utilization of a steam air heater (SAH) to exploit the waste heat of a 1000 MW single-reheat supercritical coal-fired power plant. They investigated the performance of the power plant using thermoeconomic analysis. The results imply that the payback periods for the three different case studies, including bypass flue (BPF), BPF-SAH, and BPF-SAHs, are 2.75 years, 3.42 years, and 2.36 years. In another study, Owebor et al. [
11] investigated a fully integrated combined cooling heat and power system comprising a gas turbine, solid oxide fossil fuel, a steam turbine, an organic Rankine cycle, and absorption refrigeration followed by cryogenic carbon capture and storage with a thermoeconomic and environmental approach. The net power of the complex is 147.2 MW and the exergy efficiency of their system is 39.9%. The results show a levelized energy cost and investment payback period of 0.123
and 5.2 years, respectively. Zahedi et al. [
12] assessed a quaternary combined power plant comprising a solar-integrated Brayton cycle, biogas Brayton cycle, organic Rankine cycle, and steam gas cycle. The genetic optimization algorithm was used to find the optimum site condition of the combined power plants: the exergy efficiency of the optimum condition is 61.6%, and the electricity generation cost is 0.0636 USD per kilowatt-hour. A carbon capture section, carbon amine adsorption type, was also added to the system, which decreased the system’s exergy to 50.5%. Abbaspour et al. [
13] explored the thermodynamic efficiencies of a multi-generation energy system, including a gas cycle, steam cycle, cryogenic air separation, proton exchange membrane, electrolyzer, and ammonia–urea reactor. The simulations imply 689
and 1.323 million tons of urea production yearly with a net present value of USD 7.29 billion.
Topal et al. [
14] conducted an energy and exergy analysis of a biomass co-firing power plant using olive pits in a can circulating fluidized bed power plant in Turkey. The exergy efficiency of this 157 MW electricity output plant is about 31.26%. Moreover, they concluded that increasing the turbine inlet temperature and pressure and the temperature of the compressed air and feed water leads to lower CO
2 emissions. Mohammadpour et al. [
15] performed an energy and exergy (2E) analysis for an oxy-fuel regenerative gas turbine. They considered two distinct streams for CO
2, including primary and dilution. The highest exergy destruction in the system happens in the combustion chamber. In another investigation, Abuelnuor et al. [
16] applied fundamental 2E thermodynamic analysis in a 180 MW combined power plant in Khartoum. The energy and exergy efficiency of the power plant were 38% and 49%. Bai et al. and Yan et al. [
17,
18] tried to investigate the performance of coal-fired power plants based on 2E thermodynamic analyses. The former study reported 1.046% exergy efficiency increase after enhancing the recompression supercritical CO
2 cycle; the total exergy, energy, and power efficiency were 53.41%, 94.68%, and 48.06%. The latter work simulated the integration of a trough collector system in a coal-fired power plant with a nominal electricity output of 660 MW. The exergy efficiency of the combined system highly depends on daily solar irradiance. With 300
variations in the solar intensity, the exergy efficiency fluctuates from about 33% to 57%. In [
19], a geothermal power plant accompanied by non-condensable gases in two distinct site conditions, including subcritical and supercritical, was analytically investigated. The exergy efficiencies of the subcritical and supercritical modes were 50.5% and 52%, respectively. They concluded that turbine inlet pressure has an indirect relation with the exergy performance of the supercritical cycle, while the subcritical cycle’s performance first increases and then reduces. The analysis reveals the levelized cost of energy for the subcritical and supercritical systems by 5.52
and 6.96
, respectively. Elhelw and Al Dahma [
20] studied the exergetic performance of the new Abu Qir thermal steam power plant in Alexandria with 650 MW nominal output power. The investigation was divided into full and half loads. The exergy destruction share of the boiler, turbine, and condenser is 75%, 15%, and 6%, respectively. The half load’s exergy destruction for the same devices in order is 78%, 14%, and 5%. Khaleel et al. [
21] studied the energy and exergy performance of a steam coal-fired power plant. The sensitivity analysis of the superheater pressure and temperature was investigated. Doubling the superheater pressure leads to enhanced net power output by about 8%. The superheater temperature had the same trend. Increasing the steam temperature from 539.8 to 580 °C, the net power increases by 6%. The overall energy and exergy efficiencies of this 589.47 MW power plant are 30.41% and 62.20%, respectively. Ahmadi et al. [
22] used energy, exergy, and exergoenvironmental analyses to evaluate the performance of a CHP power plant in Isfahan Petrochemical Complex, Iran. The complex aims to generate Benzene, Orthoxylene, Toluene, and Xylene. The CHP’s net power is about 18 MW. The energy and exergy efficiency of the plant are 8.22% and 7.87%. The boiler possesses the highest exergy destruction rate at 65,571 kW. Adnan et al. [
23] delved into two waste fuel power plants in two cities in Bangladesh. Taking 3 million metric tons (MMT) of municipal solid waste, Dhaka’s power plant’s net power is 169 MW, and Chattogram’s output is 83 MW. The environmental analysis shows that burning solid waste curbed carbon emissions by about 1 MMT for Dhaka and 0.5 MMT for Chattogram. Hao et al. [
24] conducted an energy and exergy analysis, along with an economic exergy analysis, of Huadian Kemen Power Plant based on its operational efficiency and its impact on the discharged heat to the surrounding environment. Their findings indicated that the construction of heat-retaining and -diversion facilities within the power plant reduced the intake water temperature and improved heat distribution, although regions with higher temperatures also experienced an increase.
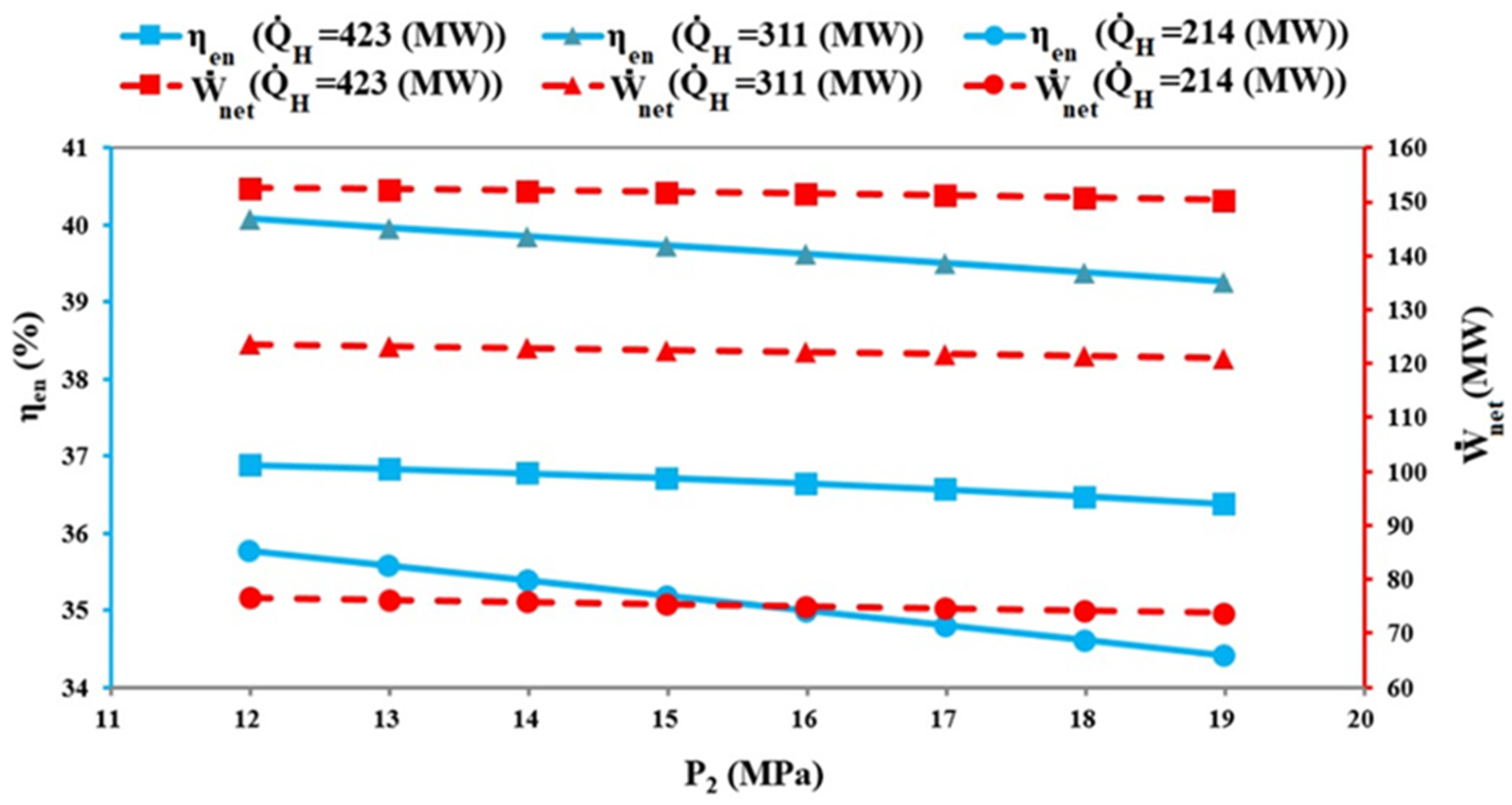
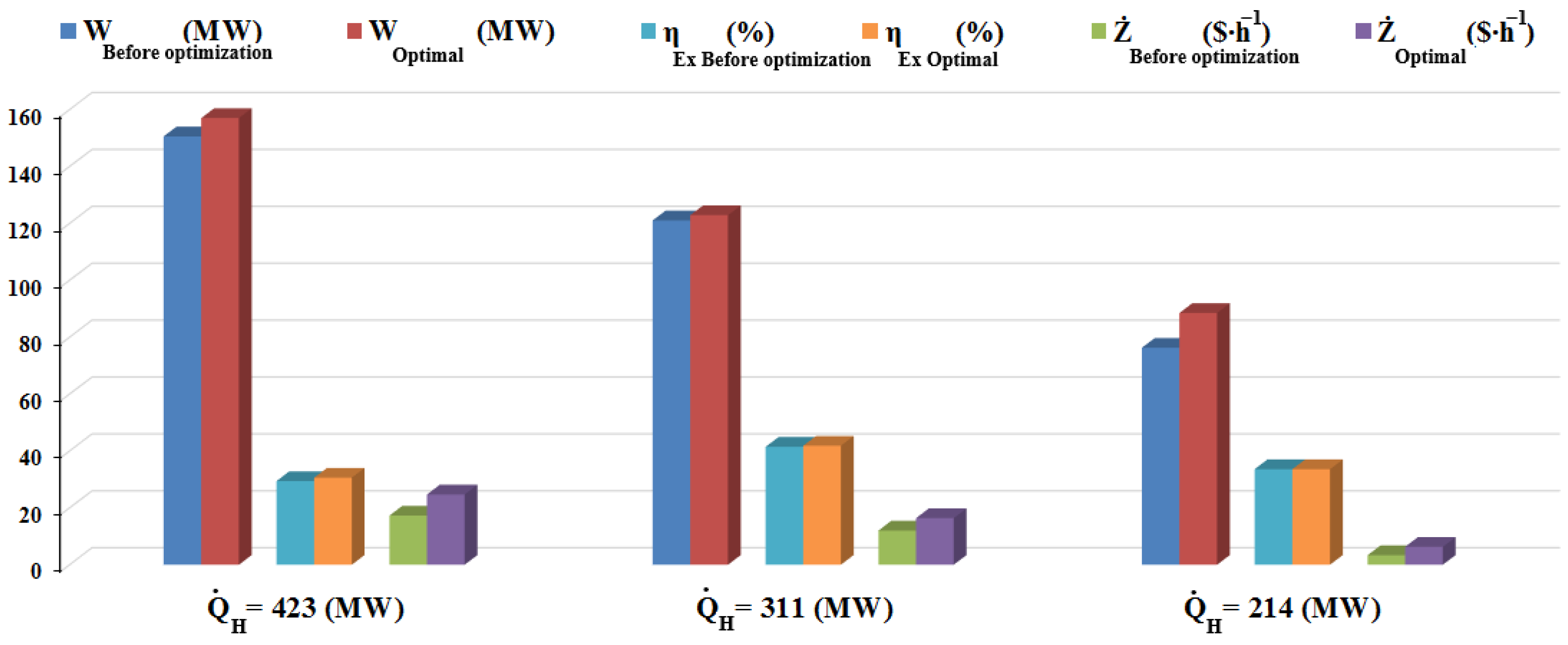
Given the paramount importance of exergy analysis evident in the reviewed literature above, this investigation evaluates the thermodynamic performance of a potential and strategic power plant in Iran: Mashhad Tous power plant. The thermodynamic analyses consist of energy, exergy, and exergoeconomic, which is the translation of exergy into economic notions. Regardless of most of the literature mimicking power plant systems through simulation, this work peruses the thermodynamic efficiencies completely using the experimental data log from the site. Three pivotal parameters, mass flow rate of the water inlet to the boiler, turbine steam inlet pressure, and ambient temperature, are considered the power plant’s input variables. The optimum working condition to maximize the network output and exergetic performance while simultaneously curbing the system’s cost is applied using Pareto-based multi-criteria. Some notable novelties of the present study are as follows:
Utilizing energy, exergy, and ecoexergy equations for the Tous power plant;
Optimizing effective parameters through a multi-objective optimization method;
The best ambient temperature has been selected based on exergy efficiency, work, and capital cost under various loads;
Employing experimental results for the validation and modeling of a power plant.