Study on Water and Salt Transport under Different Subsurface Pipe Arrangement Conditions in Severe Saline–Alkali Land in Hetao Irrigation District with DRAINMOD Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Field Test Design
2.3. Sampling, Measurement and Calculation
2.3.1. Meteorological Data
2.3.2. Irrigation Time and Water Volume
2.3.3. Soil Sampling
2.3.4. Water Sampling
2.3.5. Water Table
2.3.6. Soil Moisture Content, Salt Content, Desalting Rate and Salt Control Rate
2.4. DRAINMOD Model
2.4.1. Model Description
2.4.2. Model Input
2.5. Water and Salt Balance in Soil Profile
2.6. Shallow Groundwater Utilization and Salt Accumulation Rate
2.7. Calibration and Verification of the Models and Fitting Equations
3. Results and Analysis
3.1. Changes in Soil Water Content and Salinity
3.2. The Salt Content and Soil Desalting Rate under Experimental Conditions and the Influencing Factors
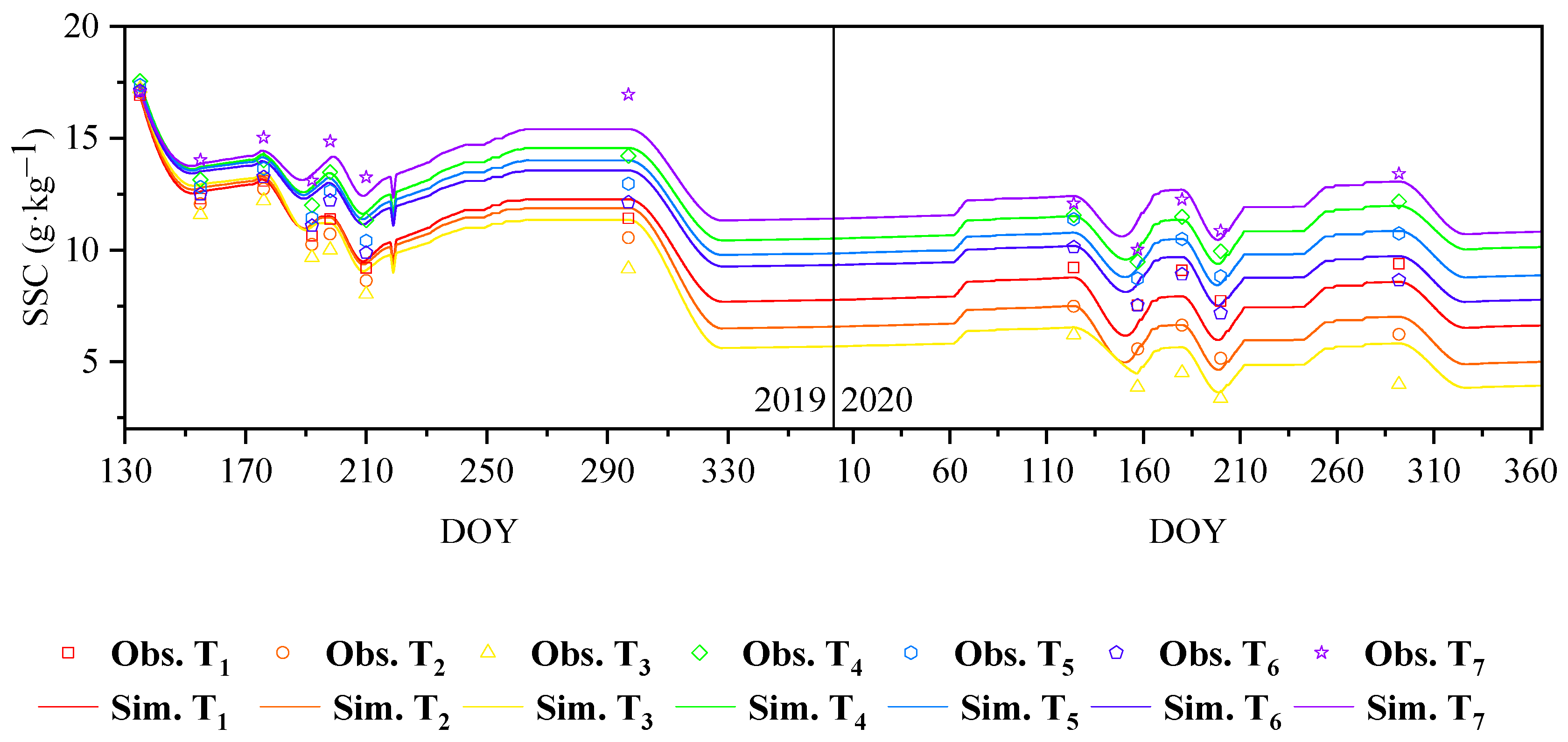
3.3. Calibration and Verification of Model Parameters
3.4. Soil Salts Simulation with DRAINMOD Model
3.5. Soil Salt Content Simulation in Existing Plot and Predicted Plot after Sunflower Planting
3.6. Analysis of Rational Layouts of Pipes
4. Discussion
4.1. Effects of Subsurface Pipe Drainage on Soil Moisture and Salinity
4.2. The Influence of Field Conditions on the Layout of Pipes
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Ao, C.; Zeng, W.; Kumar Srivastava, A.; Gaiser, T.; Wu, J. Simulating water and salt transport in subsurface pipe drainage systems with HYDRUS-2D. J. Hydrol. 2021, 592, 125823. [Google Scholar] [CrossRef]
- Dregne, H.E. Land degradation in the drylands. Arid Land Res. Manag. 2002, 16, 99–132. [Google Scholar] [CrossRef]
- Singh, A. Soil salinization and waterlogging: A threat to environment and agricultural sustainability. Ecol. Indic. 2015, 57, 128–130. [Google Scholar] [CrossRef]
- Li, P.Y.; Wu, J.H.; Qian, H. Regulation of secondary soil salinization in semi-arid regions: A simulation research in the Nanshantaizi area along the Silk Road, northwest China. Environ. Earth Sci. 2016, 75, 698. [Google Scholar] [CrossRef]
- Feng, W.Y.; Wang, T.K.; Zhu, Y.R.; Sun, F.H.; Giesy, J.P.; Wu, F.C. Chemical composition, sources, and ecological effect of organic phosphorus in water ecosystems: A review. Carbon Res. 2023, 2, 12. [Google Scholar] [CrossRef]
- Asfaw, E.; Suryabhagavan, K.V.; Argaw, M. Soil salinity modeling and mapping using remote sensing and GIS: The case of Wonji sugar cane irrigation farm, Ethiopia. J. Saudi Soc. Agric. Sci. 2018, 17, 250–258. [Google Scholar] [CrossRef]
- Li, J.; Pu, L.; Han, M.; Zhu, M.; Zhang, R.; Xiang, Y. Soil salinization research in China: Advances and prospects. J. Geogr. Sci. 2014, 24, 943–960. [Google Scholar] [CrossRef]
- Dou, X.; Shi, H.B.; Li, R.P.; Miao, Q.F.; Tian, F.; Yu, D.D. Distribution characteristics of salinity and nutrients in salinized soil profile and estimation of salt migration. Trans. Chin. Soc. Agric. 2022, 53, 279–290+330. [Google Scholar]
- Wang, Z. Salt Movement Trends in Cotton Fields with Long-Term Drip Irrigation under Mulch in Typical Oasis and Irrigation Management; China Agricultural University: Beijing, China, 2014. [Google Scholar]
- Haj-Amor, Z.; Bouri, S. Subsurface drainage system performance, soil salinization risk, and shallow groundwater dynamic under irrigation practice in an arid land. Arabian J. Sci. Eng. 2019, 44, 467–477. [Google Scholar] [CrossRef]
- Ritzema, H.; Chultz, B. Optimizing subsurface drainage practices in irrigated agriculture in the semi-arid and arid regions: Experience from Egypt, India AND Pakistan. Irrig. Drain. 2011, 60, 360–369. [Google Scholar] [CrossRef]
- Sharma, D.P.; Gupta, S.K. Subsurface drainage for reversing degradation of waterlogged saline lands. Land Degrad. Dev. 2010, 17, 605–614. [Google Scholar] [CrossRef]
- He, X.L.; Liu, H.G.; Ye, J.Y.; Yang, G.; Li, M.S.; Gong, P. Comparative investigation on soil salinity leaching under subsurface drainage and ditch drainage in Xinjiang arid region. Int. J. Agric. Biol. Eng. 2016, 9, 109–118. [Google Scholar]
- Hornbuckle, J.W.; Christen, E.W.; Faulkner, R.D. Evaluating a multi-level subsurface drainage system for improved drainage water quality. Agric. Water Manag. 2007, 89, 208–216. [Google Scholar] [CrossRef]
- Ceuppens, J.; Wopereis, M.; Miézan, K.M. Soil salinization processes in rice irrigation schemes in the Senegal river delta. Soil Sci. Soc. Am. J. 1997, 61, 1122–1130. [Google Scholar] [CrossRef]
- Salo, H.; Mellin, I.; Sikkilä, M.; Nurminen, J.; Äijö, H.; Paasonen-Kivekäs, M. Performance of subsurface drainage implemented with trencher and trenchless machineries. Agric. Water Manag. 2019, 213, 957–967. [Google Scholar] [CrossRef]
- Buckland, G.D.; Bennett, D.R.; Mikalson, D.E.; Jong, E.D.; Chang, C. Soil salinization and sodication from alternate irrigations with saline-sodic water and simulated rain. Can. J. Soil Sci. 2002, 82, 297–309. [Google Scholar] [CrossRef]
- Skaggs, R.W.; Brevé, M.A.; Gilliam, J.W. Hydrologic and water quality impacts of agricultural drainage. Crit. Rev. Environ. Sci. Technol. 1994, 24, 1–32. [Google Scholar]
- Nozari, H.; Azadi, S.; Zali, A. Experimental study of the temporal variation of drain water salinity at different drain depths and spacing in the presence of saline groundwater. Sustain. Water Resour. Manag. 2018, 4, 887–895. [Google Scholar]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Recent developments and applications of the HYDRUS computer software packages. Vadose Zone J. 2016, 15, 25. [Google Scholar] [CrossRef]
- Bailey, R.T.; Tavakoli-Kivi, S.; Wei, X. A salinity module for SWAT to simulate salt ion fate and transport at the watershed scale. Hydrol. Earth Syst. Sci. 2019, 23, 3155–3174. [Google Scholar] [CrossRef]
- Skaggs, R.W.; Youssef, M.A.; Chescheir, G.M. DRAINMOD: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1509–1522. [Google Scholar] [CrossRef]
- Dou, X.; Shi, H.B.; Li, R.P.; Miao, Q.F.; Yan, J.W.; Tian, F. Simulation and evaluation of soil water and salt transport under controlled subsurface drainage using HYDRUS-2D model. Agric. Water Manag. 2023, 273, 107899. [Google Scholar] [CrossRef]
- Addab, H.; Bailey, R.T. Simulating the effect of subsurface tile drainage on watershed salinity using SWAT. Agric. Water Manag. 2022, 262. [Google Scholar] [CrossRef]
- Hosseini, P.; Bailey, R.T. Investigating the controlling factors on salinity in soil, groundwater, and river water in a semi-arid agricultural watershed using SWAT-Salt. Sci. Total Environ. 2022, 810, 152293. [Google Scholar]
- Luo, W.; Skaggs, R.; Madani, A.; Cizikci, S.; Mavi, A. Predicting field hydrology in cold conditions with drainmod. Transactions of the ASAE. Trans. ASAE Soc. Agric.Eng. 2001, 44, 825–834. [Google Scholar]
- Youssef, M.A.; Skaggs, R.W.; Chescheir, G.M.; Gilliam, J.W. The nitrogen simulation model, DRAINMOD-N II. Trans. ASABE 2005, 48, 611–626. [Google Scholar] [CrossRef]
- Askar, M.H.; Youssef, M.A.; Chescheir, G.M.; Negm, L.M.; King, K.W.; Hesterberg, D.L. DRAINMOD Simulation of macropore flow at subsurface drained agricultural fields: Model modification and field testing. Agric. Water Manag. 2020, 242, 106401. [Google Scholar] [CrossRef]
- Moursi, H.; Youssef, M.A.; Chescheir, G.M. Development and application of DRAINMOD model for simulating crop yield and water conservation benefits of drainage water recycling. Agric. Water Manag. 2022, 266, 107592. [Google Scholar]
- Ren, D.; Huang, G.; Huang, Q.; Ramos, T.B.; Xu, X.; Huo, Z. Modeling and assessing the function and sustainability of natural patches in salt-affected agro-ecosystems: Application to tamarisk (Tamarix chinensis lour.) in Hetao, upper Yellow River basin. J. Hydrol. 2017, 552, 490–504. [Google Scholar] [CrossRef]
- Cao, Z.D.; Zhu, T.J.; Cai, X.M. Hydro-agro-economic optimization for irrigated farming in an arid region: The Hetao Irrigation District, Inner Mongolia. Agric. Water Manag. 2023, 277, 108095. [Google Scholar] [CrossRef]
- Feng, W.Y.; Yang, F.; Cen, R.; Liu, J.; Qu, Z.Y.; Miao, Q.F. Effects of straw biochar application on soil temperature, available nitrogen and growth of corn. J. Environ. Manag. 2021, 277, 111331. [Google Scholar] [CrossRef]
- Feng, Z.Z.; Miao, Q.F.; Shi, H.B.; Feng, W.Y.; Li, X.Y.; Yan, J.W. Simulation of water balance and irrigation strategy of typical sand-layered farmland in the Hetao Irrigation District, China. Agric. Water Manag. 2023, 280, 108236. [Google Scholar] [CrossRef]
- Qian, Y.Z.; Zhu, Y.; Ye, M.; Huang, J.S.; and Wu, J.W. Experiment and numerical simulation for designing layout parameters of subsurface drainage pipes in arid agricultural areas. Agric. Water Manag. 2021, 243, 106455. [Google Scholar] [CrossRef]
- Tong, W.; Chen, X.; Wen, X.; Chen, F.; Zhang, H.; Chu, Q. Applying a salinity response function and zoning saline land for three field crops: A case study in the Hetao Irrigation District, Inner Mongolia, China. J. Integr. Agric. 2015, 14, 178–189. [Google Scholar] [CrossRef]
- Bouwer, H.; van Schilfgaarde, J. Simplified method of predicting fall of water table in drained land. J. Water Resour. Prot. 1963, 11, 0288–0291. [Google Scholar]
- Kirkham, D. The Ponded Water Case. In Drainage of Agricultural Lands; Luthin, J.N., Ed.; American Society of Agronomy: Madison, WI, USA, 1957; pp. 139–181. [Google Scholar]
- Minhas, P.S.; Ramos, T.B.; Ben-Gal, A.; Pereira, L.S. Coping with salinity in irrigated agriculture: Crop evapotranspiration and water management issues. Agric. Water Manag. 2020, 227, 105832. [Google Scholar]
- Liu, M.H.; Shi, H.B.; Paredes, P.; Ramos, T.B.; Dai, L.P.; Feng, Z.Z.; Pereira, L.S. Estimating and partitioning maize evapotranspiration as affected by salinity using weighing lysimeters and the SIMDualKc model. region. Agric. Water Manag. 2022, 261, 107362. [Google Scholar] [CrossRef]
- Miao, Q.F.; Rosa, R.D.; Shi, H.B.; Paredes, P.; Zhu, L.; Dai, J.X. Modeling water use, transpiration and soil evaporation of spring wheat–maize and spring wheat–sunflower relay intercropping using the dual crop coefficient approach. Agric. Water Manag. 2016, 165, 211–229. [Google Scholar] [CrossRef]
- Rosa, R.D.; Paredes, P.; Rodrigues, G.C.; Alves, I.; Fernando, R.M.; Pereira, L.S.; Allen, R.G. Implementing the dual crop coefficient approach in interactive software. 1. Backgr. Comput. Strategy Agric. Water Manag. 2012, 103, 8–24. [Google Scholar] [CrossRef]
- Zhang, W.Z.; Zhang, Y.F. The specific yield and pore ratio of soils. J. Irrig. Drain. 1983, 2, 1–16. [Google Scholar]
- Luo, W.; Sands, G.R.; Youssef, M.; Strock, J.S.; Song, I.; Canelon, D. Modeling the impact of alternative drainage practices in the northern Corn-belt with DRAINMOD-NII. Agric. Water Manag. 2010, 97, 389–398. [Google Scholar] [CrossRef]
- Wiskow, E.; van der Ploeg, R.R. Calculation of drain spacings for optimal rainstorm flood control. J. Hydrol. 2003, 272, 163–174. [Google Scholar] [CrossRef]
- Jafari-Talukolaee, M.; Shahnazari, A.; Ahmadi, Z.M.; Darzi-Naftchali, A. Drain discharge and salt load in response to subsurface drain depth and spacing in paddy fields. J. Irrig. Drain. Eng. 2015, 141, 1–6. [Google Scholar] [CrossRef]
- Geng, X.; Boufadel, M.C. Numerical modeling of water flow and salt transport in bare saline soil subjected to evaporation. J. Hydrol. 2015, 524, 427–438. [Google Scholar] [CrossRef]
- Ghane, E.; Askar, M.H. Predicting the effect of drain depth on profitability and hydrology of subsurface drainage systems across the eastern USA. Agric. Water Manag. 2021, 258, 107072. [Google Scholar] [CrossRef]
- Darzi-Naftchali, A.; Motevali, A.; Keikha, M. The life cycle assessment of subsurface drainage performance under rice-canola cropping system. Agric. Water Manag. 2022, 266, 107579. [Google Scholar] [CrossRef]
- Sands, G.R.; Song, I.; Busman, L.M.; Hansen, B.J. The effects of subsurface drainage depth and intensity on nitrate loads in the northern cornbelt. Trans. ASABE 2008, 51, 937–946. [Google Scholar] [CrossRef]
- Krejcová, J.; Vicentini, F.; Flynn, T.; Mudrák, O.; Frouz, J. Biodiversity loss caused by subsurface pipe drainage is difficult to restore. Ecol. Eng. 2021, 170, 106336. [Google Scholar] [CrossRef]
- Schott, L.; Lagzdins, A.; Daigh, A.L.M.; Craft, K.; Pederson, C.; Brenneman, G. Drainage water management effects over five years on water tables, drainage, and yields in southeast Iowa. J. Soil Water Conserv. 2017, 72, 251–259. [Google Scholar] [CrossRef]
- Zhang, J.X.; Werner, A.D.; Lu, C.H. Improving salt leaching efficiency of subsurface drainage systems using low-permeability surface mulch. Adv. Water Resour. 2022, 162, 104147. [Google Scholar] [CrossRef]
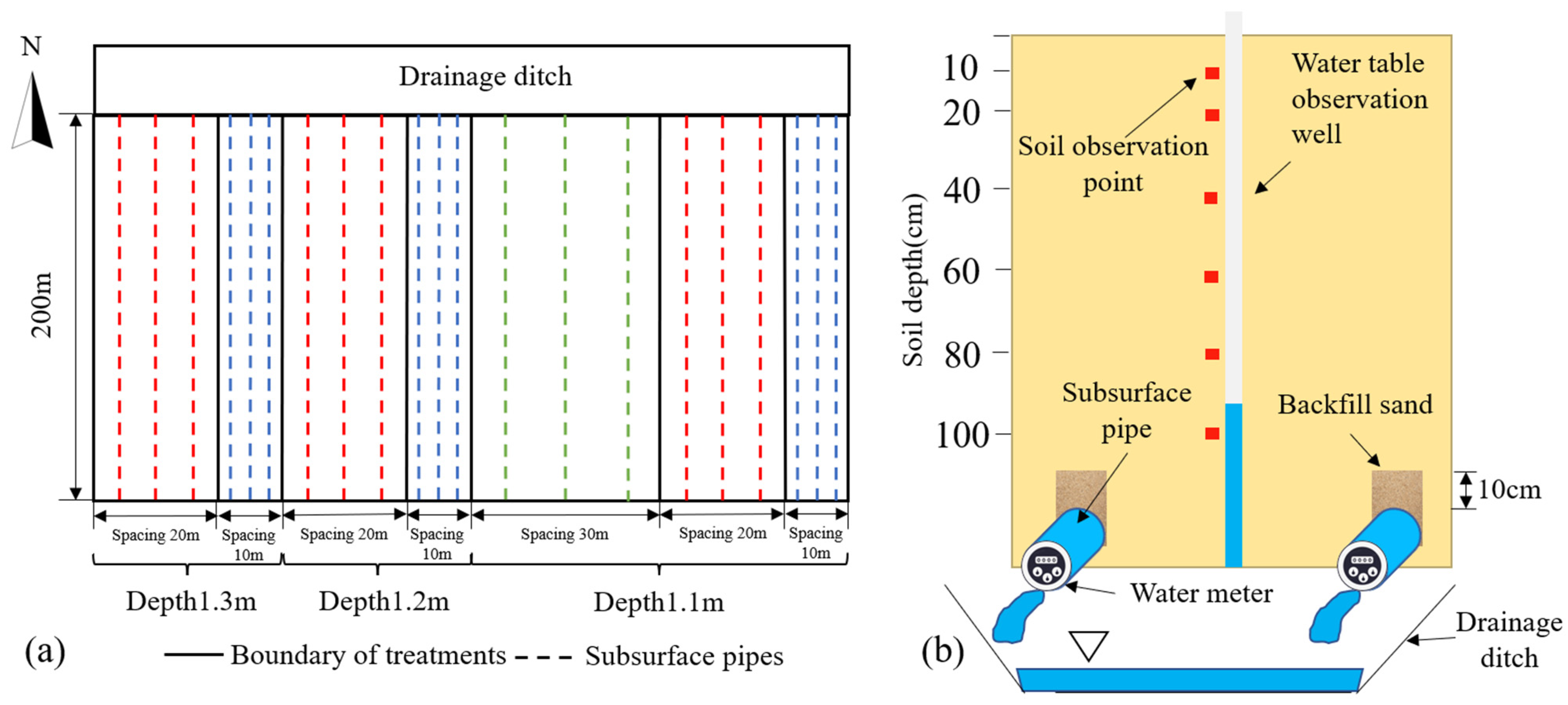


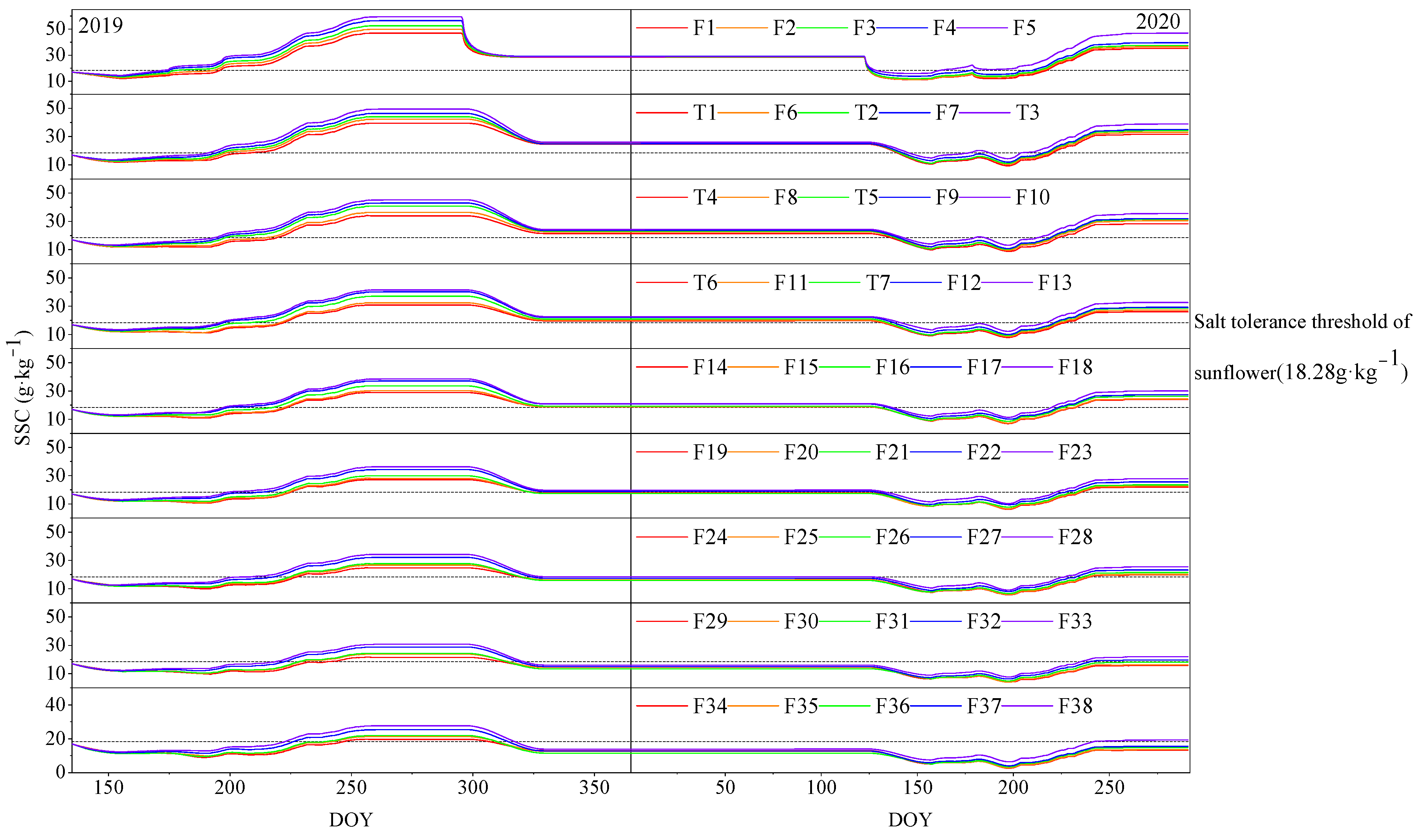

| Depth (cm) | Spacing (cm) | ||||
|---|---|---|---|---|---|
| 1000 | 1500 | 2000 | 2500 | 3000 | |
| 100 | F1 | F2 | F3 | F4 | F5 |
| 110 | T1 | F6 | T4 | F7 | T7 |
| 120 | T2 | F8 | T5 | F9 | F10 |
| 130 | T3 | F11 | T6 | F12 | F13 |
| 140 | F14 | F15 | F16 | F17 | F18 |
| 150 | F19 | F20 | F21 | F22 | F23 |
| 160 | F24 | F25 | F26 | F27 | F28 |
| 180 | F29 | F30 | F31 | F32 | F33 |
| 200 | F34 | F35 | F36 | F37 | F38 |
| Soil Layer (cm) | Particle Composition/% | Bulk Density (g·cm−3) | Soil Salt Content (g·kg−1) | pH | Field Capacity (cm3 cm−3) | ||
|---|---|---|---|---|---|---|---|
| Sand | Clay | Silt | |||||
| 0–10 | 36.6 | 4.22 | 59.18 | 1.44 | 25.23 | 7.45 | 32.35 |
| 10–20 | 32.32 | 3.86 | 63.82 | 1.45 | 21.79 | 7.60 | 33.29 |
| 20–40 | 23.98 | 2.20 | 73.82 | 1.47 | 18.22 | 7.64 | 36.61 |
| 40–60 | 8.27 | 2.47 | 89.26 | 1.48 | 15.53 | 7.72 | 35.08 |
| 60–80 | 3.36 | 5.70 | 90.94 | 1.49 | 11.79 | 7.51 | 36.33 |
| 80–100 | 12.91 | 5.02 | 82.07 | 1.49 | 10.60 | 7.62 | 36.52 |
| Parameter | Denormalization Coefficient | Standardization Coefficient | VIF | p | R2 | F |
|---|---|---|---|---|---|---|
| B | Beta | |||||
| Constant | −39.848 | - | - | 0.018 * | 0.902 | F = 101.123 p = 0.000 ** |
| So | 5.057 | 0.811 | 1.307 | 0.000 ** | ||
| I | −0.086 | −0.344 | 1.070 | 0.000 ** | ||
| s | −0.016 | −0.577 | 1.298 | 0.000 ** | ||
| d | 0.531 | 0.224 | 1.125 | 0.000 ** |
| Treatment | Time | Soil Salt Content Change (g·kg−1) | Soil Desalinization Rate (%) | Time | Soil Salt Content Change (g·kg−1) | Soil Desalinization Rate (%) | Time | Soil Salt Content Change (g·kg−1) | Soil Desalinization Rate (%) |
|---|---|---|---|---|---|---|---|---|---|
| T1 | 15 May 2019 | 4.64 | 27.38 | 26 June 2019 | 2.45 | 18.75 | 17 July 2019 | 2.19 | 19.25 |
| T2 | 4.98 | 29.23 | 2.49 | 19.51 | 2.08 | 19.40 | |||
| T3 | 6.36 | 36.93 | 2.55 | 22.71 | 1.78 | 19.77 | |||
| T4 | 4.42 | 25.19 | 2.02 | 14.39 | 2.14 | 15.86 | |||
| T5 | 4.65 | 26.77 | 2.55 | 18.89 | 1.94 | 15.95 | |||
| T6 | 4.85 | 28.32 | 2.89 | 22.58 | 1.85 | 16.74 | |||
| T7 | 3.05 | 17.88 | 1.93 | 12.81 | 1.61 | 10.83 | |||
| Treatment | Time | Soil salt content change(g·kg−1) | Soil desalinization rate (%) | Time | Soil salt content change (g·kg−1) | Soil desalinization rate (%) | |||
| T1 | 3 May 2020 | 1.69 | 18.30 | 28 June 2020 | 1.36 | 14.92 | |||
| T2 | 1.92 | 25.59 | 1.49 | 22.38 | |||||
| T3 | 2.36 | 37.94 | 1.15 | 25.43 | |||||
| T4 | 2.09 | 18.04 | 1.54 | 13.38 | |||||
| T5 | 2.65 | 23.31 | 1.67 | 15.92 | |||||
| T6 | 2.59 | 25.59 | 1.75 | 19.63 | |||||
| T7 | 2.06 | 17.03 | 1.41 | 11.47 | |||||
| Treatment | 2019 | 2020 | ||||
|---|---|---|---|---|---|---|
| MAE (cm) | RMSE (cm) | NSE | MAE (cm) | RMSE (cm) | NSE | |
| T1 | 4.11 | 21.65 | 0.76 | 3.82 | 16.01 | 0.81 |
| T2 | 4.37 | 20.35 | 0.71 | 3.51 | 13.78 | 0.70 |
| T3 | 5.07 | 28.29 | 0.69 | 4.54 | 22.98 | 0.78 |
| T4 | 4.74 | 24.61 | 0.62 | 3.85 | 16.37 | 0.80 |
| T5 | 5.25 | 29.51 | 0.64 | 4.16 | 18.98 | 0.69 |
| T6 | 5.83 | 38.32 | 0.57 | 4.77 | 24.97 | 0.75 |
| T7 | 6.15 | 41.64 | 0.60 | 5.01 | 36.90 | 0.69 |
| Treatment | 2019 | 2020 | ||||
|---|---|---|---|---|---|---|
| MAE (g·kg−1) | RMSE (g·kg−1) | NSE | MAE (g·kg−1) | RMSE (g·kg−1) | NSE | |
| T1 | 0.32 | 0.41 | 0.89 | 1.03 | 1.11 | 0.46 |
| T2 | 0.78 | 0.82 | 0.70 | 0.29 | 0.42 | 0.84 |
| T3 | 1.36 | 1.41 | 0.49 | 0.85 | 1.03 | 0.40 |
| T4 | 0.34 | 0.40 | 0.86 | 0.24 | 0.30 | 0.92 |
| T5 | 0.81 | 0.84 | 0.56 | 0.28 | 0.35 | 0.87 |
| T6 | 1.06 | 1.09 | 0.41 | 0.63 | 0.73 | 0.61 |
| T7 | 0.70 | 0.84 | 0.47 | 0.51 | 0.59 | 0.66 |
| Parameter | Denormalization Coefficient | Standardization Coefficient | VIF | p | R2 | F |
|---|---|---|---|---|---|---|
| B | Beta | |||||
| Constant | −61.548 | - | - | 0.000 ** | 0.911 | F = 678.203 p = 0.000 ** |
| So | 0.390 | 0.157 | 1.481 | 0.000 ** | ||
| I | 0.254 | 0.868 | 1.228 | 0.000 ** | ||
| s | −0.004 | −0.121 | 1.041 | 0.000 ** | ||
| d | 0.151 | 0.209 | 1.212 | 0.000 ** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, F.; Miao, Q.; Shi, H.; Li, R.; Dou, X.; Duan, J.; Liu, J.; Feng, W. Study on Water and Salt Transport under Different Subsurface Pipe Arrangement Conditions in Severe Saline–Alkali Land in Hetao Irrigation District with DRAINMOD Model. Water 2023, 15, 3001. https://doi.org/10.3390/w15163001
Tian F, Miao Q, Shi H, Li R, Dou X, Duan J, Liu J, Feng W. Study on Water and Salt Transport under Different Subsurface Pipe Arrangement Conditions in Severe Saline–Alkali Land in Hetao Irrigation District with DRAINMOD Model. Water. 2023; 15(16):3001. https://doi.org/10.3390/w15163001
Chicago/Turabian StyleTian, Feng, Qingfeng Miao, Haibin Shi, Ruiping Li, Xu Dou, Jie Duan, Jing Liu, and Weiying Feng. 2023. "Study on Water and Salt Transport under Different Subsurface Pipe Arrangement Conditions in Severe Saline–Alkali Land in Hetao Irrigation District with DRAINMOD Model" Water 15, no. 16: 3001. https://doi.org/10.3390/w15163001
APA StyleTian, F., Miao, Q., Shi, H., Li, R., Dou, X., Duan, J., Liu, J., & Feng, W. (2023). Study on Water and Salt Transport under Different Subsurface Pipe Arrangement Conditions in Severe Saline–Alkali Land in Hetao Irrigation District with DRAINMOD Model. Water, 15(16), 3001. https://doi.org/10.3390/w15163001










