The Reason for the Rise in Critical Shear Stress on Sloping Beds
Abstract
:1. Introduction
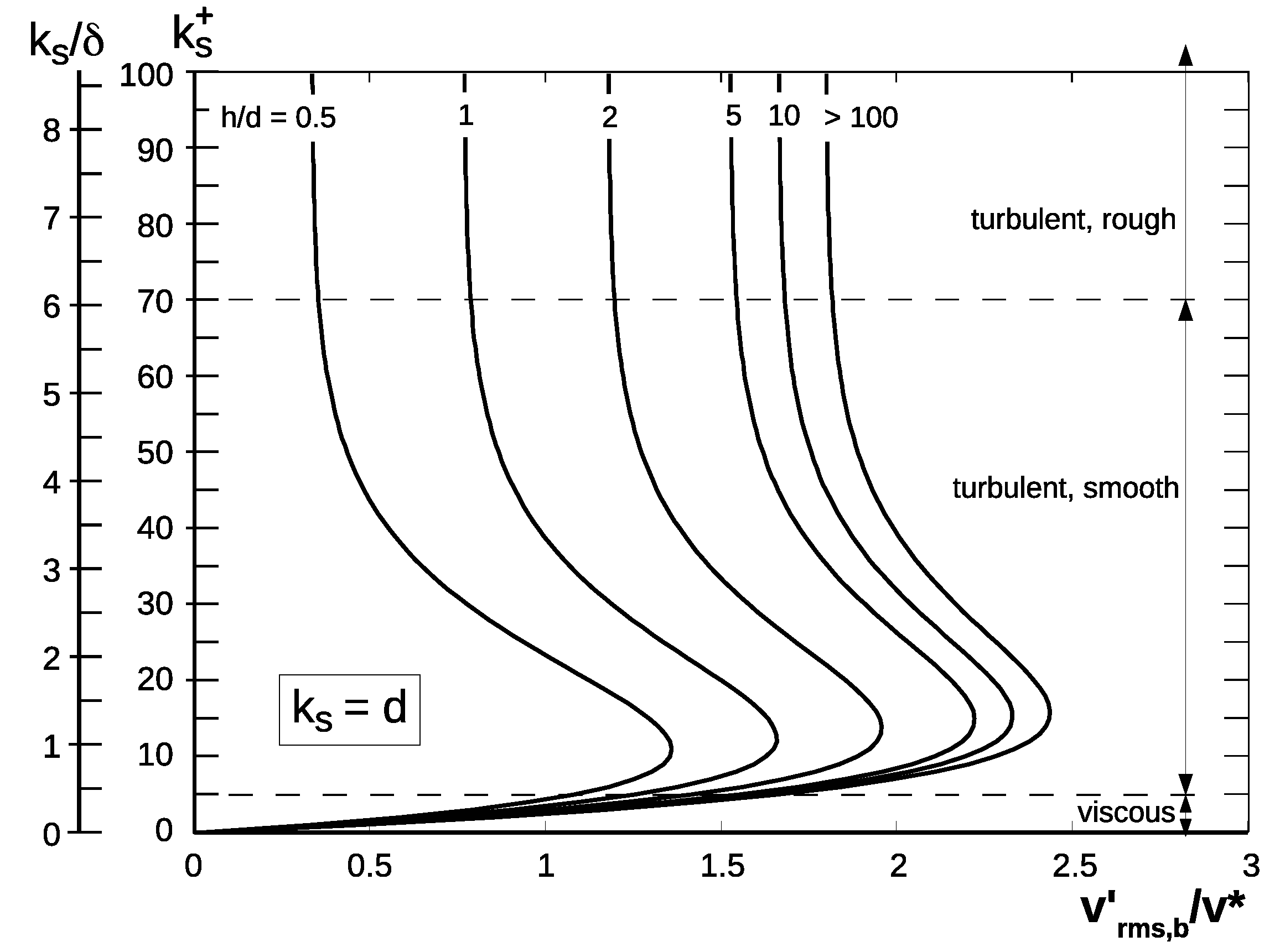
2. Turbulence Damping with Low Water Coverage
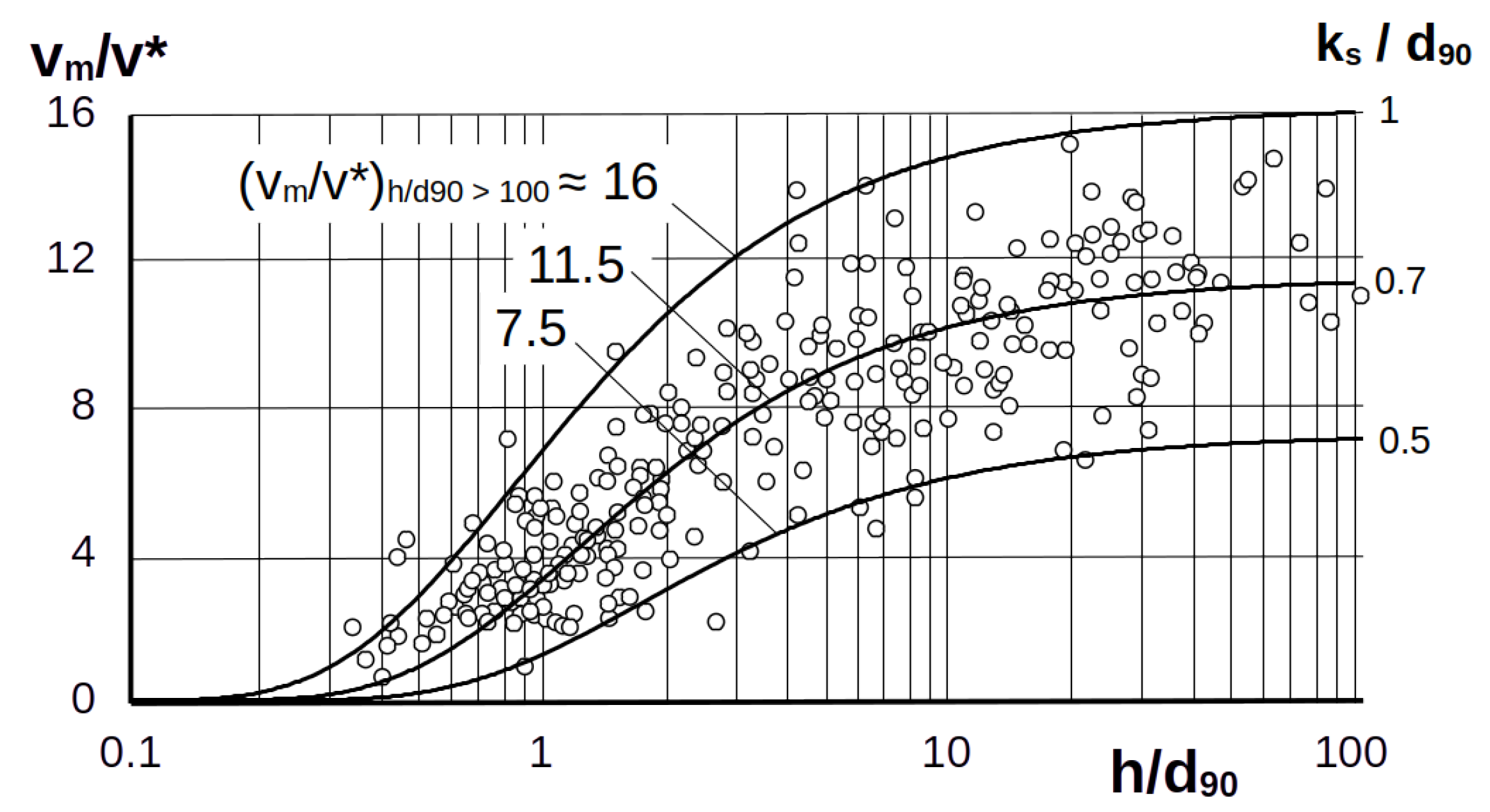
3. Beginning of Sediment Movement
3.1. Measurement Data on the Beginning of Movement at a Large Gradient and Low Water Cover
3.2. Shields Curve
3.3. Analytical Solution of the Shields Curve
3.3.1. Turbulence-Free Flow
3.3.2. Turbulent Flow
3.4. Angle of Internal Friction Determining the Onset of Motion
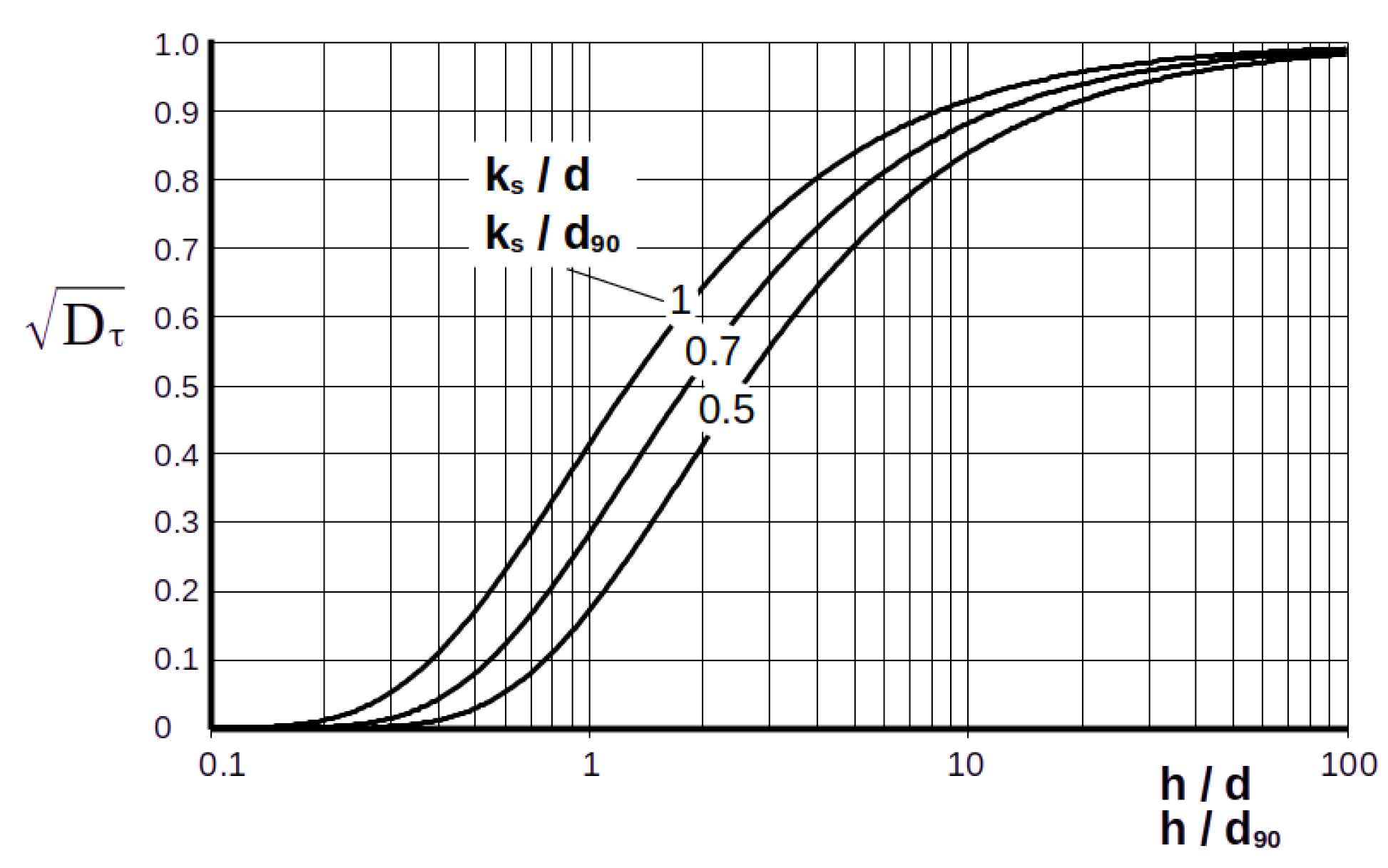
3.5. Turbulence Damping and Critical Shear Stress
3.5.1. Finite Critical Shear Stress with Complete Damping of Turbulence
3.5.2. Turbulence Damping for Exposed Particles
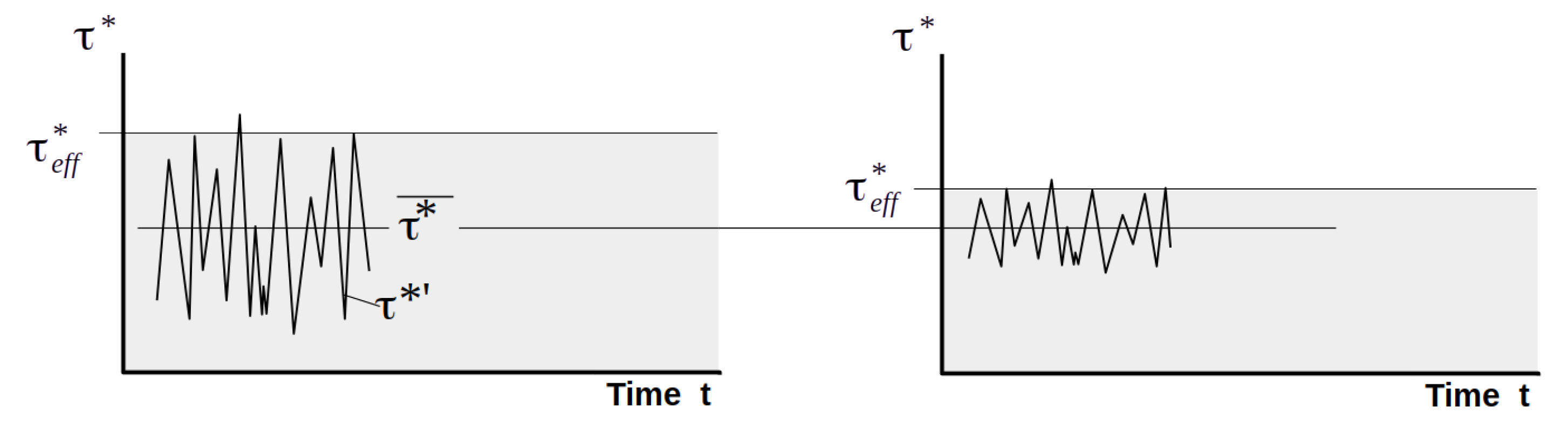
3.5.3. Degree of Movement at Start of Movement
3.6. Effect of Dynamic Friction Angle
4. Critical Shear Stress at Large Slope and Low Water Cover
5. Influence of Sediment Density
6. Summary and Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| B | Integration constant of log. velocity profile | - |
| d | Grain diameter | m |
| -Damping coefficient with low water coverage | - | |
| -Damping coefficient with respect to initiation of sediment motion | - | |
| g | Coefficient of gravity | m/s2 |
| h | Water depth | m |
| Equivalent sand roughness height, where | m | |
| = | - | |
| = , Reynolds number of grain | - | |
| n | Grain motion triggering multiple of | - |
| Mean current velocity | m/s | |
| Fluctuation values of the flow velocity | m/s | |
| Mean critical velocity | m/s | |
| Standard deviation of | m/s | |
| Standard deviation of at the grain level | m/s | |
| Shear velocity = | m/s | |
| y | Distance from the bed | m |
| = , dimensionless distance from the bed | - | |
| Inclination angle of the bed, positive downhill | ||
| Thickness of the viscous sublayer of the boundary layer | m | |
| Factor for caused by a bottom slope | - | |
| Static angle of internal friction | ||
| Angle of repose of a heap of cohesionless grains | ||
| Friction angle above which avalanches occur | ||
| Dynamic angle of internal friction | ||
| = Angle of internal friction on the sediment surface, | ||
| which is decisive for the beginning of sediment movement | ||
| Kinematic viscosity of the fluid | m2/s | |
| von Karman constant = 0.4 | - | |
| Density of fluid | kg/m3 | |
| Density of sediment | kg/m3 | |
| , relative density | - | |
| , shear stress at the bed | N/m2 | |
| Fluctuation values of shear stress due to turbulence | N/m2 | |
| , dimensionless shear stress | - | |
| = reference value for the dimensionless shear stress | ||
| at the beginning of the sediment movement according to Shields | - | |
| Indices | ||
| : | Case with low water cover | |
| or | Case with high water cover | |
| : | with inclination of the bed by the angle |
References
- Shields, A. Anwendung der Ähnlichkeitsmechanik und der Turbulenzforschung auf die Geschiebebewegung. (Application of Similarity Principles and Turbulence Research to Bed-Load Movement); Mitteilungen der Preussischen Versuchsanstalt für Wasserbau und Schiffbau: Berlin, Germany, 1936; Heft 26. (In German) [Google Scholar]
- Ashida, K.; Bayazit, M. Initiation of motion and roughness of flows in steep channels. J. Water Resour. Prot. 1973, 3, 475–484. [Google Scholar]
- Shvidchenko, A.B.; Pender, G. Flume study of the effect of relative depth on the incipient motion of coarse uniform sediments. Water Resour. Res. 2000, 36, 619–628. [Google Scholar] [CrossRef]
- Gregoretti, C. The initiation of debris flow at high slopes: Experimental results. J. Hydraul. Res. 2000, 38, 83–88. [Google Scholar] [CrossRef]
- Armanini, A.; Gregoretti, C. Incipient sediment motion at high slopes in uniform flow condition. Water Resour. Res. 2005, 41, 83–114. [Google Scholar] [CrossRef]
- Lamb, M.P.; Dietrich, W.E.; Venditti, J.G. Is the critical Shields stress for incipient sediment motion dependent on channel-bed slope? J. Geophys. Res. 2008, 113, F02008. [Google Scholar] [CrossRef]
- Recking, A. Theoretical development on the effects of changing flow hydraulics on incipient bed load motion. Water Resour. Res. 2009, 45, W04401. [Google Scholar] [CrossRef]
- Prancevic, J.P.; Lamb, M.P.; Fuller, M.F. Incipient motion across the river to debris-flow transition. Geology 2014, 42, 191–194. Available online: https://kiss.caltech.edu/papers/surface/papers/incipient.pdf (accessed on 14 July 2023).
- Prancevic, J.P.; Lamb, M.P. Unraveling bed slope from relative roughness in initial sediment motion. J. Geophys. Res. Earth Surf. 2015, 120, 474–489. [Google Scholar] [CrossRef]
- Prancevic, J.; Lamb, M. Particle friction angles in steep mountain channels. J. Geophys. Res. Earth Surf. 2015, 120, 242–259. [Google Scholar] [CrossRef]
- Zanke, U. Zum Einfluss der Turbulenz auf den Beginn der Sedimentbewegung. (On the Influence of Turbulence on the Initiation of Sediment Motion); Mitt. des Instituts für Wasserbau und Wasserwirtschaft der TU: Darmstadt, German, 2001; Heft 120. (In German) [Google Scholar]
- Zanke, U. On the influence of turbulence on the initiation of sediment motion. Int. J. Sediment Res. Beijing. 2003, 18, 17–31. [Google Scholar]
- Nezu, I.; Rodi, W. Open Channel Flow Measurements with a Laser Doppler Anemometer. ASCE J. Hydraul. Eng. 1986, 112, 335–355. [Google Scholar] [CrossRef]
- Laufer, J. The Structure of Turbulence in Fully Developed Pipe Flow; NACA-Report 1174; National Advisory Committee for Aeronautics: Edwards, CA, USA, 1954.
- Grass, A.J. Structural features of turbulent flow over smooth and rough boundaries. J. Fluid Mech. 1971, 50, 233–255. [Google Scholar] [CrossRef]
- Eckelmann, H. The structure of viscous sublayer and the adjacent wall region in a turbulent channel. J. Fluid Mech. 1974, 65, 439–459. [Google Scholar] [CrossRef]
- Steffler, P.M.; Rajaratnam, N.; Peterson, A.W. LDA measurements in open channel. J. Hyd. Eng. ASCE 1985, 111, 119–130. [Google Scholar] [CrossRef]
- Nezu, I.; Nakagawa, H. Turbulence in Open Channel Flows. In IAHR Monograph; A. A. Balkema: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Zanke, U. Hydromechanik der Gerinne und Küstengewässer (Hydromechanics of Flumes and Coastal Waters); Parey-Verlag: Berlin, Germany, 2002. (In German) [Google Scholar]
- Bezzola, G.R. Fliesswiderstand und Sohlenstabilität Natürlicher Gerinne. (Flow Resistance and Bed Stability of Natural Channels); Mitt. der VAW; ETH: Zuerich, Switzerland, 2002; Heft 173. [Google Scholar]
- Bayazit, M. Free Surface Flow in a Channel of Large Relative Roughness. JHR 1976, 14, 115–126. [Google Scholar] [CrossRef]
- Bayazit, M. Flow structure and sediment transport in steep channels. In Proceedings of the Euromech 156 ‘Mechanics of Sediment Transport’, Istanbul, Turkey, 12–14 July 1982; Sumer, M., Müller, A., Eds.; pp. 197–206. [Google Scholar]
- Rickenmann, D. Fliessgeschwindigkeit in Wildbächen und Gebirgsflüssen (Flow velocity in torrents and mountain rivers). Wasser Energie Luft 1996, 88, 298–304. (In German) [Google Scholar]
- Ruf, G. Fliessgeschwindigkeiten in der Ruetz/Stubaital, Tirol. (Flow velocities in the Ruetz/Stubaital, Tyrol). Wildbach Lawinenverbau 1990, 115, 219–227. (In German) [Google Scholar]
- Jarrett, R.D. Hydraulics of high-gradient streams. J. Hyd. Eng. ASCE 1984, 110, 1519–1539. [Google Scholar] [CrossRef]
- Bathurst, J.C. Flow resistance estimation in mountain rivers. J. Hyd. Eng. ASCE 1985, 111, 625–643. [Google Scholar] [CrossRef]
- Thompson, S.M.; Campbell, P.L. Hydraulics of a large channel paved with boulders. J. Hyd. Res. 1979, 17, 341–354. [Google Scholar] [CrossRef]
- Thorne, C.R.; Zevenbergen, L.W. Estimating mean velocity in mountain rivers. J. Hyd. Eng. ASCE 1985, 111, 612–624. [Google Scholar]
- Griffith, G.A. Flow resistance in coarse gravel bed rivers. J. Hyd. Div. ASCE 1981, 107, 899–918. [Google Scholar] [CrossRef]
- Raupach, M.R. Conditional statistics of Reynolds stress in rough-wall and smooth-wall turbulent boundary layers. J. Fluid Mech. 1981, 108, 363–382. [Google Scholar] [CrossRef]
- Lamb, M.P.; Brun, F.; Fuller, M. Hydrodynamics of steep streams with planar coarse-grained beds: Turbulence, flow resistance, and implications for sediment transport. Water Resour. Res. 2017, 53, 2240–2263. [Google Scholar] [CrossRef]
- Prancevic, J.P.; Lamb, M.P.; Fuller, M.F. Supplementary Materials for: Incipient motion across the river to debris-flow transition. Geology 2014, 43, 191–194. Available online: https://authors.library.caltech.edu/45096/7/2014067.pdf (accessed on 14 July 2023).
- Zanke, U. The beginning of sediment movement as a probability problem. In Proceedings of the Int. Sympos. Sediment Transport Modeling, New Orleans, LA, USA, 14–18 August 1989. [Google Scholar]
- Zanke, U. Zum Übergang Hydraulisch glatt - Hydraulisch rauh. (On the transition hydraulically rough-hydraulically smooth). Wasser Boden 1996, 48, 32–36. (In German) [Google Scholar]
- Zanke, U. Lösungen für das universelle Geschwindigkeitsverteilungsgesetz und die Shields-Kurve. (Solutions for the universal velocity distribution law and the Shields curve). Wasser Boden 1996, 9, 21–26. (In German) [Google Scholar]
- Reichardt, H. Vollständige Darstellung der turbulenten Geschwindigkeitsverteilung in glatten Leitungen. (Complete representation of the turbulent velocity distribution in smooth pipes). ZAMM Z. Für Angew. Math. Mech. 1951, 31, 208–219. (In German) [Google Scholar] [CrossRef]
- Zanke, U. Vorlesungsskript ’Sedimenttransport’ (Scriptum ’Sediment Transport’); Institut für Wasserbau und Wasserwirtschaft der TU Darmstadt: Darmstadt, Germany, 2004; (unpublished). [Google Scholar]
- Zanke, U.; Roland, A. Sediment Bed-Load Transport: A Standardized Notation. Geoscience 2020, 10, 368. [Google Scholar] [CrossRef]
- Hanes, D.M.; Inman, D.L. Experimental evaluation of a dynamic yield criterion for granular fluid flows. J. Geophys. Res. Solid Earth. 1985, 90, 3670. [Google Scholar] [CrossRef]
- Madsen, O.S.; Grant, W.D. Mechanics of cohesionless sediment transport in coastal waters. In Coastal Sediments; ASCE: New York, NY, USA, 1991. [Google Scholar]
- Nino, Y.; Garcia, M. Using Lagrangian particle saltation observations for bedload sediment transport modelling. Hydrol. Process. 1998, 12, 1197–1218. [Google Scholar] [CrossRef]
- Zanke, U. Neuer Ansatz zur Berechnung des Transportbeginns von Sedimenten unter Strömungseinfluss (New Approach for the Calculation of the Beginning of Sediment Transport under the Influence of Flows); Mitt. des Franzius-Instituts der Univ.: Hannover, Germany, 1977; Heft 46. (In German) [Google Scholar]
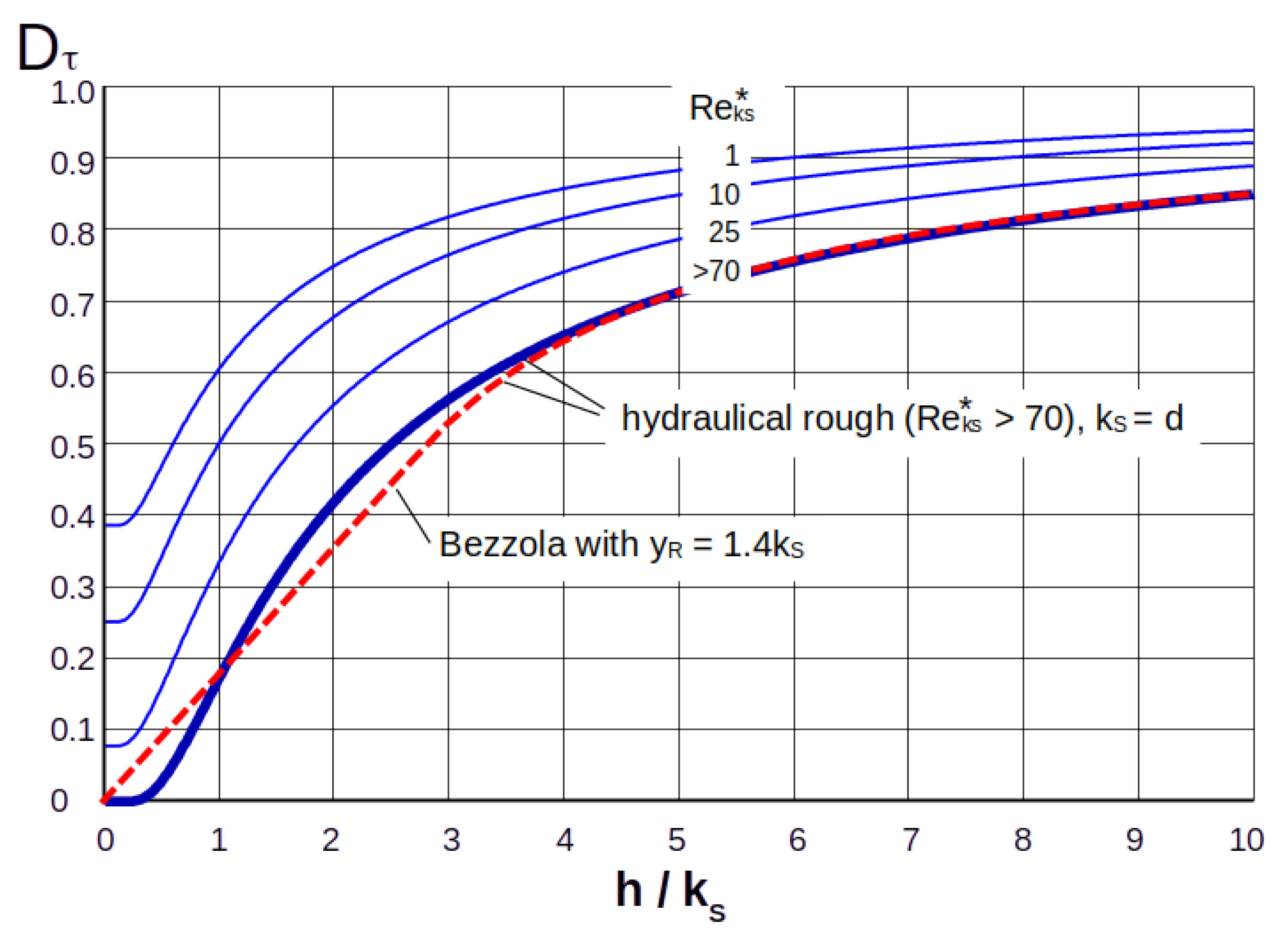
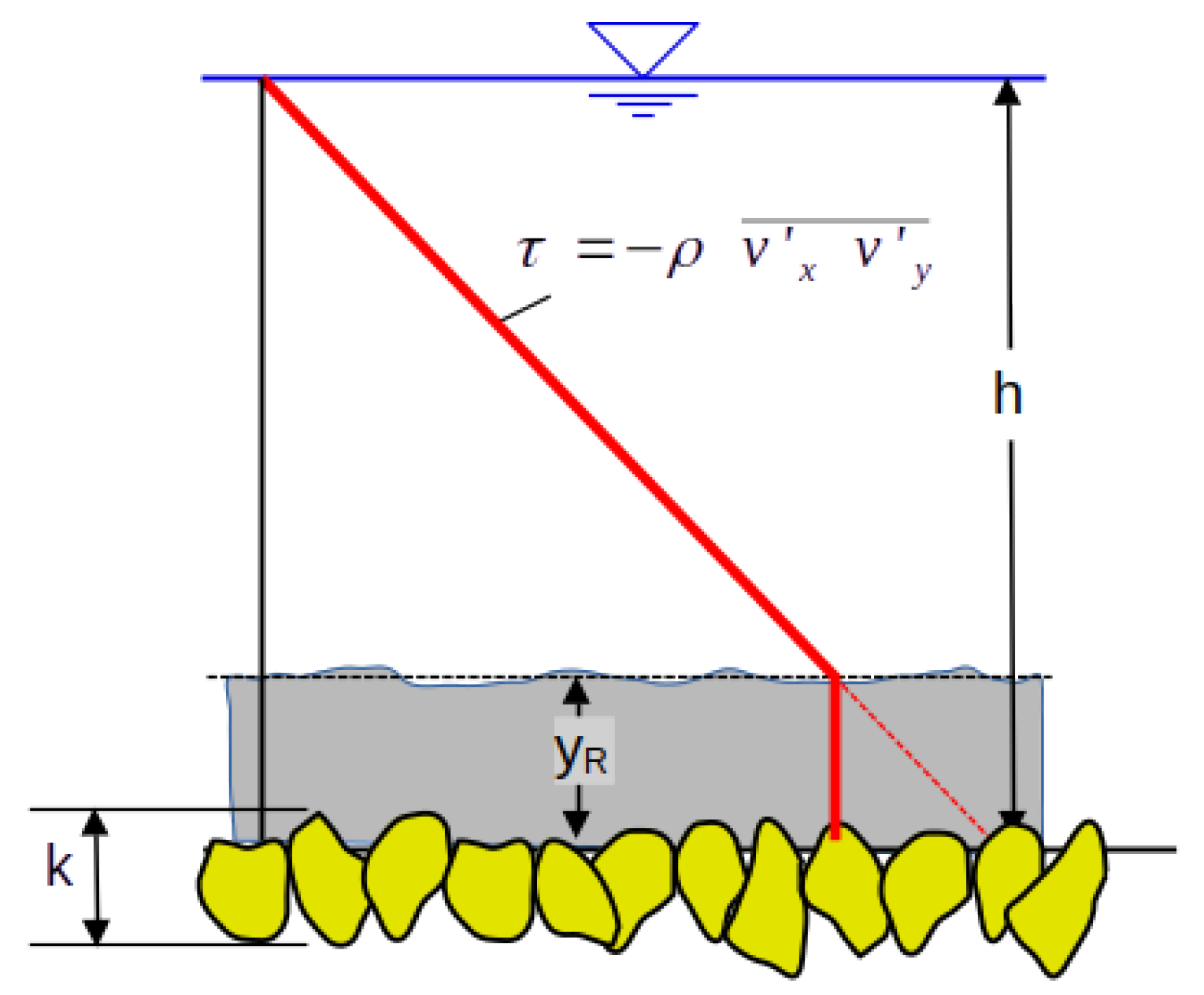
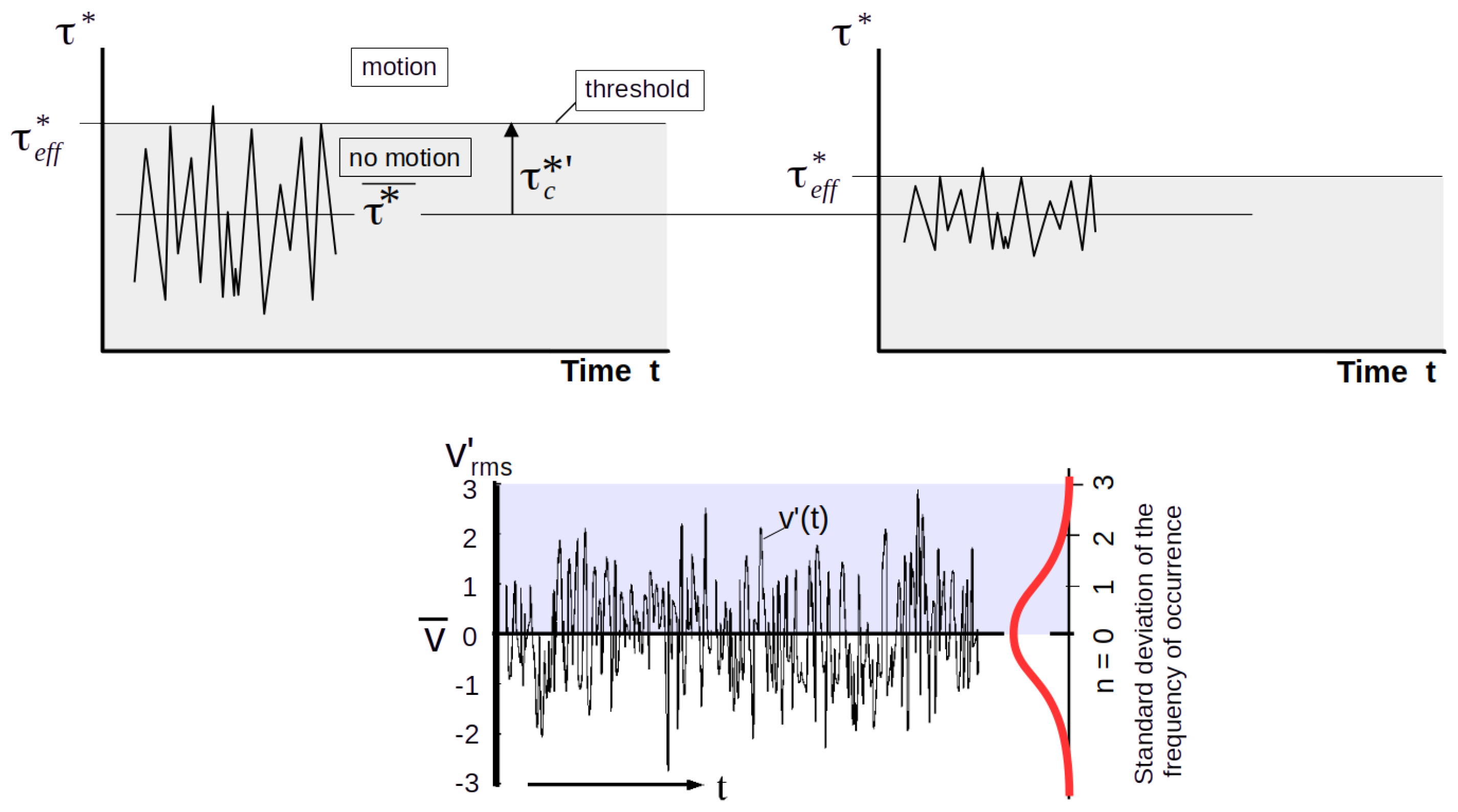
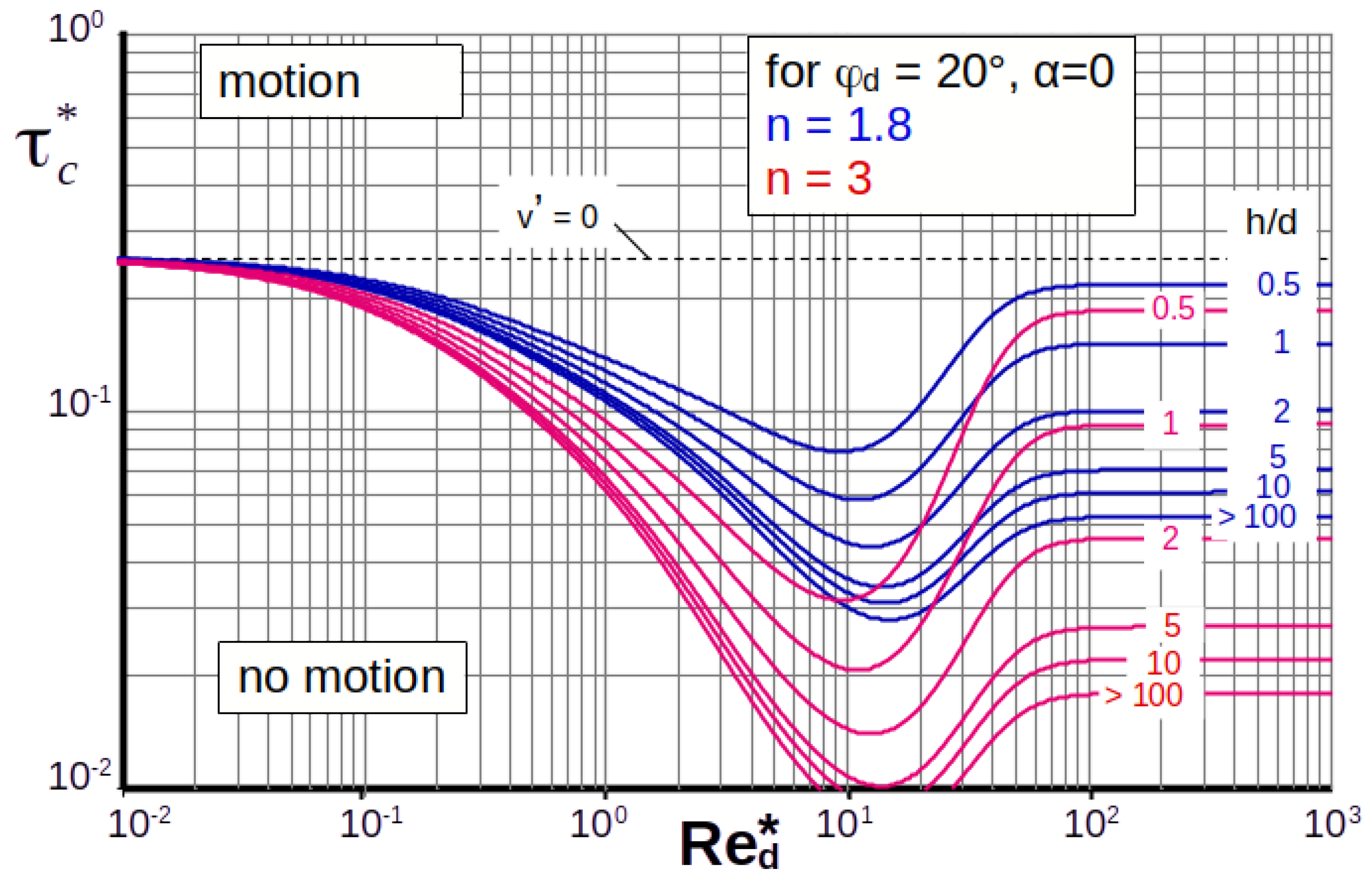
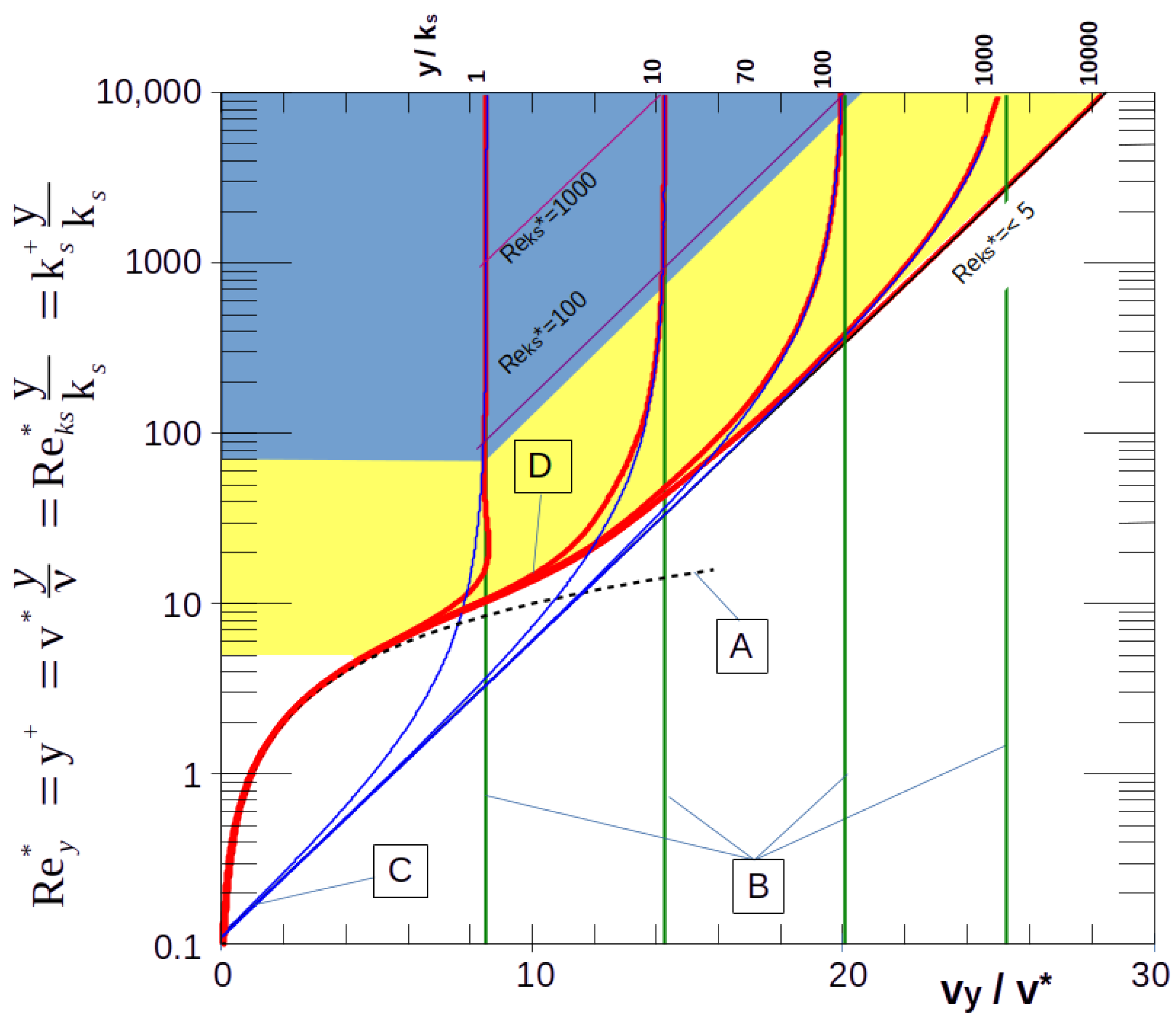
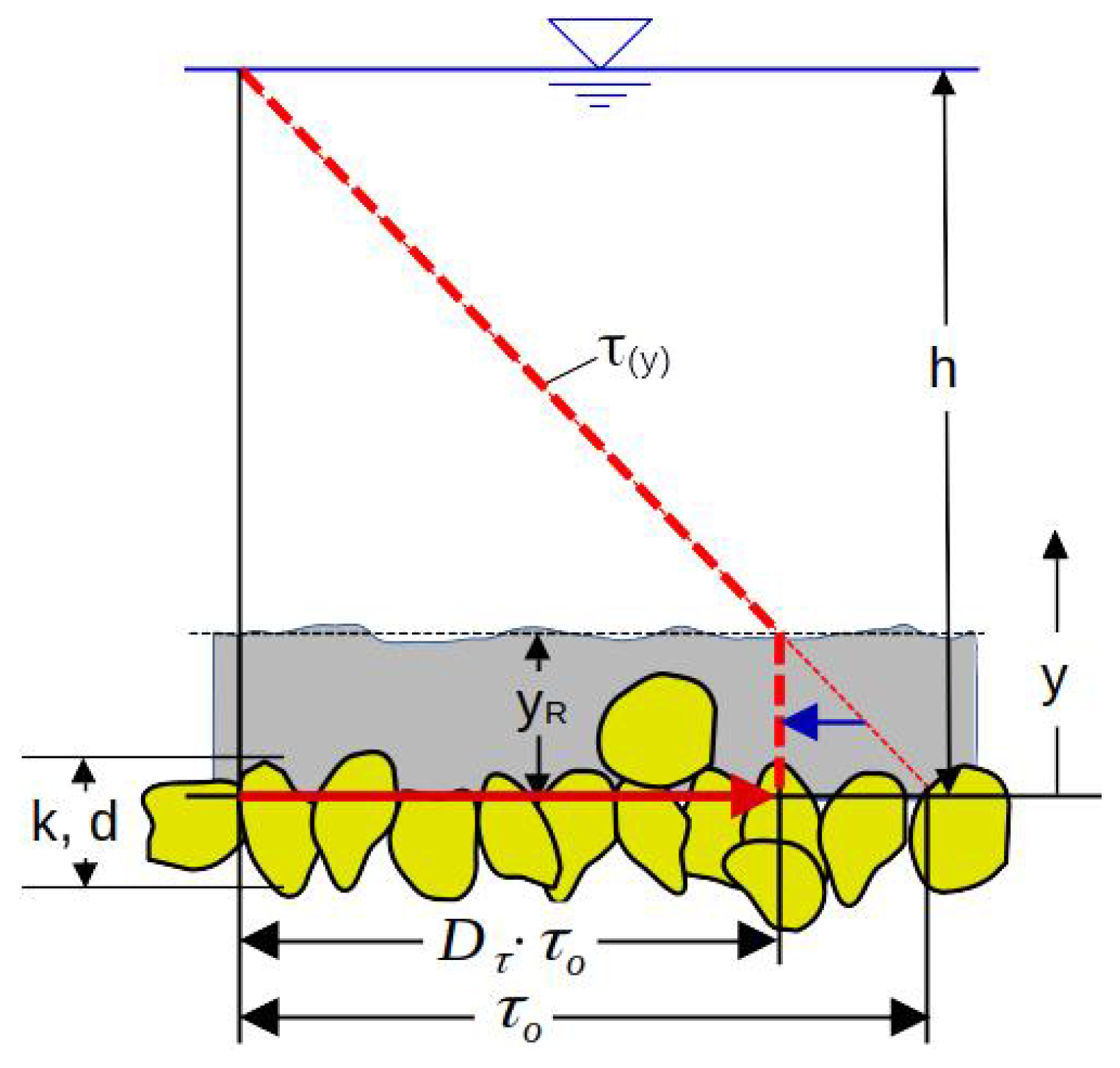
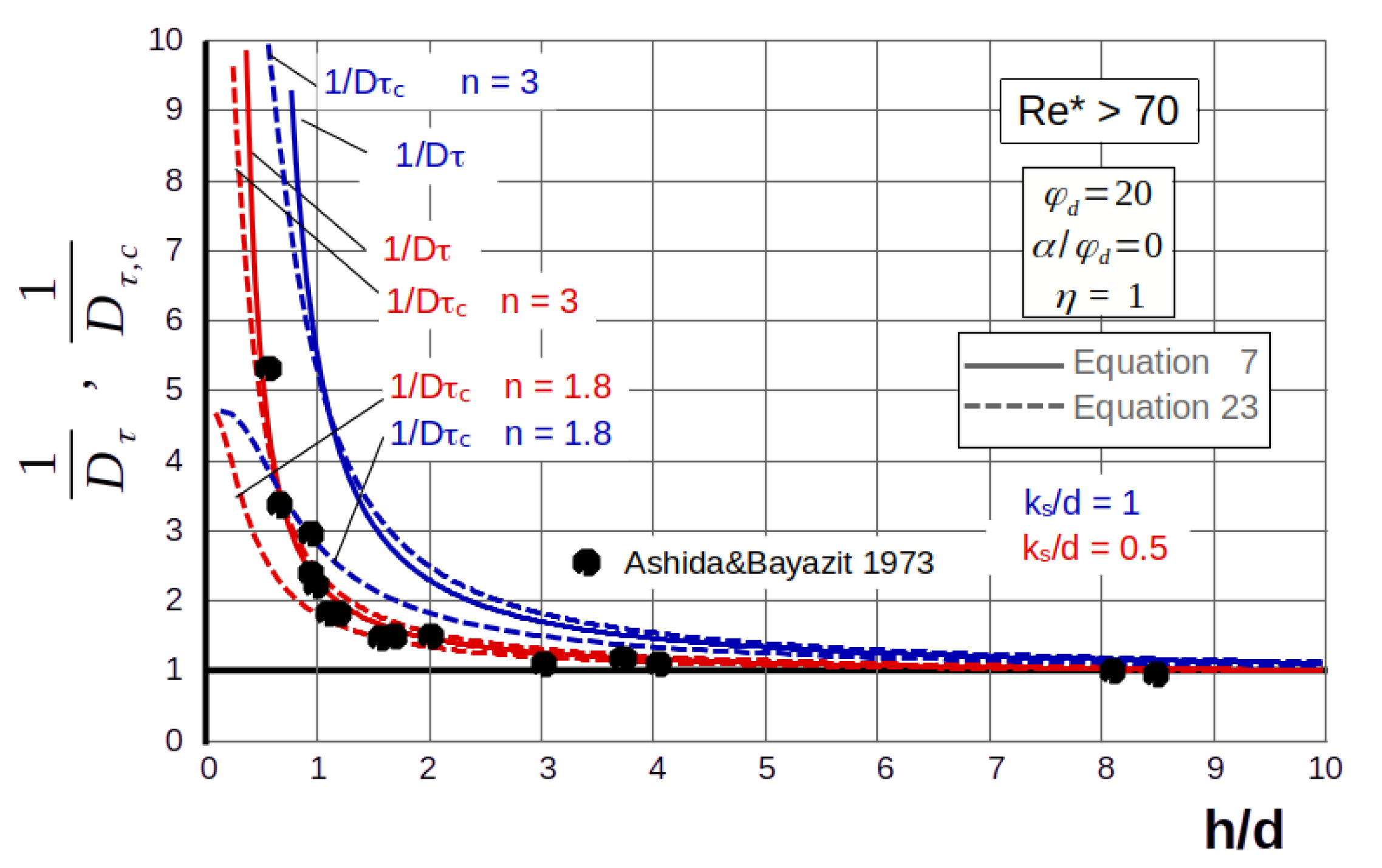
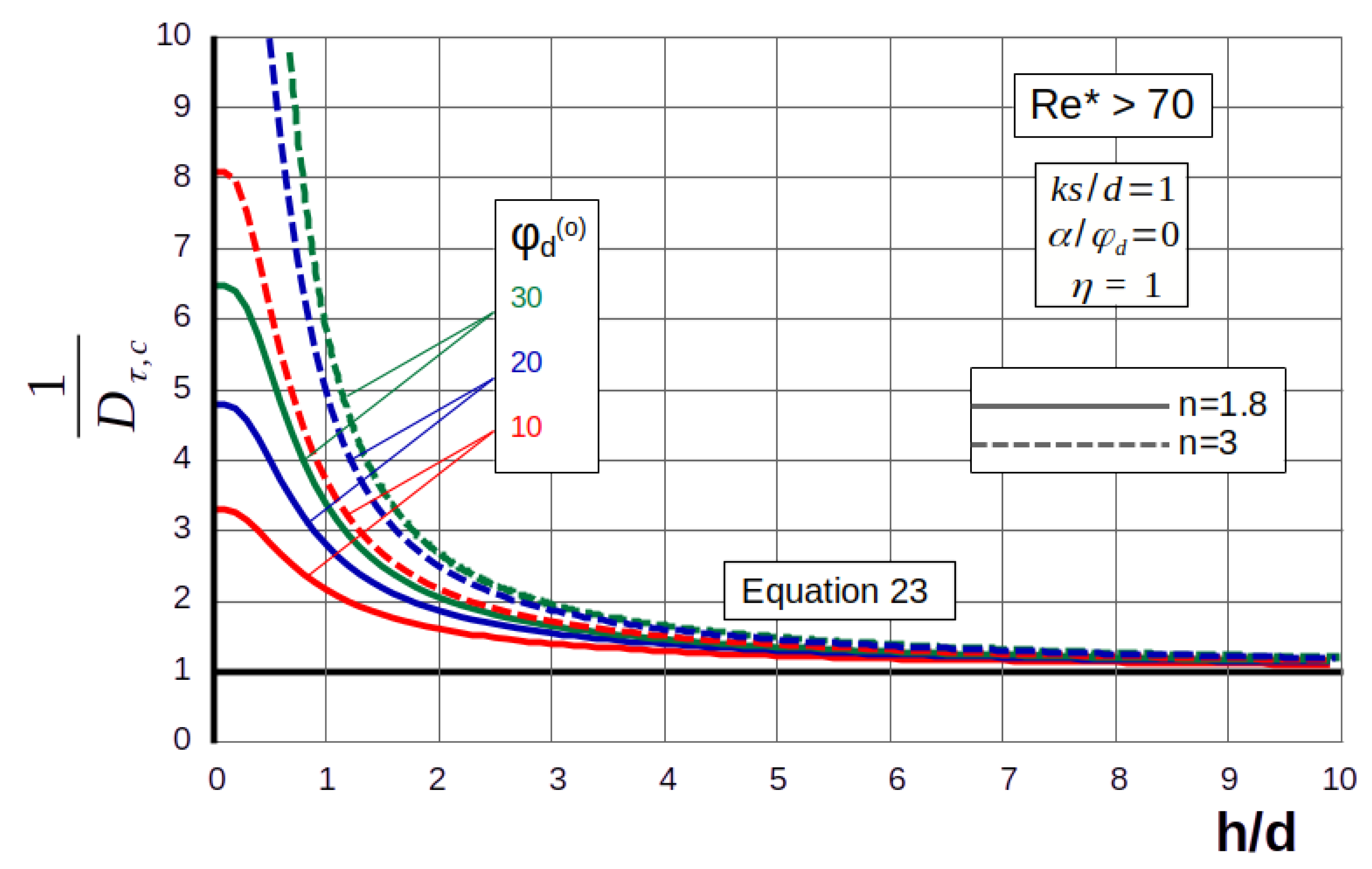

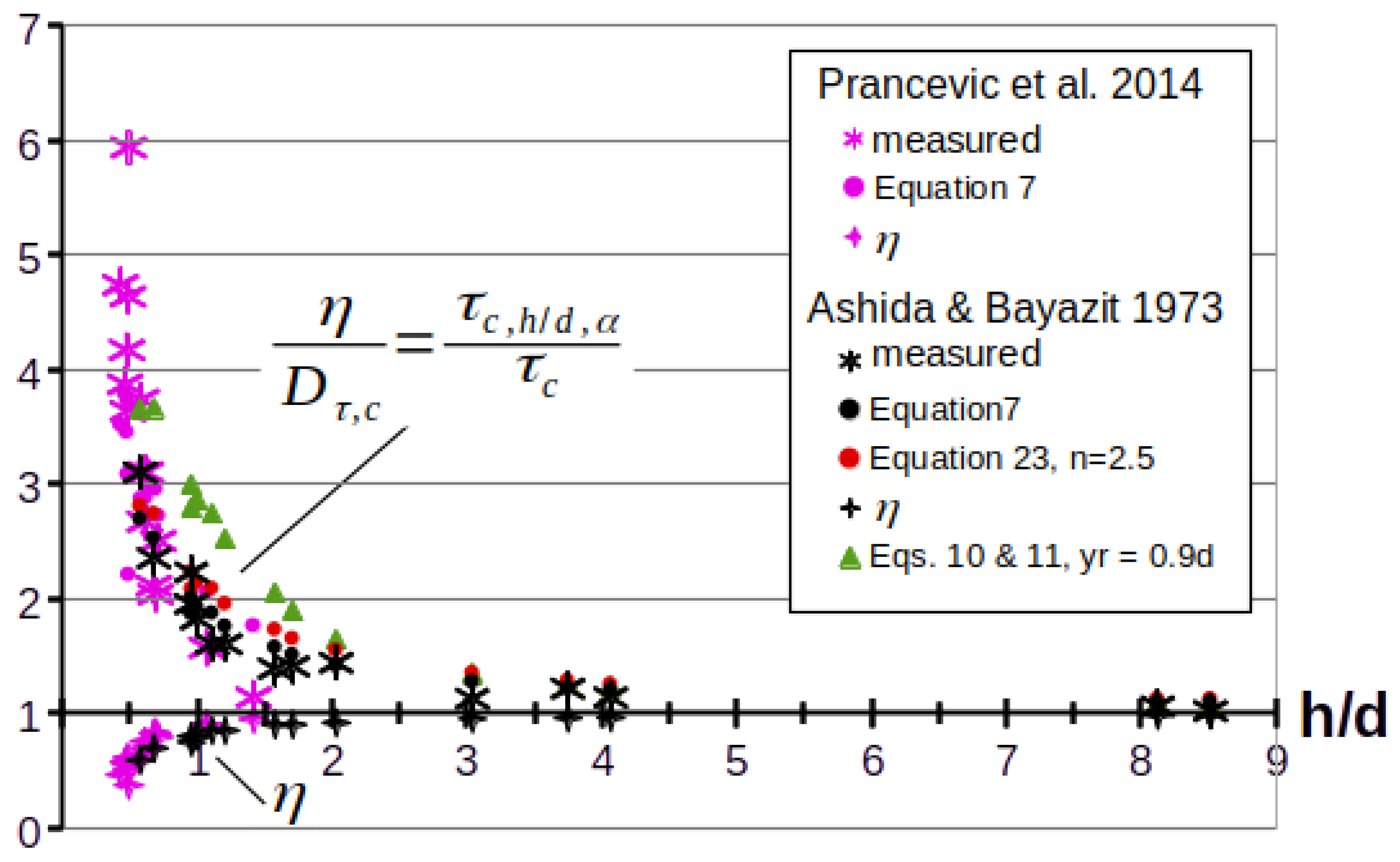
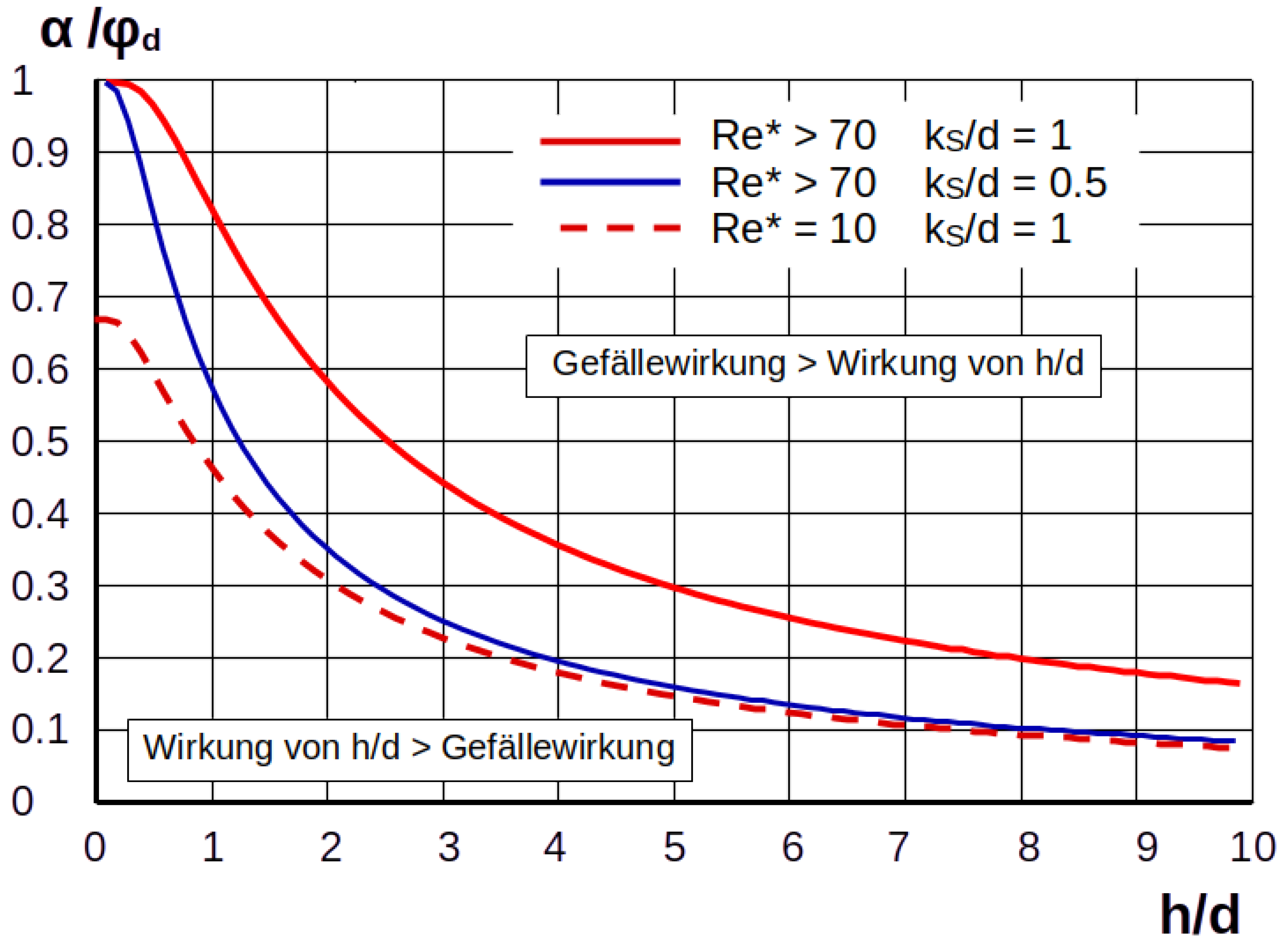
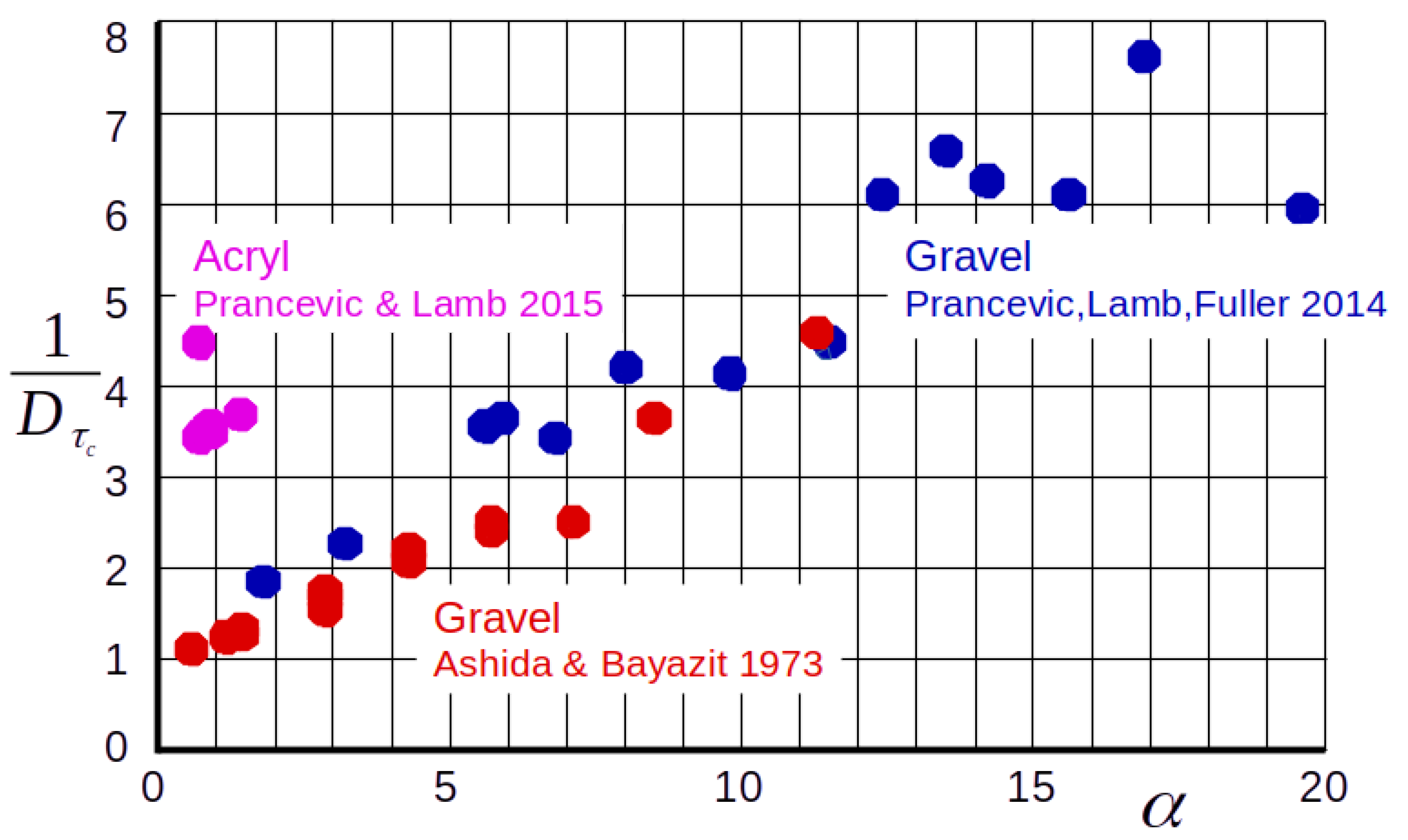
| Lowland Rivers | Mountain Streams | |
|---|---|---|
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nr. | Author | h | d | h/d | P/J | ||||||||||||
| - | o | o | - | m | m | - | - | - | - | - | - | o | - | - | - | - | |
| 1 | Ashida | 1.15 | 45.0 | 0.959 | 0.091 | 0.0225 | 1.65 | 4.07 | 1.182 | 1.134 | 0.0431 | 0.038 | 26.5 | 0.043 | 1.2416 | 1.191 | 1.051 |
| 2 | & | 2.86 | 45.0 | 0.899 | 0.036 | 0.0225 | 1.65 | 1.58 | 1.542 | 1.385 | 0.0527 | 0.038 | 26.5 | 0.108 | 1.7467 | 1.570 | 1.133 |
| 3 | Bayazit | 4.30 | 45.0 | 0.847 | 0.025 | 0.0225 | 1.65 | 1.11 | 1.891 | 1.601 | 0.0607 | 0.038 | 26.5 | 0.162 | 2.2078 | 1.869 | 1.168 |
| 4 | [2] | 5.70 | 45.0 | 0.796 | 0.022 | 0.0225 | 1.65 | 0.96 | 2.451 | 1.950 | 0.0743 | 0.038 | 26.5 | 0.215 | 2.5116 | 1.998 | 1.025 |
| 5 | “ | 8.50 | 45.0 | 0.692 | 0.015 | 0.0225 | 1.65 | 0.68 | 3.395 | 2.350 | 0.0894 | 0.038 | 26.5 | 0.321 | 3.6478 | 2.525 | 1.074 |
| 6 | “ | 11.30 | 45.0 | 0.587 | 0.013 | 0.0225 | 1.65 | 0.58 | 5.279 | 3.099 | 0.1178 | 0.038 | 26.5 | 0.427 | 4.5863 | 2.693 | 0.869 |
| 7 | “ | 0.57 | 45.0 | 0.980 | 0.097 | 0.0125 | 1.65 | 8.15 | 1.079 | 1.057 | 0.0402 | 0.038 | 26.5 | 0.022 | 1.1144 | 1.092 | 1.033 |
| 8 | “ | 1.43 | 45.0 | 0.950 | 0.036 | 0.0125 | 1.65 | 3.04 | 1.183 | 1.124 | 0.0427 | 0.038 | 26.5 | 0.054 | 1.3355 | 1.268 | 1.129 |
| 9 | “ | 2.86 | 45.0 | 0.899 | 0.020 | 0.0125 | 1.65 | 1.71 | 1.565 | 1.406 | 0.0535 | 0.038 | 26.5 | 0.108 | 1.6738 | 1.504 | 1.070 |
| 10 | “ | 4.30 | 45.0 | 0.847 | 0.014 | 0.0125 | 1.65 | 1.21 | 1.891 | 1.601 | 0.0608 | 0.038 | 26.5 | 0.162 | 2.0715 | 1.754 | 1.095 |
| 11 | “ | 5.70 | 45.0 | 0.796 | 0.012 | 0.0125 | 1.65 | 1.00 | 2.283 | 1.816 | 0.0691 | 0.038 | 26.5 | 0.215 | 2.4109 | 1.918 | 1.056 |
| 12 | “ | 7.10 | 45.0 | 0.744 | 0.011 | 0.0125 | 1.65 | 0.96 | 2.993 | 2.227 | 0.0846 | 0.038 | 26.5 | 0.268 | 2.5049 | 1.864 | 0.837 |
| 13 | “ | 0.57 | 52.0 | 0.983 | 0.054 | 0.0064 | 1.65 | 8.00 | 1.033 | 1.016 | 0.0386 | 0.038 | 30.6 | 0.019 | 1.1089 | 1.090 | 1.073 |
| 14 | “ | 1.43 | 52.0 | 0.957 | 0.024 | 0.0064 | 1.65 | 3.75 | 1.265 | 1.211 | 0.0461 | 0.038 | 30.6 | 0.047 | 1.2645 | 1.211 | 1.000 |
| 15 | “ | 2.86 | 52.0 | 0.914 | 0.013 | 0.0064 | 1.65 | 2.03 | 1.571 | 1.437 | 0.0536 | 0.038 | 30.6 | 0.094 | 1.5422 | 1.410 | 0.981 |
| 16 | Prancevic | 1.8 | 45.6 | 0.946 | 0.021 | 0.015 | 1.65 | 1.420 | 1.198 | 1.133 | 0.034 | 0.030 | 30.4 | 0.059 | 1.8584 | 1.758 | 1.551 |
| 17 | & | 3.2 | 45.6 | 0.903 | 0.016 | 0.015 | 1.65 | 1.073 | 1.734 | 1.567 | 0.047 | 0.030 | 30.4 | 0.105 | 2.2702 | 2.051 | 1.309 |
| 18 | Lamb | 5.6 | 45.6 | 0.829 | 0.010 | 0.015 | 1.65 | 0.693 | 2.453 | 2.033 | 0.061 | 0.030 | 30.4 | 0.184 | 3.5581 | 2.949 | 1.450 |
| 19 | & | 5.9 | 45.6 | 0.819 | 0.010 | 0.015 | 1.65 | 0.680 | 2.571 | 2.107 | 0.063 | 0.030 | 30.4 | 0.194 | 3.6478 | 2.989 | 1.419 |
| 20 | Fuller | 6.8 | 45.6 | 0.791 | 0.011 | 0.015 | 1.65 | 0.713 | 3.160 | 2.500 | 0.075 | 0.030 | 30.4 | 0.224 | 3.4337 | 2.717 | 1.087 |
| 21 | [8] | 8.0 | 45.6 | 0.753 | 0.009 | 0.015 | 1.65 | 0.613 | 3.541 | 2.667 | 0.080 | 0.030 | 30.4 | 0.263 | 4.1987 | 3.162 | 1.186 |
| 22 | [32] | 9.8 | 45.6 | 0.695 | 0.009 | 0.015 | 1.65 | 0.620 | 4.459 | 3.100 | 0.093 | 0.030 | 30.4 | 0.322 | 4.1345 | 2.875 | 0.927 |
| 23 | “ | 11.5 | 45.6 | 0.640 | 0.009 | 0.015 | 1.65 | 0.587 | 5.832 | 3.733 | 0.113 | 0.030 | 30.4 | 0.378 | 4.4817 | 2.869 | 0.768 |
| 24 | “ | 12.4 | 45.6 | 0.611 | 0.007 | 0.015 | 1.65 | 0.487 | 5.950 | 3.633 | 0.109 | 0.030 | 30.4 | 0.408 | 6.0996 | 3.725 | 1.025 |
| 25 | “ | 13.5 | 45.6 | 0.574 | 0.007 | 0.015 | 1.65 | 0.467 | 6.731 | 3.867 | 0.116 | 0.030 | 30.4 | 0.444 | 6.5911 | 3.786 | 0.979 |
| 26 | “ | 14.2 | 45.6 | 0.551 | 0.007 | 0.015 | 1.65 | 0.480 | 7.557 | 4.167 | 0.125 | 0.030 | 30.4 | 0.467 | 6.2547 | 3.448 | 0.828 |
| 27 | “ | 15.6 | 45.6 | 0.505 | 0.007 | 0.015 | 1.65 | 0.487 | 9.179 | 4.633 | 0.139 | 0.030 | 30.4 | 0.513 | 6.0996 | 3.079 | 0.665 |
| 28 | “ | 16.9 | 45.6 | 0.461 | 0.006 | 0.015 | 1.65 | 0.433 | 10.260 | 4.733 | 0.141 | 0.030 | 30.4 | 0.556 | 7.6199 | 3.515 | 0.743 |
| 29 | “ | 19.6 | 45.6 | 0.370 | 0.007 | 0.015 | 1.65 | 0.493 | 16.023 | 5.933 | 0.178 | 0.030 | 30.4 | 0.645 | 5.9523 | 2.204 | 0.371 |
| 30 | Prancevic | 0.7 | - | - | 0.0164 | 0.023 | 0.15 | 0.714 | - | - | 0.058 | - | - | - | 3.4354 | - | - |
| 31 | & | 0.9 | - | - | 0.0162 | 0.023 | 0.15 | 0.704 | - | - | 0.074 | - | - | - | 3.4882 | - | - |
| 32 | Lamb | 1.4 | - | - | 0.0155 | 0.023 | 0.15 | 0.676 | - | - | 0.110 | - | - | - | 3.6907 | - | - |
| 33 | [10] | 0.7 | - | - | 0.0135 | 0.023 | 0.15 | 0.588 | - | - | 0.048 | - | - | - | 4.4784 | - | - |
| 34 | 0.9 | - | - | 0.0159 | 0.023 | 0.15 | 0.690 | - | - | 0.072 | - | - | - | 3.5714 | - | - | |
| 35 | 1.4 | - | - | 0.0155 | 0.023 | 0.15 | 0.676 | - | - | 0.110 | - | - | - | 3.6907 | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zanke, U.; Roland, A.; Wurpts, A. The Reason for the Rise in Critical Shear Stress on Sloping Beds. Water 2023, 15, 2976. https://doi.org/10.3390/w15162976
Zanke U, Roland A, Wurpts A. The Reason for the Rise in Critical Shear Stress on Sloping Beds. Water. 2023; 15(16):2976. https://doi.org/10.3390/w15162976
Chicago/Turabian StyleZanke, Ulrich, Aron Roland, and Andreas Wurpts. 2023. "The Reason for the Rise in Critical Shear Stress on Sloping Beds" Water 15, no. 16: 2976. https://doi.org/10.3390/w15162976
APA StyleZanke, U., Roland, A., & Wurpts, A. (2023). The Reason for the Rise in Critical Shear Stress on Sloping Beds. Water, 15(16), 2976. https://doi.org/10.3390/w15162976






