1. Introduction
River flow forecasting is used in water resources management to address climate uncertainty, as well as in water use management, including hydropower, water supply, irrigation, shipping, flood control, and environmental protection, depending on the amount of water in river systems [
1]. A difficult area in operational hydrology is the forecasting of floods due to the melting of snow and ice in rivers in spring due to heavy precipitation and wave events in areas along river mouths [
2]. Forecasting can be performed both over short-term (from several hours to several days) and long-term (up to nine months) periods.
The main goal of hydrological forecasting is to provide the longest possible forecast with sufficient accuracy. In this case, users will be able to take the necessary optimization measures to prevent or reduce damage [
3].
The basic research and engineering tool in modern hydrology is the mathematical modeling of river runoff formation processes. In a broad sense, the term “mathematical modeling of hydrological systems” can be understood as the use of mathematics to describe the characteristic features of hydrological systems or processes. Therefore, any use of a mathematical equation to determine relationships between hydrological variables or to represent the temporal or spatial structure of a single variable can be called mathematical modeling (WMO, 2012) [
3]. The basic principle of modeling is driven by the ability to reproduce and predict the behavior of a complex object or system using a simpler and/or more flexible model (WMO, 2012) [
3]. In this work, the authors used the HBV-light conceptual model to simulate runoff. Such conceptual models include solving systems of equations based on various concepts of describing the physical processes of runoff formation. Most of the conceptual models are used in operational hydrological forecasting (WMO-No. 429). The HBV model is included in the WMO Hydrological Operational Multipurpose System (HOMS).
The HBV model has been widely applied in many areas: weir design, water resource assessment, nutrient stock assessment, and climate change studies (WMO, 2012) [
3]. In the territory of the Republic of Kazakhstan, it has been applied in the works of domestic researchers [
4,
5,
6,
7] for modeling and predicting the flow of mountain rivers.
Providing clean drinking water is a paramount strategic task, the solution of which directly affects the improvement in the quality of life of the population. Today, 97.2% of the cities and 86.4% of the villages in the Republic of Kazakhstan (RK) have access to a centralized water supply [
8]. Improving water management methods for optimizing water use, as well as protecting the population and economic facilities from floods, to a large extent depends on the possibility of improving the accuracy and timeliness of long-term forecasts of water inflow characteristics in reservoirs. In particular, the strengthening of requirements for the economic efficiency and safety of operation of hydraulic structures necessitates the involvement of additional, in addition to the existing, sources of prognostic information on the characteristics of the water regime [
9].
The steppe landscapes of Northern Kazakhstan are dominated by rivers of the Kazakh type, which are characterized by significant volumes of runoff only in the spring. The rest of the time, river flow may be minimal or absent altogether. In some years, the volume of spring floods can acquire a significant scale, which leads to economic damage to the national economy [
10].
Recently, important efforts are being undertaken to apply mathematical modeling techniques to describe the water management systems in Central Asia both in terms of water quality characteristics and resource availability [
11,
12,
13,
14,
15,
16,
17,
18]
The main purpose of this work, being its main contribution, is to simulate the water inflow into the Astana reservoir using the HBV-light model for further use in river flow forecasting. The research described in this paper is a prior contribution about this topic, providing a better understanding of the patterns of spring flood formation in the rivers under study.
2. Materials and Methods
The HBV model [
19], developed by Bergström at the Swedish Meteorological and Hydrological Institute, is a conceptual watershed model that converts precipitation, air temperature, and potential evapotranspiration into either snowmelt, runoff, or inflow into a reservoir. The model has been modified many times and different versions exist in many countries. In this study, the HBV light 2.0 version was used. The model describes the overall balance of the river as shown in Equation (1):
where P is precipitation; E—total evaporation; Q—drain; SP—snow cover; SM is soil moisture; UZ—upper groundwater zone; LZ is the lower groundwater zone; and VL is the volume of lakes.
The catchment basin is divided into private catchment areas, and it is also possible to use the altitudinal zoning method. Due to this, the HBV model can be considered as a model with semi-distributed parameters. An additional division into altitudinal zones is provided for watersheds of a certain altitudinal position. Each altitudinal zone can be subdivided into subzones according to vegetation type, such as forest and non-forest areas.
The HBV model is used to fill in gaps in runoff data series, to control data quality, to study water balance, to calculate design floods, to ensure dam safety, to study the effects of changes in runoff in a watershed, and to predict runoff [
20]. The schematic structure of the HBV model has been described by Wilk et al. [
21].
The HBV model can be viewed as a model with semi-distributed parameters; for the watershed, the altitudinal zoning method is used. This model includes routines for meteorological interpolation, calculation of snow accumulation and snowmelt, evapotranspiration, soil moisture, and runoff generalization to calculate the transformation of water movement along rivers and through lakes.
Table 1 shows the parameters used in runoff simulation (
Table 1).
The necessary input information for the model is the amount of precipitation (daily totals), air temperature (daily averages), and estimates of possible evapotranspiration. The standard model operates on the basis of monthly data on long-term averaged potential evapotranspiration, usually based on the Penman formula corrected for temperature anomalies [
22]. But in this work, the formula of N.I. Ivanov [
23] was used (Equation (2)), since there were no input data for calculating evaporation using the Penman formula:
where
T is the average monthly temperature;
r is the average monthly relative air humidity. Alternatively, daily values can be calculated as proportional to the air temperature, but with proportionality factors for monthly values. Later versions of the HBV model can work with higher temporal resolution data, i.e., hourly data.
The HBV model, when assessing the correspondence between the simulated runoff and the observed runoff, uses the generally accepted Nash–Sutcliffe (NSE) efficiency criterion (Equation (3)) [
24], called
Reff in the model [
25]
where
Qobs is the water discharge measured at the hydrological station;
Qsim is the water flow calculated using the model.
Symbols are used to interpret the obtained data. If Reff > 0.5, then the model reproduces well the dynamics of the modeled value. When the value of Reff = 1, then the model calculation is recognized as fully adequate. While Reff < 0 means that the model is considered invalid.
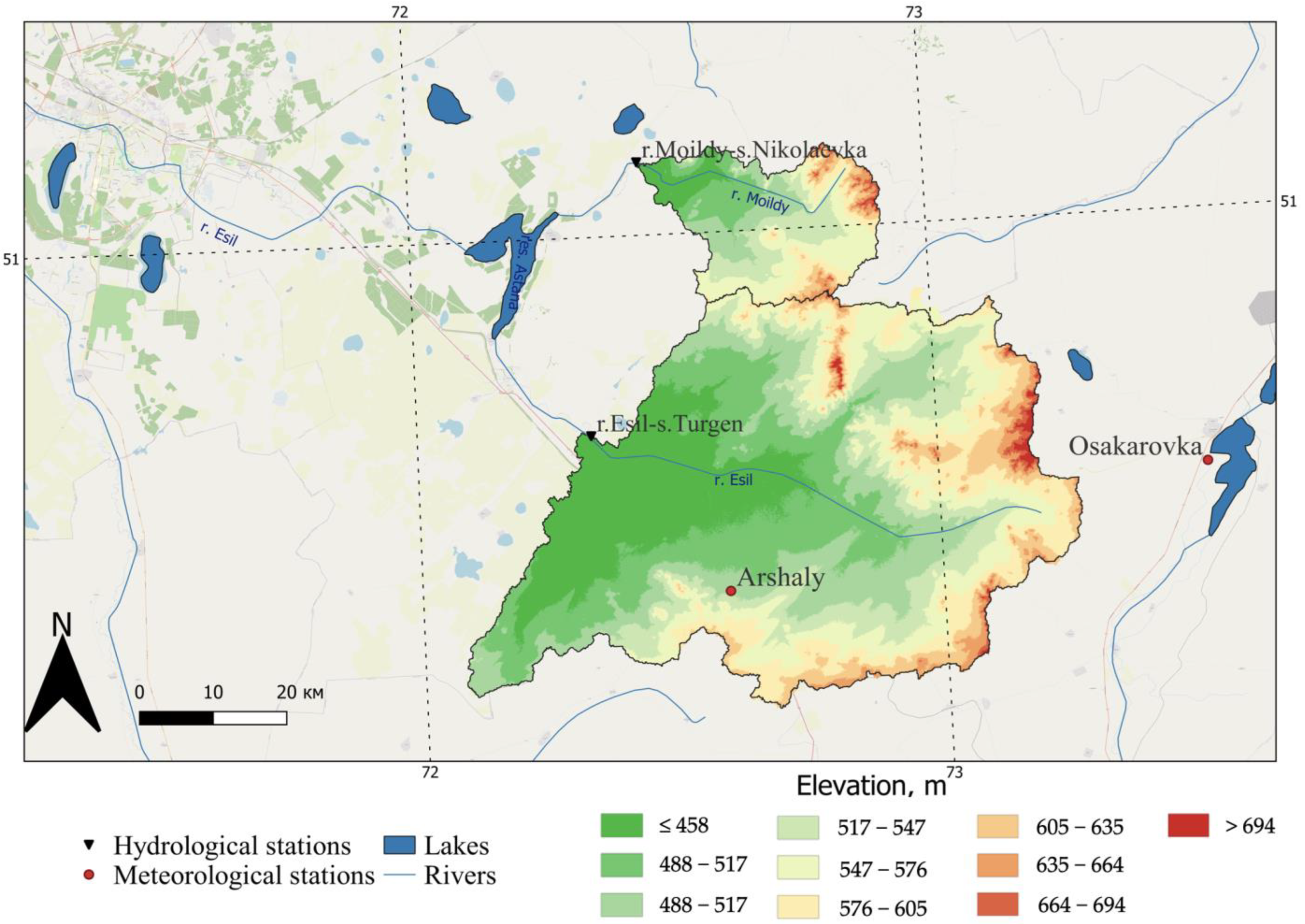
For the altitudinal analysis of the basins, three-dimensional images of the SRTM (Shuttle Radar Topography Mission) were used. The subsequent processing of a three-dimensional image is performed in the ESRI ArcGIS Desktop modules. Based on the SRTM data, a digital elevation model (DEM) was prepared for the Esil River basin at the Turgen station and for the Moildy River basin at the Nikolaevka station with a pixel extension of 30 m × 30 m [
26].
A feature of the regime of lowland rivers is that about 90% of the annual volume of water passes during the spring floods, which is due to the snow supply of the rivers. In this regard, runoff-forming processes begin in autumn, which means the beginning of the hydrological year of rivers. For this reason, the quality criteria were calculated from 1st September.
3. Description of Study Area
In this study, the authors carried out work on adapting the HBV-light conceptual model to forecast the inflow of an object important for the region for household and drinking purposes—the Astana reservoir. The Astana reservoir (area 60.9 km
2, capacity 411 million m
3) is a hydrotechnical infrastructure of long-term regulation, located on the Esil River and, among other things, provides drinking water to the capital of the Republic of Kazakhstan, Astana (
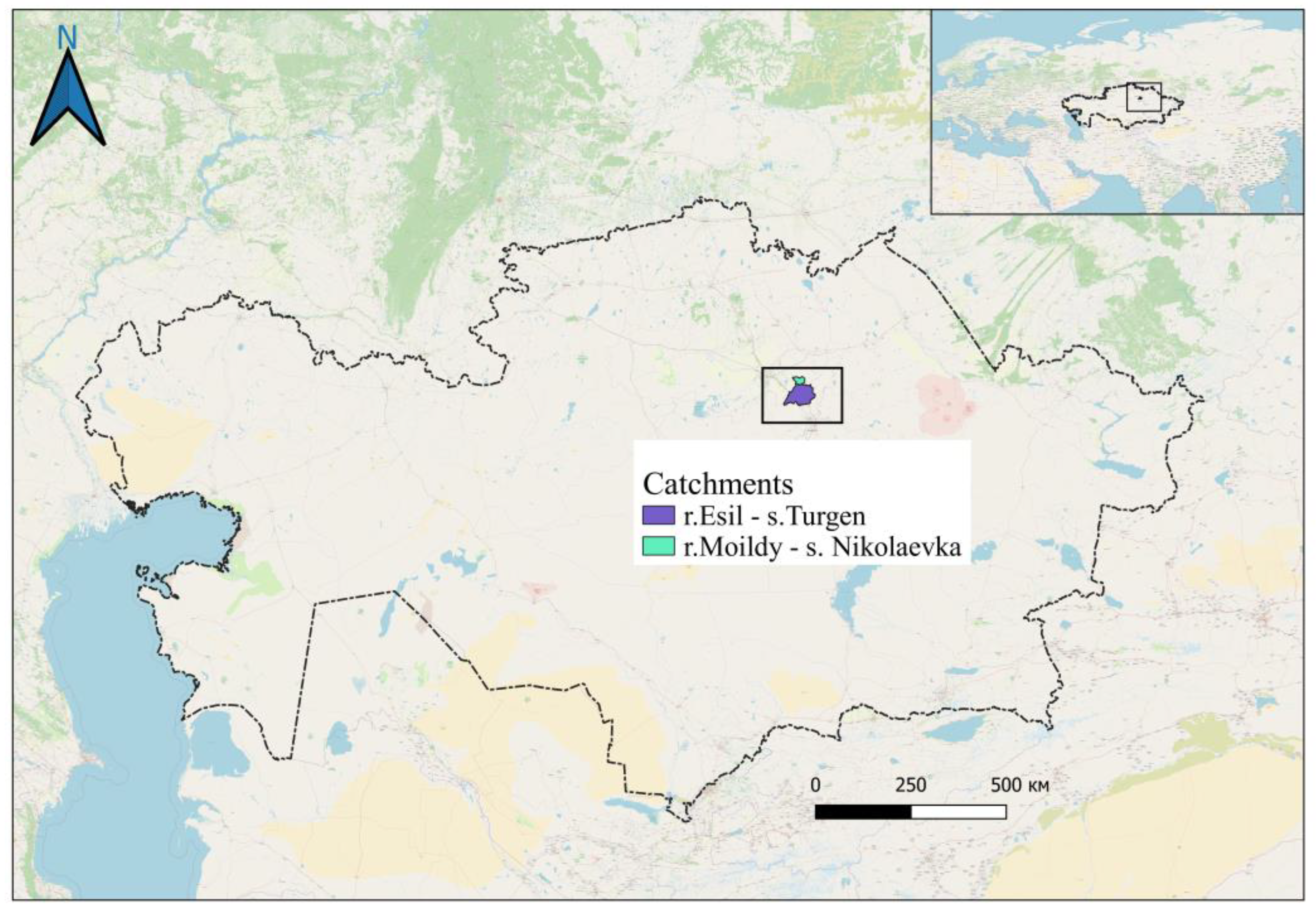
Figure 1). The main tributaries to the reservoir are the Esil and Moildy rivers.
The Esil River originates from springs in the Niyaz Mountains (the northern outskirts of the Kazakh small hills) in the Karaganda region. It enters the Akmola region 62 km away from the source. The Moildy River originates from the southwestern slopes of the Yereymentau Mountains. The riverbed makes its way among hard bedrocks—quartzites, siliceous shales, and sandstones, which cause frequent drops and rapids. Upon leaving the mountains, the rivers enter the hilly landscape. Here, among the feather-grass steppe with sparse woody vegetation, the river valleys either expand or narrow, squeezed by the bedrock hills approaching from both sides. In the widened parts of the valley, the channel strongly meanders among the alluvial deposits. There, meanders disappear, and the flow is revived due to the increase in slopes. The rivers are riparian [
27].
According to the structure of the surface, the region is a predominantly hilly plain with prevailing elevations of 300–400 m abs., which has a general slope to the west and northwest. Isolated hills and ridges rise above the plain, in some places forming small mountain ranges up to 700–800 m above sea level. The relative heights of the hills for the most part do not exceed 20–40 m, and only in the most elevated parts of the region do they reach 100–200 m or more. The uplands of the small hills have soft, smooth outlines. The steepness of the slopes is 5–10°, only rocks that are especially difficult to destroy (quartzites, etc.) form pointed peaks that stand out sharply against the general background of the flat relief. The tops of individual hills are bare. Most of the hills are covered with rubble-gravel deposits [
27].
Figure 2 shows the location of river catchments, indicating the places of observation of runoff and meteorological characteristics.
The state of the environment of the Republic of Kazakhstan is monitored by the national hydrometeorological service “Kazhydromet”. The data that were used in this work were obtained from the Kazhydromet database [
28].
Instrumental observations of the river runoff began in 1974 (the Esil River—Turgen station) and in 1973 and are still in use today. But on the Moildy River, due to certain problems, observations of the river flow were interrupted in the periods 1984, 1988–1989, 1991, 1994, and 1998–1999. Data for 2020–2022 operational data mean that the data can be corrected when they are entered into the state cadaster’s database. The table below also shows the meteorological stations whose data were used for the simulation. At the Arshaly meteorological station, observations began in 1975. This station was used for both watersheds, but for the Moildy River, the data from the Arshaly station did not give a good result, and therefore the data from the Osakarovka meteorological station were used, in which observations only began in 2008. General information about the observed data is given in
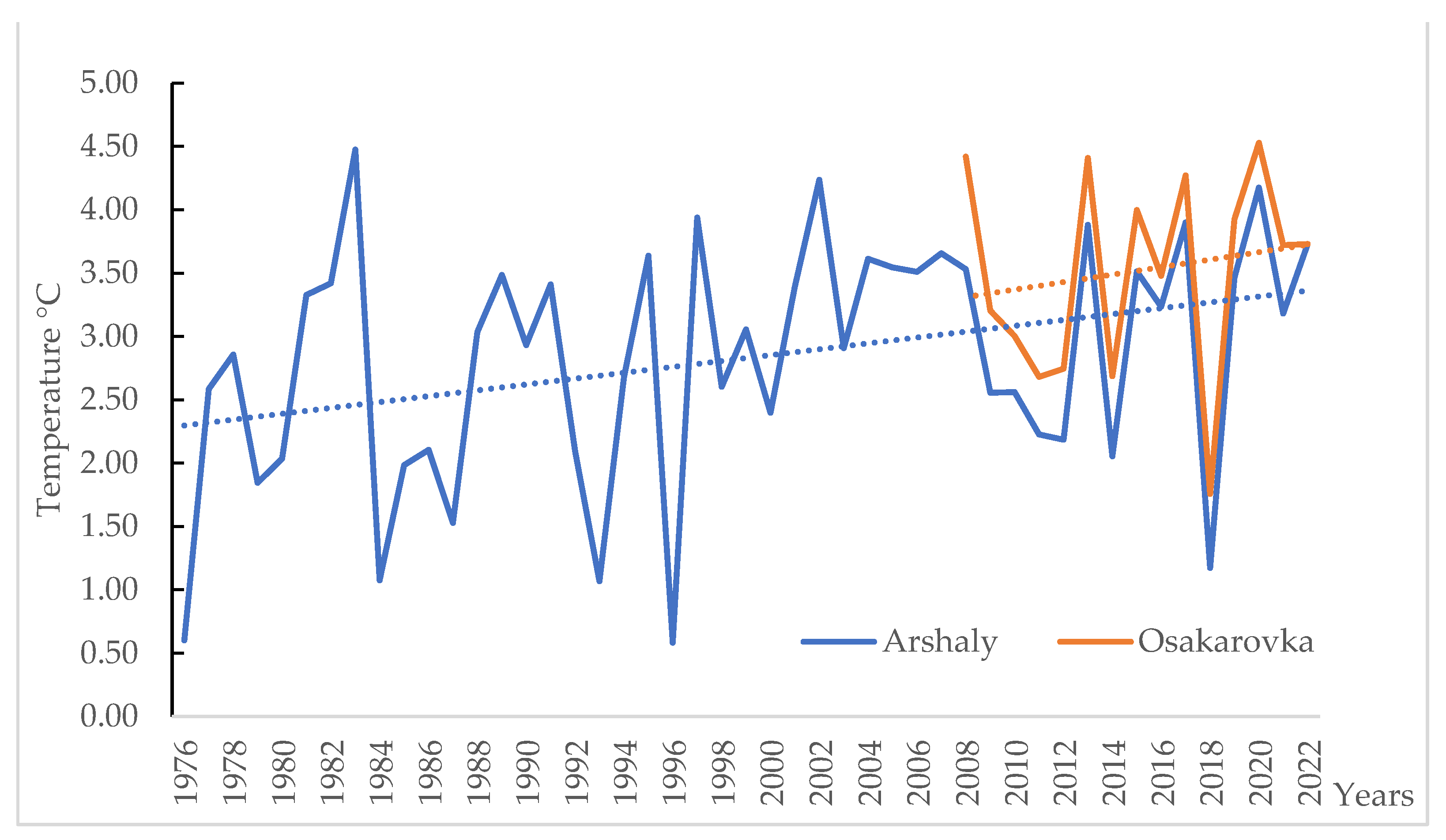
Table 2. The dynamics of the average annual air temperatures observed at the stations show an upward trend, as shown in
Figure 3.
Also, the annual course of temperatures shows synchronous fluctuations. The annual temperature variation until the end of the 1990s shows a greater amplitude and a relatively stable trend than subsequent years, as shown in
Figure 4.
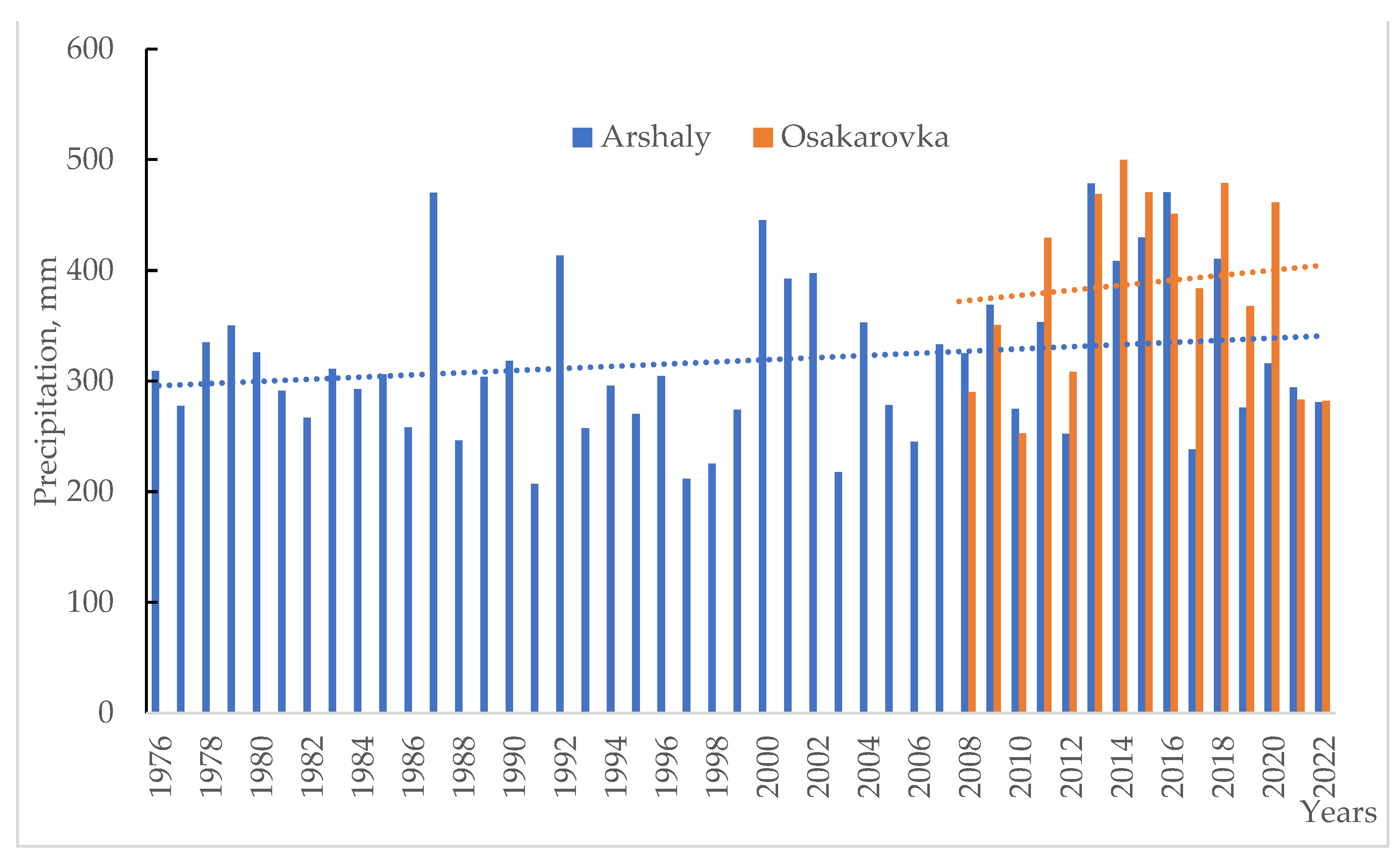
The dynamics of the annual amounts of atmospheric precipitation observed at the Arshaly station since 1976 show a slight increase. The amplitude of the amounts of precipitation at this station is 270 mm. As well as the average annual course of the temperature, the rainfall from both stations shows synchronous fluctuations. Due to the fact that in the period from 2013 to 2020, high amounts of precipitation were observed, the trend from the Osakarovka station shows a significant increase in precipitation but given the synchronism of precipitation from two meteorological stations, we can assume that the trend is also not significant at this station.
4. Model Results
The reliability of the results of the work of hydrological models of the watershed directly depends on the calibration procedure, which is usually the search for one optimal set of parameters for the study area.
The calibration method for the HBV model allows for the use of different criteria. Parameter values are chosen randomly within a given range [
5,
25] and the model is run using these parameters.
The model was calibrated automatically, based on a large number of manual calibrations (10,000 random number generations), during which the corresponding parameter values are changed until the best relationship with the observed data is obtained.
As a result of the calibration of the HBV-light model for the Esil and Moildy rivers, the best sets of parameters were determined, depending on the climatic, hydrological, and geological conditions, which are shown in
Table 3. According to [
19], when modeling the river flow, the calibration period was from 4 to 6 years.
For the warm-up period of the model, the first year of modeling was not taken into account for the final result. Also, as the hydrological year for the selected rivers starts from September, in this regard, the start of modeling was also taken from 1st September.
The parameters of the snow cover (“snow routine”) that are calculated in the HBV-light model include the threshold temperature at which precipitation is classified either as solid precipitation (actual air temperature is below the threshold value) or liquid precipitation (actual air temperature is above the threshold value). The threshold value for the Esil River was −0.92 °C and for the Moildy River, it was 0.06.
All precipitation that forms snow is multiplied by the snowfall correction factor, SFCF, which is equal to 1.19 (Esil) and 0.97 (Moildy). As well as the degree–day factor (CFMAX), which is based on the expected relationship between the ablation and air temperature, this parameter is usually expressed as the sum of positive air temperatures, i.e., the amount of melted ice or snow (mm), in a certain time interval Δt on days with positive temperatures. According to the results of the model calculation, the amount of melted snow in the studied basin is 3.49 mm (Esil) and 7.04 mm (Moildy).
The soil moisture accounting procedure is the main part of runoff control. This procedure is based on three parameters: the maximum soil moisture storage (FC), soil moisture distribution index (BETA), and soil moisture value above which evapotranspiration reaches its potential value (LP). The contribution to runoff from rain or snowmelt is small when the soil is dry and large when the soil is wet. Accordingly, the runoff coefficient depends on the soil moisture [
19]. The maximum amount of soil moisture calculated from the model is 244 mm (Esil) and 97.6 (Moildy). The value of the soil moisture, above which evapotranspiration reaches its potential value in the area under consideration, varies from the minimum to the maximum value, i.e., 0.60 (Esil) and 0.63 (Moildy), and the soil moisture distribution index is 1.85 (Esil) and 2.49 (Moildy).
The following “response routine” routine is a “response” function that converts excess moisture from the wet soil zone to runoff. Excess moisture from the zone of moistened soil accumulates in the so-called “upper reservoir” (upper soil layer). As long as there is moisture in the upper tank, it gradually seeps into the “lower tank” according to the PERC parameter. Thus, the upper soil layer is a drainage through which moisture enters the lower soil layer. In turn, the lower soil layer is a reservoir for storing groundwater in the catchment area, which contributes to the formation of runoff.
The coefficient K1 representing the accumulated runoff in the upper storage zone (SUZ) of moisture is 0.27 (Esil) and 0.15 (Moildy), and the coefficient K2 representing the accumulated runoff in the lower storage zone (SLZ) of moisture is 0.16 (Esil) and 0.09 (Moildy). The maximum rate of water infiltration is 0.78 (Esil) and 0.1 (Moildy) mm/day.
The generated runoff undergoes a transformation procedure to give the hydrograph the correct shape at the outlet of the sub-basin. The transform function is a simple triangular weight-filtering technique. The time base of the triangular distribution is equal to the value specified by the MAXBAS parameter. The MAXBAS parameter is the total daily flow, i = {1, 2,..., maxbas}. The MAXBAS function redistributes the total flow over several days, with a certain amount of precipitation falling on the basin surface affecting the catchment for no more than one day. The considered parameter for the Esil River is 5 days and for the Moildy River, it is 3.79.
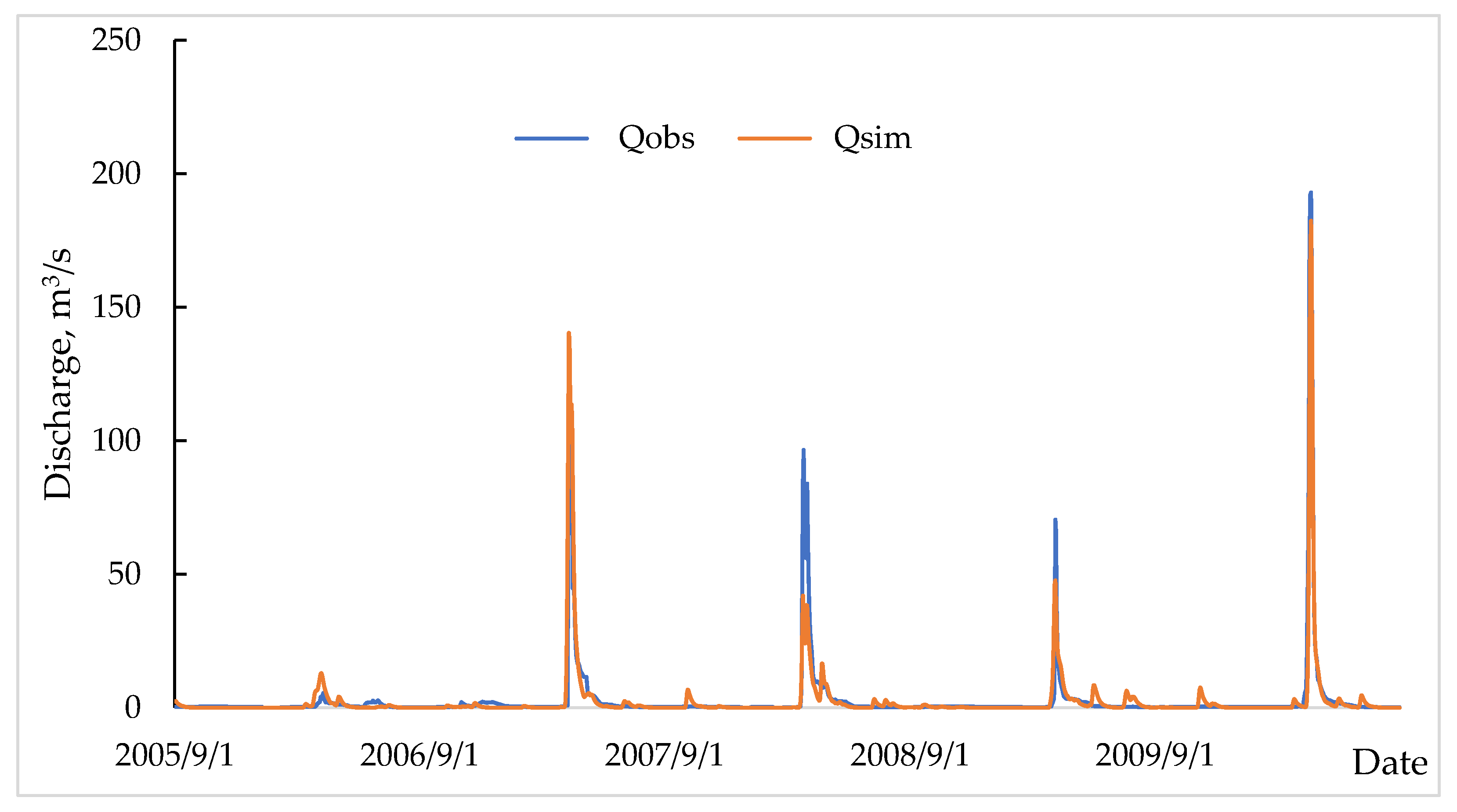
The model was run over the entire observation period from 1975 to 2020. Calibration was carried out over 4–6-year intervals. As a result of the model calibration, the best results for the Esil River were obtained for the period 2005–2010, when the model efficiency calculated by the NSE criterion was 0.85 (
Figure 5).
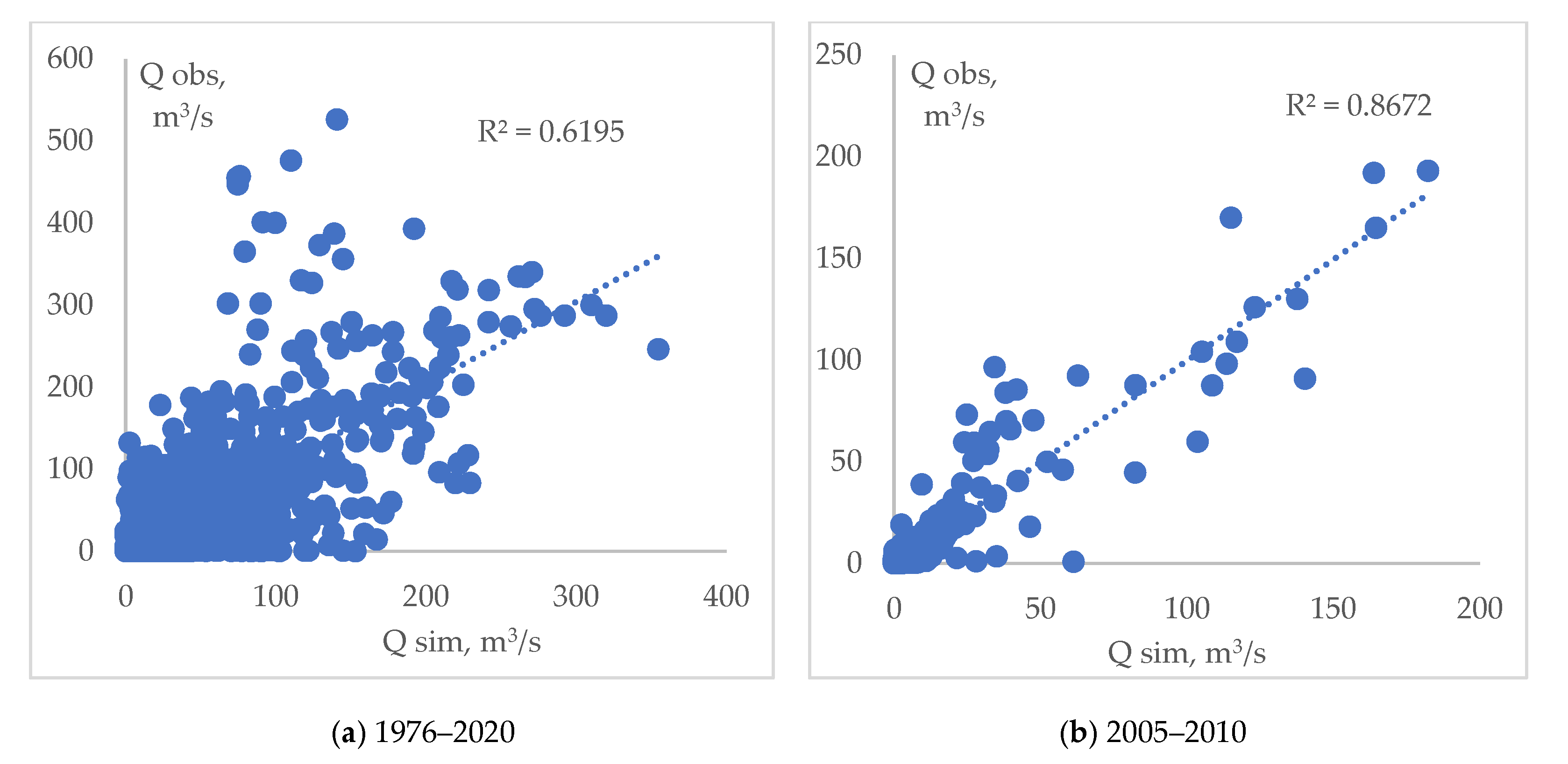
The results of the effectiveness of the HBV model for r. Esil—s. Turgen showed that the model reproduces well the dynamics of the simulated runoff. The correlation coefficient between the simulated and observed runoff for the entire observation period was 0.79, and for the period of the best calibration, it was 0.93 (
Figure 6).
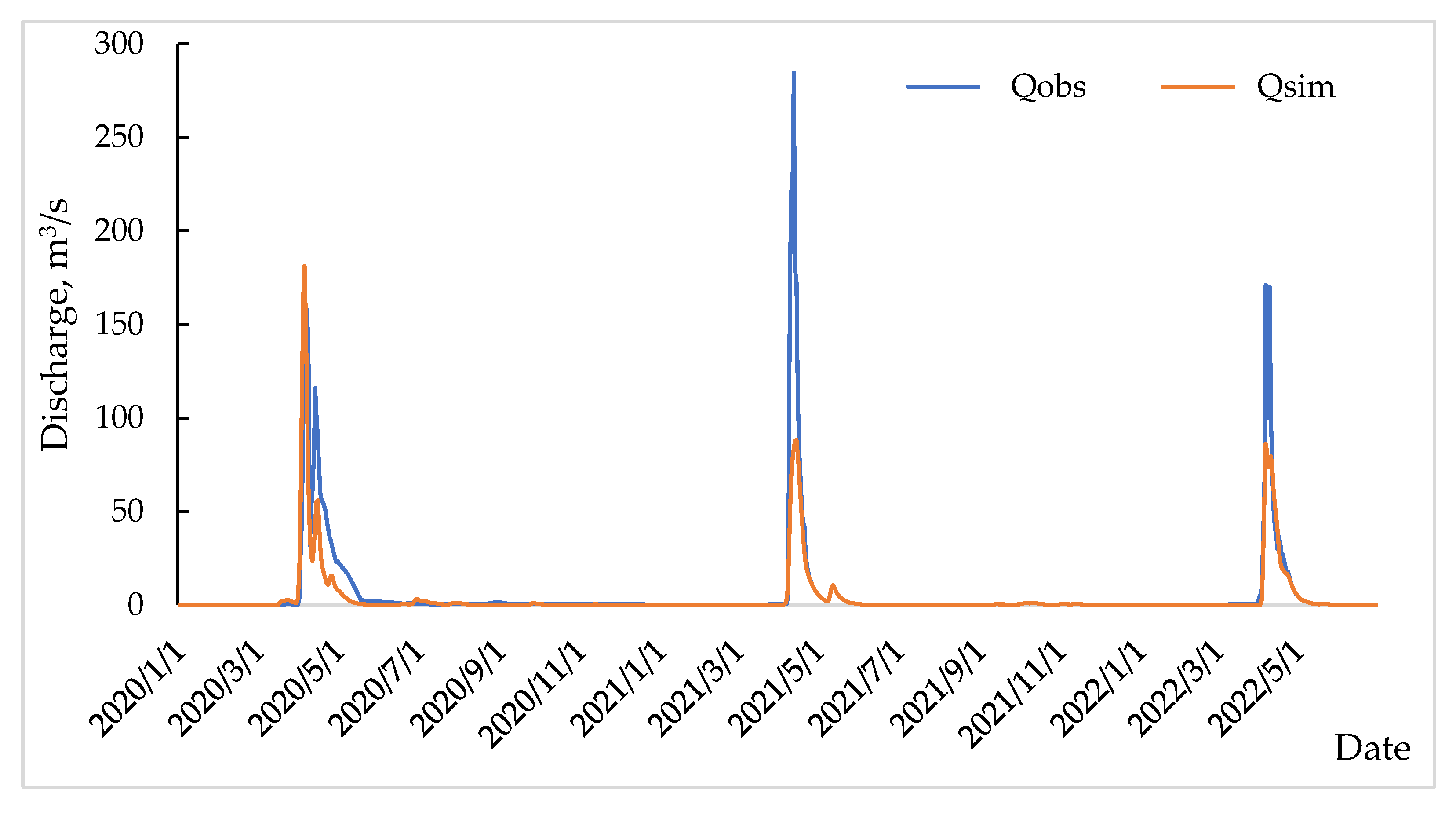
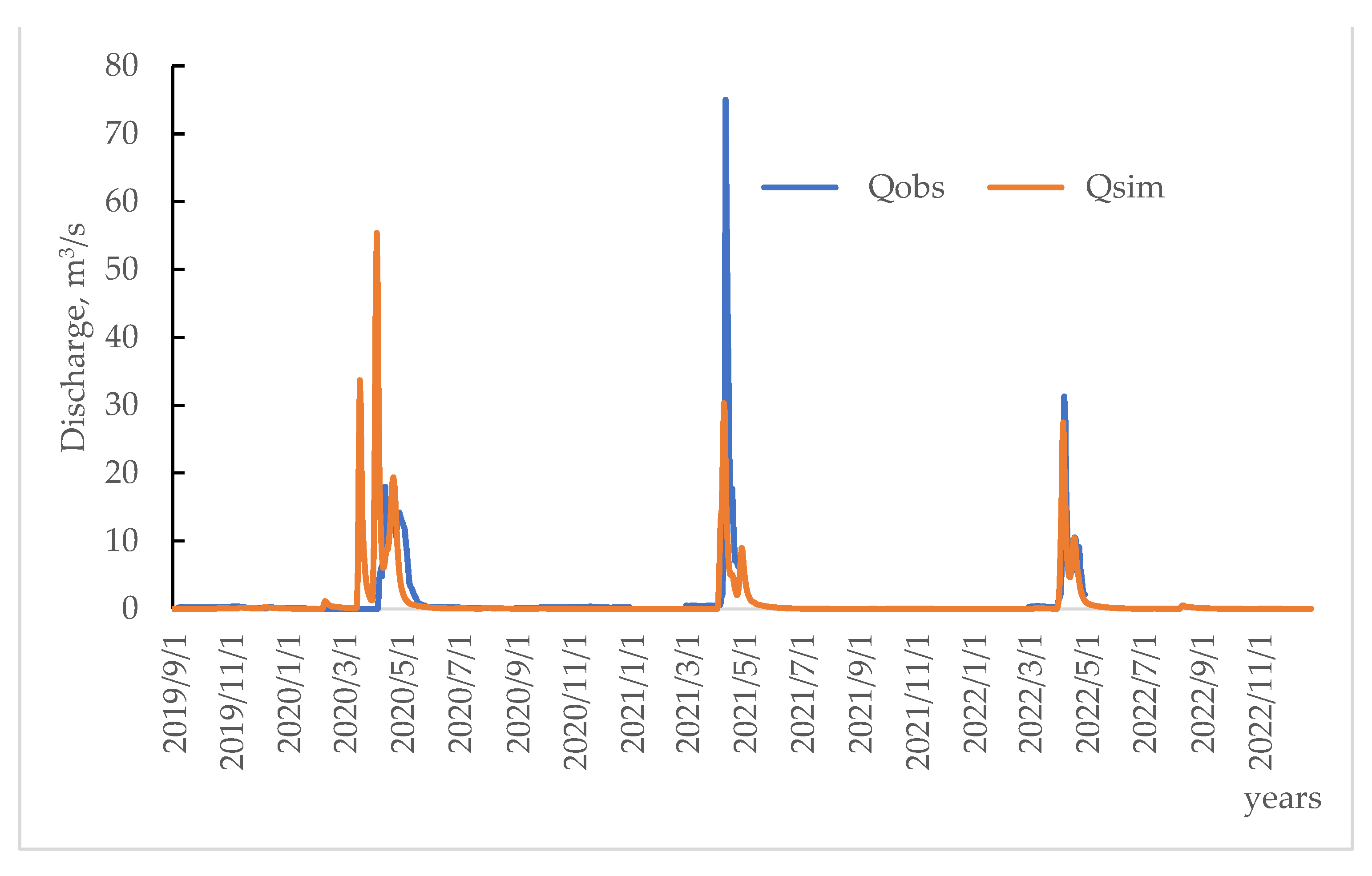
It is recommended to use the calibrated model parameters when making short-term and medium-term forecasts for water consumption/volume. In order to check the reproducibility of the observed water flow rates of the HBV model for the selected parameters, a validation process was carried out on an independent period, 2020–2022 (
Figure 7).
The observed water consumption data for 2021–2022 are operational. Due to the fact that the data will be checked for errors when entering into the state cadaster database, there may be changes in the values over the years.
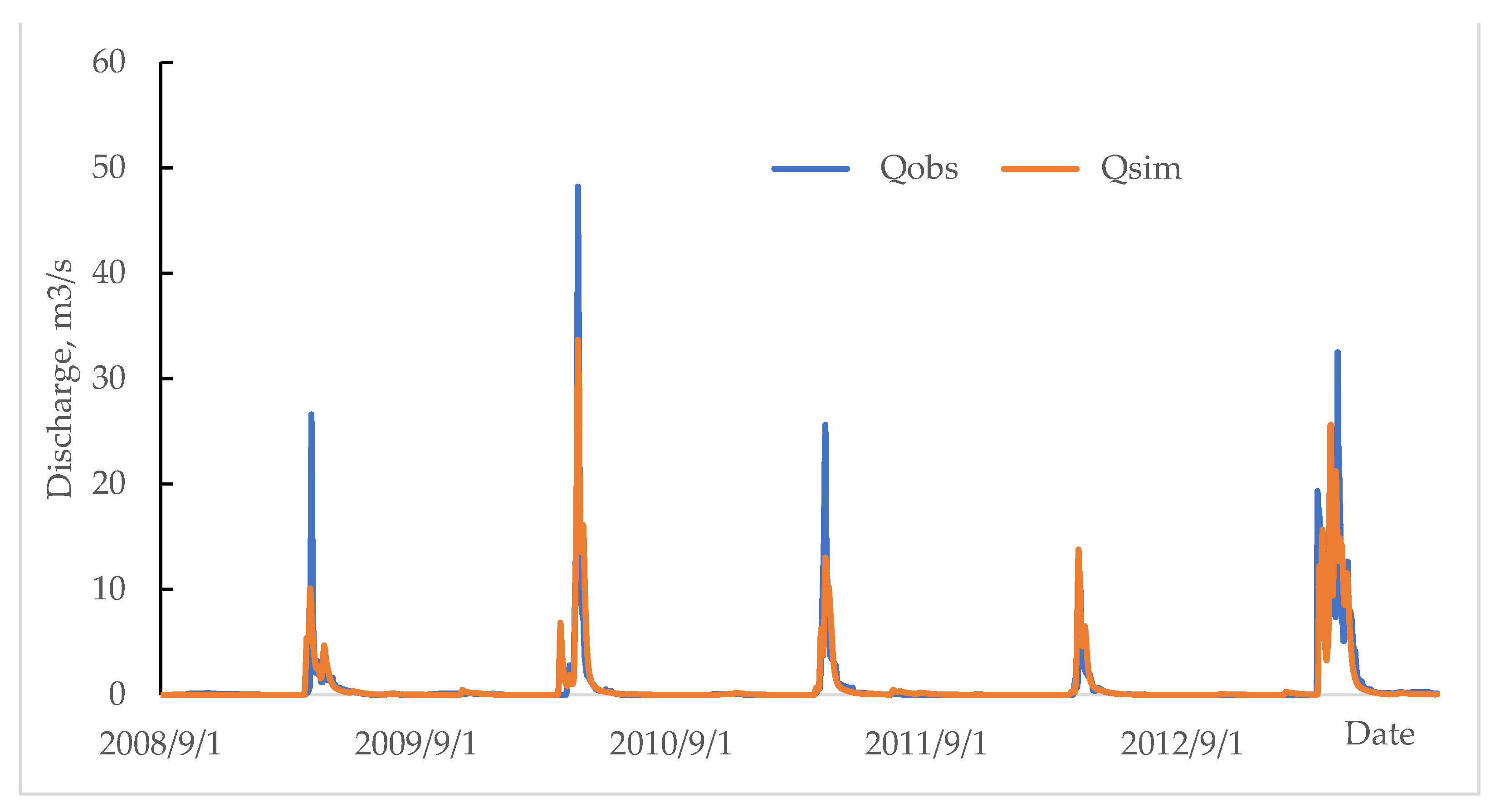
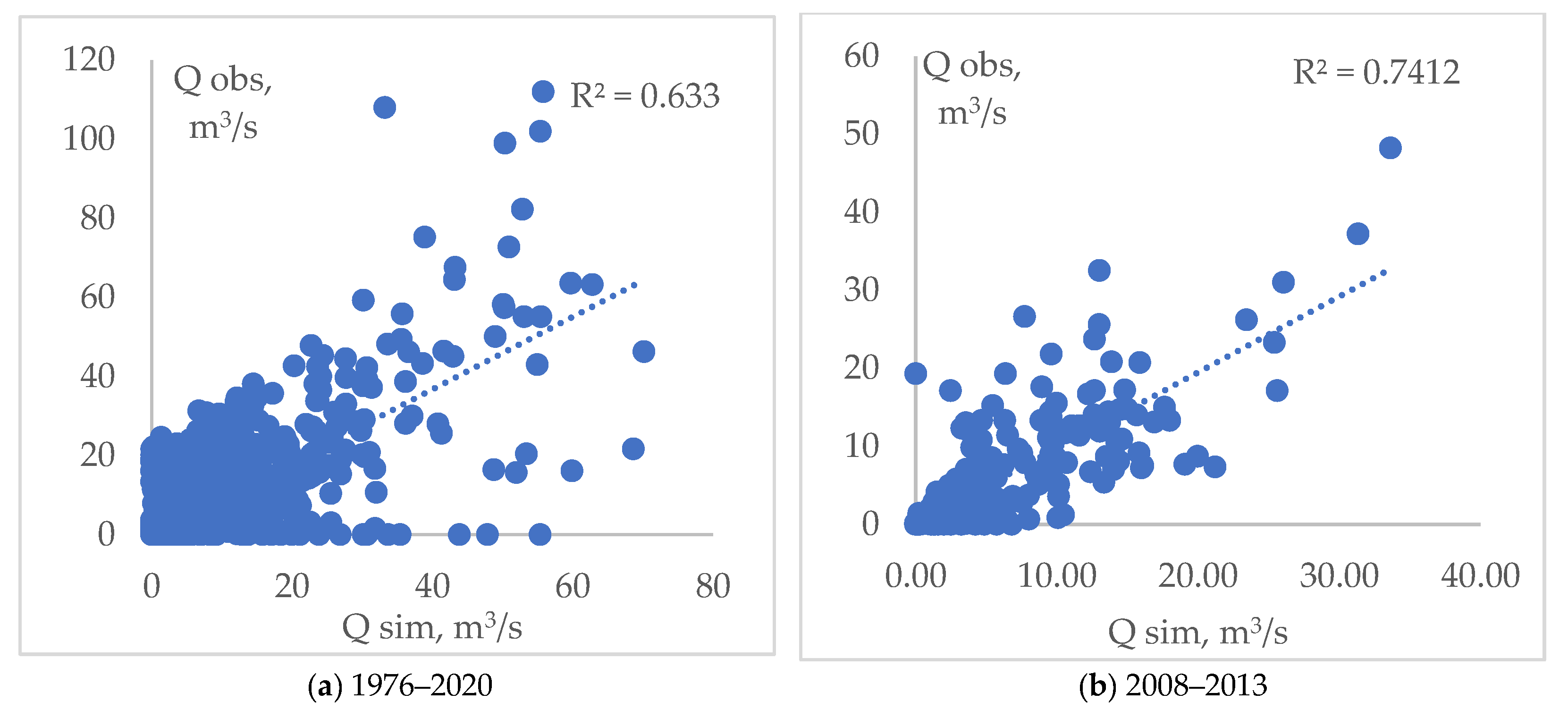
The best results for the Moildy River were obtained for the period 2008–2013, when the model efficiency calculated by the NSE criterion was 0.73 (
Figure 8).
The results of the effectiveness of the HBV model for r. Moildy—s. Nikolaevka showed that the model reproduces well the dynamics of the simulated runoff. The correlation coefficient between the simulated and observed runoff for the entire observation period was 0.79, and for the period of the best calibration, it was 0.86 (
Figure 9).
In order to check the reproducibility of the observed water flow rates of the HBV model for the selected parameters, a validation process was carried out on an independent period, 2020–2021 (
Figure 10).
5. Discussion
The best model calibration results were obtained in the last 20 years, that is, after 2000, which may be due to ongoing climate change and its impact on water resources. It should be recalled that climate change in the Central Asian region is expected to be more pronounced than in the whole world [
29]. A steady increase in the average annual air temperature is observed in the territory of all regions of Kazakhstan. On average, in the territory of Kazakhstan, the increase in the average annual air temperature is 0.32 °C every 10 years. On average, for the territory of certain regions, the growth rate is in the range from 0.23 °C/10 years (Karaganda region) to 0.54 °C/10 years (West Kazakhstan region). In all seasons, except winter, the temperature increase is statistically significant. All trends in the average annual and seasonal precipitation over the territory of Kazakhstan are statistically insignificant. There is a slight trend toward an increase in annual precipitation (by 1.1 mm/10 years), mainly due to spring season precipitation, when the increase in some western and northern regions is 10–20%/10 years. In autumn, the amount of precipitation decreases almost throughout the territory of Kazakhstan [
30].
The simulation results for the snow modulus in the Esil River exhibited higher values compared to those of the Moildy River, with the exception of the threshold temperature and the degree–day factor. The threshold temperature for the Moildy River surpasses that of the Esil River. This discrepancy might be attributed to the placement of meteorological stations situated south of the Moildy River basin. Similarly, the degree–day factor is notably larger within the Moildy River basin, potentially due to the swifter transition of meltwater to the riverbed and the relatively more rugged terrain.
Parameters governing soil conditions and runoff formation demonstrated close numerical proximity, yet the maximum soil moisture capacity near the Moildy River is more than twice that of the Esil River. Moreover, the maximum runoff traversing from the upper to the lower soil strata is sevenfold higher. This distinction can be rationalized by the prevalence of depressions in the Esil River basin that retain meltwater and the comparably larger presence of lakes within its domain, in contrast to the Moildy River basin. Notably, since runoff modeling pertains to the hydrological station, all meltwater flowing from the basin is encompassed in the model. As such, it is conceivable that the model interprets the water detained by surface depressions as soil moisture.
The calibration results for the two rivers were good and showed good modeling of the intra-annual runoff distribution, including the very economically and socially important spring flood. However, the result of the Moildy River turned out to be somewhat worse than that of the Esil River, although both rivers are very similar in terms of runoff formation and catchment area characteristics.
A difference in catchment area of seven times most likely contributed to this difference in the final result. In addition, according to the reports of an expedition that took place in 1956 in the river basin, it was found that 25% of the catchment area is inactive due to the surface retention of melt runoff during spring snowmelt. Since the catchment area of the Moildy River is relatively small, it is possible that the HBV-light model does not sufficiently take into account the retention of melt water and the time of its runoff.
In addition, the result of the calibration is affected by high water or low water in the years included in the period of the best calibration. The calibration period of the studied rivers includes all phases of water content, that is, low-water, medium-water, and high-water years, which makes it possible to take into account the parameters of various phases. However, in both cases, the calibration period does not include a very wet year. It is possible that in wet years, the forecast generated by the model will be weak.
To improve the calibration results and overall model performance, it would be beneficial to extend the calibration period to include years of extremely wet conditions. This will provide a comprehensive understanding of the behavior of the model under various hydrological conditions. In addition, further research and calibration efforts should focus on refining the representation of the catchment area and considering the dynamic processes of snowmelt retention and runoff within the modeling framework.
In addition, the inclusion of additional variables and factors, such as land cover changes, land use practices, and human intervention in water resource management, can contribute to the more accurate and reliable modeling of river systems. The complex nature of hydrological processes requires a holistic approach that encompasses many factors and their interactions.
In conclusion, although the calibration results over the past two decades have been promising, there are still aspects that can be further explored and improved. By taking into account the characteristics of the watershed, increasing the calibration period, and adding additional variables, the model can be improved to provide more accurate forecasts, especially in the case of floods and extreme hydrological conditions.
6. Conclusions
According to the daily observed data on air temperature and the amount of atmospheric precipitation at the meteorological stations of the plain and daily water discharges, the values of the parameters of the HBV-light conceptual model were obtained for modeling the runoff hydrographs of the Esil and Moildy rivers.
The catchment area of the basins for the Esil River and Moildy River were 3240 km2 and 472 km2, respectively.
Reproduction of runoff hydrographs in the HBV-light model consists of the preparation of the initial data and the selection of model parameters that allow for calculating the daily runoff layer from the temperature and precipitation at the nearest meteorological stations.
In this work, the standard structure of the model was used without taking into account the specifics of water use, land use, and land coverage in the basin, which are limitations of the model, and a limitation of this work is that the parameters were not used in operational practice.
Given the above limitations, adjusting the hydrograph for water abstraction and integrating land use and land cover data could improve the results of this work. Also, the inclusion of very wet years in the calibration period could improve the reproduction of the hydrograph in high-water years, but due to the fact that the series of high-water years is shorter than the series of dry years, these rivers will be drained within the timeframe of this work, so perhaps in the future it will be possible to include them in the calibration.
This work has shown that the application of a semi-distributed HBV model for lowland rivers is possible. In the future, there is a prospect of using the model in operational forecasts, and there is also the possibility of adapting and applying this model to other lowland rivers. In general, the quality criteria obtained for the period of calibration and validation of the models are satisfactory, and the model can, under certain conditions, be used for short-term forecasts of runoff during the flood period, as well as for assessing changes in river runoff under the conditions of modern climate change. The parameters are obtained entirely for the entire area of each basin.
The results of the calibration for the rivers show that the HBV-light conceptual model reproduces well the intra-annual runoff dynamics, including water discharges during the flood period. The peak of the flood caused by snowmelt is modeled relatively well. The amount of precipitation recorded at meteorological stations takes on random values, but during the period of snow accumulation, random fluctuations are mutually compensated. Once the applicability of the model to the Esil and Moildy rivers has been proven, its application for the hydrological modeling of both catchments provides a powerful tool to improve the water management systems that greatly influence the Astana reservoir. Future work using the HBV model will focus on the impact of climate change on the water system and the evaluation of the water reserve variations in terms of time under different scenarios.