Enhancing Urban Surface Runoff Conveying System Dimensions through Optimization Using the Non-Dominated Sorting Differential Evolution (NSDE) Metaheuristic Algorithm

Abstract

Rapid urban development and increase in construction have significantly altered the surface coverage of cities, resulting in a rise in impervious surfaces such as roofs, streets, and pavements. These changes act as barriers against rainwater infiltration into the soil, leading to a substantial increase in surface runoff. Managing surface runoff has become a critical task in civil engineering and urban planning, as it can mitigate damage and provide opportunities for utilizing excess water. However, traditional flood control and guidance systems tend to be extensive and expensive, prompting researchers to explore cost-effective alternatives that consider all design parameters and variables. In this research, we propose an innovative approach that combines the NSDE (non-dominated sorting differential evolution) metaheuristic algorithm as an optimizer with the SWMM (storm water management model) as a simulator. The objective is to design efficient surface runoff collection networks by thoroughly investigating their hydraulic behaviors. This study focuses on the Chitgar watershed in Tehran, Iran, utilizing the SWMM model and NSDE multi-objective metaheuristic algorithm to determine the optimal dimensions of the channel and its intersecting structures. The aim is to minimize costs and reduce water leakage from the network. A comparison is made between the optimized design results and the existing network plan (without any design modifications). The analysis reveals substantial reductions in water leakage for all three design scenarios: a 7.66% reduction when considering only bridges, a 7.35% reduction with only the canal, and an impressive 95.26% reduction when both the canal and bridges are incorporated. These findings demonstrate the superiority of the optimized designs in terms of cost-effectiveness and the efficient management of surface runoff.

1. Introduction

Floods annually inflict significant damage on buildings, infrastructure, and urban environments, often resulting in loss of life and immense financial losses [1]. The increased occurrence of floods can be attributed to the rapid pace of urbanization, which has led to changes in land-use and land-cover, resulting in the expansion of impervious surfaces and subsequent amplification of runoff volume [2]. This surge in runoff, accompanied by environmental pollution, road inundation, higher peak discharges, and altered flood characteristics due to atmospheric precipitation, highlights the escalating risk of urban flooding and underscores the need for attention to urban drainage and flood systems [3]. Despite these challenges, the optimal design and improvement of surface water collection systems have not received adequate consideration in many cities, leading to visible problems at the urban level [4,5]. It is essential to assess the existing potential of urban watersheds, evaluate the efficiency of drainage networks, and determine optimal dimensions in terms of hydraulics and hydrology to facilitate the safe discharge of urban floods [6]. Moreover, flood control plans are numerous and diverse, each requiring consideration of local conditions, risk mitigation, anticipated benefits, and socioeconomic factors. Therefore, selecting an appropriate plan from both technical and economic perspectives becomes crucial [7,8].

Urban runoff and flood management are critical aspects of urban planning and environmental management. As cities continue to expand and develop, the increase in impervious surfaces, such as buildings, roads, and pavements, significantly alters the natural water cycle [9]. These impervious surfaces prevent rainwater from infiltrating into the ground, leading to a surge in surface runoff. This excess water, along with pollutants accumulated on urban surfaces, poses serious challenges in terms of flooding, water quality degradation, and damage to infrastructure and property [10,11]. The occurrence of floods in urban areas has severe consequences, including economic losses, destruction of public and private property, and even loss of life. Urbanization exacerbates these risks, as land-use changes and urban development disrupt the natural flow patterns of water. The increased volume and velocity of runoff overwhelm existing drainage systems, leading to the inundation of streets, homes, and public spaces. As a result, the effective management of urban runoff and flood events is of paramount importance for sustainable urban development, environmental protection, and ensuring the safety and well-being of urban populations [12]. To address the challenges posed by urban runoff and floods, various strategies and technologies have been developed. These include the implementation of stormwater management systems, green infrastructure practices, and advanced modeling techniques to assess flood risks and optimize drainage networks [13]. Additionally, urban planners and policymakers are increasingly recognizing the importance of integrating nature-based solutions, such as rain gardens, permeable pavements, and green roofs, to mitigate the impacts of urban runoff. Through effective flood management and sustainable urban design, cities can enhance their resilience to climate change, minimize flood damages, and create healthier and more livable urban environments [14].

One of the key elements in flood management is the enhancement and strengthening of the urban surface water collection system (known as runoff conveying system, RCS). This system includes a network of drains, channels, culverts, and other infrastructure designed to collect and convey excess rainfall and stormwater runoff [15]. By improving this system, cities can effectively manage and control the movement of water during heavy rainfall events, reducing the risk of localized flooding and protecting critical infrastructure, including buildings, roads, and bridges [16,17,18,19]. The importance of an efficient RCS lies in its ability to handle the increased runoff caused by urbanization [20]. As cities expand and develop, the replacement of natural land surfaces with impervious materials, such as concrete and asphalt, reduces the ability of the soil to absorb rainfall. Consequently, a larger volume of water is directed to drainage systems, which must be adequately designed and maintained to prevent being overwhelmed and subsequently flooding [21]. An optimized RCS system, incorporating proper sizing, routing, and storage capacity, can efficiently manage the flow of water, reducing flood risks and ensuring that water is safely and effectively conveyed away from populated areas [22]. In conclusion, flood management and the improvement and strengthening of urban RCS are crucial for urban resilience and the well-being of communities. These measures not only mitigate the risks associated with urban flooding but also provide opportunities for sustainable water resource management [23]. The present study is focused on RCS and will attempt to provide an optimized model regarding RCS.

Sharifan [24] focused on investigating the uncertainty of water depth in significant manholes within drainage system pipelines located in the historical center of Shiraz, a city located in the southwest region of Iran. To simulate the complex processes of precipitation, runoff, and flow patterns in water channels, the SWMM (storm water management model) was utilized. Additionally, the Monte Carlo simulation (MCS) was employed to conduct uncertainty analysis. The findings of their research revealed notable variations in the water depth coefficient across multiple manholes, ranging from 12% to 66%. These variations highlight the significance of considering uncertainty factors when assessing water depth in drainage systems. Notably, parameters related to subbasins and rainfall were identified as having the most significant influence on peak flood discharge and its associated uncertainty. Understanding these influential parameters is essential for effective flood management and the design of robust drainage systems. Caradot et al. [25] recognized the global challenge of water management in the 21st century and placed a particular emphasis on urban flood protection as a primary objective to benefit all residents. Their study proposed a method that enables water management authorities to evaluate the services offered by urban drainage systems in terms of protection against urban flooding. By utilizing a database of sewer flood event records, the approach aimed to assess sewer flood risk and provide decisionmakers with valuable insights into the current state of affairs, rather than predicting future flood occurrences. The key aspect of this research involved adopting a comprehensive understanding of risk, which encompassed not only the vulnerabilities of the region but also the perception of urban water issues. By considering these factors, the proposed method aimed to assist beneficiaries in developing effective strategies to enhance the services provided by the urban drainage system.

Yazdi et al. [26] employed MCS as a tool for optimizing the design of urban drainage networks. In this study, a multi-objective optimization model based on Copula functions was proposed. The Copula-based model allowed for efficient exploration and optimization of multiple objectives in the design process. Additionally, the hydraulic model SWMM was utilized to simulate and evaluate the hydraulic performance of the drainage network. The integration of MCS and Copula functions provided a robust framework for the optimization of the design of urban drainage networks. By using MCS, researchers were able to capture the uncertainty and variability associated with input parameters and their impact on the performance of the network. The Copula-based multi-objective optimization approach allowed for the simultaneous consideration of various design criteria, such as minimizing flooding risks, maximizing system efficiency, and optimizing cost. Obaid et al. [27] conducted a study on the carrying capacity of the sewage network in Karbala, Iraq, using the SWMM model. The model investigated two scenarios: heavy rainfall and population increase during religious gatherings in the city of Karbala. The findings revealed that due to population growth, the sewage network lacked the capacity to handle the sewage flow, leading to overflow issues. This problem was particularly exacerbated during intense rainfall events coinciding with religious ceremonies, further exacerbating the severity of the issue. Li et al. [28] conducted a study focused on the optimal design of retention ponds under the constraints of urban stormwater control criteria. Their objective was to develop an efficient and robust method and framework for designing a retention pond network. The hydraulic simulation model, SWMM, and the modified particle swarm optimization (PSO) algorithm were employed to minimize engineering costs and mitigate the risks of flood occurrences, while considering local design criteria. To validate the proposed method, the researchers applied this model to a county in China, considering the design and size of the retention pond network, as well as various construction factors in the modeling and optimization processes. The researchers demonstrated the feasibility and credibility of the proposed framework for the multi-objective optimal design of retention ponds within the urban stormwater drainage system (USDS). The study showcased the potential and validation of the proposed method for the optimal design of multi-objective retention ponds in the USDS. The findings of their research contributed to advancing the field of urban hydrology and providing valuable insights for improving USDS control strategies, enhancing the resilience of urban areas against floods, and optimizing the design of retention pond networks.

Yazdi et al. [29] utilized the non-dominated sorting harmony search (NSHS) algorithm to achieve the optimal solution in the desirable reconstruction of urban sewer pipe networks. They compared the obtained results with the multi-objective algorithms NSGA-II and MOPSO. The results indicated the superiority of the solutions obtained using the NSHS algorithm. The NSHS algorithm proved to be effective in finding the optimal solutions for the reconstruction of urban sewer pipe networks, surpassing the performance of other multi-objective algorithms. Also, Yazdi et al. [30] employed the multi-objective optimization algorithms NSHS, NSDE, NSGA2, and SPEA2 to investigate the hydraulic efficiency of USDS. These algorithms were utilized to assess and enhance the performance of the drainage networks. By leveraging the capabilities of these optimization algorithms, the researchers aimed to optimize the hydraulic behavior of USDS, thereby improving their overall efficiency and performance. The study compared the results obtained from each algorithm, providing valuable insights into the effectiveness of different optimization approaches for enhancing the hydraulic functionality of USDS. Hooshyaripor and Yazdi [31] presented a simulation-optimization model for reducing urban flooding by integrating the NSGA2 algorithm with the SWMM model in the city of Gonbad-e Kavus. A multi-objective optimization problem with two conflicting objectives was successfully solved using the NSGA2 algorithm to identify a set of well-known optimal solutions known as the Pareto front. The study aimed to address the challenges of urban flooding through the integration of simulation and optimization techniques. By utilizing the NSGA2 algorithm, the researchers were able to find efficient solutions that mitigate the risk of urban flooding in a more integrated and comprehensive manner. The results provided valuable insights for urban planners and decisionmakers in developing effective strategies for flood management and urban resilience. Housh [32] employed the robust counterpart method to analyze the hydrological and hydraulic uncertainties in urban drainage systems. In this study, the multi-objective optimization algorithm NSGA-II was utilized, taking the reduction in flood damage costs and the total construction cost as the objective functions. By incorporating the robust counterpart approach, the researchers were able to account for uncertainties and generate robust solutions that provide reliable performance even under uncertain conditions. This approach enhances the resilience and effectiveness of urban drainage systems in mitigating the impacts of floods. Khaleghi et al. [33] focused on the Shiraz Dry River and executed the hydraulic model SWMM to simulate the flow characteristics in the area. They compared the model output with the hydrographs from the Nahr-e Azam and Chenarsoukhteh gauging stations and demonstrated a high level of accuracy, with an R2 correlation coefficient of 0.96 and a Nash–Sutcliffe coefficient of 0.91. The results indicated that SWMM is a reliable tool for predicting the effects of various management scenarios on flow characteristics. The study showcased the efficacy of SWMM in facilitating informed decision making regarding flood management strategies and assessing their impacts on the flow characteristics of the river. Basnet et al. [34] evaluated the performance of the SWMM model for estimating runoff in the Lamachaur watershed in the city of Pokhara, Nepal. They compared the calibration and validation results of the SWMM model using a rational method and found that, except for subbasin 1, the other subbasins exhibited acceptable Nash–Sutcliffe coefficients and coefficient of variation ratios. The model’s output hydrographs also exhibited a good match with the observed data. Based on these findings, the researchers concluded that the SWMM model was effective in estimating runoff in the Pokhara urban watershed and provided reliable insights for flood estimation and mitigation measures.

Stormwater management encompasses the design of effective control measures to mitigate the adverse impacts of stormwater runoff on the environment and public infrastructure. One critical aspect of stormwater management involves optimizing the dimensions of flood walls, channel embankments, and cross structures to balance multiple objectives, such as minimizing flood risk, reducing pollutant runoff, and managing construction costs. This problem presents a multi-objective optimization challenge, where various design parameters serve as decision variables, and numerous conflicting objectives need to be simultaneously considered. To address this complex task, the application of optimization algorithms, such as non-dominated sorting differential evolution (NSDE), appears promising. NSDE, a derivative of differential evolution and non-dominated sorting, holds potential for identifying a set of Pareto-optimal solutions that represent the best trade-offs between conflicting objectives, thus providing decisionmakers with a diverse range of optimal design alternatives to choose from based on their preferences and project requirements. The successful implementation of NSDE in stormwater management design relies on the utilization of accurate simulation models to assess the performance of different design alternatives under varying hydrological conditions. Through iterative evolutionary processes, NSDE explores the design space by generating and evaluating a diverse range of solutions, ultimately converging towards the Pareto-optimal front. However, it is essential to acknowledge that the application of NSDE, or any other optimization algorithm, in stormwater management demands the careful consideration of practical constraints, environmental regulations, and computational resources. Despite these challenges, the integration of NSDE holds significant promise for advancing the field of stormwater management by providing robust and efficient approaches to design environmentally sustainable and cost-effective stormwater control measures. Further research in this area is needed to fully realize the potential benefits of optimization algorithms like NSDE in improving the resilience and effectiveness of stormwater management practices [35,36,37,38,39,40]. The present article develops a systemic approach to the set of methods for improving and enhancing surface water collection systems by considering the combined and individual impact of each urban stormwater management option. It ultimately proposes the optimal and most cost-effective combination of these methods to minimize runoff and rehabilitation costs based on heuristic methods and simulation models. The multi-objective optimization algorithm, NSDE, is utilized to optimize the design of stormwater control measures and determine the dimensions of (a) flood walls; (b) channel embankments; and (c) cross-structures, which are the main objectives in this study. The NSDE algorithm is employed to solve the optimization problem of urban stormwater management. The NSDE algorithm brings several benefits to the field of urban stormwater management. One of its key advantages is its ability to handle multi-objective optimization problems. In stormwater management, there are typically multiple objectives to consider, such as minimizing runoff volume, reducing flooding risks, and minimizing infrastructure costs. The NSDE algorithm efficiently explores the trade-offs between these objectives and provides a set of Pareto-optimal solutions, giving decision-makers a range of options to choose from. Another strength of NSDE is its robustness and reliability. It effectively explores the search space, converging towards a diverse set of near-optimal solutions. This ensures that decisionmakers have a comprehensive understanding of the trade-off surface, enabling them to make informed decisions. Efficient convergence is another notable benefit of NSDE. By employing differential evolution operators, NSDE strikes a balance between exploration and exploitation. It efficiently explores different regions of the search space while converging towards optimal solutions. This makes it well-suited for optimizing complex stormwater management systems with multiple decision variables and constraints [41,42].

NSDE is also capable of handling uncertainty, a crucial aspect of urban stormwater management. With various sources of uncertainty such as rainfall variability and modeling errors, NSDE generates a diverse set of solutions that cover a range of possible scenarios. This allows decisionmakers to assess the robustness of different strategies under uncertain conditions and select the most suitable solutions. Additionally, NSDE offers flexibility and adaptability. It can be customized to incorporate specific constraints, objectives, and decision variables relevant to stormwater management. This versatility allows for the incorporation of different performance metrics, design criteria, and system constraints, making it a valuable tool for optimizing stormwater management systems [41,42].

2. Materials and Methods

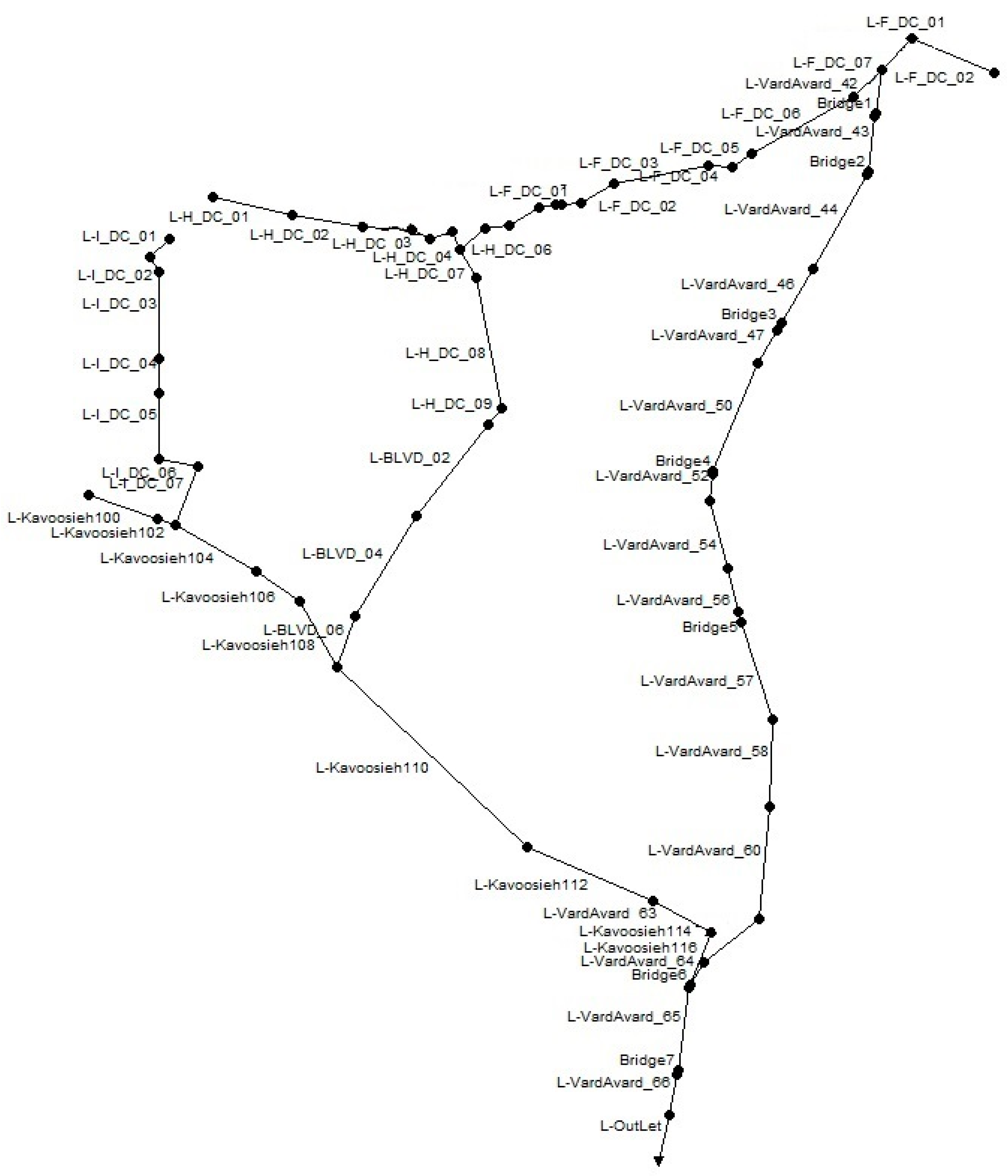
2.1. Study Area and Dataset

The study area of the Chitgar watershed in Tehran is geographically located between 507,351 to 537,325 East and 3,943,208 to 3,978,875 North, using the WGS_1984_UTM_Zone_39N coordinate system. The total area of the study is approximately 604 km², with 385 km² falling within the suburban area and 219 km² within the urban area, based on the approved 20-year city boundary of Tehran. It should be noted that the average elevation of the study area is 1931 m above sea level [43].

In terms of the city’s location, the study area extends from the eastern border of Eastern Districts 2 and 18 to the northern border of Northern Districts 2, 5, and 22, and from the western border of Western Districts 21 and 22 to the southern border of Southern Districts 21 and 18. The majority of Districts 2, 5, and 18, along with the entire areas of Districts 21 and 22, are encompassed within the scope of the current study, highlighting the extensive coverage of the study area [43]. Figure 1 illustrates the positioning of the study area in relation to the city districts and boundaries of Tehran. Figure 2 shows the study area and its main drainage network in the SWMM environment.

The Chitgar watershed in Tehran, also known as the Chitgar Lake Basin, is an important hydrological region within the city. It is located in the western part of Tehran, encompassing several districts and neighborhoods [44]. The watershed plays a significant role in managing surface water resources and mitigating the risk of urban flooding in the region. The Chitgar Lake is a prominent feature within the watershed. It is an artificial lake constructed to provide recreational space for the residents of Tehran. The lake acts as a reservoir for collecting and storing surface water runoff from the surrounding area, helping to control flooding during heavy rainfall events [43].

The watershed area consists of diverse land use patterns, including residential areas, commercial zones, industrial facilities, and open spaces. The presence of these different land uses contributes to the generation of stormwater runoff, which needs to be effectively managed to minimize the risk of flooding and protect the environment [44]. To address the water management challenges in the Chitgar watershed, various initiatives have been undertaken, including the implementation of stormwater management infrastructure, such as drainage systems, retention ponds, and green spaces. These measures aim to capture and store excess rainfall, reduce the volume of runoff, and enhance water quality before it reaches the Chitgar Lake or other water bodies in the region [43]. Additionally, hydrological studies, modeling, and monitoring activities are conducted to better understand the dynamics of the watershed and optimize water management strategies. These studies help in assessing the impact of land use changes, climate variability, and urban development on the hydrological characteristics of the Chitgar watershed [44].

The Chitgar watershed drainage network plan in Tehran province has been developed and presented in Figure 2. This plan includes the design and layout of a comprehensive network of channels, pipes, and other drainage infrastructure to efficiently manage stormwater runoff in the watershed. The plan takes into consideration factors such as topography, land use, and anticipated rainfall patterns to ensure effective drainage and minimize the risk of flooding in the area. It also incorporates measures for sediment control, erosion prevention, and water quality management. The drainage network plan aims to enhance the resilience of the Chitgar watershed by providing a robust and sustainable system for stormwater management.

2.2. Methodology

In this study, the EPA-SWMM rainfall-runoff model [45] was used to simulate urban stormwater runoff. The NSDE algorithm was employed to find the optimal design, which includes determining the required elevation increments for the different segments of the main drainage channels and optimizing the dimensions of critical structures, such as bridges and cross-sectional culverts, to minimize the outflow from the surface water collection network. The simulation and optimization models were connected in the MATLAB environment to achieve the objectives of the optimal design. Subsequently, each of the simulation and optimization models is briefly introduced.

2.2.1. The Hydraulic Simulations

The storm water management model (SWMM) is a widely utilized and comprehensive computer software package developed by the United States Environmental Protection Agency (EPA). The SWMM serves as a powerful hydrology–hydraulic simulation tool for analyzing and simulating stormwater runoff, drainage systems, and their impacts on urban areas. With its roots dating back to the late 1960s, the SWMM has undergone iterative advancements to encompass diverse stormwater management aspects [46]. Key features of SWMM include its ability to simulate hydrologic processes, such as precipitation, infiltration, and runoff generation, and its hydraulic modeling capabilities for drainage systems, incorporating pipes, channels, culverts, and storage facilities. The software version 5.1 further accommodates water quality analysis, enabling users to evaluate the transport and fate of pollutants in stormwater runoff, while also assessing the efficacy of best management practices (BMPs) and green infrastructure in mitigating water pollution. The SWMM’s versatility and applicability have led to its widespread adoption by researchers, engineers, and urban planners as an indispensable tool for understanding and designing resilient stormwater management systems to combat the challenges posed by urbanization and environmental concerns. In the realm of stormwater management and urban hydrology, the SWMM has emerged as a preeminent computational model, providing a dynamic platform for investigating complex drainage systems. Leveraging advanced hydrological methodologies and hydraulic simulations, the SWMM enables the analysis of water flow behavior, velocity, and capacity across diverse urban landscapes. Moreover, the software’s capacity to assess the impact of stormwater runoff on water quality fosters a holistic approach to environmental protection and sustainable development. By facilitating the simulation of green infrastructure practices and BMPs, the SWMM empowers decision-makers to devise effective strategies for flood control, pollution reduction, and stormwater system design. Its widespread adoption in the academic, engineering, and regulatory communities testifies to the SWMM’s significance as a fundamental tool in comprehending urban hydrology, furthering the endeavor to create resilient and ecologically sensitive urban environments. Ongoing research and updates to the software continue to enhance its capabilities, solidifying the SWMM’s position as an indispensable resource in the pursuit of integrated and efficient stormwater management solutions [47,48].

The hydraulic simulation model used in this study is the SWMM, which was developed in collaboration with the University of Florida’s Engineering Company and the Water Resources and U.S. Environmental Protection Agency from 1969 to 1971 [46]. Since then, it has been regularly updated and improved. Some of the hydraulic capabilities of this model include [49]:

• Ability to analyze flow in separate and combined sewer networks.
• Ability to analyze one-dimensional flow in both steady and unsteady states.
• Capability to model various channels and pipes with different cross-sectional shapes.
• Capability to model different hydraulic structures.
• Ability to estimate flow volume and duration of runoff from the network.
• Capability to simulate flow in free and pressurized stormwater systems.
• Capability to simulate complex networks, including networks with parallel, series, and looped pipe or channel arrangements.

In this study, the SCS (Soil Conservation Service) curve number method was used to calculate and estimate losses. The Hazen–Williams hydraulic head loss equations and continuity equation were used to calculate surface runoff. For flow routing in channels, the method of dynamic wave routing was employed. The EPA–SWMM model was chosen for its numerous and suitable capabilities in modeling complex networks, its graphical features, user-friendly interface, and its compatibility with optimization models. Additionally, its availability as a free tool further contributed to its selection in this research.

2.2.2. The Optimizations

Optimization is a method through which the best possible solution for a problem is determined based on a given objective and specified constraints, all of which are defined by mathematical functions and equations. Multi-objective optimization refers to a problem with multiple objective functions (criteria) and several constraints that collectively encompass the characteristics of the targeted system [50].

The objective of optimization in a specific case can be either maximizing or minimizing a certain function. In this study, the NSDE algorithm was utilized for optimizing the problem at hand, and the algorithm will be briefly introduced below. In recent years, the differential evolution (DE) algorithm has been introduced as a powerful and fast method for optimization problems in continuous spaces. It was initially proposed by Storn and Price in 1995 [42]. They demonstrated that this algorithm performs well in optimizing non-linear and non-differentiable functions. The main difference between genetic algorithms and the DE algorithm lies in how mutation and crossover operations are applied. After generating a new solution using a self-adaptive mutation operator and a crossover operator, the new solution is compared with the previous one, and if it is superior, it replaces the previous solution [49]. The NSDE algorithm is an evolved and multi-objective version of the DE algorithm, and the optimization process and methods of Algorithm 1 are as follows [41]:

Algorithm 1 A summary view of the process by optimization algorithm

Begin Set Npop = 100 MaxIter: Maximum number of Iteration Initialize a random population Xgi ∀I, i = 1, …, Npop Evaluate f (xig) ∀i, i = 1, …, Npop for iter = 1 to MaxIter do for i = 1 to Npop x = pop (i).Position; A = randperm(nPop) XBestPosition = pop (XBestRank).Position; XBestCost = CostFunction(XBestPosition); XWorstPosition = pop (XWorstRank).Position; XWorstCost = CostFunction(XWorstPosition); XBetterPosition = pop (XBetterRank).Position; XBetterCost = CostFunction(XBetterPosition); # Mutation operator XavgPosition = 1/3 ×(XBestPosition + XWorstPosition + XBetterPosition); XavgCost = CostFunction XavgPosition); F = unifrnd(0.1,0.8);%Pmax and Pmin recommended to be 1 and 0.1, respectively if rand < Pmax + (Pmax-Pmin) × e(it/MaxIt) y1Position = pop(1).Position + F × (pop(2).Position − pop(3).Position) + F × (pop(4).Position − pop(5).Position); y2Position = XBestPosition + F × (pop(1).Position − pop(2).Position) + F × (pop(3).Position − pop(4).Position); y3Position = pop(i).Position + F × (XBestPosition -pop(i).Position) + F × (pop(1).Position − pop(2).Position); else y1Position = XavgPosition + F1 × (XBestPosition − XBetterPosition) + F2 × (XBestPosition − XWorstPosition) + [(F1 + F2)/2] × (XBestPosition − XWorstPosition); y2Position = XavgPosition + (P2-P1) × (XBestPosition − XWorstPosition) + (P3-P2) × (XBestPosition − XWorstPosition) + (P1-P3) × (XBestPosition − XWorstPosition); y3Position = XBestPosition + F1 × (XBestPosition − XBetterPosition) + F2 × (XBestPosition − XWorstPosition); end if rand < 0.5 σ = [2×rand](1/η + 1) − 1; else σ = 1 [2-2×rand](1/η + 1); end %where σ is polynomial mutation, η is a distribution index, Ub and Lb are the lower and upper bounds of decision variable, # Crossover operator z = zeros(size(x)); j0 = randi([1 numel(x)]); for j = 1:numel(x) if j = j0 || rand <= PCR z(j) = y1Position (j) + σ × (Ub-Lb); elseif rand < 0.5 z(j) = y2Position (j); elseif rand >0.5 or rand < 0.75 z(j) = y3Position (j); else z(j) = xPosition (j); end % Apply Variable Limits z = max(z, Lb); z = min(z, Ub); NEWiPosition = z; NEWiCost = CostFunction(NEWiPosition); end

The NSDE algorithm is an evolved and multi-objective version of the differential evolution algorithm. The sequential process steps of this algorithm are as follows:

Step 1: Generating the initial population randomly and evaluating it based on the defined objective functions.

Step 2: Selecting parent individuals and generating offspring population using mutation and crossover operators.

Step 3: Sorting individuals using non-dominated sorting. The individuals in the first category form a completely non-dominated set compared to other individuals in the current population. The individuals in the second category are only dominated by the individuals in the first category, and this process continues for other categories until each individual in each category is assigned a rank based on the category number.

Step 4: Sorting individuals in each front based on the population’s crowding distance. This parameter is calculated for each individual in each group, indicating the proximity of the target sample to other individuals in that group. A higher value of this parameter leads to better diversity and range in the population set.

Step 5: Removing undesirable individuals.

Step 6: Returning to Steps 2 to 5 if the termination conditions are not met.

In the NSDE algorithm, the algorithm parameters are influential, and their values are adjusted based on the recommended values in previous research (

Table 1. Defined values for NSDE elements for volume reduction and cost minimization (adapted form Ref. [41]).

No.	Parameter	Value
1	Population Size	100
2	Mutation Rate	0.5
3	Crossover Rate	0.9
4	Scaling Factor	0.8
5	Maximum Generations	200
6	Termination Criteria	Convergence or Maximum Generations Reached

Note: The values presented in this table have been determined to reduce volume and minimize costs in the NSDE algorithm.

).

2.3. Formulation of the Optimizations

With a fixed level of investment, it is possible to reduce the volume of runoff (excess flow over channel capacity) by a certain amount using an optimal design. Further reduction requires an increase in the level of investment. Therefore, in this study, capital investment costs and runoff volume are considered as two independent and competing objectives in the multi-objective optimization model. The general formulation of the objective functions is as follows:

$$\begin{array}{ll}\hfill Min F_{{}_1 }& =Cos{t}_t=\underset{i=1}{\overset{n}{{\displaystyle \sum \hspace{0.17em}}}}Cos{t}_i^B+\underset{j=1}{\overset{m}{{\displaystyle \sum \hspace{0.17em}}}}Cos{t}_j^W\hfill \\ \hfill & =\underset{i=1}{\overset{n}{{\displaystyle \sum \hspace{0.17em}}}}{f}_1\left(H_i^B\right)+{\displaystyle {\displaystyle \sum }_{j=1}^m}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{f}_2\left(H_j^W\right)\hspace{0.17em}\hfill \end{array}$$

(1)

$$Min F_{{}_2 }={\displaystyle \sum }_{j=1}^m(V_{F,j})$$

(2)

The constraints of the optimization problem are as follows:

$$V_a\le \hspace{0.17em}\hspace{0.17em}{V}_{max}$$

(3)

$$H_i^B\in \left\{H_1^B,H_2^B,H_3^B,\dots ,H_p^B\right\}$$

(4)

$$H_i^W\in \left\{H_1^W,H_2^W,H_3^W,\dots ,H_q^W\right\}$$

(5)

$$\frac{\partial Q}{\partial x}+\frac{\partial A}{\partial t}=q$$

(6)

$$S_f=S_0-\frac{\partial y}{\partial x}-\frac{v}{g}\frac{\partial v}{\partial x}-\frac{1}{g}\frac{\partial v}{\partial t}$$

(7)

In these equations, $Cos{t}_i^B$, the cost of constructing and repairing critical cross structures (culverts) is represented by ith; $H_i^B$, the height of critical cross structures (culverts) is represented by ith; $Cos{t}_j^W$ is the cost of flood walls in the jth interval; $H_j^W$ is the height of the flood walls in the jth interval; t represents time; g represents gravity; A represents area; Q represents flow rate; m represents the number of channel intervals; n represents the number of critical cross structures (culverts); and $V_{F,j}$ the volume of the network’s flood in the jth interval which is presented in Figure 3.

In Equation (1), the objective function is to minimize the total cost of constructing bridges and flood walls. In Equation (2), the second objective function is to reduce the volume of floodwater (referring to the amount of water exiting the channel). Equations (3)–(5) represent the constraints of the optimization problem. In the first constraint, the permissible velocity in the channels is limited, and the other constraints represent the discrete values that the decision variable can take. If the design/renovation of the surface water collection system is considered, the objective functions in the optimization model will be minimizing the first and second objectives. Here, the Saint Venant equations include the continuity equation (Equation (6)) and the momentum equation (Equation (7)), which are hydraulic constraints of the problem and are implicitly satisfied by running the SWMM model.

2.4. Encoding

In solving the problem of designing a surface water collection system, the integer encoding is used. In the case of integer encoding, the number of genes in each chromosome is equal to the maximum number of proposed designs at the watershed level. In this case, the value of each gene is an integer representing the dimensions of the corresponding design. Integer encoding is particularly effective in cases where there are a large number of proposed designs (such as real case studies) and helps reduce the search space of the problem. Additionally, Figure 4 illustrates the algorithm for designing a flood control system in the modeling scenario, and the steps of this algorithm are presented in the flowchart.

2.5. Model Establishment

Hydrological and hydraulic models were developed for the drainage networks in Tehran as part of the comprehensive studies on Tehran’s surface water management plan [50]. Therefore, in this research, the same modeling approach and parameter calibration were adopted to create the utilized model. In the initial stage of modeling and design, determining the characteristics of the design rainfall, including its depth and duration along with the temporal pattern, was crucial. The depth of rainfall can be obtained using intensity–duration–frequency (IDF) relationships for the selected return period. In this method, meteorological studies provide intensity–duration–frequency curves for rainfall at 9 points in Tehran, and then, by analyzing this information, generalized curves representing short-term rainfall in Tehran were obtained. Consequently, based on the analysis of precipitation data from rain gauge stations within the Tehran metropolitan area, the following formula was suggested for short-term rainfall [51]:

i = C_Alt.RPD^−0.654

(8)

In the above equation, i represents rainfall intensity (millimeters per hour), D represents rainfall duration (minutes), and C_Alt.RP is the coefficient corresponding to the design return period (50-year return period) and average subbasin elevation. The value of the C_Alt.RP coefficient is determined based on the frequency analysis of recorded precipitation data considering the rainfall return period and has a direct relationship with the average subbasin elevation. The coefficient values for different return periods and various elevations are presented in

Table 2. Coefficients of the generalized equation of average rainfall intensity in Tehran (adapted from Ref. [41]).

Height (m)	Return Periods (Years)
	2	5	10	20	25	50	100
900	99	127	148	169	176	197	218
1000	108	138	161	184	191	214	236
1100	117	149	174	198	206	231	255
1200	125	160	187	213	221	248	274
1300	134	171	199	228	237	265	293
1400	143	182	212	242	252	282	312
1500	151	193	225	257	267	299	331
1600	160	204	238	272	283	316	350
1700	168	215	251	286	298	333	369
1800	177	226	264	301	313	350	388
1900	186	238	277	316	328	368	407
2000	194	249	290	330	344	385	426
2100	203	260	302	345	359	402	445
2200	212	271	315	360	374	419	463
2300	220	182	328	375	389	436	482
2400	229	293	341	389	405	453	501
2500	238	304	354	404	420	470	520

.

Based on previous studies, a rainfall design with a 50-year return period is recommended for the stormwater network in Tehran, and therefore, this return period has been chosen here. Additionally, based on the generated digital elevation model, the weighted average elevation of each subbasin is determined. Considering the coefficients of the generalized intensity–duration–frequency equation, the rainfall intensity for Tehran is extracted from Table 2. Furthermore, the rainfall values for each subbasin are calculated for different return periods based on a 6 h rainfall duration. The rainfall amount obtained from the 6 h duration, using the alternating block pattern (suitable for short-duration rainfall in Tehran), is distributed over time, thus determining the design rainfall. In summary, using the IDF equation, the design rainfall with a 50-year return period is estimated to be between 34 to 53 mm. In this study, the number curve method of the National Resources Conservation Service (NRCS), also known as the former Soil Conservation Service (SCS), is used to convert rainfall to net rainfall or runoff. Additionally, initial losses due to land use and soil characteristics are calculated using the SCS curve number method [52,53,54,55,56,57,58,59].

3. Results

In this study, the runoff volume for each return period has been obtained based on the output from the SWMM software version 5.1. The runoff volume for each return period is presented in Figure 5. This runoff volume represents the amount of water escaping from the stormwater channels, encompassing different return periods of the floodplain. This causes damage to the land uses within the study area located in the floodplain. Also, the longitudinal profile of the main channels of the Chitgar basin for the 50-year return period is shown in Figure 6.

As mentioned earlier, in this study, the NSDE optimization model was utilized to solve the problem of optimal design of the stormwater control system and surface water collection system for various return periods. Subsequently, the application of the optimization model for the design and presentation of the best solution for urban stormwater control system design will be provided in the case study.

In the optimization model, the decision variables are defined as follows:

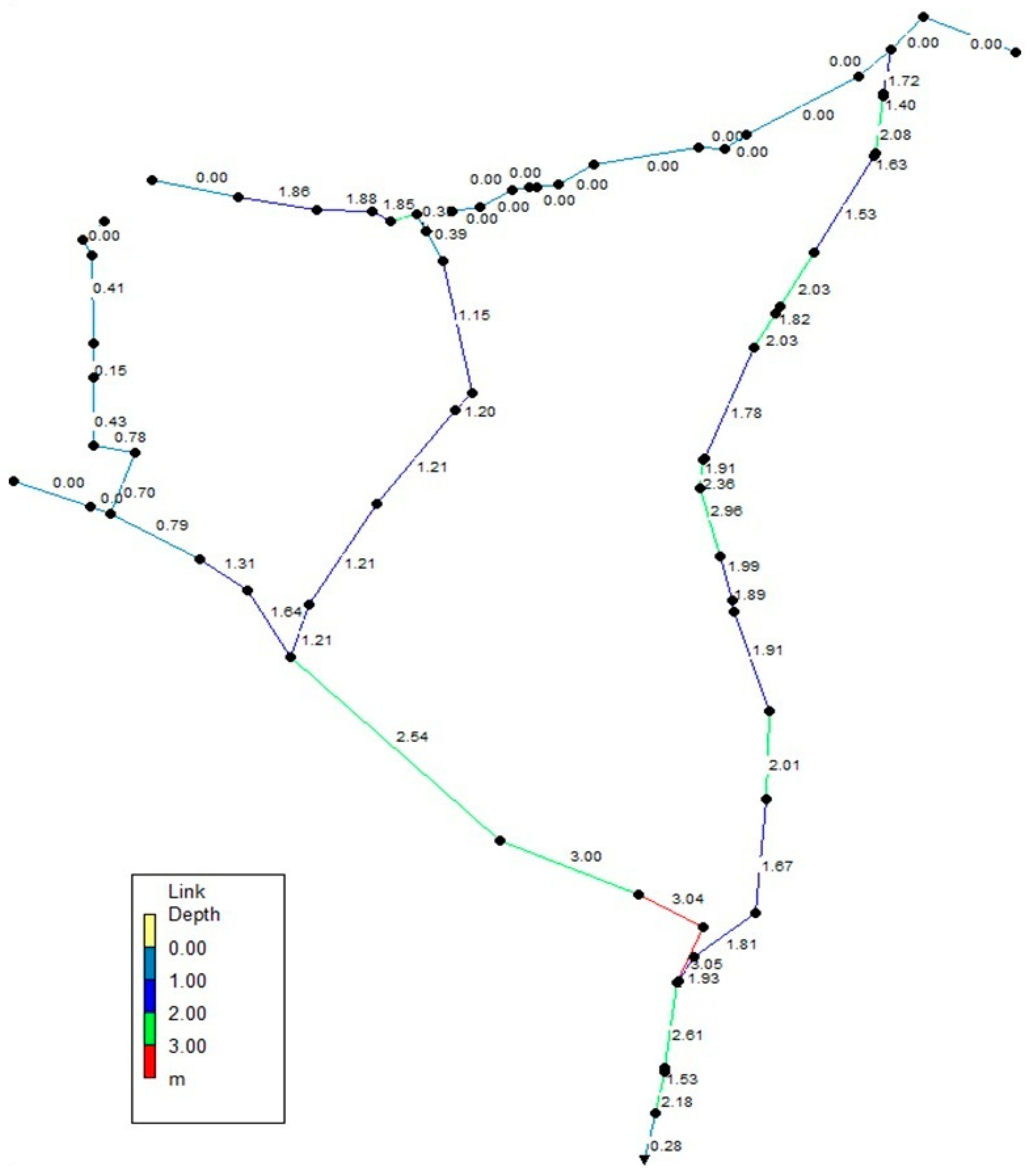
• The amount of height increase for the flood walls is defined for 16 intervals. In this variable, the corresponding channel is divided into 16 unequal parts, and the criterion is the increase in height in critical walls that may result in the overflow of the stormwater due to their low height. Increasing the height of these walls prevents water from escaping the network or minimizes its quantity (16 decision variables).
• The acceptable increase in channel width based on the required capacity for width expansion (16 decision variables).
• The increase in dimensions of cross-sectional structures or bridges (seven decision variables). In this case, based on field observations and comparing bridges that have the potential for modification, they are considered decision variables. Sometimes, the low height of the bridges increases the likelihood of water overflow from the channel and creating space for height variations in these cross-sectional structures or culverts, considering the necessary costs, can be a good option for reducing damages and the volume of water escaping from the corresponding channel.
• Since in some cases, the width of the bridges is smaller than the channel width, widening the bridges is considered a decision variable based on the maximum required capacity for expansion (seven decision variables).

Therefore, optimization has been performed in three different scenarios based on the aforementioned decision variables.

• Scenario one considers only the increase in height and widening of bridges and cross-sectional structures along the selected channel path. The number of decision variables for this scenario is 14.
• Scenario two is the case where the increase in wall height and the widening of channels and bridges are considered at different intervals for the Chitgar River basin channel. Hence, the number of decision variables for this scenario is 32.
• Scenario three includes both previous scenarios, i.e., the increase in height for bridges and cross-sectional structures, wall height, and the widening of channels and bridges. The number of decision variables in scenario three is 46 (

  Table 3. The number of decision variables in each chromosome for different optimization modes.

  Case	Number of Channels	Number of Bridges	Number of Decision Variables
  1	-	14	14
  2	32	-	32
  3	32	14	46

  ).

4. Discussion

This study determines the optimal values for increasing the height and width of flood walls in the main channel and critical cross-sectional structures (chokepoints), as well as widening walls and bridges to provide the hydraulic capacity for the passage of the 50-year return period flood. Taking into account the cost considerations and the stability of the walls, the optimization model defines the optimal design solutions.

The hydraulic modeling reveals that the existing bridges in the area sometimes hinder the passage of floods, resulting in blockages in waterways, as well as water overflow and dispersion in various areas, including streets, pedestrian paths, and residential, administrative, and commercial areas, leading to significant costs and damages. Since increasing the width of the bridges is limited by field observations and initial studies, specific changes in bridge width have been considered in the optimization model, taking into account the constraints on width variation. Therefore, the increase in height and the widening of chokepoints is considered a relevant decision variable for the cross-sectional structures in a way that optimizing them can lead to a significant reduction in the volume of the 50-year return period flood, in addition to economic considerations. The optimization model was executed for the approved 50-year return period by the urban officials in Tehran for the renovation/reconstruction of the urban stormwater collection system, and the best solutions were obtained from the optimizer for various scenarios. Figure 7 illustrates the obtained Pareto front solutions from the optimization model in three different optimization scenarios. In all three scenarios, there are solutions that are superior to the initial design (without any optimization consideration). The best performance is achieved in the third scenario, where both strategies of increasing wall height and widening, as well as bridge dimensions, are considered.

If the criterion for selecting a design is based on only one objective of the optimization problem (e.g., reducing the flood volume), the results obtained from the three approaches can be examined based on the Pareto front solutions from the optimization model. As shown in this figure, considering any of the three scenarios yields superior solutions compared to the current state without any flood control design. The superior solutions in terms of reducing the flood volume are evident, with a 7.66% reduction in the first scenario, a 7.35% reduction in the second scenario, and a 95.26% reduction in the third scenario, highlighting the superiority of all three scenarios.

As observed in the Figure 7, each point on the curve can be selected as an optimal solution. The final decision of the decisionmaker can be made based on one of the following key criteria:

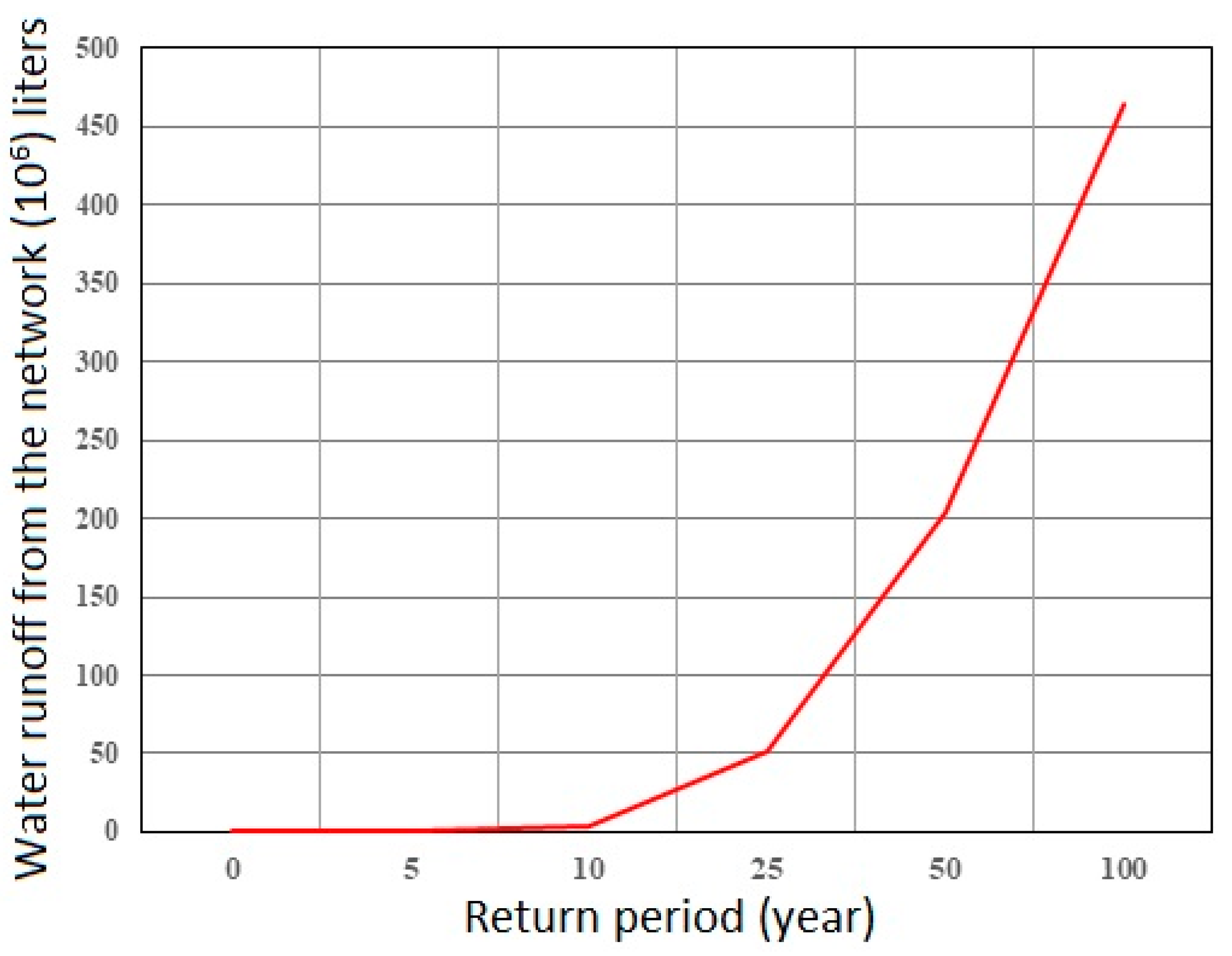
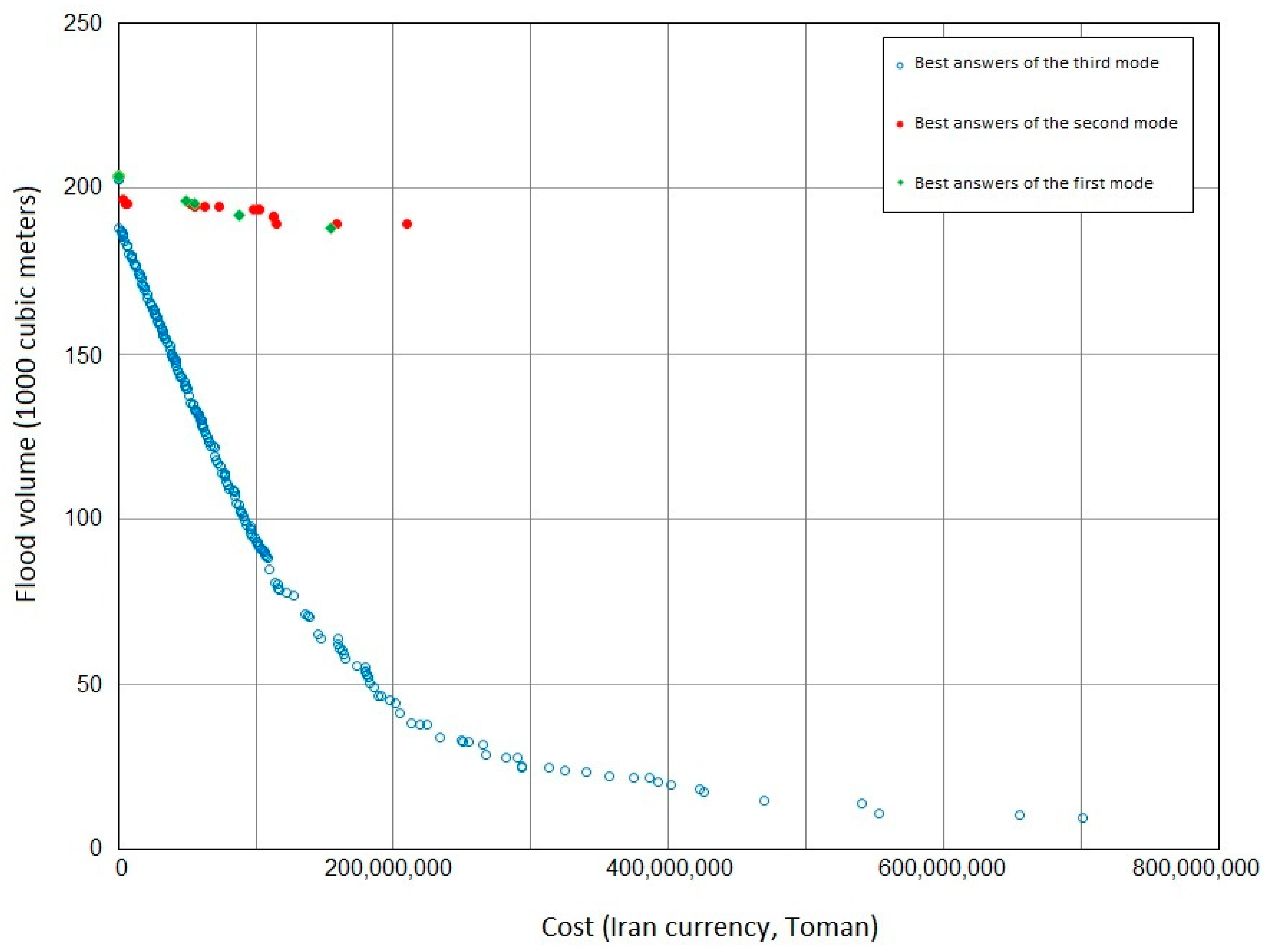
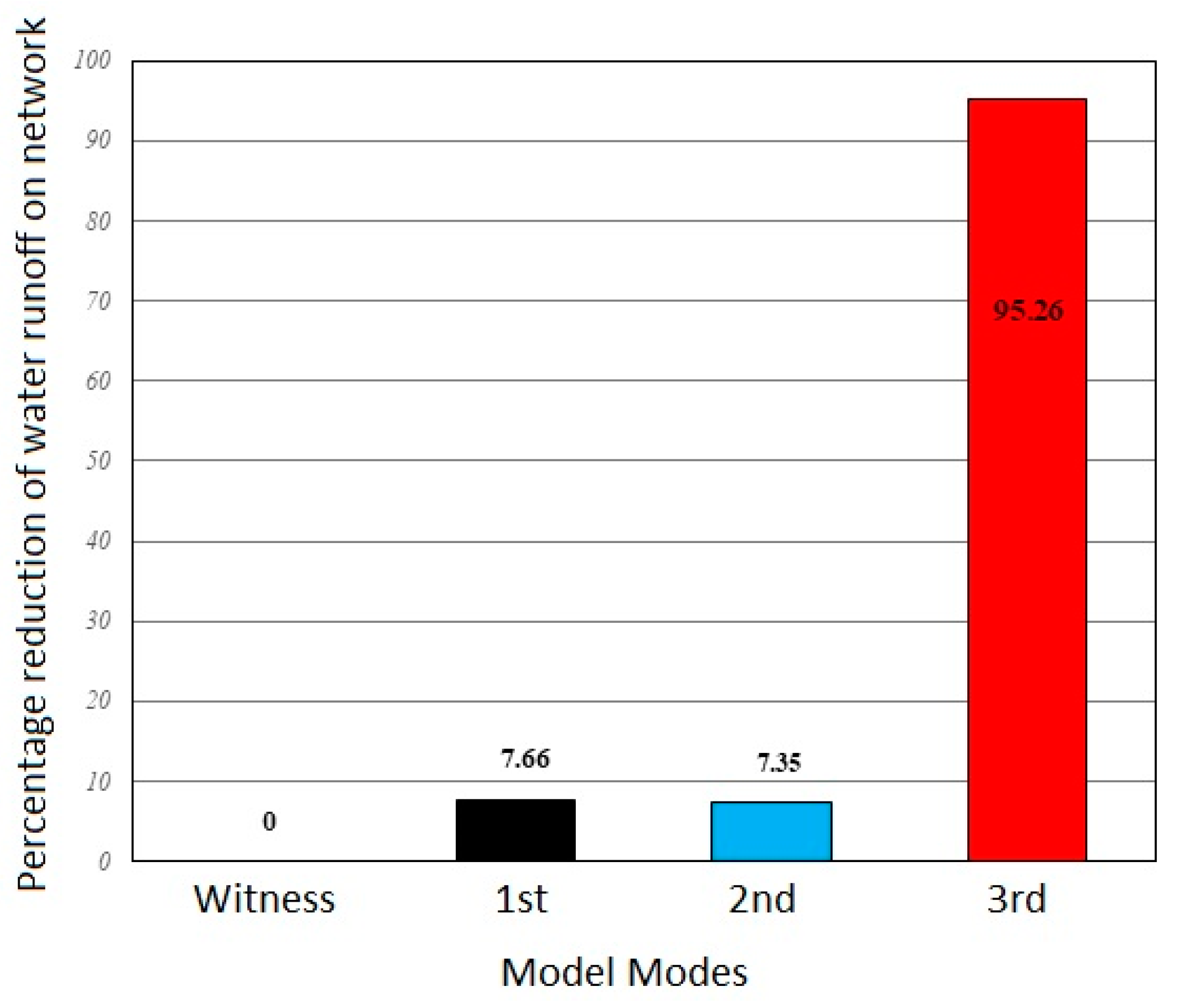
• Determining the final point based on the expected reduction in the flood volume in the study area.
• Determining the final point based on considering each of the first, second, and third scenarios, where changes are possible (generally based on the available resources of the municipality or relevant organizations for improvement in the objective function).
• Determining the final point based on a location on the curve that has an acceptable reduction in the flood volume, with a proportional decrease in the associated cost compared to the general state, and the potential for better cost-effective defense.
• Determining the final point based on the maximum approved budget for the Tehran urban stormwater management project.

Now, considering the graphs in Figure 8, the percentage reduction in water escape from the network for the first scenario, which includes considering the bridges as decision variables, is almost optimal compared to the second scenario, which considers walls as decision variables. However, overall, the superior solutions are obtained in the third scenario, which demonstrates absolute superiority over the other two scenarios and the initial state without any design.

By keeping the construction costs constant for different scenarios, the best design was determined for a specific cost range in which all three scenarios have feasible solutions. The selected cost range in which all three designs have feasible solutions is 150–150 million Tomans (unofficial unit of Iranian currency). Within this cost range, by comparing the obtained solutions, it was determined that the optimized design of the first scenario achieves a 7.67% reduction in flooding at the same fixed cost, while the second scenario achieves a 6.68% reduction, and the comprehensive design of the third scenario achieves a 64.01% reduction in flooding. This indicates the economic superiority of the overall solution of the third scenario obtained from the optimization model compared to the other two scenarios within a fixed cost range. Figure 9 illustrates the comparison performed for the three designs under the condition of fixed costs. It also demonstrates the superiority of the solutions of the first scenario over the second scenario within the selected cost range.

In accordance with the results of the modeling and optimization, the analysis of decision variable values can be described as:

Observed changes in the bridges: Based on the obtained optimal solutions, among the seven existing bridges (refer to Figure 3), it can be stated that increasing the height of bridge B6 leads to a reduction in the volume of flooding in such a way that in all the obtained optimal solutions, increasing the height of bridge B6 is one of the options for reducing the flood volume considering the changes in the throat heights. Therefore, the existence of this bridge intensifies the flood volume and the damage caused by large or small floods with a return period of 50 and 100 years. Consequently, rectifying this bridge results in a reduction in the flood volume.

In the case of bridges B2 and B4, the changes in height based on the values of decision variables in the optimal solution were not significant enough to consider changing the heights of these bridges for reducing the flood volume for the 50- and 100-year return periods. Due to the high costs of demolition and reconstruction of bridges, it is reasonable for these bridges to be overlooked and left unchanged. In terms of the remaining bridges, the changes in their heights lead to a reduction in the flood volume, and considering the obtained costs, necessary changes in the heights of these bridges are recommended. Considering the set of obtained solutions from the optimization model, it can be concluded that the wide range of changes has a limited impact on flood reduction. The obtained values are very small and insignificant, and economically, these solutions are highly logical.

Observed changes in the height and width of flood barriers: Based on the obtained solutions from the optimizer among the 16 different intervals, as we move from the upper part towards the middle of the channel, the changes in the heights of the walls become more significant. Increasing the height of the walls in the middle of the channel leads to a reduction in the flood volume. Among them, the changes in height in W1 to W6 (see Figure 2) are minimal for reducing the flood volume, and the changes in height in W9 to W16 are negligible in most of the optimal solutions, allowing us to overlook the changes in their heights. Additionally, increasing the height of walls W7 to W8 each results in a decrease in the flood volume and, consequently, the damage caused by flooding.

In the obtained optimal solutions from the optimization model, it can be mentioned that the changes in the width of the walls somehow increase from the upper part to the lower part, where the widths of walls W1, W4, W8, W12, and W15 are highly effective in reducing the flood volume, and increasing the width in these walls is necessary. Of these walls, the maximum increase in width is observed in walls W12 and W15, indicating the most sensitive and effective range for widening the walls to reduce the flood volume. Considering the multiple obtained solutions from the optimization algorithm, the optimal solution with the highest reduction in flood volume has been selected as the chosen solution. The design options related to this selected solution are presented in

Table 4. Values of decision variables in the selected optimal solution for the 50-year return period approach.

No	Variable	Value (m)	No	Variable	Value (m)	No	Variable	Value (m)
1	$H_1^B$	0.84	17	$H_3^W$	0.10	33	$W_3^W$	0.16
2	$H_2^B$	0.00	18	$H_4^W$	0.18	34	$W_4^W$	0.69
3	$H_3^B$	0.11	19	$H_5^W$	0.13	35	$W_5^W$	0.12
4	$H_4^B$	0.08	20	$H_6^W$	0.10	36	$W_6^W$	0.11
5	$H_5^B$	0.13	21	$H_7^W$	0.48	37	$W_7^W$	0.00
6	$H_6^B$	1.40	22	$H_8^W$	1.13	38	$W_8^W$	0.39
7	$H_7^B$	0.45	23	$H_9^W$	0.11	39	$W_9^W$	0.11
8	$W_1^B$	0.29	24	$H_{10}^W$	0.00	40	$W_{10}^W$	0.04
9	$W_2^B$	0.07	25	$H_{11}^W$	0.11	41	$W_{11}^W$	0.11
10	$W_3^B$	0.08	26	$H_{12}^W$	0.12	42	$W_{12}^W$	1.71
11	$W_4^B$	0.48	27	$H_{13}^W$	0.00	43	$W_{13}^W$	0.12
12	$W_5^B$	0.57	28	$H_{14}^W$	0.10	44	$W_{14}^W$	0.14
13	$W_6^B$	0.11	29	$H_{15}^W$	0.11	45	$W_{15}^W$	1.56
14	$W_7^B$	0.02	30	$H_{16}^W$	0.16	46	$W_{16}^W$	0.09
15	$H_1^W$	0	31	$W_1^W$	0.59
16	$H_2^W$	0.22	32	$W_2^W$	0

, where $W_j^B$ is the width of bridges, $H_j^B$ is the height of bridges, $H_j^W$ is the height of the wall, and $W_j^W$ is the width of the dam wall.

After obtaining the optimal solution using the algorithm and incorporating the results into the hydraulic simulation model, certain outputs of the hydraulic model are obtained. Figure 10a illustrates the water discharge rates from the studied network for various nodes. As shown, except for two nodes, the water discharge rate from the network is zero for all nodes, indicating the effectiveness and proper performance of the specific code and the optimization algorithm in reducing the flood volume and water discharge from the studied network. Figure 10b shows the maximum water depth for different nodes in the top solutions output by the simulation model. Additionally, Figure 11 also illustrates the water levels for each of the water channels. Based on the obtained outputs, it is evident that the rehabilitated channel has the necessary capacity to allow water flow, resulting in the minimum possible water discharge in the network.

5. Conclusions

The proposed algorithm in this study is a combination of various models and methods, including the multi-objective optimization model NSDE and the rainfall–runoff model SWMM. The main results obtained from the development of the models and methods used in this study are as follows.

The obtained optimal solutions with a 50-year return period demonstrate absolute improvement compared to the existing conditions without the Chitgar Channel project. Furthermore, considering the cost range considered for the optimal solutions with a 50-year return period, it was observed that the solution that incorporates both optimization scenarios for channels and cross structures or bridges is the best solution for designing/rehabilitating the system, and it is more effective in reducing flood damages. In different design scenarios with a 50-year return period, the highest reduction in damages was 95.26%, with a cost level of 700 million Tomans (unofficial unit of Iranian currency) compared to the no-project scenario.

With almost the same cost level for the optimal solution with a 50-year return period, the first scenario (only bridges) achieved a reduction of 7.66%, the second scenario (only channels) achieved a reduction of 7.35%, and the third scenario (channels + bridges) achieved a reduction of 95.26% in water discharge from the network, demonstrating the superiority of all three scenarios over the no-project scenario. Thus, the obtained results provide comprehensive information about the efficiency and relative importance of different flood control projects and rank them accordingly. Consequently, the utilization and development of these methods are necessary and essential for future studies.