Utility of Open-Access Long-Term Precipitation Data Products for Correcting Climate Model Projection in South China
Abstract
:1. Introduction
2. Materials
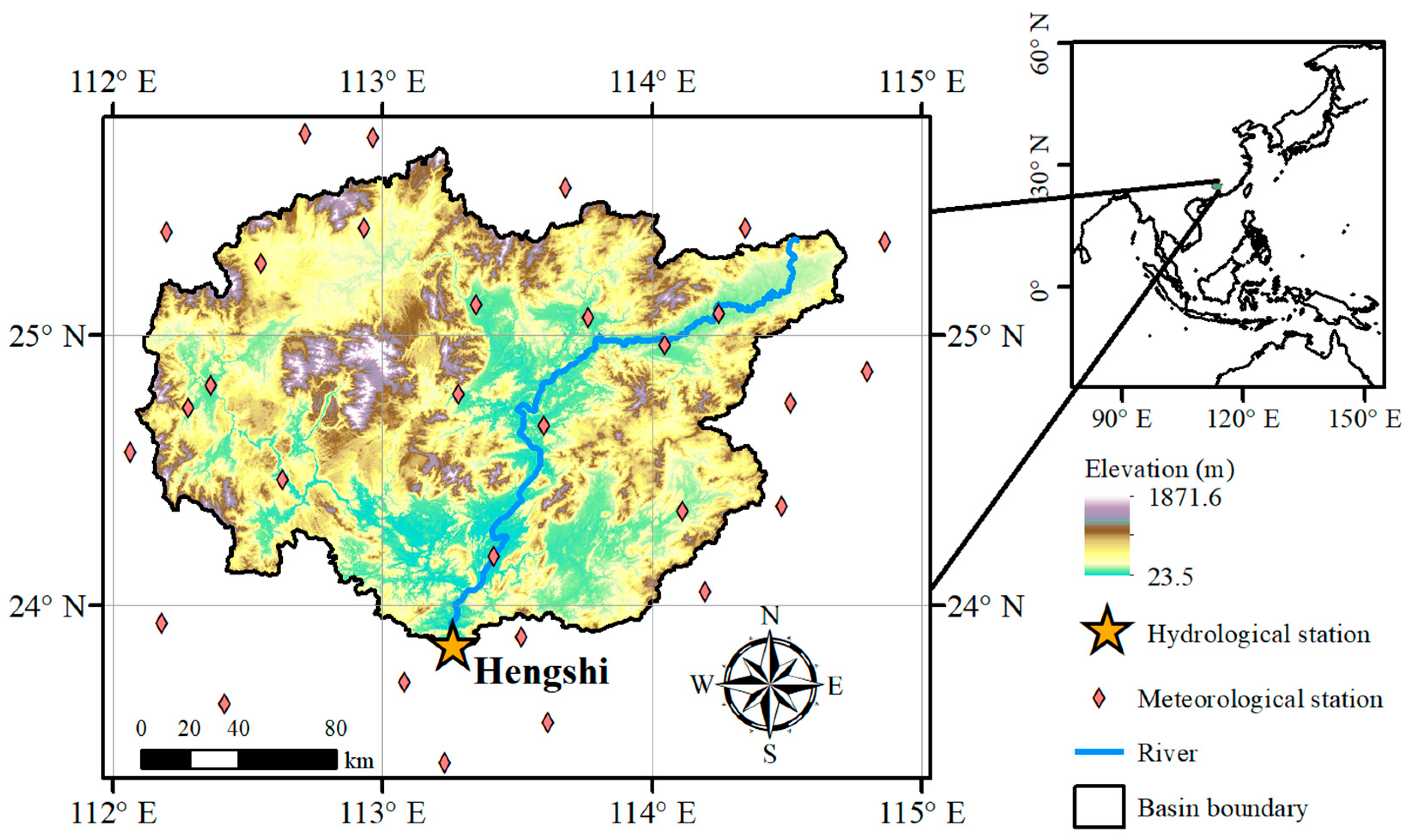
2.1. Study Area
2.2. Long-Term Quantitative Precipitation Estimation (QPE) Products
2.2.1. ERA5 Reanalysis
2.2.2. PERSIANN-CDR (PCDR)
2.2.3. CHIRPS
2.3. CMIP6 Projection Outputs
2.4. Ground-Based Observation Data
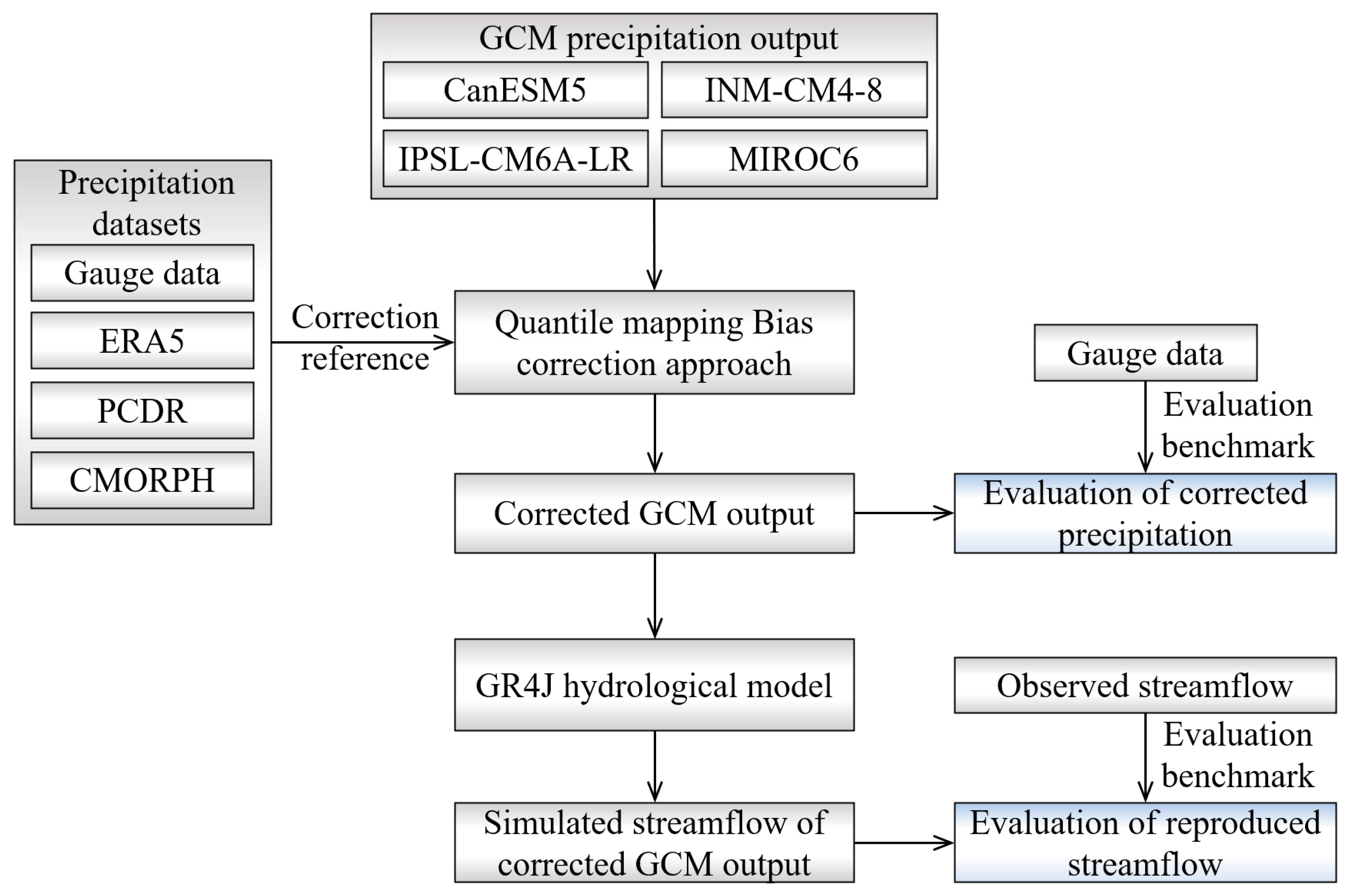
3. Methods
3.1. Quantile Mapping (QM) Statistical Bias-Correction Approach
3.2. Assessment Metrics
3.3. GR4J Hydrological Model
4. Results
4.1. Evaluation of the QPEs
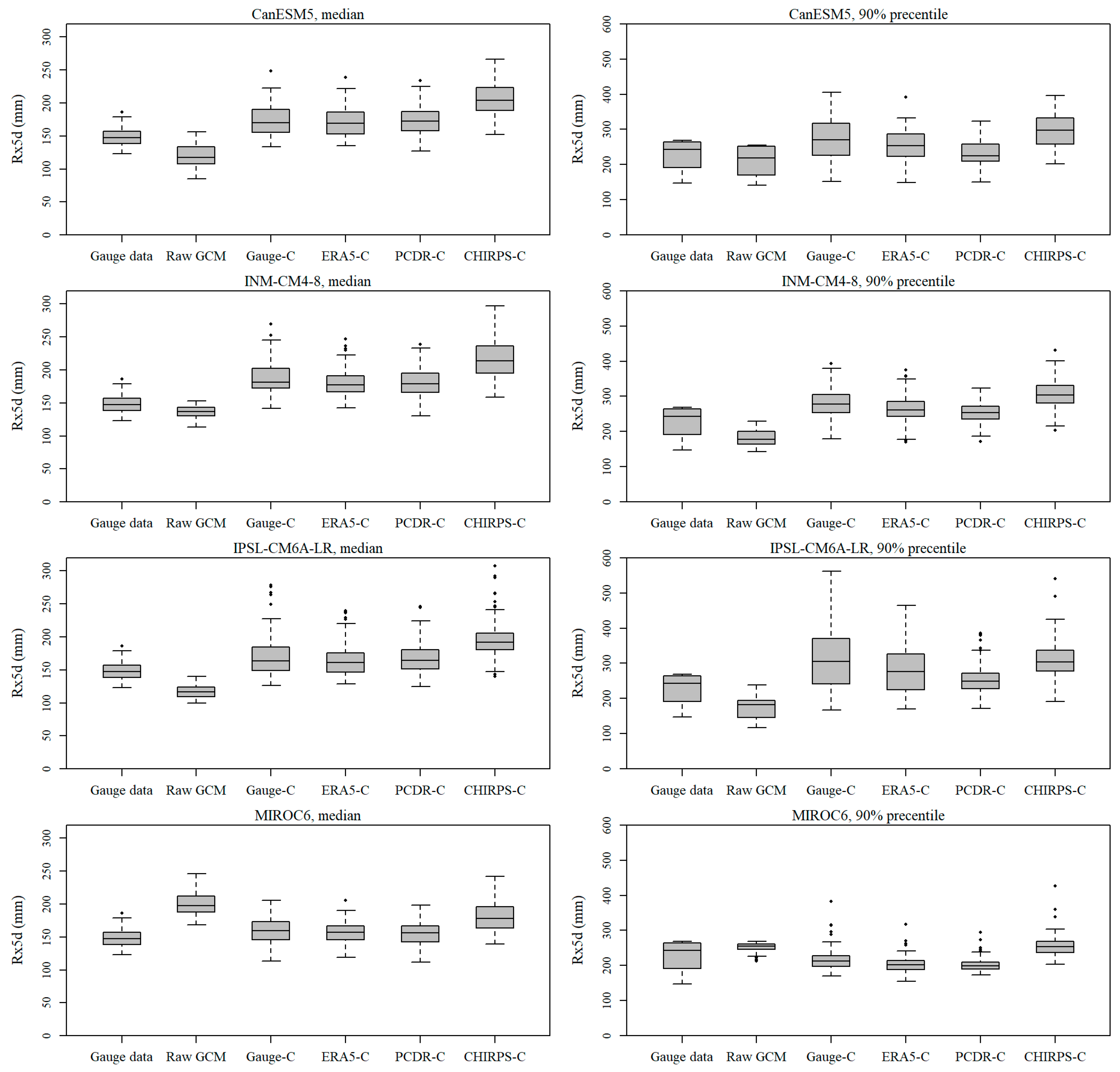
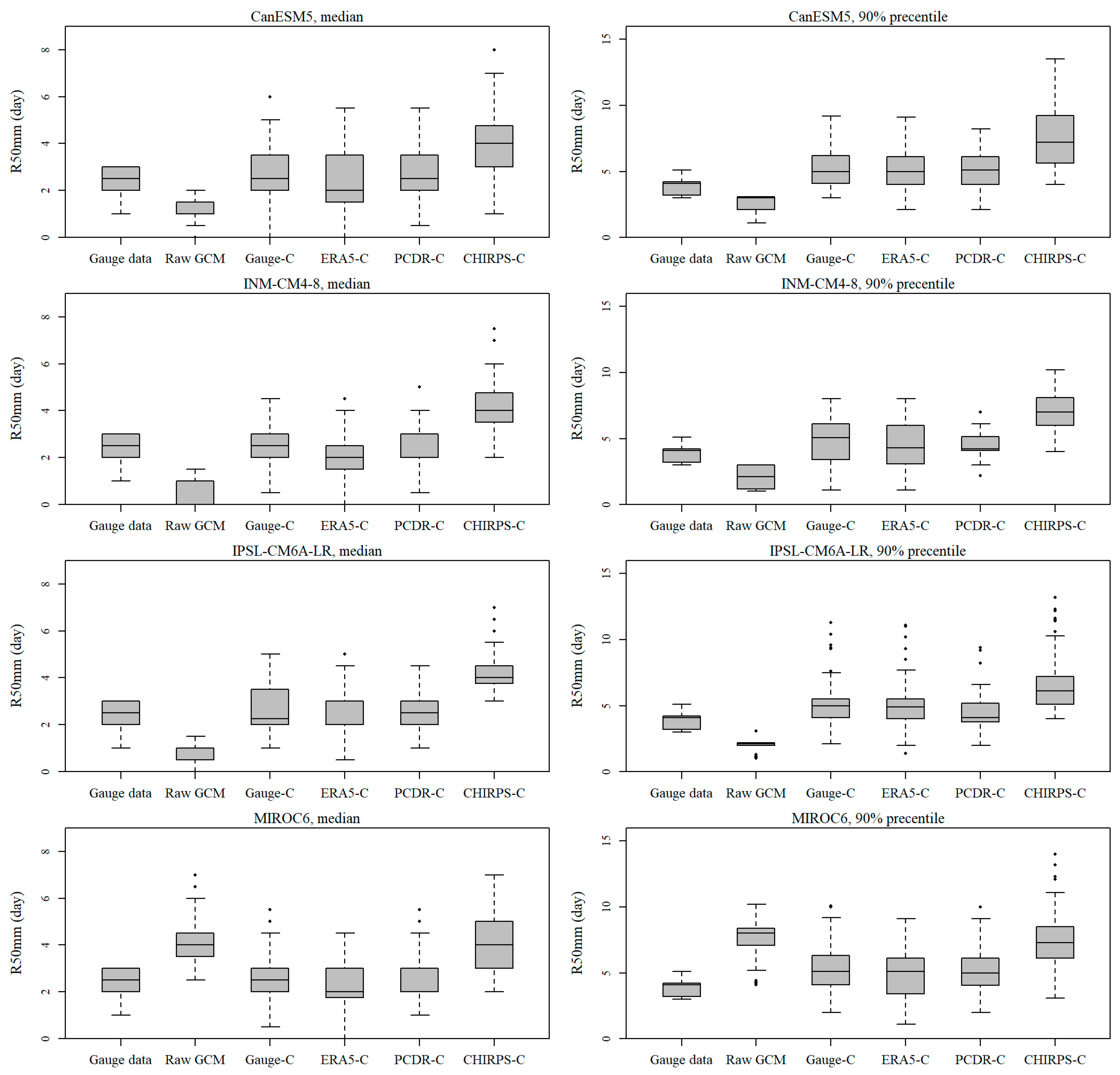
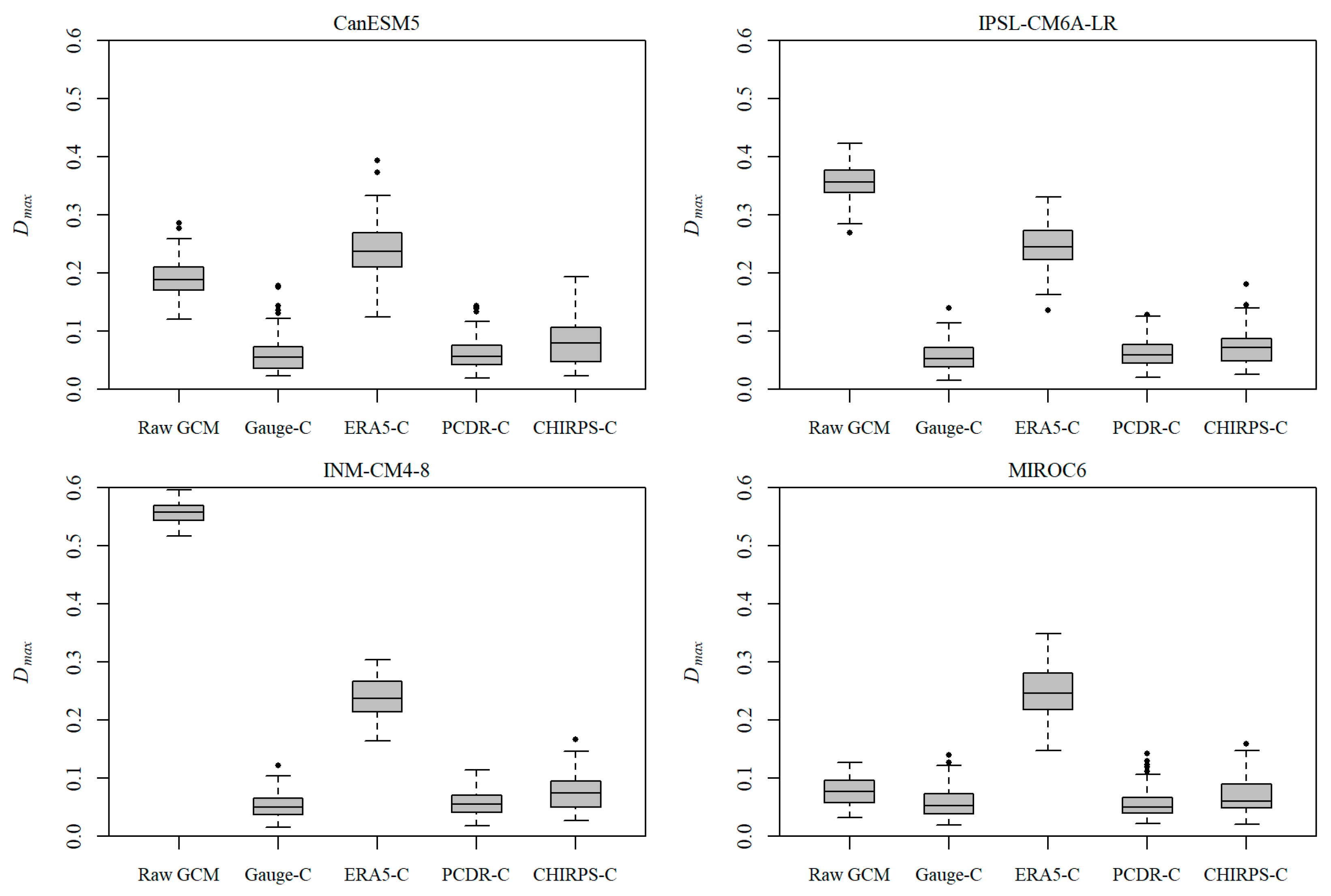
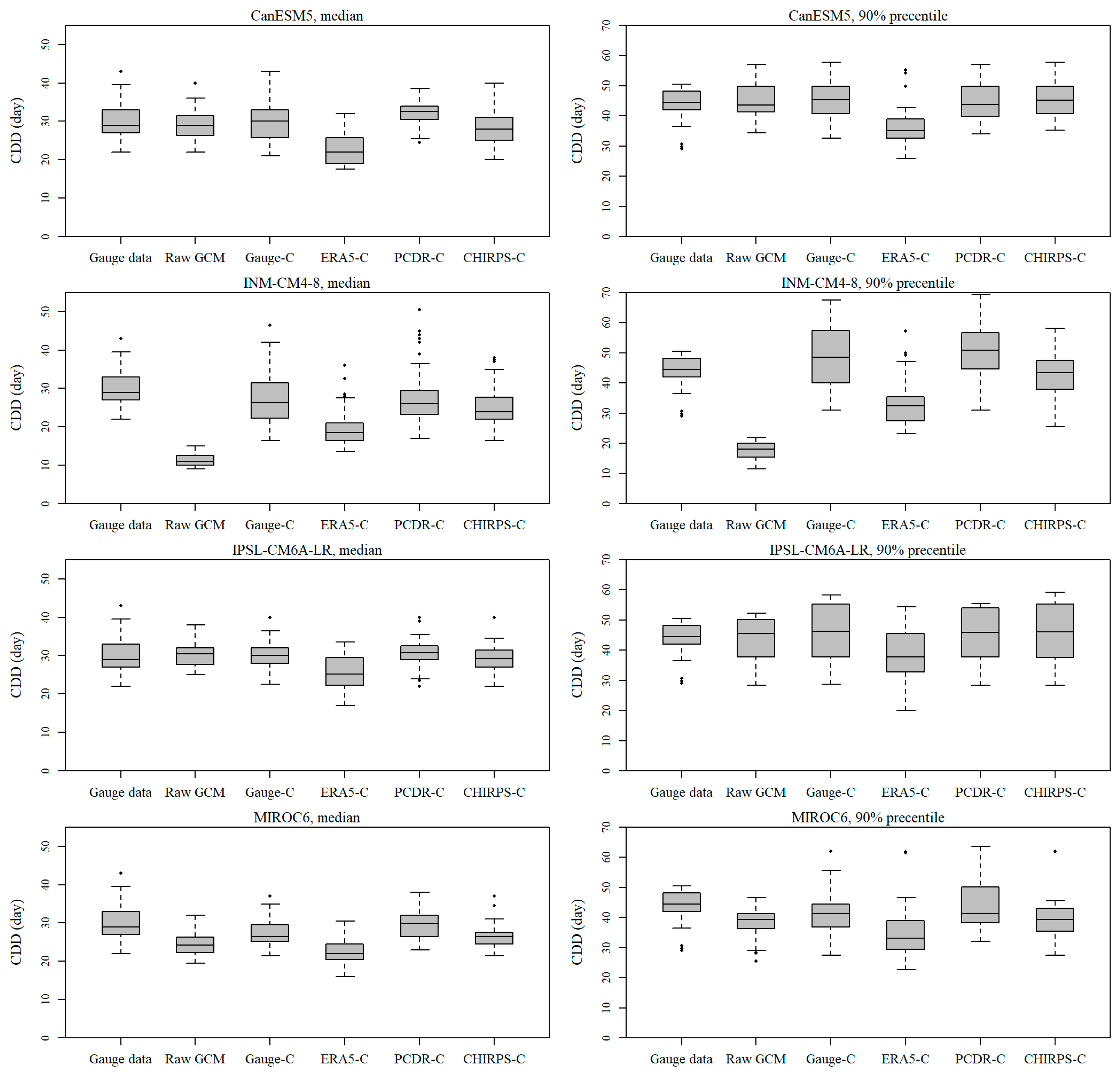
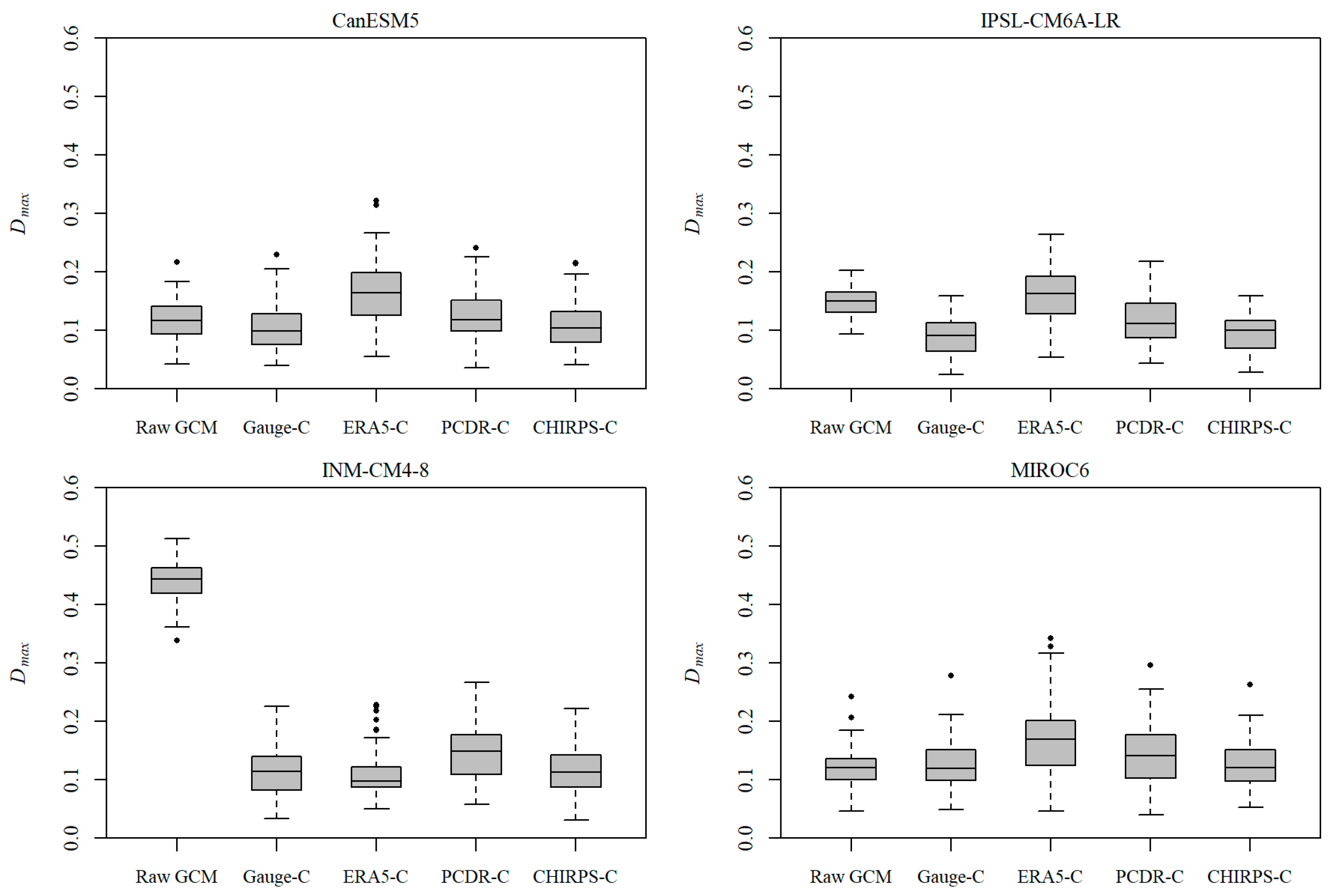
4.2. Evaluation of GCM Precipitation Outputs Bias-Corrected by QPEs
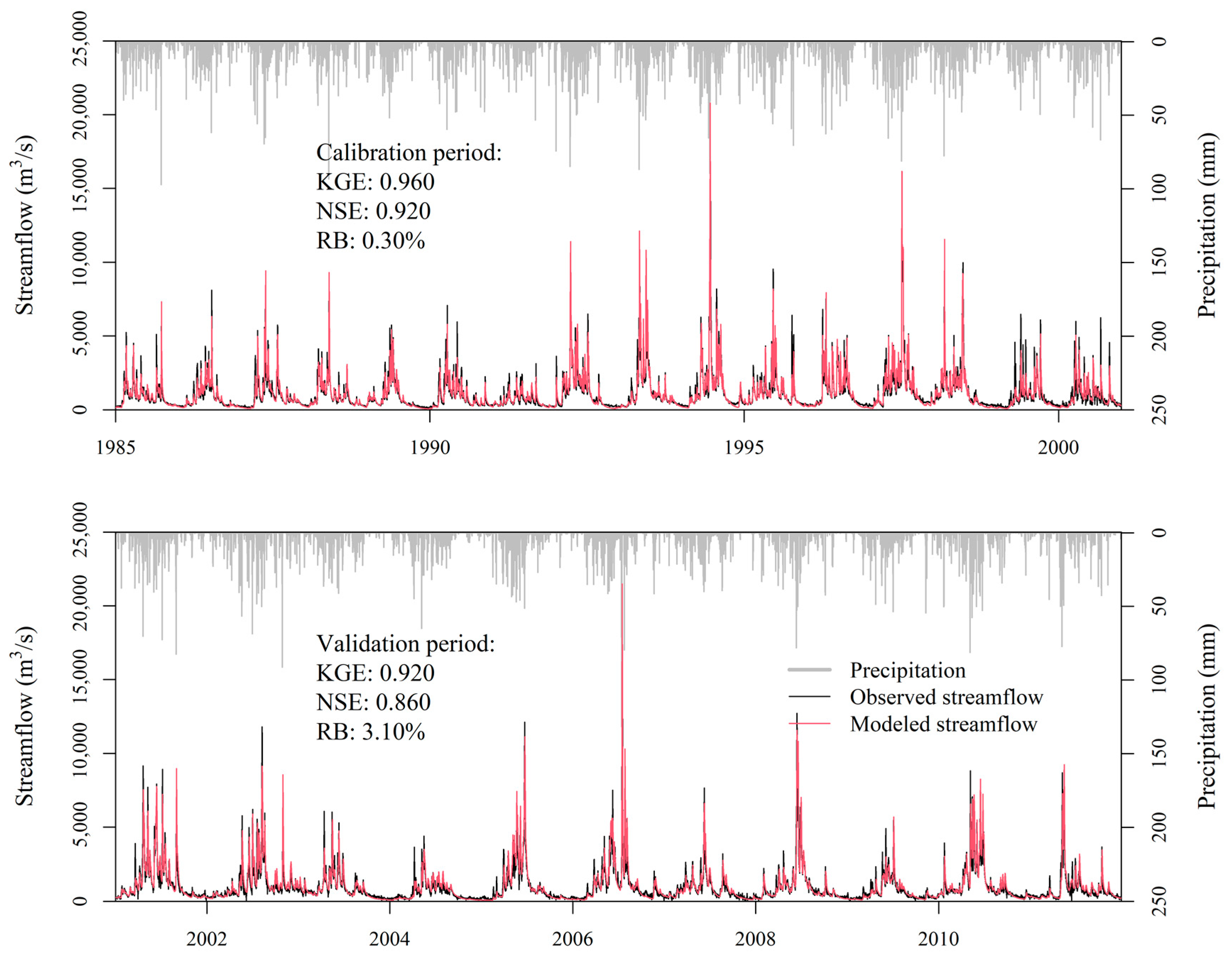
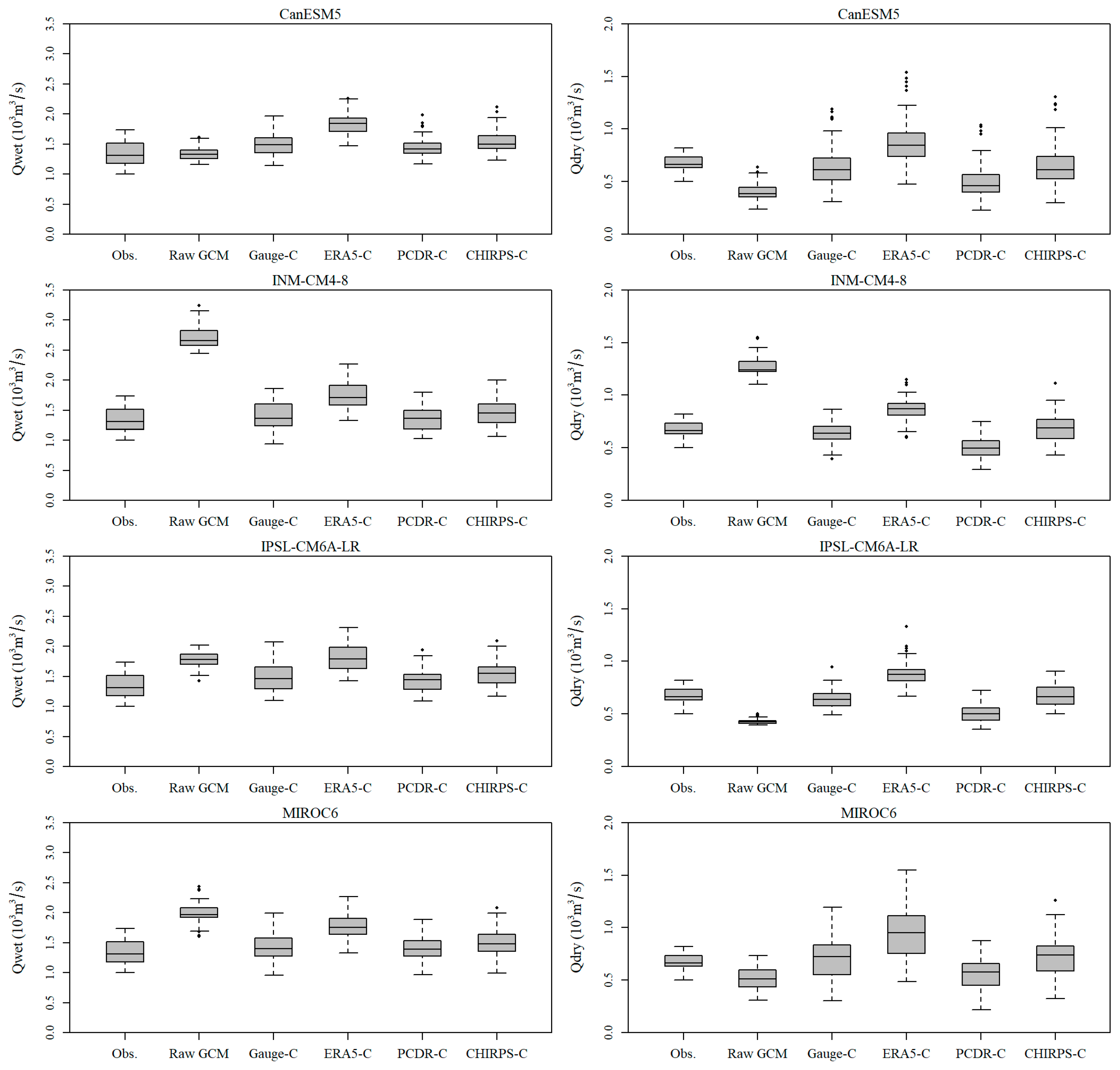
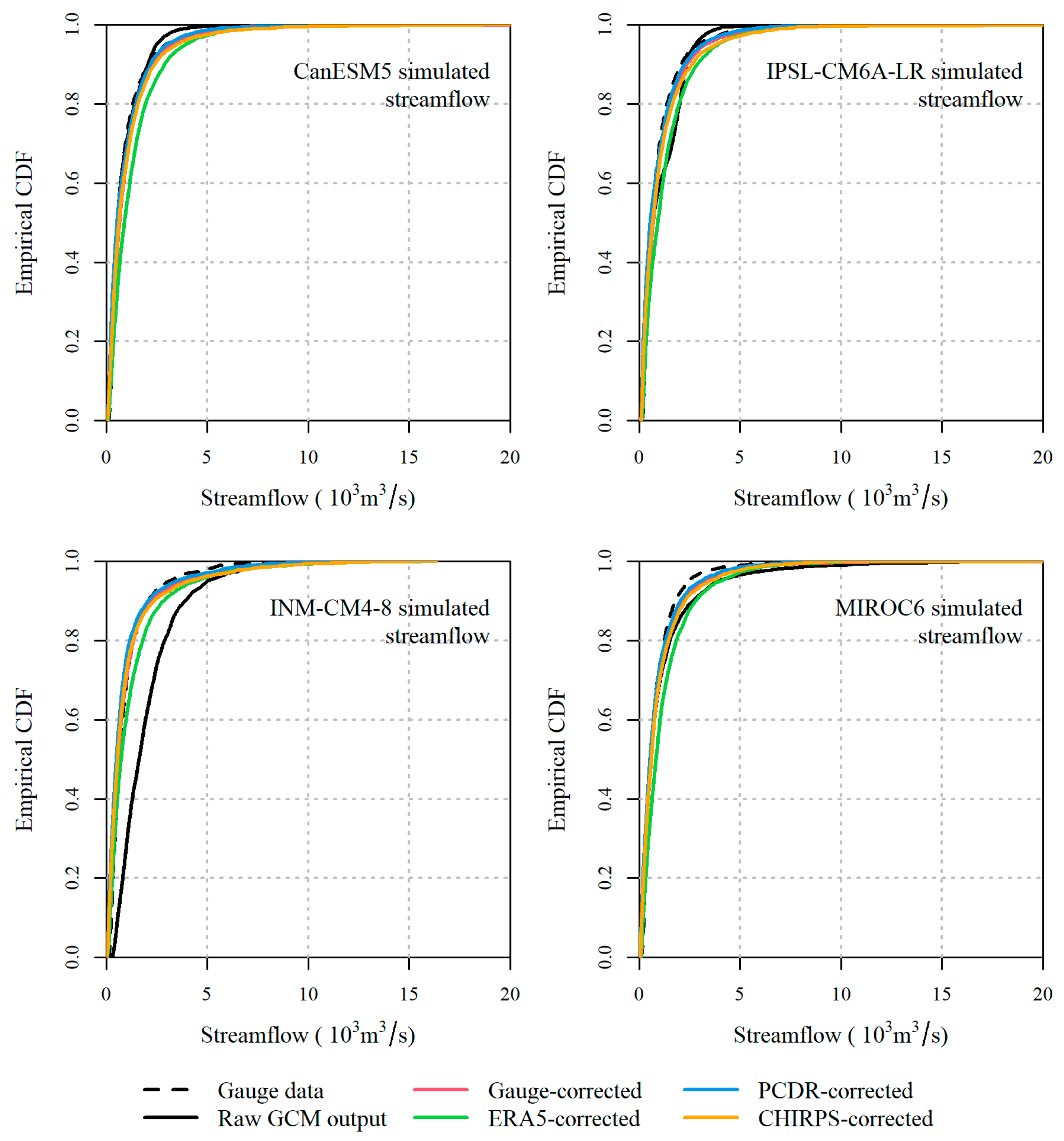
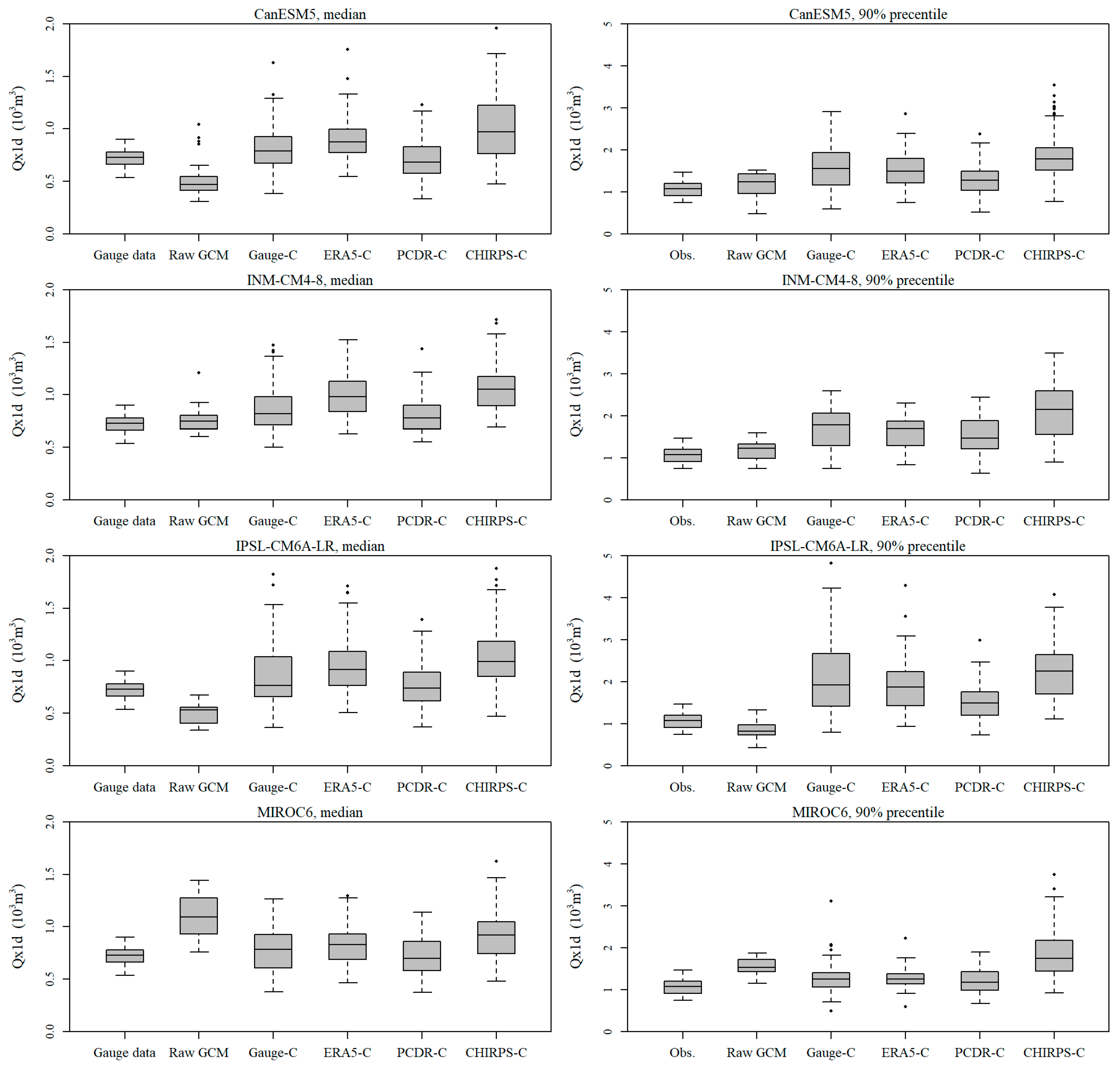
4.3. Evaluation of Simulated Streamflow of GCM Precipitation Outputs Bias-Corrected by QPEs
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CDF | Cumulated distribution functions |
| CHIRPS | Climate Hazards Group (CHG) Infrared Precipitation with Station |
| CMIP | Coupled Model Intercomparison Project |
| CMIP6 | CMIP phase 6 |
| ERA5 | The fifth generation of European Centre for Medium-Range Weather |
| Forecasts (ECMWF) Reanalysis | |
| GCM | Global Climate Model |
| GR4J | Génie Rural à 4 paramètres Journalier |
| K-S test | Kolmogorov–Smirnov test |
| KGE | Kling–Gupta efficiency coefficient |
| NSE | Nash–Sutcliffe efficiency |
| PERSIANN-CDR | Precipitation Estimation from Remotely Sensed Information using |
| Artificial Neural Networks–Climate Data Record | |
| QM | Quantile mapping |
| QPE | Quantitative precipitation estimation |
| R | Pearson correlation coefficient |
| RB | Relative bias |
| RMSE | Root mean square error |
| SCE-UA | Shuffled Complex Evolution-University of Arizona |
| WRCP | World Climate Research Programme |
Appendix A

| Extreme Index | Qx1d (m3) | Qx5d (m3) | Qn7d (m3) | |
|---|---|---|---|---|
| Median | Observation | 738.7 | 2438.9 | 116.3 |
| Modeled streamflow | 712.3 | 2581.6 | 77.7 | |
| 90% percentile (10% percentile for Qn7d) | Observation | 1132.3 | 4331.7 | 79.3 |
| Modeled streamflow | 1185.9 | 4455.4 | 52.2 | |
References
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity Is Dead: Whither Water Management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Valjarević, A.; Milanović, M.; Gultepe, I.; Filipović, D.; Lukić, T. Updated Trewartha climate classification with four climate change scenarios. Geogr. J. 2022, 188, 506–517. [Google Scholar] [CrossRef]
- Madakumbura, G.D.; Thackeray, C.W.; Norris, J.; Goldenson, N.; Hall, A. Anthropogenic influence on extreme precipitation over global land areas seen in multiple observational datasets. Nat. Commun. 2021, 12, 3944. [Google Scholar] [CrossRef] [PubMed]
- Immerzeel, W.W.; Lutz, A.F.; Andrade, M.; Bahl, A.; Biemans, H.; Bolch, T.; Hyde, S.; Brumby, S.; Davies, B.J.; Elmore, A.C.; et al. Importance and vulnerability of the world’s water towers. Nature 2020, 577, 364–369. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the GPM IMERG satellite-based precipitation products and the hydrological utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
- Zhong, R.; Zhao, T.; He, Y.; Chen, X. Hydropower change of the water tower of Asia in 21st century: A case of the Lancang River hydropower base, upper Mekong. Energy 2019, 179, 685–696. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model. Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef] [Green Version]
- Knutti, R.; Masson, D.; Gettelman, A. Climate model genealogy: Generation CMIP5 and how we got there. Geophys. Res. Lett. 2013, 40, 1194–1199. [Google Scholar] [CrossRef]
- Eyring, V.; Cox, P.M.; Flato, G.M.; Gleckler, P.J.; Abramowitz, G.; Caldwell, P.; Collins, W.D.; Gier, B.K.; Hall, A.D.; Hoffman, F.M.; et al. Taking climate model evaluation to the next level. Nat. Clim. Chang. 2019, 9, 102–110. [Google Scholar] [CrossRef] [Green Version]
- Satoh, Y.; Yoshimura, K.; Pokhrel, Y.; Kim, H.; Shiogama, H.; Yokohata, T.; Hanasaki, N.; Wada, Y.; Burek, P.; Byers, E.; et al. The timing of unprecedented hydrological drought under climate change. Nat. Commun. 2022, 13, 3287. [Google Scholar] [CrossRef]
- Pokhrel, Y.; Felfelani, F.; Satoh, Y.; Boulange, J.; Burek, P.; Gädeke, A.; Gerten, D.; Gosling, S.N.; Grillakis, M.; Gudmundsson, L.; et al. Global terrestrial water storage and drought severity under climate change. Nat. Clim. Chang. 2021, 11, 226–233. [Google Scholar] [CrossRef]
- Boulange, J.; Hanasaki, N.; Yamazaki, D.; Pokhrel, Y. Role of dams in reducing global flood exposure under climate change. Nat. Commun. 2021, 12, 417. [Google Scholar] [CrossRef]
- Wing, O.E.J.; Lehman, W.; Bates, P.D.; Sampson, C.C.; Quinn, N.; Smith, A.M.; Neal, J.C.; Porter, J.R.; Kousky, C. Inequitable patterns of US flood risk in the Anthropocene. Nat. Clim. Chang. 2022, 12, 156–162. [Google Scholar] [CrossRef]
- Barbarossa, V.; Bosmans, J.; Wanders, N.; King, H.; Bierkens, M.F.P.; Huijbregts, M.A.J.; Schipper, A.M. Threats of global warming to the world’s freshwater fishes. Nat. Commun. 2021, 12, 1701. [Google Scholar] [CrossRef]
- Xi, Y.; Peng, S.; Ciais, P.; Chen, Y. Future impacts of climate change on inland Ramsar wetlands. Nat. Clim. Chang. 2021, 11, 45–51. [Google Scholar] [CrossRef]
- Gernaat, D.E.H.J.; de Boer, H.S.; Daioglou, V.; Yalew, S.G.; Müller, C.; van Vuuren, D.P. Climate change impacts on renewable energy supply. Nat. Clim. Chang. 2021, 11, 119–125. [Google Scholar] [CrossRef]
- Zhong, R.; Zhao, T.; Chen, X. Evaluating the tradeoff between hydropower benefit and ecological interest under climate change: How will the water-energy-ecosystem nexus evolve in the upper Mekong basin? Energy 2021, 237, 121518. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Tebaldi, C.; van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.F.; Lowe, J.; et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model. Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef] [Green Version]
- Gupta, V.; Singh, V.; Jain, M.K. Assessment of precipitation extremes in India during the 21st century under SSP1-1.9 mitigation scenarios of CMIP6 GCMs. J. Hydrol. 2020, 590, 125422. [Google Scholar] [CrossRef]
- Hempel, S.; Frieler, K.; Warszawski, L.; Schewe, J.; Piontek, F. A trend-preserving bias correction—The ISI-MIP approach. Earth Syst. Dynam 2013, 4, 219–236. [Google Scholar] [CrossRef] [Green Version]
- Mishra, V.; Bhatia, U.; Tiwari, A.D. Bias-corrected climate projections for South Asia from Coupled Model Intercomparison Project-6. Sci. Data 2020, 7, 338. [Google Scholar] [CrossRef] [PubMed]
- Ehret, U.; Zehe, E.; Wulfmeyer, V.; Warrach-Sagi, K.; Liebert, J. HESS Opinions “Should we apply bias correction to global and regional climate model data”? Hydrol. Earth Syst. Sci. 2012, 16, 3391–3404. [Google Scholar] [CrossRef] [Green Version]
- Stefanidis, S.; Dafis, S.; Stathis, D. Evaluation of Regional Climate Models (RCMs) Performance in Simulating Seasonal Precipitation over Mountainous Central Pindus (Greece). Water 2020, 12, 2750. [Google Scholar] [CrossRef]
- Tolika, K.; Anagnostopoulou, C.; Maheras, P.; Vafiadis, M. Simulation of future changes in extreme rainfall and temperature conditions over the Greek area: A comparison of two statistical downscaling approaches. Glob. Planet. Chang. 2008, 63, 132–151. [Google Scholar] [CrossRef]
- Brighenti, T.M.; Gassman, P.W.; Gutowski, W.J.; Thompson, J.R. Assessing the Influence of a Bias Correction Method on Future Climate Scenarios Using SWAT as an Impact Model Indicator. Water 2023, 15, 750. [Google Scholar] [CrossRef]
- Pan, H.; Jin, Y.; Zhu, X. Comparison of Projections of Precipitation over Yangtze River Basin of China by Different Climate Models. Water 2022, 14, 1888. [Google Scholar] [CrossRef]
- Derdour, S.; Ghenim, A.N.; Megnounif, A.; Tangang, F.; Chung, J.X.; Ayoub, A.B. Bias Correction and Evaluation of Precipitation Data from the CORDEX Regional Climate Model for Monitoring Climate Change in the Wadi Chemora Basin (Northeastern Algeria). Atmosphere 2022, 13, 1876. [Google Scholar] [CrossRef]
- Zhu, Q.; Hsu, K.; Xu, Y.; Yang, T. Evaluation of a new satellite-based precipitation data set for climate studies in the Xiang River basin, southern China. Int. J. Climatol. 2017, 37, 4561–4575. [Google Scholar] [CrossRef]
- Katiraie-Boroujerdy, P.; Akbari Asanjan, A.; Chavoshian, A.; Hsu, K.; Sorooshian, S. Assessment of seven CMIP5 model precipitation extremes over Iran based on a satellite-based climate data set. Int. J. Climatol. 2019, 39, 3505–3522. [Google Scholar] [CrossRef]
- Bai, X.; Wu, X.; Wang, P. Blending long-term satellite-based precipitation data with gauge observations for drought monitoring: Considering effects of different gauge densities. J. Hydrol. 2019, 577, 124007. [Google Scholar] [CrossRef]
- Wang, P.; Bai, X.; Wu, X.; Lai, C.; Zhang, Z. Spatially continuous assessment of satellite-based precipitation products using triple collocation approach and discrete gauge observations via geographically weighted regression. J. Hydrol. 2022, 608, 127640. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method that Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.J.; Kidd, C.; Nelkin, E.J.; Sorooshian, S.; Stocker, E.F.; Tan, J.; et al. Integrated Multi-satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG). In Satellite Precipitation Measurement; Levizzani, V., Kidd, C., Kirschbaum, D.B., Kummerow, C.D., Nakamura, K., Turk, F.J., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 1, pp. 343–353. [Google Scholar]
- Boucher, O.; Servonnat, J.; Albright, A.L.; Aumont, O.; Balkanski, Y.; Bastrikov, V.; Bekki, S.; Bonnet, R.; Bony, S.; Bopp, L.; et al. Presentation and Evaluation of the IPSL-CM6A-LR Climate Model. J. Adv. Model. Earth Syst. 2020, 12, e2010M–e2019M. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteor. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Hong, Y.; Hsu, K.; Sorooshian, S.; Gao, X. Precipitation Estimation from Remotely Sensed Imagery Using an Artificial Neural Network Cloud Classification System. J. Appl. Meteorol. 2004, 43, 1834–1853. [Google Scholar] [CrossRef] [Green Version]
- Ashouri, H.; Hsu, K.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily Precipitation Climate Data Record from Multisatellite Observations for Hydrological and Climate Studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [Green Version]
- Lai, C.; Zhong, R.; Wang, Z.; Wu, X.; Chen, X.; Wang, P.; Lian, Y. Monitoring hydrological drought using long-term satellite-based precipitation data. Sci. Total Environ. 2019, 649, 1198–1208. [Google Scholar] [CrossRef]
- Zhong, R.; Zhao, T.; Chen, X.; Jin, H. Monitoring drought in ungauged areas using satellite altimetry: The Standardized River Stage Index. J. Hydrol. 2022, 612, 128308. [Google Scholar] [CrossRef]
- Babaousmail, H.; Hou, R.; Ayugi, B.; Sian, K.T.C.L.; Ojara, M.; Mumo, R.; Chehbouni, A.; Ongoma, V. Future changes in mean and extreme precipitation over the Mediterranean and Sahara regions using bias-corrected CMIP6 models. Int. J. Climatol. 2022, 42, 7280–7297. [Google Scholar] [CrossRef]
- Swart, N.C.; Cole, J.N.S.; Kharin, V.V.; Lazare, M.; Scinocca, J.F.; Gillett, N.P.; Anstey, J.; Arora, V.; Christian, J.R.; Hanna, S.; et al. The Canadian Earth System Model version 5 (CanESM5.0.3). Geosci. Model. Dev. 2019, 12, 4823–4873. [Google Scholar] [CrossRef] [Green Version]
- Volodin, E. The Mechanisms of Cloudiness Evolution Responsible for Equilibrium Climate Sensitivity in Climate Model INM-CM4-8. Geophys. Res. Lett. 2021, 48, e2021G–e96204G. [Google Scholar] [CrossRef]
- Ando, T.; Higuchi, T.; Hotta, H.; Iwakiri, T.; Jinno, T.; Kino, K.; Takano, Y.; Toda, M.; Yamazaki, K.; Suzuki, K.S. Description of MIROC6 AGCM; The University of Tokyo: Chiba, Japan, 2021. [Google Scholar]
- Cannon, A.J.; Sobie, S.R.; Murdock, T.Q. Bias Correction of GCM Precipitation by Quantile Mapping: How Well Do Methods Preserve Changes in Quantiles and Extremes? J. Clim. 2015, 28, 6938–6959. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Birnbaum, Z.W.; Tingey, F.H. One-Sided Confidence Contours for Probability Distribution Functions. Ann. Math. Stat. 1951, 22, 592–596. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Cao, D.; Li, H.; Hou, E.; Song, S.; Lai, C. Assessment and Hydrological Validation of Merged Near-Real-Time Satellite Precipitation Estimates Based on the Gauge-Free Triple Collocation Approach. Remote Sens. 2022, 14, 3835. [Google Scholar]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, W.; Fan, Z.; He, X.; Sun, W.; Chen, S.; Wen, J.; Gao, J.; Wang, J. Evaluation of the ERA5 reanalysis precipitation dataset over Chinese Mainland. J. Hydrol. 2021, 595, 125660. [Google Scholar] [CrossRef]
- Islam, M.A.; Cartwright, N. Evaluation of climate reanalysis and space-borne precipitation products over Bangladesh. Hydrol. Sci. J. 2020, 65, 1112–1128. [Google Scholar] [CrossRef]
- Jiao, D.; Xu, N.; Yang, F.; Xu, K. Evaluation of spatial-temporal variation performance of ERA5 precipitation data in China. Sci. Rep. 2021, 11, 17956. [Google Scholar] [CrossRef]
- Zhong, R.; Chen, X.; Lai, C.; Wang, Z.; Lian, Y.; Yu, H.; Wu, X. Drought monitoring utility of satellite-based precipitation products across mainland China. J. Hydrol. 2019, 568, 343–359. [Google Scholar] [CrossRef]
- Bai, X.; Wang, P.; He, Y.; Zhang, Z.; Wu, X. Assessing the accuracy and drought utility of long-term satellite-based precipitation estimation products using the triple collocation approach. J. Hydrol. 2021, 603, 127098. [Google Scholar] [CrossRef]
- Bai, X.; Shen, W.; Wu, X.; Wang, P. Applicability of long-term satellite-based precipitation products for drought indices considering global warming. J. Environ. Manag. 2020, 255, 109846. [Google Scholar] [CrossRef]
- Ombadi, M.; Nguyen, P.; Sorooshian, S.; Hsu, K. Retrospective Analysis and Bayesian Model Averaging of CMIP6 Precipitation in the Nile River Basin. J. Hydrometeorol. 2021, 22, 217–229. [Google Scholar] [CrossRef]
- Lavers, D.A.; Simmons, A.; Vamborg, F.; Rodwell, M.J. An evaluation of ERA5 precipitation for climate monitoring. Q. J. R. Meteor. Soc. 2022, 148, 3152–3165. [Google Scholar] [CrossRef]
- Zhu, Q.; Xuan, W.; Liu, L.; Xu, Y. Evaluation and hydrological application of precipitation estimates derived from PERSIANN-CDR, TRMM 3B42V7, and NCEP-CFSR over humid regions in China. Hydrol. Process 2016, 30, 3061–3083. [Google Scholar] [CrossRef]





| GCMs | Institute | Spatial Resolution (Longitude × Latitude) |
|---|---|---|
| CanESM5 | Canadian Centre for Climate Modelling and Analysis | 2.8° × 2.8° |
| INM-CM4-8 | Marchuk Institute of Numerical Mathematics, Russian Academy of Science | 2° × 1.5° |
| IPSL-CM6A-LR | Institut Pierre-Simon Laplace | 2.5° × 1.25° |
| MIROC6 | Atmosphere and Ocean Research Institute, University of Tokyo | 1.4° × 1.4° |
| Category | Index | Definition | Unit |
|---|---|---|---|
| Precipitation | SDII | Annual daily precipitation amount on wet days (precipitation ≥ 1 mm) | mm |
| Rx1d | Maximum 1-day precipitation of a year | mm | |
| Rx5d | Maximum consecutive 5-day precipitation of a year | mm | |
| R50mm | Annual count of rainstorm days (precipitation ≥ 50 mm) | day | |
| CDD | Annual maximum number of consecutive dry days (precipitation < 1 mm) | day | |
| Hydrology | Qmean | Mean annual streamflow | m3/s |
| Qwet | Wet season (April–September) mean streamflow | m3/s | |
| Qdry | Dry season (October–March) mean streamflow | m3/s | |
| Qx1d | Maximum 1-day flood water of a year | m3 | |
| Qx5d | Maximum consecutive 5-day flood water of a year | m3 | |
| Qn7d | Minimum consecutive 7-day streamflow of a year | m3 |
| Assessment Metrics | R | RMSE (mm) | RB (%) | |
|---|---|---|---|---|
| Daily scale | ERA5 | 0.83 | 5.4 | 16.8 |
| PCDR | 0.68 | 7.3 | −4.8 | |
| CHIRPS | 0.72 | 7.6 | 3.1 | |
| Monthly scale | ERA5 | 0.93 | 48.2 | 16.8 |
| PCDR | 0.94 | 37.3 | −4.8 | |
| CHIRPS | 0.96 | 30.3 | 3.1 | |
| Period | Assessment Metrics | Gauge Data | ERA5 | PCDR | CHIRPS |
|---|---|---|---|---|---|
| Calibration period (1985–2000) | KGE | 0.96 | 0.49 | 0.78 | 0.85 |
| R | 0.96 | 0.84 | 0.80 | 0.85 | |
| NSE | 0.92 | 0.42 | 0.63 | 0.70 | |
| RB (%) | 0.3 | 41.1 | −6.1 | 3.1 | |
| Calibration period (2001–2011) | KGE | 0.92 | 0.81 | 0.78 | 0.80 |
| R | 0.93 | 0.88 | 0.82 | 0.85 | |
| NSE | 0.86 | 0.74 | 0.67 | 0.66 | |
| RB (%) | 3.1 | 14.4 | −8.3 | 10.6 |
| Extreme Index | Rx1d (mm) | Rx5d (mm) | R50mm (day) | CDD (day) | |
|---|---|---|---|---|---|
| Median | Gauge data | 73.8 | 147.9 | 3 | 29.5 |
| ERA5 | 67 | 150.7 | 2 | 21.5 | |
| PCDR | 74 | 161.5 | 2 | 28 | |
| CHIRPS | 89.5 | 165.5 | 4 | 20 | |
| 90% percentile | Gauge data | 93.6 | 249.5 | 4 | 48 |
| ERA5 | 82.9 | 197.5 | 4 | 35.6 | |
| PCDR | 111 | 212.1 | 4 | 42.1 | |
| CHIRPS | 131.9 | 239.9 | 7 | 24 | |
| Extreme Index | Qx1d (m3) | Qx5d (m3) | Qn7d (m3) | |
|---|---|---|---|---|
| Median | Observation | 738.7 | 2438.9 | 116.3 |
| Gauge data | 712.3 | 2581.6 | 77.7 | |
| ERA5 | 840.3 | 3131.9 | 93.4 | |
| PCDR | 719.5 | 2541.6 | 67.3 | |
| CHIRPS | 787.9 | 2533 | 87.7 | |
| 90% percentile (10% percentile for Qn7d) | Observation | 1132.3 | 4331.7 | 79.3 |
| Gauge data | 1185.9 | 4455.4 | 52.2 | |
| ERA5 | 1184.5 | 3932.1 | 64.5 | |
| PCDR | 1069.3 | 3581.7 | 50.7 | |
| CHIRPS | 1427.1 | 4239.5 | 64.3 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, D.; Jiang, X.; Liu, S.; Chai, F.; Liu, Y.; Lai, C. Utility of Open-Access Long-Term Precipitation Data Products for Correcting Climate Model Projection in South China. Water 2023, 15, 2906. https://doi.org/10.3390/w15162906
Cao D, Jiang X, Liu S, Chai F, Liu Y, Lai C. Utility of Open-Access Long-Term Precipitation Data Products for Correcting Climate Model Projection in South China. Water. 2023; 15(16):2906. https://doi.org/10.3390/w15162906
Chicago/Turabian StyleCao, Daling, Xiaotian Jiang, Shu Liu, Fuxin Chai, Yesen Liu, and Chengguang Lai. 2023. "Utility of Open-Access Long-Term Precipitation Data Products for Correcting Climate Model Projection in South China" Water 15, no. 16: 2906. https://doi.org/10.3390/w15162906
APA StyleCao, D., Jiang, X., Liu, S., Chai, F., Liu, Y., & Lai, C. (2023). Utility of Open-Access Long-Term Precipitation Data Products for Correcting Climate Model Projection in South China. Water, 15(16), 2906. https://doi.org/10.3390/w15162906






