Encoder–Decoder Convolutional Neural Networks for Flow Modeling in Unsaturated Porous Media: Forward and Inverse Approaches
Abstract
:1. Introduction
2. Theoretical Framework and Methodology
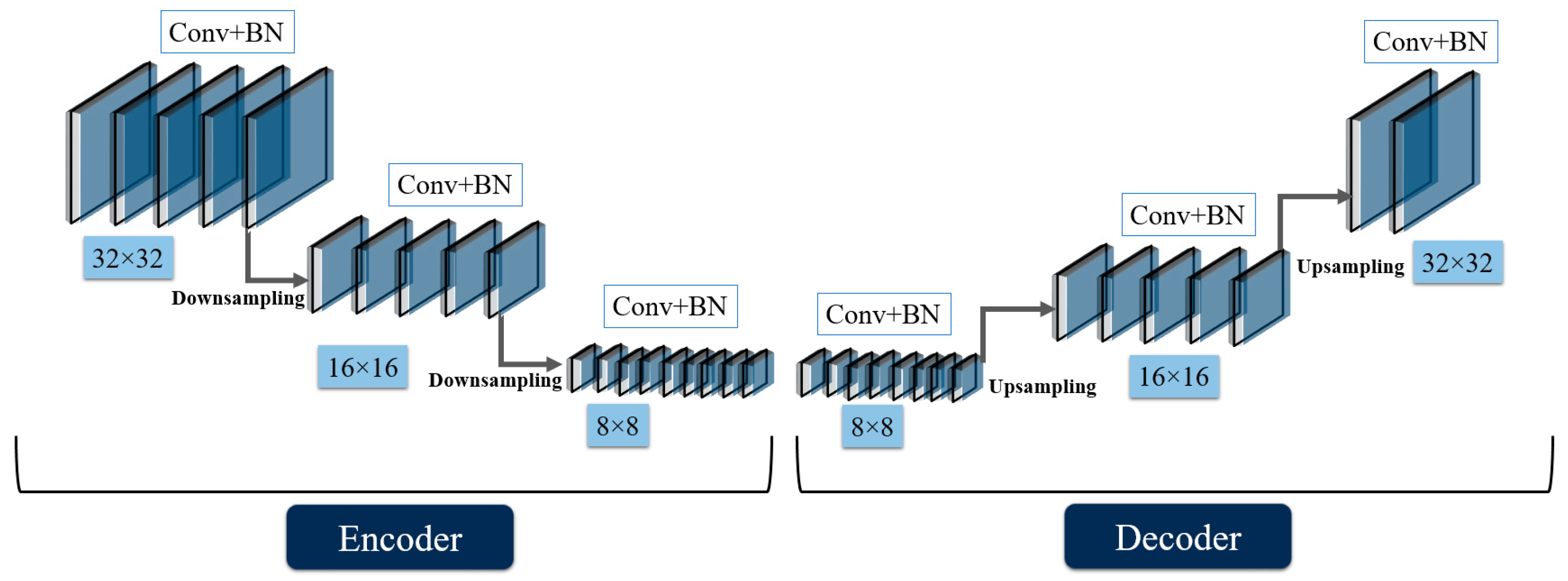
2.1. Encoder–Decoder Convolutional Neural Networks
2.2. Image-to-Image Regression Modeling
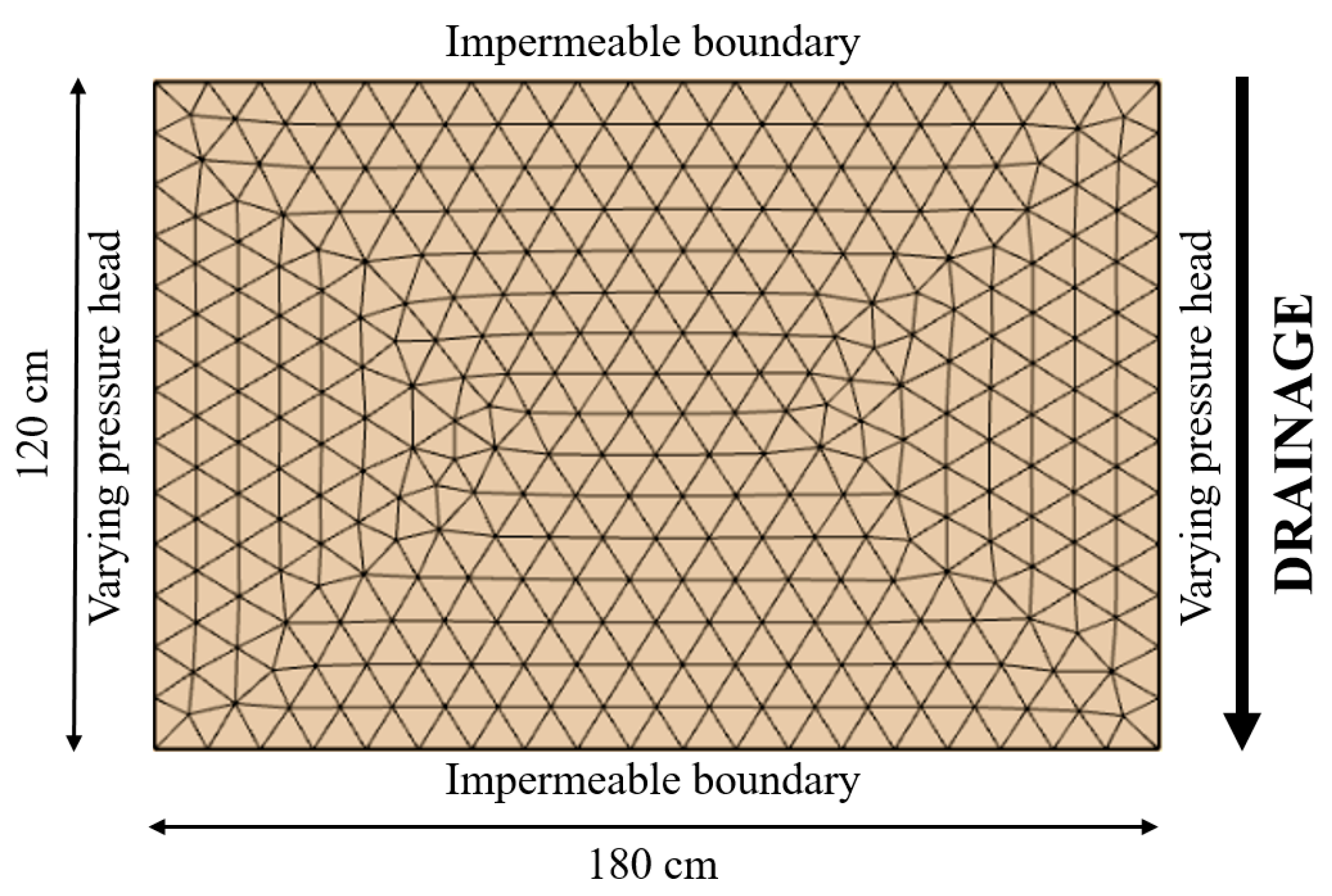
2.3. Description of the Test Case
2.3.1. Numerical Simulations
2.3.2. Measurements from the Laboratory Experiment
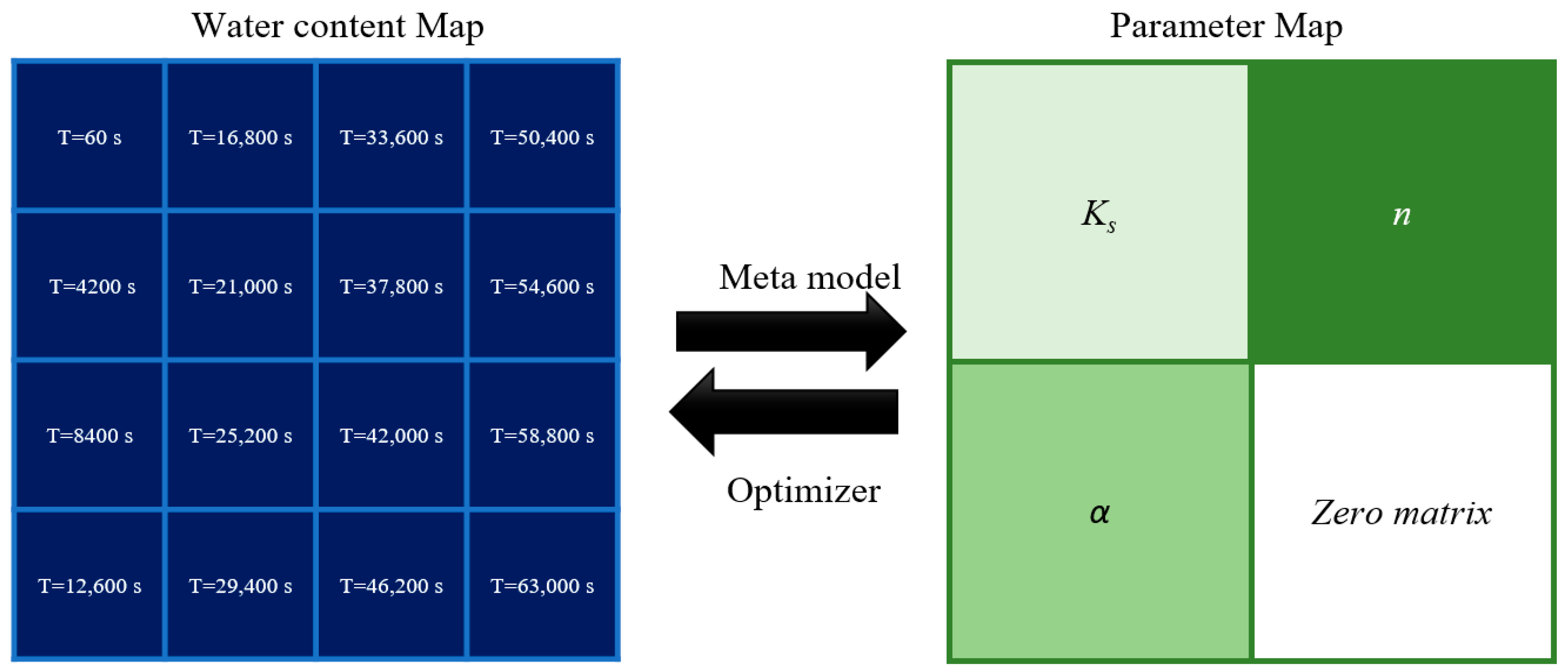
2.4. Model-Based Data Generation
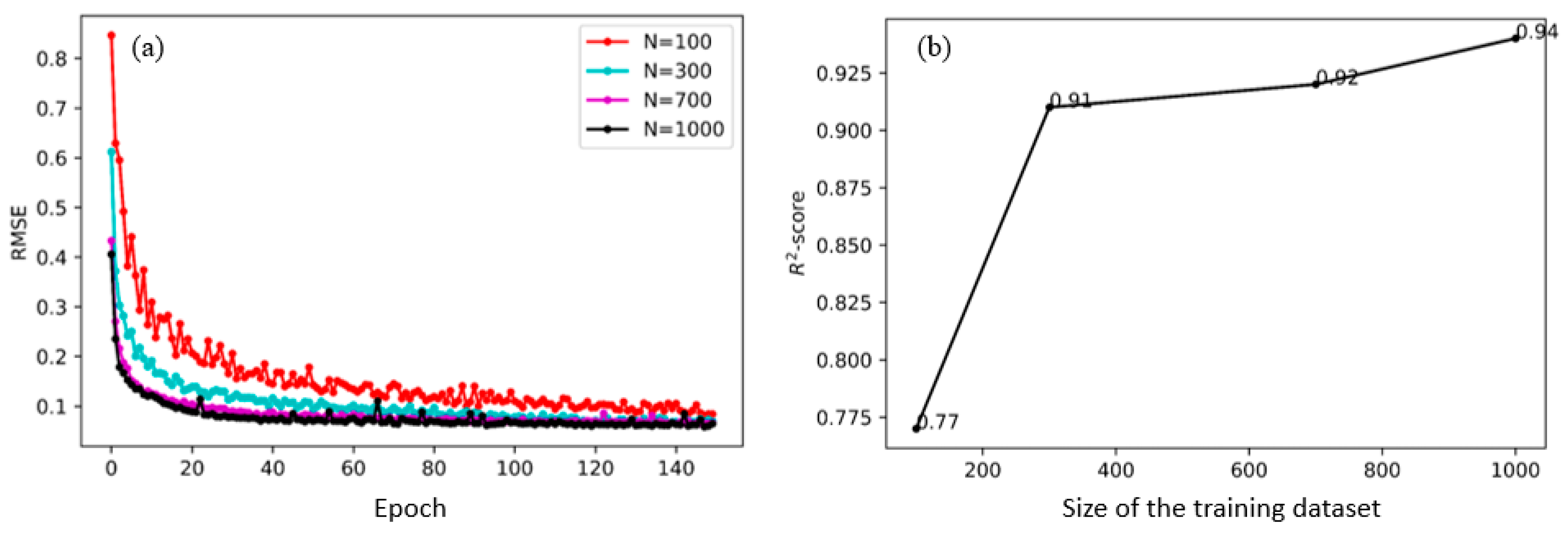
2.5. Model Training and Validation
3. Results and Discussion
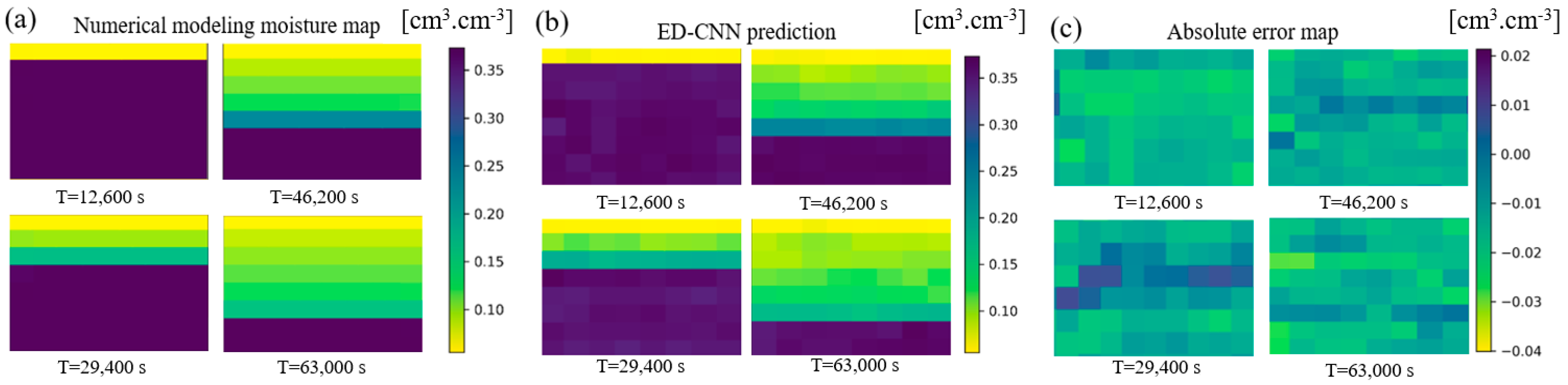
3.1. ED-CNN as Meta-Model
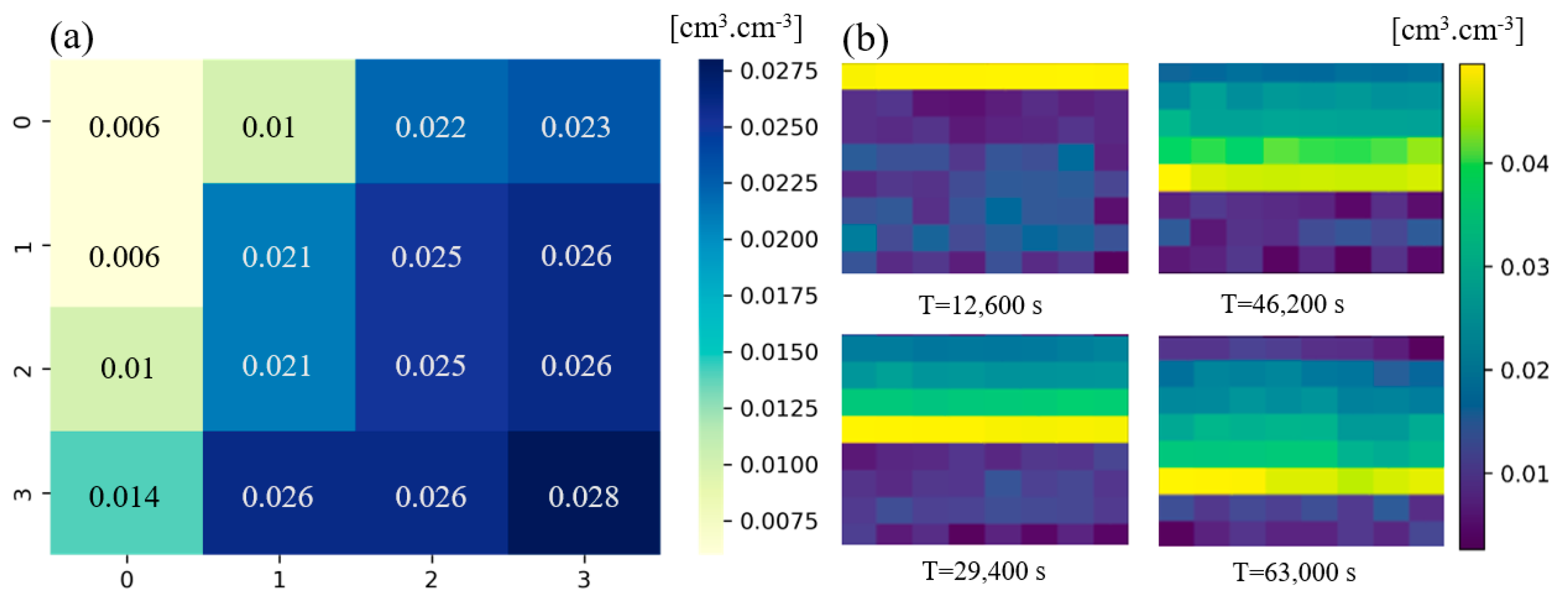
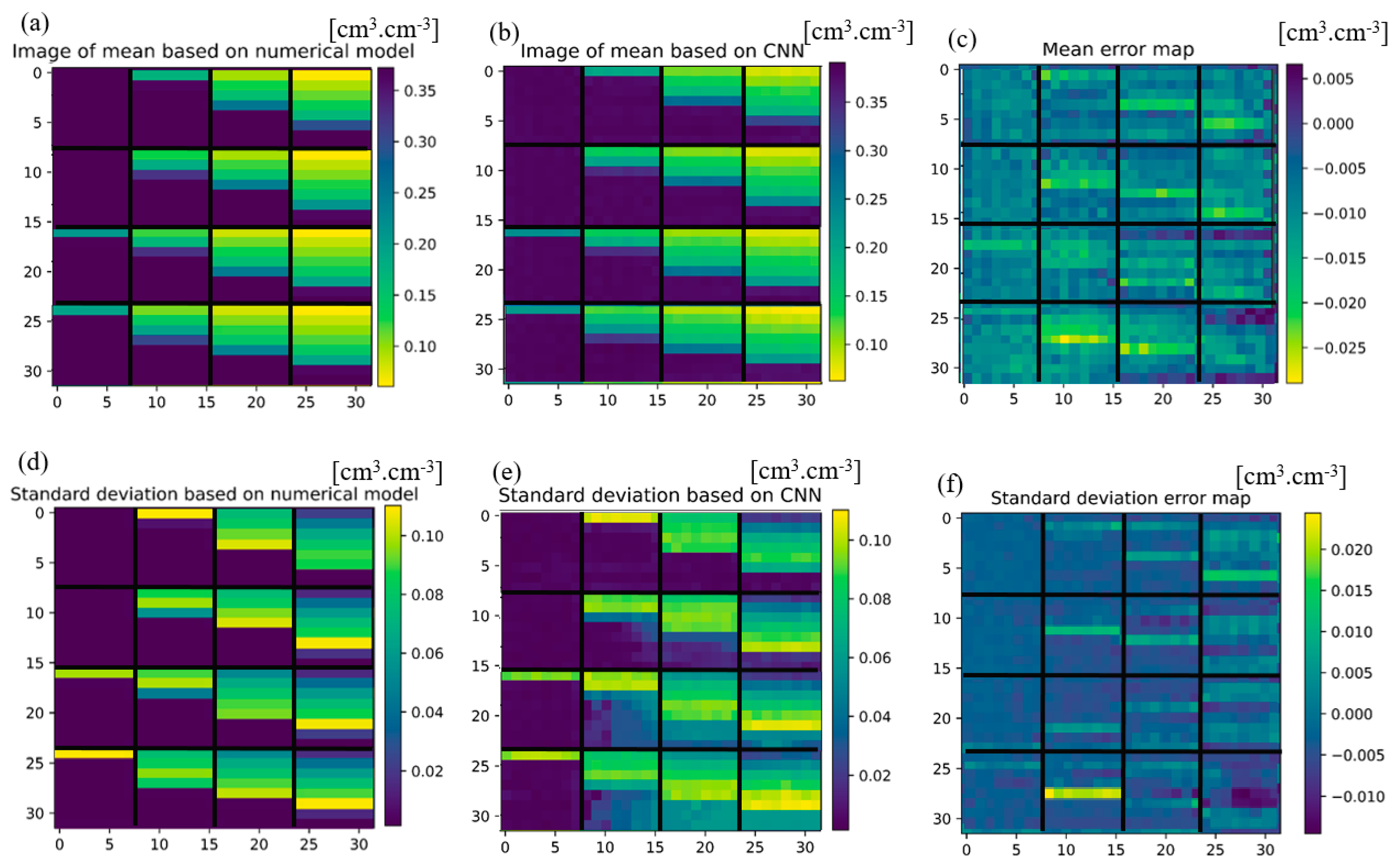
3.2. ED-CNN for Uncertainty Analysis
3.3. ED-CNN as an Optimizer
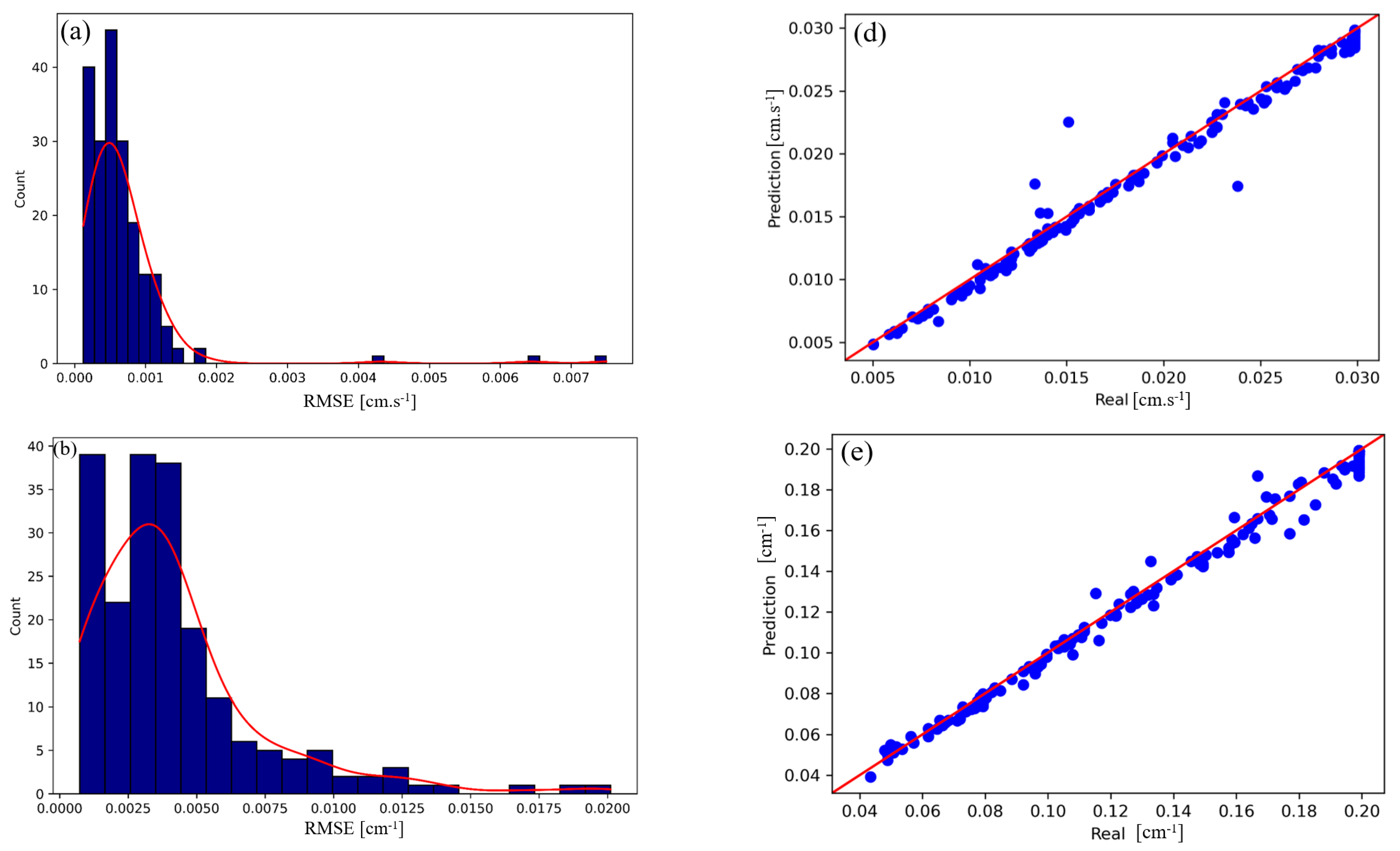
3.3.1. Model Training and Validation Using Numerical Simulation Data
3.3.2. Comparison with Previous Studies
3.3.3. Parameter Estimation Using Photographic Imaging Data
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Farthing, M.W.; Ogden, F.L. Numerical solution of Richards’ equation: A review of advances and challenges. Soil Sci. Soc. Am. J. 2017, 81, 1257–1269. [Google Scholar] [CrossRef] [Green Version]
- Rajabi, M.M.; Belfort, B.; Lehmann, F.; Weill, S.; Ataie-Ashtiani, B.; Fahs, M. An improved Kalman filtering approach for the estimation of unsaturated flow parameters by assimilating photographic imaging data. J. Hydrol. 2020, 590, 125373. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary Conduction of Liquids through Porous Mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Sklorz, S.; Kaltofen, M.; Monninkhoff, B. Application of the FEFLOW groundwater model in the Zayandeh Rud catchment. In Reviving the Dying Giant: Integrated Water Resource Management in the Zayandeh Rud Catchment, Iran; Springer: Cham, Switzerland, 2017; pp. 241–251. [Google Scholar]
- Beegum, S.; Šimůnek, J.; Szymkiewicz, A.; Sudheer, K.; Nambi, I.M. Updating the Coupling Algorithm between HYDRUS and MODFLOW in the HYDRUS Package for MODFLOW. Vadose Zone J. 2018, 17, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Dey, S.; Dhar, A. Generalized mass-conservative finite volume framework for unified saturated–unsaturated subsurface flow. J. Hydrol. 2022, 605, 127309. [Google Scholar] [CrossRef]
- Pollacco, J.; Fernández-Gálvez, J.; Ackerer, P.; Belfort, B.; Lassabatere, L.; Angulo-Jaramillo, R.; Rajanayaka, C.; Lilburne, L.; Carrick, S.; Peltzer, D. HyPix: 1D physically based hydrological model with novel adaptive time-stepping management and smoothing dynamic criterion for controlling Newton–Raphson step. Environ. Model. Softw. 2022, 153, 105386. [Google Scholar] [CrossRef]
- Li, C.; Ren, L. Estimation of unsaturated soil hydraulic parameters using the ensemble Kalman filter. Vadose Zone J. 2011, 10, 1205–1227. [Google Scholar] [CrossRef]
- Moret-Fernández, D.; Peña-Sancho, C.; Latorre, B.; Pueyo, Y.; López, M. Estimating the van Genuchten retention curve parameters of undisturbed soil from a single upward infiltration measurement. Soil Res. 2017, 55, 682–691. [Google Scholar] [CrossRef] [Green Version]
- Younes, A.; Fahs, M.; Ackerer, P. Modeling of flow and transport in saturated and unsaturated porous media. Water 2021, 13, 1088. [Google Scholar] [CrossRef]
- Liu, K.; Huang, G.; Jiang, Z.; Xu, X.; Xiong, Y.; Huang, Q.; Šimůnek, J. A gaussian process-based iterative Ensemble Kalman Filter for parameter estimation of unsaturated flow. J. Hydrol. 2020, 589, 125210. [Google Scholar] [CrossRef]
- Rajabi, M.M.; Ataie-Ashtiani, B.; Simmons, C.T. Polynomial chaos expansions for uncertainty propagation and moment independent sensitivity analysis of seawater intrusion simulations. J. Hydrol. 2015, 520, 101–122. [Google Scholar] [CrossRef]
- Zhang, J.; Man, J.; Lin, G.; Wu, L.; Zeng, L. Inverse modeling of hydrologic systems with adaptive multifidelity Markov chain Monte Carlo simulations. Water Resour. Res. 2018, 54, 4867–4886. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhang, J.; Xu, W.; Wu, L.; Zeng, L. Adaptive multi-fidelit data assimilation for nonlinear subsurface flow problems. Water Resour. Res. 2019, 55, 203–217. [Google Scholar] [CrossRef] [Green Version]
- Gadd, C.; Xing, W.; Nezhad, M.M.; Shah, A. A surrogate modelling approach based on nonlinear dimension reduction for uncertainty quantification in groundwater flow models. Transp. Porous Media 2019, 126, 39–77. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; Zheng, Y.; Wu, X.; Tian, Y.; Han, F.; Liu, J.; Zheng, C. Optimizing water resources management in large river basins with integrated surface water-groundwater modeling: A surrogate-based approach. Water Resour. Res. 2015, 51, 2153–2173. [Google Scholar] [CrossRef]
- Zhu, P.; Shi, L.; Zhu, Y.; Zhang, Q.; Huang, K.; Williams, M. Data assimilation of soil water flow via ensemble Kalman filter: Infusing soil moisture data at different scales. J. Hydrol. 2017, 555, 912–925. [Google Scholar] [CrossRef] [Green Version]
- Mady, A.; Shein, E. Support vector machine and nonlinear regression methods for estimating saturated hydraulic conductivity. Mosc. Univ. Soil Sci. Bull. 2018, 73, 129–133. [Google Scholar] [CrossRef]
- Dwelle, M.C.; Kim, J.; Sargsyan, K.; Ivanov, V.Y. Streamflow, stomata, and soil pits: Sources of inference for complex models with fast, robust uncertainty quantification. Adv. Water Resour. 2019, 125, 13–31. [Google Scholar] [CrossRef]
- Wang, H.; Gong, W.; Duan, Q.; Di, Z. Evaluation of parameter interaction effect of hydrological models using the sparse polynomial chaos (SPC) method. Environ. Model. Softw. 2020, 125, 104612. [Google Scholar] [CrossRef]
- Tran, V.N.; Kim, J. A robust surrogate data assimilation approach to real-time forecasting using polynomial chaos expansion. J. Hydrol. 2021, 598, 126367. [Google Scholar] [CrossRef]
- Bandai, T.; Ghezzehei, T.A. Physics-informed neural networks with monotonicity constraints for Richardson-Richards equation: Estimation of constitutive relationships and soil water flux density from volumetric water content measurements. Water Resour. Res. 2021, 57, e2020WR027642. [Google Scholar] [CrossRef]
- Depina, I.; Jain, S.; Mar Valsson, S.; Gotovac, H. Application of physics-informed neural networks to inverse problems in unsaturated groundwater flow. Georisk: Assess. Manag. Risk Eng. Syst. Geohazards 2022, 16, 21–36. [Google Scholar] [CrossRef]
- Chai, Y.; Liu, H.; Yu, Y.; Yang, Q.; Zhang, X.; Zhao, W.; Guo, L.; Yetemen, O. Strategies of Parameter Optimization and Soil Moisture Sensor Deployment for Accurate Estimation of Evapotranspiration Through a Data-driven Method. Agric. For. Meteorol. 2023, 331, 109354. [Google Scholar] [CrossRef]
- Shuku, T.; Phoon, K.-K. Data-driven subsurface modelling using a Markov random field model. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2023, 17, 41–63. [Google Scholar] [CrossRef]
- Lyu, B.; Hu, Y.; Wang, Y. Data-driven development of three-dimensional subsurface models from sparse measurements using Bayesian compressive sampling: A benchmarking study. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2023, 9, 04023010. [Google Scholar] [CrossRef]
- Vu, M.; Jardani, A. Mapping of hydraulic transmissivity field from inversion of tracer test data using convolutional neural networks. CNN-2T. J. Hydrol. 2022, 606, 127443. [Google Scholar] [CrossRef]
- Asher, M.J.; Croke, B.F.; Jakeman, A.J.; Peeters, L.J. A review of surrogate models and their application to groundwater modeling. Water Resour. Res. 2015, 51, 5957–5973. [Google Scholar] [CrossRef] [Green Version]
- Mo, S.; Zhu, Y.; Zabaras, N.; Shi, X.; Wu, J. Deep convolutional encoder-decoder networks for uncertainty quantification of dynamic multiphase flow in heterogeneous media. Water Resour. Res. 2019, 55, 703–728. [Google Scholar] [CrossRef] [Green Version]
- Samek, W.; Montavon, G.; Lapuschkin, S.; Anders, C.J.; Müller, K.-R. Explaining deep neural networks and beyond: A review of methods and applications. Proc. IEEE 2021, 109, 247–278. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Marrero, C.O.; Perdikaris, P.; Tartakovsky, G.D.; Barajas-Solano, D. Physics-informed deep neural networks for learning parameters and constitutive relationships in subsurface flow problems. Water Resour. Res. 2020, 56, e2019WR026731. [Google Scholar] [CrossRef]
- Stepanov, S.; Spiridonov, D.; Mai, T. Prediction of numerical homogenization using deep learning for the Richards equation. J. Comput. Appl. Math. 2023, 424, 114980. [Google Scholar] [CrossRef]
- Song, W.; Shi, L.; Hu, X.; Wang, Y.; Wang, L. Reconstructing the Unsaturated Flow Equation from Sparse and Noisy Data: Leveraging the Synergy of Group Sparsity and Physics-Informed Deep Learning. Water Resour. Res. 2023, 59, e2022WR034122. [Google Scholar] [CrossRef]
- Haruzi, P.; Moreno, Z. Modeling water flow and solute transport in unsaturated soils using physics-informed neural networks trained with geoelectrical data. Water Resour. Res. 2023, 59, e2023WR034538. [Google Scholar] [CrossRef]
- Zhu, Y.; Zabaras, N. Bayesian deep convolutional encoder–decoder networks for surrogate modeling and uncertainty quantification. J. Comput. Phys. 2018, 366, 415–447. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Yu, H.; Yuan, X.; Xu, H.; Micheal, M.; Zhang, J.; Shu, H.; Wang, G.; Wu, H. Permeability prediction of low-resolution porous media images using autoencoder-based convolutional neural network. J. Pet. Sci. Eng. 2022, 208, 109589. [Google Scholar] [CrossRef]
- Taccari, M.L.; Nuttall, J.; Chen, X.; Wang, H.; Minnema, B.; Jimack, P.K. Attention U-Net as a surrogate model for groundwater prediction. Adv. Water Resour. 2022, 163, 104169. [Google Scholar] [CrossRef]
- Davis, K.; Leiteritz, R.; Pflüger, D.; Schulte, M. Deep learning based surrogate modeling for thermal plume prediction of groundwater heat pumps. arXiv 2023, arXiv:2302.08199. [Google Scholar]
- Rajabi, M.M.; Javaran, M.R.H.; Bah, A.-o.; Frey, G.; Le Ber, F.; Lehmann, F.; Fahs, M. Analyzing the efficiency and robustness of deep convolutional neural networks for modeling natural convection in heterogeneous porous media. Int. J. Heat Mass Transf. 2022, 183, 122131. [Google Scholar] [CrossRef]
- Wen, G.; Tang, M.; Benson, S.M. Towards a predictor for CO2 plume migration using deep neural networks. Int. J. Greenh. Gas Control 2021, 105, 103223. [Google Scholar] [CrossRef]
- Jiang, Z.; Tahmasebi, P.; Mao, Z. Deep residual U-net convolution neural networks with autoregressive strategy for fluid flow predictions in large-scale geosystems. Adv. Water Resour. 2021, 150, 103878. [Google Scholar] [CrossRef]
- Wang, N.; Chang, H.; Zhang, D. Theory-guided auto-encoder for surrogate construction and inverse modeling. Comput. Methods Appl. Mech. Eng. 2021, 385, 114037. [Google Scholar] [CrossRef]
- Conway, A.M.; Durbach, I.N.; McInnes, A.; Harris, R.N. Frame-by-frame annotation of video recordings using deep neural networks. Ecosphere 2021, 12, e03384. [Google Scholar] [CrossRef]
- Kong, Z.; Zhang, C.; Lv, H.; Xiong, F.; Fu, Z. Multimodal feature extraction and fusion deep neural networks for short-term load forecasting. IEEE Access 2020, 8, 185373–185383. [Google Scholar] [CrossRef]
- Bazai, H.; Kargar, E.; Mehrabi, M. Using an encoder-decoder convolutional neural network to predict the solid holdup patterns in a pseudo-2d fluidized bed. Chem. Eng. Sci. 2021, 246, 116886. [Google Scholar] [CrossRef]
- Zaccone, G.; Karim, M.R. Deep Learning with TensorFlow: Explore Neural Networks and Build Intelligent Systems with Python; Packt Publishing Ltd.: Birmingham, UK, 2018. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Jardani, A.; Vu, T.; Fischer, P. Use of convolutional neural networks with encoder-decoder structure for predicting the inverse operator in hydraulic tomography. J. Hydrol. 2022, 604, 127233. [Google Scholar] [CrossRef]
- Xia, X.; Jiang, S.; Zhou, N.; Cui, J.; Li, X. Groundwater contamination source identification and high-dimensional parameter inversion using residual dense convolutional neural network. J. Hydrol. 2023, 617, 129013. [Google Scholar] [CrossRef]
- Belfort, B.; Weill, S.; Fahs, M.; Lehmann, F. Laboratory experiments of drainage, imbibition and infiltration under artificial rainfall characterized by image analysis method and numerical simulations. Water 2019, 11, 2232. [Google Scholar] [CrossRef] [Green Version]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef] [Green Version]
- Belfort, B.; Weill, S.; Lehmann, F. Image analysis method for the measurement of water saturation in a two-dimensional experimental flow tank. J. Hydrol. 2017, 550, 343–354. [Google Scholar] [CrossRef] [Green Version]
- Fahs, M.; Younes, A.; Lehmann, F. An easy and efficient combination of the Mixed Finite Element Method and the Method of Lines for the resolution of Richards’ Equation. Environ. Model. Softw. 2009, 24, 1122–1126. [Google Scholar] [CrossRef]
- Kumar, D.; Roshni, T.; Singh, A.; Jha, M.K.; Samui, P. Predicting groundwater depth fluctuations using deep learning, extreme learning machine and Gaussian process: A comparative study. Earth Sci. Inform. 2020, 13, 1237–1250. [Google Scholar] [CrossRef]
- Wang, N.; Chang, H.; Zhang, D. Surrogate and inverse modeling for two-phase flow in porous media via theory-guided convolutional neural network. J. Comput. Phys. 2022, 466, 111419. [Google Scholar] [CrossRef]
- Rajabi, M.M.; Ketabchi, H. Uncertainty-based simulation-optimization using Gaussian process emulation: Application to coastal groundwater management. J. Hydrol. 2017, 555, 518–534. [Google Scholar] [CrossRef]
- Tran, A.P.; Vanclooster, M.; Zupanski, M.; Lambot, S. Joint estimation of soil moisture profile and hydraulic parameters by ground-penetrating radar data assimilation with maximum likelihood ensemble filter. Water Resour. Res. 2014, 50, 3131–3146. [Google Scholar] [CrossRef]
- Shi, L.; Song, X.; Tong, J.; Zhu, Y.; Zhang, Q. Impacts of different types of measurements on estimating unsaturated flow parameters. J. Hydrol. 2015, 524, 549–561. [Google Scholar] [CrossRef]
- Hayek, M. Analytical solution to transient Richards’ equation with realistic water profiles for vertical infiltration and parameter estimation. Water Resour. Res. 2016, 52, 4438–4457. [Google Scholar] [CrossRef] [Green Version]
- Rai, P.K.; Tripathi, S. Gaussian process for estimating parameters of partial differential equations and its application to the Richards equation. Stoch. Environ. Res. Risk Assess. 2019, 33, 1629–1649. [Google Scholar] [CrossRef]
- Su, L.; Hou, L.; Zhou, B.; Shan, Y.; Duan, M.; Sun, Y.; Ning, S.; Wang, Q. Approximate analytical solution and parameter estimation for one-dimensional horizontal absorption based on the van Genuchten–Mualem model. Soil Sci. Soc. Am. J. 2021, 85, 217–234. [Google Scholar] [CrossRef]
- Yoshimoto, N.; Orense, R.P.; Tanabe, F.; Kikkawa, N.; Hyodo, M.; Nakata, Y. Measurement of degree of saturation on model ground by digital image processing. Soils Found. 2011, 51, 167–177. [Google Scholar] [CrossRef] [Green Version]




| Parameter | Interval | Unit | |
|---|---|---|---|
| [0.001, 0.03] | [cm·s−1] | ||
| Uniform | [0.001, 0.2] | [cm−1] | |
| [2, 8] | [-] |
| Layer | Kernel Size | Resolution |
|---|---|---|
| Encoder | ||
| Convolution + Batch normalization | 3 3 | 32 32 |
| Downsampling1 | 2 2 | 16 16 |
| Convolution + Batch normalization | 3 3 | 16 16 |
| Downsampling2 | 2 2 | 8 8 |
| Convolution + Batch normalization | 3 3 | 8 8 |
| Decoder | ||
| Convolution + Batch normalization | 3 3 | 8 8 |
| Upsampling1 | 2 2 | 16 16 |
| Convolution + Batch normalization | 3 3 | 16 16 |
| Upsampling2 | 2 2 | 32 32 |
| Convolution + Batch normalization | 3 3 | 32 32 |
| Hyper-Parameter | Meta-Model | Optimizer |
|---|---|---|
| Optimizer | RMSprop | Adam |
| Loss function | Mean squared error | Mean squared error |
| Samples | 1000 | 1000 |
| Test set | 200 | 200 |
| Validation set | 300 | 300 |
| Batch size | 12 | 24 |
| Epochs | 150 | 300 |
| Learning rate | 0.0001 | 0.0001 |
| Reference | Parameter Estimation Method | Estimated Hydraulic Parameters | Percentage Error (%) | ||
|---|---|---|---|---|---|
| [58] | EnKF | 3.2 | 3.6 | 1 | |
| [59] | EnKF | 20 | - | - | |
| [60] | Analytical solution | 10 | - | 10 | |
| [61] | GPPDE | 3.3 | - | 8.93 | |
| [12] | EnKF | 1 | 1 | - | |
| [62] | Analytical solution | - | 3.2 to 28 | 0.4 to 8 | |
| Current optimizer study | ED-CNN | 0.3 | 1.4 | 1 | |
| Parameter | Experiment Moisture Map as Input | Target Value |
|---|---|---|
| 0.35 | 0.37 | |
| 0.37 | 0.43 | |
| 0.45 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hajizadeh Javaran, M.R.; Rajabi, M.M.; Kamali, N.; Fahs, M.; Belfort, B. Encoder–Decoder Convolutional Neural Networks for Flow Modeling in Unsaturated Porous Media: Forward and Inverse Approaches. Water 2023, 15, 2890. https://doi.org/10.3390/w15162890
Hajizadeh Javaran MR, Rajabi MM, Kamali N, Fahs M, Belfort B. Encoder–Decoder Convolutional Neural Networks for Flow Modeling in Unsaturated Porous Media: Forward and Inverse Approaches. Water. 2023; 15(16):2890. https://doi.org/10.3390/w15162890
Chicago/Turabian StyleHajizadeh Javaran, Mohammad Reza, Mohammad Mahdi Rajabi, Nima Kamali, Marwan Fahs, and Benjamin Belfort. 2023. "Encoder–Decoder Convolutional Neural Networks for Flow Modeling in Unsaturated Porous Media: Forward and Inverse Approaches" Water 15, no. 16: 2890. https://doi.org/10.3390/w15162890
APA StyleHajizadeh Javaran, M. R., Rajabi, M. M., Kamali, N., Fahs, M., & Belfort, B. (2023). Encoder–Decoder Convolutional Neural Networks for Flow Modeling in Unsaturated Porous Media: Forward and Inverse Approaches. Water, 15(16), 2890. https://doi.org/10.3390/w15162890








