A Model Development for Thermal and Solutal Transport Analysis of Non-Newtonian Nanofluid Flow over a Riga Surface Driven by a Waste Discharge Concentration
Abstract
:1. Introduction
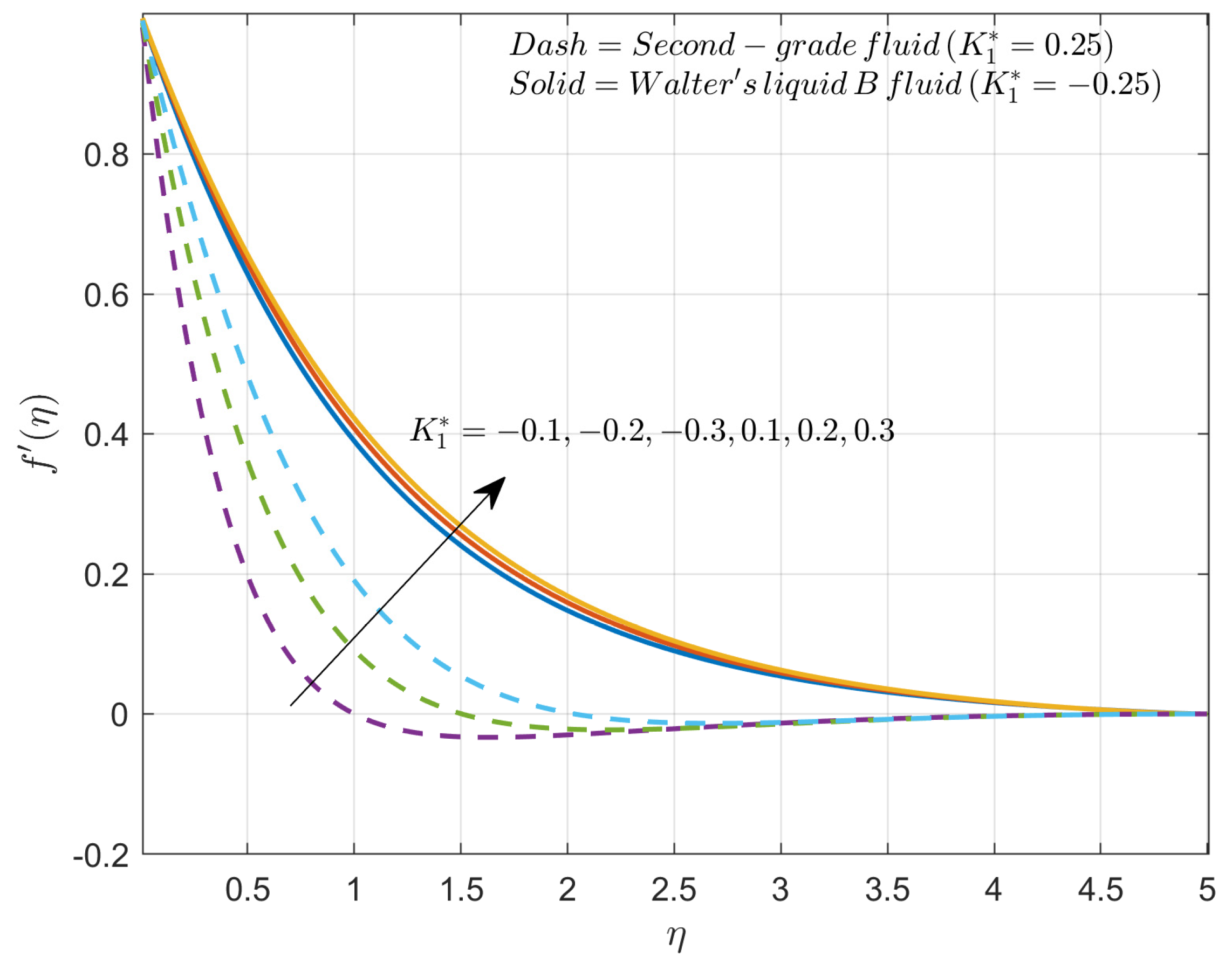
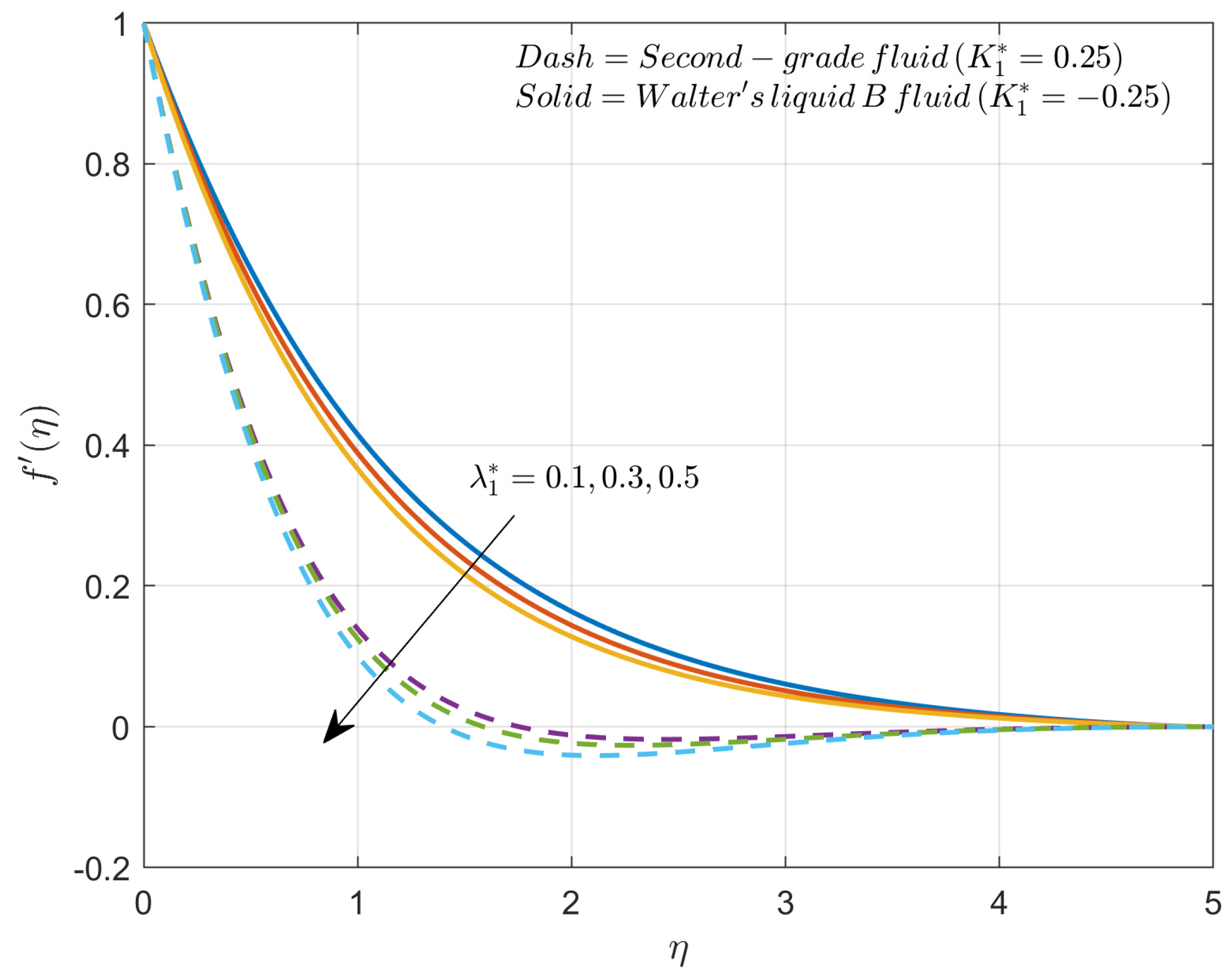
- How does the modified Hartmann number impact the velocity profile in the presence of second-grade fluid and Walter’s liquid B fluid?
- What are the behavioral changes observed in the concentration profile when external pollutant source variation parameter are varied?
- How will the local pollutant external source parameter and solid volume fractions influence the mass transfer rate?
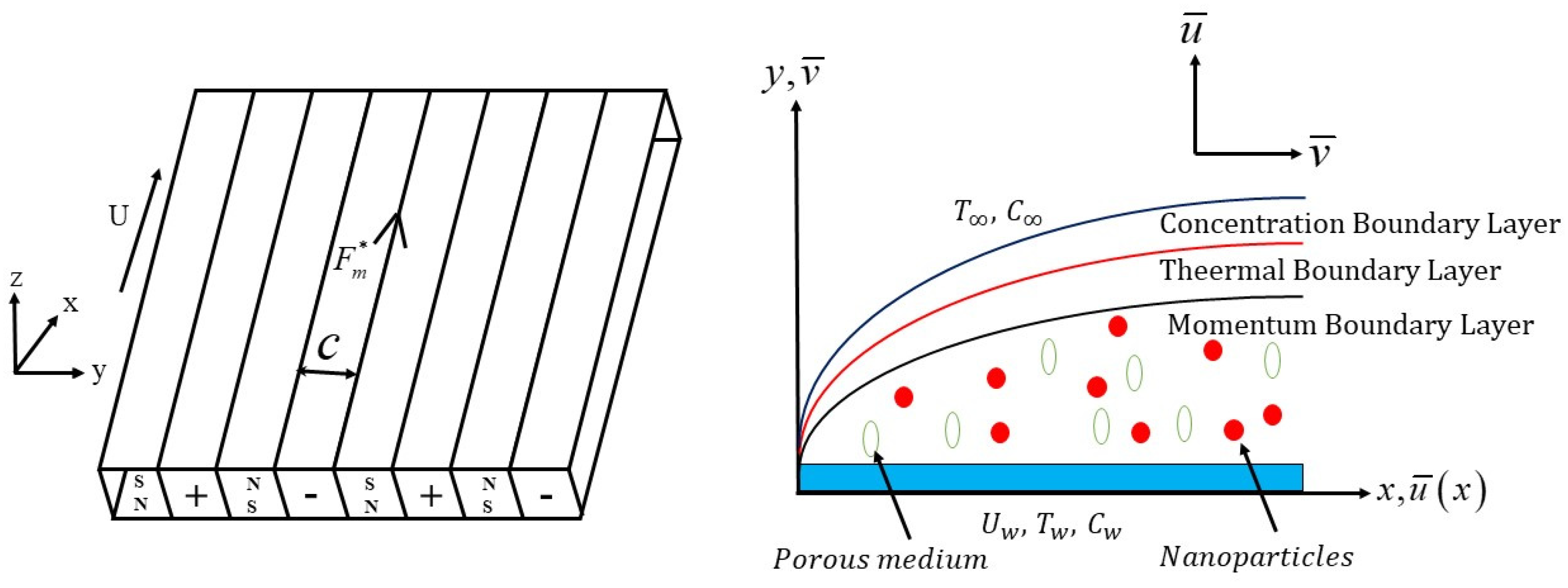
2. Mathematical Formulation
3. Numerical Scheme
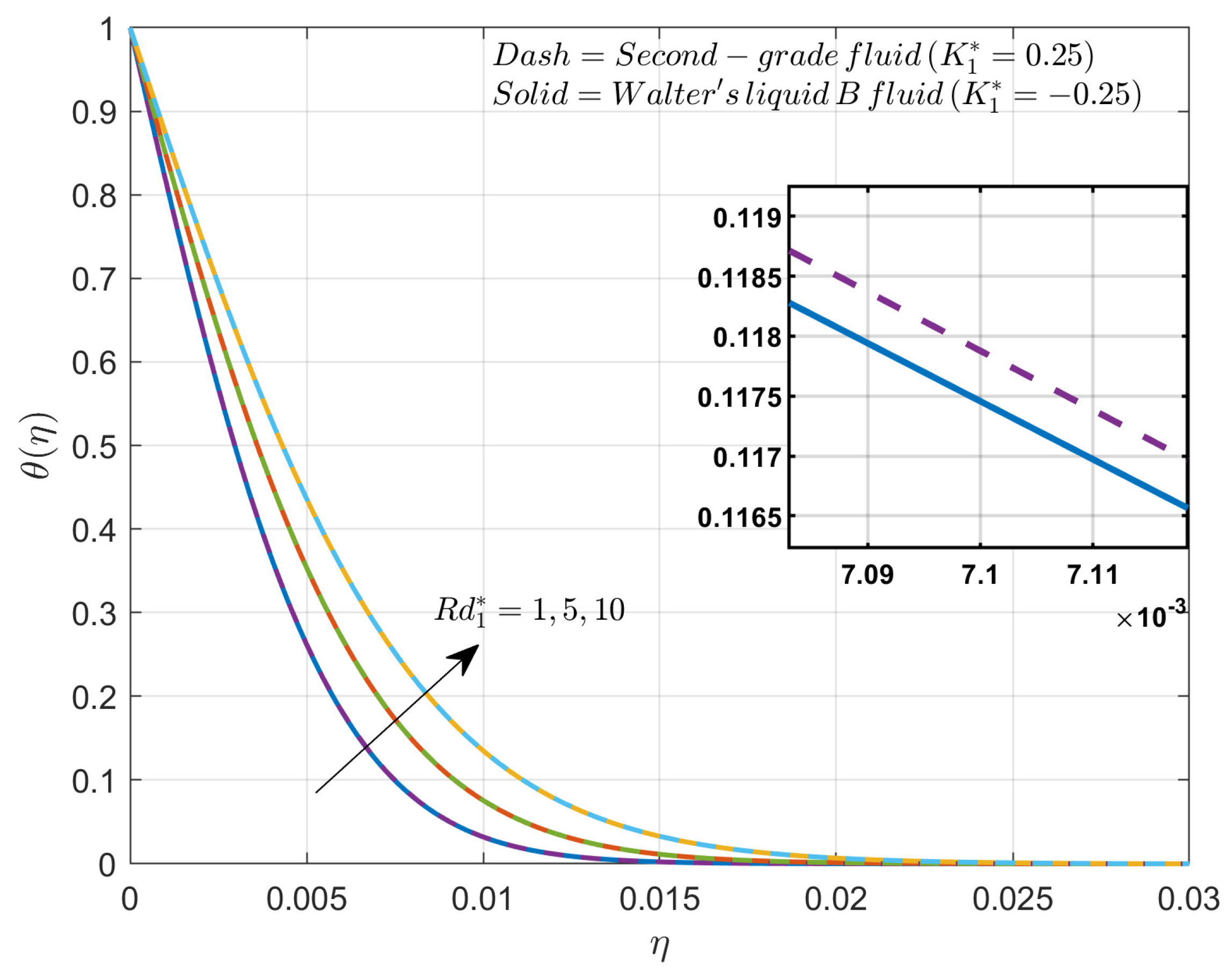
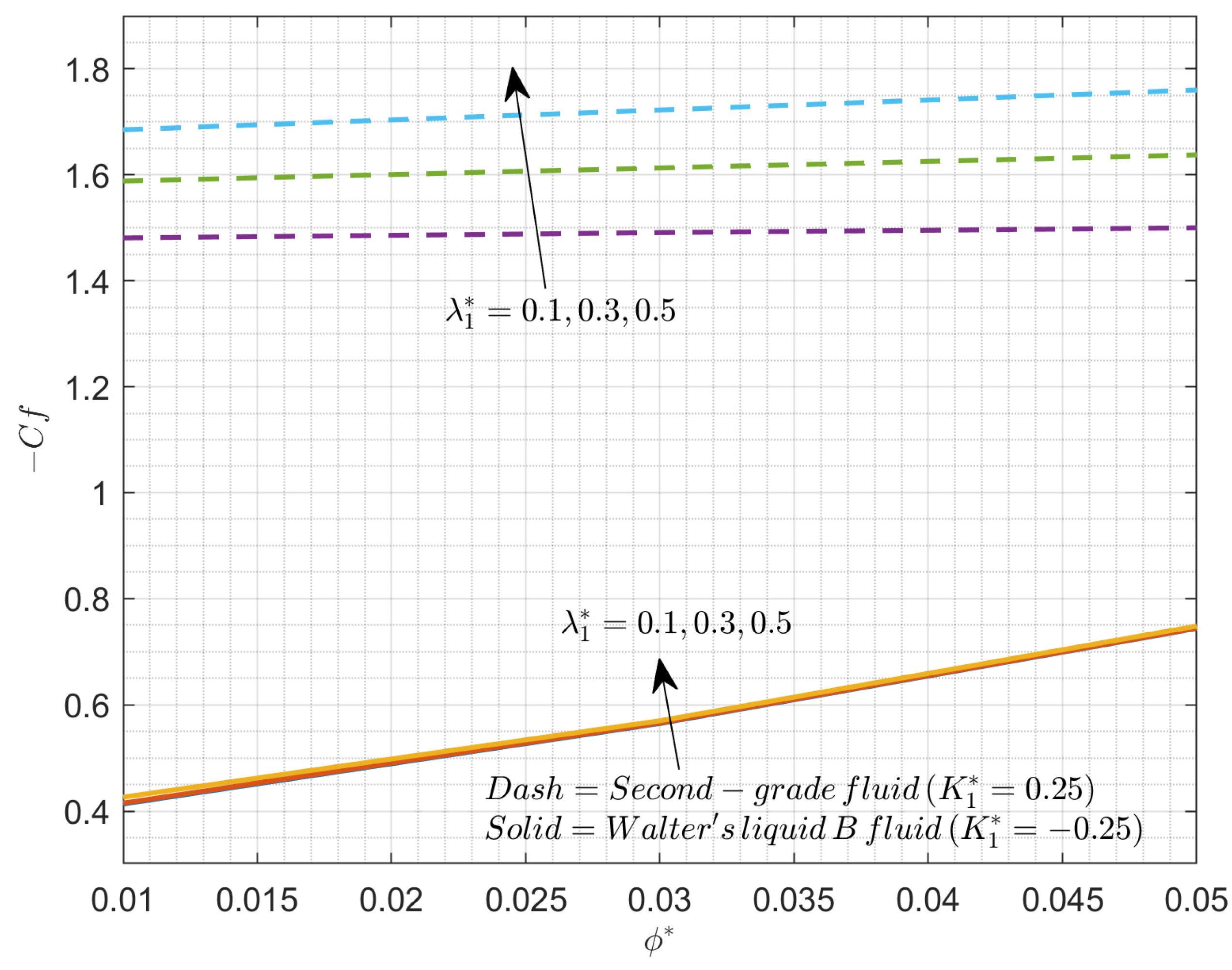
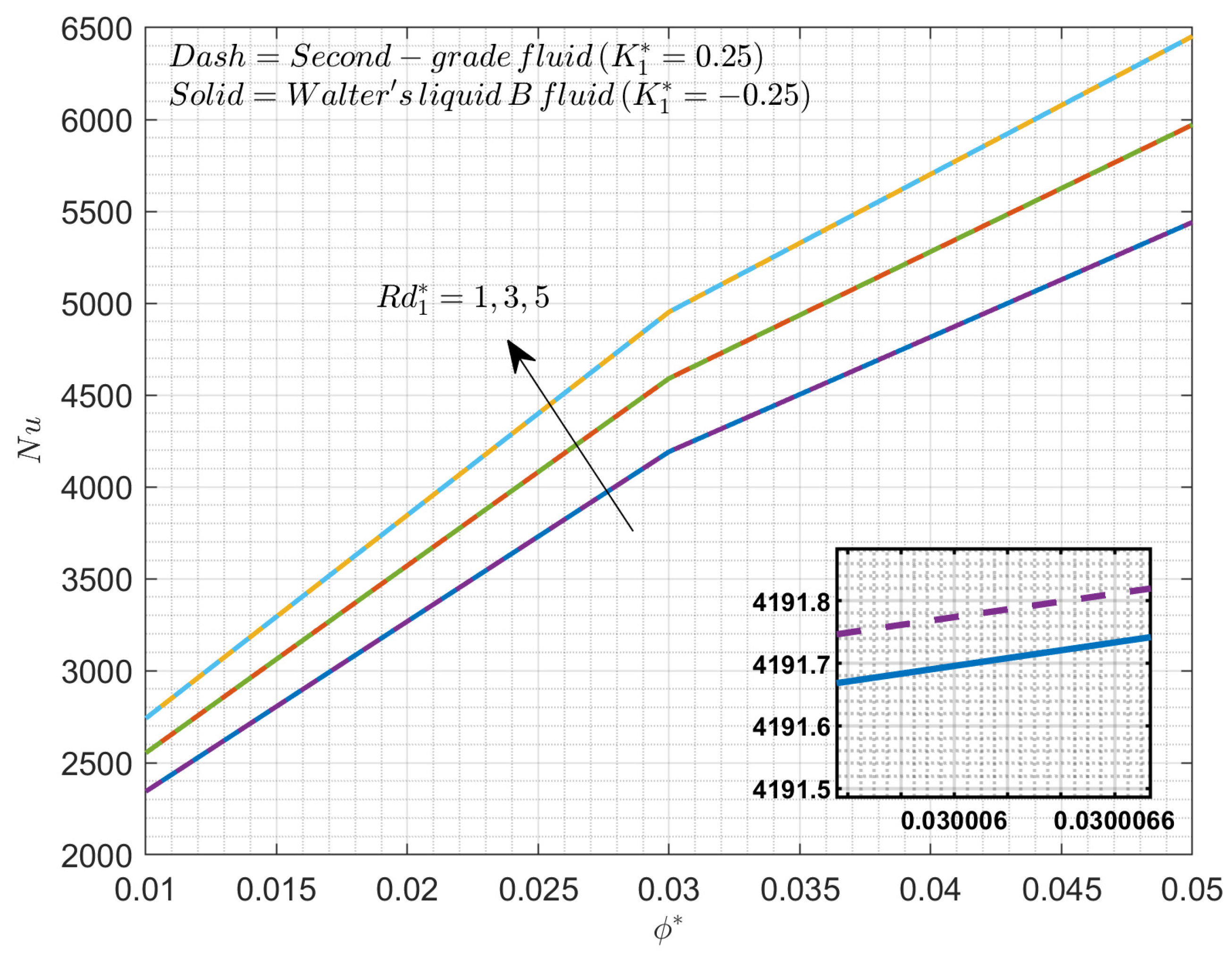
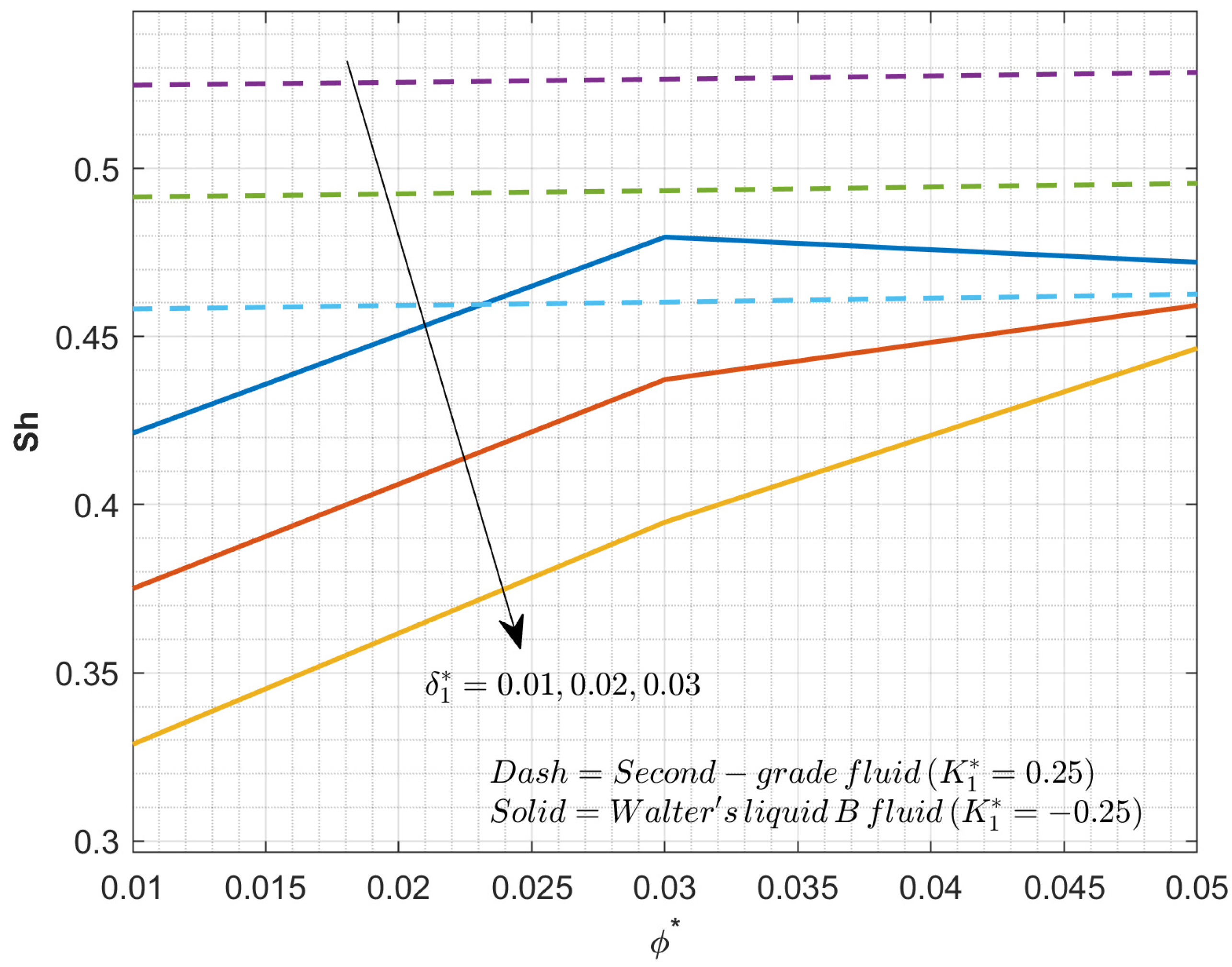
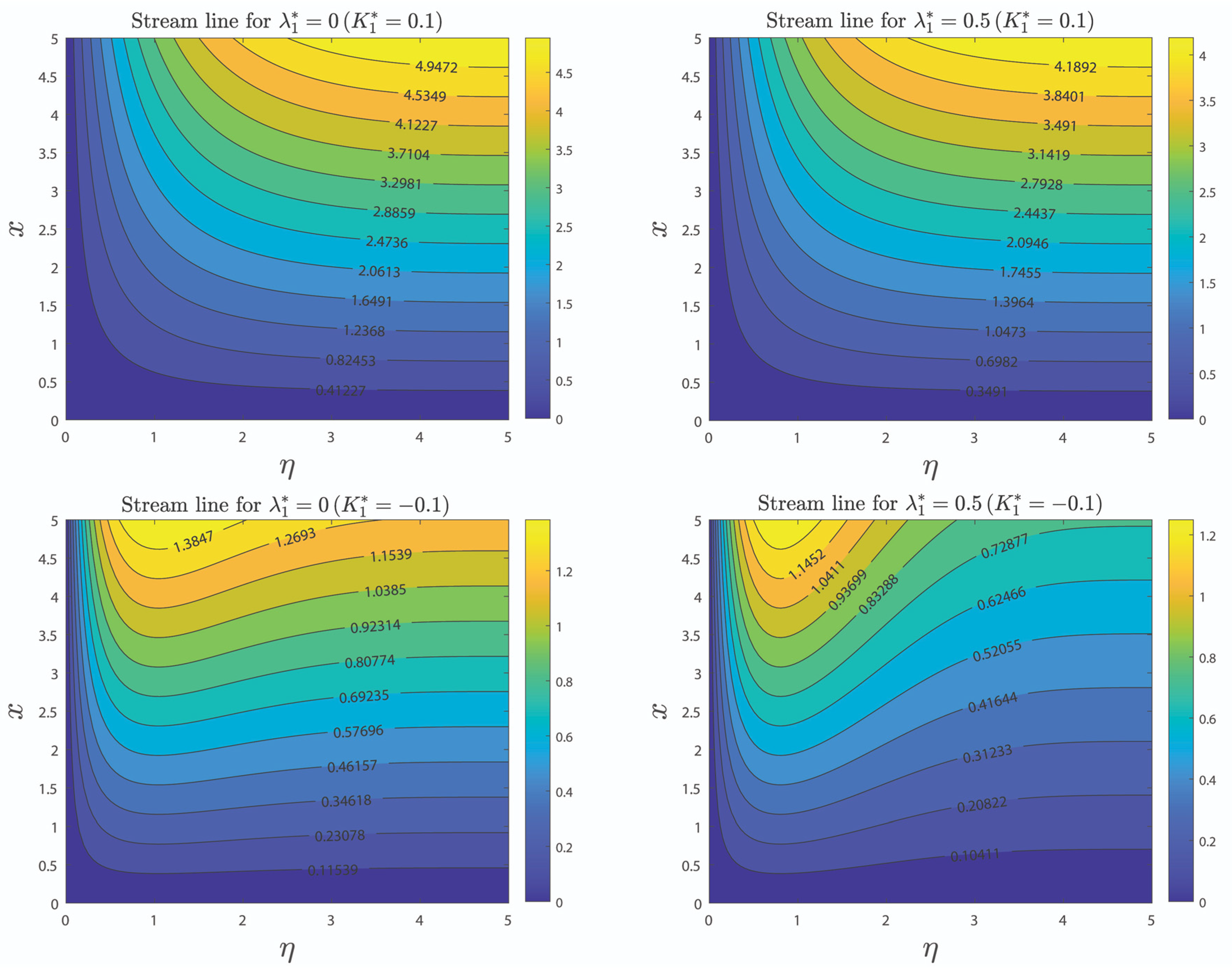
4. Results and Discussion
5. Final Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols | |
| Directions | |
| Velocity components | |
| Magnetization of permanent magnets | |
| Temperature | |
| Applied current density in electrodes | |
| Concentration | |
| Diffusivity | |
| Ambient concentration | |
| Surface concentration | |
| Uniform velocity | |
| Permeability of the porous medium | |
| Viscoelastic constraint | |
| Modified Hartmann number | |
| Radiation constant | |
| Schmidt number | |
| Local Reynolds number | |
| Skin friction | |
| Nusselt number | |
| Sherwood number | |
| Electromagnetic force | |
| Ambient temperature | |
| Heat capacitance | |
| Thermal conductivity | |
| Radiation heat flux | |
| Pollutant external source variation parameter | |
| Width of the electrodes | |
| Pollutant external source variation parameter | |
| Absorption coefficient | |
| Greek Letters | |
| Material constant | |
| Stefan–Boltzmann coefficient | |
| Parameter related to width and magnitude of electrode | |
| Porous constant | |
| Parameter related to local pollutant external source | |
| Parameter related to external pollutant source variation | |
| Solid volume fraction | |
| Dynamic viscosity | |
| Kinematic viscosity | |
| Density | |
| Thermal diffusivity | |
| Subscripts | |
| Fluid | |
| Nanofluid | |
References
- Asogwa, K.K.; Bilal, S.M.; Animasaun, I.L.; Mebarek-Oudina, F.M. Insight into the significance of ramped wall temperature and ramped surface concentration: The case of Casson fluid flow on an inclined Riga plate with heat absorption and chemical reaction. Nonlinear Eng. 2021, 10, 213–230. [Google Scholar] [CrossRef]
- Madhukesh, J.; Alhadhrami, A.; Kumar, R.N.; Gowda, R.P.; Prasannakumara, B.; Kumar, R.V. Physical insights into the heat and mass transfer in Casson hybrid nanofluid flow induced by a Riga plate with thermophoretic particle deposition. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 09544089211039305. [Google Scholar] [CrossRef]
- Xu, Y.-J.; Shah, F.; Khan, M.I.; Kumar, R.N.; Gowda, R.J.P.; Prasannakumara, B.C.; Malik, M.Y.; Khan, S.U. New modeling and analytical solution of fourth grade (non-Newtonian) fluid by a stretchable magnetized Riga device. Int. J. Mod. Phys. C 2022, 33, 2250013. [Google Scholar] [CrossRef]
- Asogwa, K.K.; Goud, B.S.; Shah, N.A.; Yook, S.-J. Rheology of electromagnetohydrodynamic tangent hyperbolic nanofluid over a stretching Riga surface featuring dufour effect and activation energy. Sci. Rep. 2022, 12, 14602. [Google Scholar] [CrossRef]
- Alshehri, A.M.; Coban, H.H.; Ahmad, S.; Khan, U.; Alghamdi, W.M. Buoyancy Effect on a Micropolar Fluid Flow Past a Vertical Riga Surface Comprising Water-Based SWCNT–MWCNT Hybrid Nanofluid Subject to Partially Slipped and Thermal Stratification: Cattaneo–Christov Model. Math. Probl. Eng. 2021, 2021, e6618395. [Google Scholar]
- Prasad, K.V.; Rajashekhar, C.; Mebarek-Oudina, F.; Animasaun, I.L.; Makinde, O.D.; Vajravelu, K.; Vaidya, H.; Mahendra, D.L. Unsteady Magnetohydrodynamic Convective Flow of a Nanoliquid via a Radially Stretched Riga Area via Optimal Homotopy Analysis Method. J. Nanofluids 2022, 11, 84–98. [Google Scholar] [CrossRef]
- Mandal, G.; Pal, D. Mixed convective-quadratic radiative MoS2–SiO2/H2O hybrid nanofluid flow over an exponentially shrinking permeable Riga surface with slip velocity and convective boundary conditions: Entropy and stability analysis. Numer. Heat Transf. Part A: Appl. [CrossRef]
- Ali, Q.; Riaz, S.; Memon, I.Q.; Chandio, I.A.; Amir, M.; Sarris, I.E.; Abro, K.A. Investigation of magnetized convection for second-grade nanofluids via Prabhakar differentiation. Nonlinear Eng. 2023, 12, 20220286. [Google Scholar] [CrossRef]
- Gowda, R.J.P.; Kumar, R.N.; Jyothi, A.M.; Prasannakumara, B.C.; Sarris, I.E. Impact of Binary Chemical Reaction and Activation Energy on Heat and Mass Transfer of Marangoni Driven Boundary Layer Flow of a Non-Newtonian Nanofluid. Processes 2021, 9, 702. [Google Scholar] [CrossRef]
- Xia, W.-F.; Animasaun, I.L.; Wakif, A.; Shah, N.A.; Yook, S.-J. Gear-generalized differential quadrature analysis of oscillatory convective Taylor-Couette flows of second-grade fluids subject to Lorentz and Darcy-Forchheimer quadratic drag forces. Int. Commun. Heat Mass Transf. 2021, 126, 105395. [Google Scholar] [CrossRef]
- Fetecau, C.; Nazar, A.; Khan, I.; Shah, N.A. First exact solution for a second grade fluid subject to an oscillating shear stress induced by a sphere. J. Nonlinear Sci. 2018, 19, 186–195. [Google Scholar]
- Shah, N.A.; Yook, S.-J.; Tosin, O. Analytic simulation of thermophoretic second grade fluid flow past a vertical surface with variable fluid characteristics and convective heating. Sci. Rep. 2022, 12, 5445. [Google Scholar] [CrossRef]
- Khan, M.I.; Qayyum, S.; Kadry, S.; Khan, W.A.; Abbas, S.Z. Irreversibility Analysis and Heat Transport in Squeezing Nanoliquid Flow of Non-Newtonian (Second-Grade) Fluid Between Infinite Plates with Activation Energy. Arab. J. Sci. Eng. 2020, 45, 4939–4947. [Google Scholar] [CrossRef]
- Hayat, T. On magnetohydrodynamic flow of second grade nanofluid over a nonlinear stretching sheet. J. Magn. Magn. Mater. 2016, 408, 99–106. [Google Scholar] [CrossRef]
- Kumar, R.N.; Prasannakumara, B.C.; Gowda, R.J.P. Impact of Diffusion-Thermo and Thermal-Diffusion on the Flow of Walters-B Fluid over a Sheet Saturated in a Porous Medium Using Local Thermal Non-Equilibrium Condition, STRPM. (n.d.). Available online: https://www.researchgate.net/publication/370042091_Impact_of_diffusion-thermo_and_thermal-diffusion_on_the_flow_of_Walters-B_fluid_over_a_sheet_saturated_in_a_porous_medium_using_local_thermal_non-equilibrium_condition (accessed on 15 April 2023).
- Wakif, A.; Animasaun, I.L.; Khan, U.; Shah, N.A.; Thumma, T. Dynamics of radiative-reactive Walters-b fluid due to mixed convection conveying gyrotactic microorganisms, tiny particles experience haphazard motion, thermo-migration, and Lorentz force. Phys. Scr. 2021, 96, 125239. [Google Scholar]
- Siddique, I.; Shah, N.A.; Abro, K.A. Thermography of ferromagnetic Walter’s-B fluid through varying thermal stratification. South Afr. J. Chem. Eng. 2021, 36, 118–126. [Google Scholar] [CrossRef]
- Qaiser, D.; Zheng, Z.; Khan, M.R. Numerical assessment of mixed convection flow of Walters-B nanofluid over a stretching surface with Newtonian heating and mass transfer. Therm. Sci. Eng. Prog. 2021, 22, 100801. [Google Scholar] [CrossRef]
- Chu, Y.-M.; Khan, N.; Khan, M.I.; Al-Khaled, K.; Abbas, N.; Khan, S.U.; Hashmi, M.S.; Qayyum, S.; Kadry, S. Thermophoresis particle deposition analysis for nonlinear thermally developed flow of Magneto-Walter’s B nanofluid with buoyancy forces. Alex. Eng. J. 2021, 60, 1851–1860. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles. In Proceedings of the 1995 International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 12–17 November 1995. [Google Scholar]
- Khan, U.; Mebarek-Oudina, F.; Zaib, A.; Ishak, A.; Bakar, S.A.; Sherif, E.-S.M.; Baleanu, D. An exact solution of a Casson fluid flow induced by dust particles with hybrid nanofluid over a stretching sheet subject to Lorentz forces. Waves Random Complex Media 2022, 1–14. [Google Scholar] [CrossRef]
- Gkountas, A.A.; Benos, L.T.; Sofiadis, G.N.; Sarris, I.E. A printed-circuit heat exchanger consideration by exploiting an Al2O3-water nanofluid: Effect of the nanoparticles interfacial layer on heat transfer. Therm. Sci. Eng. Prog. 2021, 22, 100818. [Google Scholar] [CrossRef]
- Madhukesh, J.; Shankaralingappa, B.; Gireesha, B.; Prasannakumara, B. Evaluation of heat and mass transfer characteristics in a nanofluid flow over an exponentially stretchable sheet with activation energy. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2022, 09544089221074827. [Google Scholar] [CrossRef]
- Haq, I.; Kumar, R.N.; Gill, R.; Madhukesh, J.K.; Khan, U.; Raizah, Z.; Eldin, S.M.; Boonsatit, N.; Jirawattanapanit, A. Impact of homogeneous and heterogeneous reactions in the presence of hybrid nanofluid flow on various geometries. Front. Chem. 2022, 10, 1032805. [Google Scholar] [CrossRef]
- Dogonchi, A.S.; Hashemi-Tilehnoee, M.; Waqas, M.; Seyyedi, S.M.; Animasaun, I.L.; Ganji, D.D. The influence of different shapes of nanoparticle on Cu–H2O nanofluids in a partially heated irregular wavy enclosure. Phys. A Stat. Mech. Its Appl. 2020, 540, 123034. [Google Scholar] [CrossRef]
- Gireesha, B.J.; Prasannakumara, B.C.; Umeshaiah, M.; Shashikumar, N.S. Three Dimensional Boundary Layer Flow of MHD Maxwell Nanofluid over a Non-Linearly Stretching Sheet with Nonlinear Thermal Radiation. J. Appl. Nonlinear Dyn. 2021, 10, 263–277. [Google Scholar]
- Ramesh, G.K.; Madhukesh, J.K.; Shah, N.A.; Yook, S.-J. Flow of hybrid CNTs past a rotating sphere subjected to thermal radiation and thermophoretic particle deposition. Alex. Eng. J. 2023, 64, 969–979. [Google Scholar]
- Atashafrooz, M.; Sajjadi, H.; Delouei, A.A. Simulation of combined convective-radiative heat transfer of hybrid nanofluid flow inside an open trapezoidal enclosure considering the magnetic force impacts. J. Magn. Magn. Mater. 2023, 567, 170354. [Google Scholar] [CrossRef]
- Oke, A.S.; Prasannakumara, B.C.; Mutuku, W.N.; Gowda, R.J.P.; Juma, B.A.; Kumar, R.N.; Bada, O.I. Exploration of the effects of Coriolis force and thermal radiation on water-based hybrid nanofluid flow over an exponentially stretching plate. Sci. Rep. 2022, 12, 21733. [Google Scholar]
- Alzahrani, H.A.H.; Alsaiari, A.; Madhukesh, J.K.; Kumar, R.N.; Prasanna, B.M. Effect of thermal radiation on heat transfer in plane wall jet flow of Casson nanofluid with suction subject to a slip boundary condition. Waves Random Complex Media 2022, 1–18. [Google Scholar] [CrossRef]
- Prasannakumara, B.C.; Shashikumar, N.S. Boundary Layer Flow and Heat Transfer of Nanofluid with Fluid Particle Suspension Over a Nonlinear Stretching Sheet in the Presence of Thermal Radiation. J. Nanofluids 2017, 6, 487–495. [Google Scholar] [CrossRef]
- Thumma, T.; Ahammad, N.A.; Swain, K.; Animasauan, I.L.; Mishra, S.R. Increasing effects of Coriolis force on the cupric oxide and silver nanoparticles based nanofluid flow when thermal radiation and heat source/sink are significant. Waves Random Complex Media 2022, 1–18. [Google Scholar] [CrossRef]
- Atashafrooz, M.; Sajjadi, H.; Delouei, A.A. Interacting influences of Lorentz force and bleeding on the hydrothermal behaviors of nanofluid flow in a trapezoidal recess with the second law of thermodynamics analysis. Int. Commun. Heat Mass Transf. 2020, 110, 104411. [Google Scholar] [CrossRef]
- Makinde, O.D.; Moitsheki, R.J.; Tau, B.A. Similarity reductions of equations for river pollution. Appl. Math. Comput. 2007, 188, 1267–1273. [Google Scholar] [CrossRef]
- Cintolesi, C.; Barbano, F.; Di Sabatino, S. Large-Eddy Simulation Analyses of Heated Urban Canyon Facades. Energies 2021, 14, 3078. [Google Scholar] [CrossRef]
- Chinyoka, T.; Makinde, O.D. Analysis of Nonlinear Dispersion of a Pollutant Ejected by an External Source into a Channel Flow. Math. Probl. Eng. 2010, 2010, e827363. [Google Scholar] [CrossRef]
- Southerland, V.A.; Anenberg, S.C.; Harris, M.; Apte, J.; Hystad, P.; van Donkelaar, A.; Martin, R.V.; Beyers, M.; Roy, A. Assessing the Distribution of Air Pollution Health Risks within Cities: A Neighborhood-Scale Analysis Leveraging High-Resolution Data Sets in the Bay Area, California. Environ. Health Perspect. 2021, 129, 037006. [Google Scholar] [CrossRef]
- Chinyoka, T.; Makinde, O.D. Modelling and Analysis of the Dispersal of a Polymeric Pollutant Injected into a Channel Flow of a Newtonian Liquid. Diffus. Found. Mater. Appl. 2023, 33, 23–56. [Google Scholar] [CrossRef]
- Brewster, M.Q. Thermal Radiative Transfer and Properties; John Wiley & Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Ishak, A.; Nazar, R.; Pop, I. Mixed Convection on the Stagnation Point Flow Toward a Vertical, Continuously Stretching Sheet. J. Heat Transf. 2006, 129, 1087–1090. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Entropy analysis for an unsteady MHD flow past a stretching permeable surface in nano-fluid. Powder Technol. 2014, 267, 256–267. [Google Scholar] [CrossRef]
- Das, S.; Chakraborty, S.; Jana, R.N.; Makinde, O.D. Entropy analysis of unsteady magneto-nanofluid flow past accelerating stretching sheet with convective boundary condition. Appl. Math. Mech. 2015, 36, 1593–1610. [Google Scholar]
- Alwawi, F.A.; Alkasasbeh, H.T.; Rashad, A.M.; Idris, R. Natural convection flow of Sodium Alginate based Casson nanofluid about a solid sphere in the presence of a magnetic field with constant surface heat flux. J. Phys. Conf. Ser. 2019, 1366, 012005. [Google Scholar] [CrossRef]
- Khan, A.; Khan, D.; Khan, I.; Ali, F.; Karim, F.U.; Imran, M. MHD Flow of Sodium Alginate-Based Casson Type Nanofluid Passing through a Porous Medium with Newtonian Heating. Sci. Rep. 2018, 8, 8645. [Google Scholar]



| Sl. No | Parameter Definition | Parameter Name |
|---|---|---|
| 01 | Viscoelastic constraint second-grade fluid Walter’s liquid B fluid | |
| 02 | Modified Hartmann number | |
| 03 | Parameter related to width and magnitude of electrodes | |
| 04 | Porous constraint | |
| 05 | Radiation constraint | |
| 06 | Prandtl number | |
| 07 | Parameter related to local pollutant external source | |
| 08 | Parameter related to external pollutant source variation | |
| 09 | Schmidt number | |
| 10 | Local Reynolds number | |
| 11 | ||
| 12 | ||
| 13 | ||
| Thermophysical Characteristics | Name |
|---|---|
| Specific heat capacity | |
| Dynamic viscosity | |
| Thermal conductivity | |
| Density |
| Pr | Ishak et al. [42] | Abolbashari et al. [43] | Das et al. [44] | Present Numerical Outcome |
|---|---|---|---|---|
| 0.72 | 0.8086 | 0.80863135 | 0.80876122 | 0.80876153 |
| 1.0 | 1.0000 | 1.00000000 | 1.00000000 | 1.00000000 |
| 3.0 | 1.9237 | 1.92368259 | 1.92357431 | 1.92357446 |
| 7.0 | 3.0723 | 3.07225021 | 3.07314679 | 3.07314636 |
| 10 | 3.7207 | 3.72067390 | 3.72067390 | 3.72067335 |
| Parameter | Values | Second-Grade Fluid | Walter’s Liquid B Fluid |
|---|---|---|---|
| 0.01 | 0.140264% | 0.560122% | |
| 0.02 | 0.140338% | 0.570178% | |
| 0.03 | 0.161919% | 0.601998% | |
| 0.1 | 0.140853% | 0.650966% | |
| 0.2 | 0.122659% | 0.631004% | |
| 0.3 | 0.123269% | 0.648976% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madhukesh, J.K.; Kalleshachar, V.; Kumar, C.; Khan, U.; Nagaraja, K.V.; Sarris, I.E.; Sherif, E.-S.M.; Hassan, A.M.; Chohan, J.S. A Model Development for Thermal and Solutal Transport Analysis of Non-Newtonian Nanofluid Flow over a Riga Surface Driven by a Waste Discharge Concentration. Water 2023, 15, 2879. https://doi.org/10.3390/w15162879
Madhukesh JK, Kalleshachar V, Kumar C, Khan U, Nagaraja KV, Sarris IE, Sherif E-SM, Hassan AM, Chohan JS. A Model Development for Thermal and Solutal Transport Analysis of Non-Newtonian Nanofluid Flow over a Riga Surface Driven by a Waste Discharge Concentration. Water. 2023; 15(16):2879. https://doi.org/10.3390/w15162879
Chicago/Turabian StyleMadhukesh, Javali Kotresh, Vinutha Kalleshachar, Chandan Kumar, Umair Khan, Kallur Venkat Nagaraja, Ioannis E. Sarris, El-Sayed M. Sherif, Ahmed M. Hassan, and Jasgurpreet Singh Chohan. 2023. "A Model Development for Thermal and Solutal Transport Analysis of Non-Newtonian Nanofluid Flow over a Riga Surface Driven by a Waste Discharge Concentration" Water 15, no. 16: 2879. https://doi.org/10.3390/w15162879
APA StyleMadhukesh, J. K., Kalleshachar, V., Kumar, C., Khan, U., Nagaraja, K. V., Sarris, I. E., Sherif, E.-S. M., Hassan, A. M., & Chohan, J. S. (2023). A Model Development for Thermal and Solutal Transport Analysis of Non-Newtonian Nanofluid Flow over a Riga Surface Driven by a Waste Discharge Concentration. Water, 15(16), 2879. https://doi.org/10.3390/w15162879








