Entrapped Air Removal by Hydraulic Means in Gravity Water Systems in Small Diameter Pipelines
Abstract
:1. Introduction
2. Materials and Methods
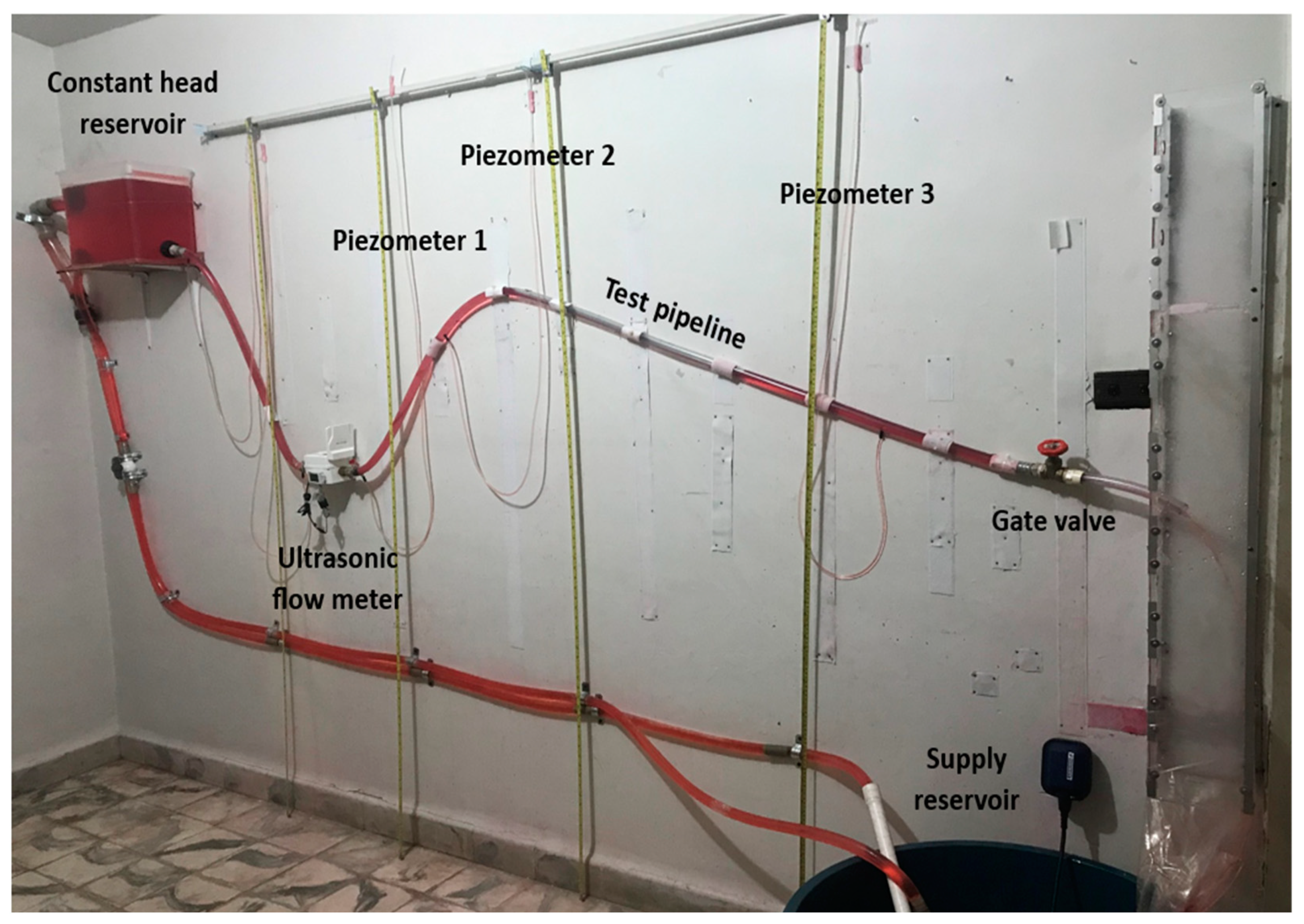
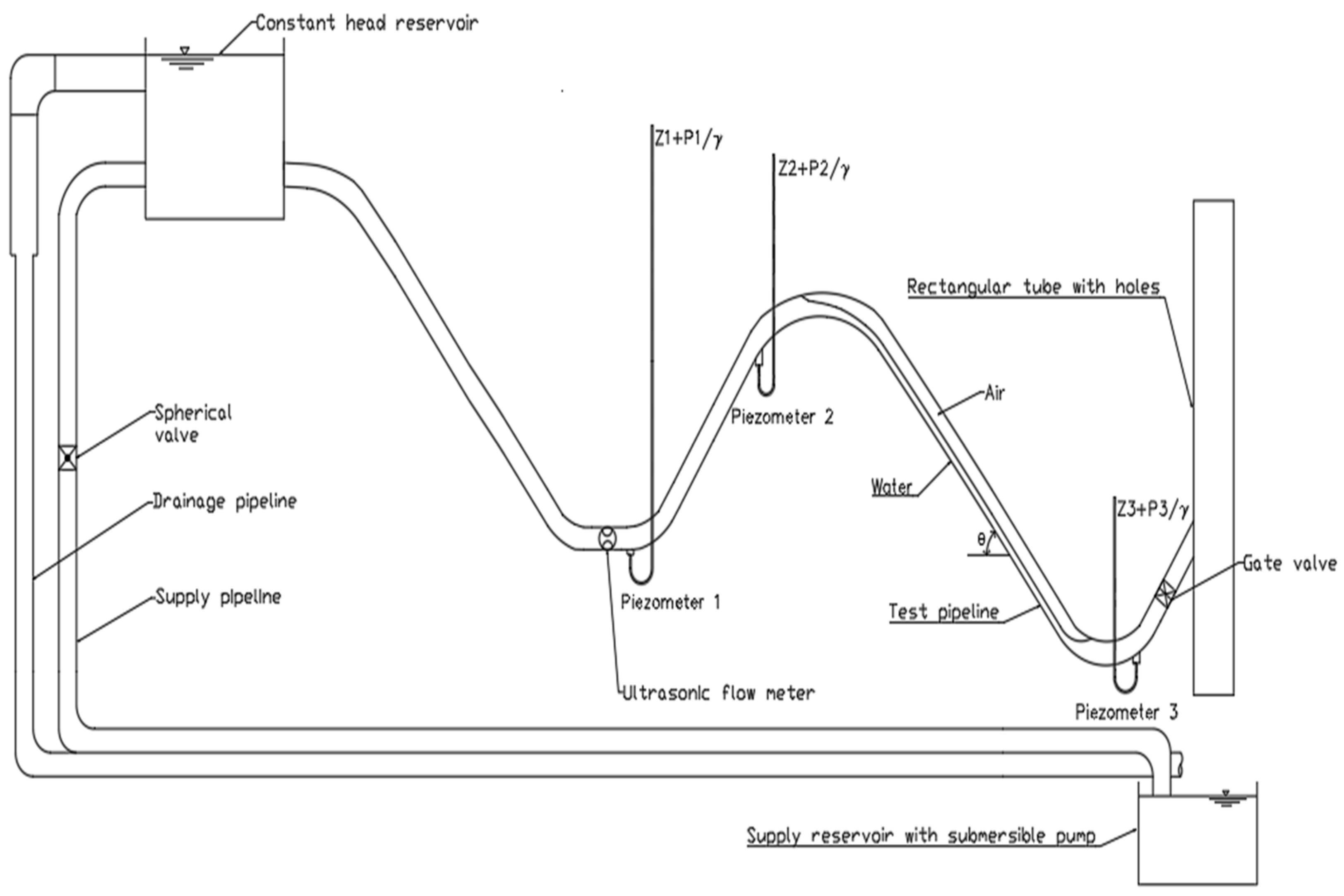
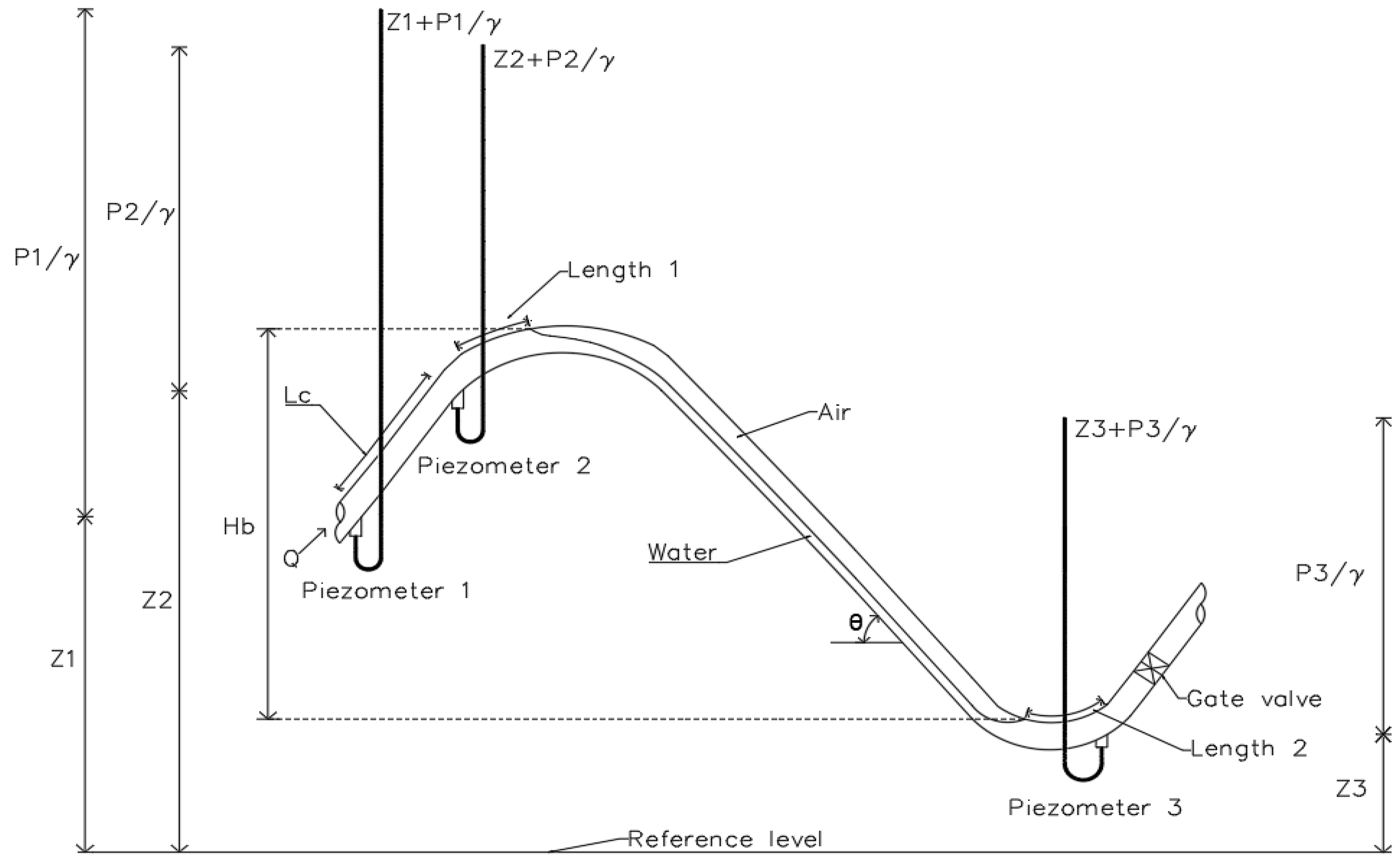
2.1. Experimental Setup
2.2. Energy Loss Generated by Entrapped Air
2.3. Air Bubbles’ Removal Due to Hydraulic Jump Turbulence
2.4. Entrapped Air Removal Due to Hydrodynamic Thrust
3. Results and Discussion
3.1. Energy Loss Generated by Entrapped Air
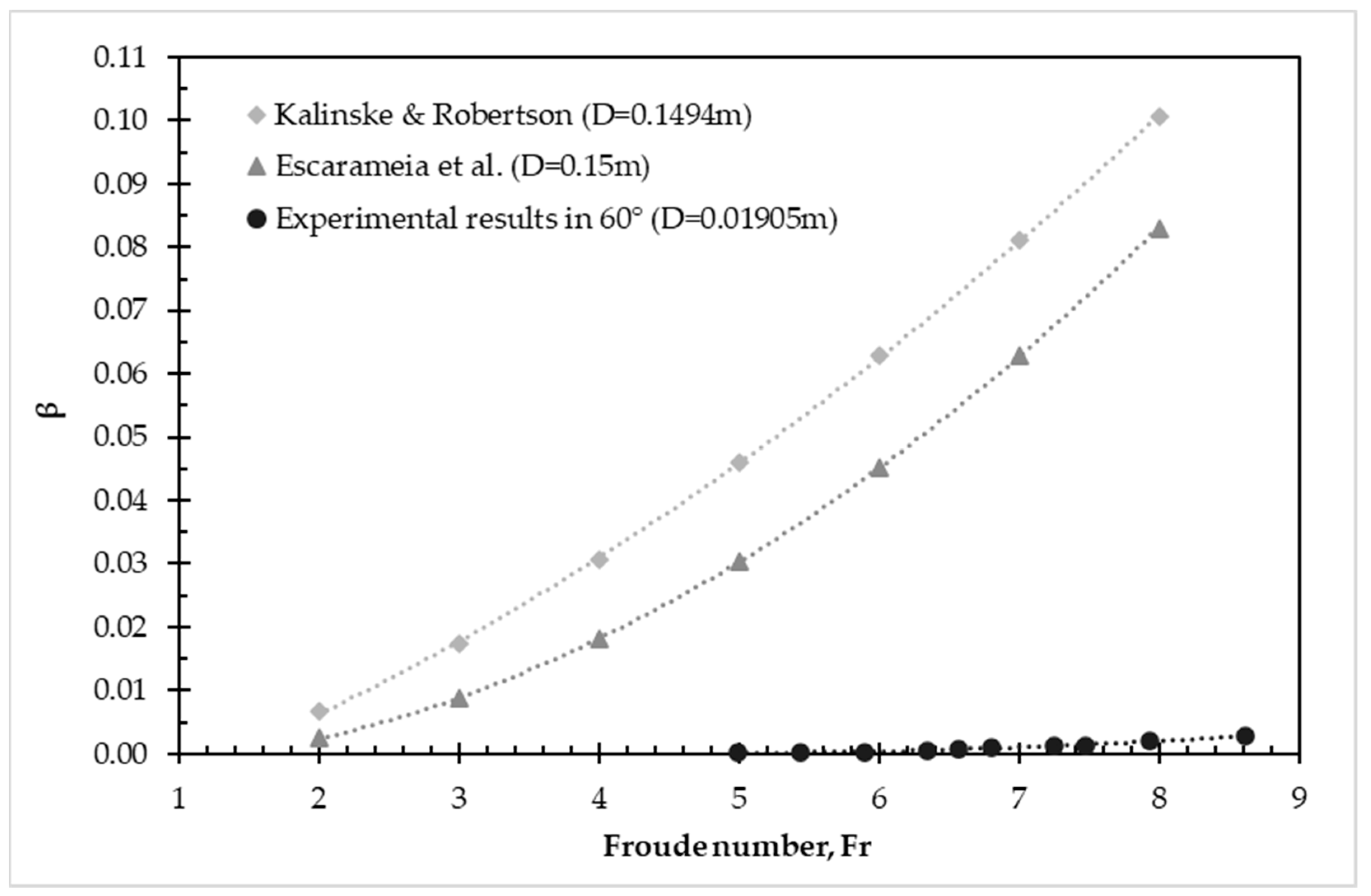
3.2. Air Bubbles’ Removal Due to Hydraulic Jump Turbulence
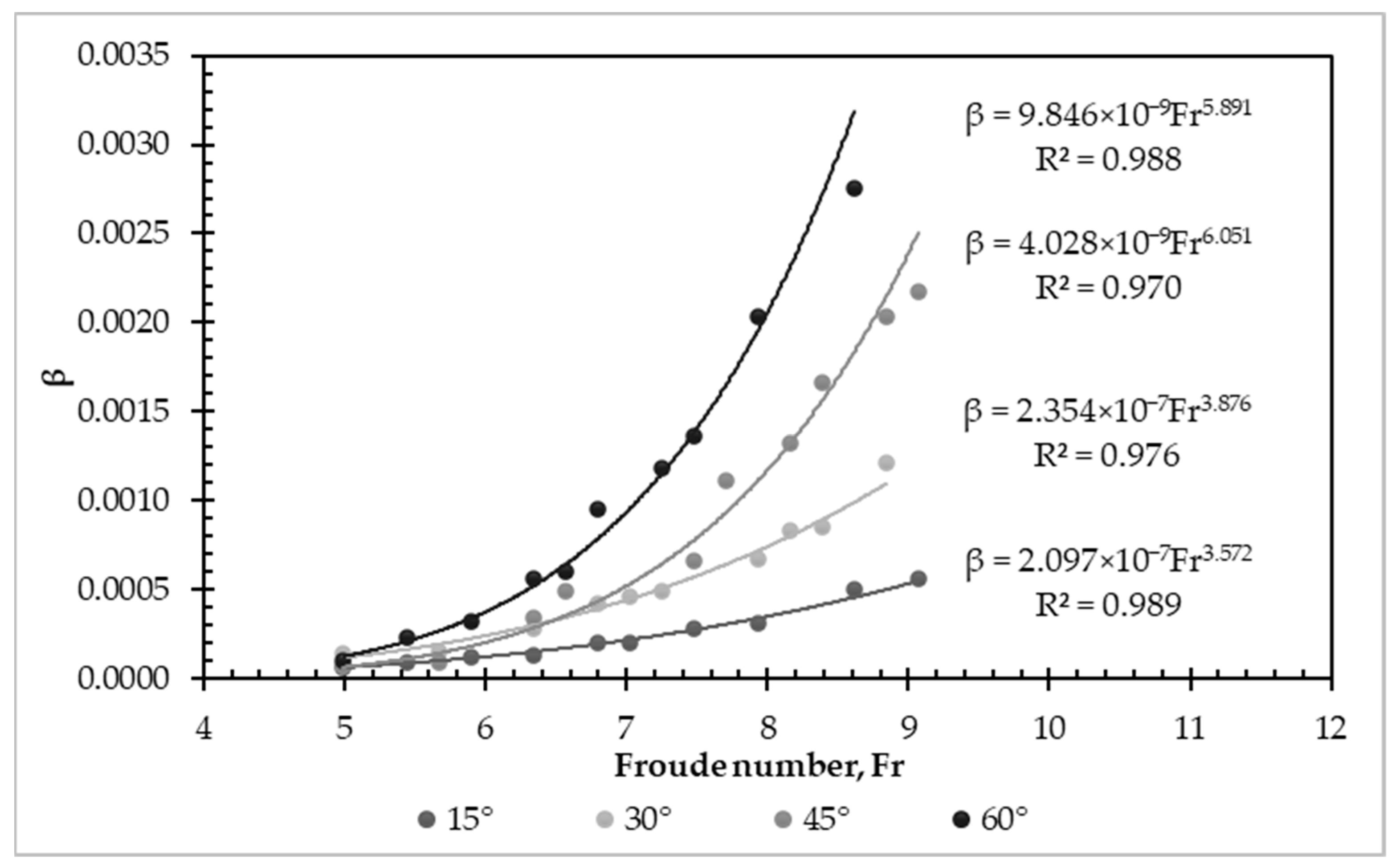
3.3. Entrapped Air Removal Due to Hydrodynamic Thrust
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ramezani, L.; Karney, B.; Malekpour, A. Encouraging effective air management in water pipelines: A critical review. J. Water Resour. Plan. Manag. 2016, 142, 04016055. [Google Scholar] [CrossRef] [Green Version]
- Stephenson, D. Effects of air valves and pipework on water hammer pressures. J. Transp. Eng. 1997, 123, 101–106. [Google Scholar] [CrossRef]
- May, D.; Allen, J.; Nelson, D. Hydraulic investigation of air in small diameter pipes. Int. J. Hydraul. Eng. 2018, 7, 51–57. Available online: http://article.sapub.org/10.5923.j.ijhe.20180703.02.html (accessed on 10 October 2022).
- Dean, J.A. Lange’s Handbook of Chemistry; McGraw-Hill, Inc.: New York, NY, USA, 1999. [Google Scholar]
- Pozos, O.; Gonzalez, C.A.; Giesecke, J.; Marx, W.; Rodal, E.A. Air entrapped in gravity pipeline systems. J. Hydraul. Res. 2010, 48, 338–347. [Google Scholar] [CrossRef]
- Colgate, D. Hydraulic Model Studies of the Flow Characteristics and Air Entrainment in the Check Towers of the Main Aqueduct, Canadian River Project Texas; Report Hyd-555; U.S. Dept. of the Bureau of Reclamation: Denver, CO, USA, 1966.
- Ochoa, L.H. Modelación de aire atrapado en flujo de agua en conductos (Modeling Entrapped Air in Water Flow in Pipelines). Ph.D. Thesis, National Autonomous University of Mexico, Mexico City, Mexico, 2005. [Google Scholar]
- Corcos, G. Air in Water Pipes: A Manual for Designers of Spring Supplied Gravity-Driven Drinking Water Rural Delivery Systems, 2nd ed.; Agua Para La Vida: Berkeley, CA, USA, 2003. [Google Scholar]
- Fuertes-Miquel, V.S.; Coronado-Hernández, O.E.; Mora-Meliá, D.; Iglesias-Rey, P.L. Hydraulic modeling during filling and emptying processes in pressurized pipelines: A literature review. Urban Water J. 2019, 16, 299–311. [Google Scholar] [CrossRef]
- Liou, C.P.; Hunt, W.A. Filling of pipelines with undulating elevation profiles. J. Hydraul. Eng. 1996, 122, 534–539. [Google Scholar] [CrossRef]
- Kalinske, A.A.; Bliss, P.H. Removal of air from pipelines by flowing water. Am. Soc. Civ. Eng. 1943, 13, 480–482. [Google Scholar]
- Kent, J.C. The Entrainment of Air by Water Flowing in Circular Conduits with Downgrade Slopes. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1952. [Google Scholar]
- Gandenberger, W. Über die wirtschaftliche und betriebssichere Gestaltung von Fernwasserleitungen (Design of Overland Water Supply Pipelines for Economy and Operational Reliability); R. Oldenbourg: Munich, Germany, 1957. [Google Scholar]
- Wisner, P.E.; Mohsen, F.N.; Kouwen, N. Removal of air from water lines by hydraulic means. J. Hydraul. Div. ACSE 1975, 101, 243–257. [Google Scholar] [CrossRef]
- Falvey, H.T. Air-Water Flow in Hydraulic Structures; Engineering Monograph 41; United States Department of the Interior, Bureau of Reclamation: Denver, CO, USA, 1980.
- Walski, T.M.; Barnhart, T.S.; Driscoll, J.M.; Yencha, R.M. Hydraulics of corrosive gas pockets in force mains. Water Environ. Res. 1994, 66, 772–778. [Google Scholar] [CrossRef]
- Escarameia, M. Investigating hydraulic removal of air from water pipelines. Proc. Inst. Civ. Eng. Water Manag. 2007, 160, 25–34. [Google Scholar] [CrossRef]
- Lauchlan, C.S.; Escarameia, M.; May, R.W.P.; Burrows, R.; Gahan, C. Air in Pipelines: A Literature Review; Report SR 649; HR Wallingford: Oxfordshire, UK, 2005. [Google Scholar]
- Lima-Neto, I.E.; de Melo-Porto, R. Performance of low-cost ejectors. J. Irrig. Drain. Eng. 2004, 130, 122–128. [Google Scholar] [CrossRef]
- Lindell, J.E.; Moore, W.P.; King, H.W. Handbook of Hydraulics, 8th ed.; McGraw-Hill Education: New York, NY, USA, 2017. [Google Scholar]
- Kalinske, A.A.; Robertson, J.M. Closed Conduit Flow. Trans. Am. Soc. Civ. Eng. 1943, 108, 1435–1447. [Google Scholar] [CrossRef]
- Pothof, I.; Clemens, F. On elongated air pockets in downward sloping pipes. J. Hydraul. Res. 2010, 48, 499–503. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Mortensen, J.D.; Barfuss, S.L.; Johnson, M.C. Scale effects of air entrained by hydraulic jumps within closed conduits. J. Hydraul. Res. 2011, 49, 90–95. [Google Scholar] [CrossRef]
- Benjamin, T.B. Gravity currents and related phenomena. J. Fluid Mech. 1968, 31, 209–248. [Google Scholar] [CrossRef]
- Zukoski, E. Influence of viscosity, surface tension and inclination on motion of long bubbles in closed tubes. J. Fluid Mech. 1966, 25, 821–837. [Google Scholar] [CrossRef] [Green Version]
- Baines, W.D.; Wilkinson, D.L. The motion of large air bubbles in ducts of moderate slope. J. Hydraul. Res. 1986, 25, 157–170. [Google Scholar] [CrossRef]
- Pothof, I.W.M.; Clemens, F.H.L.R. Experimental study of air-water flow in downward sloping pipes. Int. J. Multiph. Flow 2011, 37, 278–292. [Google Scholar] [CrossRef]
- Mosvell, G. Luft i Utslippsledninger (Air at Outfalls); Project Committee on Sewage, PRA Report 8; Norwegian Water Institute: Oslo, Norway, 1976. [Google Scholar]
- Townson, J.M. Free-Surface Hydraulics; Unwin Hyman: London, UK, 1991. [Google Scholar]
- Veronese, A. Sul Motto delle Bolle D’aria nelle Condotte D’acqua (On the Motto of Air Bubbles in the Water Pipeline); Estrato dal Fasciacolo X: Roma, Italy, 1937; Volume XIV, p. XV. [Google Scholar]
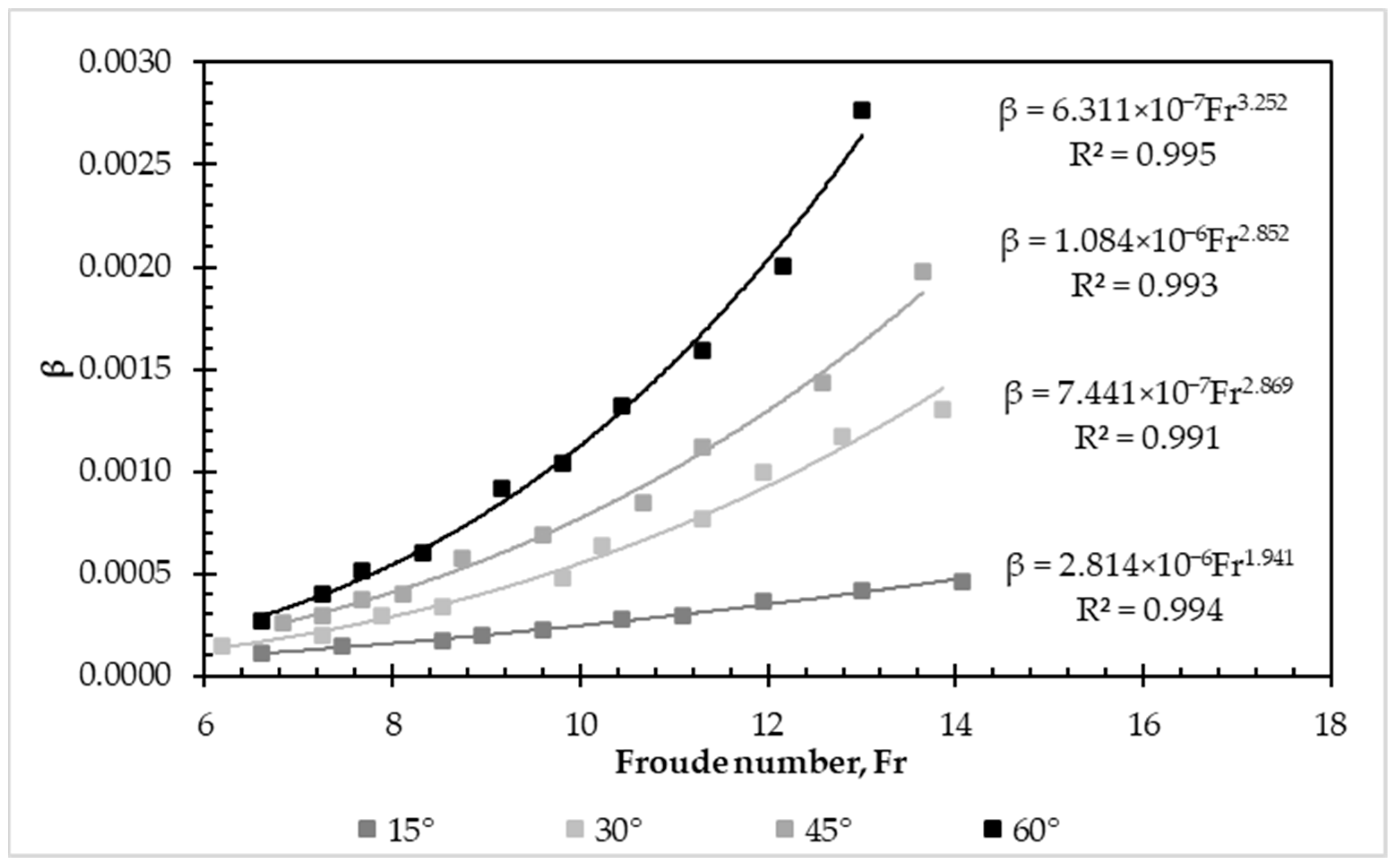
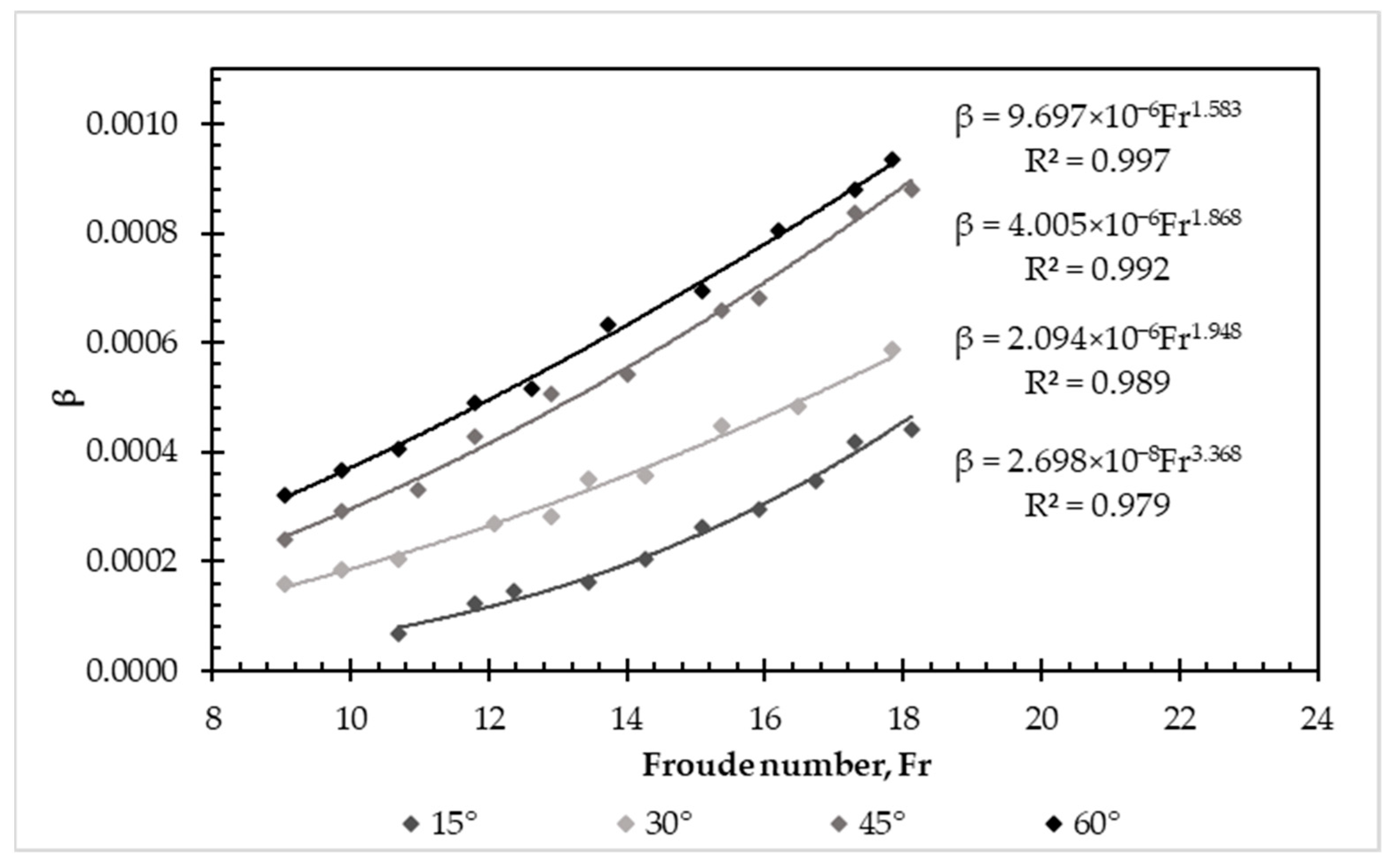
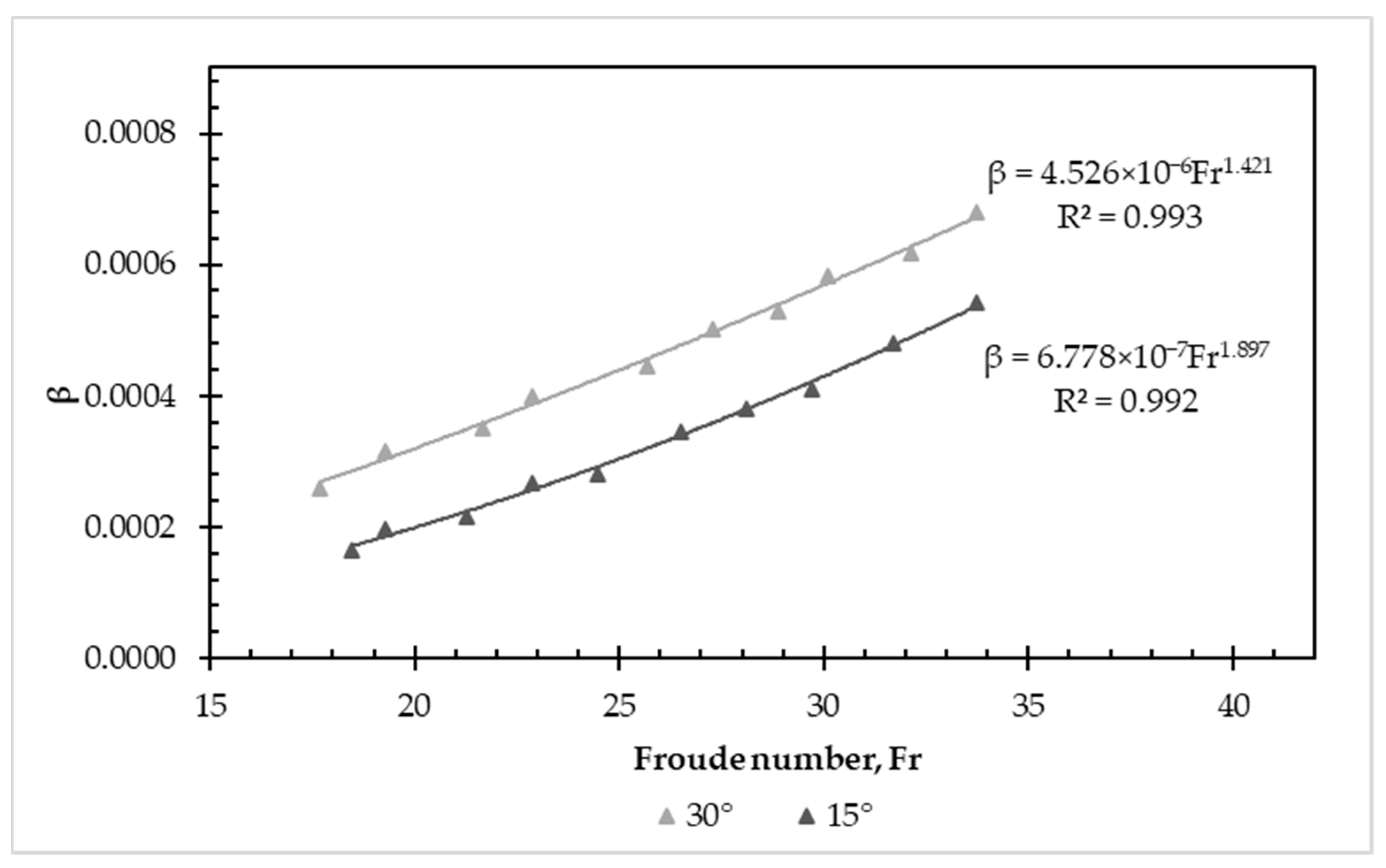
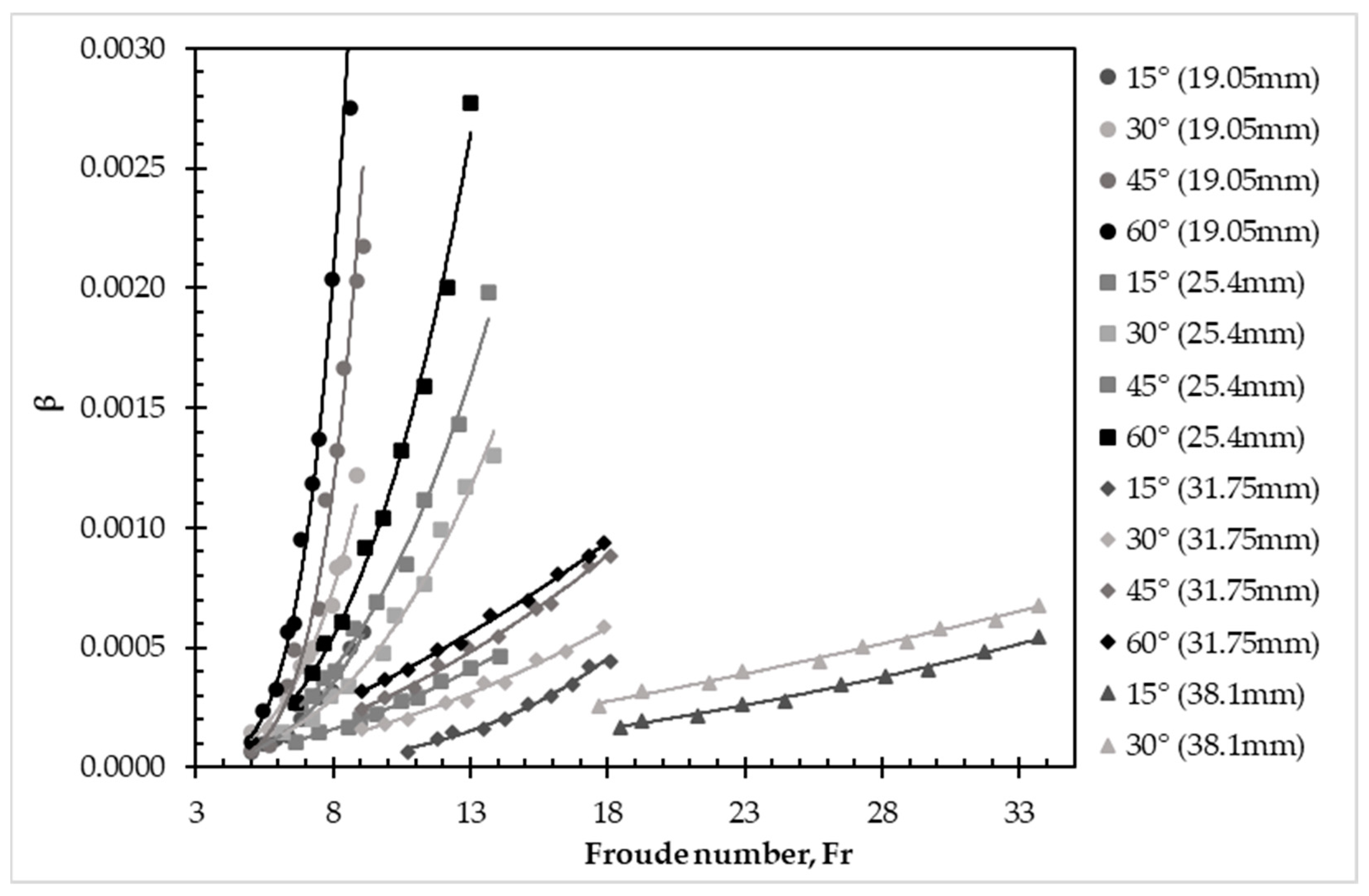

| Diameter (mm) | Downward Angle (°) | Entrapped Air Length (m) | Energy Loss Generated by Entrapped Air (m) | Percentage Difference (%) | |
|---|---|---|---|---|---|
| Calculated (Equation (1)) | Observed | ||||
| 12.7 | 15 | 0.830 | 0.206 | 0.203 | −1.35 |
| 30 | 1.032 | 0.488 | 0.495 | 1.46 | |
| 45 | 0.845 | 0.489 | 0.486 | −0.71 | |
| 60 | 0.910 | 0.767 | 0.786 | 2.07 | |
| 15.875 | 15 | 0.930 | 0.242 | 0.250 | 3.04 |
| 30 | 1.070 | 0.526 | 0.525 | −0.21 | |
| 45 | 0.825 | 0.545 | 0.565 | 3.62 | |
| 60 | 0.910 | 0.711 | 0.709 | −0.27 | |
| 19.05 | 15 | 0.860 | 0.187 | 0.190 | 1.73 |
| 30 | 0.910 | 0.382 | 0.397 | 3.72 | |
| 45 | 0.920 | 0.612 | 0.628 | 2.63 | |
| 60 | 0.950 | 0.762 | 0.787 | 3.18 | |
| 25.4 | 15 | 0.940 | 0.202 | 0.207 | 2.43 |
| 30 | 1.160 | 0.511 | 0.510 | −0.26 | |
| 45 | 1.075 | 0.653 | 0.662 | 1.42 | |
| 60 | 0.955 | 0.663 | 0.669 | 0.96 | |
| 31.75 | 15 | 0.800 | 0.155 | 0.161 | 3.97 |
| 30 | 0.855 | 0.365 | 0.360 | −1.41 | |
| 45 | 0.870 | 0.490 | 0.488 | −0.42 | |
| 60 | 0.875 | 0.564 | 0.568 | 0.74 | |
| 38.1 | 15 | 1.040 | 0.221 | 0.220 | −0.63 |
| 30 | 1.020 | 0.409 | 0.417 | 1.88 | |
| 45 | 1.025 | 0.417 | 0.415 | −0.54 | |
| 60 | 1.010 | 0.412 | 0.425 | 3.00 | |
| Downward Angle (°) | Inner Diameter (mm) | |||||
|---|---|---|---|---|---|---|
| 12.7 | 15.875 | 19.05 | 25.4 | 31.75 | 38.1 | |
| Average of the Dimensionless Air Removal Parameter | ||||||
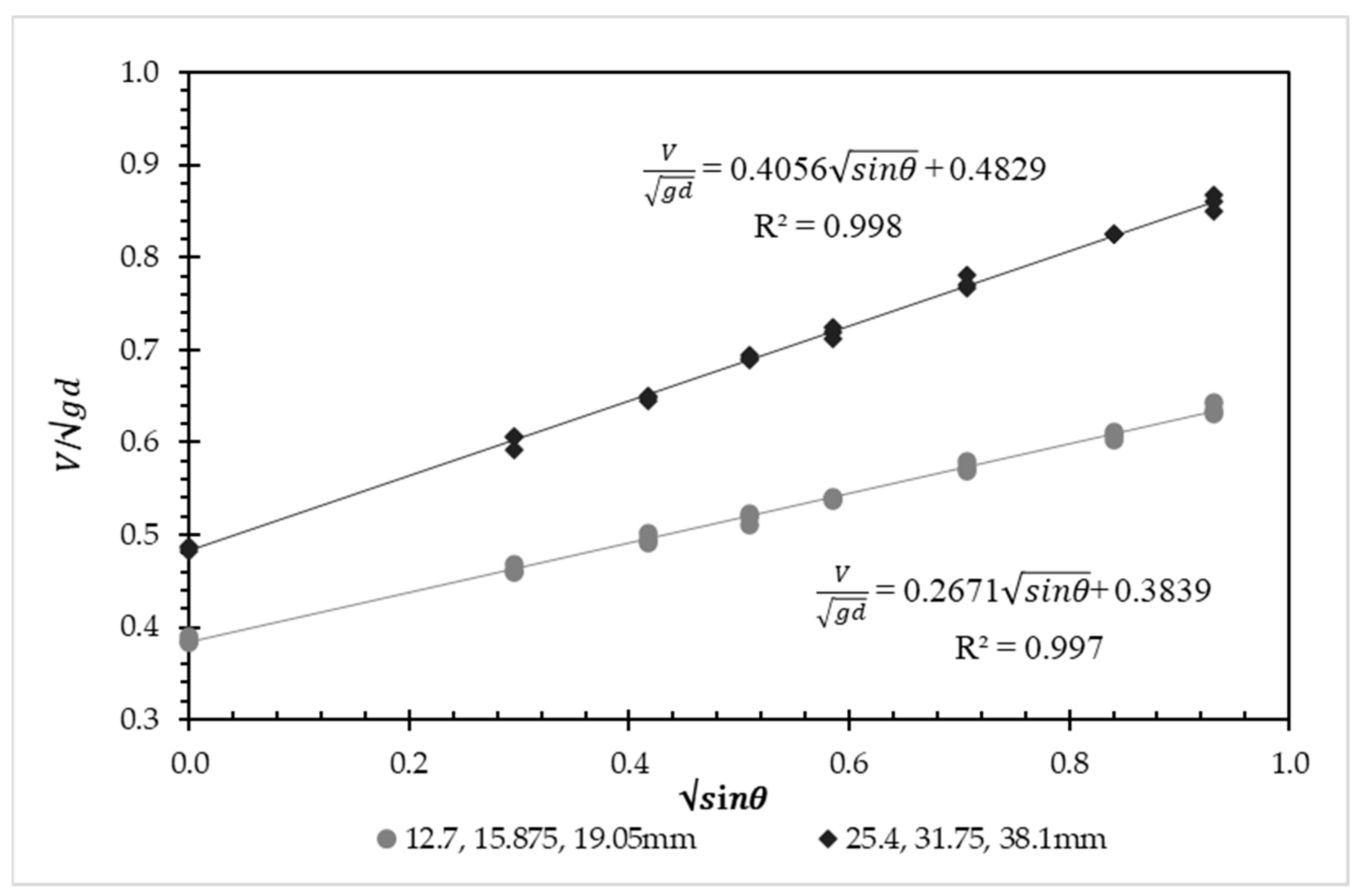
| 0 | 0.3847 | 0.3828 | 0.3896 | 0.4879 | 0.4857 | 0.4826 |
| 5 | 0.4607 | 0.4673 | 0.4585 | 0.5919 | 0.6056 | 0.6053 |
| 10 | 0.5010 | 0.4903 | 0.4951 | 0.6476 | 0.6498 | 0.6448 |
| 15 | 0.5233 | 0.5185 | 0.5113 | 0.6942 | 0.6887 | 0.6911 |
| 20 | 0.5368 | 0.5390 | 0.5397 | 0.7120 | 0.7240 | 0.7186 |
| 30 | 0.5725 | 0.5787 | 0.5689 | 0.7816 | 0.7674 | 0.7703 |
| 45 | 0.6106 | 0.6030 | 0.6071 | 0.8247 | 0.8254 | 0.8250 |
| 60 | 0.6307 | 0.6337 | 0.6428 | 0.8682 | 0.8500 | 0.8600 |
| Source of Variation | Sum of Squares | Degrees of Freedom | Mean Sum of Squares | F-Ratio | p-Value |
|---|---|---|---|---|---|
| Between groups | 0.3599 | 5 | 0.0720 | 6.652 | 1.209 × 10−4 |
| Within groups | 0.4544 | 42 | 0.0108 | ||
| Total | 0.8142 | 47 | 0.0173 |
| Diameter 1 (mm) | Diameter 2 (mm) | Absolute Difference in Averages | Q-Stat | p-Value | Difference between Diameters |
|---|---|---|---|---|---|
| 12.7 | 15.875 | 8.7 × 10−4 | 0.024 | 1.000 | No |
| 12.7 | 19.05 | 9.1 × 10−4 | 0.025 | 1.000 | No |
| 12.7 | 25.4 | 0.1735 | 4.718 | 0.021 | Yes |
| 12.7 | 31.75 | 0.1720 | 4.678 | 0.022 | Yes |
| 12.7 | 38.1 | 0.1722 | 4.682 | 0.022 | Yes |
| 15.875 | 19.05 | 4.0 × 10−5 | 0.001 | 1.000 | No |
| 15.875 | 25.4 | 0.1744 | 4.741 | 0.020 | Yes |
| 15.875 | 31.75 | 0.1729 | 4.702 | 0.021 | Yes |
| 15.875 | 38.1 | 0.1731 | 4.706 | 0.021 | Yes |
| 19.05 | 25.4 | 0.1744 | 4.742 | 0.020 | Yes |
| 19.05 | 31.75 | 0.1729 | 4.703 | 0.021 | Yes |
| 19.05 | 38.1 | 0.1731 | 4.707 | 0.021 | Yes |
| 25.4 | 31.75 | 1.4 × 10−3 | 0.039 | 1.000 | No |
| 25.4 | 38.1 | 1.3 × 10−3 | 0.035 | 1.000 | No |
| 31.75 | 38.1 | 1.4 × 10−4 | 0.004 | 1.000 | No |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quintana-Molina, E.; Prado-Hernández, J.V.; Monserrat-Viscarri, J.; Quintana-Molina, J.R. Entrapped Air Removal by Hydraulic Means in Gravity Water Systems in Small Diameter Pipelines. Water 2023, 15, 2870. https://doi.org/10.3390/w15162870
Quintana-Molina E, Prado-Hernández JV, Monserrat-Viscarri J, Quintana-Molina JR. Entrapped Air Removal by Hydraulic Means in Gravity Water Systems in Small Diameter Pipelines. Water. 2023; 15(16):2870. https://doi.org/10.3390/w15162870
Chicago/Turabian StyleQuintana-Molina, Emilio, Jorge Víctor Prado-Hernández, Joaquim Monserrat-Viscarri, and José Rodolfo Quintana-Molina. 2023. "Entrapped Air Removal by Hydraulic Means in Gravity Water Systems in Small Diameter Pipelines" Water 15, no. 16: 2870. https://doi.org/10.3390/w15162870






