Simulation of Water Quality in a River Network with Time-Varying Lateral Inflows and Pollutants
Abstract
:1. Introduction
2. River Network Hydrodynamic Model
2.1. Improvements to the Control Equation
2.2. Time-Varying Process Associated with Lateral Inflow
2.3. Calculation Method for Lateral Pollutant Concentration
3. Case Study
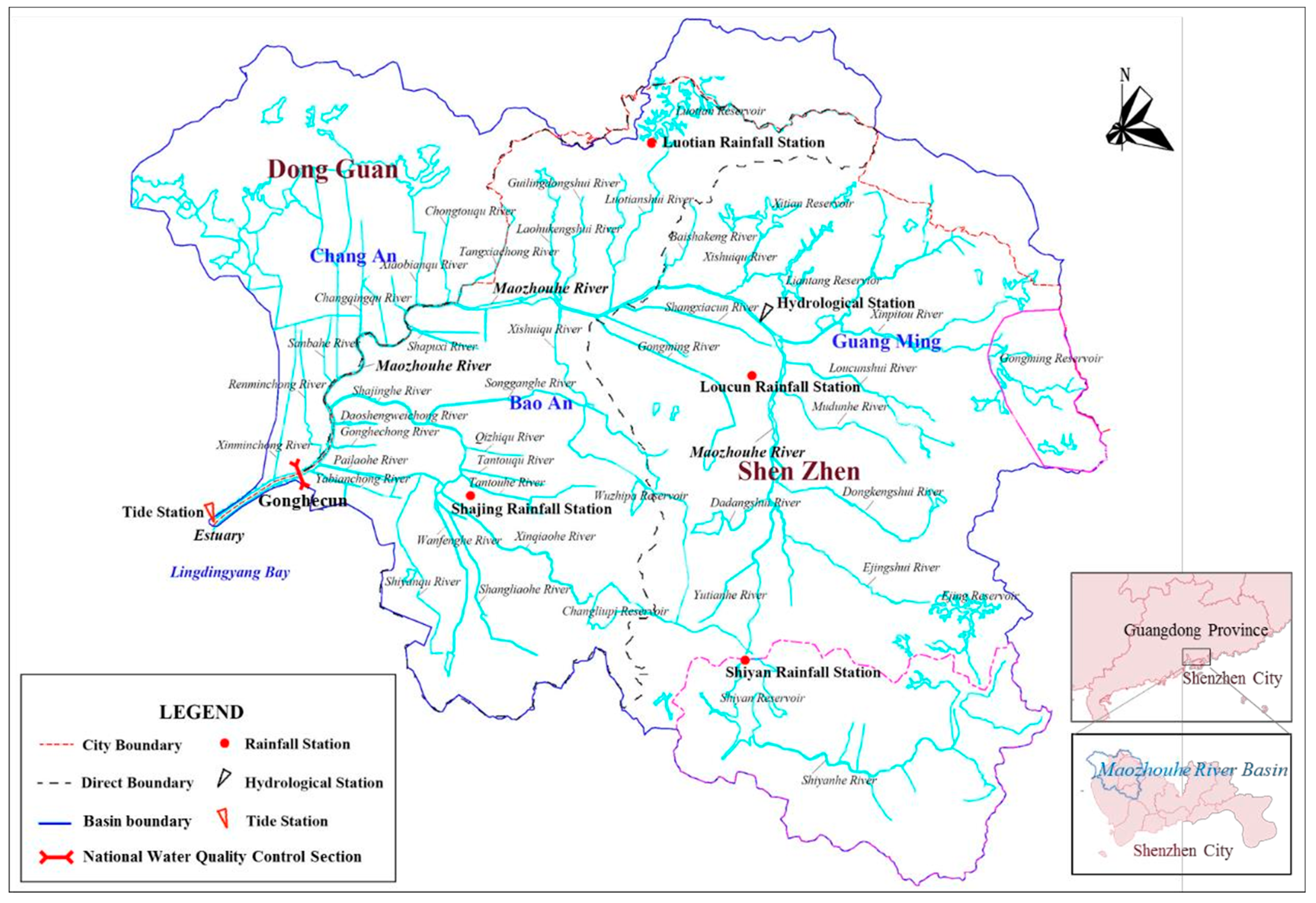
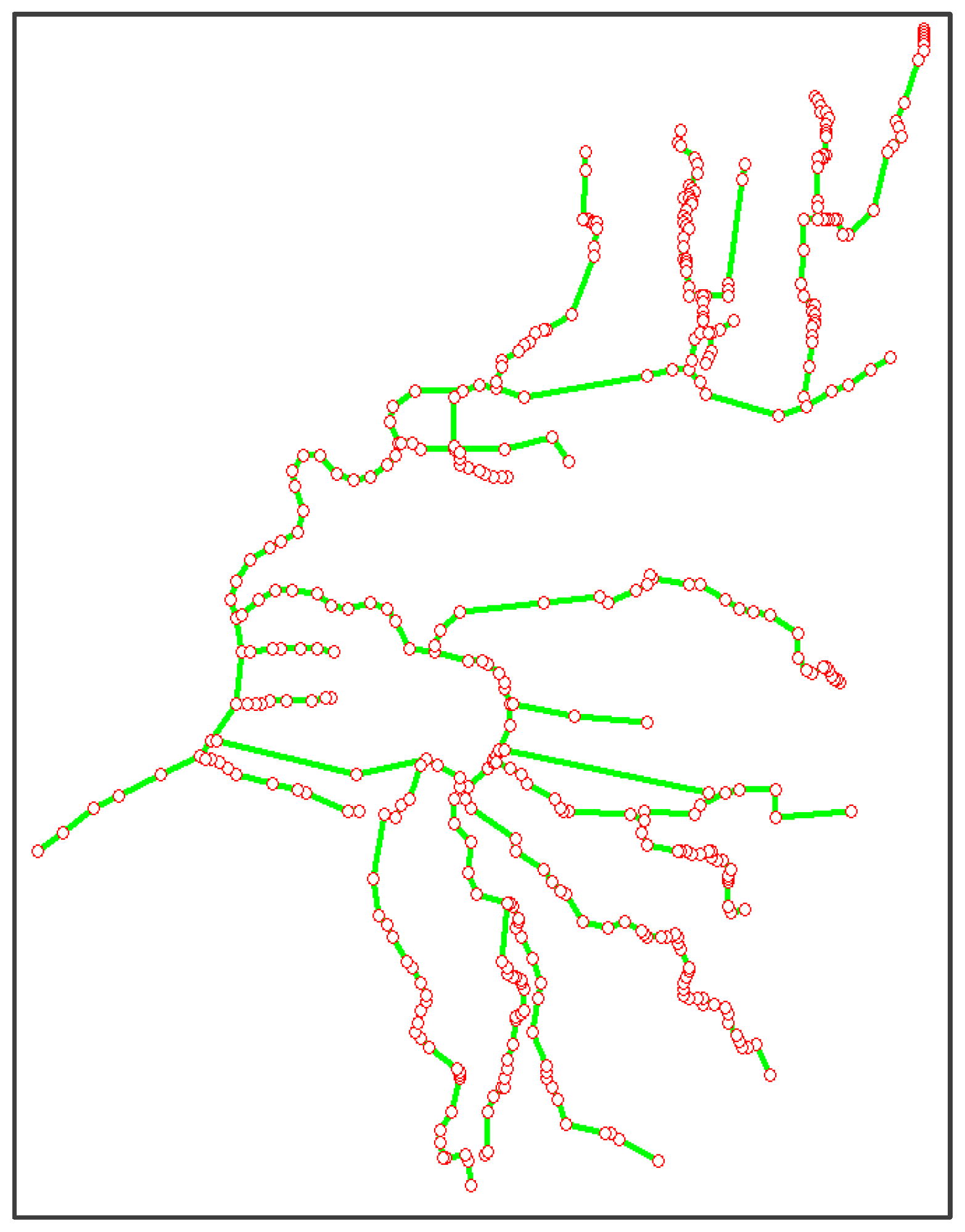
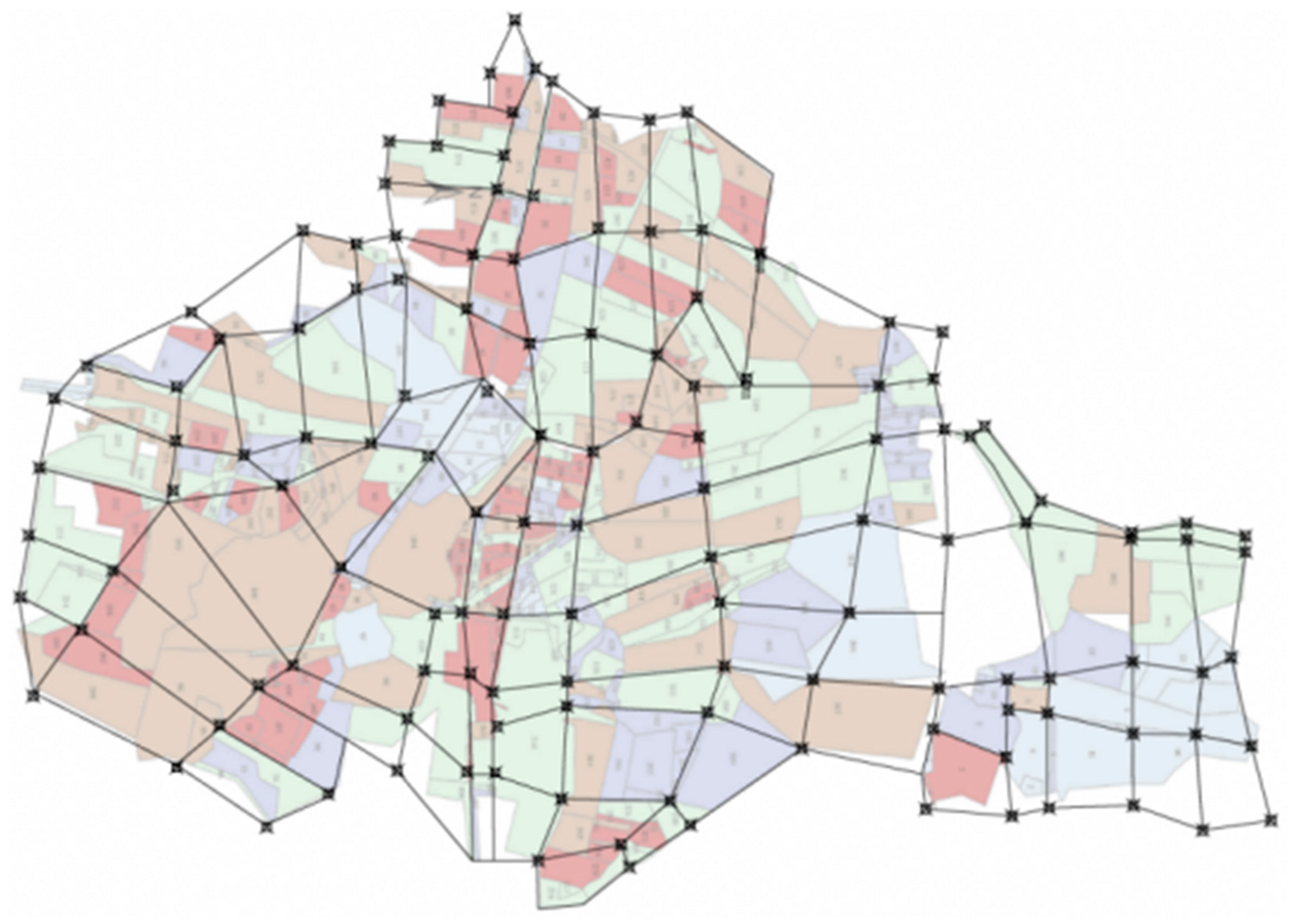
3.1. Mainstream and Tributaries of the Maozhou River
3.2. Determination of Regional Non-Point Source Chemical Oxygen Demand (COD) Load
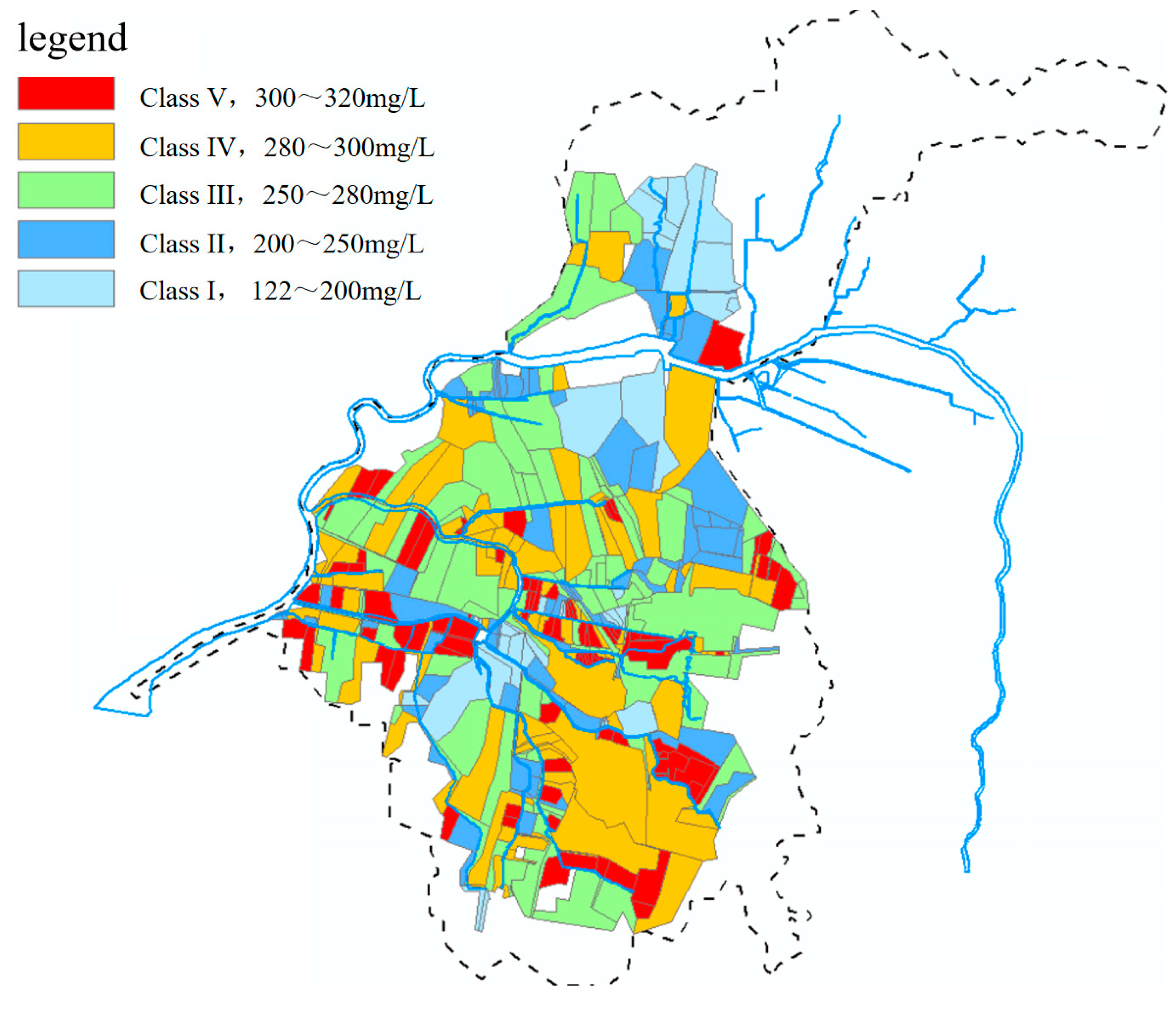
3.3. Regional Divisions and Node Pollutant Distribution
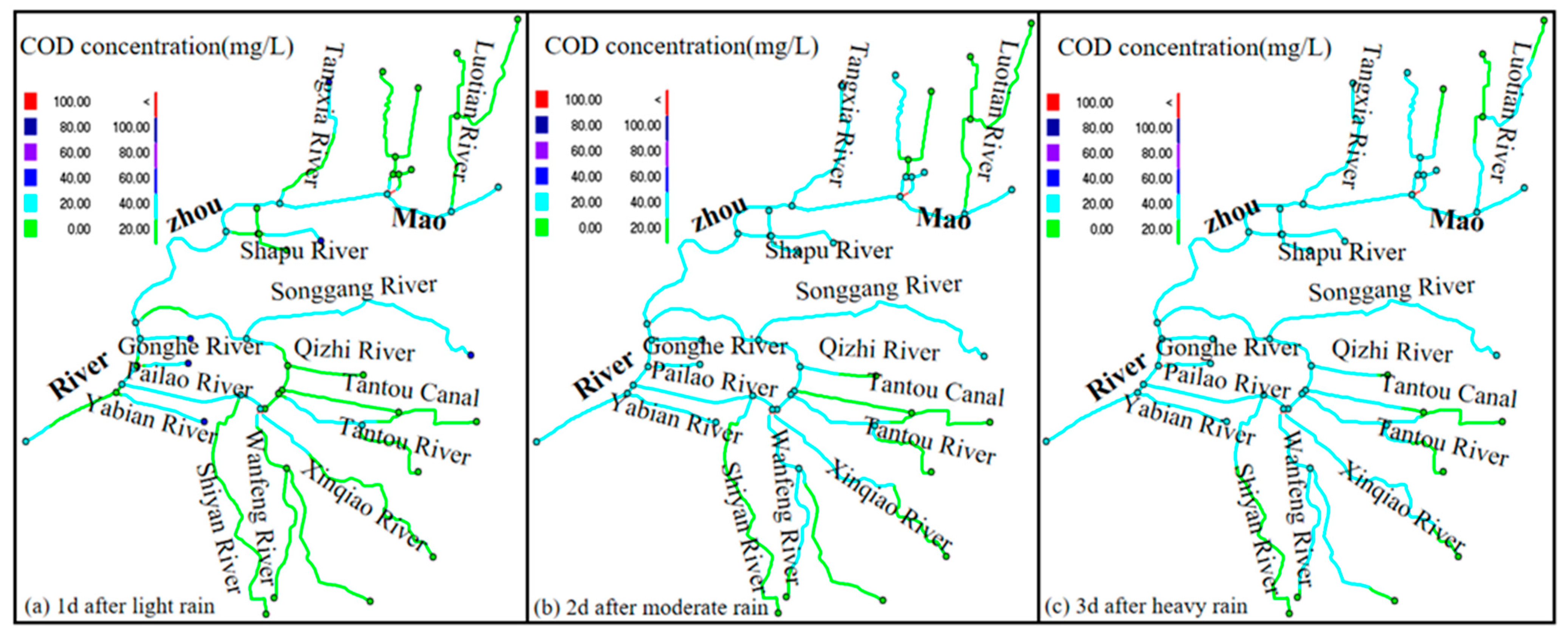
4. Results and Discussion
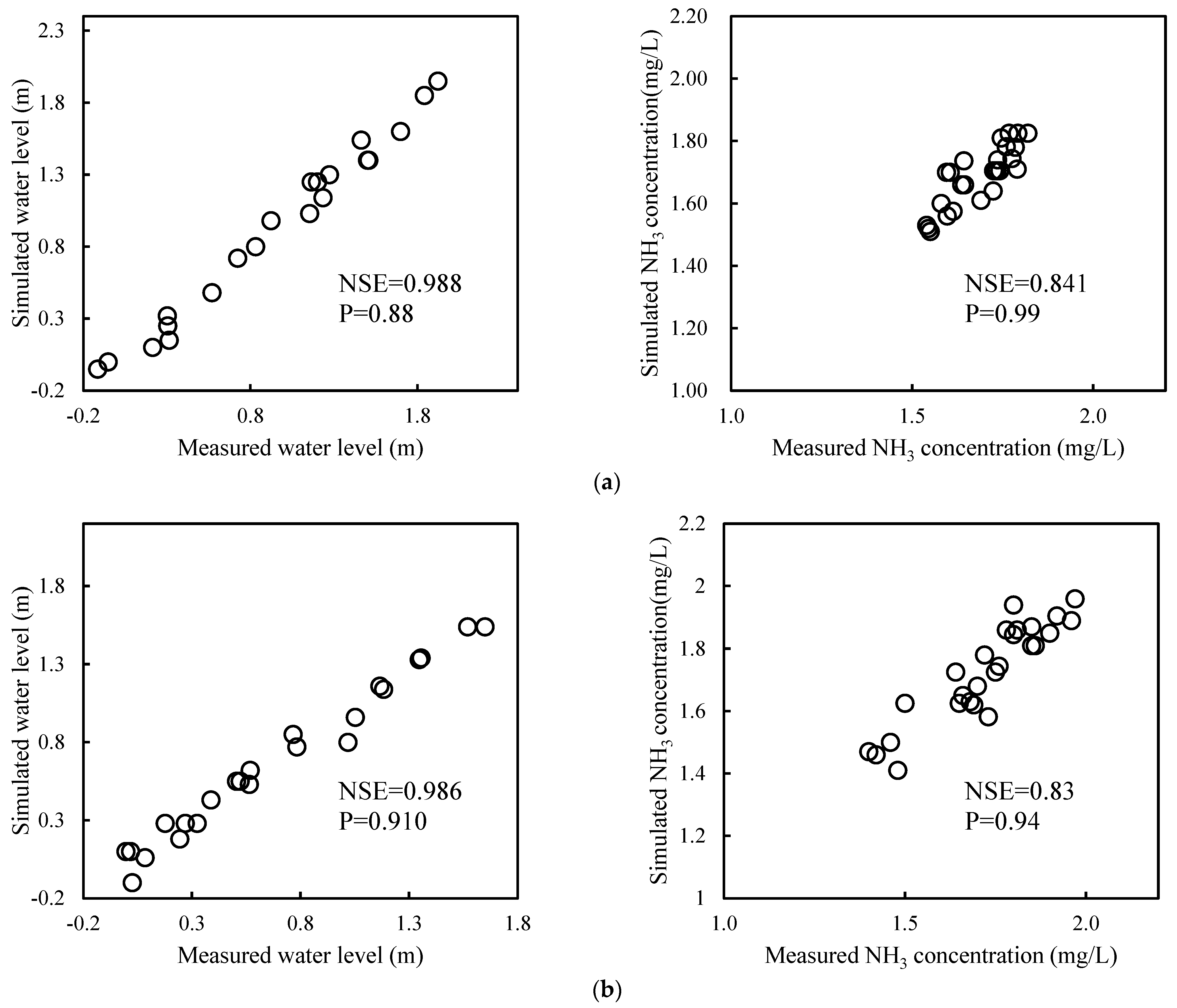
4.1. Parameter Calibration of the River Network Hydrodynamic Water Quality Model
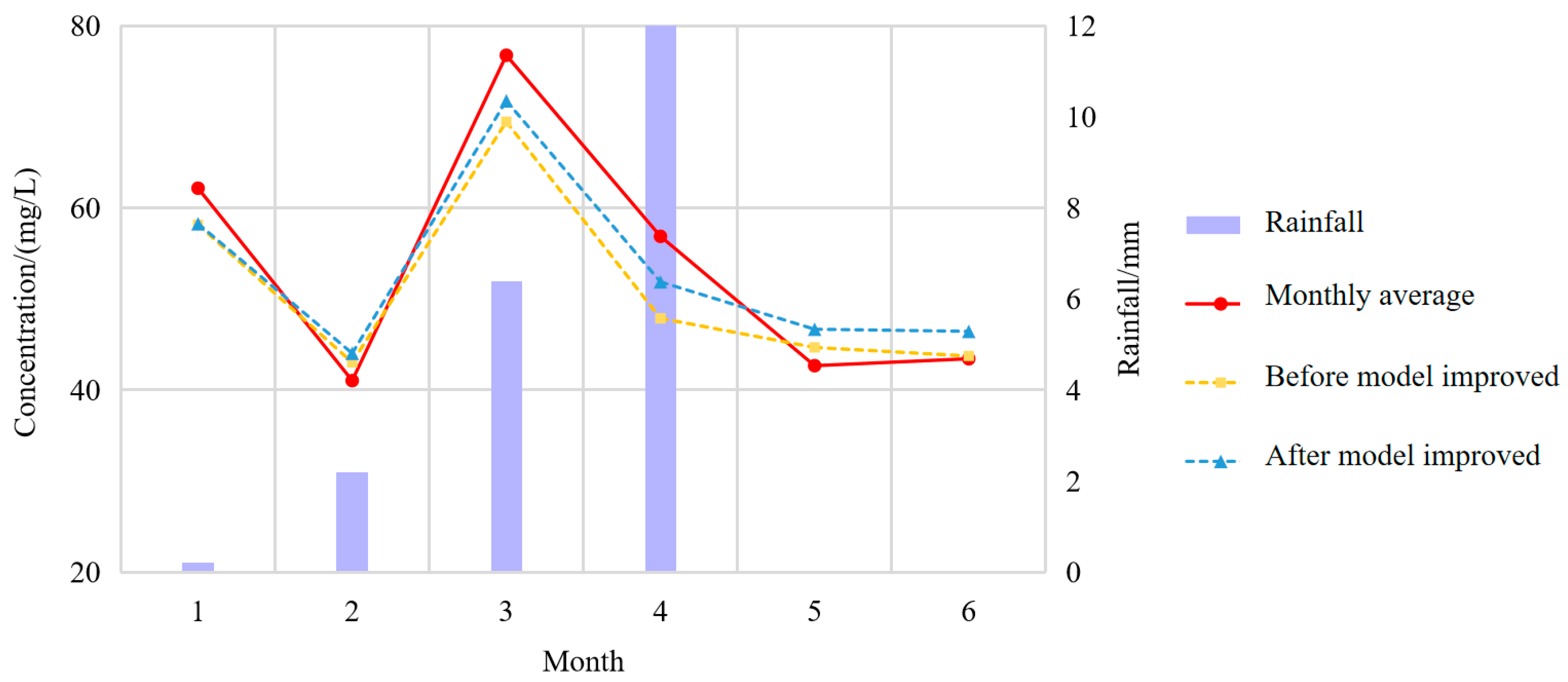
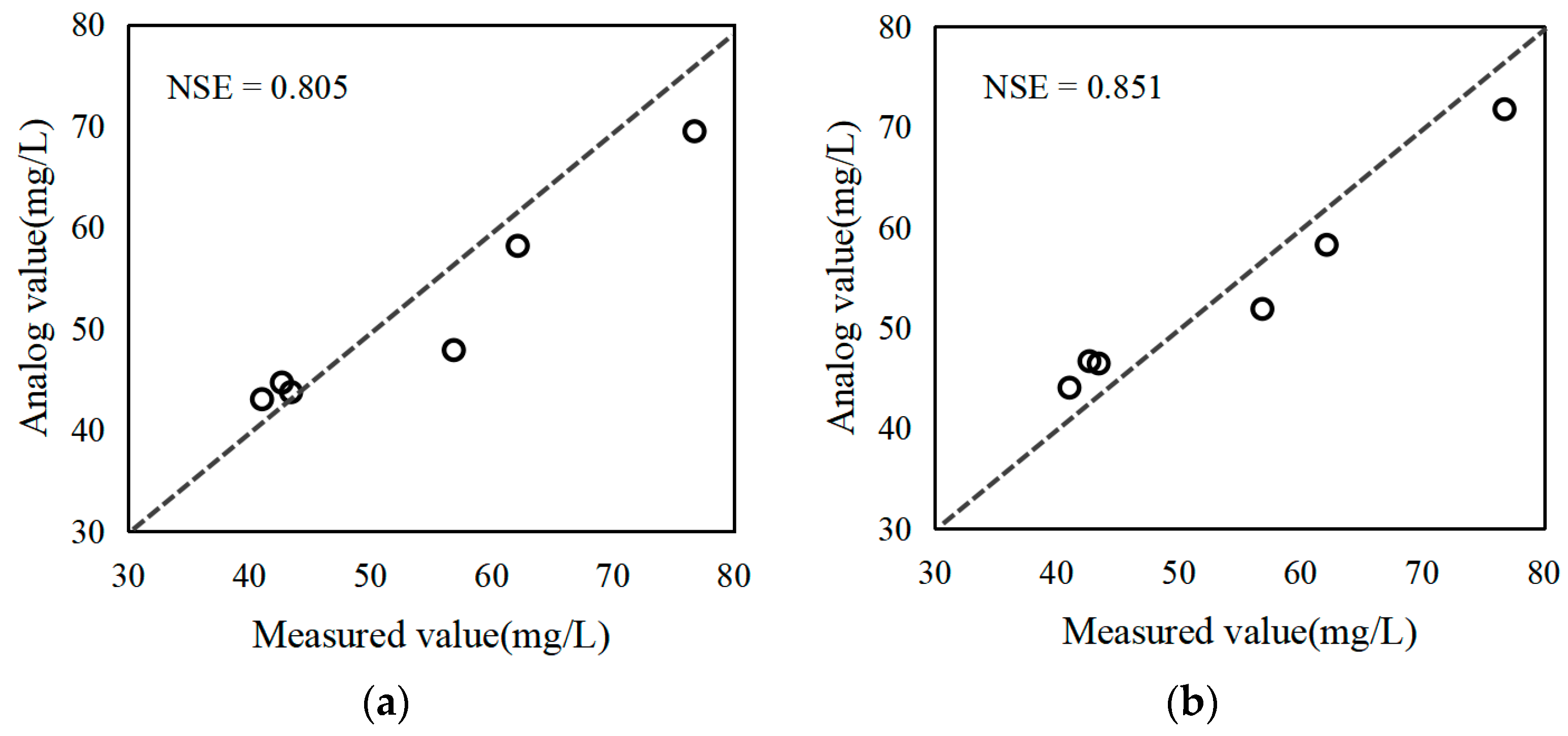
4.2. Comparative Analysis of the Improved Model
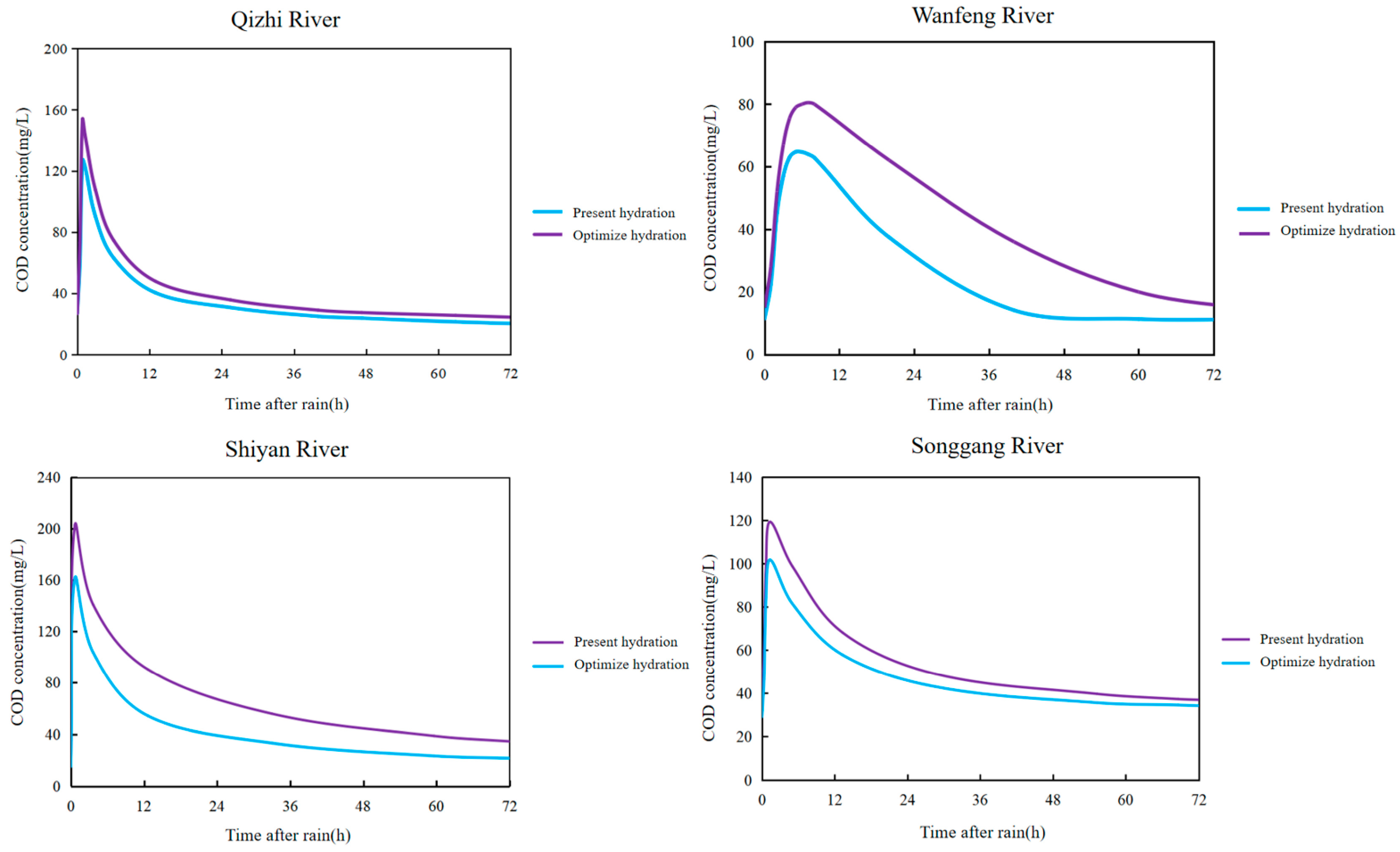
4.3. Analysis of the River Water Quality Change Law after Rain and Ecological Water Supplements Were Optimized
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Windsor, F.M.; Pereira, M.G.; Tyler, C.R.; Ormerod, S.J. Persistent contaminants as potential constraints on the recovery of urban river food webs from gross pollution. Water Res. 2019, 163, 114858. [Google Scholar] [CrossRef]
- Heeb, F.; Singer, H.; Pernet-Coudrier, B.; Qi, W.; Liu, H.; Longrée, P.; Müller, B.; Berg, M. Organic micropollutants in rivers downstream of the megacity Beijing: Sources and mass fluxes in a large-scale wastewater irrigation system. Environ. Sci. Technol. 2012, 46, 8680–8688. [Google Scholar] [PubMed] [Green Version]
- Bester, K.; Scholes, L.; Wahlberg, C.; McArdell, C.S. Sources and mass flows of xenobiotics in urban water cycles—An overview on current knowledge and data gaps. Water Air Soil Pollut. 2008, 8, 407–423. [Google Scholar] [CrossRef]
- Bouwman, L.; Goldewijk, K.K.; Van Der Hoek, K.W.; Beusen, A.H.W.; Van Vuuren, D.P.; Willems, J.; Rufino, M.C.; Stehfest, E. Exploring global changes in nitrogen and phosphorus cycles in agriculture induced by livestock production over the 1900–2050 period. Proc. Natl. Acad. Sci. USA 2013, 110, 20882–20887. [Google Scholar]
- Lin, Q.; Zhang, K.; Liu, E.; Sabatier, P.; Arnaud, F.; Shen, J. Deciphering centurial anthropogenic pollution processes in large lakes dominated by socio-economic impacts. Anthropocene 2020, 32, 100269. [Google Scholar]
- Tong, S.L.; Cui, C.F.; Bai, Y.L.; Sun, Y.; Zheng, X.H. Long-term remote monitoring the effects of rainfall and agricultural non-point sources pollution on the surface waters quality in lake Taihu. J. Mar. Sci. Technol.-Taiwan 2018, 26, 251–257. [Google Scholar]
- Xu, B.; Niu, Y.; Zhang, Y.; Chen, Z.; Zhang, L. China’s agricultural non-point source pollution and green growth: Interaction and spatial spillover. Environ. Sci. Pollut. Res. 2022, 29, 60278–60288. [Google Scholar]
- Billmire, M.; Koziol, B.W. Landscape and flow path-based nutrient loading metrics for evaluation of in-stream water quality in Saginaw Bay, Michigan. J. Great Lakes Res. 2018, 44, 1068–1080. [Google Scholar]
- Stride, B.; Abolfathi, S.; Odara MG, N.; Bending, G.D.; Pearson, J. Modeling microplastic and solute transport in vegetated flows. Water Resour. Res. 2023, 59, e2023WR034653. [Google Scholar] [CrossRef]
- Srinivas, R.; Singh, A.P.; Dhadse, K.; Garg, C. An evidence based integrated watershed modelling system to assess the impact of non-point source pollution in the riverine ecosystem. J. Clean. Prod. 2020, 246, 118963. [Google Scholar]
- Cook, S.; Chan, H.-L.; Abolfathi, S.; Bending, G.D.; Schäfer, H.; Pearson, J.M. Longitudinal dispersion of microplastics in aquatic flows using fluorometric techniques. Water Res. 2020, 170, 115337. [Google Scholar] [CrossRef]
- Goodarzi, D.; Sookhak Lari, K.; Khavasi, E.; Abolfathi, S. Large eddy simulation of turbidity currents in a narrow channel with different obstacle configurations. Sci. Rep. 2020, 10, 12814. [Google Scholar] [CrossRef]
- Tong, X.X.; Wang, J.L.; Pu, J.; Zhang, W.J.; Huang, J.Q.; Xu, W.S.; Wang, Z.G. Response of Surface Water Quality to Vegetation Cover in Shenzhen City. J. Yangtze River Sci. Res. Inst. 2022, 39, 55. [Google Scholar]
- Ghiasi, B.; Noori, R.; Sheikhian, H.; Zeynolabedin, A.; Sun, Y.; Jun, C.; Hamouda, M.; Bateni, S.M. Uncertainty quantification of granular computing-neural network model for prediction of pollutant longitudinal dispersion coefficient in aquatic streams. Sci. Rep. 2022, 12, 4610. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Jiang, J.; Lu, M.; Du, J. Spatial-temporal evolution characteristics of agricultural intensive management and its influence on agricultural non-point source pollution in China. Sustainability 2023, 15, 371. [Google Scholar] [CrossRef]
- Guan, F.; Ma, Y.H.; Zhang, D.H.; Zheng, T.; Wang, J. Agricultural non-point source pollution loads: Spatial distribution and risk assessment. Chin. Agric. Sci. Bull. 2017, 33, 61–66. [Google Scholar]
- Wang, J.; Chen, G.; Zou, G.; Song, X.; Liu, F. Comparative on plant stoichiometry response to agricultural non-point source pollution in different types of ecological ditches. Environ. Sci. Pollut. Res. 2019, 26, 647–658. [Google Scholar] [CrossRef] [PubMed]
- Lou, H.Z.; Wu, X.J.; Hao, F.H.; Yang, S.; Zhang, X. Research progress of non-point source pollution in China over the past 30 years and discussion of the future direction development. J. Environ. Sci. 2020, 40, 1535–1549. [Google Scholar]
- Zhang, F.S.; Shang, M.Z.; Zhao, P.X.; Cheng, K.Y.; Tang, Y.D.; Wei, J. Spatial analysis and simulation study of rainfall runoff pollution for a tidal river network. Environ. Sci. China 2021, 41, 1834–1841. [Google Scholar]
- Lou, S.H.; Lyu, Q.W.; Ren, K.J. Study on the selection and reconstruction of urban drainage system in high density construction area from the course of water control in Shenzhen. Water Supply Drain. China 2018, 34, 18–21. [Google Scholar]
- He, X.C.; Huang, F.F.; Ru, X.W.; Wan, D.H.; Zheng, J.L.; Wu, Q.; Zhang, L. Research on water resource control strategy and technology in typical river network area of Pearl River Delta. J. North China Univ. Water Resour. Electr. Power 2016, 37, 55–60. [Google Scholar]
- Jiang, T.; Zhu, S.L.; Zhang, Q.; Chen, X.H. Numerical simulation of water environment effect of tidal river network gate pump joint dispatch. J. Hydraul. Eng. 2011, 42, 388–395. [Google Scholar]
- Shou, C.G.; Du, H.S.; Liu, X.P. Research progress of source and mechanism of agricultural non-point source pollution in China. Appl. Ecol. Environ. Res. 2019, 17, 10611–10621. [Google Scholar] [CrossRef]
- Xu, S.M. Study on the Impact of Rainfall Runoff on Water Quality in the Main Stream of Haihe River in Tianjin; Tianjin University: Tianjin, China, 2018. [Google Scholar]
- Geng, R.Z.; Liang, X.J.; Yin, P.H.; Wang, M.; Zhou, L.L. A review: Multi-objective collaborative optimization of best management practices for non-point sources pollution control. Acta Ecol. Sin. 2019, 39, 2667–2675. [Google Scholar]
- Zhu, W.B.; Wang, J.; Xue, F.; Chen, S. From Sponge Cities to Multi-Dimensional Sponge Systems to Solve Urban Water Problems; Jiangsu Phoenix Science Press: Nanjing, China, 2018; Volume 37. [Google Scholar]
- Charters, F.; Cochrane, T.A.; O’Sullivan, A.D. Predicting event-based sediment and heavy metal loads in untreated urban run off from impermeable surfaces. Water 2020, 2, 969. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Yang, Z.; Yue, Y.; Zhong, H.; Li, D. Variation of total phosphorus concentration and loads in the upper Yangtze River and contribution of non-point sources. Water Supply 2021, 21, 1687–1700. [Google Scholar] [CrossRef]
- Zubaidah, I.; Karnaningroem, N.; Slamet, A. The Self-Purification Ability in The Rivers of Banjarmasin, Indonesia. J. Ecol. Eng. 2019, 20, 177–182. [Google Scholar] [CrossRef]
- Majed, N.; Islam, M.A. Contaminant Discharge from Outfalls and Subsequent Aquatic Ecological Risks in the River Systems in Dhaka City: Extent of Waste Load Contribution in Pollution. Front. Public Health 2022, 10, 880399. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, X.; Yang, S.; Song, Z.; Wang, Y.; Yu, Q. Basin-scale pollution loads analyzed based on coupled empirical models and numerical models. Int. J. Environ. Res. Public Health 2021, 18, 12481. [Google Scholar] [CrossRef]
- Li, C.; Zheng, X.; Zhao, F.; Wang, X.; Cai, Y.; Zhang, N. Effects of urban non-point source pollution from Baoding city on Baiyangdian lake, China. Water 2017, 9, 249. [Google Scholar] [CrossRef]
- Zhang, J. Discussion on non-point source pollution and control in water source areas. In Study of Ecological Engineering of Human Settlements; Springer: Singapore, 2020; pp. 197–211. [Google Scholar]
- Wang, H.; He, P.; Shen, C.; Wu, Z. Effect of irrigation amount and fertilization on agriculture non-point source pollution in the paddy field. Environ. Sci. Pollut. Res. 2019, 26, 10363–10373. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.; Yin, H.; Deng, J.; Li, M. Cost-effectiveness analysis of green-gray stormwater control measures for non-point source pollution. Int. J. Environ. Res. Public Health 2020, 17, 998. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, F.S.; Wei, J.; Tang, Y.D.; Cao, M.Y. Application of watershed water environmental model in the systematic management of Maozhou River basin. China Water Wastewater 2021, 37, 100–106. [Google Scholar]
- Sun, Z.L.; Chen, Y.M.; Xia, S.S.; Wu, K. Calculation of water transport capacity of river networks based on mixed models. J. Hohai Univ. 2010, 38, 144–148. [Google Scholar]
- Sun, Z.L.; Yang, E.S.; Zeng, T.L.; Zhu, L.L. Nonuniform sediment transport with lateral output in river networks. J. Hydraul. Eng. 2016, 47, 72–76, 84. [Google Scholar]
- Chen, X.; He, G.; Liu, X.; Li, B.; Peng, W.; Dong, F.; Huang, A.; Wang, W.; Lian, Q. Sub-watershed parameter transplantation method for non-point source pollution estimation in complex underlying surface environment. Land 2021, 10, 1387. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, M.; Wei, J.; Qi, J. Pollution load estimation and control countermeasures of Zhangze reservoir. Front. Environ. Sci. 2022, 10, 874124. [Google Scholar] [CrossRef]
- Xin, X.K.; Yin, W.; Li, K.F. Estimation of non-point source pollution loads with flux method in Danjiangkou Reservoir area, China. Water Sci. Eng. 2017, 10, 134–142. [Google Scholar] [CrossRef]
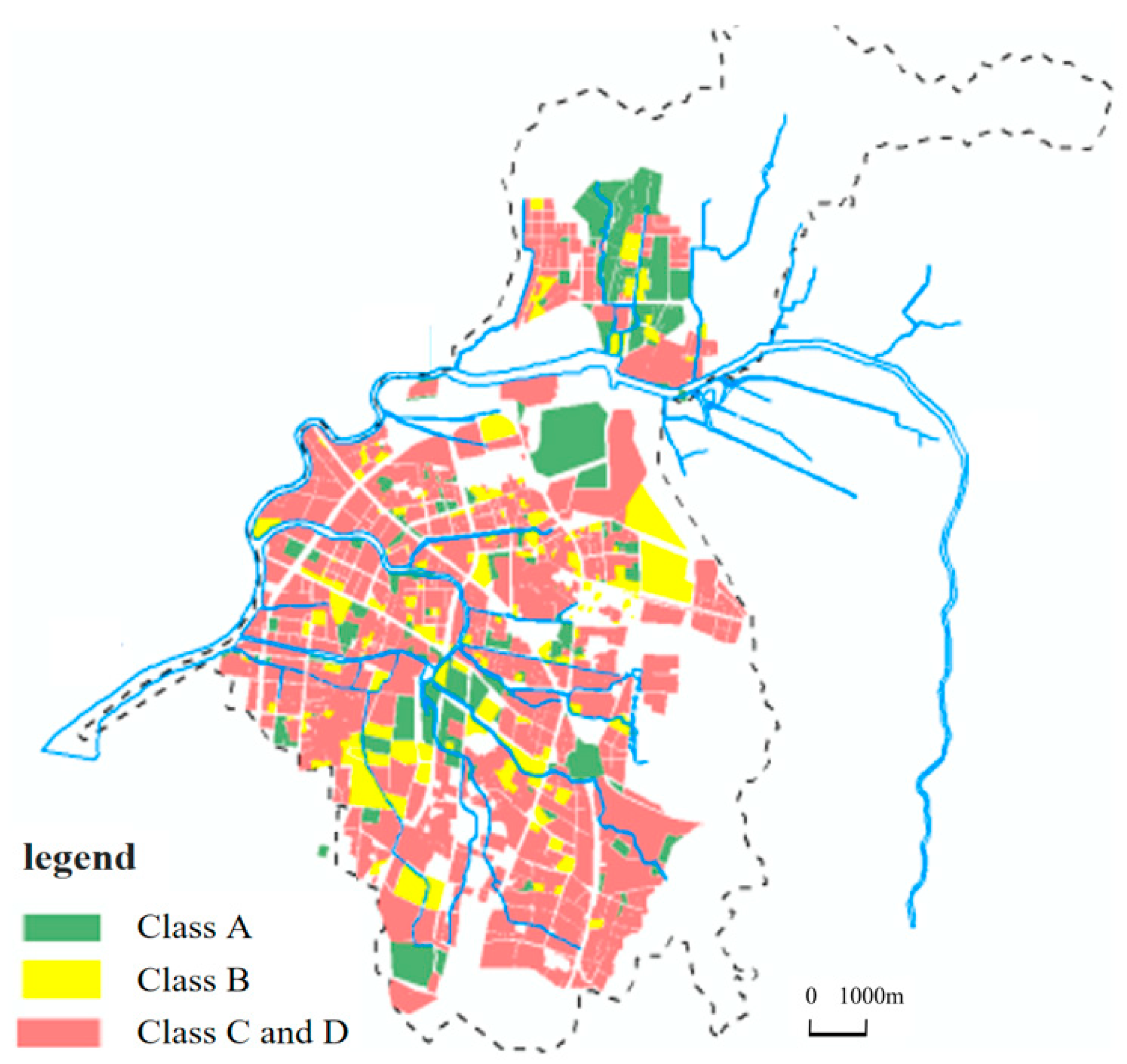


| Block | Underlay Surface Type |
|---|---|
| A | Non-urban construction land, park green space |
| B | High-end residential areas, public buildings, science and technology parks |
| C | Ordinary commercial areas, ordinary residential areas, well-managed factories or industrial areas, municipal roads |
| D | Farmers’ markets, garbage transfer stations (houses), food streets, urban villages, village-run industrial zones |
| Rivers/Canals | Water Supplement Volume (10,000 m3/d) | Water Quality Recovery Days after Moderate Rain | Remarks | ||
|---|---|---|---|---|---|
| Current Status | Optimization | Current Status | Optimization | ||
| Qizhi Canal | 2 | 2 | 1.25 | 0.75 | The water supplement site is moved upstream |
| Wanfeng R. | 2.4 | 2.4 | 1.75 | 0.8 | The water supplement site is moved upstream |
| Shajing R. | 6.5 | 6 | 0.9 | 1 | Adjust water supplement volume |
| Shangliao R. | 10.6 | 9.1 | 0.75 | 0.9 | Adjust water supplement volume |
| Songgang R. | 0 | 1 | 2.7 | 1.5 | Add water supplement sites |
| Shiyan Canal | 0 | 1 | 2.5 | 1.2 | Add water supplement sites |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Cheng, K.; Liu, J.; Guo, W.; Guo, J. Simulation of Water Quality in a River Network with Time-Varying Lateral Inflows and Pollutants. Water 2023, 15, 2861. https://doi.org/10.3390/w15162861
Sun Z, Cheng K, Liu J, Guo W, Guo J. Simulation of Water Quality in a River Network with Time-Varying Lateral Inflows and Pollutants. Water. 2023; 15(16):2861. https://doi.org/10.3390/w15162861
Chicago/Turabian StyleSun, Zhilin, Kaiyu Cheng, Jing Liu, Wenrui Guo, and Jing Guo. 2023. "Simulation of Water Quality in a River Network with Time-Varying Lateral Inflows and Pollutants" Water 15, no. 16: 2861. https://doi.org/10.3390/w15162861
APA StyleSun, Z., Cheng, K., Liu, J., Guo, W., & Guo, J. (2023). Simulation of Water Quality in a River Network with Time-Varying Lateral Inflows and Pollutants. Water, 15(16), 2861. https://doi.org/10.3390/w15162861






