Analysis of Seasonal Driving Factors and Inversion Model Optimization of Soil Moisture in the Qinghai Tibet Plateau Based on Machine Learning
Abstract
:1. Introduction
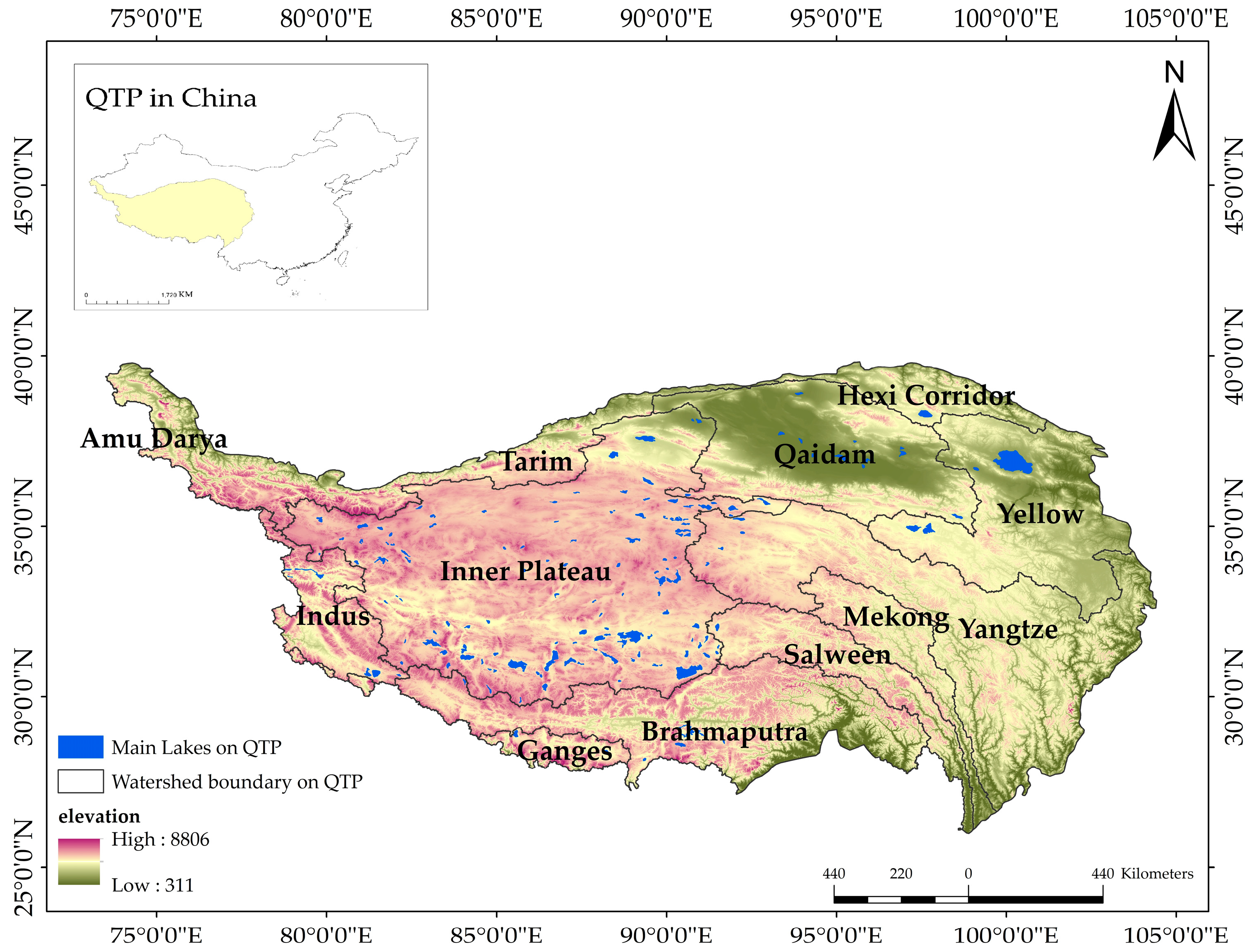
2. Materials and Methods
2.1. Sentinel-1
2.2. Basic Data
2.3. Measured Soil Moisture Data
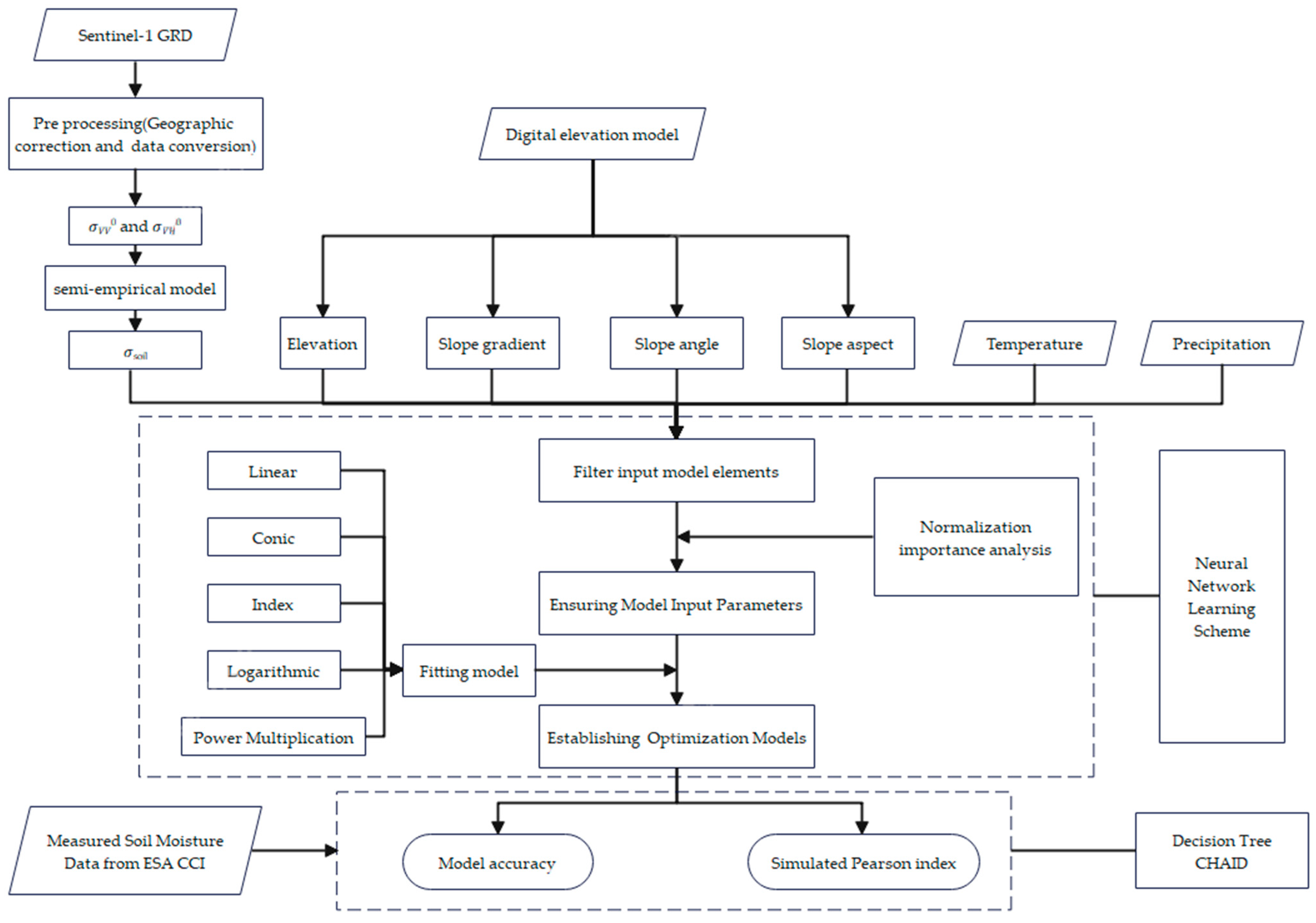
2.4. Semi-Empirical Model for Inverting Soil Moisture
2.5. Neural Network Learning Scheme
2.6. Analyzing Model Accuracy Based on Decision Tree
3. Results
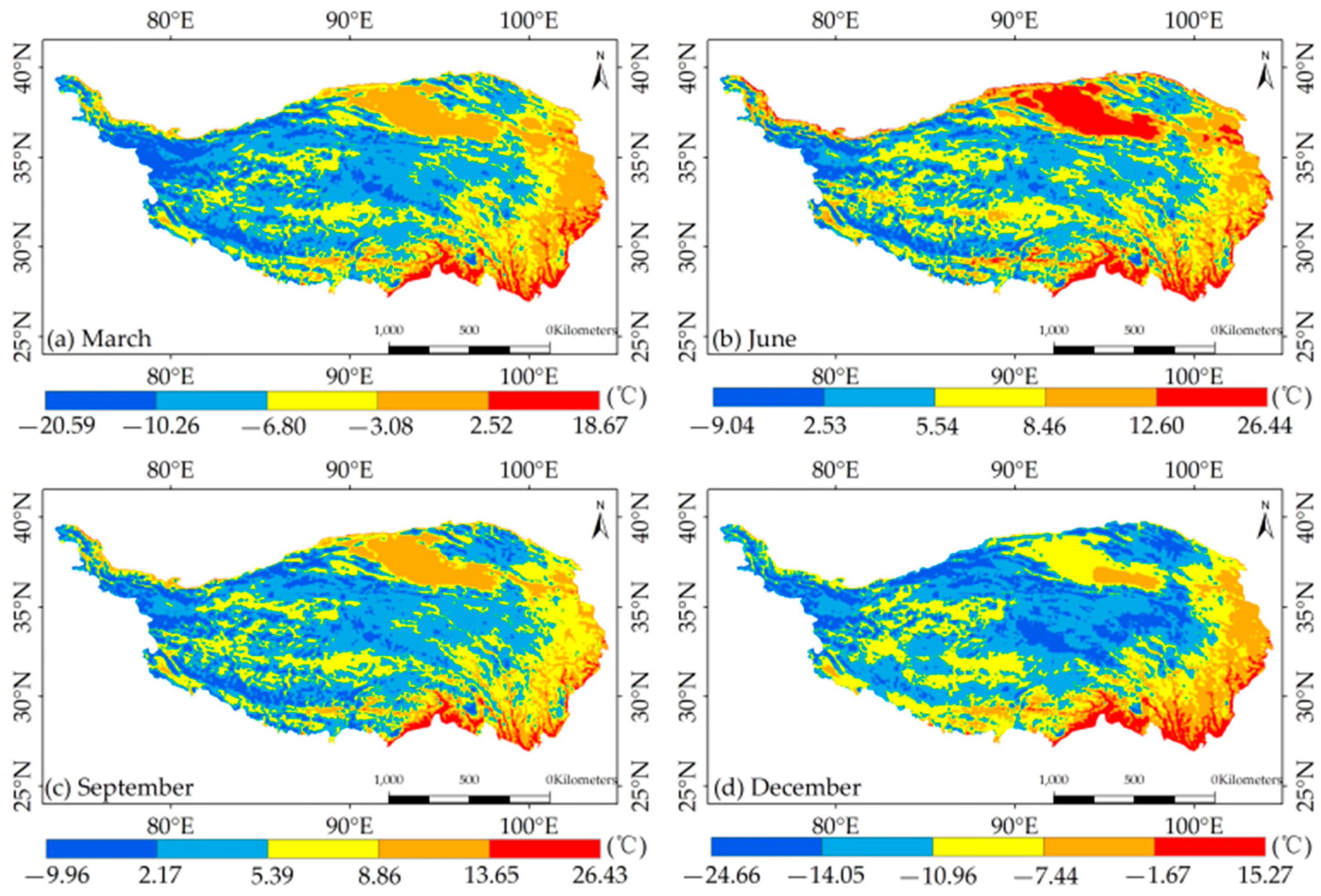
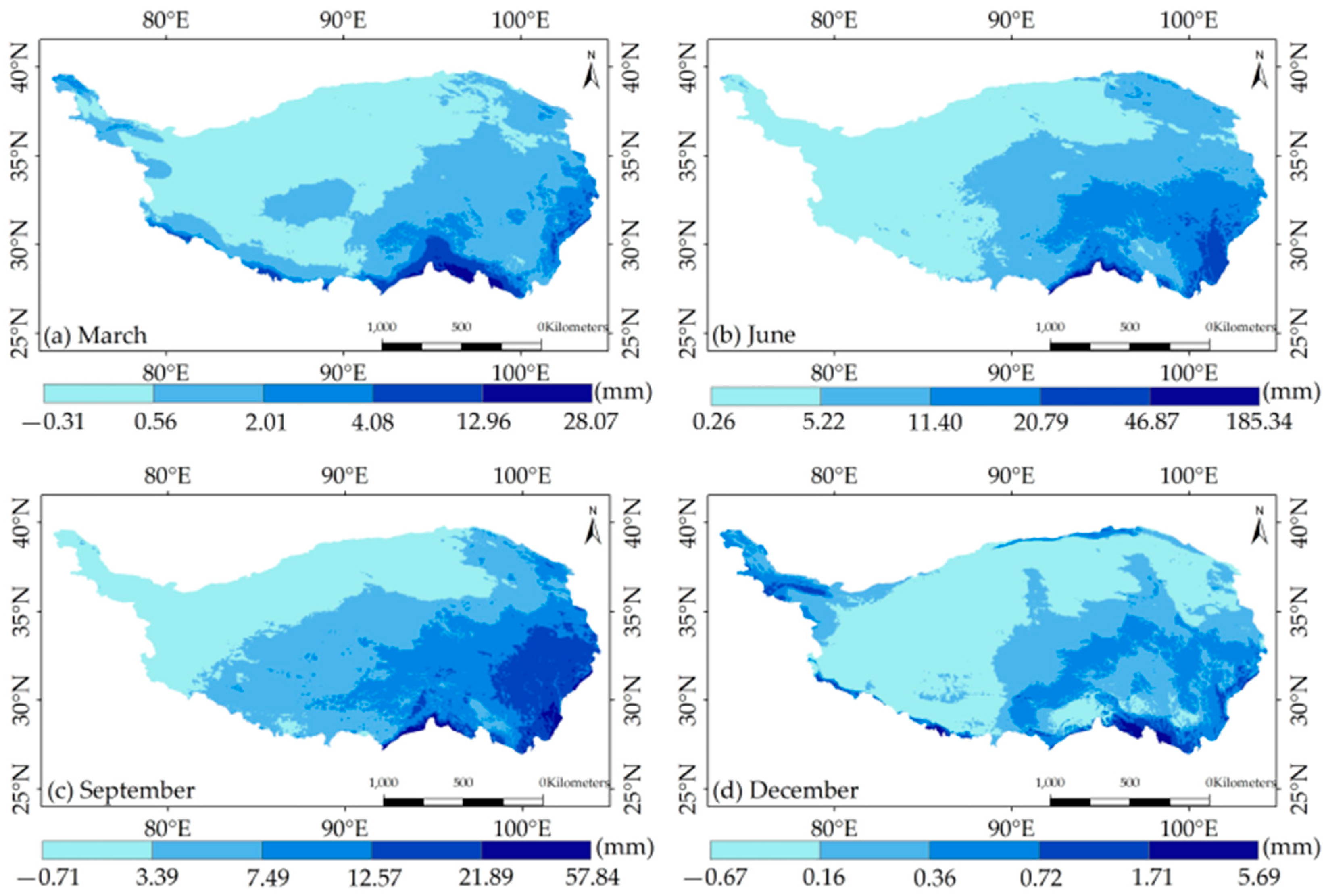
3.1. Climatic Characteristics
3.2. Significance of Factor Impact
3.3. Ensuring Model Input Parameters
3.4. Establishing an Optimization Model Based on Machine Learning Methods
3.5. Model Accuracy Verification
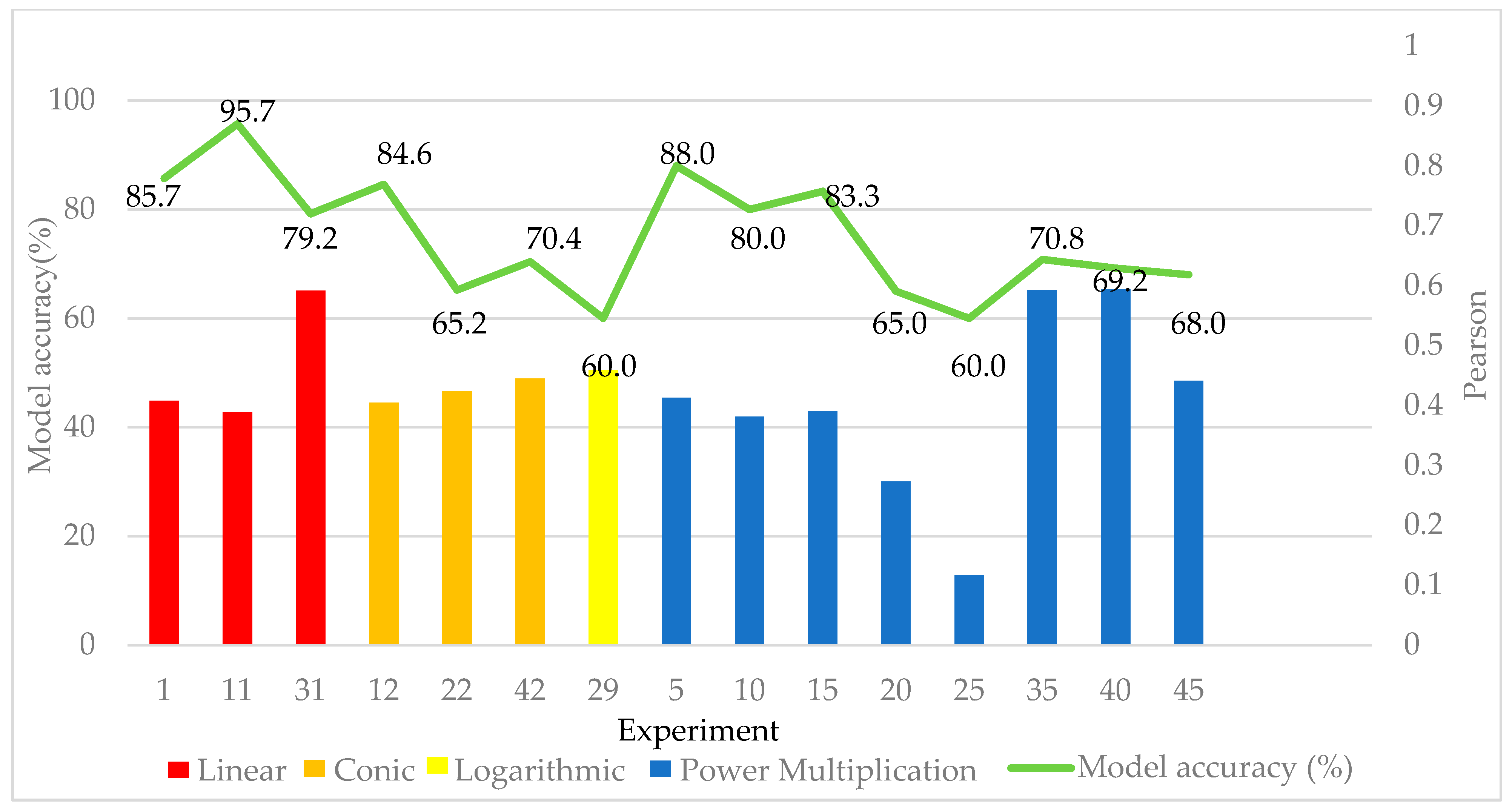
- In March, there were 15 experiments to calculate the synergistic effects of statistical elevation and precipitation, elevation and temperature, and elevation, precipitation, and temperature on the soil moisture retrieval. The experimental data showed satisfactory results, with a 0% model elimination rate. Experiments 1, 5, 10, 11, and 12 were the best models based on the Pearson index for simulated soil moisture and the designed model accuracy. The model accuracy in Experiment 11 was the highest at 95.7%. The Pearson index was 0.389, reaching the inversion accuracy requirements. Although the model accuracy in Experiment 1 was 85.7%, lower than Experiment 11, the Pearson index was 0.408, significantly higher than the inversion accuracy of the model in Experiment 11. This reaches the requirements of high accuracy and model inversion. The model accuracy in Experiment 5 was also high at 88.0%, with a Pearson index of 0.413, indicating a good model accuracy. Although the model accuracies in Experiments 10 and 12 were high at ≥80.0%, the Pearson index inverted by the model was relatively unstable and had wide variability.
- In June, three sets of experiments were designed for soil moisture in the QTP. The rates of elimination and experimental models were both high, indicating that these input parameters cannot generally reach the stability requirements of the inversion model. After comparison, the optimal fitting models were Experiments 20, 22, 25, and 29. Only the model accuracy and Pearson index of Experiment 29 were both high, with values of 60% and 0.459, respectively, reaching the model requirements. The model accuracy of Experiment 22 was 65.2%, and the Pearson index was 0.424, indicating good results. However, the Pearson index of Experiment 20 was 0.273, and that of Experiment 25 was 0.116, significantly lower than the other optimal models.
- In September, two sets of experiments were designed for soil moisture in the QTP, with satisfactory results. The model elimination rate was 10%, and Experiments 31, 35, and 40 were selected as optimal models due to their higher Pearson index and model accuracy. The accuracy and Pearson index of Experiment 31 were 79.2% and 0.592, respectively, indicating good results. The model accuracy and Pearson index for fitting soil moisture in Experiments 35 and 40 were similar, but the model accuracies were lower than in Experiment 31.
- In December, five experiments were designed for soil moisture in the QTP. The elimination rate of the model was relatively low, at 20%. The model in Experiment 42 had the highest accuracy of 70.4%, and the Pearson index was 0.445, indicating that the inversion accuracy of the model was sufficient. Experiment 41 had the highest Pearson index of 0.480.
4. Discussion
4.1. Seasonal Characteristics of Factor Influence
4.2. Optimization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shellito, P.J.; Small, E.E.; Livneh, B. Controls on surface soil drying rates observed by SMAP and simulated by the Noah land surface model. Hydrol. Earth Syst. Sci. 2018, 22, 1649–1663. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Iturbe, I.; Chen, Z.; Rinaldo, A. On the fractal structure of soil moisture fields. Adv. Water Resour. 2021, 147, 103826. [Google Scholar] [CrossRef]
- Rasheed, M.W.; Tang, J.; Sarwar, A.; Shah, S.; Saddique, N.; Khan, M.U.; Imran Khan, M.; Nawaz, S.; Shamshiri, R.R.; Aziz, M.; et al. Soil Moisture Measuring Techniques and Factors Affecting the Moisture Dynamics: A Comprehensive Review. Sustainability 2022, 14, 11538. [Google Scholar] [CrossRef]
- Shi, J.; Jiang, L.; Zhang, L.; Chen, K.S.; Wigneron, J.P.; Chanzy, A.; Jackson, T.J. Physically Based Estimation of Bare-Surface Soil Moisture With the Passive Radiometers. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3145–3153. [Google Scholar] [CrossRef]
- Zhu, W.; Wang, Y.; Jia, S. A remote sensing-based method for daily evapotranspiration mapping and partitioning in a poorly gauged basin with arid ecosystems in the Qinghai-Tibet Plateau. J. Hydrol. 2023, 616, 128807. [Google Scholar] [CrossRef]
- Rafiei Sardooi, E.; Azareh, A.; Mesbahzade, T.; Sardoo, F.; Parteli, E.; Pradhan, B. A hybrid model using data mining and multi-criteria decision-making methods for landslide risk mapping at Golestan Province, Iran. Environ. Earth Sci. 2021, 80, 487. [Google Scholar] [CrossRef]
- Zhao, Z.; Fu, R.; Liu, J.; Dai, L.; Guo, X.W.; Du, Y.; Hu, Z.; Cao, G. Response of Seasonally Frozen Ground to Climate Changes in the Northeastern Qinghai-Tibet Plateau. Front. Environ. Sci. 2022, 10, 912209. [Google Scholar] [CrossRef]
- Han, Y.; Bai, X.; Shao, W.; Wang, J. Retrieval of Soil Moisture by Integrating Sentinel-1A and MODIS Data over Agricultural Fields. Water 2020, 12, 1726. [Google Scholar] [CrossRef]
- Bai, X.; Zeng, J.; Chen, K.S.; Li, Z.; Zeng, Y.; Wen, J.; Wang, X.; Dong, X.; Su, Z. Parameter Optimization of a Discrete Scattering Model by Integration of Global Sensitivity Analysis Using SMAP Active and Passive Observations. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1084–1099. [Google Scholar] [CrossRef]
- Bai, X.; He, B.; Li, X.; Zeng, J.; Wang, X.; Wang, Z.; Zeng, Y.; Su, B. First Assessment of Sentinel-1A Data for Surface Soil Moisture Estimations Using a Coupled Water Cloud Model and Advanced Integral Equation Model over the Tibetan Plateau. Remote Sens. 2017, 9, 714. [Google Scholar] [CrossRef] [Green Version]
- Dubois, P.C.; Zyl, J.v.; Engman, T. Measuring soil moisture with imaging radars. IEEE Trans. Geosci. Remote Sens. 1995, 33, 915–926. [Google Scholar] [CrossRef] [Green Version]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An empirical model and an inversion technique for radar scattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
- Fung, A.K.; Li, Z.; Chen, K.S. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Zeng, J.; Chen, K.S.; Bi, H.; Zhao, T.; Yang, X. A Comprehensive Analysis of Rough Soil Surface Scattering and Emission Predicted by AIEM with Comparison to Numerical Simulations and Experimental Measurements. IEEE Trans. Geosci. Remote Sens. 2017, 55, 1696–1708. [Google Scholar] [CrossRef]
- Popkov, Y.S. Randomization and Entropy in Machine Learning and Data Processing. Dokl. Math. 2022, 105, 135–157. [Google Scholar] [CrossRef]
- Mauri, P.V.; Parra, L.; Mostaza-Colado, D.; Garcia, L.; Lloret, J.; Marin, J.F. The Combined Use of Remote Sensing and Wireless Sensor Network to Estimate Soil Moisture in Golf Course. Appl. Sci. 2021, 11, 11769. [Google Scholar] [CrossRef]
- Cordeiro, A.S.; Santos, S.R.d.; Moreira, F.B.; Santos, P.C.; Carro, L.; Alves, M.A.Z. Efficient Machine Learning execution with Near-Data Processing. Microprocess. Microsyst. 2022, 90, 104435. [Google Scholar] [CrossRef]
- Notarnicola, C.; Angiulli, M.; Posa, F. Soil moisture retrieval from remotely sensed data: Neural network approach versus Bayesian method. IEEE Trans. Geosci. Remote Sens. 2008, 46, 547–557. [Google Scholar] [CrossRef]
- Baghdadi, N.; Cresson, R.; El Hajj, M.; Ludwig, R.; La Jeunesse, I. Estimation of soil parameters over bare agriculture areas from C-band polarimetric SAR data using neural networks. Hydrol. Earth Syst. Sci. 2012, 16, 1607–1621. [Google Scholar] [CrossRef] [Green Version]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Pasolli, L.; Notarnicola, C.; Bruzzone, L.; Bertoldi, G.; Chiesa, S.D.; Niedrist, G.; Tappeiner, U.; Zebisch, M. Polarimetric RADARSAT-2 imagery for soil moisture retrieval in alpine areas. Can. J. Remote Sens. 2011, 37, 535–547. [Google Scholar] [CrossRef]
- Hunt, E.B. Concept Learning: An Information Processing Problem; John Wiley & Sons: Hoboken, NJ, USA, 1974. [Google Scholar]
- Cordella, L.P.; Foggia, P.; Sansone, C.; Vento, M. Learning structural shape descriptions from examples. Pattern Recognit. Lett. 2002, 23, 1427–1437. [Google Scholar] [CrossRef]
- Yuan, J.; Xiang, S.; Xia, J.; Yu, L.; Liu, S. Evaluation of Sampling Methods for Scatterplots. IEEE Trans. Vis. Comput. Graph. 2021, 27, 1720–1730. [Google Scholar] [CrossRef] [PubMed]
- Shi, N.; Naudiyal, N.; Wang, J.; Gaire, N.P.; Wu, Y.; Wei, Y.; He, J.; Wang, C. Assessing the Impact of Climate Change on Potential Distribution of Meconopsis punicea and Its Influence on Ecosystem Services Supply in the Southeastern Margin of Qinghai-Tibet Plateau. Front. Plant Sci. 2021, 12, 830119. [Google Scholar] [CrossRef]
- Zhou, C.P. The Spatial Dataset of Climate on the Tibetan Plateau (1961–2020). A Big Earth Data Platform for Three Poles. 2014. Available online: https://data.tpdc.ac.cn/en/data/ca3ce8da-fbfd-4d3c-a4ca-7a821c5f7203 (accessed on 8 July 2023).
- Shen, X.; An, R.; Quaye-Ballard, J.A.; Zhang, L.; Wang, Z. Evaluation of the European Space Agency Climate Change Initiative Soil Moisture Product over China Using Variance Reduction Factor. JAWRA J. Am. Water Resour. Assoc. 2016, 52, 1524–1535. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, Q.; Chao, L.; Ye, J.; Li, Z.; Yu, Z.; Yang, T.; Ju, Q. Ground observation-based analysis of soil moisture spatiotemporal variability across a humid to semi-humid transitional zone in China. J. Hydrol. 2019, 574, 903–914. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Ren, L.; Teuling, A.J.; Zhang, X.; Jiang, S.; Yang, X.; Wei, L.; Zhong, F.; Zheng, L. Reconstruction of ESA CCI satellite-derived soil moisture using an artificial neural network technology. Sci. Total Environ. 2021, 782, 146602. [Google Scholar] [CrossRef]
- Pan, T.; Zou, X.; Liu, Y.; Wu, S.; He, G. Contributions of climatic and non-climatic drivers to grassland variations on the Tibetan Plateau. Ecol. Eng. 2017, 108, 307–317. [Google Scholar] [CrossRef]
- Wang, X.; Yi, S.; Wu, Q.; Yang, K.; Ding, Y. The role of permafrost and soil water in distribution of alpine grassland and its NDVI dynamics on the Qinghai-Tibetan Plateau. Glob. Planet. Chang. 2016, 147, 40–53. [Google Scholar] [CrossRef]
- Bindlish, R.; Barros, A.P. Multifrequency Soil Moisture Inversion from SAR Measurements with the Use of IEM. Remote Sens. Environ. 2000, 71, 67–88. [Google Scholar] [CrossRef]
- Rawat, K.; Sehgal, V.; Pradhan, S.; Ray, S. Semi-empirical model for retrieval of soil moisture using RISAT-1 C-Band SAR data over a sub-tropical semi-arid area of Rewari district, Haryana (India). J. Earth Syst. Sci. 2018, 127, 18. [Google Scholar] [CrossRef] [Green Version]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Shi, C.; Cui, J.; Liu, X.; Zhang, Y.; Qin, N.; Luo, Y. Application of artificial neural network to predict the change of inosine monophosphate for lightly salted silver carp (hypophthalmichthys molitrix) during thermal treatment and storage. J. Food Process. Preserv. 2017, 41, e13246. [Google Scholar] [CrossRef]
- Banerjee, A. Learning Precise Spike Train–to–Spike Train Transformations in Multilayer Feedforward Neuronal Networks. Neural Comput. 2016, 28, 826–848. [Google Scholar] [CrossRef] [Green Version]
- He, Z.; Zhao, W.; Liu, H.; Chang, X. The response of soil moisture to rainfall event size in subalpine grassland and meadows in a semi-arid mountain range: A case study in northwestern China’s Qilian Mountains. J. Hydrol. 2012, 420–421, 183–190. [Google Scholar] [CrossRef]
- Mo, K.; Chen, Q.; Chen, C.; Zhang, J.; Wang, L.; Bao, Z. Spatiotemporal variation of correlation between vegetation cover and precipitation in an arid mountain-oasis river basin in northwest China. J. Hydrol. 2019, 574, 138–147. [Google Scholar] [CrossRef]
- Kizyakov, A.I.; Wetterich, S.; Günther, F.; Opel, T.; Jongejans, L.L.; Courtin, J.; Meyer, H.; Shepelev, A.G.; Syromyatnikov, I.I.; Fedorov, A.N.; et al. Landforms and degradation pattern of the Batagay thaw slump, Northeastern Siberia. Geomorphology 2023, 420, 108501. [Google Scholar] [CrossRef]
- Nguyen, V.-N.; Yariyan, P.; Amiri, M.; Dang Tran, A.; Pham, T.D.; Do, M.P.; Thi Ngo, P.T.; Nhu, V.-H.; Quoc Long, N.; Tien Bui, D. A New Modeling Approach for Spatial Prediction of Flash Flood with Biogeography Optimized CHAID Tree Ensemble and Remote Sensing Data. Remote Sens. 2020, 12, 1373. [Google Scholar] [CrossRef]
- Salzberg, S.L. C4.5: Programs for Machine Learning by J. Ross Quinlan. Morgan Kaufmann Publishers, Inc., 1993. Mach. Learn. 1994, 16, 235–240. [Google Scholar] [CrossRef] [Green Version]
- Rastogi, R.; Shim, K. PUBLIC: A Decision Tree Classifier that Integrates Building and Pruning. Data Min. Knowl. Discov. 2000, 4, 315–344. [Google Scholar] [CrossRef]
- Luchman, J. CHAID: Stata Module to Conduct Chi-Square Automated Interaction Detection; Statistical Software Components; Boston College Department of Economics: Chestnut Hill, MA, USA, 2015. [Google Scholar]
- Han, J.; Kamber, M.; Pei, J. 1—Introduction. In Data Mining, 3rd ed.; Han, J., Kamber, M., Pei, J., Eds.; Morgan Kaufmann: Boston, MA, USA, 2012; pp. 1–38. [Google Scholar]
- Zhou, Q.; Zhu, A.X.; Yan, W.; Sun, Z. Impacts of forestland vegetation restoration on soil moisture content in humid karst region: A case study on a limestone slope. Ecol. Eng. 2022, 180, 106648. [Google Scholar] [CrossRef]
- Lv, J.; Zhang, R.; Tu, J.; Liao, M.; Pang, J.; Yu, B.; Li, K.; Xiang, W.; Fu, Y.; Liu, G. A GNSS-IR Method for Retrieving Soil Moisture Content from Integrated Multi-Satellite Data That Accounts for the Impact of Vegetation Moisture Content. Remote Sens. 2021, 13, 2442. [Google Scholar] [CrossRef]
- Feng, S.; Qiu, J.; Crow, W.T.; Mo, X.; Liu, S.; Wang, S.; Gao, L.; Wang, X.; Chen, S. Improved estimation of vegetation water content and its impact on L-band soil moisture retrieval over cropland. J. Hydrol. 2023, 617, 129015. [Google Scholar] [CrossRef]
- Cai, Q.; Li, E.; Chen, J.; Tao, L.; Jiang, R. Analysis on Topographic Effect of Soil Moisture in Mountainous Areas based on Landsat-8 OLI Images. J. Eng. Sci. Technol. Rev. 2020, 13, 22–29. [Google Scholar] [CrossRef]
- Qiu, Z.; Pennock, A.; Giri, S.; Trnka, C.; Du, X.; Wang, H. Assessing Soil Moisture Patterns Using a Soil Topographic Index in a Humid Region. Water Resour. Manag. 2017, 31, 2243–2255. [Google Scholar] [CrossRef]
- Lyons, D.S.; Dobrowski, S.Z.; Holden, Z.A.; Maneta, M.P.; Sala, A. Soil moisture variation drives canopy water content dynamics across the western U.S. Remote Sens. Environ. 2021, 253, 112233. [Google Scholar] [CrossRef]
- Tan, X.; Zhang, L.; He, C.; Zhu, Y.; Han, Z.; Li, X. Applicability of cosmic-ray neutron sensor for measuring soil moisture at the agricultural-pastoral ecotone in northwest China. Sci. China Earth Sci. 2020, 63, 1730–1744. [Google Scholar] [CrossRef]
- Zhao, L.; Zou, D.; Hu, G.; Wu, T.; Du, E.; Liu, G.; Xiao, Y.; Li, R.; Pang, Q.; Qiao, Y.; et al. A synthesis dataset of permafrost thermal state for the Qinghai–Tibet (Xizang) Plateau, China. Earth Syst. Sci. Data 2021, 13, 4207–4218. [Google Scholar] [CrossRef]
- Lu, P.; Han, J.; Li, Z.; Xu, R.; Li, R.; Hao, T.; Qiao, G. Lake outburst accelerated permafrost degradation on Qinghai-Tibet Plateau. Remote Sens. Environ. 2020, 249, 112011. [Google Scholar] [CrossRef]
- Penna, D.; Borga, M.; Norbiato, D.; Dalla Fontana, G. Hillslope scale soil moisture variability in a steep alpine terrain. J. Hydrol. 2009, 364, 311–327. [Google Scholar] [CrossRef]
- Wang, J.; Bao, Y.; Zhang, Y.; Qu, J.; Zhang, W. Soil moisture inversion using multi-polarization and multi-angle ENVISAT ASAR data in surface soils of bare area and wheat-covered area. Nongye Gongcheng Xuebao/Trans. Chin. Soc. Agric. Eng. 2010, 26, 205–210. [Google Scholar] [CrossRef]
- Wei, Y.; Fang, Z.; Zhang, L.; Kang, L.; Liu, X. Estimating Soil Moisture in Semi-Arid Region by Remote Sensing Based on TM Data. In Proceedings of the 2010 International Conference on Multimedia Technology, ICMT 2010, Ningbo, China, 29–31 October 2010. [Google Scholar] [CrossRef]

| Fitting Model | Model Expression |
|---|---|
| Linear | |
| Conic | |
| Index | |
| Logarithmic | |
| Power Multiplication |
| Correlation | Influencing Factors | ||||||
|---|---|---|---|---|---|---|---|
| Elevation | Slope Gradient | Slope Angle | Slope Aspect | Temperature | Precipitation | ||
| Months | March | −0.349 * | −0.024 | −0.003 | −0.138 * | 0.193 * | 0.194 * |
| June | −0.38 * | −0.306 * | −0.203 * | −0.072 * | 0.154 * | 0.326 * | |
| September | −0.58 ** | −0.203 * | −0.29 * | 0.069 | 0.436 ** | 0.155 * | |
| December | 0.424 ** | −0.096 | 0.003 | 0.016 | −0.015 | 0.244 * | |
| Month | Test | Input Variables | Fitting Model | Month | Test | Input Variables | Fitted Model | Output Variables |
|---|---|---|---|---|---|---|---|---|
| March | 1 | MPDI, , Elevation, and Precipitation | Linear | June | 24 | MPDI, , Slope aspect, and Elevation | Logarithmic | Simulate soil moisture |
| 2 | Conic | 25 | Power Multiplication | |||||
| 3 | Index | 26 | MPDI, , Slope aspect, Temperature, and Slope gradient | Linear | ||||
| 4 | Logarithmic | 27 | Conic | |||||
| 5 | Power Multiplication | 28 | Index | |||||
| 6 | MPDI, , Elevation, and Temperature | Linear | 29 | Logarithmic | ||||
| 7 | Conic | 30 | Power Multiplication | |||||
| 8 | Index | September | 31 | MPDI, , Elevation, and Slope angle | Linear | |||
| 9 | Logarithmic | 32 | Conic | |||||
| 10 | Power Multiplication | 33 | Index | |||||
| 11 | MPDI, , Elevation, Precipitation, and Temperature | Linear | 34 | Logarithmic | ||||
| 12 | Conic | 35 | Power Multiplication | |||||
| 13 | Index | 36 | MPDI, , Elevation, and Slope aspect | Linear | ||||
| 14 | Logarithmic | 37 | Conic | |||||
| 15 | Power Multiplication | 38 | Index | |||||
| June | 16 | MPDI, , Slope aspect, and Temperature | Liner | 39 | Logarithmic | |||
| 17 | Conics | 40 | Power Multiplication | |||||
| 18 | Index | December | 41 | MPDI, , Precipitation, Temperature, and Elevation | Linear | |||
| 19 | Logarithmic | 42 | Conic | |||||
| 20 | Power Multiplication | 43 | Index | |||||
| 21 | MPDI, , Slope aspect, and Elevation | Linear | 44 | Logarithmic | ||||
| 22 | Conic | 45 | Power Multiplication | |||||
| 23 | Index |
| Month | Test | Pearson | Accuracy (%) | Month | Test | Pearson | Accuracy (%) |
|---|---|---|---|---|---|---|---|
| March | 1 | 0.408 | 85.7 | June | 24 | 0.353 | 52.5 |
| 2 | 0.415 | 82.6 | 25 | 0.116 | 60.0 | ||
| 3 | 0.4 | 93.3 | 26 | 0.219 | 45.8 | ||
| 4 | 0.378 | 77.3 | 27 | 0.363 | 43.5 | ||
| 5 | 0.413 | 88.0 | 28 | 0.14 | 43.5 | ||
| 6 | 0.348 | 82.6 | 29 | 0.459 | 60.0 | ||
| 7 | 0.339 | 85.7 | 30 | 0.448 | 40.9 | ||
| 8 | 0.306 | 92.3 | September | 31 | 0.592 | 79.2 | |
| 9 | 0.391 | 79.2 | 32 | 0.587 | 57.7 | ||
| 10 | 0.381 | 80.0 | 33 | 0.551 | 70.4 | ||
| 11 | 0.389 | 95.7 | 34 | 0.599 | 57.7 | ||
| 12 | 0.405 | 84.6 | 35 | 0.593 | 70.8 | ||
| 13 | 0.396 | 62.5 | 36 | 0.596 | 50.0 | ||
| 14 | 0.39 | 89.5 | 37 | 0.593 | 60.9 | ||
| 15 | 0.391 | 83.3 | 38 | 0.07 | 45 | ||
| June | 16 | 0.223 | 50 | 39 | 0.604 | 50 | |
| 17 | 0.191 | 47.1 | 40 | 0.594 | 69.2 | ||
| 18 | 0.140 | 50 | December | 41 | 0.48 | 57.1 | |
| 19 | 0.402 | 38.1 | 42 | 0.445 | 70.4 | ||
| 20 | 0.273 | 65.0 | 43 | −0.353 | 55.6 | ||
| 21 | 1 | 53.6 | 44 | 0.292 | 53.6 | ||
| 22 | 0.424 | 65.2 | 45 | 0.441 | 68.0 | ||
| 23 | 0.471 | 38.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Q.; Yang, J.; Zhang, L.; Sun, Z.; Sun, G.; Chen, Q.; Dou, F. Analysis of Seasonal Driving Factors and Inversion Model Optimization of Soil Moisture in the Qinghai Tibet Plateau Based on Machine Learning. Water 2023, 15, 2859. https://doi.org/10.3390/w15162859
Deng Q, Yang J, Zhang L, Sun Z, Sun G, Chen Q, Dou F. Analysis of Seasonal Driving Factors and Inversion Model Optimization of Soil Moisture in the Qinghai Tibet Plateau Based on Machine Learning. Water. 2023; 15(16):2859. https://doi.org/10.3390/w15162859
Chicago/Turabian StyleDeng, Qinghai, Jingjing Yang, Liping Zhang, Zhenzhou Sun, Guizong Sun, Qiao Chen, and Fengke Dou. 2023. "Analysis of Seasonal Driving Factors and Inversion Model Optimization of Soil Moisture in the Qinghai Tibet Plateau Based on Machine Learning" Water 15, no. 16: 2859. https://doi.org/10.3390/w15162859






