Abstract
Reservoirs are susceptible to interference from inter-basin water transfer projects intended to relieve serious water shortages. The Central Route of the South-to-North Water Division Project in China has altered the hydrological conditions and water storage status of the terminal reservoir, the Miyun Reservoir, thereby affecting the flood control reliability in the Chaobai River Basin. In this study, a dual-objective five-reservoir operation model was developed, in which reservoir releases are obtained through piecewise linear operating rules. The model considers the flooding risks both downstream of the basin and in the Miyun reservoir area. A parameterization-simulation-optimization approach was employed to obtain the Pareto-optimal front, providing decision-makers with a list of optimal rule parameters to select and match their own risk preferences. All optimized rules could ensure safe operation during the designed floods to be expected once (or more than once) every thousand years. In contrast, the current flood operation schemes largely ignore the water transfer between basins but primarily concentrate on storing water from floods. Thus, the Miyun Reservoir, whose design return period is 1000 years, can easily become filled during a 100-year flood, impeding the system’s flood control capacity. Compared to the operating rule optimized in this study, the current schemes result in a 10.5% higher upstream inundation loss and an unsatisfactory 17 million CNY of equivalent water transfer loss.
1. Introduction
Floods are natural disasters that pose significant threats to ecology, the environment, infrastructure, agriculture, and even human life. As a representative flood control infrastructure, reservoirs retain floodwater and flatten out the peak flow by intercepting heavy rainfall in flood storage and releasing it after the rainstorm. With frequent water shortages across the world, there is a growing need to operate multiple and multipurpose reservoirs such that the maximum possible water is conserved while ensuring dam safety and flood moderation [1].
Reservoir flood operation is a typical multi-objective problem, which needs to balance the conflicts of the benefits and flood damage [2,3], or flooding risks of multiple sites and different flood stages [4,5,6]. For multiple reservoir systems, it is more challenging to prioritize the flooding risk targets between the tributaries and mainstream [7], and to allocate the flood-storage capacity among reservoirs [8,9]. These characteristics pose significant modeling and optimization challenges in the flood operation of multi-reservoir systems. Single reservoir flood control research dates back to the 1936 Flood Control Act in the U.S. [10], and Windsor [11] pioneered the use of dynamic programming to optimize operation during flood periods. Multi-reservoir flood control has become a research hot topic due to the increasing water resource demand and the rapid construction of numerous dams in the past two decades, especially in developing countries [12,13,14]. The major objective of single reservoir flood control is to minimize the peak water level of the dam or the peak flow at the downstream flood control station [6,15]. Multi-reservoir systems have more complex objectives, aiming to minimize flooding risks at multiple flood control stations while also maximizing flood utilization benefits. For example, Moridi and Yazdi [16] employed an improved mixed integer linear programming to determine the optimal allocation of reservoir flood control capacity in the Karkheh multi-reservoir system. Their optimization objectives are reducing both downstream flooding damage and system hydropower loss. Lu et al. [9] applied the theory of large-scale system decomposition and coordination to balance flood control and power generation objectives for the mixed Pi River Basin. Glavan et al. [3] optimized the design of detention reservoirs using scenario-based economic analysis in the Lower Savinja Valley to ensure flood safety while preventing an unacceptable loss of crop yield.
Among the considerable attempts made to derive optimal operating policies for reservoir flood control, it usually can be achieved through implicit stochastic optimization, explicit stochastic optimization, real-time control with forecasting, and a parameterization-simulation-optimization model [12,17,18]. Each of these has its own advantages and disadvantages. Implicit stochastic optimization, also known as deterministic optimization, requires perfect foreknowledge of a flood over a lengthy time horizon [16,19], which, evidently, is not yet reached in the current flood forecasting technologies [20]. Without the presumption of perfect forecasting, explicit stochastic optimization and real-time operation using uncertainty forecast are usually applicable to single reservoir flood control [6,15,21]. Nevertheless, their application to multi-reservoir systems is computationally challenging unless operating rules can be parametrized in some way, as seen in the work of Lu et al. [9]. Parameterization-simulation-optimization involves optimizing the form of operating rules by defining them with a small number of parameters. This method is commonly used in conjunction with intelligent algorithms and widely applied in deriving reservoir scheduling rules for various purposes, including water supply [22,23], hydropower generation [24,25], and flood control [6,7]. These rules are often predefined in the form of rule curves or tables and deduced through fitting methods from optimal processes. This may involve linear regression analysis or surface fitting [18,26] or an iterative simulation-based optimization by adjusting the operating rule parameters [7,27,28]. Overall, studies on flood control for mixed-cascade reservoir systems are still rare.
The operation of reservoir systems faces abrupt hydrological changes caused by climate change and extensive human activities, such as water division. The Miyun Reservoir is the largest reservoir in North China and was the main surface water source for Beijing, the capital of China. The historical continuous decline of streamflow in the Miyun Reservoir has achieved extensive research in terms of causes, potential impacts, and future projections [29,30,31,32]. In recent years, climate change has led to an opposite increasing trend of rainfall in northern China [33], leading to a sharp increase in flood control pressure. Additionally, the water division from the Central Route of China’s South-to-North Water Transfer Project into Miyun Reservoir has increased its storage, presenting new requirements for flood control scheduling. However, the current reservoir in operation under the influence of inter-basin water transfer predominantly focuses on water supply issues [34,35]. The impact of inter-basin water transfer on flood control situations and thus flood control rule adjustments remain lacking. The Chaobai River Basin, with the Miyun Reservoir as its major controlling infrastructure, was chosen as a case study to demonstrate the optimization of multi-reservoir flood control operations.
The rest of this paper is organized as follows. Section 2 provides detailed information about the study area and the formation of operating rules and optimization models for the mixed five-reservoir system. Section 3 describes the impact of SNWDP on the Miyun Reservoir and the optimization results. The conclusions are drawn in Section 4.
2. Methods and Materials
2.1. Chaobai River Basin
The study area is the Chaobai River Basin (39°46′–41°49′ N, 115°25′–117°35′ E) in northern China (Figure 1a). The watershed covers an area of 19,400 km2 and has a diverse topography, with higher elevations in the northern region and a gradual decrease in elevation towards the southeast. It is characterized by two major tributaries, namely the Chao River and the Bai River, which merge at the Miyun Reservoir and form the Chaobai River downstream of the reservoir. The annual precipitation and runoff are around 553 mm (range 500–700) and 1653 million m3 (range 615–4320) [36]. The major flood season is June–August. Over 70% of the annual rainfall occurs during this period, predominantly in the form of intense and localized downpours [37].
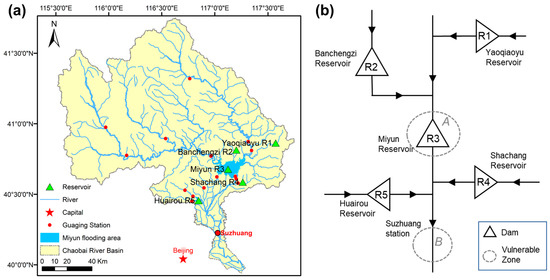
Figure 1.
Location of the Chaobai River Basin (a) and the schematic diagram of the mixed five-reservoir flood control system (b).
The flood control system in the Chaobai River Basin consists of a cascade of five reservoirs: the Yaoqiaoyu Reservoir (R1), Banchengzi Reservoir (R2), Miyun Reservoir (R3), Shachang Reservoir (R4), and Huairou Reservoir (R5). The layout is depicted in Figure 1b and numbered from upstream to downstream. The respective flood control characteristic parameters are listed in Table 1. The reservoirs are designed with different seismic intensity levels: R1 and R2 are at 7 degree and the downstream R3, R4, and R5 have a higher design seismic intensity level of 8 degree. Among these reservoirs, the Miyun Reservoir serves as the pivotal control project along the main stream of the basin, with a total storage capacity of 4375 million m3 [38] and a drainage area of approximately 90% of the basin’s total area. The Miyun Reservoir has long been the sole surface water resource for Beijing through the Jingmi Canal. Since the introduction of water transfer from the Central Route of the SNWDP in 2015, the reservoir’s role shifted to serving as an emergency strategic water resource reserve.

Table 1.
Characteristic parameters of the Chaobai River flood control system. In the last three rows, the characteristic water level [m3], and in parentheses the respective storage [106 m3], for each reservoir are given.
2.2. Multi-Reservoir Flood Control Operation Model
The general goal for reservoir flood control is to ensure the safety of both the reservoir itself and the downstream flood control stations. In general, the model objectives during the floods are (1) to minimize the vulnerability (or economic losses) caused by flooding of the reservoir in terms of the reservoir risk water level and the duration of such a high level, and (2) to minimize the damage due to peak outflow from the reservoir at critical locations downstream of the reservoir.
Flood control in the study area is unique because both the upstream reservoir area and downstream flood space have undergone significant urbanization, and the urban development within the Beijing metropolitan area has placed extremely high demands on flood safety in Miyun Reservoir. The flood control objects in this study are (1) the upstream Miyun Reservoir area (Zone A in Figure 1) and (2) the downstream Suzhuang flood control station (Zone B).
The potential inundation losses in the Miyun Reservoir area are due to the continuous decline in the reservoir water level over the past few decades [30]. The long-term exposed reservoir’s original inundation area has been developed and inhabited by humans. The flooding risk of the area upstream of the Miyun Reservoir is simulated using the economic losses of human settlements, infrastructure, and agriculture. Forested areas will be submerged when the water level is between 152 m (the flood limited water level, FLWL) and 155 m. When the water level exceeds 155 m, seven towns will be submerged. When the water level reaches 158.5 m (the check flood level, CFL), the water supply security will be impaired. The standardized inundation losses at different water levels under the CFL are collected and calculated (Figure 2a). Therefore, flooding damage can occur at any time when the water level is higher than the FLWL, which is unique and unlike others that are a threat only when the risky water level is exceeded.
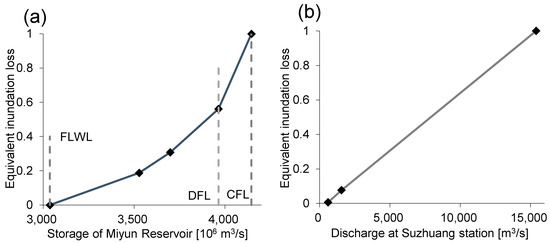
Figure 2.
Relationships between inundation loss in the Miyun Reservoir area and the reservoir storage (a), and the downstream losses and discharge in the Suzhuang flood control section (b).
The downstream area of the Chaobai River Basin has important towns and a major transport railway and highway. The Suzhuang station is designated as the flood control site. The discharge is jointly managed by the Miyun (R3), Shachang (R4), and Huairou (R5) reservoirs. The safe carrying capacity at Suzhuang station is 600 m3/s, exceeding which would result in varying degrees of flooding. Through flood routing simulations, the extent of inundation and damage in the channel can be determined. Figure 2b illustrates the relationship between the total discharge and the downstream losses due to flooding.
The inundation losses in the Chaobai River Basin are semi-quadratic (or linear) functions of the decision variables. To simplify the model calculation and ensure the stability of the optimization process across time periods, we use the quadratic function instead of the flooding damage as the target and normalized it as follows:
These objectives are subjective to the following constraints.
Water balance constraint
Reservoir water storage or level constraint
Outflow constraint
where, and are the beginning and ending storages of reservoir in period t (m3), respectively. Specifically, is the ending storage of the Miyun Reservoir. and are the storages corresponding to the flood limited water level and designed flood level (m3), respectively. are the natural inflow (m3/s), reservoir outflow (m3/s), and reservoir water level (m), respectively. The intermediate flow between reservoirs, i.e., regions between the reservoir and the flood control section, is ignored. The Miyun Reservoir (R3) receives the discharges from the Yaoqiaoyu Reservoir (R1) and the Banchengzi Reservoir (R2). , , and are the discharges of the Miyun (R3), Shachang (R4), and Huairou (R5) reservoirs (m3/s), the sum of which is the flow rate at the downstream Suzhuang flood control section. and are the lower and upper limits of the reservoir water level (m), respectively, and are typically the dead water level and check flood level (CFL), respectively, during the flood season. and are the boundaries of the outflow constraints and are equal to the ecological flow requirement and the reservoir spillway capacity of the respective reservoir at the check flood level (m3/s).
2.3. Operating Rules
Flood control operating rules are used to make release decisions based on the current hydrological conditions, such as the reservoir water level and incoming flow rates, thereby achieving conservative safety operation during a flood. These rules can be established using empirical relationships, simulation models, and optimization methods. The release schemes are usually presented in the form of tables or mathematical functions, with
where (i.e., in Equations (2) and (5)) is the reservoir release to be decided (m3/s), which is usually a piecewise parametric function of the reservoir states, i.e., the inflow (m3/s) and water level (m). , , , and , k = 1,2,…K, are the hierarchical boundaries of the classified reservoir inflow and water level.
In general, reservoirs follow uniform rules when confronted with frequent flood events. However, a uniform parameterization scheme cannot adequately address the specific flood safety requirements for the Chaobai River Basin. Distinct parameters have been proposed for a similar set of rules for each reservoir, to cope with floods with different frequencies. We use the following widely used linear decision rules [7,27,39] with hourly regulation and four-lever hierarchy:
In the case of extreme floods with a return period of over 100 years (e.g., 1000-year-flood), the form of the rule needs to be slightly modified for reservoirs other than the Miyun Reservoir. The discharge increases with :
where the reservoir release is decided as a linear function of both the reservoir inflow and the water level. is the reservoir inflow from the flood hydrograph and upstream releases (m3/s); , , and are the maximum allowable discharges (m3/s) under FLWL, DFL, and CFL, respectively. The parameters , , and are the decision variables that need to be optimized in this study.
2.4. Investigated Floods
The 100-year design flood hydrographs for each reservoir area are illustrated in Figure 3. Table 2 lists the peak flood discharges for each reservoir under different return periods. By proportionally scaling the representative floods using the peak flows and 3-day flood quantities (not shown), the 72-h design flood hydrographs for different frequencies are obtained.
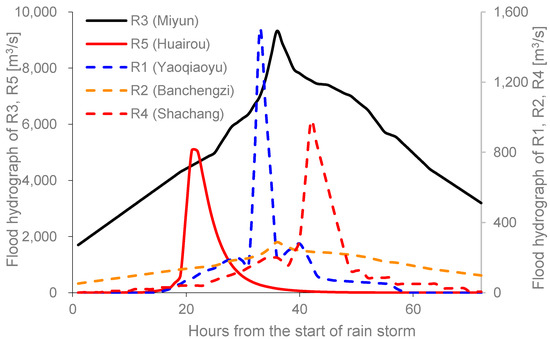
Figure 3.
72-h designed flood hydrographs for the designed 100-year-flood.

Table 2.
Low-recurrence-interval design flood peak flow discharge.
2.5. NSGA-II Solving Method
Due to the non-differentiable nature of the predefined operating rules (Section 2.3) and the nonlinear relationship between rule parameters and flood damage, classical optimization methods like linear programming are not suitable for optimizing the model. Instead, a simulation-based optimization approach is employed to derive the rule parameters.
In this paper, the non-dominated sorting genetic algorithm II algorithm (NSGA-II) [40] is implemented to identify the large set of Pareto solutions to this simulation-optimization multi-objective model (Section 2.2). The NSGA-II eliminates the need for explicit coordination among multiple objectives and enhances the basic genetic algorithm by incorporating fast non-dominated sorting and crowding distance mechanisms. An elite preservation strategy in NSGA-II ensures diverse solutions that effectively approach the Pareto optimal front in a wide and uniform manner. Hojjati et al. [41] have found that NSGA-II provides better approximations of the true Pareto optimal surface, depicting tradeoffs between objectives, compared to multi-objective particle swarm optimization. The NSGA-II algorithm is well-established and has been demonstrated to have strong optimization capabilities in both theoretical test functions and practical production problems [25,40]. The obtained Pareto front provides valuable insights into available compromising strategies for decision-makers.
The operating rules (Section 2.3) are optimized for various representative flood frequencies, starting from the FLWL of each reservoir. For each representative flood (Section 2.4), a set of initial decision variables (i.e., the rule parameters) is randomly generated. Simulation methods are then used to sequentially update the reservoir states. The operation process and objective function values are evaluated (Section 2.2). Optimized using the NSGA-II algorithm, all non-dominated optimal solutions, including the Pareto front and corresponding rule parameters, are obtained.
3. Results and Discussion
3.1. Impact of Inter-Basin Water Transfer on the Flood Control Situation of the Miyun Reservoir
Figure 4 illustrates the historical annual end-of-year storage of the Miyun Reservoir. Before 1995, the reservoir’s water level was close to the FLWL, which has undergone multiple adjustments [39] and currently stands at 152 m (3037 million m3). Since then, a combination of factors including reduced rainfall, has led to consistently low reservoir storage (Figure 4). Flood control was not a major consideration during the flood season. Instead, the reservoir intercepted all incoming floodwater for non-flood season water supply.
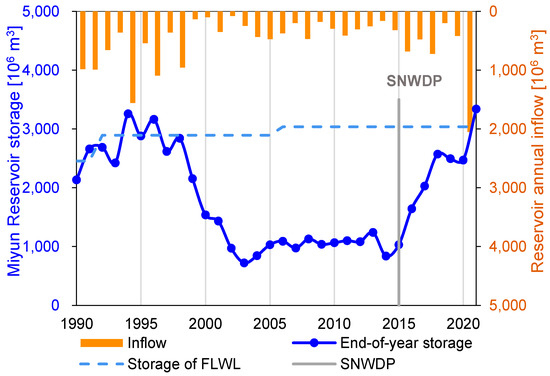
Figure 4.
Annual available water resources into the Miyun Reservoir (including external transfer), end-of-year reservoir storage, and the historical flood limited water level (FLWL) from 1990 to 2021. The Central Route of the South-to-North Water Diversion Project (SNWDP) commenced water transfer in 2015.
The Miyun reservoir began to receive water from the Central Route of the SNWDP in 2015, accounting for approximately 10–30% of the total inflow to the reservoir. Along with the decreasing water supply and increasing trend of extreme floods recently, water storage in the Miyun Reservoir has been steadily rising and reached its peak in 2021 (Figure 4). During the flood season in 2021, the basin experienced 63% more precipitation than the average, and the historically largest flood event, which occurred from 30 July to 2 August. With these changes, the reservoir now seeks to maximize water storage due to the high cost of inter-basin water transfer while mitigating potential losses caused by heavy rainfall. The discharge during flood regulation consists of a combination of upstream floodwater and water transferred from southern China. Consequently, the equivalent economic losses of the Miyun Reservoir discharge can be evaluated as the product of the discharge volume and the unit price of the transferred water.
3.2. Flood Regulation
Taking the 20-year flood (within design standard) and 1000-year flood (beyond design standard) events as examples, Figure 5 shows the Pareto front of the dual-objective model using the NSGA-II method. Objective F1 aims to minimize the water level of the Miyun Reservoir, thus reducing the losses due to inundation in the reservoir area (Equation (1)). Objective F2 focuses on controlling the system downstream discharge in the Suzhuang section, thus constraining the flooding risk in the downstream river channel (Equation (2)). These objectives are in competition and reducing one will enlarge the other. Under the two different frequency floods, the upstream target values are in a similar range, but the downstream target values are six times larger for the 1000-year flood than for the 20-year flood (Figure 5).
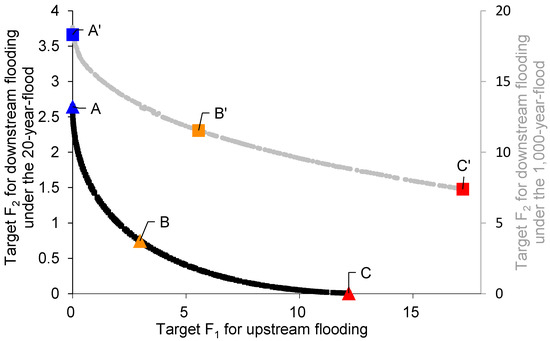
Figure 5.
The Pareto front for the dual-objective operation model under a 20-year flood and a 1000-year flood. The six points (A, B, C, A’, B’, and C’) represent the six solutions under different flood conditions and distinct objective prioritization.
Each point on the Pareto front represents an optimal solutions alternative obtained through the optimization of the reservoir operation. Figure 5 and Figure 6a,b show a comparison of the reservoir operation process under the 20-year flood. The blue point (line) labeled A on the Pareto front indicates full focus on minimizing upstream inundation (objective F1). In this case, the water level of the Miyun Reservoir remains relatively stable at the FLWL (Figure 6a). To achieve this, almost all inflow is discharged, leading to high flow rates in the Suzhuang station, and the peak value even surpasses the system’s natural inflow (Figure 6b). As the concern shifts toward prioritizing the downstream flood safety (the trade-off point B on the Pareto front), the reservoir storage gradually increases (orange curve in Figure 6a) from the FLWL (3037 million m3) to 154.7 m (3422 million m3) within 72 h. In return, the system release exhibits a noticeable peak attenuation effect (Figure 6b). The goal of red point (curve) C is to minimize downstream flooding by intercepting as much incoming floodwater as possible in the Miyun Reservoir.
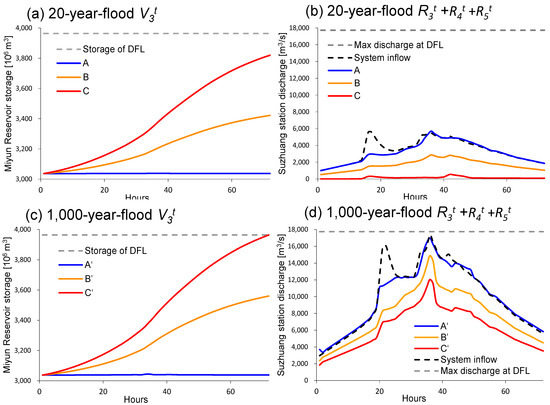
Figure 6.
The reservoir operation process in terms of the Miyun Reservoir storage (a,c) and the basin’s downstream total discharge (b,d) corresponding to the points A, B, C, A’, B’, and C’ in Figure 5.
Under the 1000-year flood, the system is still capable of safeguarding the entire basin (Figure 6c,d). None of the selected three scenarios causes the water level of the Miyun Reservoir to surpass the DFL. As the system’s designed flood has two peaks, the reservoirs effectively capture the first peak while the attenuation effect on the second peak is noticeably diminished. This weakness can be attributed to the shrinking flood control storage of the reservoirs during the operation.
The optimal decision variables (i.e., rule parameters) under each frequency design flood are provided in the Supplementary Materials (Table S1). The rule-based operation typically involves two steps: (1) evaluation of the magnitude of the incoming flood by comparing the forecast peak flow and quantity to the historical flood records; and (2) releasing the water according to the operating rules with the corresponding parameters and Equations (6)–(8).
3.3. Compariosn to the Current Operating Rules
The existing flood control rules for the five reservoirs listed in Table 3 are designed independently for the single-objective single-reservoir condition. In general, the reservoir discharge varies in different characteristic water level ranges. When reservoir storage is below the FLWL, all incoming floodwater is stored in the reservoirs. When water level exceeds FLWL, reservoirs with small flood control capacity, i.e., R1, R2, and R4, are designed to discharge either up to the maximum capacity or at predetermined flow rates. The Miyun Reservoir (R3) and Huairou Reservoir (R5) adjust their discharge considering the inflow rate more extensively, with small release under low inflow conditions and high release when there is a significant inflow.

Table 3.
The current flood control operating rules for individual reservoirs and the optimized rule parameters for the integrated operation of the five reservoirs on the Chaobai River when confronting a 100-year flood.
Taking the 100-year flood as an example, the current rules lead to greater flood control loss in both the upstream and downstream areas compared to the dual-objective multi-reservoir integrated optimization result (Figure 7a). For illustrative purposes, we compare the current rules with the closest optimal Pareto solution, the rule parameters of which are listed in Table 3.
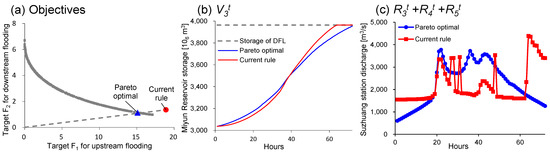
Figure 7.
Comparison of operation under current rules and optimized rules in terms of the objective values (a), the Miyun Reservoir storage process (b), and the basin’s downstream total discharge (c).
Under the current rules, the primary focus of the Miyun Reservoir is on inflow interception, regardless of the background of the SNWDP. The reservoir tends to fill up prematurely, thus reducing its flood control capacity in the latter stages. It is evident from the storage process shown in Figure 7b that the current rules could rapidly increase the water level to the DFL, after which all inflow must be released. Conversely, the optimized rules (blue curve in Figure 7b) allow for water storage at lower inflow rates and dynamically adjust the outflow proportionally to the inflow and storage, resulting in more gradual filling. The optimized rules, with emphasis on reservoir storage, i.e., discharging in response to both incoming water and dynamic changes in storage, lead to a more continuous reservoir outflow process. This helps avoid the frequent abrupt changes in discharge observed under the current rules (Figure 7c).
In terms of flood damage, the current rules for a 100-year flood lead to 10.5% more loss in the upstream reservoir area compared to the optimized rules. Downstream inundation losses are similar, but the Miyun Reservoir incurs an additional 7.4 million m3 spill. Assuming a unit water price of 2.33 CNY for the water transferred to Beijing via the Central Route of the SNWDP [42], the surplus water is worth about around 17 million CNY.
4. Conclusions
In this study, a multi-objective model for mixed-reservoir flood control operation was developed. The operating rules were optimized using the NSGA-II algorithm. The mixed five-reservoir system in the Chaobai River Basin was selected because the major flood control reservoir, the Miyun Reservoir, has been significantly influenced in terms of both its water inflow and demand by the Central Route of the SNWDP. Unlike conventional flood control models whose upstream risk is dam overtopping, the Miyun Reservoir faces unique challenges: the upstream reservoir area faces inundation loss as long as the water level exceeds the FLWL and the loss increases non-linearly with the increasing inundation depth. The piecewise linear rules are directly proportional to the inflow and reservoir storage. These linear rules are operational simplicity and in line with the current operation schemes in the Chaobai River Basin. An integrated simulation-optimization frame is adopted for the joint reservoirs. This means that the rules are optimized by accounting for the interplay, such as the compensation effects, among the reservoirs, thereby yielding more reasonable rules than optimizing each reservoir independently.
The model provides a range of rule parameter combinations that accommodate the different preferences of the targets. A comparison with the current flood operating rules revealed that the optimized rules can avoid premature reservoir filling and decrease inundation losses in the Miyun Reservoir area and downstream of the basin.
In this study, different combinations of rule parameters are proposed to address floods of varying frequencies. While these combinations could effectively handle floods of the corresponding magnitudes, the effectiveness of the operating rules in different flood coincidences in the mainstream and tributaries has not been investigated. In addition, only piecewise linear operating rules are considered. To enhance the adaptability and robustness of the system flood control operation, future research should leverage the optimized parameter library derived from designed floods and the actual normal flood events. The performances of other types of operating rules should be compared to determine the most suitable rules for the control of basin-wide floods in future studies. The operating rules and rule parameters could be further adjusted to provide more dynamic decision support for operators under typical flood conditions and incorporating real-time weather forecasts.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/w15152817/s1, Table S1: Parameters for operating rules.
Author Contributions
Conceptualization, W.W. and Y.L. (Yueyi Liu); methodology and formal analysis, W.W. and H.Z.; data resources, F.Z. and Y.L. (Yajing Lu); writing—original draft preparation, W.W., H.Z. and J.Z. All authors provided critical feedback and helped shape the manuscript and revision. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financially supported by the National Natural Science Foundation of China (U2040206), (52179009) and (51909035).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jain, S.K.; Shilpa, L.S.; Rani, D.; Sudheer, K.P. State-of-the-art review: Operation of multi-purpose reservoirs during flood season. J. Hydrol. 2023, 618, 129165. [Google Scholar] [CrossRef]
- Wan, W.; Zhao, J.; Lund, J.R.; Zhao, T.; Lei, X.; Wang, H. Optimal Hedging Rule for Reservoir Refill. J. Water Res. Plan. Man. 2016, 142, 4016051. [Google Scholar] [CrossRef]
- Glavan, M.; Cvejić, R.; Zupanc, V.; Knapič, M.; Pintar, M. Agricultural production and flood control dry detention reservoirs: Example from Lower Savinja Valley, Slovenia. Environ. Sci. Policy 2020, 114, 394–402. [Google Scholar] [CrossRef]
- Ding, W.; Zhang, C.; Cai, X.; Li, Y.; Zhou, H. Multi-objective hedging rules for flood water conservation. Water Resour. Res. 2017, 53, 1963–1981. [Google Scholar] [CrossRef]
- Zhao, T.; Zhao, J.; Lund, J.R.; Yang, D. Optimal Hedging Rules for Reservoir Flood Operation from Forecast Uncertainties. J. Water Res. Plan. Man. 2014, 140, 4014041. [Google Scholar] [CrossRef]
- Chou, F.N.; Wu, C. Stage-wise optimizing operating rules for flood control in a multi-purpose reservoir. J. Hydrol. 2015, 521, 245–260. [Google Scholar] [CrossRef]
- Lei, X.; Zhang, J.; Wang, H.; Wang, M.; Khu, S.; Li, Z. Deriving mixed reservoir operating rules for flood control based on weighted non-dominated sorting genetic algorithm II. J. Hydrol. 2018, 564, 967–983. [Google Scholar] [CrossRef]
- Meng, X.; Chang, J.; Wang, X.; Wang, Y.; Wang, Z. Flood control operation coupled with risk assessment for cascade reservoirs. J. Hydrol. 2019, 572, 543–555. [Google Scholar] [CrossRef]
- Lu, Q.; Zhong, P.; Xu, B.; Zhu, F.; Huang, X.; Wang, H.; Ma, Y. Stochastic programming for floodwater utilization of a complex multi-reservoir system considering risk constraints. J. Hydrol. 2021, 599, 126388. [Google Scholar] [CrossRef]
- Arnold, J.L. The Evolution of the 1936 Flood Control Act; Office of History; US Army Corps of Engineers: Fort Belvoir, VA, USA, 1988.
- Windsor, J.S. Optimization model for the operation of flood control systems. Water Resour. Res. 1973, 9, 1219–1226. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal operation of multireservoir systems: State-of-the-art review. J. Water Res. Plan. Man. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Guo, S.; Chen, J.; Li, Y.; Liu, P.; Li, T. Joint operation of the multi-reservoir system of the Three Gorges and the Qingjiang cascade reservoirs. Energies 2011, 4, 1036–1050. [Google Scholar] [CrossRef]
- Rahimi, H.; Ardakani, M.K.; Ahmadian, M.; Tang, X. Multi-reservoir utilization planning to optimize hydropower energy and flood control simultaneously. Environ. Process. 2020, 7, 41–52. [Google Scholar] [CrossRef]
- Qi, Y.; Yu, J.; Li, X.; Wei, Y.; Miao, Q. Reservoir flood control operation using multi-objective evolutionary algorithm with decomposition and preferences. Appl. Soft Comput. 2017, 50, 21–33. [Google Scholar] [CrossRef]
- Moridi, A.; Yazdi, J. Optimal allocation of flood control capacity for multi-reservoir systems using multi-objective optimization approach. Water Resour. Manag. 2017, 31, 4521–4538. [Google Scholar] [CrossRef]
- Ahmad, A.; El-Shafie, A.; Razali, S.F.M.; Mohamad, Z.S. Reservoir optimization in water resources: A review. Water Resour. Manag. 2014, 28, 3391–3405. [Google Scholar] [CrossRef]
- Celeste, A.B.; Billib, M. Evaluation of stochastic reservoir operation optimization models. Adv. Water Resour. 2009, 32, 1429–1443. [Google Scholar] [CrossRef]
- Kim, Y.; Sun, B.; Kim, P.; Jo, M.; Ri, T.; Pak, G. A study on optimal operation of gate-controlled reservoir system for flood control based on PSO algorithm combined with rearrangement method of partial solution groups. J. Hydrol. 2021, 593, 125783. [Google Scholar] [CrossRef]
- Zhao, T.; Cai, X.; Yang, D. Effect of streamflow forecast uncertainty on real-time reservoir operation. Adv. Water Resour. 2011, 34, 495–504. [Google Scholar] [CrossRef]
- Shim, K.; Fontane, D.G.; Labadie, J.W. Spatial decision support system for integrated river basin flood control. J. Water Res. Plan. Man. 2002, 128, 190–201. [Google Scholar] [CrossRef]
- Wan, W.; Zhao, J.; Wang, J. Revisiting water supply rule curves with hedging theory for climate change adaptation. Sustainability 2019, 11, 1827. [Google Scholar] [CrossRef]
- Chen, L.; McPhee, J.; Yeh, W.W.G. A diversified multiobjective GA for optimizing reservoir rule curves. Adv. Water Resour. 2007, 30, 1082–1093. [Google Scholar] [CrossRef]
- Afshar, A.; Shafii, M.; Haddad, O.B. Optimizing multi-reservoir operation rules: An improved HBMO approach. J. Hydroinform. 2011, 13, 121–139. [Google Scholar] [CrossRef]
- Liu, P.; Guo, S.; Xu, X.; Chen, J. Derivation of Aggregation-Based Joint Operating Rule Curves for Cascade Hydropower Reservoirs. Water Resour. Manag. 2011, 25, 3177–3200. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, P.; Wang, H.; Lei, X.; Zhou, Y. A Bayesian model averaging method for the derivation of reservoir operating rules. J. Hydrol. 2015, 528, 276–285. [Google Scholar] [CrossRef]
- Liu, P.; Li, L.; Chen, G.; Rheinheimer, D.E. Parameter uncertainty analysis of reservoir operating rules based on implicit stochastic optimization. J. Hydrol. 2014, 514, 102–113. [Google Scholar] [CrossRef]
- Nourani, V.; Rouzegari, N.; Molajou, A.; Hosseini Baghanam, A. An integrated simulation-optimization framework to optimize the reservoir operation adapted to climate change scenarios. J. Hydrol. 2020, 587, 125018. [Google Scholar] [CrossRef]
- Bao, Z.; Fu, G.; Wang, G.; Jin, J.; He, R.; Yan, X.; Liu, C. Hydrological projection for the Miyun Reservoir basin with the impact of climate change and human activity. Quatern Int. 2012, 282, 96–103. [Google Scholar] [CrossRef]
- Wang, Z. Status and causes of storage change in Miyun Reservoir. Beijing Water 2013, 13–16. (In Chinese) [Google Scholar]
- Xu, W.; Zhao, J.; Zhao, T.; Wang, Z. Adaptive Reservoir Operation Model Incorporating Nonstationary Inflow Prediction. J. Water Res. Plan. Man. 2014, 141, 4014099. [Google Scholar] [CrossRef]
- Ma, H.; Yang, D.; Tan, S.K.; Gao, B.; Hu, Q. Impact of climate variability and human activity on streamflow decrease in the Miyun Reservoir catchment. J. Hydrol. 2010, 389, 317–324. [Google Scholar] [CrossRef]
- Yao, J.; Sun, S.; Zhai, H.; Feger, K.; Zhang, L.; Tang, X.; Li, G.; Wang, Q. Dynamic monitoring of the largest reservoir in North China based on multi-source satellite remote sensing from 2013 to 2022: Water area, water level, water storage and water quality. Ecol. Indic. 2022, 144, 109470. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, H.; Liang, G.; Xu, H. Optimal Operation of Bidirectional Inter-Basin Water Transfer-Supply System. Water Resour. Manag. 2015, 29, 3037–3054. [Google Scholar] [CrossRef]
- Wan, W.; Guo, X.; Lei, X.; Jiang, Y.; Wang, H. A novel optimization method for multi-reservoir operation policy derivation in complex inter-basin water transfer system. Water Resour. Manag. 2018, 32, 31–51. [Google Scholar] [CrossRef]
- Wang, Y.; Xue, X.; Zhang, X. The Drought Assessment and Its Impact Analysis in Chaobai River Basin from 1980 to 2012. Clim. Chang. Res. Lett. 2014, 3, 52–60. [Google Scholar] [CrossRef]
- Zhou, X.; Pan, X.; Zhu, Y.; Hu, Y. Research of the Mean Annual Water Balance during 1980–2013 in Chaobai River Basin. J. Nat. Resour. 2016, 31, 649–657. (In Chinese) [Google Scholar] [CrossRef]
- Hu, Y.; Zhou, L.; Yan, M.; Dong, X.; Wu, Z.; Wei, C. The Valuation and Compensation Policies Suggestions of Main Capitals and Services of Miyun Reservoir. J. Nat. Resour. 2007, 22, 497–506. (In Chinese) [Google Scholar]
- Zhang, M.; Xue, Z.; Pan, L.; Wang, Z. Analysis on dispatching potential of Miyun Reservoir for extreme rainstorm under high water level condition. Beijing Water 2023, 7–13. (In Chinese) [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Hojjati, A.; Monadi, M.; Faridhosseini, A.; Mohammadi, M. Application and comparison of NSGA-II and MOPSO in multi-objective optimization of water resources systems. J. Hydrol. Hydromech. 2018, 66, 323–329. [Google Scholar] [CrossRef]
- Crow-Miller, B.; Webber, M. Of maps and eating bitterness: The politics of scaling in China’s South-North Water Transfer Project. Political Geogr. 2017, 61, 19–30. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).