Simulation and Prediction Algorithm for the Whole Process of Debris Flow Based on Multiple Data Integration
Abstract
:1. Introduction
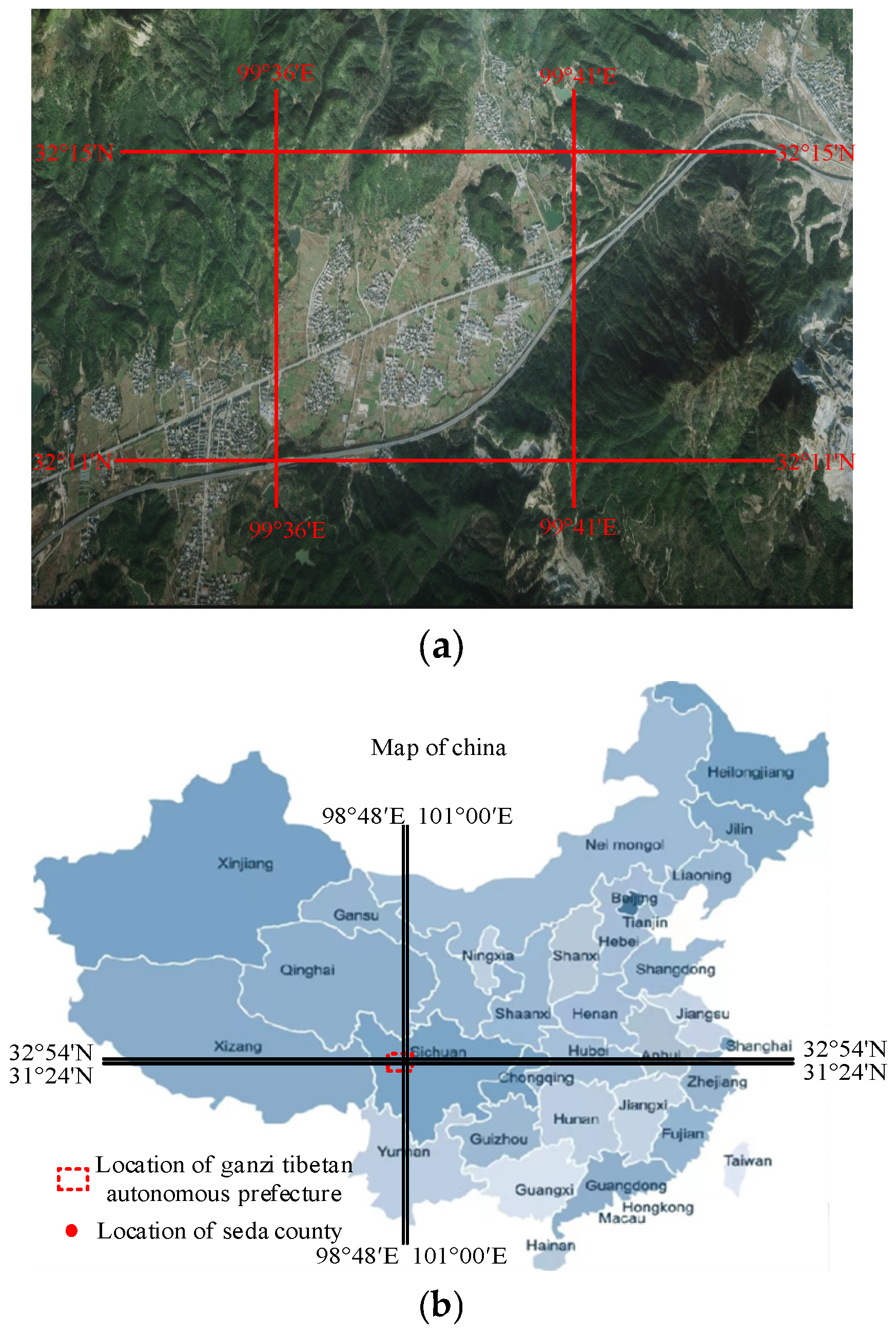
2. Simulation and Prediction of the Whole Process of Debris Flow Based on Multiple Data Integration
2.1. Multi-Source Data Integration Method of Debris-Flow Prediction GIS Based on Middleware
2.1.1. Multi-Source Data Integration Structure Based on Data Middleware Mode
2.1.2. Realization of GIS Multiple Data Integration for Debris-Flow Prediction
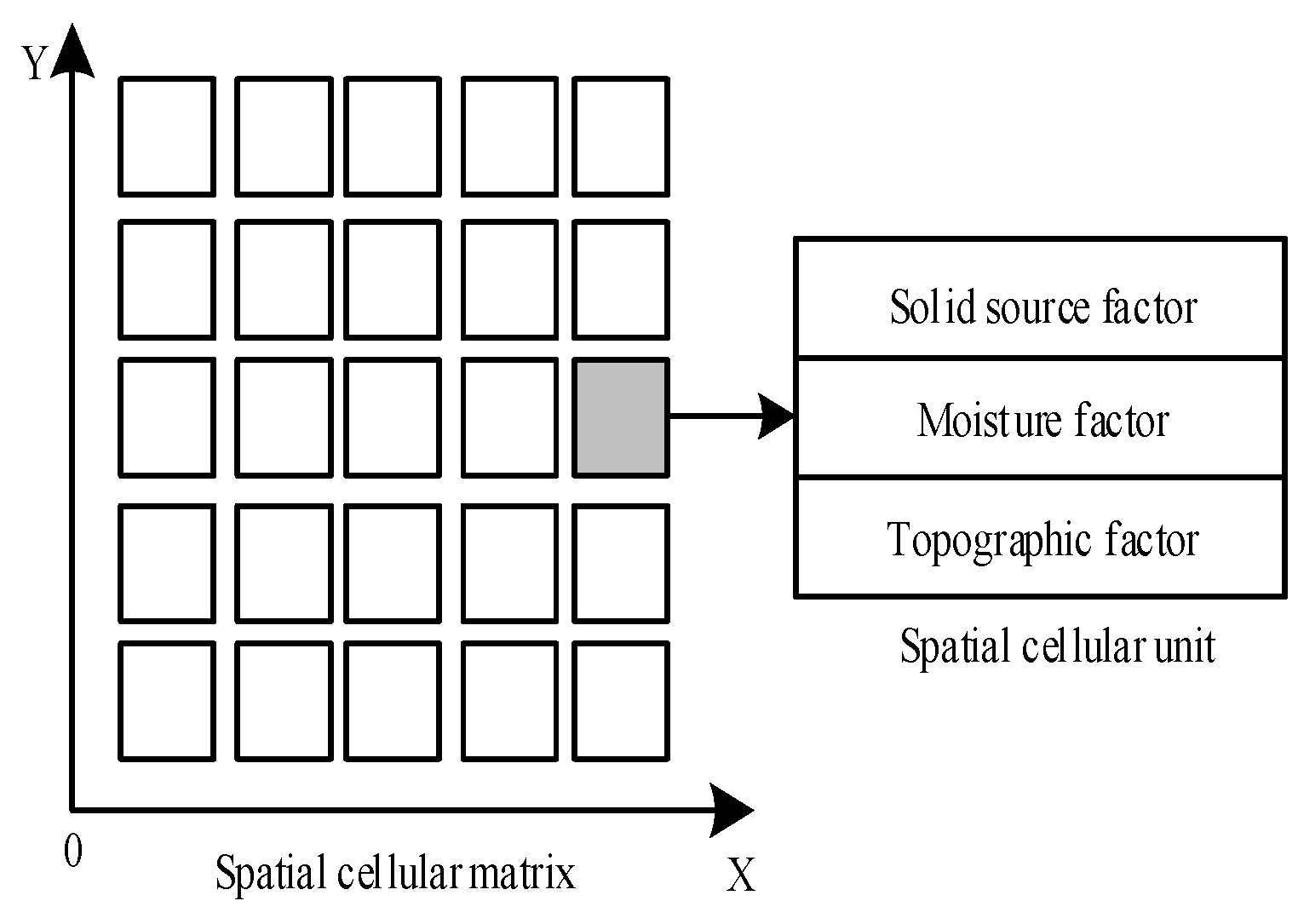
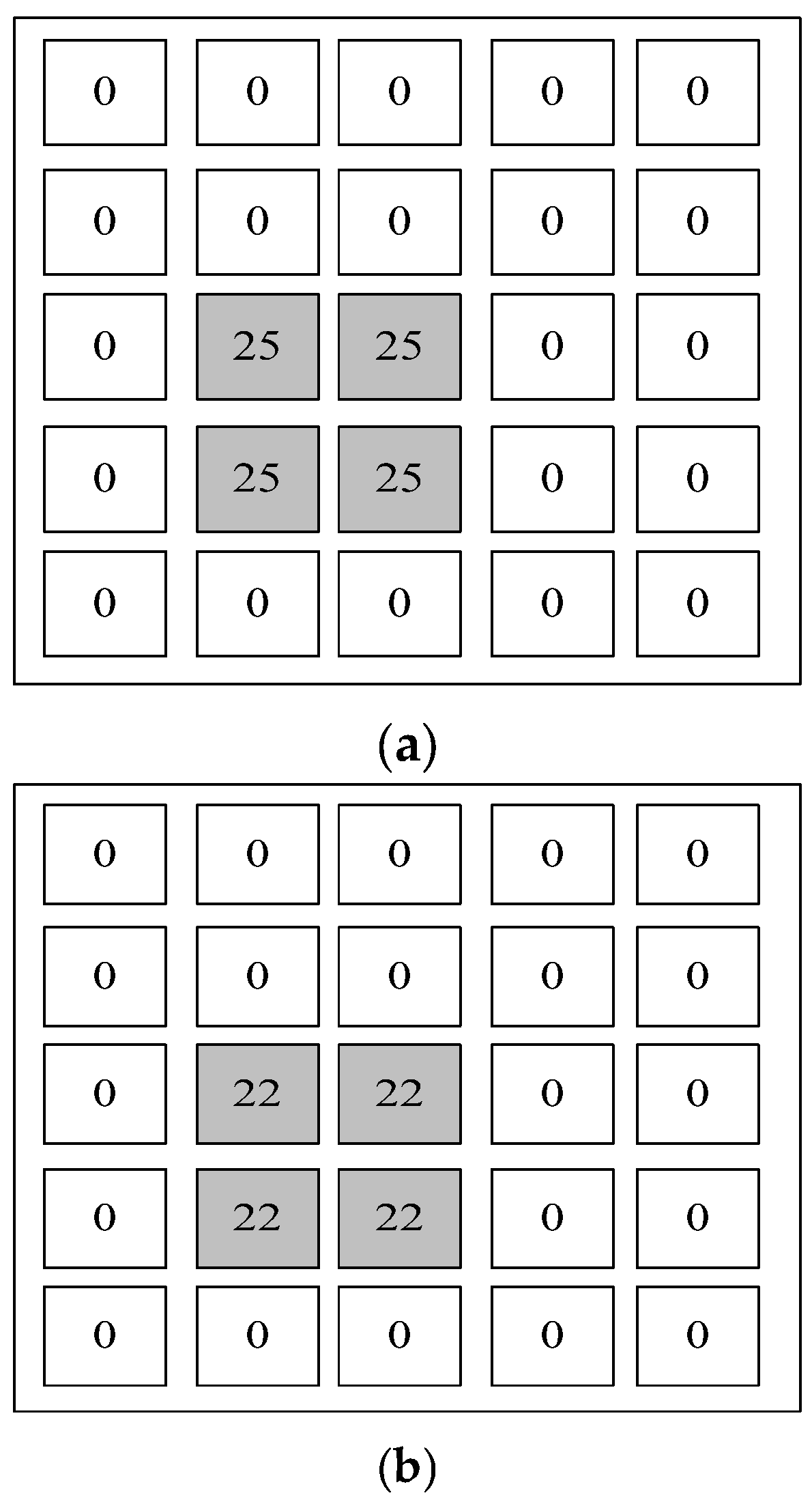
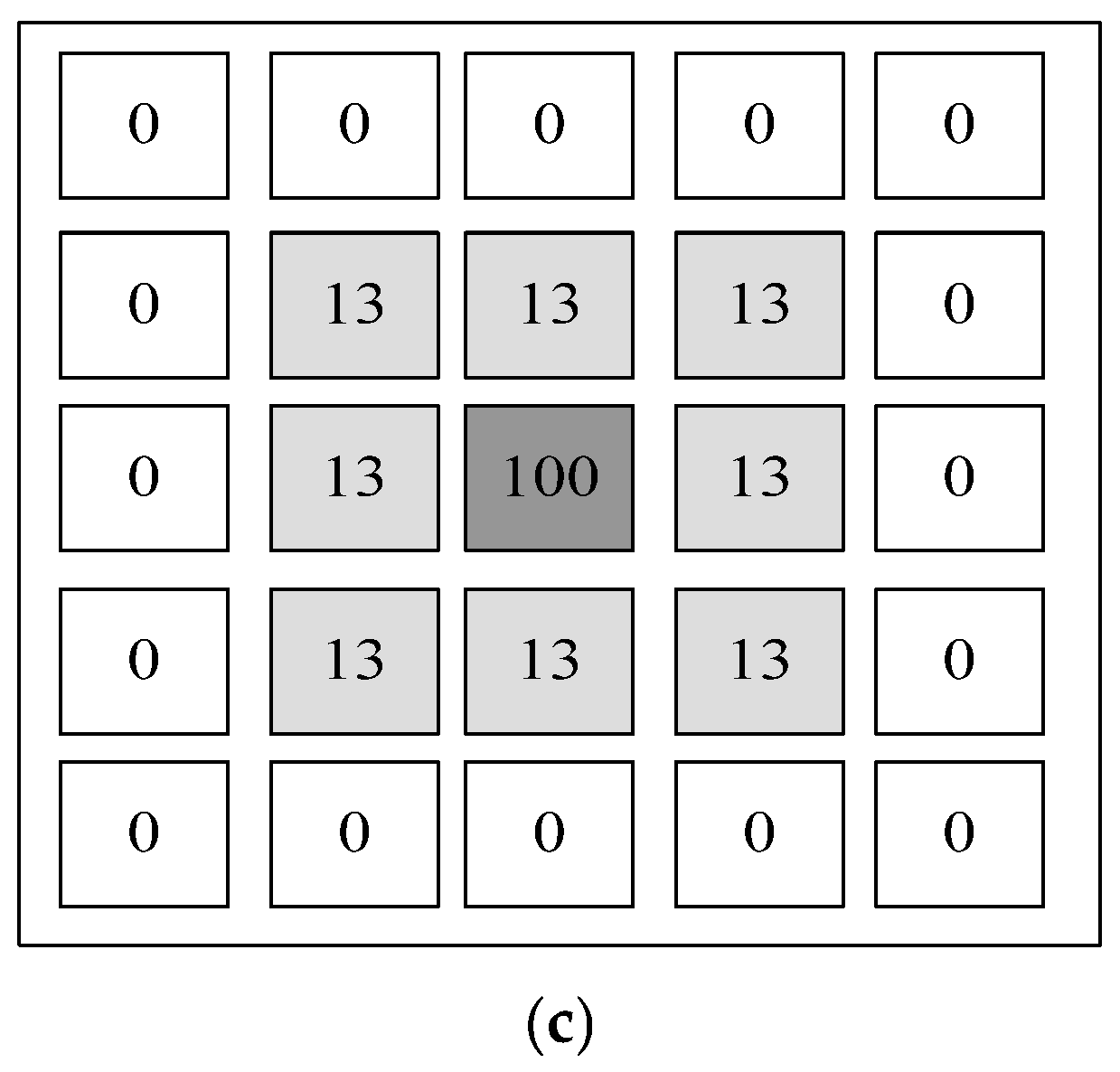
2.2. Construction of Spatial Cell Simulation Model of Debris Flow
2.3. Prediction Algorithm for the Whole Process of Debris Flow
2.3.1. Establishment of Debris-Flow Prediction Index System
2.3.2. Dimension Reduction in Debris-Flow Prediction Index Data Based on Improved Kernel Principal Component Analysis
2.3.3. Prediction Algorithm of Debris Flow Based on Support Vector Machine
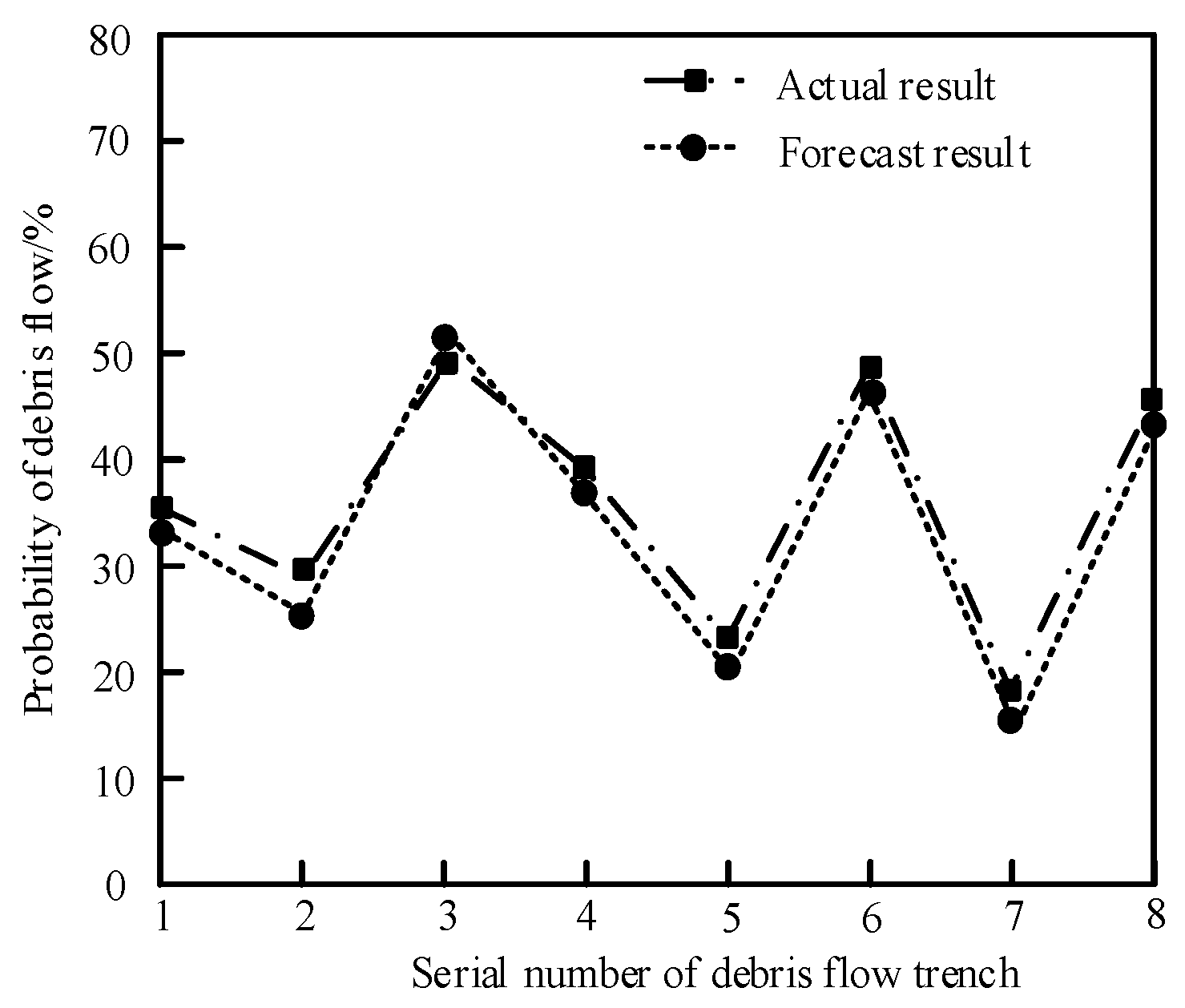
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, D.H.; Cheon, E.; Lim, H.H.; Choi, S.K.; Lee, S.R. An artificial neural network model to predict debris-flow volumes caused by extreme rainfall in the central region of south korea. Eng. Geol. 2020, 281, 105979–105985. [Google Scholar] [CrossRef]
- Feng, Q.; Zhao, Y.; Meng, X.; Su, X.; Yue, D. Application of machine learning to debris flow susceptibility mapping along the china-pakistan karakoram highway. Remote Sens. 2020, 12, 2933–2945. [Google Scholar]
- Wu, S.; Chen, J.; Xu, C.; Zhou, W.; Yao, L.; Yue, W.; Cui, Z. Susceptibility assessments and validations of debris-flow events in meizoseismal areas: Case study in china’s longxi river watershed. Nat. Hazards Rev. 2020, 21, 05019005.1–05019005.13. [Google Scholar] [CrossRef]
- Yang, H.; Haque, M.E.; Song, K. Experimental study on the effects of physical conditions on the interaction between debris flow and baffles. Phys. Fluids 2021, 33, 056601–056612. [Google Scholar] [CrossRef]
- Mcguire, L.A.; Youberg, A.M. What drives spatial variability in rainfall intensity-duration thresholds for post-wildfire debris flows? insights from the 2018 buzzard fire, nm, usa. Landslides 2020, 17, 2385–2399. [Google Scholar] [CrossRef]
- Su, C.C.; Liu, H.Y. Three-Dimensional Modeling and Simulation of Large Scene Variable Terrain Characteristics in Disaster-prone Areas. Comput. Simul. 2021, 38, 210–213+257. [Google Scholar]
- Yang, Z.-Q.; Wei, L.; Liu, Y.-Q.; He, N.; Zhang, J.; Xu, H.-H. Discussion on the Relationship between Debris Flow Provenance Particle Characteristics, Gully Slope, and Debris Flow Types along the Karakoram Highway. Sustainability 2023, 15, 5998. [Google Scholar] [CrossRef]
- Ren, G.L.; Li, F.M.; Wang, Q.T.; Zeng, Z.P. Dynamic response and failure analysis of steel strand under low speed impact. Ordnance Mater. Sci. Eng. 2023, 46, 96–104. [Google Scholar]
- Ahrari, A.; Elsayed, S.; Sarker, R.; Essam, D.; Coello, C. Adaptive multilevel prediction method for dynamic multimodal optimization. IEEE Trans. Evol. Comput. 2021, 25, 463–477. [Google Scholar] [CrossRef]
- Yang, L.; Xu, W.; Zhang, X.; Sang, B. Multi-granulation method for information fusion in multi-source decision information system. Int. J. Approx. Reason. 2020, 122, 47–65. [Google Scholar] [CrossRef]
- Jia, X.; Guo, B. Reliability analysis for complex system with multi-source data integration and multi-level data transmission. Reliab. Eng. Syst. Saf. 2022, 217, 104–118. [Google Scholar] [CrossRef]
- Banihabib, M.E.; Jurik, L.; Kazemi, M.S.; Soltani, J.; Tanhapour, M. A hybrid intelligence model for the prediction of the peak flow of debris floods. Water 2020, 12, 2246–2253. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, M.; Zhang, J.; Ding, P.; He, N.; Yang, Y. Effect of initial water content on soil failure mechanism of loess mudflow disasters. Front. Ecol. Evol. 2023, 11, 1141155. [Google Scholar] [CrossRef]
- Debelak, A.M.; Bareither, C.A.; Mahmoud, H. Finite-element model of impact loading and deformation of a flexible steel ring-net debris-flow barrier. Nat. Hazards Rev. 2020, 21, 04020026–04020032. [Google Scholar] [CrossRef]
- Moreno, E.; Dialami, N.; Cervera, M. Modeling of spillage and debris floods as Newtonian and viscoplastic Bingham flows with free surface with mixed stabilized finite elements. J. Non-Newton. Fluid Mech. 2021, 290, 104512. [Google Scholar] [CrossRef]
- Viktoriia, K.; Tatyana, V.; Anastasiia, V. Comparison of Debris Flow Modeling Results with Empirical Formulas Applied to Russian Mountains Areas. Open J. Geol. 2020, 10, 92–110. [Google Scholar]
- Yan, Y.; Zhang, Y.; Hu, W.; Xiao-jun, G.; Chao, M.; Zi-ang, W.; Qun, Z. A multiobjective evolutionary optimization method based critical rainfall thresholds for debris flows initiation. J. Mt. Sci. 2020, 17, 1860–1873. [Google Scholar] [CrossRef]
- Jia, X.; Cheng, Z.; Guo, B. Reliability analysis for system by transmitting, pooling and integrating multi-source data. Reliab. Eng. Syst. Saf. 2022, 224, 108471.1–108471.16. [Google Scholar] [CrossRef]
- Kattel, P.; Khattri, K.B.; Pudasaini, S.P. A multiphase virtual mass model for debris flow. Int. J. Non-Linear Mech. 2021, 129, 103638–103645. [Google Scholar] [CrossRef]
- Tsunetaka, H.; Hotta, N.; Imaizumi, F.; Hayakawa, Y.S.; Masui, T. Variation in rainfall patterns triggering debris flow in the initiation zone of the ichino-sawa torrent, ohya landslide, japan. Geomorphology 2021, 375, 107529–107536. [Google Scholar] [CrossRef]
- Wang, Y.C.; Kentaro, I.; Iyan, E.M.; Keisuke, A.; Narumi, T.; Kenichi, S.; Hitoshi, K.; Hiroto, A.; Yoshiaki, S. Data assimilation using high-frequency radar for tsunami early warning: A case study of the 2022 tonga volcanic tsunami. JGR Solid Earth 2023, 128, e2022JB025153. [Google Scholar] [CrossRef]


| Target Layer | Criterion Layer | Index Layer |
|---|---|---|
| Debris-flow prediction | Base factor | Relative height difference |
| Slope grade | ||
| Soil texture | ||
| Vegetation coverage | ||
| Erosion intensity | ||
| Stratigraphic lithology | ||
| Response factor | Mass of loose material in slope | |
| Disaster sensitivity | ||
| Inducible factor | Rainfall in the first 7 days | |
| 24 h rainfall | ||
| Maximum hourly rainfall |
| Index Name | Normalized Results |
|---|---|
| Relative height difference | 0.852 |
| Soil texture | 0.751 |
| Erosion intensity | 0.254 |
| Stratigraphic lithology | 0.162 |
| Disaster sensitivity | 0.284 |
| 24 h rainfall | 0.394 |
| Maximum hourly rainfall | 0.584 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, M.; Qi, X. Simulation and Prediction Algorithm for the Whole Process of Debris Flow Based on Multiple Data Integration. Water 2023, 15, 2778. https://doi.org/10.3390/w15152778
Fang M, Qi X. Simulation and Prediction Algorithm for the Whole Process of Debris Flow Based on Multiple Data Integration. Water. 2023; 15(15):2778. https://doi.org/10.3390/w15152778
Chicago/Turabian StyleFang, Min, and Xing Qi. 2023. "Simulation and Prediction Algorithm for the Whole Process of Debris Flow Based on Multiple Data Integration" Water 15, no. 15: 2778. https://doi.org/10.3390/w15152778
APA StyleFang, M., & Qi, X. (2023). Simulation and Prediction Algorithm for the Whole Process of Debris Flow Based on Multiple Data Integration. Water, 15(15), 2778. https://doi.org/10.3390/w15152778





