Effects of Biomass and Soil Water Content Distribution on Cosmic Ray Neutron Probe Measurement
Abstract
:1. Introduction
2. Materials and Methods
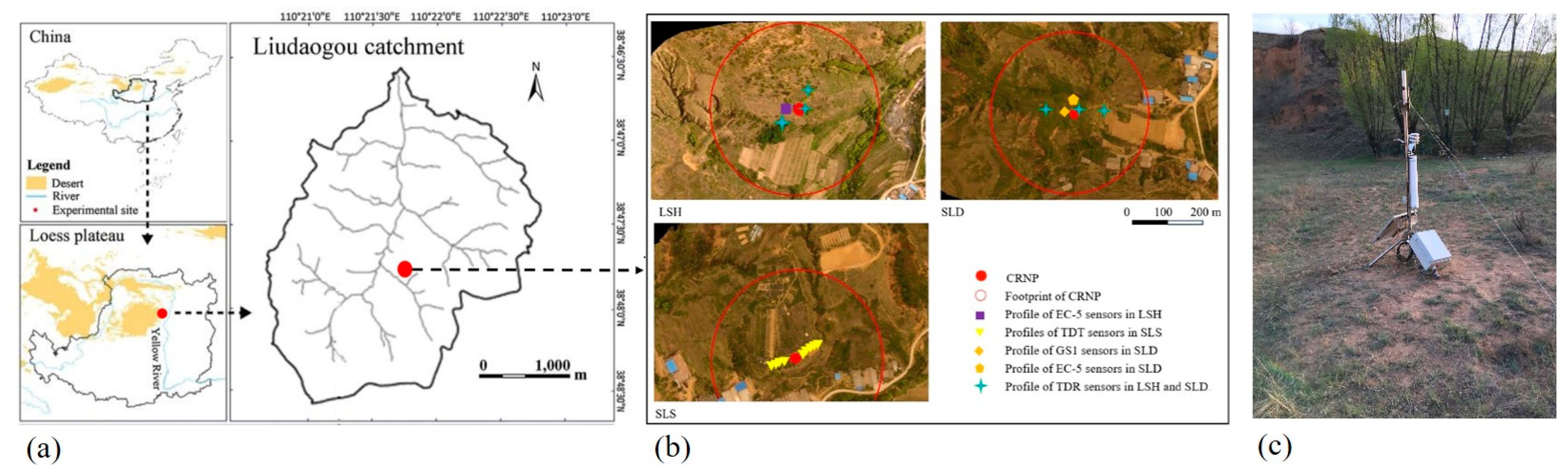
2.1. Site Description
2.2. SWC Sensors
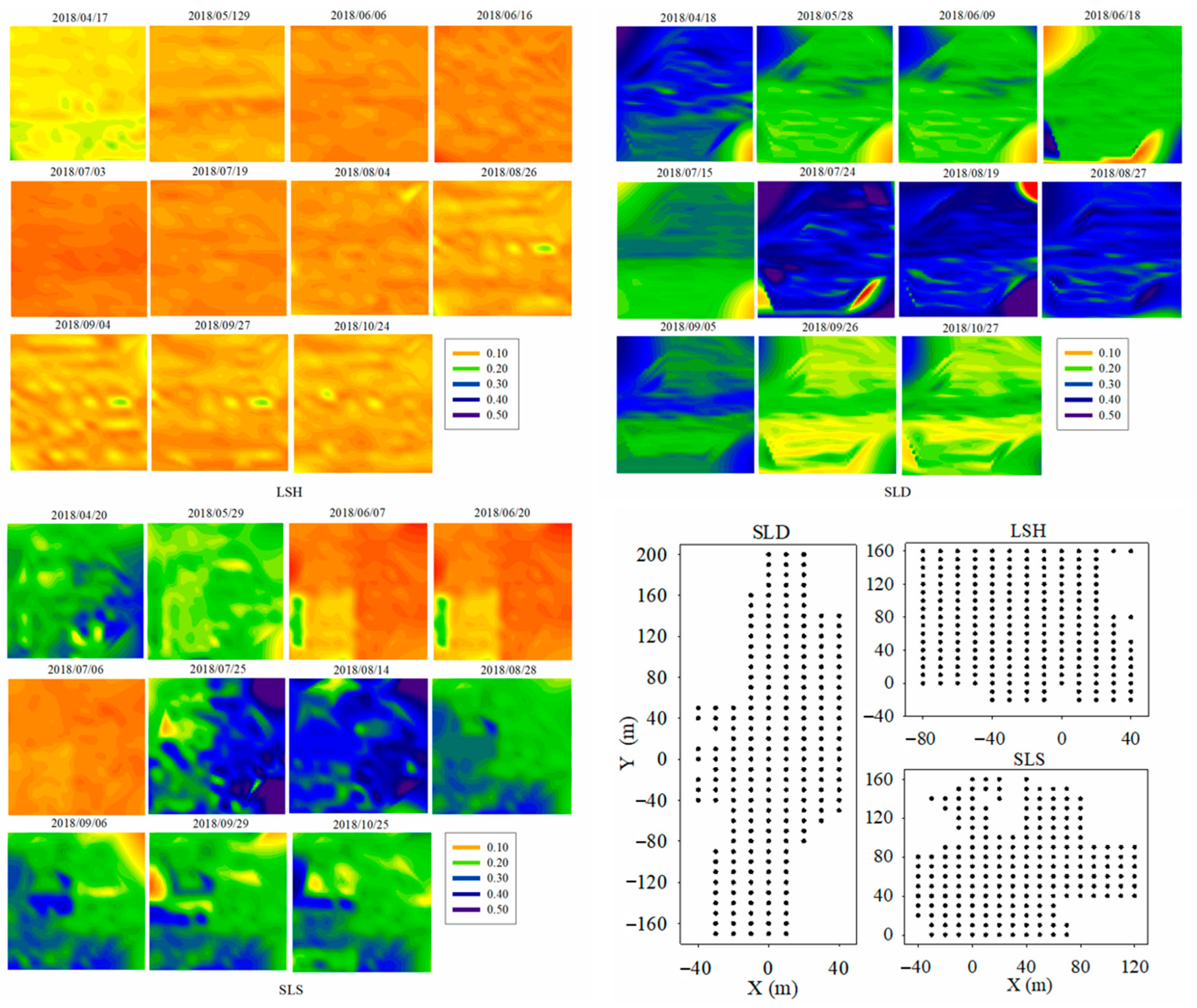
2.3. The Spatial Distribution of SWC
2.4. The CRNPs
2.4.1. Horizontal and Vertical Footprints of the CRNPs
2.4.2. Calibration of Neutron Intensity and the CRNPs
2.4.3. Calibration Soil Sampling
2.4.4. Vegetation Correction
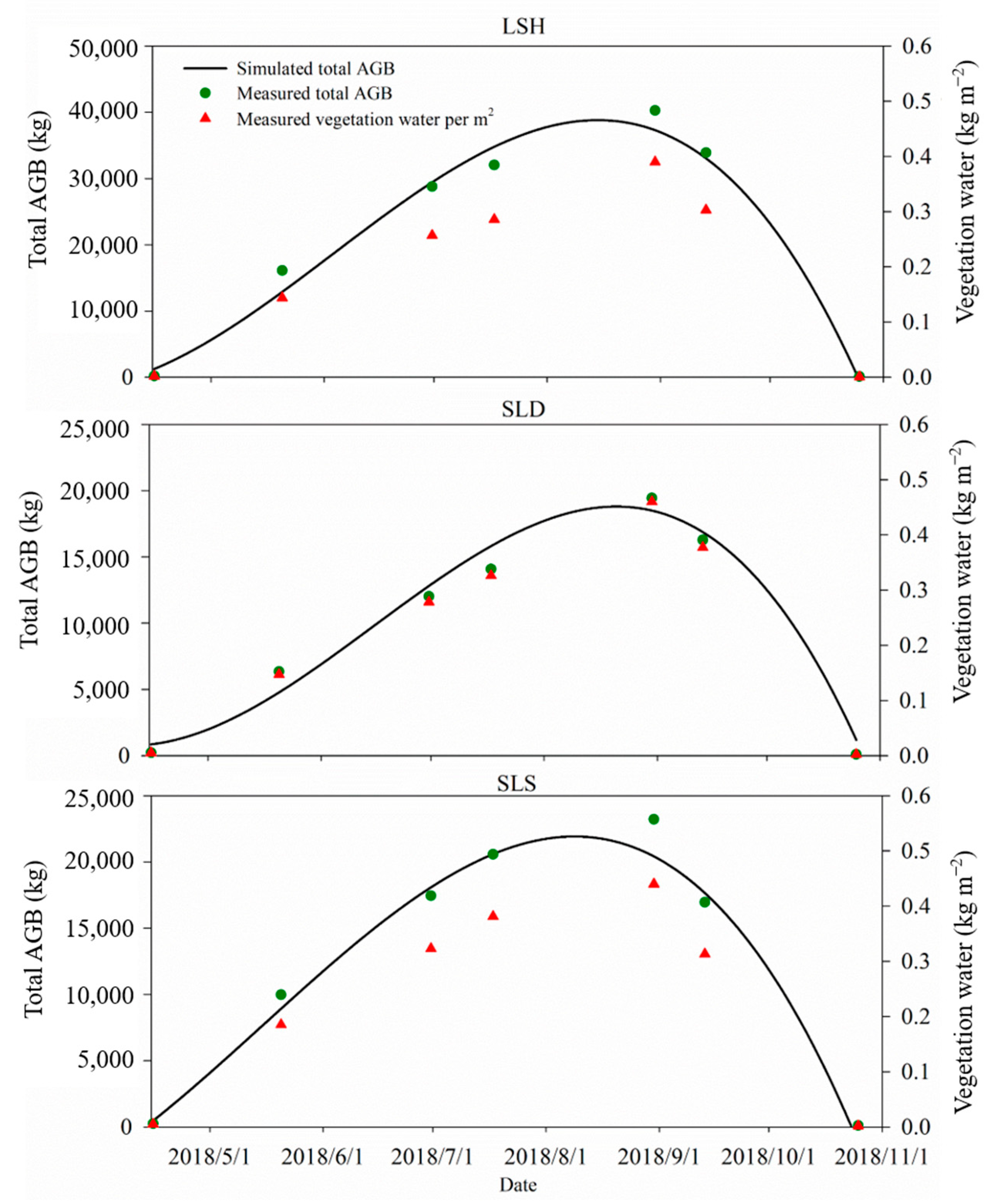
2.5. Biomass Measurement
3. Results
3.1. The Calculation of the N0 and Footprint of a CRNP
3.2. The Spatial Distribution of SWC
3.3. The Effects of Vegetation on CRNPs
3.4. The Effects of the Spatial Distribution of Vegetation on CRNPs
4. Discussion
4.1. Calculating and Selecting N0
4.2. The Effects of the SWC Spatial Distribution on the CRNP Output
4.3. Effects of Vegetation on CRNPs
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kodama, M.; Kudo, S. Response of atmospheric neutron fluxes to soil moisture content. Sci. Pap. Inst. Phys. Chem. Res. 1985, 79, 99–103. [Google Scholar]
- Zreda, M.; Desilets, D.; Ferré, T.P.A.; Scott, R.L. Scott. Measuring soil moisture content non-invasively at intermediate spatial scale using cosmic-ray neutrons. Geophys. Res. Lett. 2008, 35, L21402. [Google Scholar] [CrossRef] [Green Version]
- Andreasen, M.; Jensen, K.H.; Desilets, D.; Franz, T.E.; Zreda, M.; Bogena, H.R.; Looms, M. Status and perspectives on the cosmic-ray neutron method for soil moisture estimation and other environmental science applications. Vadose Zone J. 2017, 16, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Fan, J.; Wang, S.; Yong, C.; Ge, J.; You, W. Application and accuracy of cosmic-ray neutron probes in three soil textures on the Loess Plateau, China. J. Hydrol. 2018, 569, 449–461. [Google Scholar] [CrossRef]
- Rosolem, R.; Hoar, T.; Arellano, A.; Anderson, J.L.; Shuttleworth, W.J.; Zeng, X.; Franz, T.E. Translating aboveground cosmic-ray neutron intensity to high frequency soil moisture profiles at sub-kilometer scale. Hydrol. Earth Syst. Sci. 2014, 18, 4363–4379. [Google Scholar] [CrossRef] [Green Version]
- Zreda, M.; Shuttleworth, W.J.; Zeng, C.; Desilets, D.; Franz, T.; Rosolem, R. COSMOS: The COsmic-ray Soil Moisture Observing System. Hydrol. Earth Syst. Sci. 2012, 16, 4079–4099. [Google Scholar] [CrossRef] [Green Version]
- Franz, T.E.; Zreda, M.; Rosolem, R.; Ferre, T. A universal calibration function for determination of soil moisture with cosmic-ray neutrons. Hydrol. Earth Syst. Sci. 2013, 17, 453–460. [Google Scholar] [CrossRef] [Green Version]
- Shuttleworth, J.; Rosolem, R.; Zreda, M.; Franz, T. The COsmic-ray Soil Moisture Interaction Code (COSMIC) for use in data assimilation. Hydrol. Earth Syst. Sci. 2013, 10, 1097–1125. [Google Scholar] [CrossRef] [Green Version]
- Desilets, D.; Zreda, M.; Ferre, T.P.A. Nature’s neutron probe: Land surface hydrology at an elusive scale with cosmic rays. Water Resour. Res. 2010, 46, W11505. [Google Scholar] [CrossRef] [Green Version]
- Baatz, R.; Bogena, H.R.; Franssen, H.H.; Huisman, J.A.; Qu, W.; Montzka, C.; Vereecken, H. Calibration of a catchment scale cosmic-ray probe network: A comparison of three parameterization methods. J. Hydrol. 2014, 516, 231–244. [Google Scholar] [CrossRef]
- Desilets, D.; Zreda, M. On scaling cosmogenic nuclide production rates for altitude and latitude using cosmic-ray measurements. Earth Planet. Sci. Lett. 2001, 193, 213–225. [Google Scholar] [CrossRef]
- Rosolem, R.; Shuttleworth, W.J.; Zreda, M.; Franz, T.E.; Zeng, X.; Kurc, S.A. The effect of atmospheric water vapor on neutron count in the cosmic-ray soil moisture observing system. J. Hydrometeorol. 2013, 14, 1659–1671. [Google Scholar] [CrossRef] [Green Version]
- Baatz, R.; Bogena, H.R.; Franssen, H.J.H.; Huisman, J.A.; Montzka, C.; Vereecken, H. An empirical vegetation correction for soil water content quantification using cosmic ray probes. Water Resour. Res. 2015, 51, 2030–2046. [Google Scholar] [CrossRef] [Green Version]
- Baroni, G.; Oswald, S.E. A scaling approach for the assessment of biomass changes and rainfall interception using cosmic-ray neutron sensing. J. Hydrol. 2015, 525, 264–276. [Google Scholar] [CrossRef]
- Desilets, D.; Zreda, M. Footprint diameter for a cosmic-ray soil moisture probe: Theory and monte carlo simulations. Water Resour. Res. 2013, 49, 3566–3575. [Google Scholar] [CrossRef]
- Franz, T.E.; Zreda, M.; Ferre, T.P.A.; Rosolem, R.; Zweck, C.; Stillman, S.; Zeng, X.; Shuttleworth, W.J. Measurement depth of the cosmic ray soil moisture probe affected by hydrogen from various sources. Water Resour. Res. 2012, 48, W08515. [Google Scholar] [CrossRef] [Green Version]
- Köhli, M.; Schrön, M.; Zreda, M.; Schmidt, U.; Dietrich, P.; Zacharias, S. Footprint characteristics revised for field-scale soil moisture monitoring with cosmic-ray neutrons. Water Resour. Res. 2015, 51, 5772–5790. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Cao, R.; Shao, M.; Liang, Y. Footprint radius of a cosmic-ray neutron probe for measuring soil-water content and its spatiotemporal variability in an alpine meadow ecosystem. J. Hydrol. 2018, 558, 1–8. [Google Scholar] [CrossRef]
- Schattan, P.; Baroni, G.; Oswald, S.E.; Schöber, J.; Fey, C.; Kormann, C.; Huttenlau, M.; Achleitner, S. Continuous monitoring of snowpack dynamics in alpine terrain by aboveground neutron sensing. Water Resour. Res. 2017, 53, 3615–3634. [Google Scholar] [CrossRef]
- Peterson, A.M.; Helgason, W.D.; Ireson, A.M. Estimating field scale root zone soil moisture using the cosmic-ray neutron probe. Hydrol. Earth Syst. Sci. 2016, 20, 1373–1385. [Google Scholar] [CrossRef] [Green Version]
- Bogena, H.R.; Huisman, J.A.; Baatz, R.; Franssen, H.J.H.; Vereecken, H. Accuracy of the cosmic-ray soil water content probe in humid forest ecosystems: The worst case scenario. Water Resour. Res. 2013, 49, 5778–5791. [Google Scholar] [CrossRef] [Green Version]
- Villarreyes, R.C.A.; Baroni, G.; Oswald, S.E. Integral quantification of seasonal soil moisture changes in farmland by cosmic-ray neutrons. Hydrol. Earth Syst. Sci. 2011, 15, 3843–3859. [Google Scholar] [CrossRef] [Green Version]
- Evans, J.G.; Ward, H.C.; Blake, J.R.; Hewitt, E.J.; Morrison, R.; Fry, M.; Ball, L.A.; Doughty, L.C.; Libre, J.W.; Hitt, O.E. Soil water content in southern england derived from a cosmic-ray soil moisture observing system—COSMOS-UK. Hydrol. Process. 2016, 30, 4987–4999. [Google Scholar] [CrossRef] [Green Version]
- Hawdon, A.; Mcjannet, D.; Wallace, J. Calibration and correction procedures for cosmic-ray neutron soil moisture probes located across Australia. Water Resour. Res. 2014, 50, 5029–5043. [Google Scholar] [CrossRef]
- Franz, T.E.; Wahbi, A.; Vreugdenhil, M.; Weltin, G.; Heng, L.; Oismueller, M.; Strauss, P.; Dercon, G.; Desilts, D. Using cosmic-ray neutron probes to monitor landscape scale soil water content in mixed land use agricultural systems. Appl. Environ. Soil Sci. 2016, 2016, 4323742. [Google Scholar] [CrossRef] [Green Version]
- Coopersmith, E.J.; Cosh, M.H.; Daughtry, C. Field-scale moisture estimates using cosmos sensors: A validation study with temporary networks and leaf-area-indices. J. Hydrol. 2014, 519, 637–643. [Google Scholar] [CrossRef]
- Tian, Z.; Li, Z.; Liu, G.; Li, B.; Ren, T. Soil water content determination with cosmic-ray neutron sensor: Correcting aboveground hydrogen effects with thermal/fast neutron ratio. J. Hydrol. 2016, 540, 923–933. [Google Scholar] [CrossRef]
- Jakobi, J.; Huisman, J.A.; Vereecken, H.; Diekkrüger, B.; Bogena, H.R. Cosmic ray neutron sensing for simultaneous soil water content and biomass quantification in drought conditions. Water Resour. Res. 2018, 54, 7383–7402. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.Z.; Huang, M.B.; Warrington, D.N. Black locust transpiration responses to soil water availability as affected by meteorological factors and soil texture. Pedosphere 2015, 25, 57–71. [Google Scholar] [CrossRef]
- Shao, M.A.; Yang, W.Z.; Li, Y.S. Study on soil water availability in Loess region. J. Hydraul. Eng-Asce. 1987, 8, 40–46. (In Chinese) [Google Scholar]
- Zhao, C.L.; Jia, X.X.; Zhu, Y.J.; Shao, M.A. Long-term temporal variations of soil water content under different vegetation types in the Loess Plateau, China. Catena 2017, 158, 55–62. [Google Scholar] [CrossRef]
- Tang, K.; Hou, Q.; Wang, B.; Zhang, P. The environment background and administration way of Wind-Water Erosion Crisscross Region and Shenmu experimental area on the Loess Plateau. Mem. NISWC Acad. Sin. MWR 1993, 18, 2–15. (In Chinese) [Google Scholar]
- Zhu, Y.; Shao, M. Spatial distribution of surface rock fragment on hill-slopes in a small catchment in wind-water erosion crisscross region of the Loess Plateau. Sci. China Ser. D Earth Sci. 2008, 51, 862–870. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, L.; Dou, S. Agrology; Chemical Industry Publishing House: Beijing, China, 2005; pp. 197–199. [Google Scholar]
- Zhao, P.; Shao, M.; Zhuang, J. Fractal features of particle size redistributions of deposited soils on the dam farmlands. Soil Sci. 2009, 174, 403–407. [Google Scholar] [CrossRef]
- Lin, C.G. Agrology; Agricultural Publishing House: Beijing, China, 1983; pp. 219–220. [Google Scholar]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef] [Green Version]
- Avery, W.A.; Finkenbiner, C.; Franz, T.E.; Wang, T.; Nguy-Robertson, A.L.; Suyker, A.; Arkebauer, T.; Munoz-Arriola, F. Incorporation of globally available datasets into the roving cosmic-ray neutron probe method for estimating field-scale soil water content. Hydrol. Earth Syst. Sci. 2016, 20, 3859–3872. [Google Scholar] [CrossRef] [Green Version]
- Heidbüchel, I.; Güntner, A.; Blume, T. Use of cosmic-ray neutron sensors for soil moisture monitoring in forests. Hydrol. Earth Syst. Sci. 2016, 20, 1269–1288. [Google Scholar] [CrossRef] [Green Version]
- Han, X.; Rui, J.; Xin, L.; Wang, S. Soil moisture estimation using cosmic-ray soil moisture sensing at heterogeneous farmland. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1659–1663. [Google Scholar]
- Zhu, X.; Shao, M.; Jia, X.; Huang, L.; Zhu, J.; Zhang, Y. Application of temporal stability analysis in depth-scaling estimated soil water content by cosmic-ray neutron probe on the northern Tibetan Plateau. J. Hydrol. 2017, 546, 299–308. [Google Scholar] [CrossRef]
- Zheng, H.; Cheng, T.; Zhou, M.; Li, D.; Yao, X.; Tian, Y.; Cao, W.; Zhu, Y. Improved estimation of rice aboveground biomass combining textural and spectral analysis of UAV imagery. Precis. Agric. 2018, 20, 611–629. [Google Scholar] [CrossRef]
- Birth, G.S.; Mcvey, G.R. Measuring the color of growing turf with a reflectance spectrophotometer. Agron. J. 1968, 60, 640–643. [Google Scholar] [CrossRef]
- Hornbuckle, B.; Irvin, S.; Franz, T.; Rosolem, R.; Zweck, C. The potential of the COSMOS network to be a source of new soil moisture information for SMOS and SMAP. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 1243–1246. [Google Scholar]
- Jiang, N.; Shao, M.A.; Wei, H.; Wang, Y.Q. Characteristics of water circulation and balance of typical vegetations at plot scale on the Loess Plateau of China. Environ. Earth Sci. 2013, 70, 157–166. [Google Scholar] [CrossRef]
- Yu, B.; Liu, G.; Liu, Q.; Wang, X.; Feng, J.; Huang, C. Soil moisture variations at different topographic domains and land use types in the semi-arid Loess Plateau, China. Catena 2018, 165, 125–132. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, M.; Zhang, C.; Han, X.; Mao, T.; Jia, X. Choosing an optimal land-use pattern for restoring eco-environments in a semiarid region of the Chinese Loess Plateau. Ecol. Eng. 2015, 74, 213–222. [Google Scholar] [CrossRef]
- Camille, L.; Philippe, B.; Guillaume, J.; Bruno, R.; Sylvain, L.; Baret, F. Assessment of unmanned aerial vehicles imagery for quantitative monitoring of wheat crop in small plots. Sensors 2008, 8, 3557–3585. [Google Scholar]
- Boon, M.A.; Tesfamichael, S. Wetland vegetation integrity assessment with low altitude multispectral uav imagery. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 55–62. [Google Scholar] [CrossRef] [Green Version]
- Yue, J.; Yang, G.; Tian, Q.; Feng, H.; Xu, K.; Zhou, C. Estimate of winter-wheat above-ground biomass based on uav ultrahigh- ground-resolution image textures and vegetation indices. ISPRS J. Photogramm. 2019, 150, 226–244. [Google Scholar] [CrossRef]
- Villoslada, M.; Bergamo, T.F.; Ward, R.D.; Joyce, C.B.; Sepp, K. A novel UAV-based approach for biomass prediction and grassland structure assessment in coastal meadows. Ecol. Indic. 2021, 122, 107227. [Google Scholar] [CrossRef]
- Zhang, H.; Tang, Z.; Yang, B.; Meng, B.; Qin, Y.; Sun, Y.; Lv, Y.Y.; Zhang, J.G.; Yi, S.H. A non-destructive method for rapid acquisition of grassland aboveground biomass for satellite ground verification using UAV RGB images. Glob. Ecol. Conserv. 2022, 33, e01999. [Google Scholar] [CrossRef]
- Franz, T.E.; Zreda, M.; Rosolem, R.; Hornbuckle, B.K.; Shuttleworth, W.J. Ecosystem-scale measurements of biomass water using cosmic ray neutrons. Geophys. Res. Lett. 2013, 40, 3929–3933. [Google Scholar] [CrossRef]
- Kodama, M.; Nakai, K.; Kawasaki, S.; Wada, M. An application of cosmic-ray neutron measurements to the determination of the snow-water equivalent. J. Hydrol. 1979, 41, 85–92. [Google Scholar] [CrossRef]
- Liu, C.; Jia, X.; Ren, L.; Zhu, X.; Shao, M. Evaluation of the soil water content of two managed ecosystems using cosmic-ray neutron sensing on China’s Loess Plateau. Eur. J. Soil Sci. 2023, 74, e13339. [Google Scholar] [CrossRef]
- Brogi, C.; Pisinaras, V.; Koehli, M.; Dombrowski, O.; Franssen, H.; Babakos, K.; Chatzi, A. Monitoring Irrigation in Small Orchards with Cosmic-Ray Neutron Sensors. Sensors 2023, 23, 2378. [Google Scholar] [CrossRef]
- Chen, X.; Song, W.; Shi, Y.; Liu, W.; Lu, Y.; Pang, Z.; Chen, X. Application of Cosmic-Ray Neutron Sensor Method to Calculate Field Water Use Efficiency. Water 2022, 14, 1518. [Google Scholar] [CrossRef]
- Finkenbiner, C.E.; Franz, T.E.; Gibson, J.; Heeren, D.M.; Luck, J. Integration of hydrogeophysical datasets and empirical orthogonal functions for improved irrigation water management. Precis. Agric. 2019, 20, 78–100. [Google Scholar] [CrossRef] [Green Version]
- Franz, T.E.; Wahbi, A.; Zhang, J.; Vreugdenhil, M.; Heng, L.; Dercon, G.; Strauss, P.; Brocca, L.; Wagner, W. Practical data products from cosmic-ray neutron sensing for hydrological applications. Front. Water 2020, 2, 9. [Google Scholar] [CrossRef] [Green Version]
- Jeong, J.; Cho, S.; Lee, S.; Kim, K.; Lee, Y.; Lee, C.; Lee, S.; Choi, M. A Study on Domestic Applicability for the Korean Cosmic-Ray Soil Moisture Observing System. Korean J. Remote Sens. 2023, 39, 233–246. [Google Scholar]
- Dimitrova-Petrova, K.; Geris, J.; Wilkinson, M.; Rosolem, R.; Verrot, L.; Lilly, A.; Soulsby, C. Opportunities and challenges in using catchment-scale storage estimates from cosmic ray neutron sensors for rainfall-runoff modelling. J. Hydrol. 2020, 586, 124878. [Google Scholar] [CrossRef]
- Raghuram, A.; Mounika, N.; Basha, B.; Moghal, A. Soil Water Characteristic Curves of Soils Exhibiting Different Plasticity. Int. J. Geosynth. Ground Eng. 2023, 9, 25. [Google Scholar] [CrossRef]




| LSH | SLD | SLS | |
|---|---|---|---|
| Bulk density (g cm−3) | 1.56 | 1.35 | 1.34 |
| Soil total porosity (%) | 41.13 | 47.27 | 49.43 |
| Sand content (2−0.02 mm, %) | 84.20 | 15.73 | 51.91 |
| Silt content (0.02–0.002 mm, %) | 6.50 | 62.67 | 36.10 |
| Clay content (<0.002 mm, %) | 9.30 | 21.60 | 11.99 |
| Organic matter content (g kg−1) | 0.19 | 1.49 | 0.22 |
| Saturated hydraulic conductivity (cm h−1) | 35.45 | 9.86 | 22.21 |
| Field capacity (cm3 cm−3) | 0.11 | 0.33 | 0.28 |
| Soil type | Loamy sand | Silty loam | Sandy loam |
| Terrain | Hilly | Check dam | Sloped |
| Plot | Sensor Type | Plant Species | Depth of Sensors (m) | Distance between Profile and CRNP (m) | Number of Profiles |
|---|---|---|---|---|---|
| LSH | TDR310S | Caragana korshinskii | 0.10, 0.20, 0.50, 1, 2, and 4 | 0.5 | 1 |
| TDR310S | Artemisia | 0.10, 0.20, 0.50, 1, 2, and 4 | 30 | 1 | |
| TDR310S | Salix matsudana | 0.10, 0.20, 0.50, 1, 2, and 4 | 30 | 1 | |
| SLD | TDR310S | Artemisia | 0.10, 0.20, 0.50, 1, 2, and 4 | 0.5 | 1 |
| TDR310S | Caragana korshinskii | 0.10, 0.20, 0.50, 1, 2, and 4 | 72 | 1 | |
| TDR310S | Zea mays Linn.Sp. | 0.10, 0.20, 0.50, 1, and 2 | 70 | 1 | |
| SLS | TDT | Medicago sativa | 0.05, 0.15 | 7.5, 12.5, and 17.5 | 3 |
| TDT | Artemisia | 0.05, 0.15 | 2.5, 2.5, and 7.5 | 3 | |
| TDT | Glycine max | 0.05, 0.15 | 12.5, 17.5, and 22.5 | 3 |
| r (m) | CFoC | Segment | wh |
|---|---|---|---|
| 50 | 0.298 | 0–50 | 0.431 |
| 100 | 0.471 | 50–100 | 0.250 |
| 150 | 0.594 | 100–150 | 0.178 |
| 200 | 0.692 | 150–200 | 0.142 |
| Date | N0 | RMSE (cm3 cm−3) | |||||
|---|---|---|---|---|---|---|---|
| LSH | SLD | SLS | LSH | SLD | SLS | Total | |
| 27 June 2016 | 5109 | 6176 | 4930 | 0.099 | 0.151 | 0.102 | 0.120 |
| 23 July 2016 | 4677 | 6295 | 4316 | 0.051 | 0.030 | 0.100 | 0.068 |
| 5 October 2016 | 3763 | 5254 | 4246 | 0.119 | 0.171 | 0.080 | 0.121 |
| 6 May 2017 | 4547 | 5179 | 5323 | 0.088 | 0.09 | 0.106 | 0.099 |
| Plot | Radial Segment (m) | 0–50 | 50–100 | 100–150 | 150–200 | Total |
|---|---|---|---|---|---|---|
| LSH | Area (m2) | 7850 | 23,550 | 39,250 | 41,213 | 111,863 |
| Above-ground biomass (kg m–2) | 0.30 | 0.38 | 0.40 | 0.33 | 0.36 | |
| Vegetation water (kg m–2) | 0.32 | 0.40 | 0.43 | 0.36 | 0.39 | |
| SLD | Area (m2) | 7850 | 11,775 | 9812 | 13,737 | 43,175 |
| Above-ground biomass (kg m–2) | 0.54 | 0.44 | 0.58 | 0.32 | 0.45 | |
| Vegetation water (kg m–2) | 0.59 | 0.47 | 0.55 | 0.30 | 0.46 | |
| Area (m2) | 7137 | 17,663 | 14,719 | 13,738 | 53,969 | |
| SLS | Above-ground biomass (kg m–2) | 0.40 | 0.39 | 0.53 | 0.39 | 0.43 |
| Vegetation water (kg m–2) | 0.43 | 0.41 | 0.52 | 0.41 | 0.44 |
| Plots | RMSE without Vegetation Calibration (cm3 cm−3) | RMSE of Three Vegetation Calibrations without Horizontal Weighting (cm3 cm–3) | RMSE of Three Vegetation Calibrations with Horizontal Weighting (cm3 cm–3) | ||||
|---|---|---|---|---|---|---|---|
| Veg–N0 | Veg–N/N0 | Veg–WSWC | Veg–N0 | Veg–N/N0 | Veg–WSWC | ||
| LSH | 0.053 | 0.022 | 0.030 | 0.034 | 0.020 | 0.024 | 0.028 |
| SLD | 0.100 | 0.068 | 0.078 | 0.082 | 0.062 | 0.072 | 0.078 |
| SLS | 0.127 | 0.032 | 0.052 | 0.041 | 0.011 | 0.035 | 0.032 |
| Date | LSH | SLD | SLS | |||
|---|---|---|---|---|---|---|
| SD | CV | SD | CV | SD | CV | |
| 17 April | 0.013 | 0.086 | 0.033 | 0.105 | 0.036 | 0.142 |
| 28 May | 0.011 | 0.105 | 0.021 | 0.091 | 0.021 | 0.099 |
| 9 June | 0.008 | 0.089 | 0.010 | 0.127 | 0.038 | 0.407 |
| 20 June | 0.008 | 0.090 | 0.010 | 0.127 | 0.038 | 0.408 |
| 5 July | 0.008 | 0.116 | 0.028 | 0.217 | 0.010 | 0.122 |
| 24 July | 0.018 | 0.116 | 0.050 | 0.131 | 0.064 | 0.202 |
| 4 August | 0.014 | 0.148 | 0.046 | 0.125 | 0.053 | 0.160 |
| 26 August | 0.018 | 0.164 | 0.025 | 0.076 | 0.031 | 0.120 |
| 4 September | 0.021 | 0.189 | 0.150 | 0.571 | 0.096 | 0.420 |
| 27 September | 0.018 | 0.164 | 0.035 | 0.186 | 0.031 | 0.120 |
| 24 October | 0.018 | 0.164 | 0.027 | 0.081 | 0.096 | 0.420 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Shi, L.; Zhao, X.; Fan, J. Effects of Biomass and Soil Water Content Distribution on Cosmic Ray Neutron Probe Measurement. Water 2023, 15, 2766. https://doi.org/10.3390/w15152766
Wang Q, Shi L, Zhao X, Fan J. Effects of Biomass and Soil Water Content Distribution on Cosmic Ray Neutron Probe Measurement. Water. 2023; 15(15):2766. https://doi.org/10.3390/w15152766
Chicago/Turabian StyleWang, Qiuming, Liang Shi, Xu Zhao, and Jun Fan. 2023. "Effects of Biomass and Soil Water Content Distribution on Cosmic Ray Neutron Probe Measurement" Water 15, no. 15: 2766. https://doi.org/10.3390/w15152766
APA StyleWang, Q., Shi, L., Zhao, X., & Fan, J. (2023). Effects of Biomass and Soil Water Content Distribution on Cosmic Ray Neutron Probe Measurement. Water, 15(15), 2766. https://doi.org/10.3390/w15152766









