Urban Flood Runoff Modeling in Japan: Recent Developments and Future Prospects
Abstract
1. Introduction
2. Brief History on Urban Runoff Modeling in Japan
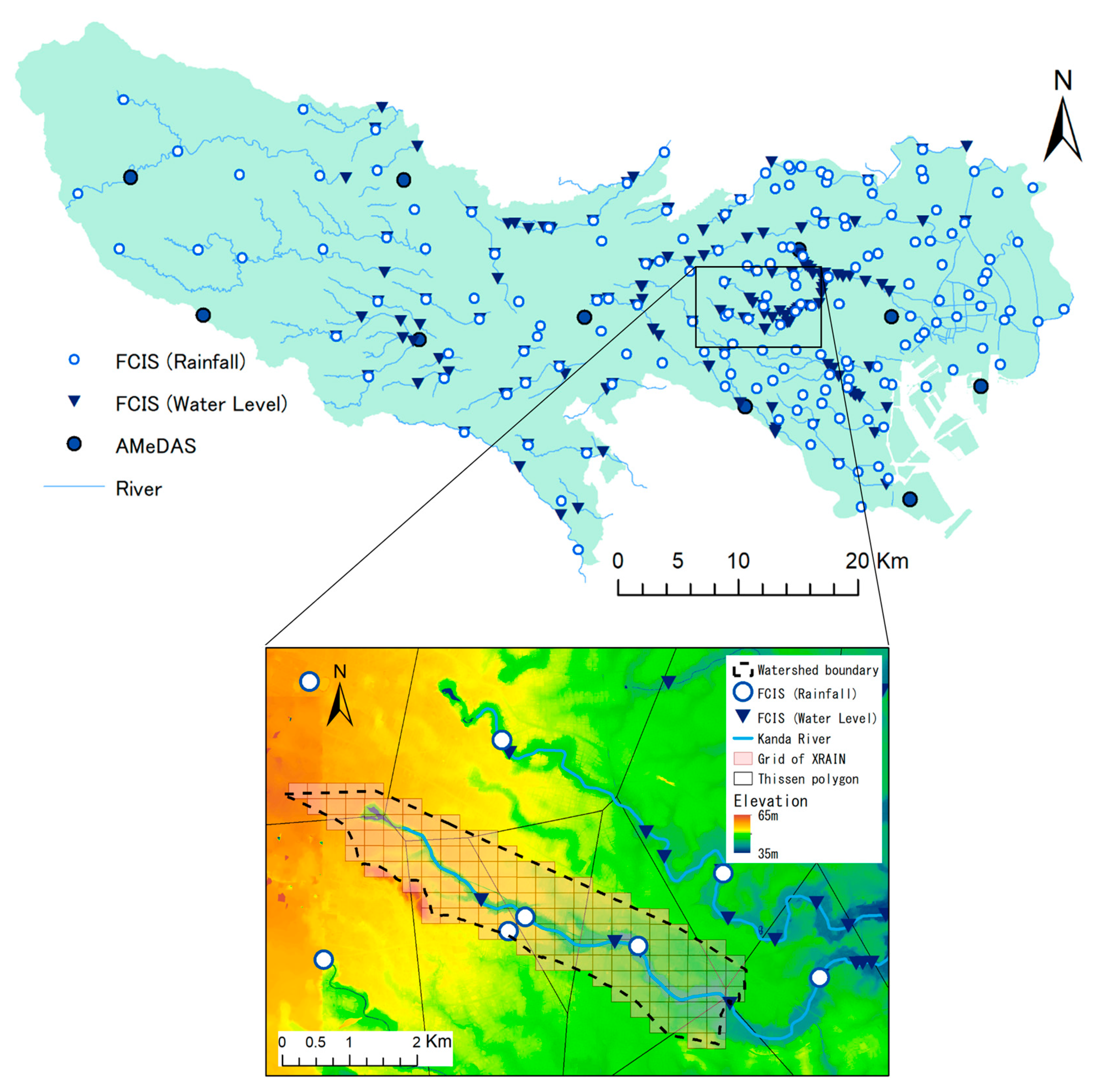
3. Rainfall and Water Level Observation System in Japan
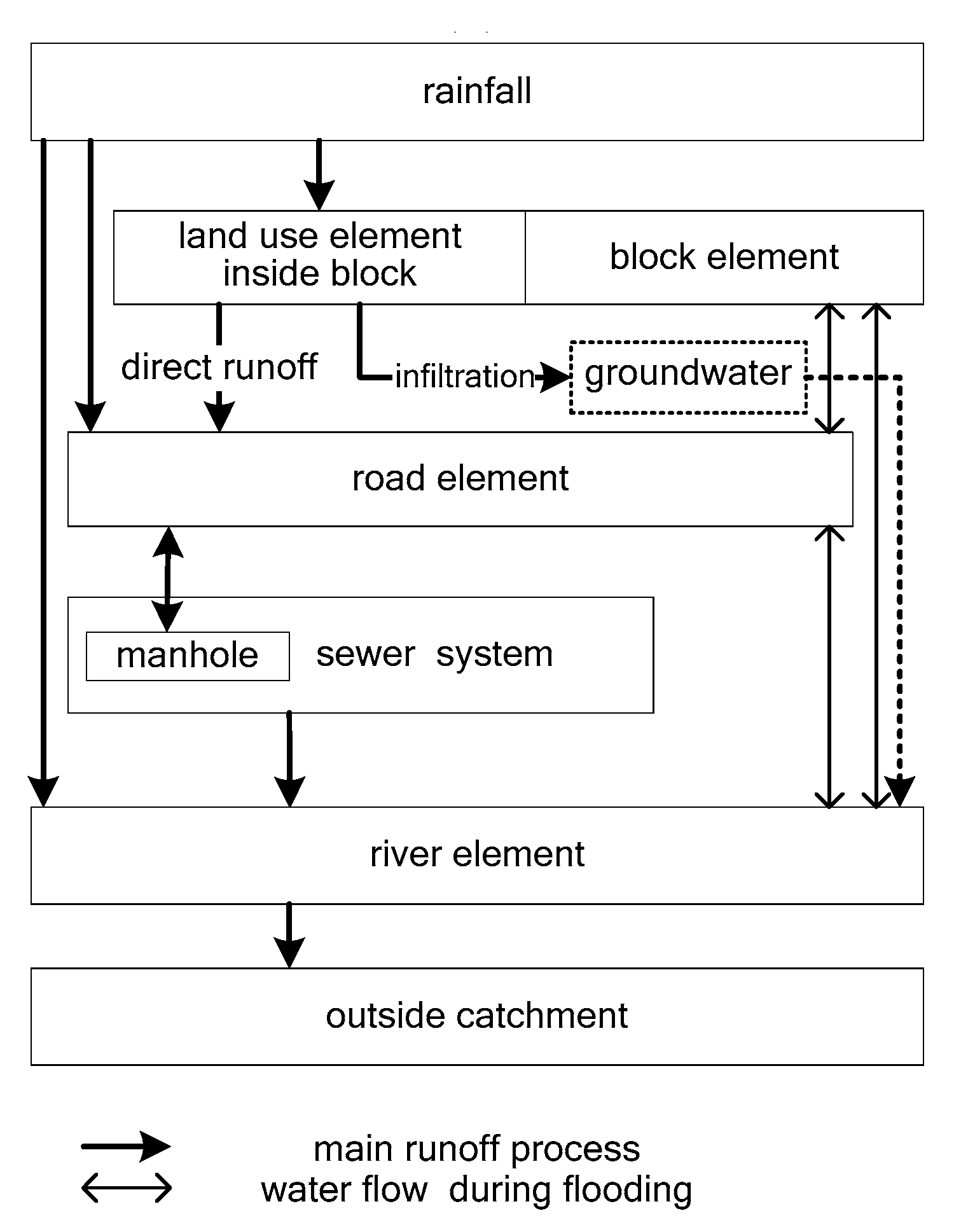
4. Storage Function Model in Urban Watersheds
4.1. Conventional SF Models
4.2. Urban Storage Function (USF) Model
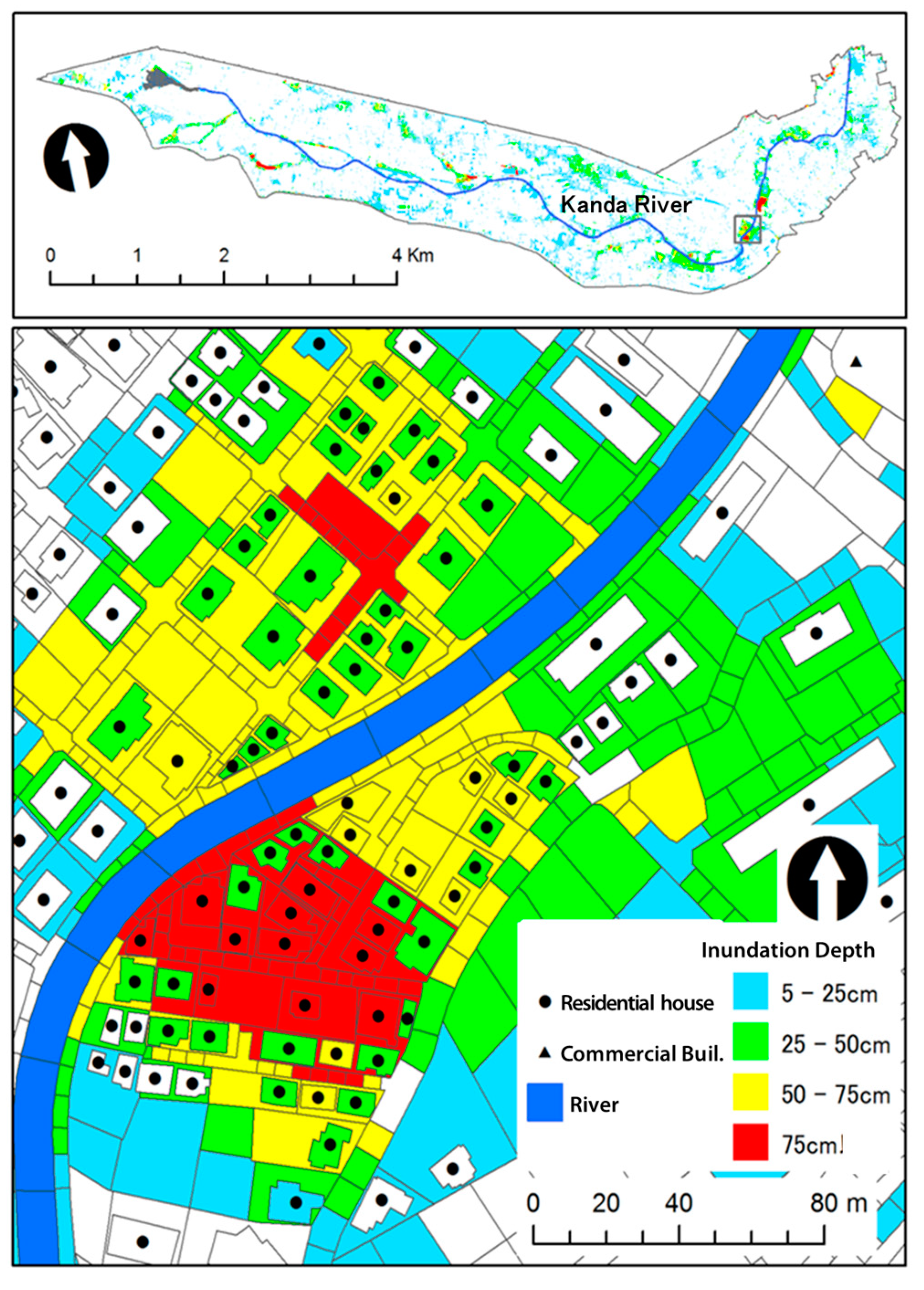
4.3. Application of the USF Model in an Urban Watershed
4.4. Runoff Prediction by USF Using XRAIN Data in an Urban Watershed
4.5. AI-Based Flood Runoff Modeling in Urban Watersheds
5. Distributed Physical Models in Urban Watersheds
5.1. Background
5.2. Representation of Urban Structures in Distributed Physical Models
5.3. Structured Grid
5.4. Curvilinear Grid
5.5. Unstructured Grid
5.6. Road Network
5.7. Urban Landscape GIS Delineation
5.8. TSR Model
5.8.1. Outline of Tokyo Storm Runoff (TSR) Model
5.8.2. Model Application to Urban Watershed
6. Concluding Remarks and Future Prospects
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Year | Ref. No. | Model/Method Name | Remarks |
|---|---|---|---|
| 1954 | [58] | Kinematic Wave Theory | Hillslope runoff analysis. |
| 1955 | [59] | Kinematic Wave Theory | Characteristic curve method is used for hillslope runoff analysis. |
| 1955 | ([60]) | Kinematic Wave Theory | River flow tracking analysis. |
| 1961 | [18] | Storage Function Model | The original storage function model was developed. |
| 1967 | [1] | - | The first paper in Japan that quantitatively describe urban flood runoff mechanisms. |
| 1967 | ([81]) | Storage Function Model | The Prasad storage function model was developed. |
| 1972 | [17] | Tank Model | The original tank model was developed. |
| 1972 | [55] | Modified RRL Method | The model was applied to urban watersheds. |
| 1976 | [51] | Kinematic Wave Theory | Concentration time of flood by urbanization was studied. |
| 1977 | [54] | Quasi-Linear Storage Model | The model was applied to urban watersheds. |
| 1979 | ([30]) | TOPMODEL | A watershed hydrologic model that combines the advantages of a concentrated constant model with the effects of runoff contribution rate changes and the dispersion of stormwater due to channel network runoff. |
| 1980 | [79] | Storage Function Model | Explanatory paper of the model. |
| 1980 | [111] | 2D Diffusive Model (Structured Grid) | Pioneering model for inundation calculations. |
| 1982 | [2] | - | A study of flood runoff changes in hilly basins by urbanization. |
| 1982 | [57] | Kinematic Wave Theory | The effects of urbanization on flood runoff was analyzed. |
| 1982 | [50] | Rational Method | Application of Rational Method to urbanized channels. |
| 1982 | [82] | Storage Function Model | Relationship with kinematic wave model was studies |
| 1985 | [3] | - | The effect of field moisture distribution on runoff was analyzed. |
| 1985 | [4] | - | A review of runoff changes due to urbanization is made. |
| 1985 | [85] | Storage Function Model | Comparison of various SF models |
| 1991 | [63] | Kinematic Wave Model | Application for an urban watershed by dividing it into rectangular sub-watersheds. |
| 1992 | ([31]) | Xinanjiang Model | Rainfall-runoff, distributed, basin model. |
| 1995 | ([33]) | SHE/SHESED | Basin-scale water flow and sediment transport modeling system. |
| 1995 | ([34]) | Institute of Hydrology Distributed Model | The model uses established flow equations for surface and subsurface. |
| 1995 | ([35]) | HBV Model | Lumped (or semi-distributed) bucket-type (conceptual) catchment model. |
| 1995 | [64] | Diffusion Wave Model Dynamic Wave Model | Comparison with kinematic wave model for nonstationary and unsteady river channel flow. |
| 1995 | [91] | Tank Model | Tank model parameter estimation using global optimization methods, |
| 1996 | [65] | Doken Model | Distributed model for real-time flood forecasting. |
| 1997 | [67] | Kinematic Wave Model | Model parameters were obtained using GIS information. |
| 1998 | [52] | Rational Model | Application for small urban rivers. |
| 1998 | [122] | 2D Diffusive Wave Model (Curvilinear Grid) | Pioneer research on flood flow considering the influence of buildings and road structures. |
| 1999 | [22] | Storage Function Model | Proposal of SF model considering loss mechanisms that directly uses the observed rainfall and runoff. |
| 1999 | [25] | Distributed Runoff Model | Evaluation of the permeable pavement and the house infiltration system. |
| 1999 | [125] | 2D Diffusive Wave Model (Road Network) | Proposal of road network model in an urban area. |
| 2000 | [84] | Storage Function Model (Hoshi’s Model) | Proposal of four-parameter SF model that directly uses the observed rainfall and runoff. |
| 2000 | [112] | 2D Diffusive Model (Structured Grid) | The model of [112] was extended to include inflows from mountain watersheds and sewer overflows. |
| 2001 | [26] | A Distributed Hydrological Model-WEP Model | WEP model that evaluates the effects of stormwater detention ponds and infiltration trenches in urban watersheds. |
| 2002 | [121] | 2D Diffusive Model (Structured/Curvilinear /Unstructured Grid) | Proposal of a flood runoff analysis model considering urban area characteristics. |
| 2004 | [119] | NILIM2.0 2D Diffusive Model | A standard method used to prepare municipal flood maps in Japan. |
| 2007 | [39] | TSR Model | TSR model in the early development stage. The model is a physically based distributed model, which was applied for an urban catchment using polygon feature GIS data. |
| 2008 | [86] | Storage Function Model | Proposal of SF model considering outflow through combined sewer system. |
| 2008 | [123] | Flood Disaster Deduction System (Dual Drainage, Unstructured Grid) | Consideration of sewer flows in surface flooding models that use 2D full shallow-water equations. |
| 2009 | [23] | Urban storage function (USF) Model | Proposal of USF Model that directly uses the observed rainfall and runoff. |
| 2010 | ([36]) | HYPE Model | Dynamic and semi-distributed hydrological model integrating fluxes of water, nutrients, and other substances. |
| 2010 | [124] | Flood Disaster Reduction System (Dual Drainage, Unstructured Grid) | The numerical simulation for inundation flows with flood control system was carried out. |
| 2011 | [118] | 2D Diffusive Model (Structured Grid) | Formulating the impact of buildings on flood flows. |
| 2011 | [126] | 1D Saint-Venant Equations (Dual Drainage, Road Network) | Numerical analysis of inundation in the region of downtown Tokyo with residence area. |
| 2012 | [6] | Dual drainage model TSR model (Urban Landscape GIS) | TSR model was proposed that is a distributed urban storm runoff event model with a vector-based catchment. |
| 2012 | [28] | RRI model | RRI model was proposed that is a 2D model capable of simultaneously analyzing rainfall-runoff and flood inundation. |
| 2012 | [38] | Urban Landscape GIS Delineation | Permeable area ratio of 10m-mesh land use classification was studied. |
| 2012 | [53] | Synthesized Rational Model | Theoretical derivation of the synthesized rational formula. |
| 2012 | [97] | USF Model | Real-time runoff forecasting of the model using particle filter. |
| 2013 | [98] | USF Model | Real-time runoff forecasting of the model using the Kalman filter. |
| 2013 | [132] | TSR model (Urban Landscape GIS) | TSR model considering the flooding process of buildings. |
| 2015 | [92] | Distributed Model SCE-UA Method | Parameter identification of a distributed runoff model using SCE-UA method. |
| 2016 | [40] | Urban Landscape GIS Delineation | Impervious area ratios of grid-based land use classifications were assessed. |
| 2016 | [100] | XRAIN Data | Precision evaluation of XRAIN data in a small urban watershed. |
| 2016 | [104] | Deep Learning (DL) Method | Development of the real-time river stage prediction method using DL approach. |
| 2017 | [62] | Various Numerical Methods | Review paper for surface water flow numerical analysis. |
| 2017 | [83] | Baseflow Estimation Method | Baseflow estimation using recursive digital filters. |
| 2017 | [102] | XRAIN Data | Spatiotemporal characteristic analysis of XRAIN data. |
| 2017 | [103] | XRAIN Data | Spatiotemporal correlation analysis of XRAIN data focused on torrential rainfall events at each ground observation point. |
| 2017 | [106] | Machine Learning (ML) Method | Real-time forecasting of water levels in sewer system by the method. |
| 2017 | [110] | Deep Neural Network (DNN) Model Distributed Model | Proposal of real-time river stage prediction model by combining DNN and a distributed model. |
| 2018 | ([43]) | SWMM | Drainage area characterization for evaluating green infrastructure. |
| 2018 | ([66]) | IFAS (Integrated Flood Analysis System) | Flood forecasting in watersheds with inadequate water level observations. |
| 2018 | [88] | Storage Function Model | An effective storage function model for an urban watershed was investigated. |
| 2018 | [99] | USF Model XRAIN Data | Reproducibility of hydrograph by USF model using different rainfall datasets was studied. |
| 2018 | [101] | XRAIN Data | Precision of 1-minute XRAIN data in a small urban watershed was studied. |
| 2018 | [105] | DL Method | Application of DL method to long-term prediction of dam inflow. |
| 2018 | [113] | Integrated Model with InfoWorks and WEB-DHM | A river channel and sewer model were built by integrating InfoWorks into WEB-DHM. |
| 2019 | [21] | HYPE Model | HYPE model using EEA Urban Atlas. |
| 2019 | [94] | USF Model | Parameter uncertainty of USF model was evaluated. |
| 2019 | [95] | USF Model | Proposal of a generalized USF model considering spatial rainfall distribution. |
| 2019 | [107] | USF Model DL Method | Possibility of emulating USF model by DL method was studied for benchmark virtual hyeto and hydrograph. |
| 2019 | [108] | Neural Network Method DL Method | Comparison of emulation ability for the USF model by the two methods. |
| 2019 | ([114]) | HE-C-RAS | HEC-RAS was used to generate flood inundation and develop a risk map under the different rainfall scenarios. |
| 2020 | [27] | TSR model | TSR model, considering green infrastructure. |
| 2020 | [96] | Generalized Storage Function Model | Proposal of a generalized storage function model for the water level estimation. |
| 2020 | [109] | DL Method | Prediction evaluation of hydrograph by the method using an observed urban dataset. |
| 2021 | ([115]) | HEC-RAS | Building representation method by HEC-RAS 2-D and evaluation of the influence of fluid forces on buildings. |
| 2023 | [77] | Time Series Method | Water level forecasting based on time series analysis in an urban watershed. |
References
- Kinoshita, T. Runoff changes due to urbanization. Civ. Eng. Technol. Mat. 1967, 9, 11–15. (In Japanese) [Google Scholar]
- Takahashi, Y.; Izumi, K.; Ando, Y.; Kanao, K. Change of flood runoff in hilly basins by urbanization. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1982, 26, 261–266. (In Japanese) [Google Scholar]
- Yamada, T.; Ishii, F.; Yamazaki, K.; Iwatani, K. On relation between distribution of field moisture capacity and runoff characteristics in small basins. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1985, 29, 25–30. (In Japanese) [Google Scholar]
- Kadoya, M. A review of the study on runoff changes due to urbanization. J. Jpn. Soc. Civ. Eng. 1985, 363, 23–34. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Takahashi, Y. City and Water; Iwanami Shinsho: Tokyo, Japan, 1988; pp. 1–34. (In Japanese) [Google Scholar]
- Amaguchi, H.; Kawamura, A.; Olsson, J.; Takasaki, T. Development and testing of a distributed urban storm runoff event model with a vector-based catchment. J. Hydrol. 2012, 420–421, 205–215. [Google Scholar] [CrossRef]
- Tamai, N. River Engineering; Ohmsha: Tokyo, Japan, 1999; pp. 55–95. (In Japanese) [Google Scholar]
- Ishihara, S.; Takasaki, T.; Kawamura, A.; Amaguchi, H. Background of new development plan and future development methods of urban rivers in Tokyo metropolis. Adv. River Eng. 2014, 20, 437–442. (In Japanese) [Google Scholar]
- Kanae, S. Characteristics of localized torrential rainfall (so-called guerrilla rainfall). J. Hydrol. Syst. 2009, 73, 11–16. (In Japanese) [Google Scholar]
- Nakakita, E.; Yamaguchi, K.; Yamabe, H. A study on detecting origin of localized torrential rainfall using volume scanning radar. DPRI Annu. 2009, 52, 547–562. (In Japanese) [Google Scholar]
- Ushiyama, M. A study of relationship between “Guerilla Heavy Rainfall” and disaster. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2011, 67, I_505–I_510. (In Japanese) [Google Scholar] [CrossRef]
- Fujibe, F.; Togawa, H.; Sakata, M. Long-term change and spatial anomaly of warm season afternoon precipitation in Tokyo. SOLA 2009, 5, 17–20. [Google Scholar] [CrossRef]
- Seino, N.; Aoyagi, T.; Tsuguti, H. Numerical Simulation of Urban Impact on Precipitation in Tokyo: How does Urban Temperature Rise Affect Precipitation? Urban Clim. 2018, 23, 8–35. [Google Scholar] [CrossRef]
- Kawamura, A. Urban flooding and its countermeasures. In Urban Technology, Revised ed.; Graduate School of Urban Infrastructure and Environment, Tokyo Metropolitan University, Ed.; Gihodo Pub.: Tokyo, Japan, 2016; pp. 235–249. (In Japanese) [Google Scholar]
- Singh, V.P. Watershed modeling. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Res. Pub.: Denver, CO, USA, 1995; pp. 1–22. [Google Scholar]
- JSCE Committee on Hydroscience and Hydraulic Engineering. Hydroscience Formulary; JSCE: Tokyo, Japan, 1999; pp. 35–47. (In Japanese) [Google Scholar]
- Sugawara, M. Rainfall-Runoff Analysis; Kyoritsu Pub: Tokyo, Japan, 1972; p. 257. (In Japanese) [Google Scholar]
- Kimura, T. Storage Function Model. Civ. Eng. J. 1961, 3, 36–43. (In Japanese) [Google Scholar]
- Kawamura, A. Inverse problems in hydrology. In Introduction to Inverse Problems in Civil Engineering; Jpn. Soc. Civil Eng.; Maruzen: Tokyo, Japan, 2000; pp. 24–30. (In Japanese) [Google Scholar]
- Hino, M. What have hydrologists done and what should we do? What should we do from now on? J. Jpn. Soc. Hydrol. Water Res. 1996, 9, 3–16. (In Japanese) [Google Scholar]
- Tanouchi, H.; Olsson, J.; Lindstrom, G.; Kawamura, A.; Amaguchi, H. Improving urban runoff contributions in multi-basin hydrological simulation by the HYPE model using EEA Urban Atlas. Hydrology 2019, 6, 28. [Google Scholar] [CrossRef]
- Baba, H.; Hoshi, K.; Hashimoto, N. Synthetic storage routing model coped with loss mechanisms. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1999, 43, 1085–1090. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Takasaki, T.; Kawamura, A.; Amaguchi, H.; Araki, K. Storage function model considering urban runoff process. J. Jpn. Soc. Civ. Eng. B 2009, 65, 217–230. (In Japanese) [Google Scholar] [CrossRef]
- Shiiba, M.; Tachikawa, Y.; Ichikawa, Y. Hydrology and Hydraulic Engineering Planning Studies; Kyoto University Press: Kyoto, Japan, 2013; pp. 351–371. (in Japanese) [Google Scholar]
- Hanaki, T.; Suharyanto, A.; Sugio, S. Investigation of flood control by rainwater infiltration facilities in urbanized watershed. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1999, 48, 37–42. (In Japanese) [Google Scholar] [CrossRef]
- Jia, Y.; Ni, G.; Kinouchi, T.; Yoshitani, J.; Kawahara, Y.; Suetsugi, T. Study on effects of storm-water detention facilities in an urbanized watershed using distributed model. Jpn. Soc. Civ. Eng. Hydraul. Conf. 2001, 45, 109–114. (In Japanese) [Google Scholar] [CrossRef]
- Amaguchi, H.; Kawamura, A. A proposal of urban runoff model considering green infrastructures and its application. J. Jpn. Soc. Civ. Eng. Ser. G (Environ. Res.) 2020, 76, I_319–I_325. (In Japanese) [Google Scholar] [CrossRef]
- Sayama, T.; Ozawa, G.; Kawakami, T.; Nabesaka, S.; Fukami, K. Rainfall-runoff-inundation analysis of the 2010 Pakistan flood in the Kabul River basin. Hydrol. Sci. J. 2012, 57, 298–312. [Google Scholar] [CrossRef]
- Public Works Research Institute. RRI Model. Available online: http://www.icharm.pwri.go.jp/research/rri/rri_top.html (accessed on 18 November 2022).
- Beven, K.J.; Kirkby, M.J. A physically based variable contributing area model of basin hydrology. Hydrol. Sci. Bull. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Zhoa, R.J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Ren, L.; Yuan, F. The Xinanjiang model on a digital basin platform. In Watershed Models; Singh, V.P., Frevert., D.K., Eds.; CRC Press: Boca Raton, FL, USA, 2006; pp. 179–208. [Google Scholar]
- Bathurst, J.C.; Wicks, J.M.; O’Connell, P.E. The SHE/SHESED basin scale water flow and sediment transport modelling system. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Res. Pub.: Denver, CO, USA, 1995; pp. 563–594. [Google Scholar]
- Calver, A.; Wood, W.L. The Institute of Hydrology Distributed Model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Res. Pub.: Denver, CO, USA, 1995; pp. 595–626. [Google Scholar]
- Bergström, S. The HBV Model. In Computer Models of Watershed Hydrology; Singh, V.P., Ed.; Water Res. Pub.: Denver, CO, USA, 1995; pp. 443–476. [Google Scholar]
- Lindström, G.; Pers, C.P.; Rosberg, R.; Strömqvist, J.; Arheimer, B. Development and test of the HYPE (Hydrological Predictions for the Environment) model—A water quality model for different spatial scales. Hydrol. Res. 2010, 41, 295–319. [Google Scholar] [CrossRef]
- SMHI, HYPE. Available online: https://www.smhi.se/en/research/research-departments/hydrology/hype-1.7994 (accessed on 18 November 2022).
- Koga, T.; Kawamura, A.; Amaguchi, H. Study on permeable area ratio of 10m-mesh land use classification using advanced GIS delineation in the upper Kanda River basin. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2012, 68, I_505–I_510. (In Japanese) [Google Scholar]
- Amaguchi, H.; Kawamura, A.; Takasaki, T. Physically based distributed flood runoff model for an urban catchment using polygon feature GIS data. J. Jpn. Soc. Civ. Eng. B 2007, 63, 206–223. (In Japanese) [Google Scholar] [CrossRef]
- Koga, T.; Kawamura, A.; Amaguchi, H.; Tanouchi, H. Assessing impervious area ratios of grid-based land-use classifications on an example of an urban watershed. Hydrol. Sci. J. 2016, 61, 1728–1739. [Google Scholar] [CrossRef]
- Sample, D.J.; Heaney, J.P.; Wright, L.; Koustas, R. Geographic information systems, decision support systems, and urban storm-water management. J. Water Plan. Man. 2001, 127, 155–161. [Google Scholar] [CrossRef]
- Rodriguez, F.; Andrieu, H.; Creutin, J.D. Surface runoff in urban catchments: Morphological identification of unit hydrographs from urban databanks. J. Hydrol. 2003, 283, 146–168. [Google Scholar] [CrossRef]
- Lee, J.G.; Nietch, C.T.; Panguluri, S. Drainage area characterization for evaluating green infrastructure using the storm water management model. Hydrol. Earth Syst. Sci. 2018, 22, 2615–2635. [Google Scholar] [CrossRef]
- Japan Society of Hydrology and Water Resources. Handbook of Hydrology and Water Resources; Asakura: Tokyo, Japan, 1997; p. 636. (In Japanese) [Google Scholar]
- JSCE Committee on Hydroscience and Hydraulic Engineering. Hydroscience Formulary, 1985 ed.; JSCE: Tokyo, Japan, 1985; pp. 151–172, 713. (In Japanese) [Google Scholar]
- JSCE Committee on Hydroscience and Hydraulic Engineering. Hydroscience Formulary, 1971 ed.; JSCE: Tokyo, Japan, 1971; p. 616. (In Japanese) [Google Scholar]
- JSCE Committee on Hydroscience and Hydraulic Engineering. Hydroscience Formulary, 1963 ed.; JSCE: Tokyo, Japan, 1963; p. 603. (In Japanese) [Google Scholar]
- Morita, S. Urban Flood Risk Analysis; Forum 8: Tokyo, Japan, 2014; pp. 3–75. (In Japanese) [Google Scholar]
- Matsubayashi, U. Runoff mechanism and characteristics in urban areas. In Handbook of Hydrology and Water Resources; Jpn Soc. Hydrol. Water Res.; Asakura: Tokyo, Japan, 1997; pp. 146–148. (In Japanese) [Google Scholar]
- Ishikawa, K.; Sato, K.; Izumi, K. Applicability of rational method to the urbanized channels in Tokyo. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1982, 26, 267–272. (In Japanese) [Google Scholar]
- Kadoya, M.; Fukushima, A. Concentration time of flood in small or medium river basin. DPRI Annu. 1976, 19B, 143–152. (In Japanese) [Google Scholar]
- Tanioka, Y.; Fukuoka, S.; Taniguchi, M.; Koyama, Y. Characteristics of floods in small urban rivers. J. Jpn. Soc. Civ. Eng. 1998, 586, 1–12. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Watanabe, A.; Sasada, T.; Watanabe, N.; Yamada, T. Theoretical derivation of synthesized rational formula. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2012, 68, I_499–I_504. (In Japanese) [Google Scholar]
- Hashimoto, T.; Hasegawa, T. A runoff model to evaluate land use change. Civ. Eng. J. 1977, 19, 221–226. (In Japanese) [Google Scholar]
- Yamaguchi, T.; Matsubara, S.; Yamamori, T. Second report of rainfall-runoff study in an urban area -Runoff estimation by modified R.R.L. method. Civ. Eng. J. 1972, 14, 34–39. (In Japanese) [Google Scholar]
- Matsubayashi, U. Runoff model for urban watersheds. In Handbook of Hydrology and Water Resources; Jpn. Soc. Hydrol. Water Res.; Asakura: Tokyo, Japan, 1997; pp. 148–151. (In Japanese) [Google Scholar]
- Sukegawa, N.; Kitagawa, Y. A rainfall-runoff simulation model for assessing the effect of urbanization on flood runoff. Proc. Jan. Soc. Civ. Eng. 1982, 325, 51–59. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Iwagaki, Y.; Sueishi, T. On the unsteady flow in open channels with uniform lateral inflow—Hydraulic studies on the run-off phenomena of rain water, 1st report. J. Jpn. Soc. Civ. Eng. 1954, 39, 575–583. (In Japanese) [Google Scholar]
- Sueishi, T. On the run-off analysis by the method of characteristics hydraulic studies on the run-off phenomena of rain water, 2nd report. J. Jpn. Soc. Civ. Eng. 1955, 29, 74–87. (In Japanese) [Google Scholar] [CrossRef]
- Lighthill, M.J.; Whitham, G.B. On kinematic waves: 1. Flood movement in long rivers. Proc. R. Soc. 1955, 229, 281–316. [Google Scholar]
- Singh, V.P.; Jain, S.K. Rainfall-Runoff Modeling. In Handbook of Applied Hydrology, 2nd ed.; Singh, V.P., Ed.; McGraw-Hill Education: New York, NY, USA, 2016; Chapter 59; pp. 59-1–59-8. [Google Scholar]
- Kimura, M.; Tanaka, T.; Azechi, I.; Nakatani, K.; Yamazaki, D.; Yoshioka, H. Interdisciplinary perspective of surface water flow numerical analysis. J. Jpn. Soc. Hydrol. Water Res. 2017, 30, 307–334. (In Japanese) [Google Scholar] [CrossRef]
- Ando, Y.; Nabeyama, T.; Nishijima, S. Flood runoff analysis of urban watersheds. J. Urban Res. 1991, 41, 69–89. (In Japanese) [Google Scholar]
- Fujimura, K.; Ando, Y.; Maeda, M. A study on stormwater runoff model of urban lowland basin. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1995, 39, 61–66. (In Japanese) [Google Scholar] [CrossRef]
- Suzuki, T.; Terakawa, Y.; Matsuura, T. Development of physics-based distributed model for operational hydrological forecasting. Civ. Eng. J. 1996, 38, 26–31. (In Japanese) [Google Scholar]
- Shahzad, A.; Gabriel, H.F.; Haider, S.; Mubeen, A.; Siddiqui, M.J. Development of a flood forecasting system using IFAS: A case study of scarcely gauged Jhelum and Chenab river basins. Arab. J. Geosci. 2018, 11, 383. [Google Scholar]
- Chikamori, H.; Oka, T.; Takara, K.; Okubo, G. Fundamental Study on Application of Geographic Information System to Construction of Rainfall-Runoff Model of Urbanized Area. DPRI Annu. 1997, B 40, 137–144. (In Japanese) [Google Scholar]
- Ministry of Land, Infrastructure, Transport and Tourism. Investigation Guidelines for River Sand and Gravel Management Technology Standards, Survey Edition; MLIT: Tokyo, Japan, 2016; Chapter 3. [Google Scholar]
- Kawamura, A. Status quo and perspectives of flood runoff analysis for urban watersheds. J. Jpn. Soc. Hydrol. Water Res. 2018, 31, 451–466. (In Japanese) [Google Scholar] [CrossRef]
- Shibuo, Y.; Furumai, H. Advances in Urban Stormwater Management in Japan: A Review. J. Disaster Res. 2021, 16, 310–320. [Google Scholar] [CrossRef]
- Water Management and Land Conservation Bureau. Available online: https://www5.river.go.jp/ (accessed on 27 March 2023).
- Water Management and Land Conservation Bureau. River Disaster Prevention Information. Available online: https://city.river.go.jp/kawabou/reference/index01.html (accessed on 27 March 2023).
- Japan Meteorological Agency. Automated Meteorological Data Acquisition System 2020. Available online: https://www.jma.go.jp/jma/en/Activities/amedas/amedas.html (accessed on 10 November 2022).
- Ministry of Land, Infrastructure, Transport and Tourism. X-Band MP Radar Network. Available online: http://mp-radar.bosai.go.jp/ (accessed on 18 November 2022).
- Schilling, W. Rainfall data for urban hydrology: What do we need? Atmos. Res. 1991, 27, 5–21. [Google Scholar] [CrossRef]
- Fabry, F.; Bellon, A.; Duncan, M.R.; Austin, G.L. High resolution rainfall measurements by radar for very small basins: The sampling problem reexamined. J. Hydrol. 1994, 161, 415–428. [Google Scholar] [CrossRef]
- Koyama, N.; Sakai, M.; Yamada, T. Study on a Water-Level-Forecast Method Based on a Time Series Analysis of Urban River Basins—A Case Study of Shibuya River Basin in Tokyo. Water 2023, 15, 161. [Google Scholar] [CrossRef]
- Tokyo Metropolitan Government—Flood Control Integrated Information System. Available online: https://www.kasen-suibo.metro.tokyo.lg.jp/im/uryosuii/tsim0102g_en.html (accessed on 10 November 2022).
- Kadoya, M.; Nagai, A. Runoff analysis methods (Part 10) Storage method—Flood runoff analysis by the storage function model. J. Jpn. Soc. Agric. Civ. Eng. 1980, 48, 43–50. [Google Scholar]
- Holmes, R.R., Jr. Streamflow Ratings. In Handbook of Applied Hydrology, 2nd ed.; Singh, V.P., Ed.; McGraw-Hill Education: New York, NY, USA, 2016; Chapter 6; pp. 6-1–6-14. [Google Scholar]
- Prasad, R. A nonlinear hydrologic system response model. J. Hydraul. Div. 1967, 93, 201–222. [Google Scholar] [CrossRef]
- Hoshi, K.; Yamaoka, T. A relationship between kinematic wave and storage routing models. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1982, 26, 273–278. (In Japanese) [Google Scholar]
- Padiyedath, S.G.; Kawamura, A.; Amaguchi, H.; Azhikodan, G. Baseflow estimation for tropical wet and dry climate region using recursive digital filters. J. Jpn. Soc. Civ. Eng. Ser. G (Environ. Res.) 2017, 73, 9–16. [Google Scholar] [CrossRef]
- Hoshi, K.; Baba, H.; Hashimoto, A. Development of a storage function method for tracking floods in watershed and channel systems. Adv. River Eng. 2000, 6, 297–302. (In Japanese) [Google Scholar]
- Takasao, T.; Takara, K.; Kusuhashi, H. Comparative study of storage function models of flood runoff. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1985, 29, 245–250. (In Japanese) [Google Scholar]
- Takasaki, T.; Kawamura, A.; Amaguchi, H. Development of the storage function model for urban flood considering the outflow through combined sewer system. J. Jpn. Soc. Hydrol. Water Res. 2008, 21, 228–241. (In Japanese) [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure, Transport and Tourism. History of the Sewerage System. Available online: https://www.mlit.go.jp/crd/city/sewerage/data/basic/rekisi.html (accessed on 31 January 2023). (In Japanese).
- Padiyedath, S.G.; Kawamura, A.; Takasaki, T.; Amaguchi, H.; Azhikodan, G. An effective storage function model for an urban watershed in terms of hydrograph reproducibility and Akaike information criterion. J. Hydrol. 2018, 563, 657–668. [Google Scholar] [CrossRef]
- Kawamura, A.; Marabtene, T. Evolutionary computing: Genetic algorithms. In Handbook of Applied Hydrology, 2nd ed.; Singh, V.P., Ed.; McGraw-Hill Education: New York, NY, USA, 2016; Chapter 13; pp. 13-1–13-4. [Google Scholar]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 3–4, 265–284. [Google Scholar] [CrossRef]
- Tanakamaru, H. Parameter estimation for the tank model using global optimization. J. Jpn. Soc. Agric. Civ. Eng. 1995, 178, 503–512. (In Japanese) [Google Scholar]
- Matsubara, T.; Tsuchida, K.; Hibiya, M. Study on parameter identification of distributed runoff model using SCE-UA method. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2015, 71, I_265–I_270. (In Japanese) [Google Scholar]
- Akaike, H. Likelihood of a model and information criteria. J. Econom. 1981, 16, 3–14. [Google Scholar] [CrossRef]
- Padiyedath, S.G.; Kawamura, A.; Takasaki, T.; Amaguchi, H.; Azhikodan, G. A bootstrap approach for the parameter uncertainty of an urban-specific rainfall runoff model. J. Hydrol. 2019, 579, 1–18. [Google Scholar] [CrossRef]
- Padiyedath, S.G.; Kawamura, A.; Takasaki, T.; Amaguchi, H.; Azhikodan, G. A generalized urban storage function model considering spatial rainfall distribution. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2019, 75, I_223–I_228. [Google Scholar] [CrossRef] [PubMed]
- Padiyedath, S.G.; Kawamura, A.; Amaguchi, H.; Takasaki, T.; Azhikodan, G. A generalized storage function model for the water level estimation using rating curve relationship. Water Res. Man. 2020, 34, 2603–2619. [Google Scholar]
- Takasaki, T.; Kawamura, A.; Amaguchi, H.; Ishihara, S. Real-time runoff forecasting characteristics of urban storage function model using particle filter. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2012, 68, I_511–I_516. (In Japanese) [Google Scholar]
- Takasaki, T.; Kawamura, A.; Amaguchi, H.; Ishihara, S. Real-time runoff forecasting characteristics of Urban Storage Function Model using Kalman filter. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2013, 69, I_457–I_480. (In Japanese) [Google Scholar]
- Yonese, Y.; Kawamura, A.; Tonotsuka, A.; Amaguchi, H. Runoff characteristics using XRAIN in a small urban watershed. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2018, 74, I_97–I_102. (In Japanese) [Google Scholar]
- Yonese, Y.; Kawamura, A.; Amaguchi, H.; Tonotsuka, A. Precision evaluation of X-band MP radar rainfall in a small urban watershed by comparison to 1-minute ground observation rainfall data. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2016, 72, I_217–I_222. (In Japanese) [Google Scholar]
- Yonese, Y.; Kawamura, A.; Amaguchi, H.; Tonotsuka, A. Study on the precision of 1-minute X-band MP radar rainfall data in a small urban watershed. Int. J. Sustain. Dev. Plan. 2018, 13, 614–625. [Google Scholar] [CrossRef]
- Yonese, Y.; Kawamura, A.; Amaguchi, H.; Tonotsuka, A. Spatiotemporal characteristic analysis of X-band MP radar rainfall in a small urban watershed on the movement of rainfall area. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2017, 73, I_217–I_222. (In Japanese) [Google Scholar]
- Tonotsuka, A.; Kawamura, A.; Yonese, Y.; Amaguchi, H. Spatiotemporal correlation characteristics of X-band MP radar rainfall in a small urban watershed focused on torrential rainfall events at each ground observation point. J. Jpn. Soc. Civ. Eng. Ser. G (Environ. Res.) 2017, 73, I_261–I_268. (In Japanese) [Google Scholar]
- Hitokoto, M.; Sakuraba, M.; Sei, Y. Development of the real-time river stage prediction method using deep learning. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2016, 72, I_187–I_192. (In Japanese) [Google Scholar] [CrossRef] [PubMed]
- Tamura, K.; Nanou, S.; Miura, S.; Yamawaki, M.; Kaneko, H. Application of deep learning to long-term prediction of dam inflow toward efficiency of the flood control operation. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2018, 74, I_1327–I_1332. (In Japanese) [Google Scholar] [CrossRef]
- Hida, Y.; Chiha, H.; Asaoka, Y.; Nagabayashi, H. Real-time forecasting for water levels in sewer by machine learning and inundation simulation. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2017, 73, I_649–I_654. (In Japanese) [Google Scholar] [CrossRef]
- Fujizuka, S.; Kawamura, A.; Amaguchi, H.; Takasaki, T. Emulation of urban runoff model by deep learning for benchmark virtual hyeto and hydrograph. J. Jpn. Soc. Civ. Eng. Ser. G (Environ. Res.) 2019, 75, I_289–I_296. (In Japanese) [Google Scholar] [CrossRef]
- Fujizuka, S.; Kawamura, A.; Amaguchi, H.; Takasaki, T. Emulation performance evaluation of urban runoff model by neural network and deep learning. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2019, 75, I_229–I_234. (In Japanese) [Google Scholar] [CrossRef]
- Fujizuka, S.; Kawamura, A.; Amaguchi, H.; Takasaki, T. Rainfall runoff benchmark test by deep learning model using urban medium and small river basin dataset. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2020, 76, I_355–I_360. (In Japanese) [Google Scholar] [CrossRef]
- Hitokoto, M.; Sakuraba, M. Hybrid deep neural network and distributed rainfall-runoff model for the real-time river stage prediction. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2017, 73, I_22–I_34. (In Japanese) [Google Scholar] [CrossRef]
- Iwasa, Y.; Inoue, K.; Mizutori, M. Hydraulic analysis of overland flood flows by means of numerical method. DPRI Annu. 1980, 23, 305–317. (In Japanese) [Google Scholar]
- Toda, K.; Inoue, K.; Murase, S.; Ichikawa, Y.; Yokoo, H. Inundation analysis due to heavy rainfall in urban area. J. Jpn. Soc. Civ. Eng. 2000, 663, 1–10. (In Japanese) [Google Scholar] [CrossRef]
- Shibuo, Y.; Lee, S.; Sanuki, H.; Yoshimura, K.; Tajima, Y.; Sato, S.; Furumai, H. Development of couped river and sewer network model for improved water level prediction in urban rivers. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2018, 74, I_1357–I_1362. (In Japanese) [Google Scholar]
- Rangari, V.A.; Umamahesh, N.V.; Bhatt, C.M. Assessment of inundation risk in urban floods using HEC RAS 2D. Mod. Earth Syst. Environ. 2019, 5, 1839–1851. [Google Scholar] [CrossRef]
- Mustafa, A.; Szydłowski, M. Application of different building representation techniques in HEC-RAS 2-D for urban flood modeling using the Toce River experimental case. PeerJ 2021, 2, e11667. [Google Scholar] [CrossRef] [PubMed]
- Rosenzweig, B.R.; Cantis, P.H.; Kim, Y.; Cohn, A.; Grove, K.; Brock, J.; Yesuf, P.; Mistry, P.; Welty, C. The value of urban flood modeling. Earth’s Future 2021, 9, e2020EF001739. [Google Scholar] [CrossRef]
- Amaguchi, H.; Tsubaki, R. On the inundation prediction, present state and matters to be resolved. Adv. River Eng. 2015, 21, 425–430. (In Japanese) [Google Scholar]
- Miura, S.; Kawamura, I.; Kimura, I.; Miura, A. Study on inundation flow analysis method in densely populated urban area on alluvial fan. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2011, 67, I_979–I_984. (In Japanese) [Google Scholar] [CrossRef]
- Nakamura, T.; Sasaki, Y.; Mizukusa, K. A guide of application for flood analysis models in the urban areas. Technical Note of NILM 2004, No. 202. Available online: https://www.nilim.go.jp/lab/bcg/siryou/tnn/tnn0202pdf/ks0202.pdf (accessed on 10 November 2022).
- Inokawa, N.; Kobayashi, K. Analysis of flooding in underground space using 1m mesh elevation data and study of evacuation risk. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2022, 78, I_1415–I_1420. (In Japanese) [Google Scholar] [CrossRef]
- Kawaike, K.; Inoue, K.; Hayashi, H.; Toda, K. Development of inundation flow model in urban area. J. Jpn. Soc. Civ. Eng. 2002, 698, 1–10. (In Japanese) [Google Scholar] [CrossRef]
- Fukuoka, S.; Kawashima, M.; Yokoyama, H.; Mizuguchi, M. The numerical simulation of flood-induced flows in urban residential area and the study of damage reduction. J. Jpn. Soc. Civ. Eng. 1998, 600, 23–36. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Akiyama, J.; Shigeeda, M.; Tanabe, T. Dynamic network model for free-surface-pressurized flows and its applicability to sewer network in the urban area. Adv. River Eng. 2008, 14, 425–430. Available online: http://library.jsce.or.jp/jsce/open/00906/2008/14-0241.pdf (accessed on 25 July 2023). (In Japanese).
- Akiyama, J.; Shigeeda, M.; Kozono, Y. Numerical model for rainfall-runoff and flood inundation processes and its application for Iizuka city. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 2010, 54, 919–924. Available online: http://library.jsce.or.jp/jsce/open/00028/2010/54-0154.pdf (accessed on 25 July 2023). (In Japanese).
- Inoue, K.; Kawaike, K.; Hayashi, H. Inundation flow modeling in urban area. Proc. Hydraul. Conf. Jpn. Soc. Civ. Eng. 1999, 43, 533–538. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Sekine, M. Numerical analysis of inundation in the region of downtown Tokyo with residence area. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2011, 67, 70–85. (In Japanese) [Google Scholar] [CrossRef]
- Sekine, M.; Kamata, T.; Hosono, Y.; Shibuya, Y. Inundation process in three cities of Musashino, Mitaka, and Chofu for the largest possible torrential rainfall. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2022, 78, I_427–I_432. (In Japanese) [Google Scholar] [CrossRef]
- Araki, T.; Amaguchi, H.; Kawamura, A.; Takasaki, T. Development of a groundwater recharge model for an urban catchment using urban landscape GIS delineation and its simulation for actual catchment. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2012, 68, 109–124. (In Japanese) [Google Scholar]
- Tanouchi, H.; Amaguchi, H.; Kawamura, A.; Nakagawa, N. Development of an automated construction algorithm of advanced delineation GIS data using 1:2500 topological map. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2013, 69, I_523–I_528. (In Japanese) [Google Scholar]
- Tanouchi, H.; Amaguchi, H.; Kawamura, A.; Nakagawa, N.; Koga, T. Study on an automated construction method of minute road segments aiming at urban storm runoff analysis. Theory Appl. GIS 2014, 22, 25–34. (In Japanese) [Google Scholar] [CrossRef]
- Tanouchi, H.; Amaguchi, H.; Kawamura, A.; Koga, T.; Hagiwara, Y. Automated construction method of polygonal blocks for an urban watershed. J. Jpn. Soc. Hydrol. Water Res. 2015, 26, 298–303. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Amaguchi, H.; Nagasaka, T.; Kawamura, A.; Takasaki, T.; Nakagawa, N. A proposal of storm runoff model considering process of building inundation for an urban catchment. Adv. River Eng. 2013, 19, 211–216. (In Japanese) [Google Scholar]
- Amaguchi, H.; Kawamura, A. Development of a storm runoff model considering process of individual building inundation. Int. J. Saf. Secur. Eng. 2016, 6, 570–581. [Google Scholar]
- Bonacci, O. Floods: New Concepts merge—Old problems remain. In Proceedings of the 15th International Symposium on Water Management and Hydraulic Engineering, Primošten, Croatia, 6–8 September 2017. [Google Scholar]
- Mercado, J.M.R.; Kawamura, A.; Medina, R. An expanded interpretive structural modeling analysis of the barriers to integrated flood risk management adaptation in Metro Manila. Water 2023, 15, 1029. [Google Scholar] [CrossRef]
- Koike, T. Evolution of Japan’s flood control planning and policy in response to climate change risks and social changes. Water Policy 2021, 23, 77–84. [Google Scholar] [CrossRef]


| No. | Models | Storage Equation | Continuity Equation |
|---|---|---|---|
| 1 | Linear (3-PAR) | ||
| 2 | Kimura (4-PAR) | ||
| 3 | Prasad (5-PAR) | ||
| 4 | Hoshi (6-PAR) | ||
| 5 | USF (7-PAR) |
| Geometry | Image | Characteristics (a) Objective; (b) Features; (c) Land use; (d) Handling of Buildings; (e) Surface Flow Equations |
|---|---|---|
| Structured Grid [118,119,120] |  |
|
| Curvilinear Grid [121,122] | 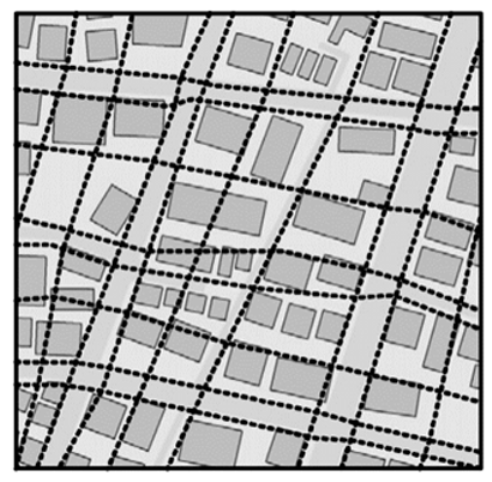 |
|
| Unstructured Grid [123,124] |  |
|
| Road Network [125,126] | 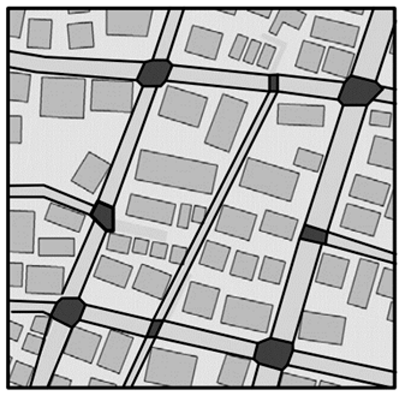 |
|
| Urban Landscape Delineation [6] |  |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kawamura, A.; Amaguchi, H.; Olsson, J.; Tanouchi, H. Urban Flood Runoff Modeling in Japan: Recent Developments and Future Prospects. Water 2023, 15, 2733. https://doi.org/10.3390/w15152733
Kawamura A, Amaguchi H, Olsson J, Tanouchi H. Urban Flood Runoff Modeling in Japan: Recent Developments and Future Prospects. Water. 2023; 15(15):2733. https://doi.org/10.3390/w15152733
Chicago/Turabian StyleKawamura, Akira, Hideo Amaguchi, Jonas Olsson, and Hiroto Tanouchi. 2023. "Urban Flood Runoff Modeling in Japan: Recent Developments and Future Prospects" Water 15, no. 15: 2733. https://doi.org/10.3390/w15152733
APA StyleKawamura, A., Amaguchi, H., Olsson, J., & Tanouchi, H. (2023). Urban Flood Runoff Modeling in Japan: Recent Developments and Future Prospects. Water, 15(15), 2733. https://doi.org/10.3390/w15152733






