Experimental and Modeling Evaluation of Impacts of Different Tillage Practices on Fitting Parameters of Kostiakov’s Cumulative Infiltration Empirical Equation
Abstract
:1. Introduction
2. Materials and Methods
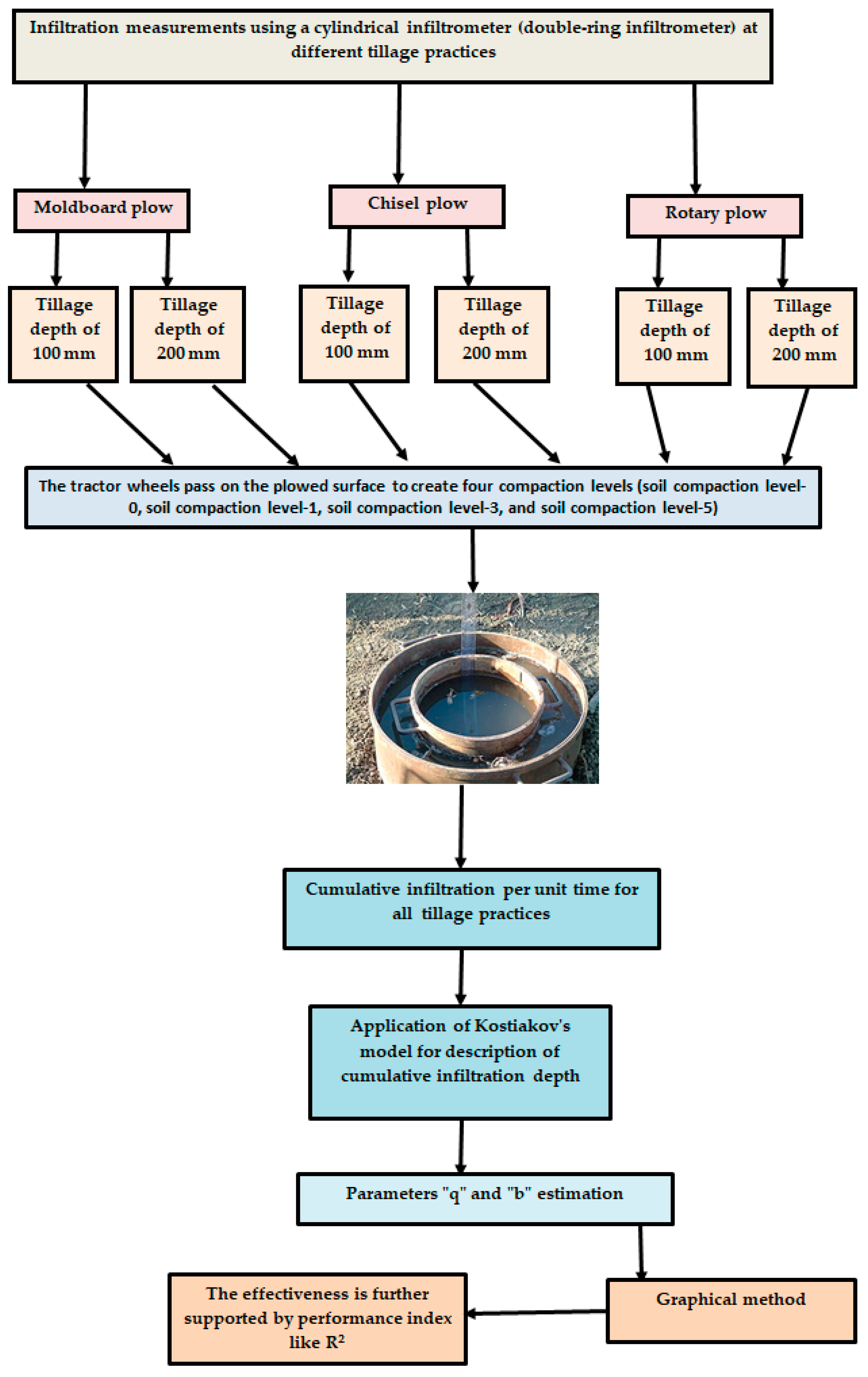
2.1. Procedures of the First Stage of the Research (the Experimental Work)
2.2. Double-Ring Infiltration Experiments
2.3. Determination of Kostiakov Equation Fitting Parameters for Cumulative Infiltration (the Second Stage of the Research)
2.4. Statistical Analysis
2.5. Procedures of the Third Stage of the Research (Data Mining Algorithms)
2.6. Statistical Criteria for Evaluation of Regression Data Mining Algorithms
3. Results and Discussion
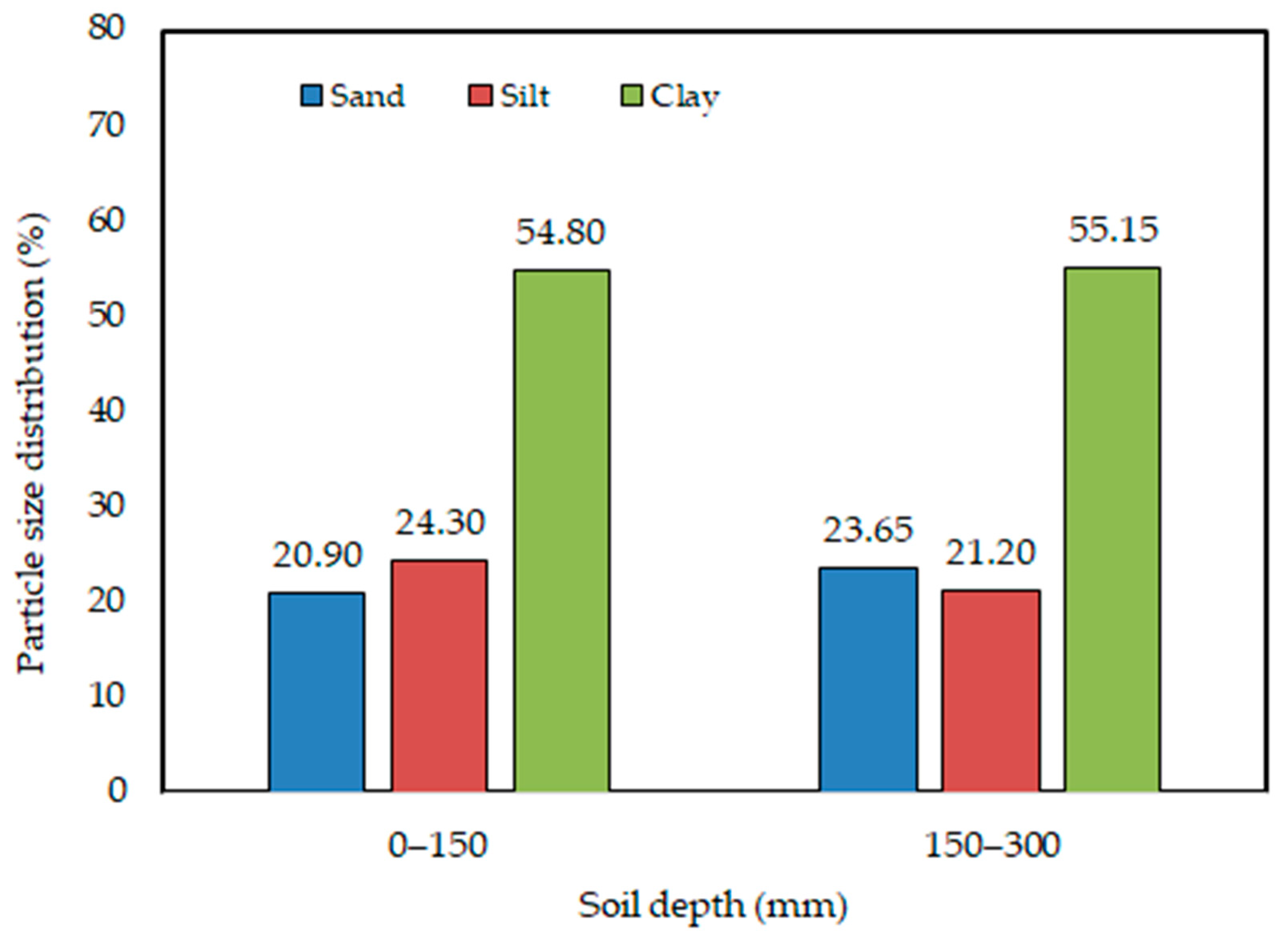
3.1. Data Analysis of the First Stage of the Research (the Experimental Work) for Soil Mean Weight Diameter
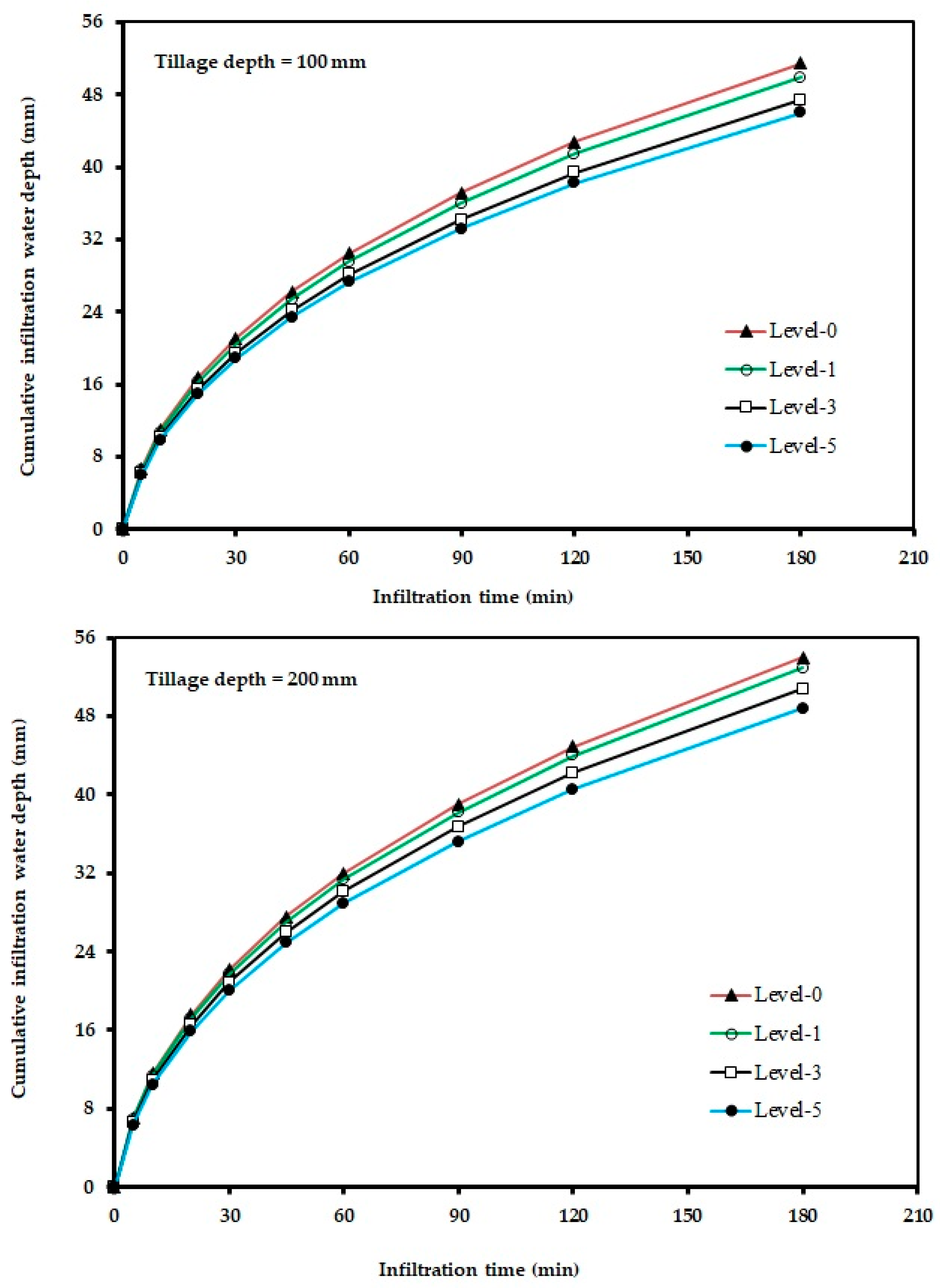
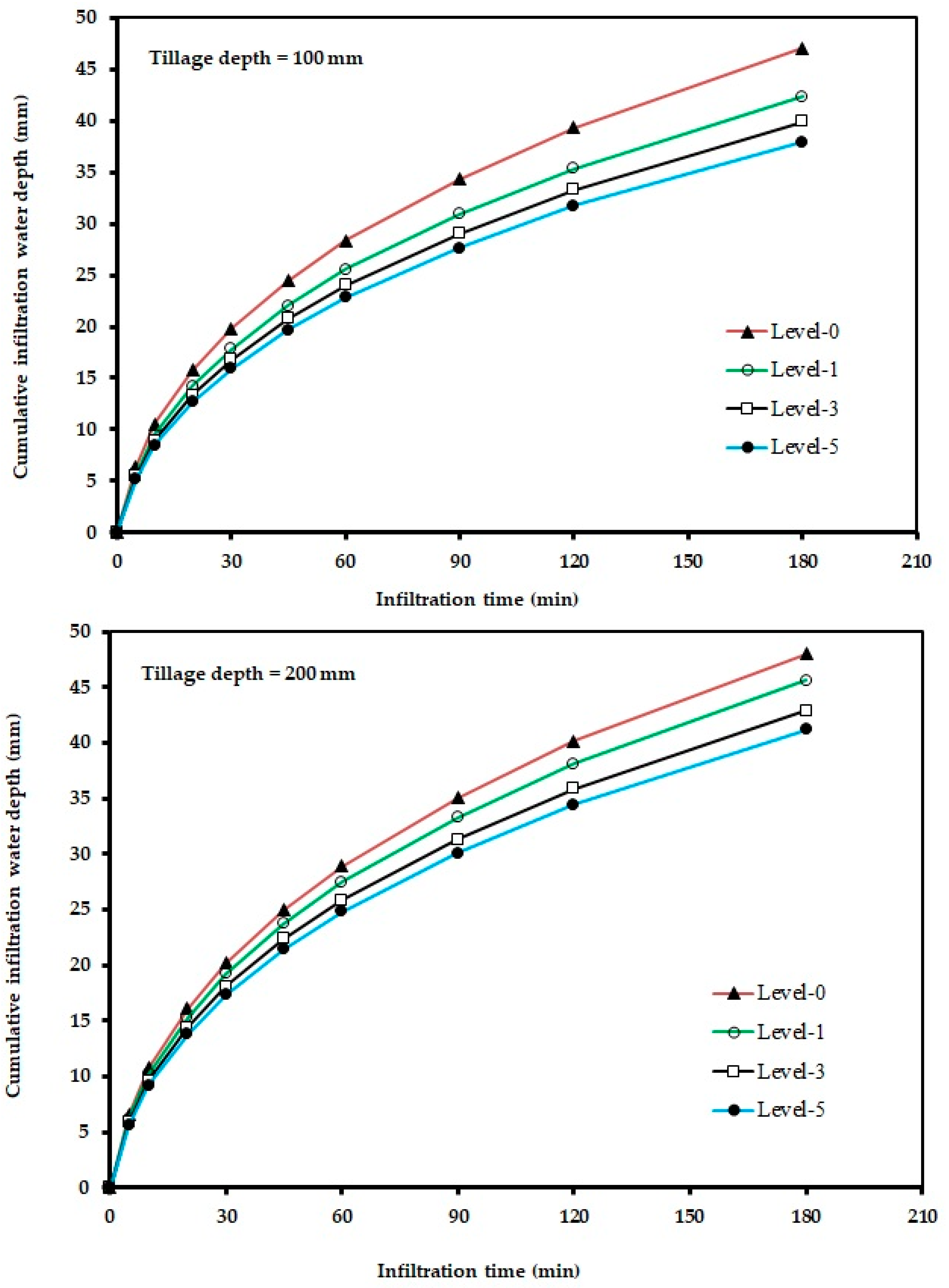
3.2. Data Analysis of the Second Stage of the Research (Water Cumulative Infiltration Depths)
3.3. Kostiakov Fitting Parameters
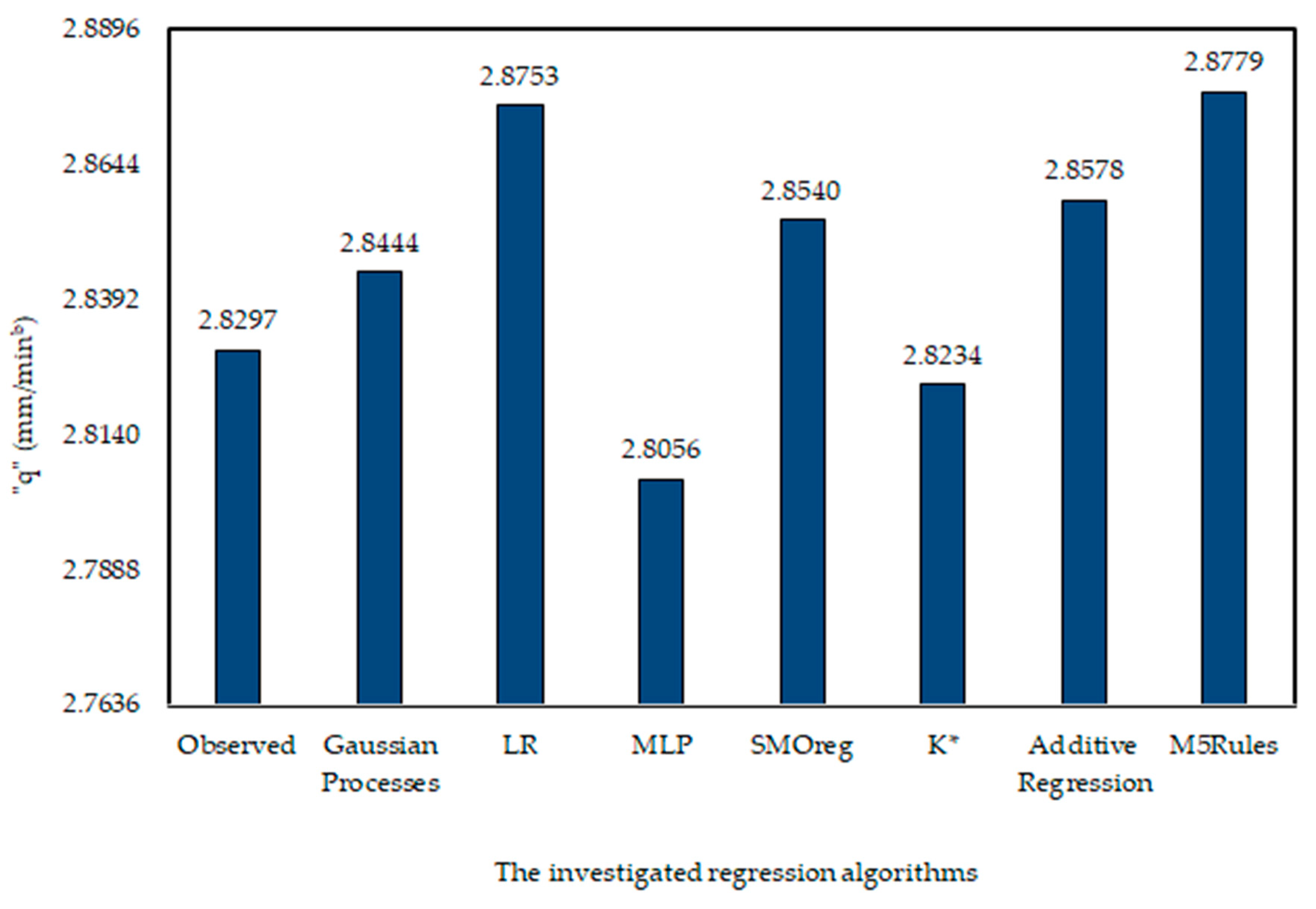
3.4. Data Analysis of the Third Stage of the Research (Data Mining Algorithms)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mahapatra, S.; Jha, M.K.; Biswal, S.; Senapati, D. Assessing variability of infiltration characteristics and reliability of infiltration models in a tropical sub-humid region of India. Sci. Rep. 2020, 10, 1515. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, Y.; Huang, N.; Gong, J.; Shao, X.; Zhang, J.; Zhao, T. A simplified infiltration model for predicting cumulative infiltration during vertical line source irrigation. Water 2018, 10, 89. [Google Scholar] [CrossRef] [Green Version]
- Amami, R.; Ibrahimi, K.; Sher, F.; Milham, P.; Ghazouani, H.; Chehaibi, S.; Hussain, Z.; Iqbal, H.M.N. Impacts of Different tillage practices on soil water infiltration for sustainable agriculture. Sustainability 2021, 13, 3155. [Google Scholar] [CrossRef]
- Ahuchaogu, I.I.; Emit, I.; Etuk, A.I. Effects of tillage methods on soil infiltration rate in UYO, Nigeria. Cont. J. Eng. Sci. 2015, 10, 10–20. [Google Scholar]
- Villanueva, J.J.M.; García, V.M.V.; Alberich, M.V.E.; Huerta, A.G.; Arriaga, M.R.; Rodríguez, F.G. MEAN infiltration speed in a vertisol under different tillage systems. Terra Latinoam. 2015, 33, 95–99. [Google Scholar]
- Osanyinpeju, K.; Dada, P.O. Soil porosity and water infiltration as influenced by tillage practices on federal university of agriculture Abeokuta, Ogun State, Nigeria soil. Int. J. Latest Technol. Eng. Manag. Appl. Sci. 2018, 7, 2278–2540. [Google Scholar]
- Atta-Darkwa, T.; Asare, A.; Amponsah, W.; Oppon, E.D.; Agbeshie, A.A.; Budu, M.; Larbi, I.; Akolgo, G.A.; Quaye, D.N.D. Performance evaluation of infiltration models under different tillage operations in a tropical climate. Sci. Afr. 2022, 17, e01318. [Google Scholar] [CrossRef]
- Mohammadshirazi, F.; Brown, V.K.; Heitman, J.L.; McLaughlin, R.A. Effects of tillage and compost amendment on infiltration in compacted soils. J. Soil Water Conserv. 2016, 71, 443–449. [Google Scholar] [CrossRef] [Green Version]
- Rahman, S.M.; Islam, A. Effects of tillage depth on infiltration characteristics of two Bangladesh soils having plowpans. Soil Tillage Res. 1989, 13, 407–412. [Google Scholar] [CrossRef]
- Ibeje, A.O.; Osuagwu, J.C.; Onosakponome, O.R. Impacts of land use on infiltration. World J. Eng. Res. Technol. 2018, 4, 95–102. [Google Scholar]
- Dahak, A.; Boutaghane, H.; Merabtene, T. Parameter estimation and assessment of infiltration models for Madjez Ressoul Catchment, Algeria. Water 2022, 14, 1185. [Google Scholar] [CrossRef]
- Sajjadi, S.-A.-H.; Mirzaei, M.; Nasab, A.F.; Sarkardeh, H. Effect of soil Physical Properties on infiltration rate. Geomech. Eng. 2016, 10, 727–736. [Google Scholar] [CrossRef]
- Mattar, M.A.; Alazba, A.A.; Zin El-Abedin, T.K. Forecasting furrow irrigation infiltration using artificial neural networks. Agric. Water Manag. 2015, 148, 63–71. [Google Scholar] [CrossRef]
- Ogbe, V.B.; Jayeoba, O.J.; Ode, S.O. Comparison of four soil infiltration models on a sandy soil in Lafia, Southern Guinea Savanna Zone of Nigeria. PAT 2011, 7, 116–126. [Google Scholar]
- Zolfaghari, A.A.; Mirzaee, S.; Gorji, M. Comparison of different models for estimating cumulative infiltration. Int. J. Soil Sci. 2012, 7, 108–115. [Google Scholar] [CrossRef] [Green Version]
- Patle, G.T.; Sikar, T.T.; Rawat, K.S.; Singh, S.K. Estimation of infiltration rate from soil properties using regression model for cultivated land. Geol. Ecol. Landsc. 2019, 3, 1–13. [Google Scholar] [CrossRef]
- Al-Ghobari, H.M. Modeling soil infiltration under variables of application rate and number of irrigation. J. King Saud Univ. Agric. Sci. 2003, 15, 185–194. [Google Scholar]
- Mishra, S.K.; Tyagi, J.V.; Singh, V.P. Comparison of infiltration models. J. Hydrol. Process. 2003, 17, 2629–2652. [Google Scholar] [CrossRef]
- Haghiabi, A.H.; Abedi-koupai, J.; Heidarpour, M.; Mohammadzadeh-Habili, J. A new method for estimating the parameters of Kostiakov and modified Kostiakov infiltration equations. World Appl. Sci. J. 2011, 15, 129–135. [Google Scholar]
- Adindu, R.U.; Kelechi, K.I.; Chigbu Timothy, O.; Ike-Amadi, C.A. Application of Kostiakov’s infiltration model on the soils of Umudike, Abia State–Nigeria. Am. J. Environ. Eng. 2014, 4, 1–6. [Google Scholar]
- Elmarazky, M.S.A.; Aboukarima, A.M.; Guirguis, A.E.; Egela, M.I. Water infiltration as affected by tillage methods, plowing depth and wheel traffic. J. Agric. Sci. Mansoura Univ. 2007, 32, 2019–2033. [Google Scholar]
- Hossne García, A.J.; Jesús, M.N.; Smith, I.J.; Velázquez, P.; Leiva, L.M.G.; Gil, A. Effects of compaction, moisture and depth on the parameters of the Kostiakov equation. ESPAMCIENCIA J. 2021, 12, 56–68. [Google Scholar] [CrossRef]
- Al-Sulaiman, A.; Aboukarima, A.M.; Zayed, M.F. Prediction of Kostiakov parameters of cumulative infiltration based on soil and water characteristics. Egypt. J. Agric. Res. 2015, 93, 273–291. [Google Scholar]
- Sihag, P.; Singh, B.; Sepah, S.A.; Mehdipour, V. Modeling the infiltration process with soft computing techniques. ISH J. Hydraul. Eng. 2018, 26, 138–152. [Google Scholar] [CrossRef]
- Sihag, P.; Tiwari, N.K.; Ranjan, S. Support vector regression-based modeling of cumulative infiltration of sandy soil. ISH J. Hydraul. Eng. 2020, 26, 44–50. [Google Scholar] [CrossRef]
- Zakwan, M. Assessment of dimensionless form of Kostiakov model. Aquademia: Water Environ. Technol. 2017, 1, 1. [Google Scholar] [CrossRef]
- Kashi, H.; Emamqolizadeh, S.; Qorbani, H.; Hashemi, S.A.A. Estimation of soil infiltration using artificial neural network and linear regression in agricultural lands. J. Environ. Eros. Res. 2013, 3, 19–34. [Google Scholar]
- Angelaki, A.; Singh, S.; Singh, V.; Sihag, P. Estimation of models for cumulative infiltration of soil using machine-learning methods. ISH J. Hydraul. Eng. 2021, 27, 162–169. [Google Scholar] [CrossRef]
- Vand, A.S.; Sihag, P.; Singh, B.; Zand, M. Comparative evaluation of infiltration models. KSCE J. Civ. Eng. 2018, 22, 4173–4184. [Google Scholar] [CrossRef]
- Singh, B.; Sihag, P.; Singh, K. Modelling of impact of water quality on infiltration rate of soil by random forest regression. Model. Earth Syst. Environ. 2017, 3, 999–1004. [Google Scholar] [CrossRef]
- Panahi, M.; Khosravi, K.; Ahmad, S.; Panahi, S.; Heddam, S.; Melesse, A.; Omidvar, E.; Lee, C. Cumulative infiltration and infiltration rate prediction using optimized deep learning algorithms: A study in Western Iran. J. Hydrol. Reg. Stud. 2021, 35, 100825. [Google Scholar] [CrossRef]
- Salifu, A.; Abagale, F.; Kranjac-Berisavljevic, G. Estimation of infiltration models’ parameters using regression analysis in irrigation fields of Northern Ghana. Open J. Soil Sci. 2021, 11, 164–176. [Google Scholar] [CrossRef]
- Seongyun, K.; Karahan, G.; Sharma, M.; Pachepsky, Y. Estimating parameters of empirical infiltration models from the global dataset using machine learning. Int. Agrophys. 2021, 35, 73–81. [Google Scholar] [CrossRef]
- Tiwari, N.K.; Sihag, P.; Ranjan, S. Modeling of infiltration of soil using adaptive neuro-fuzzy inference system (ANFIS). J. Eng. Technol. Educ. 2017, 11, 13–21. [Google Scholar]
- Sayari, S.; Mahdavi-Meymand, A.; Zounemat-Kermani, M. Irrigation water infiltration modeling using machine learning. Comput. Electron. Agric. 2021, 180, 105921. [Google Scholar] [CrossRef]
- Voorhees, W.B.; Evans, S.D.; Warnes, D.D. Effect of preplant wheel traffic on soil compaction, water use and growth of spring wheat. Soil Sci. Soc. Am. J. 1985, 49, 215–220. [Google Scholar] [CrossRef]
- Li, Y.; Ma, Z.; Liu, Y.; Cui, Z.; Mo, Q.; Zhang, C.; Sheng, H.; Wang, W. Variation in soil aggregate stability due to land use changes from Alpine grassland in a high-altitude watershed. Land 2023, 12, 393. [Google Scholar] [CrossRef]
- Kostiakov, A.N. On the dynamics of the coefficient of water percolation in soils and on the necessity of studying it from a dynamic point of view for the purposes of amelioration. Soc. Soil Sci. 1932, 14, 17–21. [Google Scholar]
- Uloma, A.R.; Samuel, A.C.; Kingsley, I.K. Estimation of Kostiakov’s infiltration model parameters of some sandy loam soils of Ikwuano–Umuahia. Nigeria. Open Trans. Geosci. 2014, 1, 34–38. [Google Scholar] [CrossRef]
- Khaliq, A.; Iqbal, M.; Anwar, S. Evaluation of Kostiakov infiltration equation parameters from irrigation advance in level basins. Pak. J. Agri. Sci. 1994, 31, 258–264. [Google Scholar]
- El-Bakhshwan, M.H.; Aboukarima, A.M.; Hemeda, S.G. Impact of mixing biogas liquid manure with soil on water infiltration under flood irrigation system. Asian Res. J. Agric. 2016, 1, 1–12. [Google Scholar] [CrossRef]
- Gebl, M.A. Simplified approach for determination of parameters for Kostiakov’s infiltration equation. Water Pract. Technol. 2022, 17, 2435–2446. [Google Scholar] [CrossRef]
- Garner, S.R. WEKA: The Waikato Environment for Knowledge Analysis. In Proceedings of the New Zealand Computer Science Research Students Conference; 1995; pp. 57–64. [Google Scholar]
- SAS. User’s Guide, Statistical Analysis System; SAS Ins., Inc.: Cary, NC, USA, 1986. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Ian Witten, H. The WEKA Data Mining Software: An Update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Frank, E.; Hall, M.; Trigg, L.; Holmes, G.; Witten, I.H. Data mining in bioinformatics using Weka. Bioinformatics 2004, 20, 2475–2481. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alencar, D.; Carvalho, D.; Koenders, E.; Mourao, F.; Rocha, L. Devising a computational model based on data mining techniques to predict concrete compressive strength. Procedia Comput. Sci. 2017, 108, 455–464. [Google Scholar] [CrossRef]
- Cleary, J.G.; Trigg, L.E. k*: An instance-based learner using an entropic distance measure. In Proceedings of the 12th International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995; pp. 108–114. [Google Scholar]
- Wang, K. Introduction to Gaussian Process Regression, Part 1: The Basics. 2022. Available online: https://medium.com/data-science-at-microsoft/introduction-to-gaussian-process-regression-part-1-the-basics-3 (accessed on 8 March 2023).
- Shevade, S.; Keerthi, S.; Bhattacharyya, C.; Murthy, K. Improvements to the SMO algorithm for SVM regression. IEEE Trans. Neural Netw. 2000, 11, 1188–1193. [Google Scholar] [CrossRef] [Green Version]
- Tso, G.K.; Yau, K.K. Predicting electricity energy consumption: A comparison of regression analysis, decision tree and neural networks. Energy 2007, 32, 1761–1768. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann Pub: Cambridge, MA, USA, 2005. [Google Scholar]
- Wormstrand, O. Electricity Price Prediction. A Comparison of Machine Learning Algorithms. Master’s Thesis, Ostfold University College, Halden, Norway, 2011. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Chaudhari, M.S.; Choudhari, N.K. Study of various rainfall estimation & prediction techniques using data mining. Am. J. Eng. Res. (AJER) 2017, 6, 137–139. [Google Scholar]
- Brouwer, C.; Goffeau, A.; Heibloem, M. Irrigation Water Management: Training Manual No. 1-Introduction to Irrigation. FAO—Food and Agriculture Organization of the United Nations. 1985. Available online: http://www.fao.org/docrep/r4082e/r4082e00.htm#Contents (accessed on 1 April 2023).
- Romkens, M.J.; Luk, M.S.H.; Poesen, J.W.A.; Mermut, A.R. Rainfall infiltration into loess soils from different geographic regions. Catena 1995, 25, 21–32. [Google Scholar] [CrossRef]
- Hwang, S.I.; Powers, S.E. Using particle-size distribution models to estimate soil hydraulic properties. Soil Sci. Soc. Am. 2003, 67, 1103–1112. [Google Scholar] [CrossRef]
- Hamza, M.A.; Anderson, W.K. Soil compaction in cropping systems: A review of the nature, causes, and possible solutions. Soil Tillage Res. 2005, 82, 121–145. [Google Scholar] [CrossRef]
- Khadr, K.A. Effect of some primary tillage implement on soil pulverization and specific energy. Misr. J. Agric. Eng. 2008, 25, 731–745. [Google Scholar] [CrossRef]
- Hajabbasi, M.A.; Hemmat, A. Tillage impacts on aggregate stability and crop productivity in a clay-loam soil in central Iran. Soil Tillage Res. 2000, 56, 205–212. [Google Scholar] [CrossRef]
- Çarman, K. Effect of different tillage systems on soil properties and wheat yield in middle Anatolia. Soil Tillage Res. 1997, 40, 201–207. [Google Scholar] [CrossRef]
- Boydas, M.G.; Turgut, N. Effect of tillage implements and operating speeds on soil physical properties and wheat emergence. Turk. J. Agric. For. 2007, 31, 399–412. [Google Scholar]
- Carter, M.R. Characterization of soil physical properties and organic matter under long-term primary tillage in a humid climate. Soil Tillage Res. 1996, 38, 251–263. [Google Scholar] [CrossRef]
- Naseer, S.; Kadhim, A.; Subr, K. Effect of tillage with chisel plow on soil mean weight diameter and porosity. Iraqi J. Agric. Sci. 2012, 33, 33–41. [Google Scholar]
- Yassen, H.A.; Hassan, H.M.; Hammadi, I.A. Effects of plowing depth using different plow types on some physical properties of soil. AMA 1992, 23, 21–24. [Google Scholar]
- Ramezani, N.; Sayyad, G.A.; Barzegar, A.R. Tractor wheel compaction effect on soil water infiltration, hydraulic conductivity and bulk density. Malays. J. Soil Sci. 2017, 21, 47–61. [Google Scholar]
- Barzegar, A.R.; Hashemi, A.M.; Herbert, S.J.; Asoodar, M.A. Interactive effects of tillage system and soil water content on aggregate size distribution for seedbed preparation in Fluvisols in southwest Iran. Soil Tillage Res. 2004, 78, 45–52. [Google Scholar] [CrossRef]
- Yadav, R.K.; Singh, P.; Singh, S.K. Performance analysis of rotavator and other tillage implement driven by the tractor. Int. J. Agric. Eng. 2017, 10, 590–594. [Google Scholar] [CrossRef]
- Moret, D.; Arrué, J.L. Characterizing soil water-conducting macro- and mesoporosity as influenced by tillage using tension infiltrometry. Soil Sci. Soc. Am. J. 2007, 71, 500–506. [Google Scholar] [CrossRef] [Green Version]
- Flowers, M.D.; Lal, R. Axle load and tillage effects on soil physical properties and soybean grain yield on a Mollic ochraqualf in Northwest Ohio. Soil Tillage Res. 1998, 48, 21–35. [Google Scholar] [CrossRef]
- Reicosky, D.C. Long term effect of moldboard plowing on tillage induced CO2 loss. In Agricultural Practices and Policies for Carbon Sequestration in Soil; Kimble, J.M., Lal, R., Follet, R.F., Eds.; CRC/Lewis: Boca Raton, FL, USA, 2002; pp. 87–97. [Google Scholar]
- Ankeny, M.D.; Kaspar, T.C.; Horton, R. Characterization of tillage and traffic effects on unconfined infiltration measurements. Soil Sci. Soc. Am. J. 1990, 54, 837–840. [Google Scholar] [CrossRef] [Green Version]
- Al-Ghazal, A.A. Effect of tillage practices and compaction on infiltration rate of sandy soils. Pak. J. Biol. Sci. 2000, 3, 1443–1446. [Google Scholar] [CrossRef] [Green Version]
- Mbagwu, J.S.C. Testing the goodness of fit of infiltration models for highly permeable soils under different tropical soil management systems. Soil Tillage Res. 1995, 34, 199–205. [Google Scholar] [CrossRef]
- Al-Matroud, S.S. Evaluation of Irrigation Water Quality and its Effect on Soil Infiltration Rate in Riyadh Region. Master’s Thesis, College of Agriculture, King Saud University, Riyadh, Saudi Arabia, 2003. (In Arabic). [Google Scholar]
- Eze, P.C.; Musa, J.J. Prediction of infiltration rates of fallow and cultivated soils in Minna, Southern Guinea Savanna zone of Nigeria. J. Soil Water Conserv. 2022, 21, 337–344. [Google Scholar] [CrossRef]
- Fok, Y.-S. Derivation of Lewis-Kostiakov intake equation. J. Irrig. Drain. Eng. 1986, 112, 164–171. [Google Scholar] [CrossRef]
- Dixon, R.M.; Simanton, J.R.; Lane, L.J. Simple Time-Power Functions for Rainwater Infiltration and Runoff. Arizona-Nevada Academy of Science. 1978. Available online: http://hdl.handle.net/10150/301042 (accessed on 1 April 2023).
- Guzmán-Rojo, D.B.; Bautista, E.; Gonzalez-Trinidad, J.; Bronson, K.F. Variability of furrow infiltration and estimated infiltration parameters in a macroporous soil. J. Irrig. Drain. Eng. 2019, 145, 16. [Google Scholar] [CrossRef] [Green Version]
- Teixeira, S.; Guimarães, A.M.; Proença, C.A.; da Rocha, J.C.F.; Caires, E.F. Data mining algorithms for prediction of soil organic matter and clay based on Vis-NIR Spectroscopy. Int. J. Agric. For. 2014, 4, 310–316. [Google Scholar]
- Bushara, N.O.; Abraham, A. Weather forecasting in Sudan using machine learning schemes. J. Netw. Innov. Comput. 2014, 2, 309–317. [Google Scholar]
- Sihag, P.; Singh, S. Modeling of Infiltration Rate Using Data Mining Models. Conference Paper (I-CONCEPTS-18/). 2018. Available online: http://www.gjesr.com/Issues%20PDF/I-CONCEPTS-18/32.pdf (accessed on 10 March 2023).
- Khasraei, A.; Abyaneh, H.Z.; Jovzi, M.; Albaji, M. Determining the accuracy of different water infiltration models in lands under wheat and bean cultivation. J. Hydrol. 2021, 603, 127122. [Google Scholar] [CrossRef]







| Class | Algorithms | Description |
|---|---|---|
| Rule | M5Rules | By using separate-and-conquer, this generates a decision list for regression issues. It employs M5 to construct a model tree in each cycle, turning the “best” leaf into a rule [47]. |
| Meta | Additive Regression | A fitting model’s residuals are adjusted interactively for prediction while taking earlier iterations into account [47]. |
| Lazy | KStar (K*) | An entropy-based distance function is used to calculate how similar the training examples are in order to make predictions [48]. |
| Function | Gaussian Processes | Regression without hyper-parameter tweaking is performed. This measures the match between arguments to forecast the value using lazy learning [49]. |
| SMOreg | The algorithm is dependent on the support vector machine method for regression predictions [50]. |
| Source of Variation | Degrees of Freedom | Anova SS | Mean Square | F-Value | p-Values |
|---|---|---|---|---|---|
| Replicates | 2 | 2.45 | 1.2 | 4.53 | 0.0160 |
| TI | 2 | 21,752.6 | 10,876.3 | 40,159.1 | <0.0001 |
| NTT | 3 | 6587.7 | 2195.9 | 8108.07 | <0.0001 |
| TD | 1 | 168.2 | 168.2 | 621.01 | <0.0001 |
| 6 | 1583.9 | 263.9 | 974.70 | <0.0001 | |
| 2 | 40.4 | 20.2 | 74.65 | <0.0001 | |
| 3 | 1.3 | 0.44 | 1.64 | 0.1942 | |
| 6 | 0.32 | 0.053 | 0.20 | 0.9762 |
| Treatments | Mean MWD (mm) |
|---|---|
| Moldboard plow | 57.86 a |
| Chisel plow | 32.98 b |
| Rotary plow | 15.50 c |
| LSD (5%) | 0.30 |
| Soil compaction level-0 | 47.84 a |
| Soil compaction level-1 | 40.67 b |
| Soil compaction level-3 | 30.52 c |
| Soil compaction level-5 | 22.76 d |
| LSD (5%) | 0.35 |
| Tillage depth (100 mm) | 33.92 b |
| Tillage depth (200 mm) | 36.98 a |
| LSD (5%) | 0.25 |
| Soil MWD (mm) | Number of Tractor Wheel Passes on the Plowed Soil Surface (-) | Tillage Depth (mm) | Replicates | “q” (mm/minb) | “b” (Dimensionless) |
|---|---|---|---|---|---|
| 75.5 | 0 | 104 | R1 | 2.979 | 0.5595 |
| 77.6 | 0 | 108 | R2 | 2.963 | 0.5637 |
| 74.8 | 0 | 103 | R3 | 2.962 | 0.5634 |
| 80.4 | 0 | 189 | R1 | 3.128 | 0.5595 |
| 79.7 | 0 | 201 | R2 | 3.124 | 0.5627 |
| 80.5 | 0 | 197 | R3 | 3.119 | 0.5627 |
| 63.4 | 1 | 105 | R1 | 2.889 | 0.5595 |
| 65.2 | 1 | 98 | R2 | 2.888 | 0.5627 |
| 62.8 | 1 | 106 | R3 | 2.879 | 0.5627 |
| 69.1 | 1 | 198 | R1 | 3.065 | 0.5595 |
| 68.5 | 1 | 204 | R2 | 3.051 | 0.5631 |
| 69.2 | 1 | 189 | R3 | 3.063 | 0.5624 |
| 46.9 | 3 | 102 | R1 | 2.745 | 0.5595 |
| 48.2 | 3 | 104 | R2 | 2.735 | 0.5627 |
| 46.5 | 3 | 105 | R3 | 2.738 | 0.5636 |
| 52.5 | 3 | 194 | R1 | 2.943 | 0.5595 |
| 52.1 | 3 | 198 | R2 | 2.926 | 0.5640 |
| 52.6 | 3 | 189 | R3 | 2.941 | 0.5621 |
| 34.3 | 5 | 98 | R1 | 2.663 | 0.5595 |
| 35.2 | 5 | 97 | R2 | 2.651 | 0.5632 |
| 33.9 | 5 | 108 | R3 | 2.642 | 0.5647 |
| 39.9 | 5 | 198 | R1 | 2.825 | 0.5595 |
| 39.6 | 5 | 194 | R2 | 2.801 | 0.5647 |
| 40.0 | 5 | 197 | R3 | 2.818 | 0.5625 |
| Soil MWD (mm) | Number of Tractor Wheel Passes on the Plowed Soil Surface (-) | Tillage Depth (mm) | Replicates | “q” (mm/minb) | “b” (Dimensionless) |
|---|---|---|---|---|---|
| 43.0 | 0 | 104 | R1 | 2.918 | 0.546 |
| 44.2 | 0 | 107 | R2 | 2.900 | 0.551 |
| 42.6 | 0 | 106 | R3 | 2.900 | 0.551 |
| 45.8 | 0 | 195 | R1 | 2.976 | 0.546 |
| 45.4 | 0 | 203 | R2 | 2.971 | 0.550 |
| 45.9 | 0 | 198 | R3 | 2.966 | 0.550 |
| 36.1 | 1 | 107 | R1 | 2.626 | 0.546 |
| 37.2 | 1 | 102 | R2 | 2.623 | 0.550 |
| 35.8 | 1 | 114 | R3 | 2.615 | 0.550 |
| 39.4 | 1 | 207 | R1 | 2.827 | 0.546 |
| 39.1 | 1 | 197 | R2 | 2.812 | 0.551 |
| 39.5 | 1 | 207 | R3 | 2.824 | 0.550 |
| 26.8 | 3 | 104 | R1 | 2.469 | 0.546 |
| 27.5 | 3 | 103 | R2 | 2.457 | 0.550 |
| 26.5 | 3 | 98 | R3 | 2.460 | 0.551 |
| 30.0 | 3 | 187 | R1 | 2.658 | 0.546 |
| 29.7 | 3 | 197 | R2 | 2.639 | 0.552 |
| 30.0 | 3 | 198 | R3 | 2.655 | 0.550 |
| 19.5 | 5 | 102 | R1 | 2.345 | 0.546 |
| 20.1 | 5 | 99 | R2 | 2.332 | 0.551 |
| 19.3 | 5 | 108 | R3 | 2.322 | 0.553 |
| 22.8 | 5 | 201 | R1 | 2.551 | 0.546 |
| 22.6 | 5 | 194 | R2 | 2.526 | 0.553 |
| 22.8 | 5 | 198 | R3 | 2.543 | 0.550 |
| Soil MWD (mm) | Number of Tractor Wheel Passes on the Plowed Soil Surface (-) | Tillage Depth (mm) | Replicates | “q” (mm/minb) | “b” (Dimensionless) |
|---|---|---|---|---|---|
| 20.2 | 0 | 98 | R1 | 2.679 | 0.5424 |
| 20.8 | 0 | 104 | R2 | 2.660 | 0.5475 |
| 20.0 | 0 | 103 | R3 | 2.660 | 0.5471 |
| 21.5 | 0 | 195 | R1 | 2.813 | 0.5424 |
| 21.4 | 0 | 198 | R2 | 2.808 | 0.5464 |
| 21.6 | 0 | 198 | R3 | 2.803 | 0.5463 |
| 17.0 | 1 | 104 | R1 | 2.599 | 0.5424 |
| 17.5 | 1 | 111 | R2 | 2.595 | 0.5464 |
| 16.8 | 1 | 109 | R3 | 2.587 | 0.5463 |
| 18.5 | 1 | 198 | R1 | 2.701 | 0.5424 |
| 18.4 | 1 | 196 | R2 | 2.684 | 0.5469 |
| 18.5 | 1 | 198 | R3 | 2.696 | 0.5461 |
| 12.6 | 3 | 97 | R1 | 2.469 | 0.5424 |
| 12.9 | 3 | 98 | R2 | 2.457 | 0.5463 |
| 12.5 | 3 | 97 | R3 | 2.460 | 0.5475 |
| 14.1 | 3 | 197 | R1 | 2.593 | 0.5424 |
| 14.0 | 3 | 195 | R2 | 2.574 | 0.5480 |
| 14.1 | 3 | 189 | R3 | 2.589 | 0.5457 |
| 9.2 | 5 | 104 | R1 | 2.296 | 0.5424 |
| 9.4 | 5 | 98 | R2 | 2.283 | 0.5471 |
| 9.1 | 5 | 108 | R3 | 2.272 | 0.5490 |
| 10.7 | 5 | 198 | R1 | 2.411 | 0.5424 |
| 10.6 | 5 | 187 | R2 | 2.385 | 0.5491 |
| 10.7 | 5 | 187 | R3 | 2.402 | 0.5463 |
| Source of Variation | DF | p-Values | |
|---|---|---|---|
| “q” (mm/minb) | “b” (Dimensionless) | ||
| TI | 2 | <0.0001 | <0.0001 |
| NTT | 3 | 0.0152 | 0.9868 |
| TD | 1 | 0.0902 | 0.2770 |
| 6 | 0.9950 | 1.000 | |
| 2 | 0.9714 | 0.9954 | |
| 3 | 0.9967 | 0.9355 | |
| 6 | 1.0000 | 1.000 | |
| Treatments | Mean Fitting Parameters | |
|---|---|---|
| “q” (mm/minb) | “b” (Dimensionless) | |
| Moldboard plow | 2.89736 a | 0.5619581 a |
| Chisel plow | 2.66316 b | 0.5493522 b |
| Rotary plow | 2.56147 c | 0.5454777 c |
| LSD (5%) | 0.0782 | 0.0015 |
| Soil compaction level-0 | 2.78313 a | 0.5521947 a |
| Soil compaction level-1 | 2.73002 ba | 0.5521412 a |
| Soil compaction level-3 | 2.67475 b | 0.5522829 a |
| Soil compaction level-5 | 2.64142 b | 0.5524318 a |
| LSD (5%) | 0.0903 | 0.0017 |
| Tillage depth (200 mm) | 2.73479 a | 0.5525892 a |
| Tillage depth (100 mm) | 2.67987 a | 0.5519362 a |
| LSD (5%) | 0.0639 | 0.0012 |
| Regression Algorithm | WEKA Information |
|---|---|
| M5Rules | Scheme: weka.classifiers.rules.M5Rules -M 4.0 |
| Additive Regression | Scheme: weka.classifiers.meta.AdditiveRegression -S 1.0 -I 10 -W weka.classifiers.trees.DecisionStump |
| KStar (K*) | Scheme: weka.classifiers.lazy.KStar -B 20 -M a |
| Gaussian Processes | Scheme: weka.classifiers.functions.GaussianProcesses -L 1.0 -N 0 -K “weka.classifiers.functions.supportVector.RBFKernel -C 250007 -G 1.0” |
| SMOreg | Scheme: weka.classifiers.functions.SMOreg -C 1.0 -N 0 -I “weka.classifiers.functions.supportVector.RegSMOImproved -L 0.001 -W 1 -P 1.0E-12 -T 0.001 -V” -K “weka.classifiers.functions.supportVector.PolyKernel -C 250007 -E 1.0” |
| LR | Scheme: weka.classifiers.functions.LinearRegression -S 0 -R 1.0E-8 |
| MLP | Scheme: weka.classifiers.functions.MultilayerPerceptron -L 0.3 -M 0.2 -N 500 -V 0 -S 0 -E 20 -H a |
| Regression Algorithm | “q” (mm/minb) | “b” (Dimensionless) |
|---|---|---|
| Gaussian Processes | 1.60 | 1.62 |
| Linear Regression | 0.01 | 0.01 |
| Multilayer Perceptron | 0.15 | 0.17 |
| SMOreg | 0.01 | 0.04 |
| KStar (K*) | 0.00 | 0.00 |
| Additive Regression | 0.03 | 0.02 |
| M5Rules | 0.25 | 0.25 |
| Regression Algorithm | “q” (mm/minb) | “b” (Dimensionless) | ||||
|---|---|---|---|---|---|---|
| MAE | RMSE | Correlation Coefficient | MAE | RMSE | Correlation Coefficient | |
| M5Rules | 0.0575 | 0.0702 | 0.946 | 0.0021 | 0.0028 | 0.808 |
| Additive Regression | 0.0459 | 0.0638 | 0.926 | 0.0026 | 0.0042 | 0.564 |
| KStar (K*) | 0.0179 | 0.0228 | 0.997 | 0.0021 | 0.0027 | 0.805 |
| SMOreg | 0.0373 | 0.0771 | 0.948 | 0.0019 | 0.0026 | 0.828 |
| Multilayer Perceptron (MLP) | 0.0425 | 0.0910 | 0.951 | 0.0013 | 0.0026 | 0.962 |
| Linear Regression (LR) | 0.0544 | 0.0667 | 0.947 | 0.0023 | 0.0029 | 0.786 |
| Gaussian Processes | 0.0604 | 0.0817 | 0.959 | 0.0033 | 0.0042 | 0.711 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdel-Sattar, M.; Al-Obeed, R.S.; Al-Hamed, S.A.; Aboukarima, A.M. Experimental and Modeling Evaluation of Impacts of Different Tillage Practices on Fitting Parameters of Kostiakov’s Cumulative Infiltration Empirical Equation. Water 2023, 15, 2673. https://doi.org/10.3390/w15142673
Abdel-Sattar M, Al-Obeed RS, Al-Hamed SA, Aboukarima AM. Experimental and Modeling Evaluation of Impacts of Different Tillage Practices on Fitting Parameters of Kostiakov’s Cumulative Infiltration Empirical Equation. Water. 2023; 15(14):2673. https://doi.org/10.3390/w15142673
Chicago/Turabian StyleAbdel-Sattar, Mahmoud, Rashid S. Al-Obeed, Saad A. Al-Hamed, and Abdulwahed M. Aboukarima. 2023. "Experimental and Modeling Evaluation of Impacts of Different Tillage Practices on Fitting Parameters of Kostiakov’s Cumulative Infiltration Empirical Equation" Water 15, no. 14: 2673. https://doi.org/10.3390/w15142673





