Statistical Analysis and Modeling of Suspended Sediment Yield Dependence on Environmental Conditions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Natural and Anthropogenic Conditions for the Formation of Suspended Sediment Yield in Rivers in the Study Area
2.2. Gauging Station Data
2.3. Basin Approach
2.4. Model Input Data
2.5. Analysis Methods
3. Results and Discussion
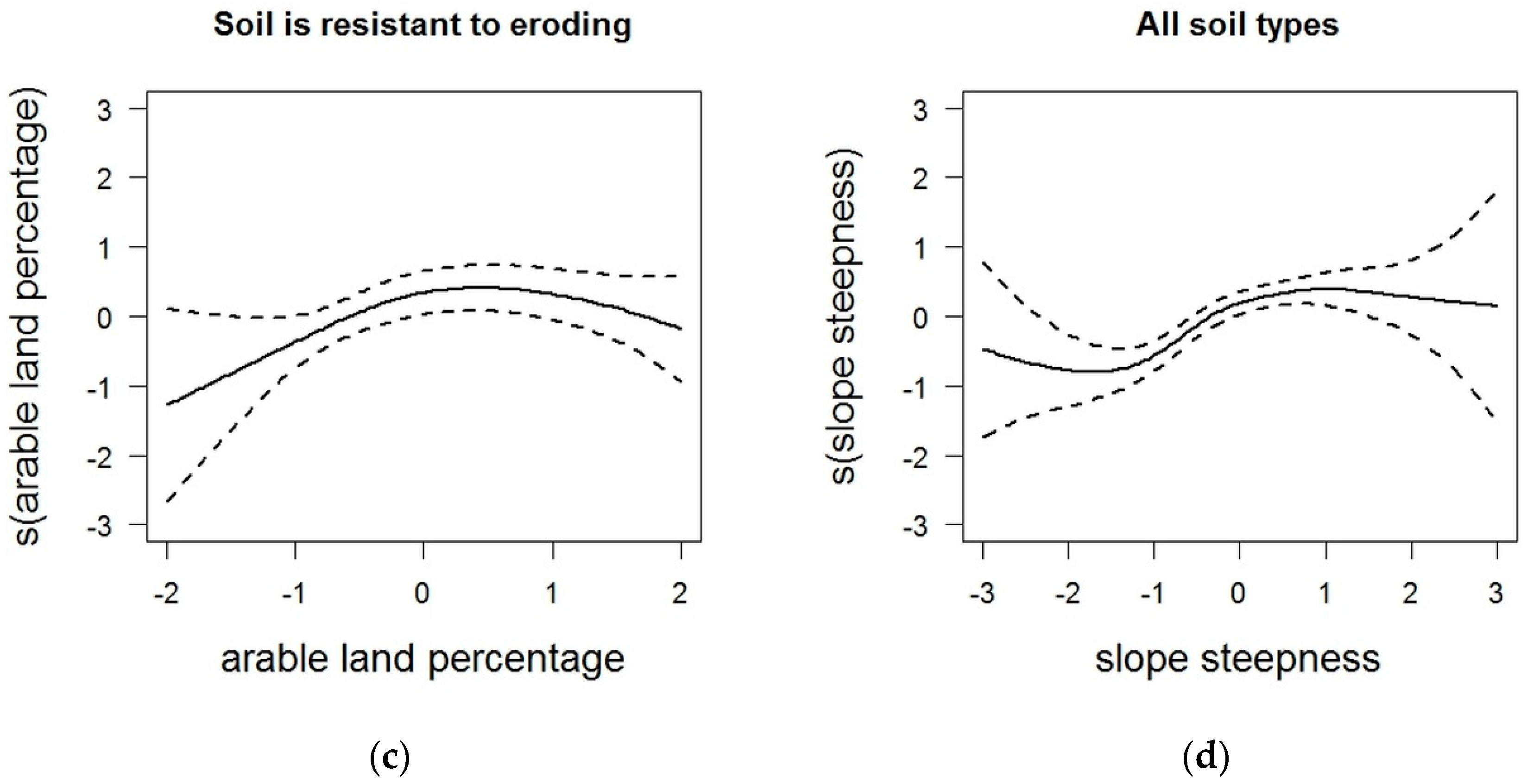
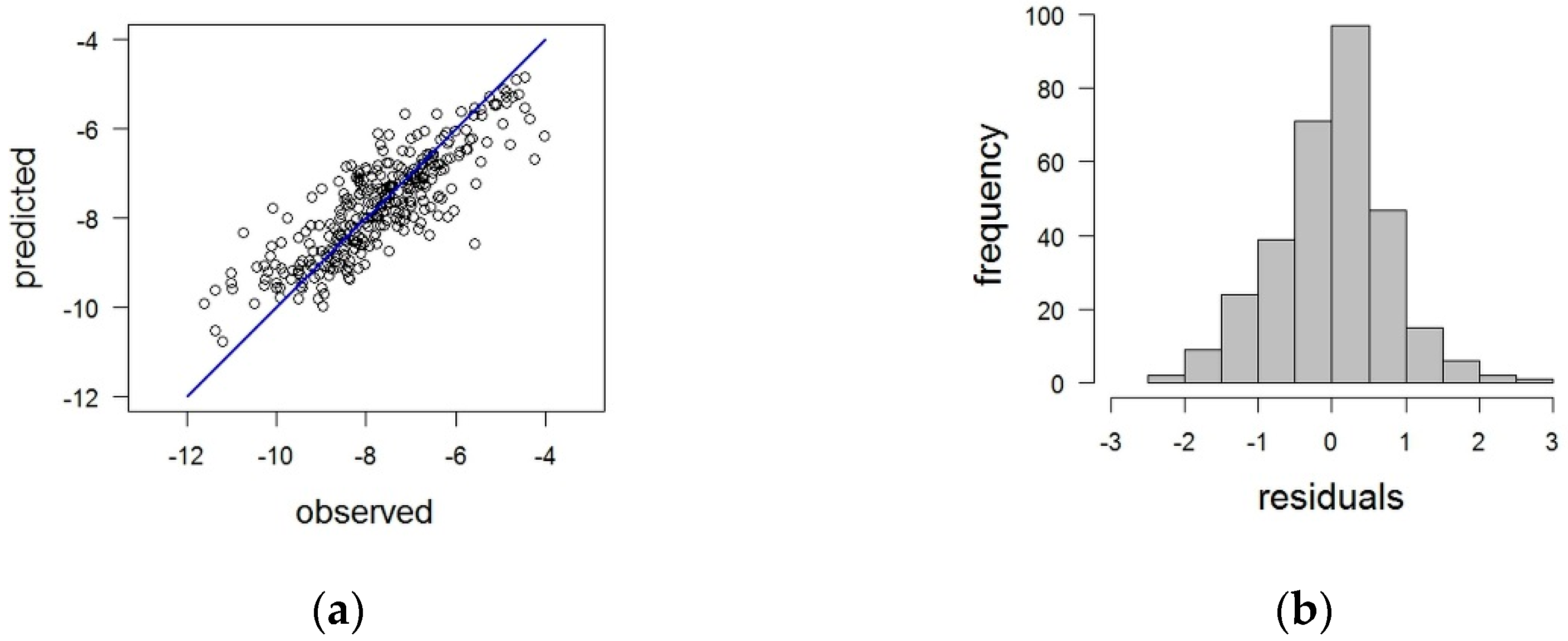
3.1. Constructed Models
3.2. Spatial Prediction of Suspended Sediment Yield for Unexplored Areas
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kocherin, D.I. The mean long-term, annual and monthly run-off in the European part of Union. Trans. Mosc. Inst. Transp. Eng. 1927, 6, 55–94. (In Russian) [Google Scholar]
- Zaykov, B.D.; Belinkov, S.Y. Average Long-Term Water Runoff of the USSR; State Hydrological Institute: Saint Petersburg, Russia, 1937. [Google Scholar]
- Zaykov, B.D. Average runoff and its distribution in the year on the territory of the USSR. Federal Serv. Russia Hydrometeorol. Monitor. Environ. 1946, 4, 13–32. [Google Scholar]
- Lopatin, G.V. Sediments of the rivers of the USSR (Formation and transfer); Geografgiz: Moscow, Russia, 1952. (In Russian) [Google Scholar]
- Karaushev, A.V.; Leningrad. (Eds.) Sediment Runoff, Its Study and Geographical Distribution; Hydrometeoizdat: Saint Petersburg, Russia, 1977. (In Russian) [Google Scholar]
- Dedkov, A.P.; Mozzherin, V.I. Erosion and Suspended Sediment on the Earth; Publishing house KSU: Kazan, Russia, 1984. (In Russian) [Google Scholar]
- Magritsky, D.V. Factors and regularities of territorial and long-term variability of sediment load to the seas of the Russian Arctic. Probl. Geogr. 2016, 142, 444–466. (In Russian) [Google Scholar]
- Chalov, S.R. River Sediments in Erosion-Channel Systems. Dissertation for the Doctor of Geographical Sciences. Ph.D. Thesis, Moscow State University, Moscow, Russia, 2021. (In Russian). [Google Scholar]
- Maltsev, K.; Yermolaev, O.; Mozzherin, V. Mapping and spatial analysis of suspended sediment yields from the Russian Plain. IAHS-AISH Publ. 2012, 356, 251–258. [Google Scholar]
- Tsyplenkov, A.S. Formation of suspended sediment runoff in the basins of small mountain rivers: General patterns and regional features. Dissertation for the degree of Candidate of Geographical Sciences. Ph.D. Thesis, Moscow State University, Moscow, Russia, 2019. (In Russian). [Google Scholar]
- Alekseevskij, N.I.; Frolova, N.L.; Antonova, M.M.; Igonina, M.I. Assessment of climate change impacts on water regime and river runoff in the Volga river basin. Water Chem. Ecol. 2013, 4, 3–12. [Google Scholar]
- Kuchment, L.S.; Gelfan, A.N.; Kondratiev, S.A.; Lavrov, S.A. Improving the scientific and methodological base of calculations and forecasts of river run-off based on physical and mathematical models of its formation. In Proceedings of the VII All-Russian Congress, Saint Petersburg, Russia, 19–21 November 2013. [Google Scholar]
- Motovilov, Y.G. ECOMAG: A distributed model of runoff formation and pollution transformation in river basins. IAHS Publ. 2013, 361, 227–234. [Google Scholar]
- Koren’, V.I. Mathematical Models in River Flow Forecasts; Hydrometeoizdat: Saint Petersburg, Russia, 1991. (In Russian) [Google Scholar]
- Goldberg, E.; Scheringer, M.; Buchelic, T.D.; Hungerbühler, K. Prediction of nanoparticle transport behavior from physicochemical properties: Machine learning provides insights to guide the next generation of transport models. Environ. Sci. Nano 2015, 2, 352–360. [Google Scholar] [CrossRef] [Green Version]
- Gomez-Flores, A.; Bradford, S.A.; Hong, G.; Kim, H. Statistical analysis, machine learning modeling, and text analytics of aggregation attachment efficiency: Mono and binary particle systems. J. Hazard. Mater. 2023, 454, 131482. [Google Scholar] [CrossRef]
- Shelutko, V.A.; Dolinnaya, S.J. Issues of Linearization of Relationships and Normalization of Initial Series in Calculations Using Regression Equations. Sci. Notes Russ. State Hydrometeorol. Univ. 2015, 38, 230–239. (In Russian) [Google Scholar]
- Oudin, L. Spatial proximity, physical similarity, regression and ungauged catchments: A comparison of regionalization approaches based on 913 French catchments. Water Resour. Res. 2008, 44, 1–15. [Google Scholar] [CrossRef]
- Gordeeva, S.M.; Malininn, V.N. On predicting annual runoff of large rivers of European Russia based on decision trees method. Sci. Notes Russ. State Hydrometeorol. Univ. 2018, 50, 53–56. [Google Scholar]
- Duan, L.M.; Liu, T.X.; Wang, X.X.; Luo, Y.Y.; Wu, L. Development of a regional regression model for estimating annual runoff in the Hailar river basin of China. J. Water Resour. Prot. 2010, 2, 934–943. [Google Scholar] [CrossRef] [Green Version]
- Barbarossa, V.; Huijbregts, M.; Hendriks, A.J.; Beusen, A.; Clavreul, J.; King, H.; Schipper, A.M. Developing and testing a global-scale regression model to quantify mean annual streamflow. J. Hydrol. 2017, 544, 479–487. [Google Scholar] [CrossRef] [Green Version]
- Patel, S.; Hardaha, M.K.; Seetpal, M.K.; Madankar, K.K. Multiple linear regression model for stream flow estimation of Wainganga river. Am. J. Water Sci. Eng. 2016, 2, 1–5. [Google Scholar]
- Di, C.L.; Yang, X.H.; Xia, X.H.; Chen, X.J.; Li, J.Q. Multi-scale modeling of the response of runoff to climate change. Therm. Sci. 2014, 18, 1511–1516. [Google Scholar] [CrossRef]
- Aalto, R.; Dunne, T.; Guyot, J.L. Geomorphic Controls on Andean Denudation Rates. J. Geol. 2006, 114, 85–99. [Google Scholar] [CrossRef] [Green Version]
- Milliman, J.D.; Syvitski, J.P.M. Geomorphic/Tectonic Control of Sediment Discharge to the Ocean: The Importance of Small Mountainous Rivers. J. Geol. 1992, 100, 525–544. [Google Scholar] [CrossRef]
- Jansen, I.M.L.; Painter, R.B. Predicting suspended sediment yield from climate and topography. J. Hydrol. 1974, 21, 371–380. [Google Scholar] [CrossRef]
- Ning, D.; Zhang, M.; Ren, S.; Hou, Y.; Yu, L.; Meng, Z. Predicting hydrological response to forest changes by simple statistical models: The selection of the best indicator of forest changes with a hydrological perspective. IOP Conf. Ser. Earth Environ. Sci. 2017, 52, 012059. [Google Scholar] [CrossRef]
- Vanacker, V.; von Blanckenburg, F.; Govers, G.; Molina, A.; Poesen, J.; Deckers, J.; Kubik, P. Restoring dense vegetation can slow mountain erosion to near natural benchmark levels. Geology 2007, 35, 303–306. [Google Scholar] [CrossRef]
- Terskij, P.N.; Zhbakov, K.K.; Miheeva, A.I. The correlation between morphometric characteristics, landscape drivers of flow generation and the characteristics of maximum and mean annual river flow in the Avacha river catchment (Kamchatka). Res. Aquat. Biolog. Resour. Kamchatka North-West Part Pac. Ocean 2017, 46, 51–65. [Google Scholar]
- Syvitski, J.P.; Vörösmarty, C.J.; Kettner, A.J.; Green, P. Impact of humans on the flux of terrestrial sediment to the global coastal ocean. Science 2005, 308, 376–380. [Google Scholar] [CrossRef] [PubMed]
- Chalov, S.R.; Shkol’nyi, D.I.; Promakhova, E.V.; Romanchenko, A.O.; Leman, V.N. Formation of the sediment yield in areas of mining of placer deposits. Geogr. Nat. Resour. 2015, 36, 124–131. [Google Scholar] [CrossRef]
- River Basins of the European Part of Russia. Available online: http://bassepr.kpfu.ru/ (accessed on 8 June 2023).
- Yermolaev, O.P.; Mukharamova, S.S.; Maltsev, K.A.; Ivanov, M.A.; Ermolaeva, P.O.; Gayazov, A.I.; Lisetskii, F.N. Geographic Information System and Geoportal River basins of the European Russia. IOP Conf. Ser. Earth Environ. Sci. 2018, 107, 012108. [Google Scholar] [CrossRef]
- Yermolaev, O.; Mukharamova, S.; Vedeneeva, E. River runoff modeling in the European territory of Russia. Catena 2021, 203, 105327. [Google Scholar] [CrossRef]
- Ermolaev, O.P.; Maltsev, K.A.; Mukharamova, S.S.; Kharchenko, S.V.; Vedeneeva, E.A. Cartographic model of river basins of European Russia. Geogr. Nat. Resour. 2017, 38, 131–138. [Google Scholar] [CrossRef]
- Danielson, J.J.; Gesch, D.B. Global Multi-Resolution Terrain Elevation Data 2010 (GMTED2010). U.S. Geological Survey Open-File Report 2011–1073; 2011. Available online: https://pubs.usgs.gov/of/2011/1073/pdf/of2011-1073.pdf (accessed on 8 June 2023).
- Lindsay, J.B. The Whitebox Geospatial Analysis Tools project and open-access GIS. In Proceedings of the GIS Research UK 22nd Annual Conference, Scotland, UK, 16–18 April 2014. [Google Scholar] [CrossRef]
- All-Russian Research Institute of Hydrometeorological. Available online: http://meteo.ru (accessed on 8 June 2023).
- Buligina, O.; Razuvayev, V.; Aleksandrova, T. Daily Temperature and Precipitation Data for Russia and U.S.S.R. Stations (TTTR). Patent № 2014620942, 31 March 2014. [Google Scholar]
- Unified State Register of Soil Resources of Russia. Available online: https://egrpr.esoil.ru/ (accessed on 8 June 2023).
- Bartalev, S.A.; Plotnikov, D.E.; Loupian, E.A. Mapping of arable land in Russia using multi-year time series of MODIS data and the LAGMA classification technique. Remote Sens. Lett. 2016, 7, 269–278. [Google Scholar] [CrossRef]
- Dobson, A.J. An Introduction to Generalized Linear Models; Chapman & Hall CRC: New York, NY, USA, 2002. [Google Scholar]
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models; Chapman & Hall CRC: London, UK, 1990. [Google Scholar]
- Wood, S.N. Generalized Additive Models: An Introduction with R; Chapman & Hall: London, UK, 2006. [Google Scholar]
- Zuur, A.F.; Saveliev, A.A.; Ieno, E.N. Zero Inflated Models and Generalized Linear Mixed Models with R; Highland Statistics Ltd.: Newburgh, NY, USA, 2012. [Google Scholar]
- Zuur, A.F.; Saveliev, A.A.; Ieno, E.N. A Beginner’s Guide to Generalized Additive Mixed Models with R; Highland Statistics Ltd.: Newburgh, NY, USA, 2014. [Google Scholar]
- Sakamoto, Y.; Ishiguro, M.; Kitagawa, G. Akaike Information Criterion Statistics; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1986. [Google Scholar]
- Seber, D. Linear Regression Analysis; Mir: Moscow, Russia, 1980. (In Russian) [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- The R Project for Statistical Computing. Available online: http://www.R-project.org/ (accessed on 8 June 2023).
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team. nlme: Linear and Nonlinear Mixed Effects Models. R Package Version 3.1. 2014. Available online: https://cran.r-project.org/web/packages/nlme/nlme.pdf (accessed on 8 June 2023).
- Ribeiro, J.R.P.J.; Diggle, P.J. geoR: A package for geostatistical analysis. R-NEWS 2001, 1, 15–18. [Google Scholar]
- Alekseevskiy, N.I. Formation and Movement of River Sediments; Publishing House of Moscow State University: Moscow, Russia, 1998. (In Russian) [Google Scholar]
- Walling, D.E.; Fang, D. Recent trends in the suspended sediment loads of the world’s rivers. Glob. Planet. Change 2003, 39, 111–126. [Google Scholar] [CrossRef]
- Dedkov, A.P.; Mozzherin, V.I. Global suspended sediment yield to the ocean: Natural and anthropogenic components. Eros. Riverbed Process. 2000, 3, 15–23. (In Russian) [Google Scholar]
- The National Atlas of Russia; Roskartography: Moscow, Russia, 2007; Volume 2. (In Russian)
- Borrelli, P.; Robinson, D.A.; Fleischer, L.R.; Lugato, E.; Ballabio, C.; Alewell, C.; Meusburger, K.; Modugno, S.; Schütt, B.; Ferro, V.; et al. An assessment of the global impact of 21st century land use change on soil erosion. Nat. Commun. 2017, 8, 2013. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Milliman, J.D.; Farnsworth, K.L. River Discharge to the Coastal Ocean: A Global Synthesis. Camb. Univ. Press 2013, 24, 143–160. [Google Scholar] [CrossRef]
- Syvitski, J.P.M.; Kettner, A. Sediment flux and the Anthropocene. Phil. Trans. R. Soc. A 2011, 369, 957–975. [Google Scholar] [CrossRef] [PubMed]
- Syvitski, J.P.M.; Milliman, J.D. Geology, geography, and humans battle for dominance over the delivery of fluvial sediment to the coastal ocean. J. Geol. 2007, 115, 1–19. [Google Scholar] [CrossRef] [Green Version]

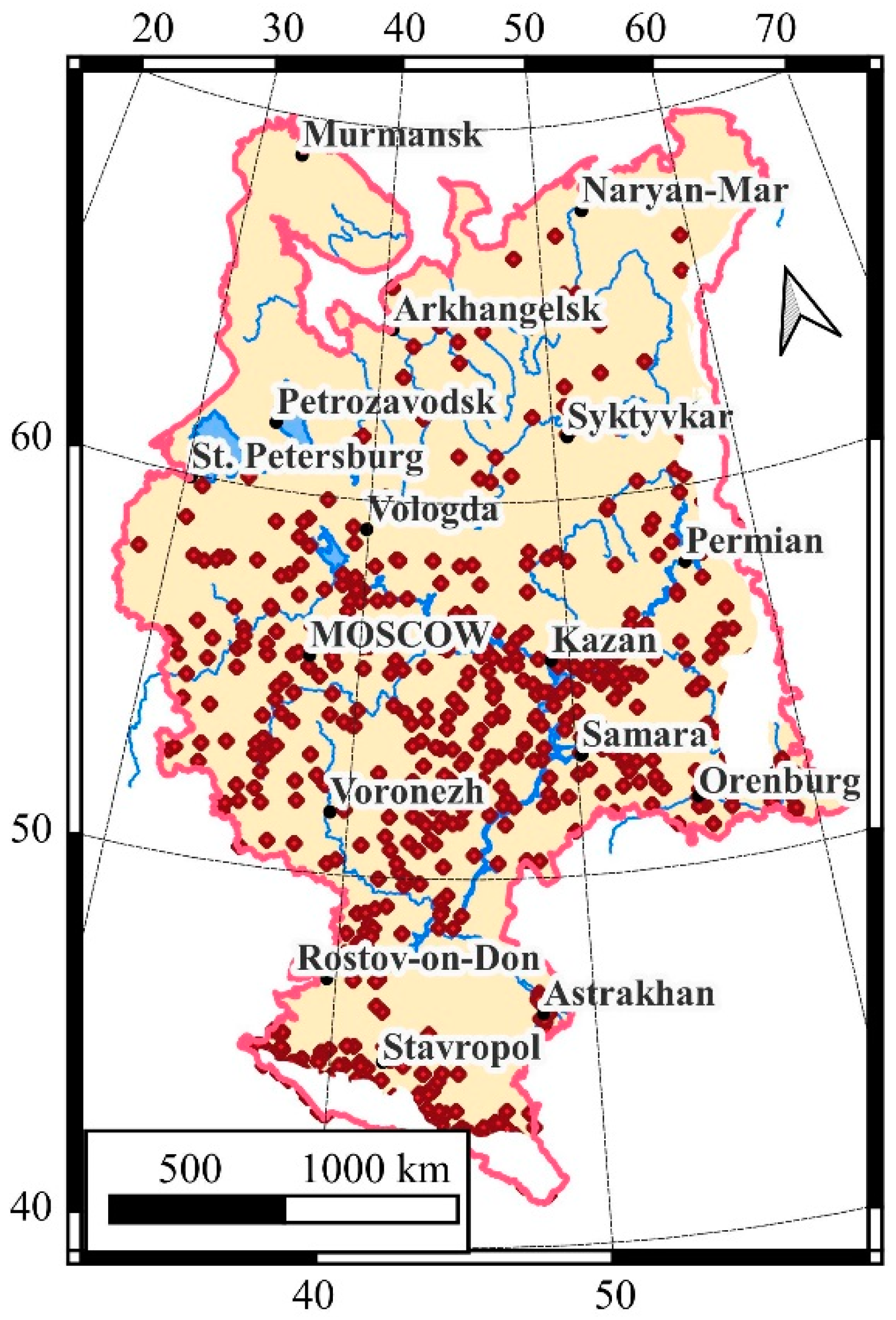




| Landscape Zone | Square, % |
|---|---|
| Tundra and forest-tundra | 8.8 |
| Northern taiga | 11.8 |
| Middle taiga | 16.2 |
| Southern taiga | 14.8 |
| Mixed and broad-leaved | 18.5 |
| Forest-steppe | 8.5 |
| Steppe | 16.9 |
| Semi-desert and desert | 4.6 |
| Basin Area, sq. km | Number of Observation Years | ||||||
|---|---|---|---|---|---|---|---|
| 1 to 10 | 10 to 20 | 20 to 30 | 30 to 40 | Over 40 | Total | % | |
| under 500 | 29 | 18 | 11 | 3 | 5 | 66 | 17.1 |
| 500–1000 | 14 | 15 | 12 | 5 | 2 | 48 | 12.5 |
| 1000–5000 | 64 | 50 | 22 | 11 | 14 | 161 | 41.8 |
| 5000–10,000 | 13 | 10 | 11 | 3 | 4 | 41 | 10.6 |
| 10,000–50,000 | 20 | 9 | 10 | 10 | 9 | 58 | 15.1 |
| 50,000–100,000 | 4 | 0 | 3 | 0 | 1 | 8 | 2.1 |
| over 100,000 | 1 | 1 | 0 | 0 | 1 | 3 | 0.8 |
| total | 145 | 103 | 69 | 32 | 36 | 385 | 100 |
| % | 37.7 | 26.8 | 17.9 | 8.3 | 9.4 | 100 | |
| Explanatory Variables {X} | Data Source | Data Format |
|---|---|---|
| The terrain conditions | ||
| Average height Average steepness of slopes Average exposure Profile and plan curvatures Slope length Relief erosion potential | GMTED2010 with spatial resolution 250 m [36] | Raster data |
| Climatic characteristics | ||
| Annual precipitation Annual precipitation in May-August (heavy rain season) Precipitation for cold and warm periods of the year Variation coefficient of annual precipitation Annual average air temperature Average air temperature in January and in July Sum of active temperatures (sum of average daily temperatures for days when the temperature is above 10 °C) Average highs and lows of temperature Average amplitude of temperature Standard deviation of temperature Hydrothermic coefficient | Daily temperature and precipitation data on meteostations of Russia and USSR [38,39] | ASCII |
| The geological conditions | ||
| Class of pre-Quaternary deposits (predominant) | The “State geological map of the USSR of pre-Quaternary deposits” at a 1:1,000,000 scale | Vector data |
| The soil conditions | ||
| Type of soil (predominant) Type of soil-forming rock (predominant) | The Unified State Register of Soil Resources of Russia [40] | Vector data |
| Land cover/land use | ||
| Forest cover share Grassland cover share Brushwood cover share Swamp cover share Arable land share | TerraNorte RLC Map of the Russian Terrestrial Ecosystems, ver. 2015) (the Institute of Space Research of the Russian Academy of Sciences) [41] | Raster data |
| Landscape zones | ||
| Type of landscape (predominant) Subtype of landscape (predominant) | The “USSR Landscape Map” at a 1:2,500,000 scale | Vector data |
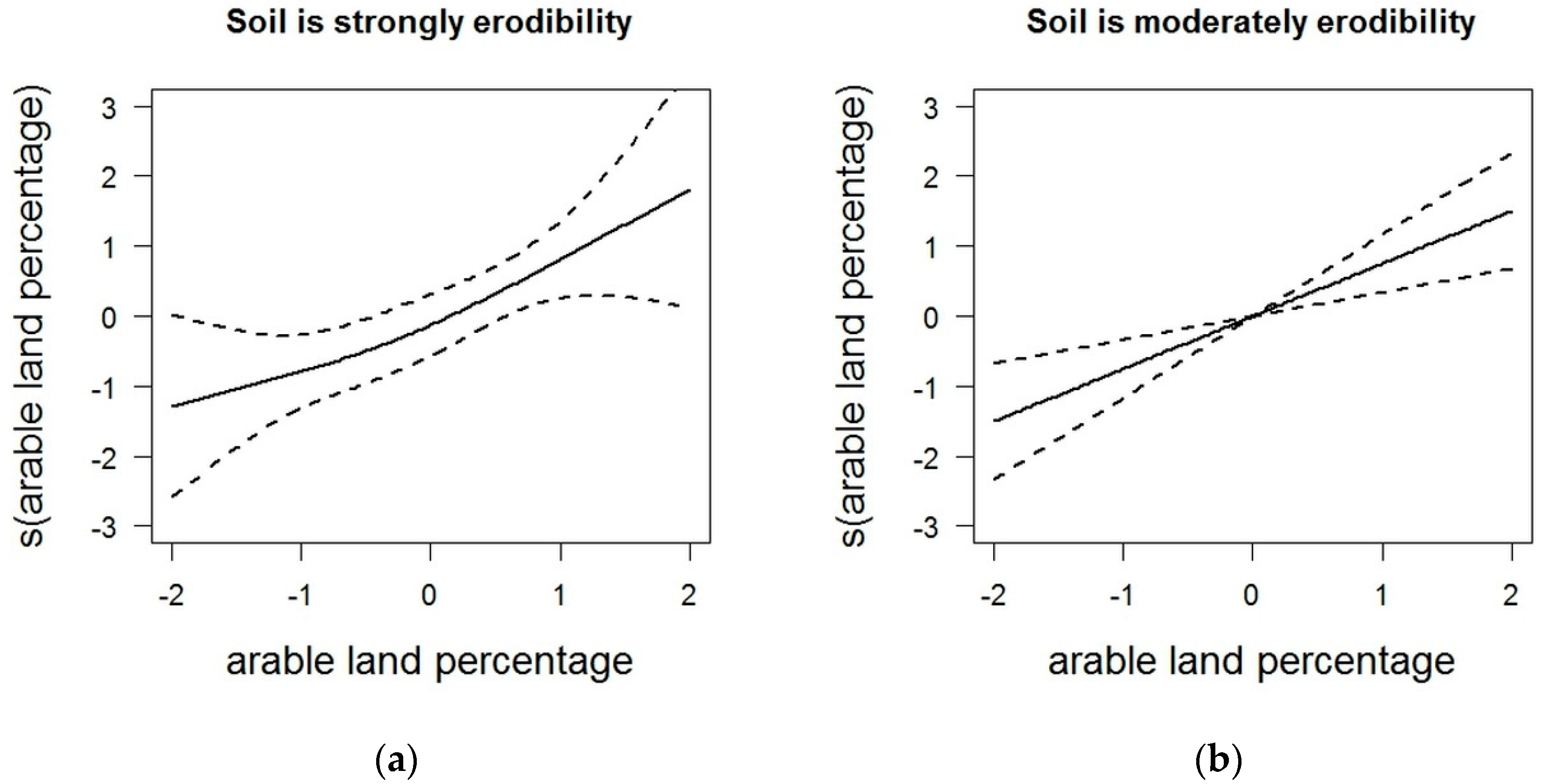
| Explanatory Variables | Transform | The Rank of Soil and Soil-Forming Rock Erodibility | Linear Model Coefficients |
|---|---|---|---|
| Average steepness of slopes | log | strongly erodibility | 0.176 |
| moderately erodibility | 0.684 | ||
| slightly erodibility | 0.592 | ||
| resistant to eroding | 0.333 | ||
| very resistant to eroding | 0.077 | ||
| Percentage of arable land | strongly erodibility | 1.673 | |
| moderately erodibility | 1.231 | ||
| slightly erodibility | 0.682 | ||
| resistant to eroding | 0.077 | ||
| very resistant to eroding | 0.198 | ||
| Water runoff per unit area | log | strongly erodibility | 1.246 |
| moderately erodibility | 0.718 | ||
| slightly erodibility | 0.405 | ||
| resistant to eroding | 0.503 | ||
| very resistant to eroding | 0.607 | ||
| Area of catchment | log | strongly erodibility | −0.038 |
| moderately erodibility | −0.083 | ||
| slightly erodibility | −0.237 | ||
| resistant to eroding | −0.192 | ||
| very resistant to eroding | −0.083 | ||
| Longitude | 0.408 | ||
| Latitude | −0.333 | ||
| Constant | −7.309 |
| Methods | ME | MdE | MAE | RMSE | WAPE | SE | R-Squared adj. |
|---|---|---|---|---|---|---|---|
| GLM | 8.8 | 0.0 | −0.005 | 0.746 | 1.031 | −0.096 | 0.993 |
| GAM | 11.8 | 0.0 | 0.064 | 0.592 | 0.845 | −0.076 | 0.781 |
| Landscape Zone | Min | 5% Quantile | Mean | Median | 95% Quantile | Max |
|---|---|---|---|---|---|---|
| Tundra and forest-tundra | 2.1 | 4.4 | 12.4 | 10.0 | 26.4 | 83.4 |
| Northern taiga | 2.1 | 3.8 | 12.1 | 10.8 | 24.4 | 91.1 |
| Middle taiga | 2.3 | 3.9 | 12.5 | 10.0 | 27.9 | 119.4 |
| Southern taiga | 1.8 | 2.5 | 11.8 | 6.4 | 34.0 | 116.1 |
| Mixed and broad-leaved | 0.8 | 2.9 | 25.1 | 13.9 | 90.0 | 226.5 |
| Forest-steppe | 0.6 | 5.2 | 33.5 | 28.0 | 87.2 | 158.4 |
| Steppe | 0.2 | 2.2 | 36.9 | 18.1 | 147.1 | 889.1 |
| Semi-desert and desert | 0.3 | 0.8 | 2.9 | 1.6 | 9.5 | 34.5 |
| Total | 0.24 | 46.2 | 17.3 | 10.9 | 46.2 | 1127.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yermolaev, O.; Mukharamova, S. Statistical Analysis and Modeling of Suspended Sediment Yield Dependence on Environmental Conditions. Water 2023, 15, 2639. https://doi.org/10.3390/w15142639
Yermolaev O, Mukharamova S. Statistical Analysis and Modeling of Suspended Sediment Yield Dependence on Environmental Conditions. Water. 2023; 15(14):2639. https://doi.org/10.3390/w15142639
Chicago/Turabian StyleYermolaev, Oleg, and Svetlana Mukharamova. 2023. "Statistical Analysis and Modeling of Suspended Sediment Yield Dependence on Environmental Conditions" Water 15, no. 14: 2639. https://doi.org/10.3390/w15142639





