Advancing Water Quality Research: K-Nearest Neighbor Coupled with the Improved Grey Wolf Optimizer Algorithm Model Unveils New Possibilities for Dry Residue Prediction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Database
2.2. Modeling Method
3. Results and Discussion
3.1. Factors Affecting Water Quality and Dry Residue
3.2. KNN Model
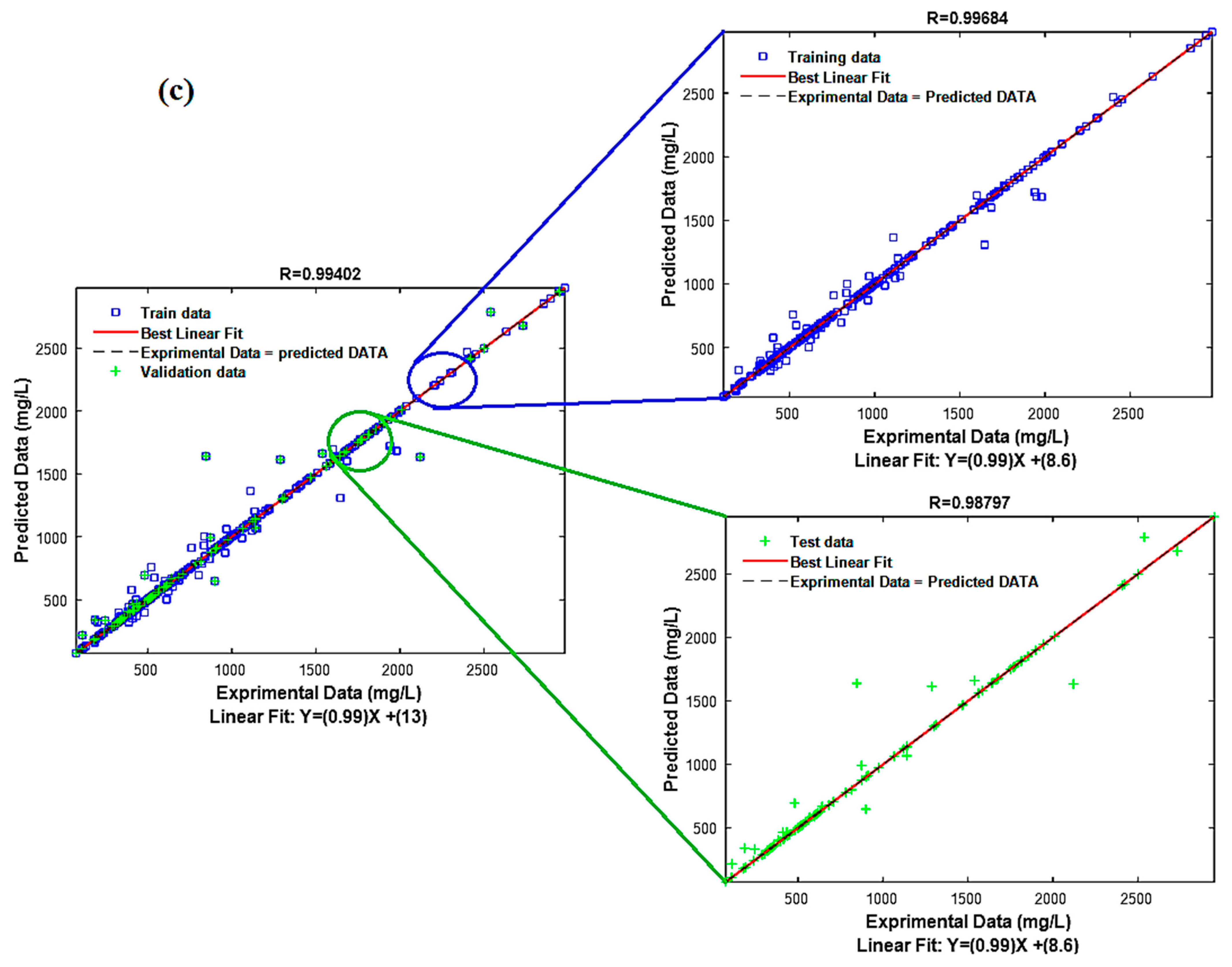
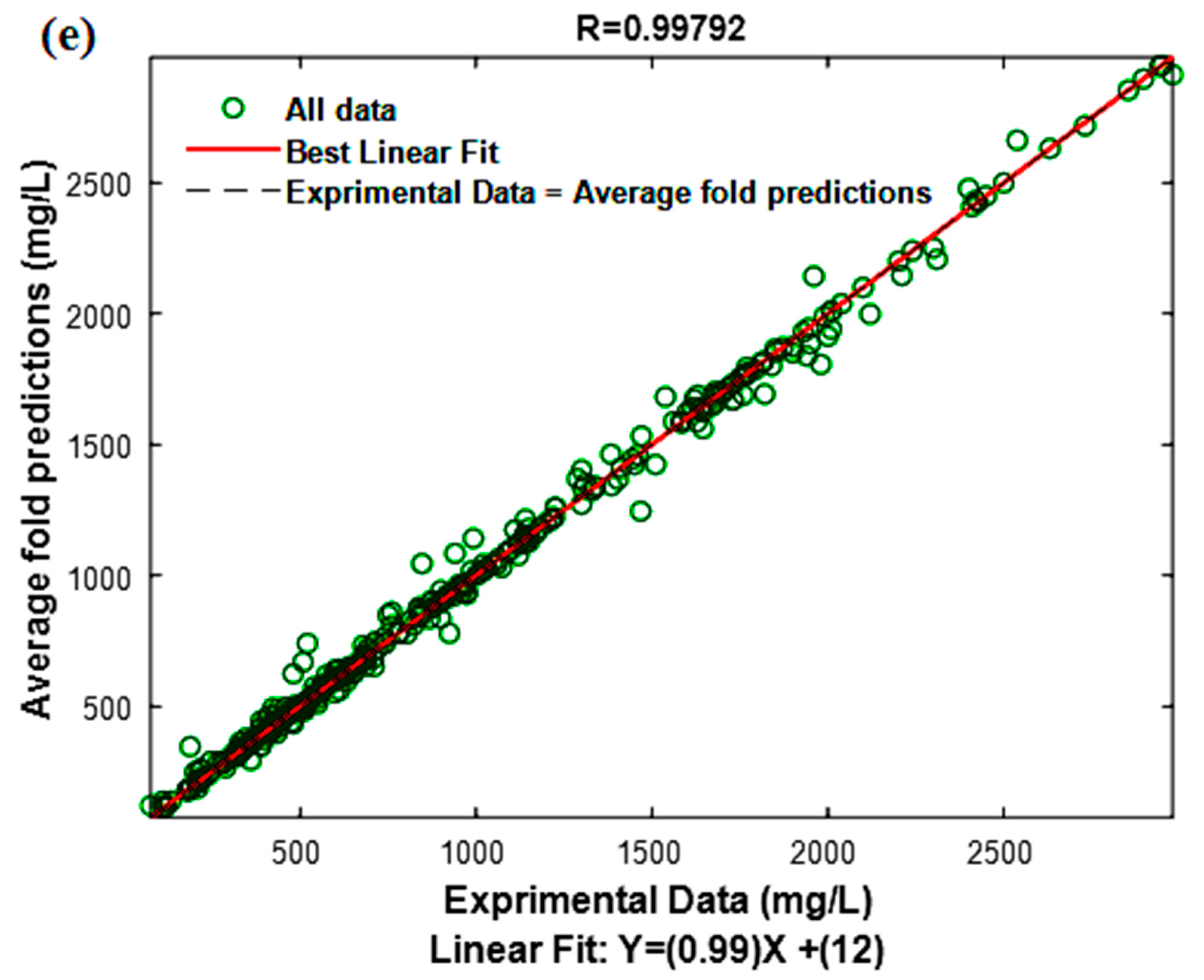
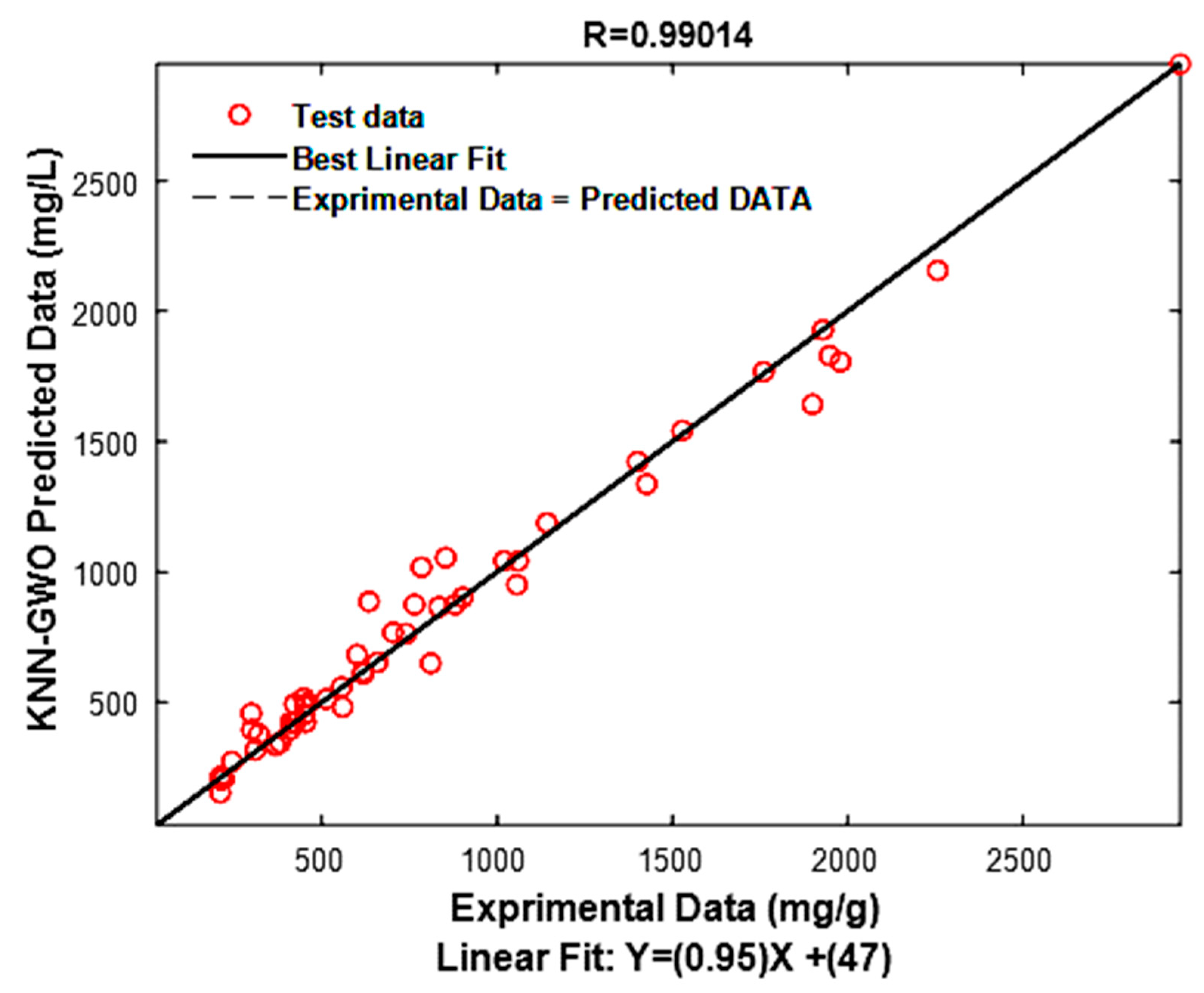
3.3. Model Performance Test
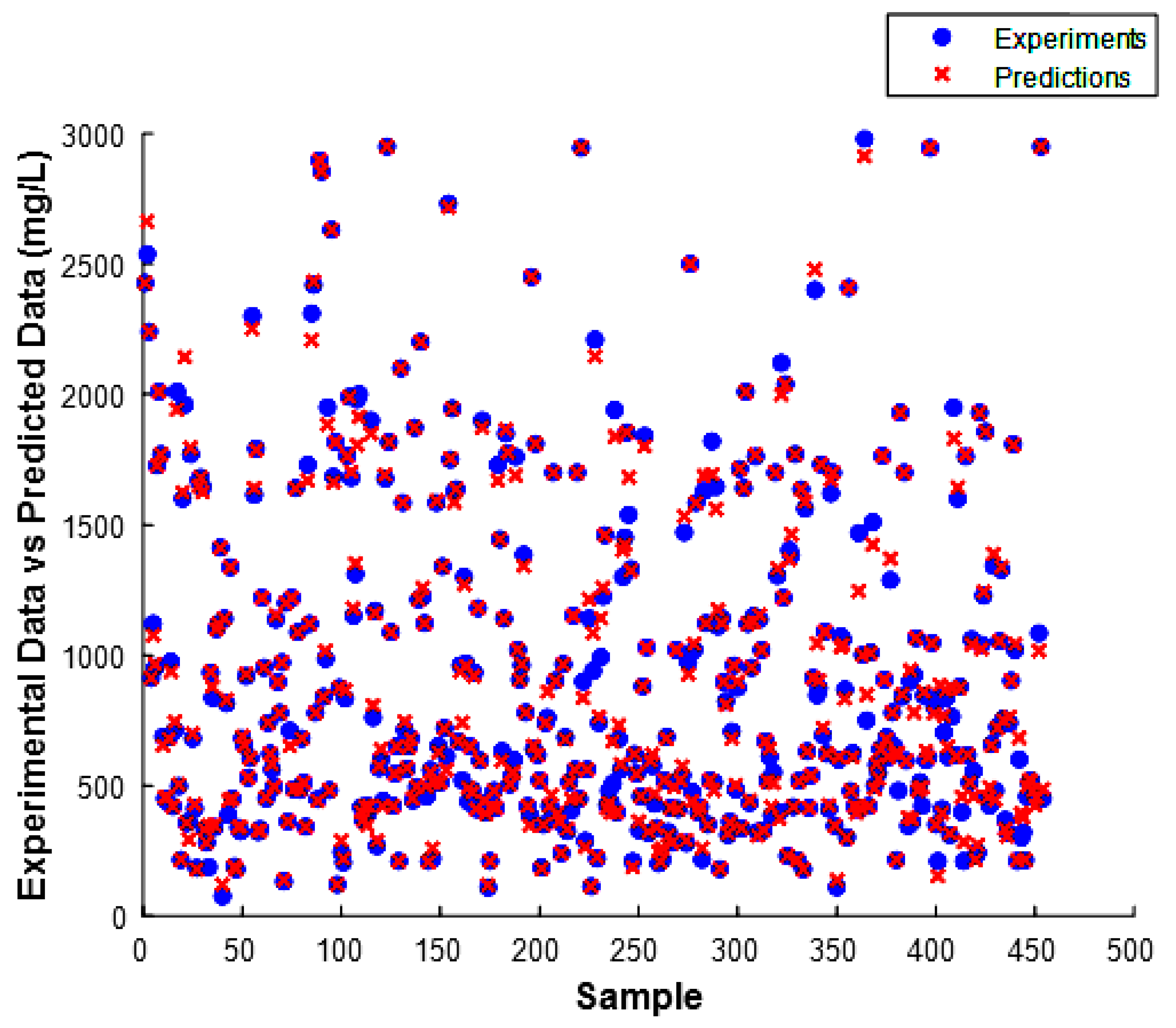
3.4. Analysis of Model Residuals
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kılıç, Z. The Importance of Water and Conscious Use of Water. Int. J. Hydrol. 2020, 4, 239–241. [Google Scholar] [CrossRef]
- Deng, W.; Wang, G.; Zhang, X. A Novel Hybrid Water Quality Time Series Prediction Method Based on Cloud Model and Fuzzy Forecasting. Chemom. Intell. Lab. Syst. 2015, 149, 39–49. [Google Scholar] [CrossRef]
- Hamid, A.; Bhat, S.U.; Jehangir, A. Local Determinants Influencing Stream Water Quality. Appl. Water Sci. 2020, 10, 24. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.R.; Cai, Y.J.; Sun, P.D.; Chen, B. The Use of Combined Neural Networks and Genetic Algorithms for Prediction of River Water Quality. J. Appl. Res. Technol. 2014, 12, 493–499. [Google Scholar] [CrossRef]
- Ho, J.Y.; Afan, H.A.; El-Shafie, A.H.; Koting, S.B.; Mohd, N.S.; Jaafar, W.Z.B.; Lai Sai, H.; Malek, M.A.; Ahmed, A.N.; Mohtar, W.H.M.W.; et al. Towards a Time and Cost Effective Approach to Water Quality Index Class Prediction. J. Hydrol. 2019, 575, 148–165. [Google Scholar] [CrossRef]
- Tahraoui, H.; Amrane, A.; Belhadj, A.-E.; Zhang, J. Modeling the Organic Matter of Water Using the Decision Tree Coupled with Bootstrap Aggregated and Least-Squares Boosting. Environ. Technol. Innov. 2022, 27, 102419. [Google Scholar] [CrossRef]
- Tahraoui, H.; Belhadj, A.-E.; Triki, Z.; Boudella, N.R.; Seder, S.; Amrane, A.; Zhang, J.; Moula, N.; Tifoura, A.; Ferhat, R.; et al. Mixed Coagulant-Flocculant Optimization for Pharmaceutical Effluent Pretreatment Using Response Surface Methodology and Gaussian Process Regression. Process Saf. Environ. Prot. 2022, 169, 909–927. [Google Scholar] [CrossRef]
- Tahraoui, H.; Belhadj, A.-E.; Amrane, A.; Houssein, E.H. Predicting the Concentration of Sulfate Using Machine Learning Methods. Earth Sci. Inform. 2022, 15, 1023–1044. [Google Scholar] [CrossRef]
- Collivignarelli, M.C.; Abbà, A.; Benigna, I.; Sorlini, S.; Torretta, V. Overview of the Main Disinfection Processes for Wastewater and Drinking Water Treatment Plants. Sustainability 2017, 10, 86. [Google Scholar] [CrossRef] [Green Version]
- Tahraoui, H.; Belhadj, A.-E.; Hamitouche, A.-E. Prediction of the Bicarbonate Amount in Drinking Water in the Region of Médéa Using Artificial Neural Network Modelling. Kem. U Ind. Časopis Kemičara Kem. Inženjera Hrvat. 2020, 69, 595–602. [Google Scholar] [CrossRef]
- Tahraoui, H.; Belhadj, A.-E.; Hamitouche, A.-E.; Bouhedda, M.; Amrane, A. Predicting the Concentration of Sulfate (So4 2–) in Drinking Water Using Artificial Neural Networks: A Case Study: Médéa-Algeria. Desalination Water Treat. 2021, 217, 181–194. [Google Scholar] [CrossRef]
- Rajaee, T.; Khani, S.; Ravansalar, M. Artificial Intelligence-Based Single and Hybrid Models for Prediction of Water Quality in Rivers: A Review. Chemom. Intell. Lab. Syst. 2020, 200, 103978. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Amendolia, S.R.; Cossu, G.; Ganadu, M.L.; Golosio, B.; Masala, G.L.; Mura, G.M. A Comparative Study of K-Nearest Neighbour, Support Vector Machine and Multi-Layer Perceptron for Thalassemia Screening. Chemom. Intell. Lab. Syst. 2003, 69, 13–20. [Google Scholar] [CrossRef]
- Altman, N.S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. Am. Stat. 1992, 46, 175–185. [Google Scholar]
- Kotsiantis, S.B.; Zaharakis, I.; Pintelas, P. Supervised Machine Learning: A Review of Classification Techniques. Emerg. Artif. Intell. Appl. Comput. Eng. 2007, 160, 3–24. [Google Scholar]
- Alpaydin, E. Introduction to Machine Learning; MIT Press: Cambridge, MA, USA, 2020; ISBN 0-262-04379-3. [Google Scholar]
- Zamouche, M.; Chermat, M.; Kermiche, Z.; Tahraoui, H.; Kebir, M.; Bollinger, J.-C.; Amrane, A.; Mouni, L. Predictive Model Based on K-Nearest Neighbor Coupled with the Gray Wolf Optimizer Algorithm (KNN_GWO) for Estimating the Amount of Phenol Adsorption on Powdered Activated Carbon. Water 2023, 15, 493. [Google Scholar] [CrossRef]
- Adithiyaa, T.; Chandramohan, D.; Sathish, T. Optimal Prediction of Process Parameters by GWO-KNN in Stirring-Squeeze Casting of AA2219 Reinforced Metal Matrix Composites. Mater. Today Proc. 2020, 21, 1000–1007. [Google Scholar] [CrossRef]
- Huang, H.; Wang, Q.; He, X.; Wu, Y.; Xu, C. Association between Polyfluoroalkyl Chemical Concentrations and Leucocyte Telomere Length in US Adults. Sci. Total Environ. 2019, 653, 547–553. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Olbert, A.I. A Review of Water Quality Index Models and Their Use for Assessing Surface Water Quality. Ecol. Indic. 2021, 122, 107218. [Google Scholar] [CrossRef]
- Rodier, J.; Legube, B.; Merlet, N.; Brunet, R. L’analyse de L’eau-9e éd.: Eaux Naturelles, Eaux Résiduaires, Eau de Mer; Dunod: Malakoff Cedex, France, 2009; ISBN 978-2-10-054179-9. [Google Scholar]
- Sinha, P.; Sinha, P. Comparative Study of Chronic Kidney Disease Prediction Using KNN and SVM. Int. J. Eng. Res. 2015, 4, 608–612. [Google Scholar] [CrossRef]
- Ahmed, R.; Rangaiah, G.P.; Mahadzir, S.; Mirjalili, S.; Hassan, M.H.; Kamel, S. Memory, Evolutionary Operator, and Local Search Based Improved Grey Wolf Optimizer with Linear Population Size Reduction Technique. Knowl.-Based Syst. 2023, 110297. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. I-GWO and Ex-GWO: Improved Algorithms of the Grey Wolf Optimizer to Solve Global Optimization Problems. Eng. Comput. 2021, 37, 509–532. [Google Scholar] [CrossRef]
- Yahoum, M.M.; Toumi, S.; Hentabli, S.; Tahraoui, H.; Lefnaoui, S.; Hadjsadok, A.; Amrane, A.; Kebir, M.; Moula, N.; Assadi, A.A. Experimental Analysis and Neural Network Modeling of the Rheological Behavior of Xanthan Gum and Its Derivatives. Materials 2023, 16, 2565. [Google Scholar] [CrossRef] [PubMed]
- Belsley, D.A.; Kuh, E.; Welsch, R.E. Regression Diagnostics: Identifying Influential Data and Sources of Collinearity; Wiley: Hoboken, NJ, USA, 1980; ISBN 978-0-471-05856-4. [Google Scholar]
- Hong, S.H.; Lee, M.W.; Lee, D.S.; Park, J.M. Monitoring of Sequencing Batch Reactor for Nitrogen and Phosphorus Removal Using Neural Networks. Biochem. Eng. J. 2007, 35, 365–370. [Google Scholar] [CrossRef]
- Bousselma, A.; Abdessemed, D.; Tahraoui, H.; Amrane, A. Artificial Intelligence and Mathematical Modelling of the Drying Kinetics of Pre-Treated Whole Apricots. Kem. U Ind. 2021, 70, 651–667. [Google Scholar] [CrossRef]
- Bouchelkia, N.; Tahraoui, H.; Amrane, A.; Belkacemi, H.; Bollinger, J.-C.; Bouzaza, A.; Zoukel, A.; Zhang, J.; Mouni, L. Jujube Stones Based Highly Efficient Activated Carbon for Methylene Blue Adsorption: Kinetics and Isotherms Modeling, Thermodynamics and Mechanism Study, Optimization via Response Surface Methodology and Machine Learning Approaches. Process. Saf. Environ. Prot. 2022, 170, 513–535. [Google Scholar] [CrossRef]
- Zamouche, M.; Tahraoui, H.; Laggoun, Z.; Mechati, S.; Chemchmi, R.; Kanjal, M.I.; Amrane, A.; Hadadi, A.; Mouni, L. Optimization and Prediction of Stability of Emulsified Liquid Membrane (ELM): Artificial Neural Network. Processes 2023, 11, 364. [Google Scholar] [CrossRef]
- Tahraoui, H.; Belhadj, A.-E.; Moula, N.; Bouranene, S.; Amrane, A. Optimisation and Prediction of the Coagulant Dose for the Elimination of Organic Micropollutants Based on Turbidity. Kem. U Ind. 2021, 70, 675–691. [Google Scholar] [CrossRef]
- Manssouri, I.; Manssouri, M.; El Kihel, B. Fault Detection by K-Nn Algorithm and Mlp Neural Networks in a Distillation Column: Comparative Study. J. Inf. Intell. Knowl. 2011, 3, 201. [Google Scholar]
- Manssouri, I.; El Hmaidi, A.; Manssouri, T.E.; El Moumni, B. Prediction Levels of Heavy Metals (Zn, Cu and Mn) in Current Holocene Deposits of the Eastern Part of the Mediterranean Moroccan Margin (Alboran Sea). IOSR J. Comput. Eng. 2014, 16, 117–123. [Google Scholar] [CrossRef]
- Dolling, O.R.; Varas, E.A. Artificial Neural Networks for Streamflow Prediction. J. Hydraul. Res. 2002, 40, 547–554. [Google Scholar] [CrossRef]
- Post, G.B.; Atherholt, T.B.; Cohn, P.D. Water quality and treatment: A handbook on drinking water. In Health and Aesthetic Aspects of Drinking Water, 6th ed.; McGraw-Hill: New York, NY, USA, 2011; pp. 2.1–2.100. [Google Scholar]
- Boyd, C.E. Water Quality: An Introduction; Springer Nature: Berlin/Heidelberg, Germany, 2019; ISBN 3-030-23335-9. [Google Scholar]
- Bartram, J.; Ballance, R. Water Quality Monitoring: A Practical Guide to the Design and Implementation of Freshwater Quality Studies and Monitoring Programmes; CRC Press: Boca Raton, FL, USA, 1996; ISBN 0-419-22320-7. [Google Scholar]
- WHO. Guidelines for Drinking-Water Quality; World Health Organization: Geneva, Switzerland, 2004; Volume 1, ISBN 92-4-154638-7. [Google Scholar]
- Staff, A. Water Quality: Principles and Practices of Water Supply Operations; American Water Works Assoc.: Denver, CO, USA, 2003. [Google Scholar]
- Csuros, M.; Csuros, C. Environmental Sampling and Analysis for Metals; CRC Press: Boca Raton, FL, USA, 2016; ISBN 1-4200-3234-8. [Google Scholar]
- Rice, E.W.; Bridgewater, L.; Association, A.P.H. Standard Methods for the Examination of Water and Wastewater; American Public Health Association: Washington, DC, USA, 2012; Volume 10. [Google Scholar]
- Nollet, L.M.; De Gelder, L.S. Handbook of Water Analysis; CRC Press: Boca Raton, FL, USA, 2000; ISBN 0-8493-8486-9. [Google Scholar]
- Graindorge, J.; Landot, É. La Qualité de L’eau Potable: Techniques et Responsabilités; Territorial éditions; Territorial: Voiron, France, 2018; ISBN 2-8186-1418-X. [Google Scholar]
- Debieche, T.H. Evolution de La Qualité Des Eaux (Salinité, Azote et Métaux Lourds) Sous L’effet de la Pollution Saline, Agricole et Industrielle: Application à la Basse Plaine de la Seybouse Nord-Est Algérien; University of Franche-Comté: Besançon, France, 2002. [Google Scholar]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4. [Google Scholar]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012; ISBN 0-262-30432-5. [Google Scholar]





| Variables | Symbol | Unit | Min | Mean | Max | STD |
|---|---|---|---|---|---|---|
| Inputs | ||||||
| Conductivity | X1 | µS/cm | 223 | 1263.98 | 3570 | 754.59 |
| Turbidity | X2 | NTU | 0.10 | 7.87 | 1024 | 58.57 |
| Potential hydrogen | X3 | – | 2.10 | 9.62 | 797 | 37.07 |
| Hardness | X4 | mg/L | 8.13 | 53.42 | 160 | 24.27 |
| Calcium | X5 | mg/L | 16.03 | 121.87 | 360.72 | 47.40 |
| Magnesium | X6 | mg/L | 0 | 55.20 | 218.70 | 36.91 |
| Total alkalimetric titre | X7 | °F | 6.50 | 117.71 | 663 | 133.39 |
| Bicarbonate | X8 | mg/L | 6.74 | 200.11 | 495.20 | 117.01 |
| Chlorides | X9 | mg/L | 10.50 | 150.76 | 609.39 | 125.91 |
| Nitrogen dioxide | X10 | mg/L | 0 | 0.01 | 0.50 | 0.07 |
| Ammonium | X11 | mg/L | 0 | 0.02 | 1.05 | 0.14 |
| Nitrates | X12 | mg/L | 0 | 8.13 | 195.09 | 15.89 |
| Phosphate | X13 | mg/L | 0 | 1.28 | 288 | 19.09 |
| Sulfate | X14 | mg/L | 10.55 | 342.25 | 1457 | 287.37 |
| Sodium | X15 | mg/L | 0 | 122.05 | 460 | 121.67 |
| Potassium | X16 | mg/L | 0.005 | 6.92 | 805 | 37.92 |
| Manganese | X17 | mg/L | 0 | 0.007 | 0.21 | 0.02 |
| Iron | X18 | mg/L | 0 | 0.013 | 0.53 | 0.03 |
| Aluminum | X19 | mg/L | 0 | 0.005 | 0.90 | 0.04 |
| Organic matter | X20 | mg/L | 0 | 3.26 | 29.20 | 3.86 |
| Output | ||||||
| Dry residue | Y | mg/L | 29 | 916.01 | 2980 | 635.64 |
| Number of Neighbors | R/R2/R2adj | RMSE/EPM | ||||
|---|---|---|---|---|---|---|
| Train | VAL | ALL | Train | VAL | ALL | |
| 1st fold | ||||||
| 3 | 0.9958 | 0.9951 | 0.9956 | 56.0000 | 70.2000 | 59.9000 |
| 0.9916 | 0.9902 | 0.9911 | 2.7000 | 3.2000 | 2.8000 | |
| 0.9910 | 0.9877 | 0.9907 | ||||
| 2nd fold | ||||||
| 5 | 0.9948 | 0.9924 | 0.9941 | 65.8000 | 79.3000 | 69.4000 |
| 0.9896 | 0.9848 | 0.9882 | 3.2000 | 4.3000 | 3.5000 | |
| 0.9888 | 0.9809 | 0.9876 | ||||
| 3rd fold | ||||||
| 6 | 0.9968 | 0.9880 | 0.9940 | 48.5000 | 110.9000 | 69.5000 |
| 0.9937 | 0.9761 | 0.9881 | 2.2000 | 5.1000 | 2.9000 | |
| 0.9932 | 0.9700 | 0.9874 | ||||
| 4th fold | ||||||
| 7 | 0.9930 | 0.9948 | 0.9935 | 75.7000 | 63.0000 | 72.7000 |
| 0.9861 | 0.9897 | 0.9869 | 3.0000 | 3.8000 | 3.2000 | |
| 0.9851 | 0.9871 | 0.9863 | ||||
| The average of the folds | ||||||
| / | / | / | 0.9979 | / | / | 41.2000 |
| 0.9958 | 3.1000 | |||||
| 0.9956 | ||||||
| R | R2 | R2adj | RMSE | EPM |
|---|---|---|---|---|
| 0.9901 | 0.9804 | 0.9685 | 87.7000 | 9.6000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tahraoui, H.; Toumi, S.; Hassein-Bey, A.H.; Bousselma, A.; Sid, A.N.E.H.; Belhadj, A.-E.; Triki, Z.; Kebir, M.; Amrane, A.; Zhang, J.; et al. Advancing Water Quality Research: K-Nearest Neighbor Coupled with the Improved Grey Wolf Optimizer Algorithm Model Unveils New Possibilities for Dry Residue Prediction. Water 2023, 15, 2631. https://doi.org/10.3390/w15142631
Tahraoui H, Toumi S, Hassein-Bey AH, Bousselma A, Sid ANEH, Belhadj A-E, Triki Z, Kebir M, Amrane A, Zhang J, et al. Advancing Water Quality Research: K-Nearest Neighbor Coupled with the Improved Grey Wolf Optimizer Algorithm Model Unveils New Possibilities for Dry Residue Prediction. Water. 2023; 15(14):2631. https://doi.org/10.3390/w15142631
Chicago/Turabian StyleTahraoui, Hichem, Selma Toumi, Amel Hind Hassein-Bey, Abla Bousselma, Asma Nour El Houda Sid, Abd-Elmouneïm Belhadj, Zakaria Triki, Mohammed Kebir, Abdeltif Amrane, Jie Zhang, and et al. 2023. "Advancing Water Quality Research: K-Nearest Neighbor Coupled with the Improved Grey Wolf Optimizer Algorithm Model Unveils New Possibilities for Dry Residue Prediction" Water 15, no. 14: 2631. https://doi.org/10.3390/w15142631
APA StyleTahraoui, H., Toumi, S., Hassein-Bey, A. H., Bousselma, A., Sid, A. N. E. H., Belhadj, A.-E., Triki, Z., Kebir, M., Amrane, A., Zhang, J., Assadi, A. A., Chebli, D., Bouguettoucha, A., & Mouni, L. (2023). Advancing Water Quality Research: K-Nearest Neighbor Coupled with the Improved Grey Wolf Optimizer Algorithm Model Unveils New Possibilities for Dry Residue Prediction. Water, 15(14), 2631. https://doi.org/10.3390/w15142631









