Advances in Frazil Ice Evolution Mechanisms and Numerical Modelling in Rivers and Channels in Cold Regions
Abstract
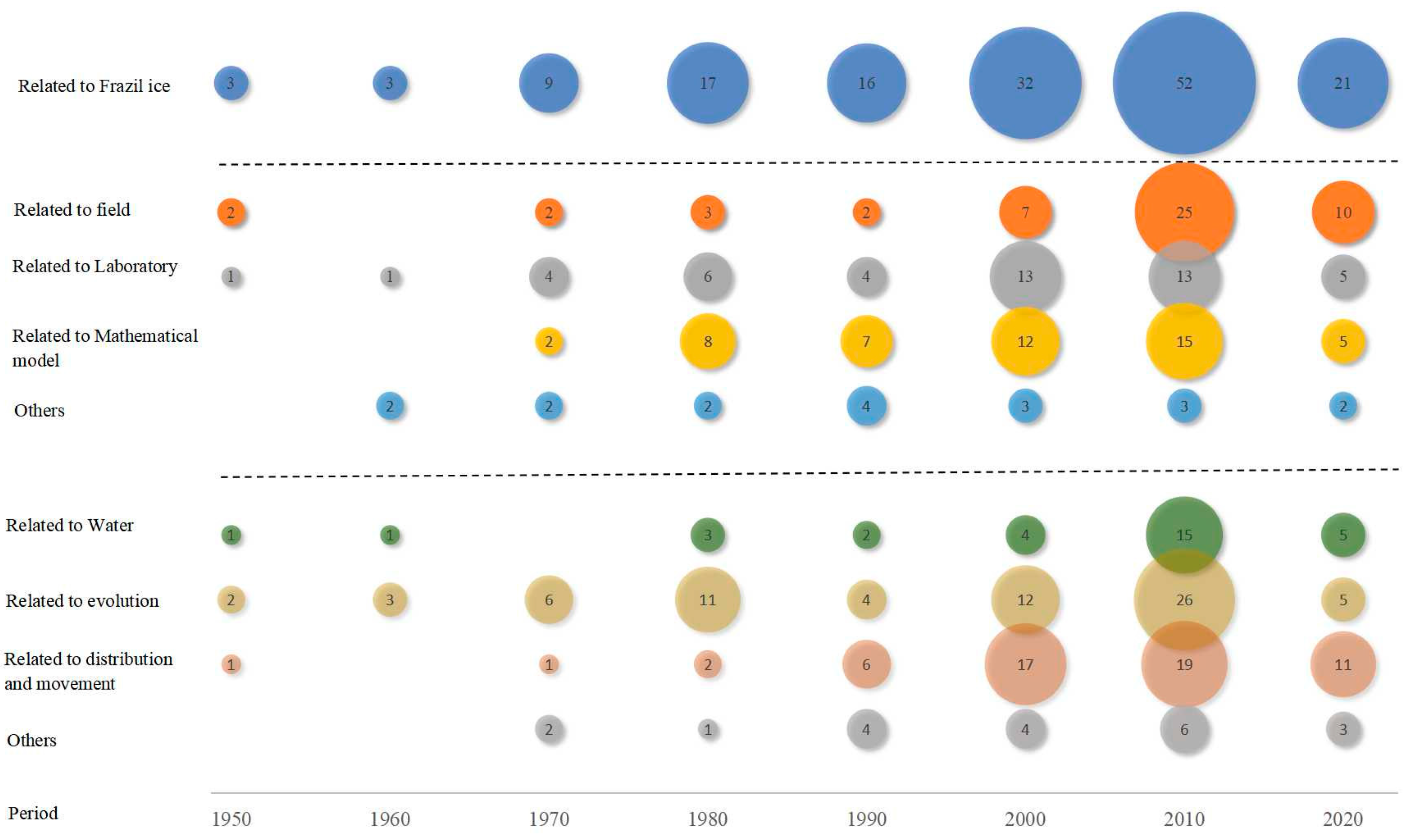
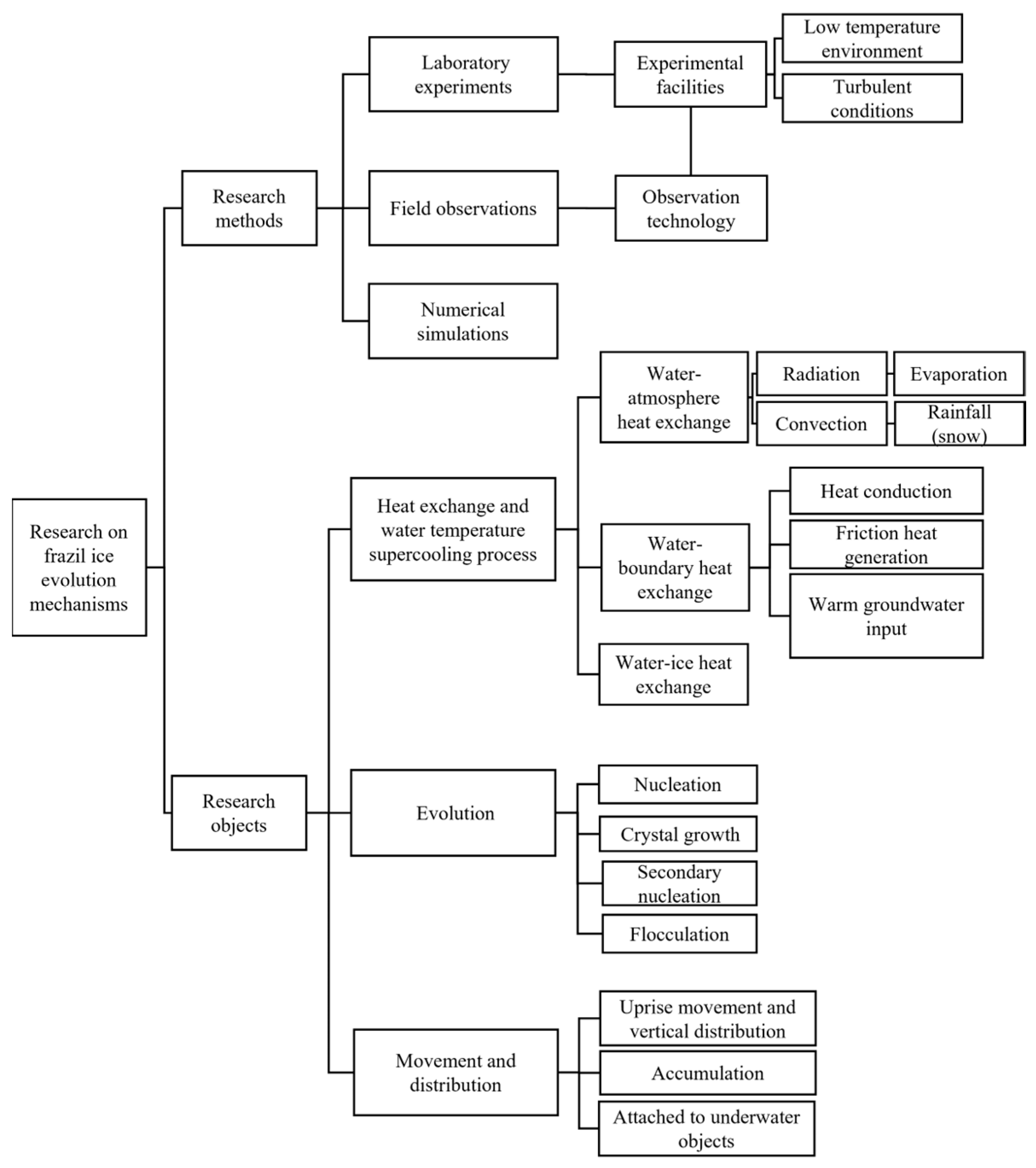
:1. Introduction
2. Laboratory Studies and Field Observation
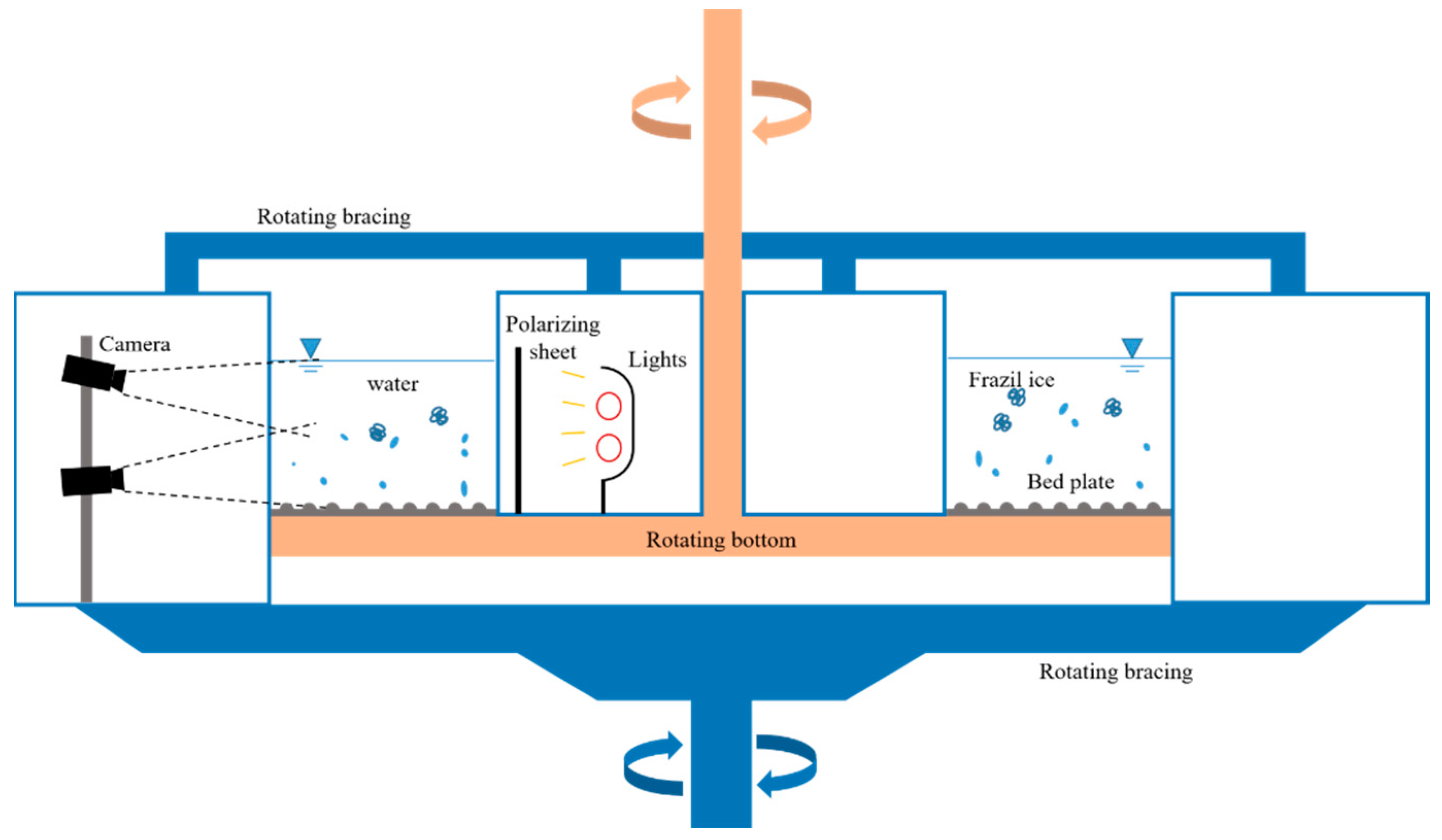
2.1. Laboratory Studies
2.1.1. Experimental Facilities
2.1.2. Observation Instruments
2.2. Field Observation
3. Heat Exchange and Supercooling Processes
3.1. Heat Exchange
3.1.1. Water–Atmosphere Heat Exchange
3.1.2. Water–Boundary Heat Exchange
3.1.3. Water–Ice Heat Exchange
| Model | No. | Year | Researcher | Formula | Remark |
|---|---|---|---|---|---|
| Heat transfer between water and air | 1 | 1984 | Shen [7] | is the heat transfer between water and air; is short-wave radiation, cal·cm−2·day−1 is the conductive heat transfer, cal·cm−2·day−1; is the incoming short-wave radiation, cal·cm−2·day−1; is the cloud cover in tenths; = 0.0017; c = 0.55; d = 0.052; , mb; is a coefficient, similar to the evapo-condensation flux; | |
| 2 | 1991 | Lai [74] | °C−1 °C; °C; | ||
| 3 | 2015 | Richard [67] | means the water experiences a heat loss or negative heat flux, and means the opposite; is the air temperature, °C; is the water albedo for long-wave radiation (approximately equal to 0.03); is the short-wave water surface albedo; is the air density; is the effective wind speed at a reference height; , , and , are the drag coefficients and heat transfer coefficients for sensible and latent heat, respectively is the specific heat of air; is the latent heat of vaporization (or sublimation); is the rate of falling snow mass per unit area; and are the temperature at the surface and the potential temperature (the temperature that a parcel of fluid would acquire if adiabatically brought to a standard reference pressure) at a reference height, respectively; are the humidity at the surface and the potential specific humidity at a reference height, respectively; | ||
| Heat transfer between water and frazil ice | 4 | 1984 | Omstedt [75] | is the coefficient of the heat exchange between water and ice; is the Nusselt number, is the radius of the spherical ice particles, i = 1, 2…. | |
| 5 | 1985 | Omstedt [76] | is the thickness of the ice crystal; | ||
| 6 | 1994 | Svensson [77] | |||
| 7 | 1984 | Daly [12] | For large particles, i.e., m* > 1: | ; is the “turbulent” Nusselt number; is the Prandtl Number; is the turbulence intensity; U is the mean flow velocity. | |
| 8 | 2007 | Holland [69] | A correction to “Frazil evolution in channels” by Lars Hammar and Hung-Tao Shen [70]. |
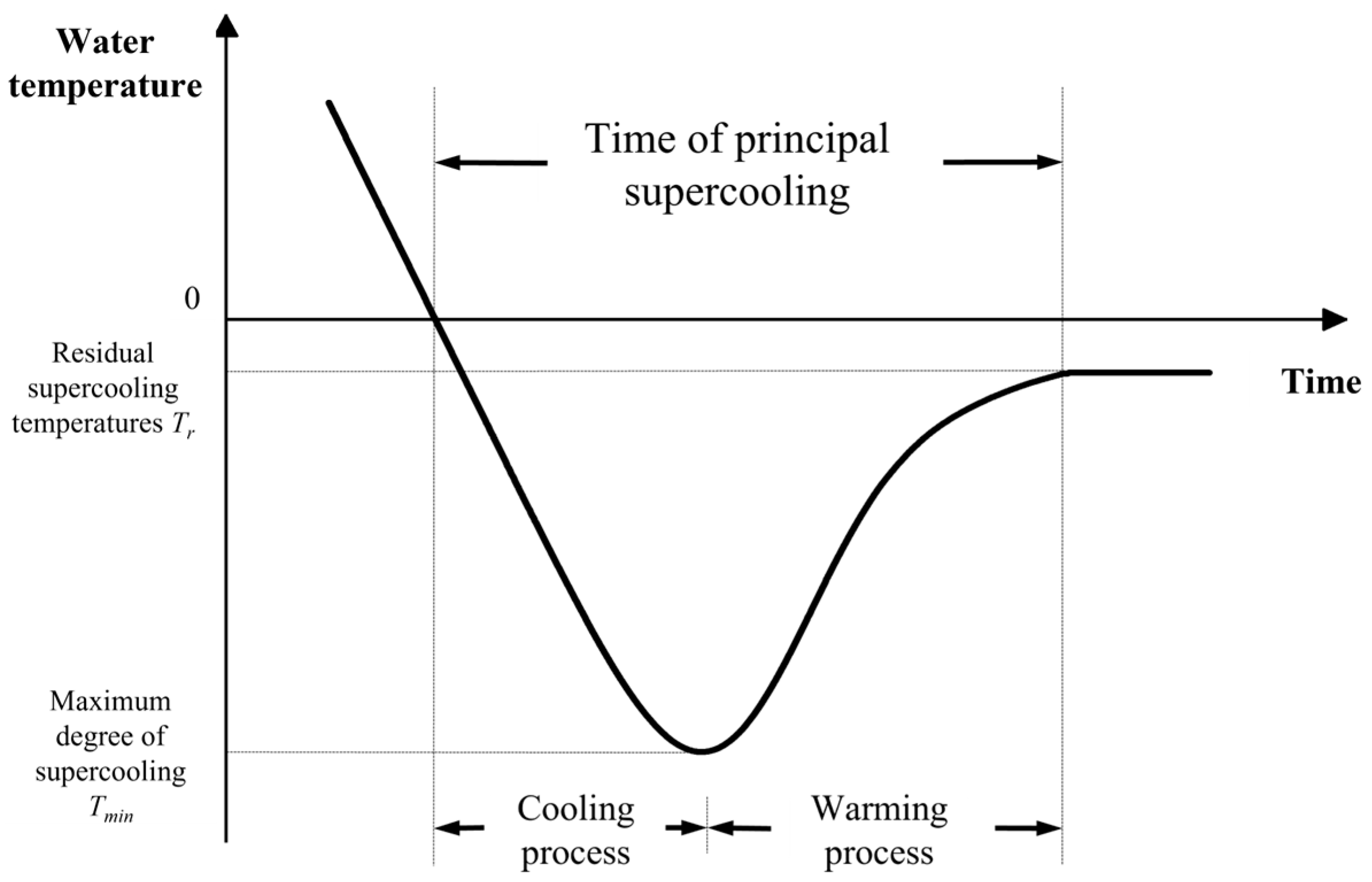
3.2. Supercooling Process
4. Frazil Ice Generation and Evolution
4.1. Nucleation
4.2. Crystal Growth
4.3. Secondary Nucleation and Flocculation
5. Frazil Ice Movement and Distribution
5.1. Uprise Movement and Vertical Distribution
5.2. Frazil Ice Accumulation
5.3. Attachment to Underwater Objects
6. Conclusions
- (1)
- The need for more applications of signal acquisition systems and image acquisition systems in field observations, and a close link between data from signal measurement systems and specific characteristics from image acquisition technology.
- (2)
- The need for a rational approach to determining the evolution of frazil ice generation by the water temperature subcooling process.
- (3)
- The need for numerical models for the initial nucleation process of frazil ice.
- (4)
- The need for new observation techniques to observe the dynamic processes of frazil ice collisions; then, more studies and new models on the secondary nucleation and flocculation of frazil ice.
- (5)
- The need for more studies on frazil ice movement and distribution and new three-dimensional frazil ice movement and distribution models for simulating frazil ice at complex cross sections of rivers and channels.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hicks, F. An overview of river ice problems: CRIPE07 guest editorial. Cold Reg. Sci. Technol. 2009, 55, 175–185. [Google Scholar] [CrossRef]
- Beltaos, S.; Prowse, T.D.; Carter, T. Ice regime of the lower Peace River and ice-jam flooding of the Peace-Athabasca Delta. Hydrol. Process. 2006, 20, 4009–4029. [Google Scholar] [CrossRef]
- Makkonen, L.; Tikanmaki, M. Modelling frazil and anchor ice on submerged objects. Cold Reg. Sci. Technol. 2018, 151, 64–74. [Google Scholar] [CrossRef]
- Ashton, G.D. Frazil Ice, 49th ed.; Academic Press: Madison, WI, USA, 1983; pp. 271–289. [Google Scholar] [CrossRef]
- Schneck, C.C.; Ghobrial, T.R.; Loewen, M.R. Laboratory study of the properties of frazil ice particles and flocs in water of different salinities. Cryosphere 2019, 13, 2751–2769. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Li, Z.; Xiu, Y.; Li, C.; Zhang, B.; Deng, Y. Microstructural characteristics of frazil particles and the physical properties of frazil ice in the yellow river, China. Crystals 2021, 11, 617. [Google Scholar] [CrossRef]
- Shen, H.T.; Chiang, L.A. Simulation of growth and decay of river ice cover. J. Hydraul. Eng. 1984, 110, 958–971. [Google Scholar] [CrossRef]
- Ye, S.Q.; Doering, J.; Shen, H.T. A laboratory study of frazil evolution in a counter-rotating flume. Can. J. Civ. Eng. 2004, 31, 899–914. [Google Scholar] [CrossRef]
- Mcfarlane, V.; Loewen, M.; Hicks, F. Measurements of the evolution of frazil ice particle size distributions. Cold Reg. Sci. Technol. 2015, 120, 45–55. [Google Scholar] [CrossRef]
- Barrette, P.D. Understanding frazil ice: The contribution of laboratory studies. Cold Reg. Sci. Technol. 2021, 189, 103334. [Google Scholar] [CrossRef]
- Hanley, T.; Michel, B. Laboratory formation of border ice and frazil slush. Can. J. Civ. Eng. 1977, 4, 153–160. [Google Scholar] [CrossRef]
- Daly, S.F. Frazil Ice Dynamics; US Army Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 1984.
- Daly, S.F.; Colbeck, S.C. Frazil ice measurements in Crrel’s flume facility. In Proceedings of the IAHR Symposium on Ice, Iowa City, IA, USA, 7–31 August 1986; pp. 427–438. [Google Scholar]
- Andres, D.D. Nucleation and frazil production during the supercooling period. In Proceedings of the Workshop on Hydraulics of Ice-Covered Rivers, Edmonton, AB, Canada, 1–2 June 1982; pp. 148–175. [Google Scholar]
- Michel, B. Theory of formation and deposit of frazil ice. In Proceedings of the 20th Annual Eastern Snow Conference, Quebec City, QC, Canada, 14–15 February 1963; pp. 130–148. [Google Scholar]
- Carstens, T. Experiments with supercooling and ice formation in flowing water. Geofys. Publ. 1966, 26, 1–18. [Google Scholar]
- Hanley, T.O.D.; Michel, B. Temperature patterns during the formation of border ice and frazil in a laboratory tank. In Proceedings of the 3rd International Symposium on Ice Problems, Hanover, NH, USA, 18–21 August 1975; pp. 211–220. [Google Scholar]
- Tsang, G.; Hanley, T.O. Frazil Formation in Water of Different Salinities and Supercoolings. J. Glaciol. 1985, 31, 74–85. [Google Scholar] [CrossRef] [Green Version]
- Ettema, R.; Karim, M.F.; Kennedy, J.F. A Study of Frazil Ice Formation; Army Cold Regions Research and Engineering Laboratory (CRREL): Hanover, NH, USA, 1984. [CrossRef]
- Mcfarlane, V.; Loewen, M.; Hicks, F. Laboratory measurements of the rise velocity of frazil ice particles. Cold Reg. Sci. Technol. 2014, 106, 120–130. [Google Scholar] [CrossRef]
- Mcfarlane, V.J. Laboratory Studies of Suspended Frazil Ice Particles; University of Alberta: Edmonton, AB, Canada, 2014. [Google Scholar]
- Mcfarlane, V.; Loewen, M.; Hicks, F. Field measurements of suspended frazil ice. Part I: A support vector machine learning algorithm to identify frazil ice particles. Cold Reg. Sci. Technol. 2019, 165, 102812. [Google Scholar] [CrossRef]
- Richard, M.; Cornett, A. NRC Frazil Ice Research Facility. In Proceedings of the Annual Conference—Canadian Society for Civil Engineering, Laval, QC, Canada, 2–5 June 2019. [Google Scholar]
- Clark, S.; Doering, J. Laboratory Experiments on Frazil-Size Characteristics in a Counterrotating Flume. J. Hydraul. Eng. 2006, 132, 94–101. [Google Scholar] [CrossRef]
- Clark, S.; Doering, J. Experimental investigation of the effects of turbulence intensity on frazil ice characteristics. Can. J. Civ. Eng. 2008, 35, 67–79. [Google Scholar] [CrossRef]
- Ye, S. A Physical and Mathematical Study of the Supe Rcooling Process and Frazil Evolution; University of Manitoba: Winnipeg, MB, Canada, 2002. [Google Scholar]
- Daly, S.F. Report on Frail Ice; International Association for Hydraulics Research, Working Group on Thermal Regimes: Madrid, Spain, 1994. [Google Scholar]
- Schaefer, V.J. The formation of frazil and anchor ice in cold water. Eos Trans. Am. Geophys. Union 1950, 31, 885–893. [Google Scholar] [CrossRef]
- Arakawa, K.; Higuchi, K. Studies on the Freezing of Water (I). J. Fac. Sci. Hokkaido Univ. II 1952, 4, 201–209. [Google Scholar]
- Schmidt, C.C.; Glover, J.R. A frazil ice concentration measuring system using a laser doppler velocimeter. J. Hydraul. Res. 1975, 13, 299–314. [Google Scholar] [CrossRef]
- Tsang, G. An instrument for measuring frazil concentration. Cold Reg. Sci. Technol. 1985, 10, 235–249. [Google Scholar] [CrossRef]
- Daly, S.F.; Rand, J.H. Development of an underwater frazil-ice detector. Cold Reg. Sci. Technol. 1990, 18, 77–82. [Google Scholar] [CrossRef]
- Pegau, W.S.; Paulson, C.A.; Zaneveld, J.R.V. Optical measurements of frazil concentration. Cold Reg. Sci. Technol. 1996, 24, 341–353. [Google Scholar] [CrossRef]
- Marko, J.R.; Jasek, M. Sonar detection and measurements of ice in a freezing river I: Methods and data characteristics. Cold Reg. Sci. Technol. 2010, 63, 121–134. [Google Scholar] [CrossRef]
- Marko, J.R.; Jasek, M. Sonar detection and measurement of ice in a freezing river II: Observations and results on frazil ice. Cold Reg. Sci. Technol. 2010, 63, 135–153. [Google Scholar] [CrossRef]
- Marko, J.R.; Topham, D.R. Laboratory measurements of acoustic backscattering from polystyrene pseudo-ice particles as a basis for quantitative characterization of frazil ice. Cold Reg. Sci. Technol. 2015, 112, 66–86. [Google Scholar] [CrossRef]
- Ghobrial, T.R.; Loewen, M.R.; Hicks, F. Laboratory calibration of upward looking sonars for measuring suspended frazil ice concentration. Cold Reg. Sci. Technol. 2012, 70, 19–31. [Google Scholar] [CrossRef]
- Lever, J.H.; Daly, S.F.; Rand, J.H.; Furey, D. A frazil concentration meter. In Proceedings of the International Association for Hydraulic Research Symposium on Ice, Banff, Alberta, 15–19 June 1992; pp. 1362–1376. [Google Scholar]
- Doering, J.C.; Morris, M.P. A digital image processing system to characterize frazil ice. Can. J. Civ. Eng. 2003, 30, 1–10. [Google Scholar] [CrossRef]
- Gilfilian, R.; Kline, W.; Osterkamp, T.; Benson, C. Ice formation in a small Alaskan stream. In Proceedings of the Symposia on the Role of Snow and Ice in Hydrology: Properties and Processes, Banff, AB, Canada, 6–20 September 1972; pp. 505–512. [Google Scholar]
- Richard, M.; Morse, B.; Daly, S.F.; Emond, J. Quantifying suspended frazil ice using multi-frequency underwater acoustic devices. River Res. Appl. 2011, 27, 1106–1117. [Google Scholar] [CrossRef]
- Ghobrial, T.R.; Loewen, M.R.; Hicks, F.E. Characterizing suspended frazil ice in rivers using upward looking sonars. Cold Reg. Sci. Technol. 2013, 86, 113–126. [Google Scholar] [CrossRef]
- Marko, J.R.; Jasek, M. Acoustic Detection and Study of Frazil Ice in a Freezing River during the 2004–2005 and 2005–2006 Winters. In Proceedings of the 19th IAHR International Symposium on Ice, Vancouver, BC, Canada, 6–11 July 2008; pp. 1–13. [Google Scholar]
- Marko, J.R.; Jasek, M. Multifrequency analyses of 2011–2012 Peace River SWIPS frazil backscattering data. Cold Reg. Sci. Technol. 2015, 110, 102–119. [Google Scholar] [CrossRef]
- Dmitrenko, I.A.; Wegner, C.; Kassens, H.; Kirillov, S.A.; Krumpen, T.; Heinemann, G.; Helbig, A.; Schröder, D.; Hölemann, J.A.; Klagge, T.; et al. Observations of supercooling and frazil ice formation in the Laptev Sea coastal polynya. J. Geophys. Res. Ocean. 2010, 115, C05015. [Google Scholar] [CrossRef] [Green Version]
- Ito, M.; Ohshima, K.I.; Fukamachi, Y.; Simizu, D.; Iwamoto, K.; Matsumura, Y.; Mahoney, A.R.; Eicken, H. Observations of supercooled water and frazil ice formation in an Arctic coastal polynya from moorings and satellite imagery. Ann. Glaciol. 2015, 56, 307–314. [Google Scholar] [CrossRef] [Green Version]
- Ito, M.; Ohshima, K.I.; Fukamachi, Y.; Mizuta, G.; Kusumoto, Y.; Nishioka, J. Observations of frazil ice formation and upward sediment transport in the Sea of Okhotsk: A possible mechanism of iron supply to sea ice. J. Geophys. Res. Ocean. 2017, 122, 788–802. [Google Scholar] [CrossRef]
- Ito, M.; Fukamachi, Y.; Ohshima, K.I.; Shirasawa, K. Observational evidence of supercooling and frazil ice formation throughout the water column in a coastal polynya in the Sea of Okhotsk. Cont. Shelf Res. 2020, 196, 104072. [Google Scholar] [CrossRef]
- Ito, M.; Ohshima, K.I.; Fukamachi, Y.; Mizuta, G.; Kusumoto, Y.; Kikuchi, T. Underwater frazil ice and its suspension depth detected from ADCP backscatter data around sea ice edge in the Sea of Okhotsk. Cold Reg. Sci. Technol. 2021, 192, 103382. [Google Scholar] [CrossRef]
- Frazer, E.K.; Langhorne, P.J.; Leonard, G.H.; Robinson, N.J.; Schumayer, D. Observations of the Size Distribution of Frazil Ice in an Ice Shelf Water Plume. Geophys. Res. Lett. 2020, 47, e2020GL090498. [Google Scholar] [CrossRef]
- Osterkamp, T.E.; Gosink, J.P. Frazil ice formation and ice cover development in interior Alaska streams. Cold Reg. Sci. Technol. 1983, 8, 43–56. [Google Scholar] [CrossRef]
- Mcfarlane, V.; Loewen, M.; Hicks, F. Measurements of the size distribution of frazil ice particles in three Alberta rivers. Cold Reg. Sci. Technol. 2017, 142, 100–117. [Google Scholar] [CrossRef]
- Mcfarlane, V.; Loewen, M.; Hicks, F. Field measurements of suspended frazil ice. Part II: Observations and analyses of frazil ice properties during the principal and residual supercooling phases. Cold Reg. Sci. Technol. 2019, 165, 102796. [Google Scholar] [CrossRef]
- Turcotte, B.; Morse, B.; Anctil, F. Cryologic continuum of a steep watershed. Hydrol. Process. 2014, 28, 809–822. [Google Scholar] [CrossRef]
- Turcotte, B.; Morse, B.; Anctil, F. Impacts of precipitation on the cryologic regime of stream channels. Hydrol. Process. 2012, 26, 2653–2662. [Google Scholar] [CrossRef]
- Cook, S.J.; Waller, R.I.; Knight, P.G. Glaciohydraulic supercooling: The process and its significance. Prog. Phys. Geogr. 2006, 30, 577–588. [Google Scholar] [CrossRef]
- Caissie, D.; El-Jabi, N.; Satish, M. Modeling of Maximum Daily Water Temperatures in a Small Stream Using Air Temperatures. J. Hydrol. 2001, 251, 14–28. [Google Scholar] [CrossRef]
- Evans, E.C.; Mcgregor, G.R.; Petts, G.E. River energy budgets with special reference to river bed processes. Hydrol. Process. 1998, 12, 575–595. [Google Scholar] [CrossRef]
- Turcotte, B.; Morse, B.; Anctil, F. The hydro-cryologic continuum of a steep watershed at freezeup. J. Hydrol. 2014, 508, 397–409. [Google Scholar] [CrossRef]
- Maheu, A.; St-Hilaire, A.; Caissie, D.; El-Jabi, N. Understanding the Thermal Regime of Rivers Influenced by Small and Medium Size Dams in Eastern Canada. River Res. Appl. 2016, 32, 2032–2044. [Google Scholar] [CrossRef]
- Lind, L.; Alfredsen, K.; Kuglerová, L.; Nilsson, C. Hydrological and thermal controls of ice formation in 25 boreal stream reaches. J. Hydrol. 2016, 540, 797–811. [Google Scholar] [CrossRef]
- Jing, Z.; Kang, L. High-order scheme for the source-sink term in a one-dimensional water temperature model. PLoS ONE 2017, 12, e0173236. [Google Scholar] [CrossRef] [Green Version]
- Kalke, H.; Mcfarlane, V.; Ghobrial, T.R.; Loewen, M.R. Field measurements of supercooling in the North Saskatchewan River. In Proceedings of the Committee on River Ice Processes and the Environment 20th Workshop on the Hydraulics of Ice Covered Rivers, Ottawa, ON, Canada, 14–16 May 2019; pp. 1–16. [Google Scholar]
- Mcfarlane, V.; Clark, S.P. A detailed energy budget analysis of river supercooling and the importance of accurately quantifying net radiation to predict ice formation. Hydrol. Process. 2021, 35, e14056. [Google Scholar] [CrossRef]
- Boyd, S.; Ghobrial, T.; Loewen, M. Analysis of the surface energy budget during supercooling in rivers. Cold Reg. Sci. Technol. 2023, 205, 103693. [Google Scholar] [CrossRef]
- Ashton, G.D. River and Lake Ice Engineering; Water Resources Publications: Littleton, CO, USA, 1986. [Google Scholar]
- Richard, M.; Morse, B.; Daly, S.F. Modeling frazil ice growth in the St. Lawrence river. Can. J. Civ. Eng. 2015, 42, 592–608. [Google Scholar] [CrossRef] [Green Version]
- Shen, H.T.; Ruggles, R.W. Winter Heat Budget and Frazil Ice Production in the Upper St. Lawrence River. Jawra J. Am. Water Resour. Assoc. 1982, 18, 251–256. [Google Scholar] [CrossRef]
- Holland, P.R.; Feltham, D.L.; Daly, S.F. On the Nusselt number for frazil ice growth—A correction to “Frazil evolution in channels” by Lars Hammar and Hung-Tao Shen. J. Hydraul. Res. 2007, 45, 421–424. [Google Scholar] [CrossRef]
- Rees Jones, D.W.; Wells, A.J. Solidification of a disk-shaped crystal from a weakly supercooled binary melt. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2015, 92, 022406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hammar, L.; Shen, H.T. Frazil evolution in channels. J. Hydraul. Res. 1995, 33, 291–306. [Google Scholar] [CrossRef]
- Ye, S.Q.; Doering, J. Simulation of the supercooling process and frazil evolution in turbulent flows. Can. J. Civ. Eng. 2004, 31, 915–926. [Google Scholar] [CrossRef]
- Wang, S.M.; Doering, J.C. Numerical simulation of supercooling process and frazil ice evolution. J. Hydraul. Eng. 2005, 131, 889–897. [Google Scholar] [CrossRef]
- Lal, A.M.W.; Shen, H.T. Mathematical model for river ice processes. J. Hydraul. Eng. 1991, 117, 851–867. [Google Scholar] [CrossRef] [Green Version]
- Omstedt, A.; Svensson, U. Modeling supercooling and ice formation in a turbulent Ekman layer. J. Geophys. Res. 1984, 89, 735–744. [Google Scholar] [CrossRef]
- Omstedt, A. On Supercooling and Ice Formation in Turbulent Sea-water. J. Glaciol. 1985, 31, 263–271. [Google Scholar] [CrossRef]
- Svensson, U.; Omstedt, A. Simulation of supercooling and size distribution in frazil ice dynamics. Cold Reg. Sci. Technol. 1994, 22, 221–233. [Google Scholar] [CrossRef]
- Jones, D.W.R.; Wells, A.J. Frazil-ice growth rate and dynamics in mixed layers and sub-ice-shelf plumes. Cryosphere 2018, 12, 25–38. [Google Scholar] [CrossRef] [Green Version]
- Hanley, T.O.; Tsang, G. Formation and properties of frazil in saline water. Cold Reg. Sci. Technol. 1984, 8, 209–221. [Google Scholar] [CrossRef]
- Clark, S.; Doering, J.C. Effect of turbulence intensity on frazil formation. In Proceedings of the 18th International IAHR Ice Symposium, Sapporo, Japan, 28 August 2006; pp. 267–275. [Google Scholar]
- Clark, S.P.; Doering, J.C. Frazil flocculation and secondary nucleation in a counter-rotating flume. Cold Reg. Sci. Technol. 2009, 55, 221–229. [Google Scholar] [CrossRef]
- Boyd, S.; Ghobrial, T.; Loewen, M.; Jasek, M.; Evans, J. A study of supercooling in rivers. Cold Reg. Sci. Technol. 2022, 194, 103455. [Google Scholar] [CrossRef]
- Boyd, S.; Ghobrial, T.; Loewen, M. Observations of supercooling in rivers. In Proceedings of the 25th IAHR International Symposium on Ice, Trondheim, Norway, 23–25 November 2020; pp. 1–10. [Google Scholar]
- Howley, R.; Ghobrial, T.R.; She, Y. Thermal regime in the North Saskatchewan River in Edmonton. In Proceedings of the CGU HS Committee on River Ice Processes and the Environment 20th Workshop on the Hydraulics of Ice Covered Rivers, Ottawa, ON, Canada, 14–16 May 2019; pp. 1–19. [Google Scholar]
- Omstedt, A. Modelling frazil ice and grease ice formation in the upper layers of the ocean. Cold Reg. Sci. Technol. 1985, 11, 87–98. [Google Scholar] [CrossRef]
- Svensson, U.; Omstedt, A. Numerical simulations of frazil ice dynamics in the upper layers of the ocean. Cold Reg. Sci. Technol. 1998, 28, 29–44. [Google Scholar] [CrossRef]
- Wang, S.M.; Doering, J.C. Development of a mathematical model of frazil ice evolution based on laboratory tests using a counter-rotating flume. Can. J. Civ. Eng. 2007, 34, 210–218. [Google Scholar] [CrossRef]
- Abbà, A.; Olla, P.; Valdettaro, L. Numerical analysis of frazil ice formation in turbulent convection. In Proceedings of the Springer Proceedings in Physics, Delhi, India, 12–16 December 2016; pp. 299–303. [Google Scholar]
- Blackburn, J.; She, Y. A comprehensive public-domain river ice process model and its application to a complex natural river. Cold Reg. Sci. Technol. 2019, 163, 44–58. [Google Scholar] [CrossRef]
- Michel, B. From the Nucleation of Ice Crystals in Clouds to the Formation of Frazil Ice in Rivers. In Proceedings of the Conference on Physics of Snow and Ice, Sapporo, Japan, 14–19 August 1967; pp. 129–136. [Google Scholar]
- Osterkamp, T.E.; Gilfilian, R.E. Nucleation characteristics of stream water and frazil ice nucleation. Water Resour. Res. 1975, 11, 926–928. [Google Scholar] [CrossRef]
- Sosso, G.C.; Tribello, G.A.; Zen, A.; Pedevilla, P.; Michaelides, A. Ice formation on kaolinite: Insights from molecular dynamics simulations. J. Chem. Phys. 2016, 145, 211927. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Osterkamp, T. Frazil Ice Formation: A Review. J. Hydraul. Div. 1978, 104, 1239–1255. [Google Scholar] [CrossRef]
- Osterkamp, T.E.; Gosink, J.P. An Investigation of Frazil and Anchor Ice: Formation, Properties, Evolution and Dynamics; Alaska University: Fairbanks, AK, USA, 1985. [Google Scholar]
- Osterkamp, T. Frazil-Ice Nucleation by Mass-Exchange Processes at the Air-Water Interface. J. Glaciol. 1978, 19, 619–625. [Google Scholar] [CrossRef] [Green Version]
- Chow, R.; Mettin, R.; Lindinger, B.; Kurz, T.; Lauterborn, W. The importance of acoustic cavitation in the sonocrystallisation of ice—High speed observations of a single acoustic bubble. In Proceedings of the 2003 IEEE Ultrasonics Symposium, Honolulu, HI, USA, 5–8 October 2003; pp. 1447–1450. [Google Scholar]
- Zhang, Z.; Sun, D.W.; Zhu, Z.; Cheng, L. Enhancement of Crystallization Processes by Power Ultrasound: Current State-of-the-Art and Research Advances. Compr. Rev. Food Sci. Food Saf. 2015, 14, 303–316. [Google Scholar] [CrossRef]
- Schremb, M.; Roisman, I.V.; Tropea, C. Transient effects in ice nucleation of a water drop impacting onto a cold substrate. Phys. Rev. E 2017, 95, 022805. [Google Scholar] [CrossRef]
- Jackson, K.A.; Uhlmann, D.R.; Hunt, J.D. On the nature of crystal growth from the melt. J. Cryst. Growth 1967, 1, 1–36. [Google Scholar] [CrossRef]
- Fujioka, T. Study of Ice Growth in Slightly Undercooled Water; Carnegie-Mellon University: Pittsburgh, PA, USA, 1978. [Google Scholar]
- Colbeck, S. The Slow Growth of Ice Crystals in Water; U.S. Army Cold Regions Research & Engineering Laboratory: Hanover, NH, USA, 1992.
- Smedsrud, L.H.; Jenkins, A. Frazil ice formation in an ice shelf water plume. J. Geophys. Res. Ocean. 2004, 109, C03025. [Google Scholar] [CrossRef] [Green Version]
- Dempsey, D.E.; Langhorne, P.J.; Robinson, N.J.; Williams, M.J.M.; Haskell, T.G.; Frew, R.D. Observation and modeling of platelet ice fabric in McMurdo Sound, Antarctica. J. Geophys. Res. Ocean. 2010, 115, C01007. [Google Scholar] [CrossRef]
- Richard, M. Field Investigation of Freshwater Frazil Ice Dynamics. Ph.D. Thesis, Laval University, Quebec City, QC, Canada, 2011. [Google Scholar]
- Hughes, K.G.; Langhorne, P.J.; Leonard, G.H.; Stevens, C.L. Extension of an Ice Shelf Water plume model beneath sea ice with application in McMurdo Sound, Antarctica. J. Geophys. Res. C Ocean. 2014, 119, 8662–8687. [Google Scholar] [CrossRef]
- Ettema, R.; Karim, M.F.; Kennedy, J.F. Laboratory experiments on frazil ice growth in supercooled water. Cold Reg. Sci. Technol. 1984, 10, 43–58. [Google Scholar] [CrossRef]
- Evans, T.W.; Sarofim, A.F.; Margolis, G. Models of secondary nucleation attributable to crystal-crystallizer and crystal-crystal collisions. AIChE J. 1974, 20, 959–966. [Google Scholar] [CrossRef]
- Daly, S.F. Evolution of frazil ice. In Proceedings of the IAHR International Symposium on Ice, Vancouver, BC, Canada, 6–11 July 2008; pp. 29–47. [Google Scholar]
- Morse, B.; Richard, M. A field study of suspended frazil ice particles. Cold Reg. Sci. Technol. 2009, 55, 86–102. [Google Scholar] [CrossRef]
- Ye, S.; Doering, J. Frazil size and flow turbulence. In Proceedings of the 11th Workshop on River Ice, Ottawa, ON, Canada, 18 December 2001; pp. 364–374. [Google Scholar]
- Liou, C.P.; Ferrick, M.G. A model for vertical frazil distribution. Water Resour. Res. 1992, 28, 1329–1337. [Google Scholar] [CrossRef]
- Ye, S.; Doering, J. A model for the vertical distribution of frazil ice. In Proceedings of the 12th Workshop on the Hydraulics of Ice Covered Rivers, Edmonton, AB, Canada, 19–20 June 2003; pp. 1–11. [Google Scholar]
- Wang, J.; Li, Q.g.; Sui, J.y. Floating rate of frazil ice particles in flowing water in bend channels—A three-dimensional numerical analysis. J. Hydrodyn. 2010, 22, 19–28. [Google Scholar] [CrossRef]
- Wang, X.; Jiang, Z.; Zhang, A.; Zhou, Z.; An, J. Two-phase flow numerical simulation of a bend-type ice sluice in the diversion water channel of powerhouse. Cold Reg. Sci. Technol. 2012, 81, 36–47. [Google Scholar] [CrossRef]
- Liu, M.; Fan, Q.; Guo, H. Frazil ice jam risk assessment method for water transfer projects based on design scheme. Water Sci. Technol. Water Supply 2020, 20, 3038–3051. [Google Scholar] [CrossRef]
- Shen, H.T.; Wang, D. Under Cover Transport and Accumulation of Frazil Granules. J. Hydraul. Eng. 1995, 121, 184–195. [Google Scholar] [CrossRef]
- Sui, J.; Wang, J.; Balachandar, R.; Sun, Z.; Wang, D. Accumulation of frazil ice along a river bend. Can. J. Civ. Eng. 2008, 35, 158–169. [Google Scholar] [CrossRef]
- Ettema, R.; Kirkil, G.; Daly, S. Frazil ice concerns for channels, pump-lines, penstocks, siphons, and tunnels in mountainous regions. Cold Reg. Sci. Technol. 2009, 55, 202–211. [Google Scholar] [CrossRef]
- Fu, H.; Guo, X.L.; Yang, K.L.; Wang, T.; Guo, Y.X. Ice accumulation and thickness distribution before inverted siphon. J. Hydrodyn. 2017, 29, 61–67. [Google Scholar] [CrossRef]
- Murray, A.; Essel, E.; Dow, K. Particle image velocimetry investigation of void seepage through a simulated ice jam. Cold Reg. Sci. Technol. 2022, 196, 103493. [Google Scholar] [CrossRef]
- Chen, P.; Cheng, T.; Wang, J.; Cao, G. Accumulation and evolution of ice jams influenced by different ice discharge: An experimental analysis. Front. Earth Sci. 2023, 10, 1054040. [Google Scholar] [CrossRef]
- Sui, J.; Wang, J.; He, Y.; Krol, F. Velocity profiles and incipient motion of frazil particles under ice cover. Int. J. Sediment Res. 2010, 25, 39–51. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Sui, J.; Karney, B. Formation and movement of ice accumulation waves under ice cover—An experimental study. J. Hydrol. Hydromech. 2019, 67, 171–178. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.; Sui, J.; Cao, G.; Cheng, T. Waved-Shape Accumulation of Ice Jam—Analysis and Experimental Study. Water 2022, 14, 3945. [Google Scholar] [CrossRef]
- Hou, Z.; Wang, J.; Sui, J.; Song, F.; Li, Z. Impact of Local Scour around a Bridge Pier on Migration of Waved-Shape Accumulation of Ice Particles under an Ice Cover. Water 2022, 14, 2193. [Google Scholar] [CrossRef]
- Arden, R.S.; Wigle, T.E. Dynamics of ice formation in the Upper Niagara River. In Proceedings of the Role of Snow and Ice in Hydrology, IAHS-UNESCO-WMO, Banff, AB, Canada, 6–20 September 1972; pp. 1296–1313. [Google Scholar]
- Marcotte, N. Anchor ice in Lachine Rapids results of observations and analysis. In Proceedings of the 7th IAHR International Symposium on Ice, Hamburg, Germany, 27–31 August 1984; Hamburgische Schiffbau-Versuchsanst GmbH: Hamburg, Germany, 1984; pp. 151–160. [Google Scholar]
- Parkinson, F.E. Anchor ice effects on water levels in Lake St. Louis, St. Lawrence River at Montreal. In Proceedings of the Third Workshop on the Hydraulics of River Ice, Fredericton, NB, Canada, 20 June 1984; Canadian Geophysical Union: Montreal, QC, Canada, 1984; pp. 345–370. [Google Scholar]
- Devik, O. Freezing Water and Supercooling: Anchor Ice and Frazil Ice. J. Glaciol. 1949, 1, 307–309. [Google Scholar] [CrossRef] [Green Version]
- Hirayama, K.; Terada, K.; Sato, M.; Hirayama, K.; Sasmoto, M.; Yamazaki, M. Field measurements of anchor and frazil ice. In Proceedings of the 9th Workshop on River Ice, Fredericton, NB, Canada, 24–26 September 1997; pp. 141–151. [Google Scholar]
- Hammar, L.; Shen, H.T. Anchor ice growth in channels. In Proceedings of the 8th Workshop on the Hydraulics of Ice Covered Rivers, Kamloops, BC, Canada, 16–18 August 1997; 1995; pp. 77–92. [Google Scholar]
- Hammar, L.; Kerr, D.J.; Shen, H.T.; Liu, L. Anchor ice formation in gravel-bedded channels. In Proceedings of the 13th IAHR International Symposium on Ice, Beijing, China, 27–31 August 1996; pp. 843–850. [Google Scholar]
- Doering, J.C.; Bekeris, L.E.; Morris, M.P.; Dow, K.E.; Girling, W.C. Laboratory study of anchor ice growth. J. Cold Reg. Eng. 2001, 15, 60–67. [Google Scholar] [CrossRef]
- Kerr, D.J.; Shen, H.T.; Daly, S.F. Evolution and hydraulic resistance of anchor ice on gravel bed. Cold Reg. Sci. Technol. 2002, 35, 101–114. [Google Scholar] [CrossRef]
- Qu, Y.X.; Doering, J. Laboratory study of anchor ice evolution around rocks and on gravel beds. Can. J. Civ. Eng. 2007, 34, 46–55. [Google Scholar] [CrossRef]
- Bisaillon, J.F.; Bergeron, N.E. Modeling anchor ice presence-absence in gravel bed rivers. Cold Reg. Sci. Technol. 2009, 55, 195–201. [Google Scholar] [CrossRef]
- Stickler, M.; Alfredsen, K.T. Anchor ice formation in streams: A field study. Hydrol. Process. 2009, 23, 2307–2315. [Google Scholar] [CrossRef]
- Dubé, M.; Turcotte, B.; Morse, B. Inner structure of anchor ice and ice dams in steep channels. Cold Reg. Sci. Technol. 2014, 106–107, 194–206. [Google Scholar] [CrossRef]
- Ghobrial, T.R.; Loewen, M.R. Continuous in situ measurements of anchor ice formation, growth, and release. Cryosphere 2021, 15, 49–67. [Google Scholar] [CrossRef]
- Daly, S.F.; Barrette, P.D. Prevention of Water Intake Blockage by Ice during Supercooling Events. J. Cold Reg. Eng. 2023, 37, 03122001. [Google Scholar] [CrossRef]
- Daly, S.F. Frazil Ice Blockage of Intake Trash Racks. In Cold Regions Technical Digest; U.S. Government Printing Office: Washington, DC, USA, 1991; Volume 91, pp. 1–12. [Google Scholar]
- Chen, Z.; Ettema, R.; Lai, Y. Ice-tank and numerical study of frazil ingestion by submerged intakes. J. Hydraul. Eng. 2004, 130, 101–111. [Google Scholar] [CrossRef]
- Daly, S.F.; Ettema, R. Frazil ice blockage of water intakes in the Great Lakes. J. Hydraul. Eng. 2006, 132, 814–824. [Google Scholar] [CrossRef]
- Richard, M.; Morse, B. Multiple frazil ice blockages at a water intake in the St. Lawrence River. Cold Reg. Sci. Technol. 2008, 53, 131–149. [Google Scholar] [CrossRef]
- Wang, Y.; Politano, M.; Ho, H.C.; Muste, M.; Michell, F.; Stallings, J. Assessment of ice plugging of a cooling water intake by a numerical model. J. Hydraul. Res. 2014, 52, 81–92. [Google Scholar] [CrossRef]
- Wang, Y.; Politano, M.; Muste, M.; Stallings, J.; Michell, F. A 3D numerical model to evaluate the effect of shutting down a once-through cooling system on the ice transport to existing intakes. In Proceedings of the 34th IAHR Congress 2011—Balance and Uncertainty: Water in a Changing World, Brisbane, Australia, 26 June–1 July 2011; International Association for Hydro-Environment Engineering and Research (IAHR): Beijing, China; pp. 3279–3287. [Google Scholar]
- Kempema, E.W.; Ettema, R. Fish, ice, and wedge-wire screen water intakes. J. Cold Reg. Eng. 2016, 30, 04015004. [Google Scholar] [CrossRef]


| No. | Year | Researcher | Formula | Remark |
|---|---|---|---|---|
| 1 | 1994 | Svensson [77] | is the active freezing area per crystal, is the density of ice; L is the latent heat of ice. | |
| 2 | 1995 | Hammar [71] | is the volumetric concentration of frazil in the k-th size fraction; is the frazil buoyant velocity of the k-th size fraction; is the source term due to the thermal growth of frazil ice; is the source/sink term due to secondary nucleation and flocculation. |
| No. | Year | Researcher | Formula | Remark |
|---|---|---|---|---|
| 1 | 1994 | Svensson [77] | N represents the number of particle size groups; i represents the i-th size is the number change in the i-th particle size group due to secondary nucleation; is the relative velocity; is the gravitational rise’s velocity; is the turbulent dissipation rate; is the kinematic viscosity; d is the crystal diameter; is the average number of crystals per unit volume; | |
| 2 | 1995 | Hammar [71] | is the rate of collisional energy transfer to the crystals per unit volume of fluid; are the collision efficiency functions for differential rising and turbulent shear, respectively; | |
| 3 | 1974 | Evans [107] | is the nucleation rate; is the number of crystals generated per unit of collision energy and is expected to be a function of parameters including supercooling , the salt concentration , the crystal size , and the agitation power . The author believes that the mixing power can be replaced by hydraulic conditions such as the turbulence intensity or dissipation rate in natural water flow calculations. is the rate of the energy transfer to the crystals by a collision. and are the components of contributed to by collisions between crystals driven by gravity and turbulence, respectively. is the crystal frequency distribution; is the average crystal size; ; , are the crystal radii of crystal–crystal collisions; and are the densities of the fluid and crystal, respectively. |
| No. | Year | Researcher | Formula | Remark |
|---|---|---|---|---|
| 1 | 1994 | Svensson [76] | is the number change in the i-th size is the ratio between the volumes of particles of two neighboring radius intervals; is the radius of ice particles in the minimum radius group; | |
| 1995 | Hammar [70] | are the number concentration of the i-th- and j-th-sized particles, respectively, where each collision per unit volume reduces the local number concentration of i-th- and j-th-class particles by one; is the new particle volume due to each collision; is the volume of the ice nucleus size class. |
| No. | Year | Researcher | Technique and Method | Laboratory or Field | Size of Frazil Ice (Diameter) |
|---|---|---|---|---|---|
| 1 | 1950 | Schaefer [28] | Microscope | Laboratory | 1–5 mm |
| 2 | 1952 | Arakawa et al. [29] | The shadow photograph method | Laboratory | 0.1–3 mm |
| 3 | 1983 | Osterkamp et al. [51] | Camera | Field | Mostly 0.1 to 1 mm, up to 3–5 mm |
| 4 | 2006 | Clark et al. [80] | Image acquisition and post-processing technique | Laboratory | Approximately 0.3–5 mm |
| 5 | 2012 | Ghobrial et al. [37] | Microscope equipped with a digital camera | Laboratory | 0.25–4.25 mm |
| 6 | 2015 | McFarlane et al. [9] | Image acquisition and post-processing technique | Laboratory | 0.022–5.5 mm |
| 7 | 2017 | McFarlane et al. [52] | Image acquisition and post-processing technique | Field | Mean of 0.32–1.2 mm |
| 8 | 2019 | McFarlane et al. [53] | Image acquisition and post-processing technique | Field | 0.034–5.83 mm |
| 9 | 2022 | Richard et al. [23] | Image acquisition technique | Laboratory | Approximately 1 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Lian, J.; Zhao, X.; Guo, Q.; Yang, D. Advances in Frazil Ice Evolution Mechanisms and Numerical Modelling in Rivers and Channels in Cold Regions. Water 2023, 15, 2582. https://doi.org/10.3390/w15142582
Chen Y, Lian J, Zhao X, Guo Q, Yang D. Advances in Frazil Ice Evolution Mechanisms and Numerical Modelling in Rivers and Channels in Cold Regions. Water. 2023; 15(14):2582. https://doi.org/10.3390/w15142582
Chicago/Turabian StyleChen, Yunfei, Jijian Lian, Xin Zhao, Qizhong Guo, and Deming Yang. 2023. "Advances in Frazil Ice Evolution Mechanisms and Numerical Modelling in Rivers and Channels in Cold Regions" Water 15, no. 14: 2582. https://doi.org/10.3390/w15142582
APA StyleChen, Y., Lian, J., Zhao, X., Guo, Q., & Yang, D. (2023). Advances in Frazil Ice Evolution Mechanisms and Numerical Modelling in Rivers and Channels in Cold Regions. Water, 15(14), 2582. https://doi.org/10.3390/w15142582









