Evaluating Urban Stream Flooding with Machine Learning, LiDAR, and 3D Modeling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Machine Learning
2.2.1. Data Preparation
2.2.2. Prophet Algorithm
2.2.3. Performance Analysis
2.3. Terrestrial LiDAR and 3D River Channel Modeling
2.4. Upstream Volume Calculations
3. Results
3.1. Machine Learning
3.2. LiDAR 3D Models and Upstream Volume Calculations
4. Discussion
Methodology Applications
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, S.; Tachikiawa, Y.; Takara, K. Recent flood disasters and progress of disaster management system in Korea. Annu. Disaster Prev. Res. Inst. 2007, 50, 15–31. [Google Scholar]
- Walsh, C.J.; Roy, A.H.; Feminella, J.W.; Cottingham, P.D.; Groffman, P.M.; Morgan, R.P. The urban stream syndrome: Current knowledge and the search for a cure. J. N. Am. Benthol. Soc. 2005, 24, 706–723. [Google Scholar] [CrossRef]
- Wilson, C.; Weng, Q. Assessing surface water quality and its relation with urban land cover changes in the Lake Calumet Area, Greater Chicago. Envion. Manag. 2010, 45, 1096–1111. [Google Scholar] [CrossRef]
- Wilby, R.; Perry, G.L.W. Climate change, biodiversity and the urban environment: A critical review based on London, UK. Prog. Phys. Geogr. 2006, 30, 73–98. [Google Scholar] [CrossRef]
- Sun, N.; Yearsley, J.; Baptiste, M.; Cao, Q.; Lettenmaier, D.; Nijssen, B. A spatially distributed model for assessment of the effects of changing land use and climate change on urban stream quality. Hydrol. Process. 2016, 30, 4779–4798. [Google Scholar] [CrossRef]
- Bell, C.D.; McMillan, S.K.; Clinton, S.M.; Jefferson, A.J. Hydrologic response to stormwater control measures in urban watersheds. J. Hydrol. 2016, 541, 1488–1500. [Google Scholar] [CrossRef] [Green Version]
- Konrad, C.P.; Booth, D.B. Hydrological changes in urban streams and their ecological significance. Am. Fish. Soc. Symp. 2005, 47, 157–177. [Google Scholar]
- Paul, M.J.; Meyer, J.L. Streams in the urban landscape. Annu. Rev. Ecol. Syst. 2001, 32, 333–365. [Google Scholar] [CrossRef]
- Awadallah, M.O.; Juarez, A.; Alfredsen, K. Comparison between topographic and bathymetric LiDAR terrain models in flood inundation estimations. Remote Sens. 2022, 14, 227. [Google Scholar] [CrossRef]
- Ourloglou, O.; Stefanidis, K.; Dimitriou, E. Assessing nature-based and classical engineering solutions for flood-risk reduction in urban streams. J. Ecol. Eng. 2020, 21, 46–56. [Google Scholar] [CrossRef]
- Kolakovic, S.; Kolakovic, S.; Fabian, J.; Jeftenic, G.; Trajkovic, S. River floodplain 1D/2D hydraulic modeling combined with recent LiDAR DTM technology. Tech. Gaz. 2021, 28, 880–890. [Google Scholar] [CrossRef]
- Bruno, L.S.; Mattos, T.S.; Oliveira, T.S.; Almagro, A.; Rodrigues, D.B.B.R. Hydrological and hydraulic modeling applied to flash flood event in a small urban stream. Hydrology 2022, 9, 223. [Google Scholar] [CrossRef]
- Brunner, G.W. HEC-RAS 5.0 Hydraulic Reference Manual; US Army Corps of Engineers: Washington, DC, USA, 2016.
- Baek, S.S.; Pyo, J.; Chun, J.A. Prediction of water level and water quality using a CNN-LSTM combined deep learning approach. Water 2020, 12, 3399. [Google Scholar] [CrossRef]
- Phan, T.; Nguyen, X.H. Combining statistical machine learning models with ARIMA for water level forecasting: The case of the Red River. Adv. Water Resour. 2020, 142, 103656. [Google Scholar] [CrossRef]
- Ghorpade, P.; Gadge, A.; Lende, A.; Chordiya, H.; Gosavi, G.; Mishra, A.; Hooli, B.; Ingle, Y.S.; Shaikh, N. Flood forecasting using machine learning: A review. In Proceedings of the 8th International Conference on Smart Computing and Communication (ICSCC), Kochi, India, 1–3 July 2021. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef] [Green Version]
- Sahoo, B.B.; Jha, R.; Singh, A.; Kumar, D. Long short-term memory (LSTM) recurrent neural network for low-flow hydrological time series forecasting. Acta Geophys. 2019, 67, 1471–1481. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, A. Large-scale assessment of Prophet for multi-step ahead forecasting of monthly streamflow. Adv. Geosci. 2018, 45, 147–153. [Google Scholar] [CrossRef] [Green Version]
- Munoz, P.; Orellana-Alvevar, J.; Bendix, J.; Feyen, J.; Celleri, R. Flood early warning systems using machine learning techniques: The case of the Tomebamba Catchment at the southern Andes of Ecuador. Hydrology 2021, 8, 183. [Google Scholar] [CrossRef]
- Nevo, S.; Morin, E.; Rosenthal, A.G.; Metzger, A.; Barshai, C.; Weitzner, D.; Voloshin, D.; Kratzert, F.; Elidan, G.; Dror, G.; et al. Flood forecasting with machine learning models in an operational framework. Hydrol. Earth Syst. Sci. 2022, 26, 4013–4032. [Google Scholar] [CrossRef]
- Rasheed, Z.; Aravamudan, A.; Sefidmazgi, A.G.; Anagnostopoulos, G.C.; Nikolopoulos, E.I. Advancing flood warning procedures in ungauged basins with machine learning. J. Hydrol. 2022, 609, 127736. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Feng, W.; Huang, H. Short term real-time rolling forecast of urban river water levels based on LSTM: A case study in Fuzhou City, China. Int. J. Eng. Res. Public Health 2021, 18, 9287. [Google Scholar] [CrossRef] [PubMed]
- Koyama, M.; Sakai, M.; Yamada, T. Study on water-level-forecast method based on a time series analysis of urban river basins—A case study of Shibuya River Basin in Tokyo. Water 2022, 15, 161. [Google Scholar] [CrossRef]
- Moon, H.; Yoon, S.; Moon, Y. Urban flood forecasting using a hybrid modeling approach based on a deep learning technique. Hydroinformatics 2023, 25, 593–610. [Google Scholar] [CrossRef]
- Wanginger, U. Introduction to LiDAR. In LiDAR; Weitkamp, C., Ed.; Springer Series in Optical Sciences; Springer: New York, NY, USA, 2005; Volume 102, pp. 1–18. ISBN 9780387400754. [Google Scholar]
- Liu, X. Airborne LiDAR for DEM generation: Some critical issues. Prog. Phys. Geogr. 2008, 32, 31–49. [Google Scholar] [CrossRef]
- Young, A.P.; Olsen, M.J.; Driscoll, N.; Flick, R.E.; Gutierrez, R.; Guza, R.T.; Johnstone, E.; Kuester, F. Comparison of airborne and terrestrial Lidar estimates of seacliff erosion in Southern California. Photogramm. Eng. Remote Sens. 2010, 76, 421–427. [Google Scholar] [CrossRef] [Green Version]
- Williams, K.; Olsen, M.J.; Roe, G.V.; Glennie, C. Synthesis of transportation applications of mobile LiDAR. Remote Sens. 2013, 5, 4652–4692. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.; Joyce, J.; Phillips, D.; Shrestha, R.; Carter, W. Delineating and defining the boundaries of an active landslide in the rainforest of Puerto Rico using a combination of airborne and terrestrial LiDAR data. Landslides 2013, 10, 503–513. [Google Scholar] [CrossRef]
- Dong, W. 3D modeling of UC Berkeley’s Strawberry Creek using terrestrial LiDAR. In Proceedings of the Environmental Sciences Senior Thesis Symposium, Berkeley, CA, USA, 14 April 2018; pp. 1–34. [Google Scholar]
- Myers, D.T.; Rediske, R.R.; McNair, J.N. Measuring streambank erosion: A comparison of erosion pins, total station, and terrestrial laser scanner. Water 2019, 11, 1846. [Google Scholar] [CrossRef] [Green Version]
- Costabile, P.; Costanzo, C.; Lorenzo, G.; Santis, R.S.; Penna, N.; Macchione, F. Terrestrial and airborne laser scanning and 2-D modeling for 3-D flood hazard maps in urban areas: New opportunities and perspectives. Environ. Modell. Sofw. 2021, 135, 104889. [Google Scholar] [CrossRef]
- Ramacgabdran, R.; Fernandez, Y.B.; Truckell, I.; Constantiono, C.; Casselden, R.; Leinster, P.; Casado, M.R. Strategies for the characterization of microtopographic features that influence surface water flooding. Remote Sens. 2023, 15, 1912. [Google Scholar] [CrossRef]
- Bolick, M.M.; Post, C.J.; Naser, M.Z.; Mikhailova, E.A. Comparison of machine learning algorithms to predict dissolved oxygen in an urban stream. Environ. Sci. Pollut. Res. 2023, 30, 78075–78096. [Google Scholar] [CrossRef] [PubMed]
- U.S. Climate Data. Available online: https://www.usclimatedata.com/climate/pickens/south-carolina/united-states/ussc0270 (accessed on 3 April 2023).
- Esswein, S.; Hallstrom, J.; Post, C.J.; White, D.; Eidson, G. Augmenting hydrologic information systems with streaming water resource data. In Proceedings of the South Carolina Water Resources Conference, Columbia, SC, USA, 13–14 October 2010. [Google Scholar]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2017, 72, 37–45. [Google Scholar] [CrossRef]
- Harvey, A.; Peters, S. Estimation procedures for structural time series models. J. Forecast. 1990, 9, 89–108. [Google Scholar] [CrossRef]
- Chowdari, K.K.; Barma, S.D.; Bhat, N.; Girisha, R.; Gouda, K.C. Evaluation of ARIMA, Facebook Prophet, and a boosting algorithm framework for monthly precipitation prediction of a semi-arid district of north Karnataka, India. In Proceedings of the Fourth International Conference on Emerging Research in Electronics, Computer Science, and Technology (ICERECT), Mandya, India, 26–27 December 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Xiao, Q.; Zhou, L.; Xiang, X.; Liu, L.; Liu, X.; Li, X.; Ao, T. Integration of hydrological model and time series model for improving the runoff simulation: A case study on BTOP modeling in Zhou River Basin, China. Appl. Sci. 2022, 12, 6883. [Google Scholar] [CrossRef]
- Khatibi, R.; Ghorbani, M.A.; Naghipour, L.; Jothiprakash, V.; Fathima, T.A.; Fazelifard, M.H. Inter-comparison of time series models of lake levels predicted several modeling strategies. J. Hydrol. 2014, 511, 530–545. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Naghshara, S.; Salih, S.Q.; Kim, S.; Malik, A.; Ghorbani, M.A. Lake water modeling using newly developed hybrid data intelligence model. Theor. Appl. Climatol. 2020, 141, 1285–1300. [Google Scholar] [CrossRef]
- Du, N.; Liang, X. Short-term water level prediction of Hongze Lake by Prophet-LSTM combined model based on LAE. In Proceedings of the 7th International Conference on Hydraulic and Civil Engineering & Smart Water Conservancy and Intelligent Disaster Reduction Forum, Nanjing, China, 6–8 November 2021. [Google Scholar]
- Tornevi, A.; Bergstedt, O.; Forsber, B. Precipitation effects on microbial pollution in a river: Lag structures and seasonal effect modification. PLoS ONE 2014, 9, e98546. [Google Scholar] [CrossRef]
- Van Vliet, M.T.H.; Ludwig, F.; Zwolsman, J.J.G.; Weedon, G.P.; Kabat, P. Global river temperatures and sensitivity to atmospheric warming and changes in river flow. Water Resour. Res. 2011, 47, W02544. [Google Scholar] [CrossRef]
- Oo, H.T.; Zin, W.W.; Kyi, C.C.T. Analysis of streamflow response to changing climate conditions using SWAT model. Civil. Eng. J. 2020, 6, 194–209. [Google Scholar] [CrossRef] [Green Version]
- Morrill, J.C.; Bales, R.C.; Conklin, M.H. Estimating stream temperature from air temperature: Implications for future water quality. J. Environ. Eng. 2005, 131, 139–146. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Peterson, A. River water temperature in relation to local air temperature in the Mackensize and Yukon Basins. Arctic 2017, 70, 47–58. [Google Scholar] [CrossRef]
- Campolo, M.; Andreussi, P.; Soldati, A. River flood forecasting with a neural network model. Water Resour. Res. 1999, 35, 1191–1197. [Google Scholar] [CrossRef]
- Fleischmann, A.; Fan, F.; Collischonn, B.; Collischonn, W.; Pontes, P.; Ruhoff, A. Precipitation as a proxy for climate variables: Application for hydrological modelling. Hydrol. Sci. Res. 2019, 64, 361–379. [Google Scholar] [CrossRef]
- Harvey, R.; Lye, L.; Khan, A.; Paterson, R. The influence of air temperature on water temperature and the concentration of dissolved oxygen in Newfoundland Rivers. Can. Water Resour. J. 2013, 36, 171–192. [Google Scholar] [CrossRef]
- Rajwa-Kuligiewicz, A.; Bialik, R.J.; Rowinski, P.M. Dissolved oxygen and water temperature dynamics in lowland rivers over various timescales. J. Hydrol. Hydromech. 2015, 63, 353–363. [Google Scholar] [CrossRef] [Green Version]
- Irvine, K.N.; Richey, J.E.; Holtgrieve, G.W.; Sarkkula, J.; Sampson, M. Spatial and temporal variability of turbidity, dissolved oxygen, conductivity, temperature, and fluorescence in the lower Mekong River- Tonle Sap system identified using continuous monitoring. Int. J. River Basin Manag. 2011, 9, 151–168. [Google Scholar] [CrossRef]
- Ouali, D.; Chebana, F.; Ouarda, T.B.M.J. Fully nonlinear statistical and machine-learning approaches for hydrological frequency estimation at ungauged sites. J. Adv. Model. Earth Syst. 2017, 9, 1292–1306. [Google Scholar] [CrossRef]
- Wang, W.; Chau, K.; Cheng, C.; Qiu, L. A comparison of performance of several intelligence methods for forecasting monthly discharge time series. J. Hydrol. 2009, 374, 294–306. [Google Scholar] [CrossRef] [Green Version]
- Reich, N.G.; Lessler, J.; Sakrejda, K.; Lauer, S.A.; Iamsirithanworn, S.; Cummings, D.A.T. Case study in evaluating time series prediction models using the relative means absolute error. Am. Stat. 2016, 70, 285–292. [Google Scholar] [CrossRef] [Green Version]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE, and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Molnar, C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable; Learnpub: Victoria, BC, Canada, 2019. [Google Scholar]
- LiDAR USA. Surveyor 32. Available online: https://www.lidarusa.com/surveyor-32-uav-and-mms.html (accessed on 27 April 2023).
- Isenburg, M. LAStools, Efficient LiDAR Processing Software. Version 1.4, Academic. Available online: https://rapidlasso.com/LAStools (accessed on 27 April 2023).
- Chow, T.E.; Hodgson, M.E. Effects of lidar post-spacing and DEM resolution to mean slope estimation. Int. J. Geogr. Inf. Sci. 2009, 23, 1277–1295. [Google Scholar] [CrossRef]
- ESRI. ArcScene, version 10.8.1; ESRI: Redlands, CA, USA, 2023.
- Sun, X.Y.; Newham, L.T.H.; Croke, B.F.W.; Norton, J.P. Three complementary methods for sensitivity analysis of a water quality model. Environ. Modell. Softw. 2012, 37, 19–29. [Google Scholar] [CrossRef]
- Abrahart, R.J.; See, L.M. Neural network modeling of non-linear hydrological relationships. Hydrol. Earth Syst. Sci. 2007, 11, 1563–1579. [Google Scholar] [CrossRef] [Green Version]
- Asha, J.; Rishidas, S.; Santhosh Kumar, S.; Reena, P. Analysis of temperature prediction using random forest and Facebook Prophet algorithms. In Proceedings of the International Conference on Innovative Data Communication Technologies and Application (ICIDCA), Coimbatore, India, 17–18 October 2019; pp. 432–439. [Google Scholar]
- Okonkwo, S.; Ukoha, P.; Adedoyin, E.; Adewoye, R. Time series analysis of precipitation in Lake Chad using the Prophet Forecasting procedure. In Proceedings of the 4th International Conference of Professional Statisticians Society of Nigeria (PSSN), Ilorin, Nigeria, 24–27 August 2020. [Google Scholar]
- Sulasikin, A.; Nugraha, Y.; Kanggrawan, J.I.; Suherman, A.L. Monthly rainfall prediction using the Facebook Prophet model for flood mitigation in Central Jakarta. In Proceedings of the International Conference on ICT for Smart Society (ICISS), Bandung, Indonesia, 2–4 August 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Aguilera, H.; Guardiola-Albert, C.; Naranjo-Fernandez, N.; Kohfahl, C. Towards flexible groundwater-level prediction for adaptive water management: Using Facebook’s Prophet forecasting approach. Hydrol. Sci. J. 2019, 64, 1504–1518. [Google Scholar] [CrossRef]
- Elovitz, K.M. Understanding what humidity does and why. ASHRAE J. 1999, 41, 84. [Google Scholar]
- Bao, J.; Sherwood, S.C.; Alexander, L.V.; Evans, J.P. Future increases in extreme precipitation exceed observed scaling rates. Nat. Clim. Change 2017, 7, 128–132. [Google Scholar] [CrossRef]
- Fatdillah, E.; Rehan, B.M.; Rameshwaran, P.; Bell, V.A.; Zulkafli, Z.; Yusuf, B.; Sayers, P. Spatial estimates of flood damage and risk are influenced by the underpinning DEM resolution: A case study in Kuala Lumpur, Malaysia. Water 2022, 14, 2208. [Google Scholar] [CrossRef]
- Sampson, C.C.; Fewtrell, T.J.; Duncan, A.; Shaad, K.; Horritt, M.S.; Bates, P.D. Use of terrestrial laser scanning data to drive decimetric resolution urban inundation models. Adv. Water Resour. 2012, 41, 1–17. [Google Scholar] [CrossRef]
- Turner, A.B.; Colby, J.D.; Csontos, R.M.; Batten, M. Flood modeling using a synthesis of multi-platform LiDAR data. Water 2013, 5, 1533–1560. [Google Scholar] [CrossRef] [Green Version]
- Ozdemir, H.; Sampson, C.C.; De Almeida, G.A.M.; Bates, P.D. Evaluating scale and roughness effects in urban flood modeling using terrestrial LiDAR data. Hydrol. Earth Syst. Sci. 2013, 17, 4015–4030. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Sarma, A.K.; Hack, J. Cost-effective optimization of nature based solutions for reducing urban floods considering limited space availability. Environ. Proc. 2020, 7, 297–319. [Google Scholar] [CrossRef]
- Maspo, N.; Harun, A.N.B.; Goto, M.; Cheros, F.; Haron, N.A.; Nawi, M.N.M. Evaluation of machine learning approach in flood prediction scenarios and its input parameters: A systematic review. In Proceedings of the 7th AUN/SEED-Net Regional Conference on National Disaster, Kuala Lumpar, Malaysia, 25–26 November 2019; Volume 479. [Google Scholar] [CrossRef]
- Motta, M.; Neto, M.C.; Sarmento, P. A mixed approach for urban flood prediction using machine learning and GIS. Int. J. Disaster Risk Res. 2021, 56, 102154. [Google Scholar] [CrossRef]
- Brecheisen, Z.S.; Richter, D. Gully-erosion estimation and terrain reconstruction using analyses of microtropographic roughness and LiDAR. Catena 2021, 202, 105264. [Google Scholar] [CrossRef]
- Wolter, C.F.; Schilling, K.E.; Palmer, J.A. Quantifying the extent of eroding streambanks in Iowa. J. Am. Water Resour. Assoc. 2021, 57, 391–405. [Google Scholar] [CrossRef]




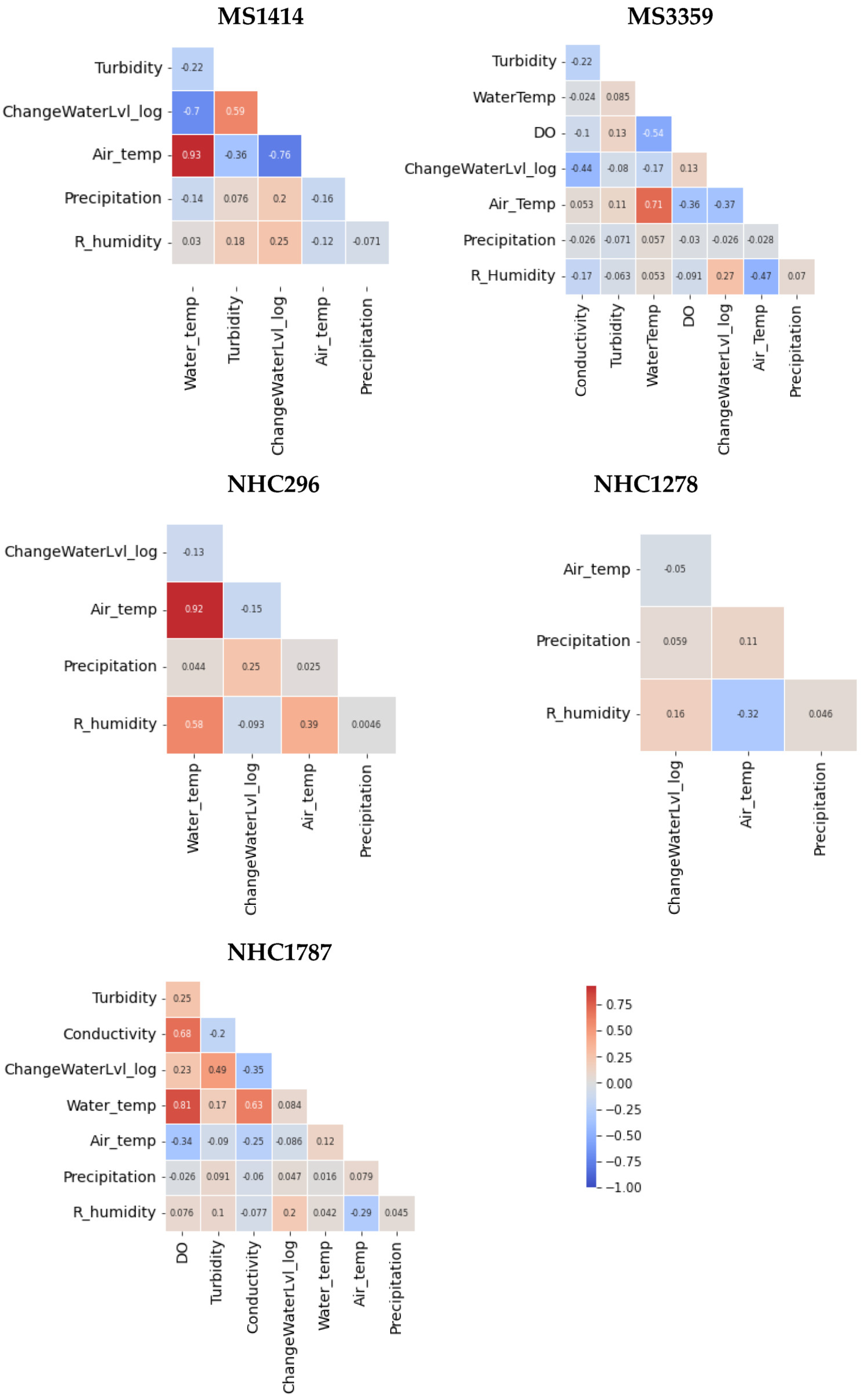
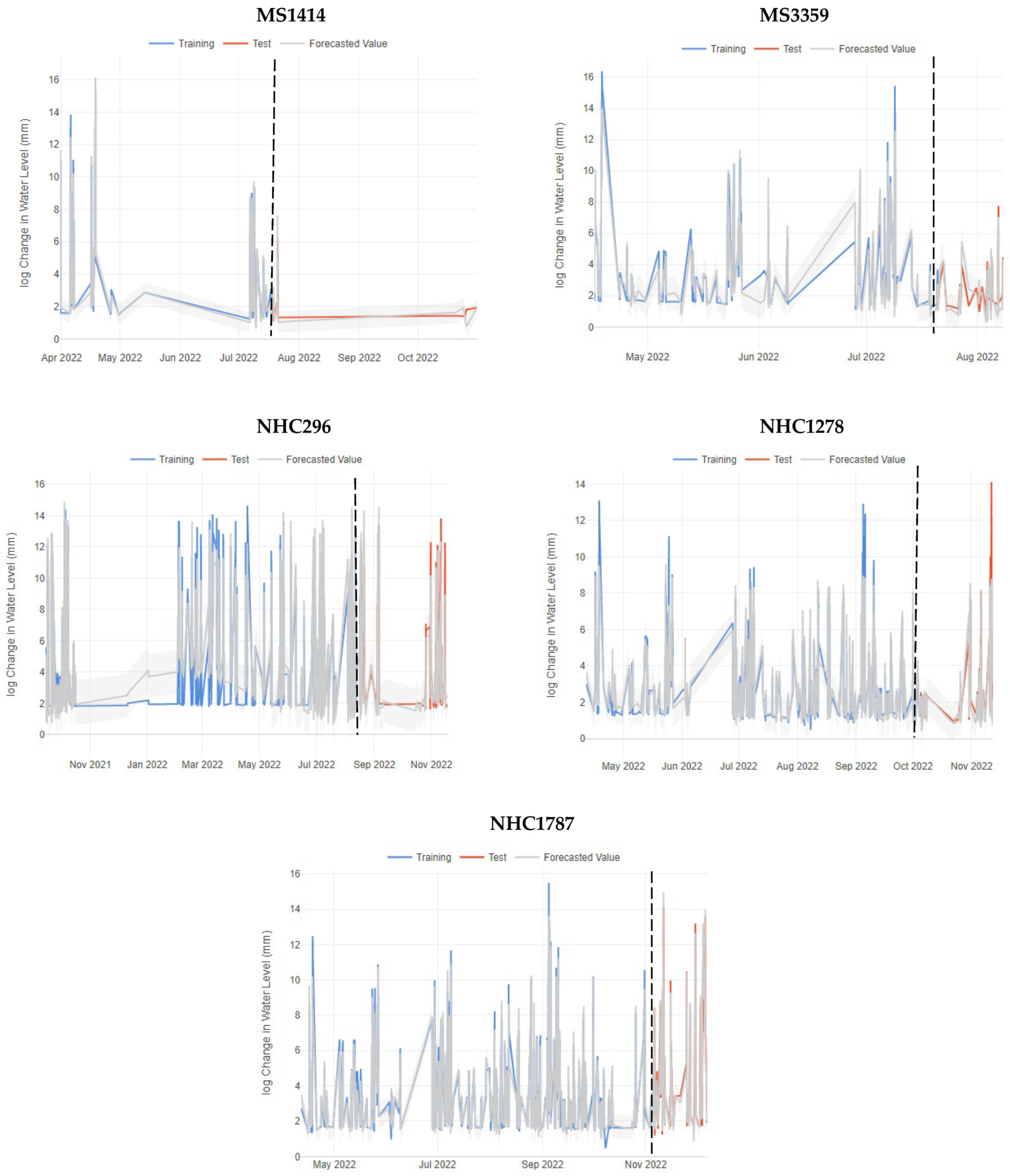


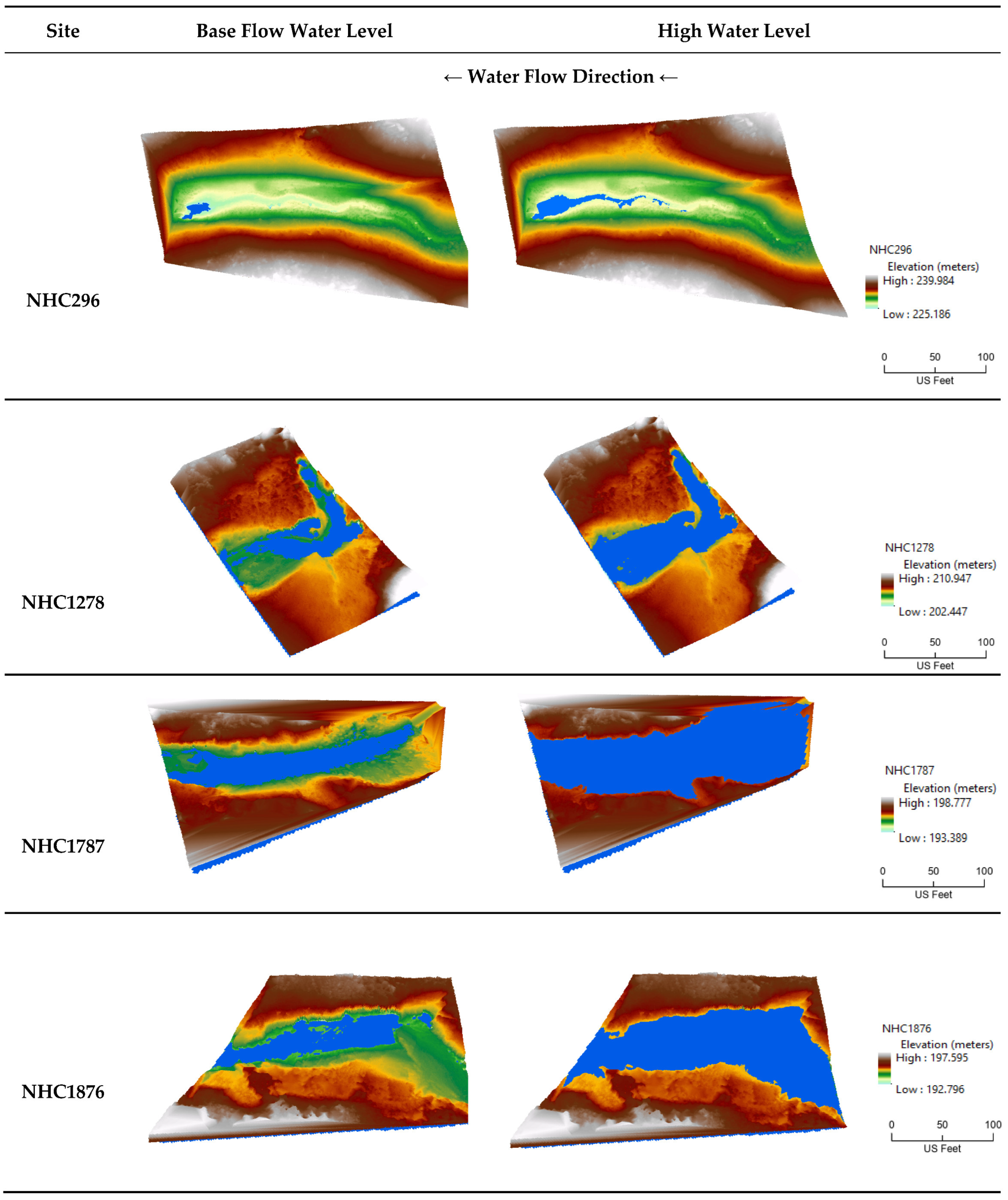
| Site Name | Data Available | Temporal Resolution | Variables | Number of Records | Closest Weather Station |
|---|---|---|---|---|---|
| MS1414 | 3/31/2022–10/31/2022 | 13 min | Water temperature (°C), turbidity (NTUs), air temperature (°C), precipitation (mm), relative humidity (%) | 363 | Weather station 1 |
| MS3359 | 4/16/2022–8/8/2022 | 14 min | Dissolved oxygen (% saturation), turbidity (NTUs), conductivity (µS/m), water temperature (°C), air temperature (°C), precipitation (mm), relative humidity (%) | 573 | Weather station 3 |
| NHC296 | 9/14/2021–11/18/2022 | 12 min | Water temperature (°C), air temperature (°C), precipitation (mm), relative humidity (%) | 2598 | Weather station 2 |
| NHC1278 | 4/11/2022–11/12/2022 | 12 min | Air temperature (°C), precipitation (mm), relative humidity (%) | 1473 | Weather station 3 |
| NHC1787 | 4/11/2022–12/7/2022 | 11 min | Dissolved oxygen (% saturation), turbidity (NTUs), conductivity (µS/m), water temperature (°C), air temperature (°C), precipitation (mm), relative humidity (%) | 1828 | Weather station 3 |
| Station Name | RMSE | MAE | R2 |
|---|---|---|---|
| MS1414 | 0.446 | 0.318 | 0.986 |
| MS3359 | 0.535 | 0.433 | 0.944 |
| NHC296 | 1.002 | 0.710 | 0.927 |
| NHC1278 | 0.813 | 0.485 | 0.909 |
| NHC1787 | 0.729 | 0.442 | 0.964 |
| Site Name | Point Spacing (m) | Point Density (m2) | DEM Resolution (m) | Mean Slope (%) |
|---|---|---|---|---|
| MS292 | 0.006 | 27,778 | 0.03 | 36.5 |
| MS1414 | 0.004 | 62,500 | 0.03 | 27.2 |
| MS3359 | 0.01 | 10,000 | 0.028 | 33.6 |
| NHC296 | 0.008 | 15,625 | 0.024 | 27.6 |
| NHC1278 | 0.009 | 12,346 | 0.032 | 27.0 |
| NHC1787 | 0.009 | 12,346 | 0.024 | 26.5 |
| NHC1876 | 0.008 | 15,625 | 0.024 | 29.9 |
| BG1128 | 0.006 | 27,778 | 0.018 | 27.6 |
| Site Information | Base Flow | High Water Level | Increase in Volume | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Name | Catchment Area (m2) | Water Level Elevation (m) | Upstream Volume (m3) | Two Foot Cross Section Volume (m3) | Water Level Elevation (m) | Upstream Volume (m3) | Two Foot Cross Section Volume (m3) | Upstream Volume (m3) | Two Foot Cross Section Volume (m3) |
| MS292 | 1333.4 | 224.2 | 5.26 | 0.095 | 224.83 | 44.85 | 1.24 | 39.59 | 1.145 |
| MS1414 | 390.5 | 208.1 | 21.58 | 0.33 | 208.87 | 200.30 | 2.45 | 178.72 | 2.12 |
| MS3359 | 1338.9 | 187.3 | 345.33 | 0.13 | 188.35 | 928.99 | 2.64 | 583.66 | 2.51 |
| NHC296 | 3628.2 | 228.5 | 13.39 | 1.03 | 229.5 | 52.03 | 3.24 | 38.64 | 2.21 |
| NHC1278 | 956.4 | 205.5 | 61.22 | 0.13 | 205.93 | 135.63 | 1.37 | 74.41 | 1.24 |
| NHC1787 | 822.8 | 194.8 | 25.97 | 0.38 | 195.86 | 352.82 | 4.68 | 326.85 | 4.3 |
| NHC1876 | 412.4 | 194 | 7.69 | 0.47 | 194.9 | 107.41 | 2.91 | 99.72 | 2.44 |
| BG1128 | 685.3 | 205 | 7.80 | 0.02 | 205.4 | 48.55 | 0.22 | 40.75 | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bolick, M.M.; Post, C.J.; Naser, M.Z.; Forghanparast, F.; Mikhailova, E.A. Evaluating Urban Stream Flooding with Machine Learning, LiDAR, and 3D Modeling. Water 2023, 15, 2581. https://doi.org/10.3390/w15142581
Bolick MM, Post CJ, Naser MZ, Forghanparast F, Mikhailova EA. Evaluating Urban Stream Flooding with Machine Learning, LiDAR, and 3D Modeling. Water. 2023; 15(14):2581. https://doi.org/10.3390/w15142581
Chicago/Turabian StyleBolick, Madeleine M., Christopher J. Post, M. Z. Naser, Farhang Forghanparast, and Elena A. Mikhailova. 2023. "Evaluating Urban Stream Flooding with Machine Learning, LiDAR, and 3D Modeling" Water 15, no. 14: 2581. https://doi.org/10.3390/w15142581
APA StyleBolick, M. M., Post, C. J., Naser, M. Z., Forghanparast, F., & Mikhailova, E. A. (2023). Evaluating Urban Stream Flooding with Machine Learning, LiDAR, and 3D Modeling. Water, 15(14), 2581. https://doi.org/10.3390/w15142581










