Numerical Simulation of Sediment Transport in Unsteady Open Channel Flow
Abstract
:1. Introduction
2. Governing Equations
2.1. Nonequilibrium Sediment Transport Model
2.2. Numerical Methods
2.2.1. Godunov-Type Finite Volume Method
2.2.2. HLLC Approximated Riemann Solver
2.2.3. Well-Balanced Scheme for the VDSWEs
3. Results
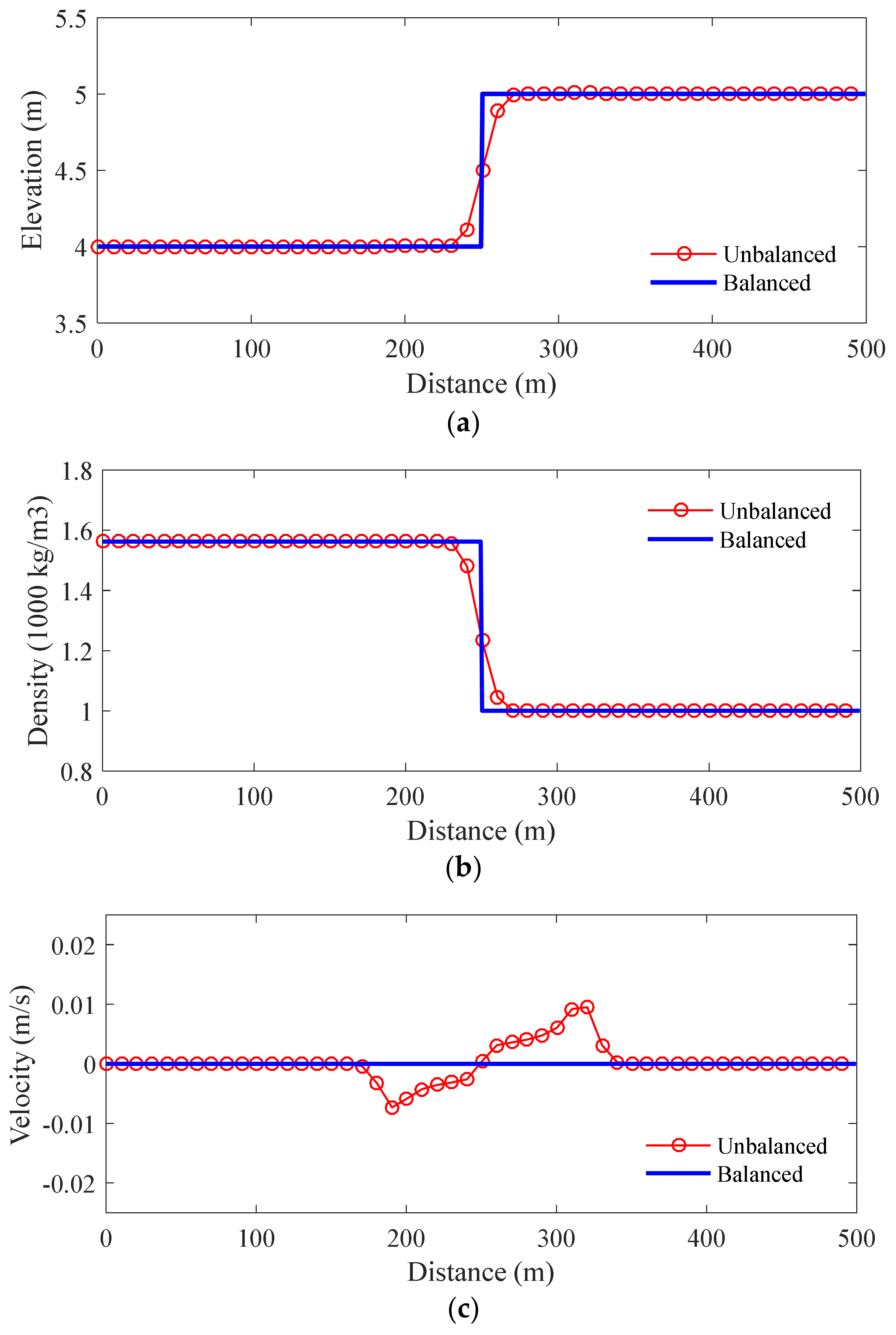
3.1. Case 1: Standing Contact-Discontinuity
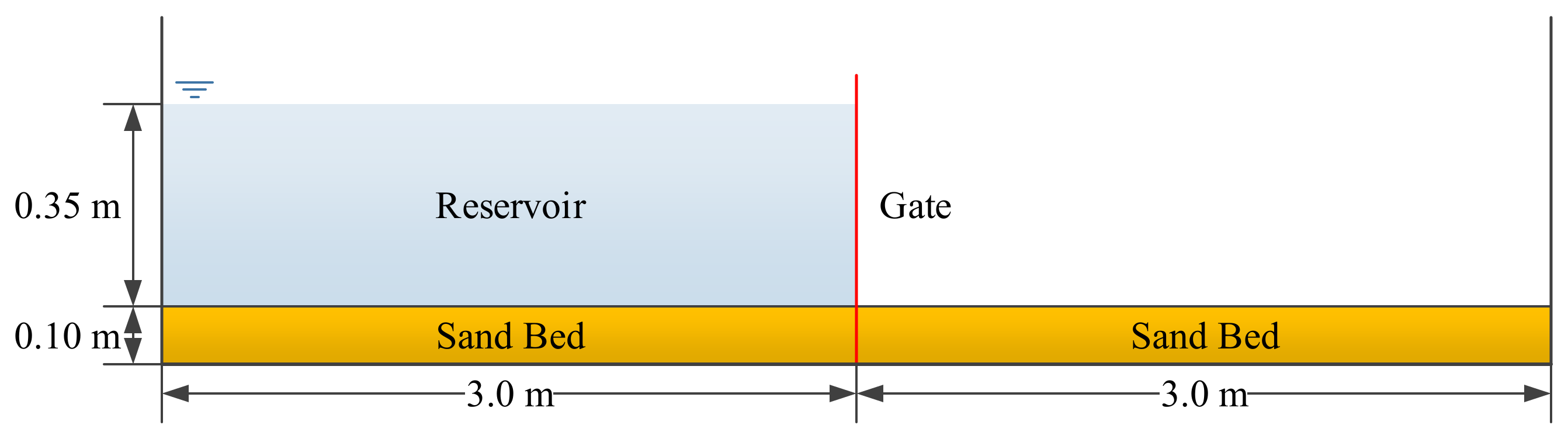
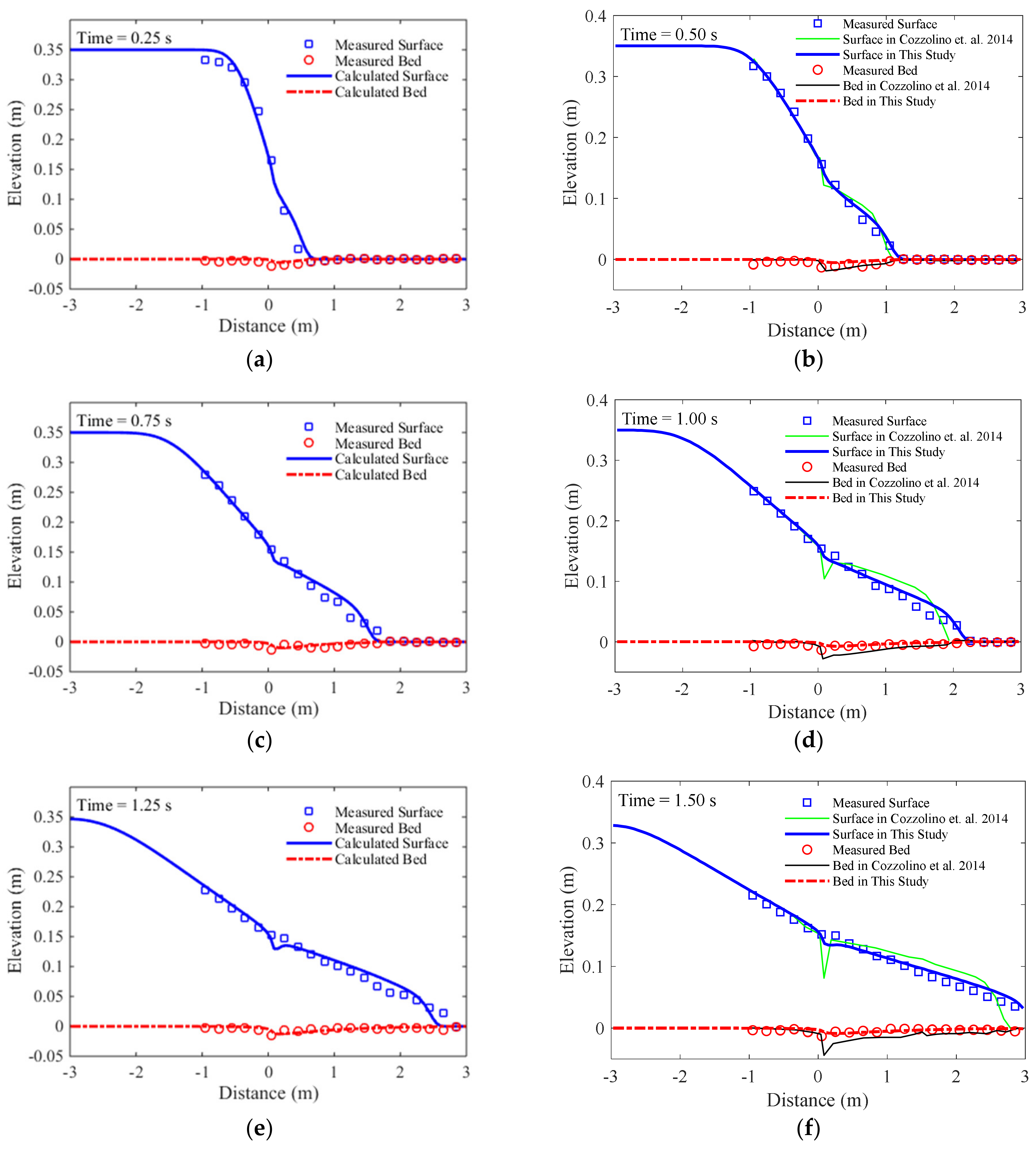
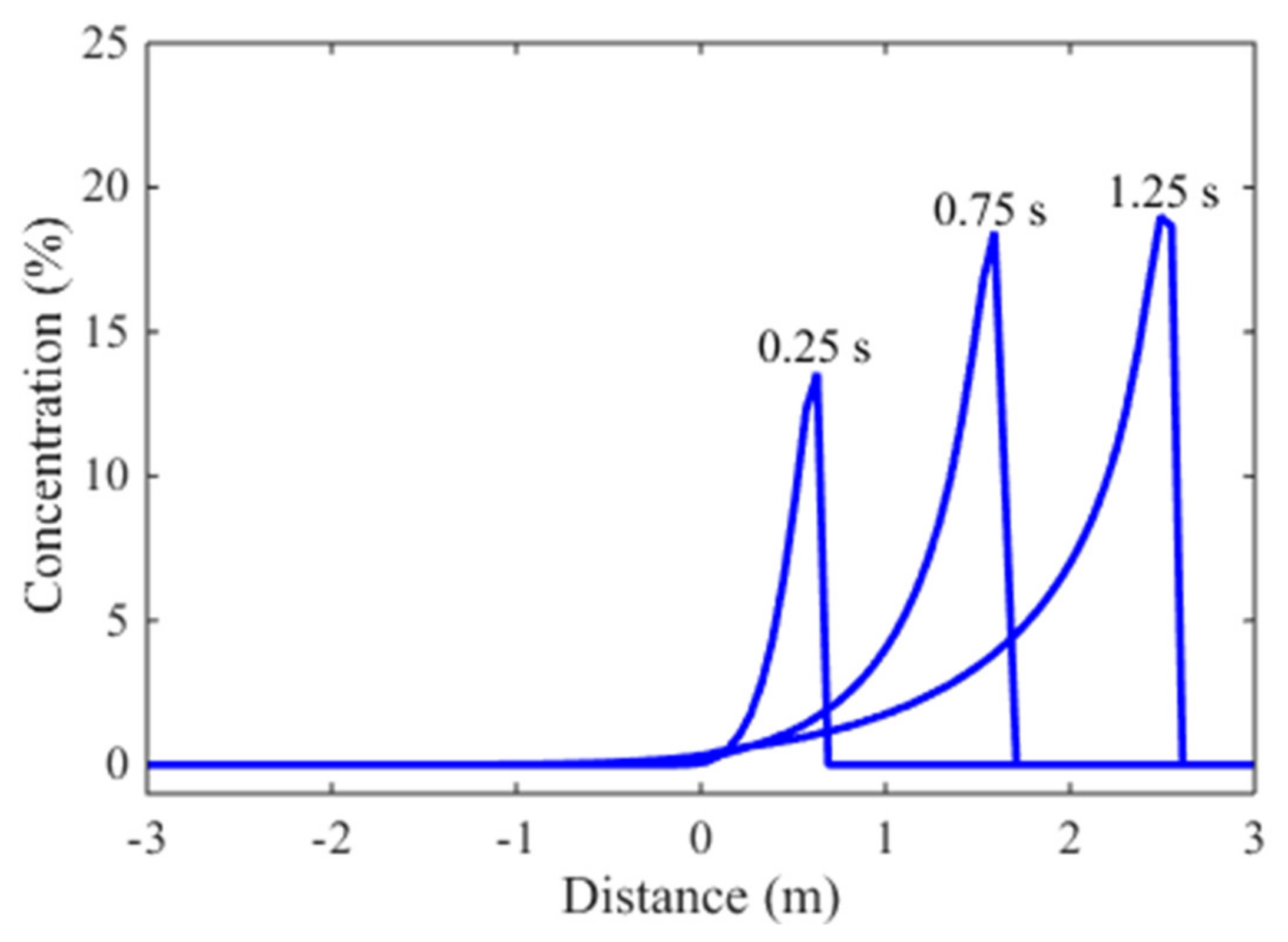
3.2. Case 2: One-Dimensional Dam-Break Flow over Mobile Bed
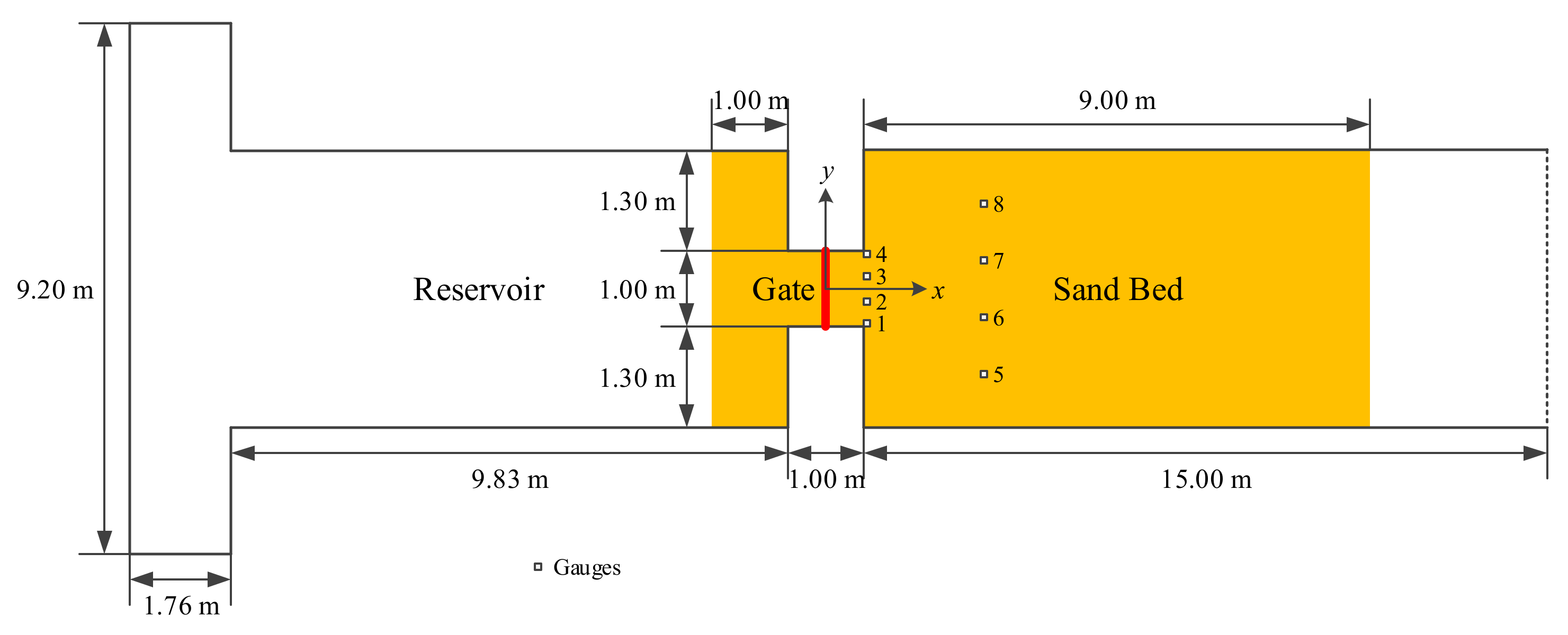
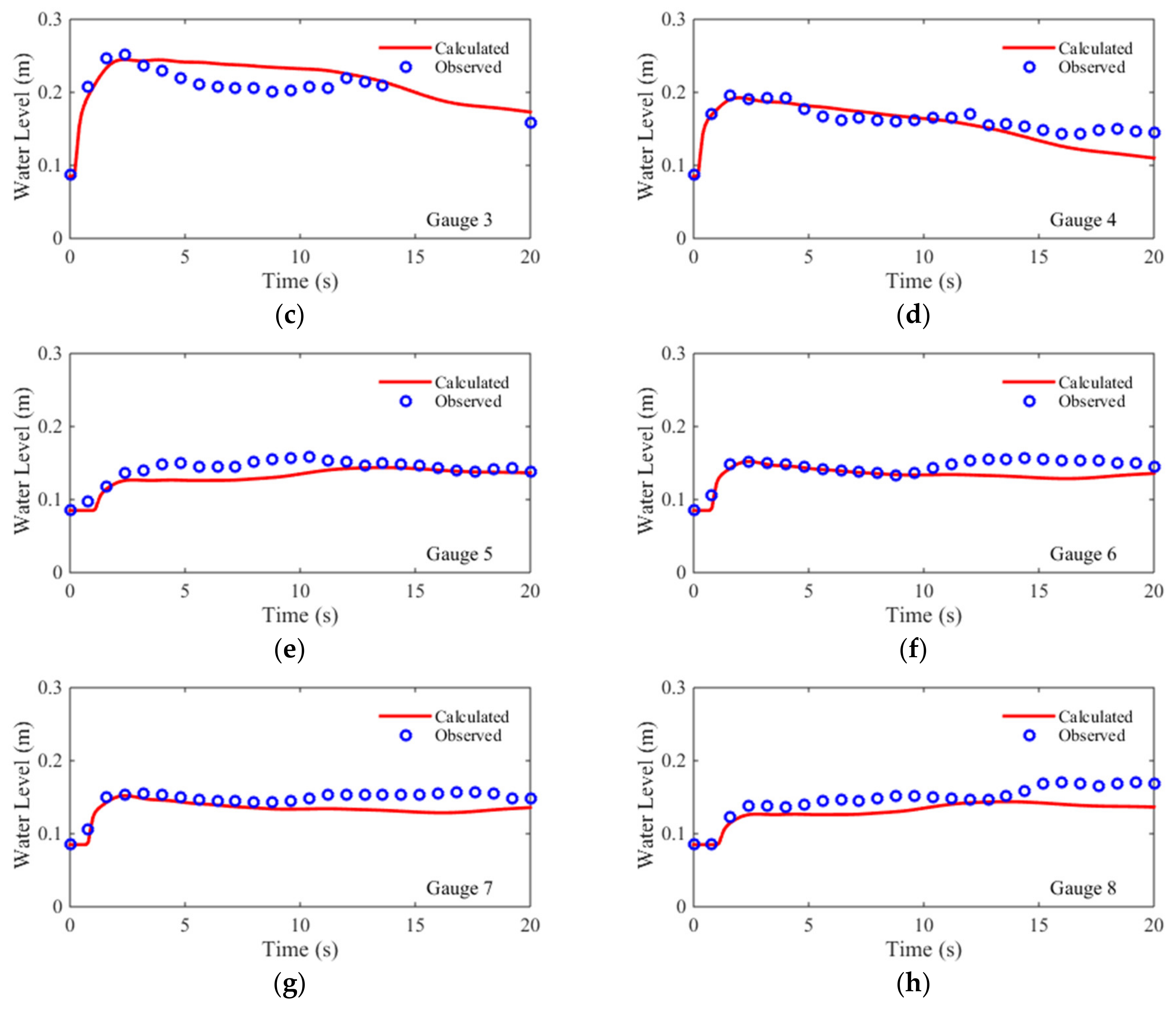
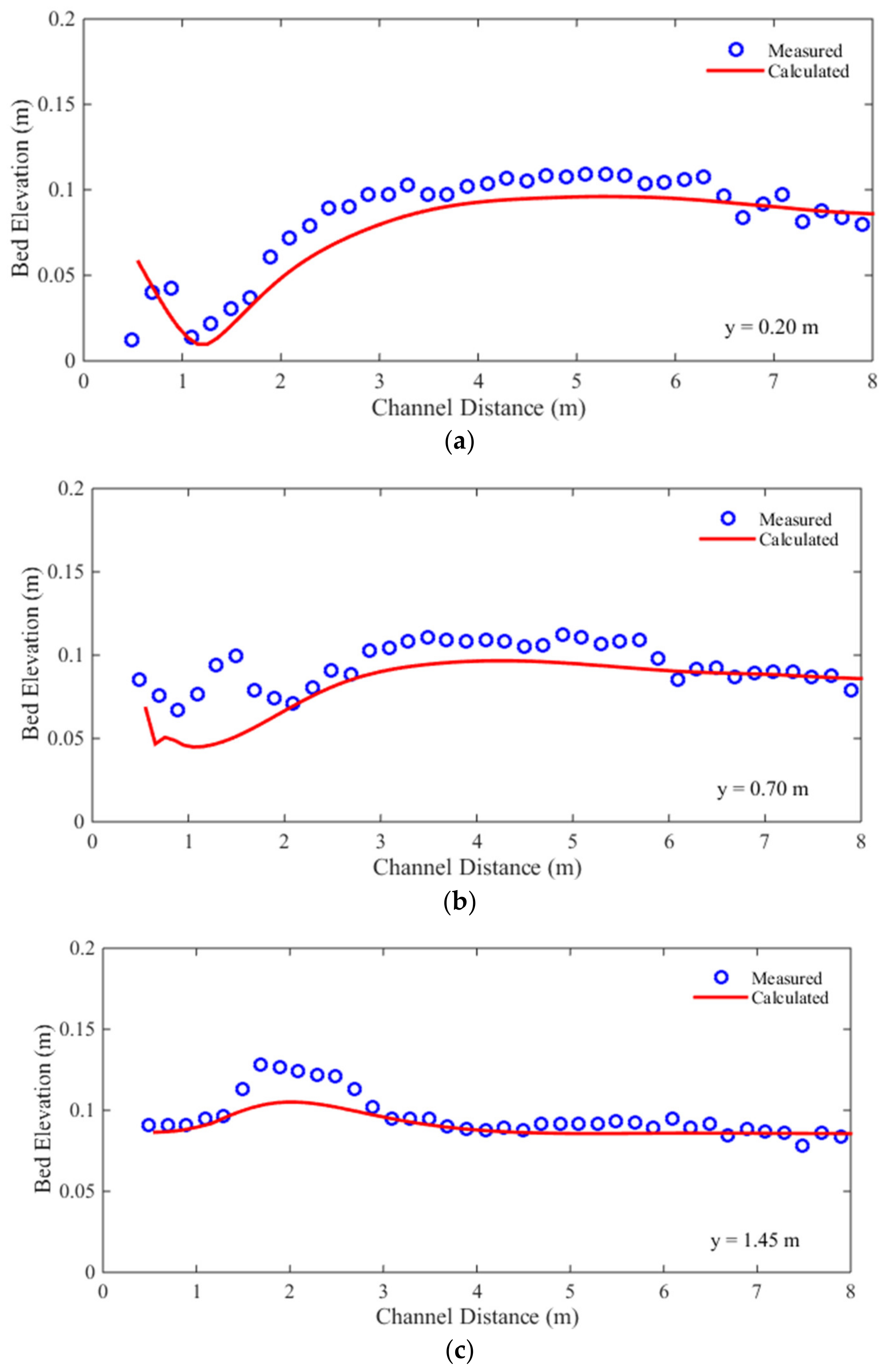
3.3. Case 3: Two-Dimensional Dam-Break Flow over Mobile Bed
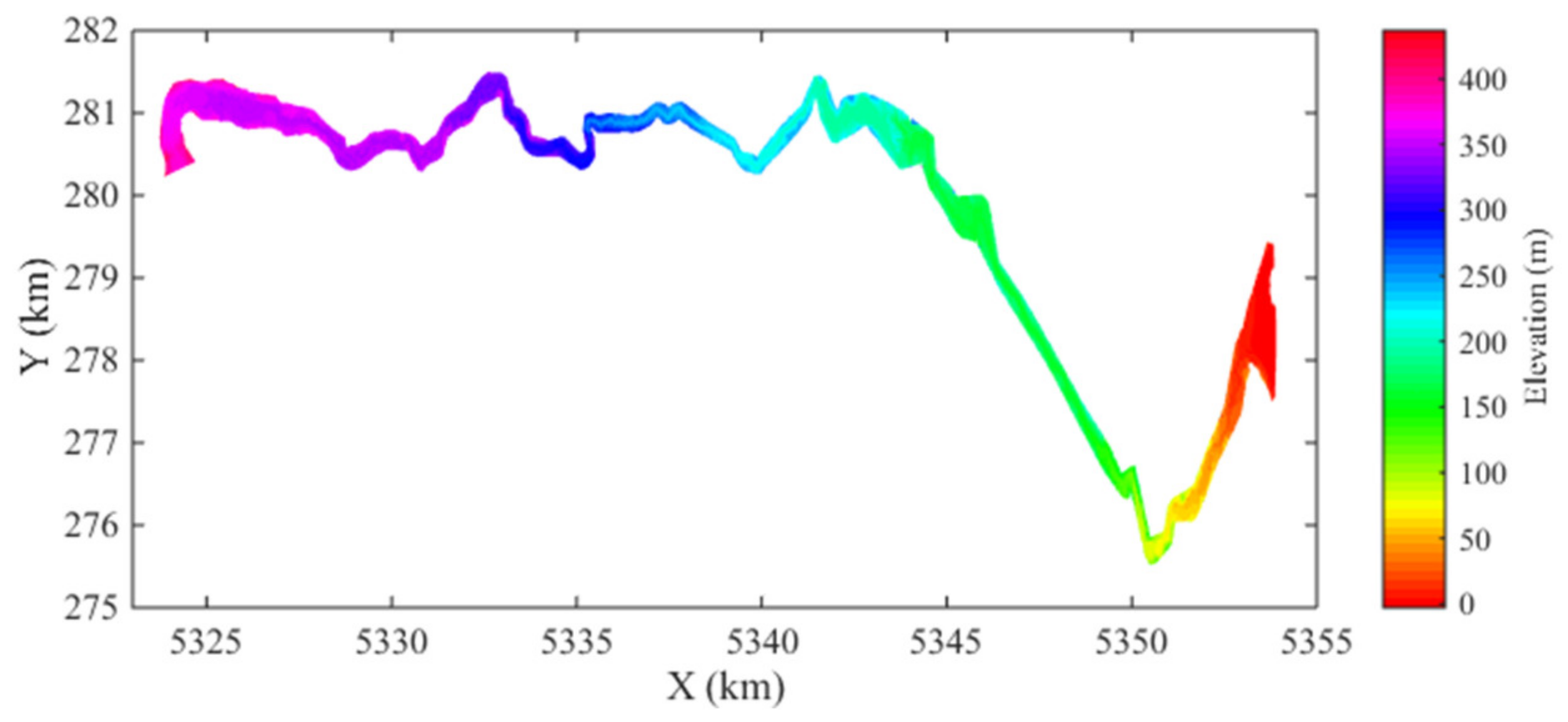
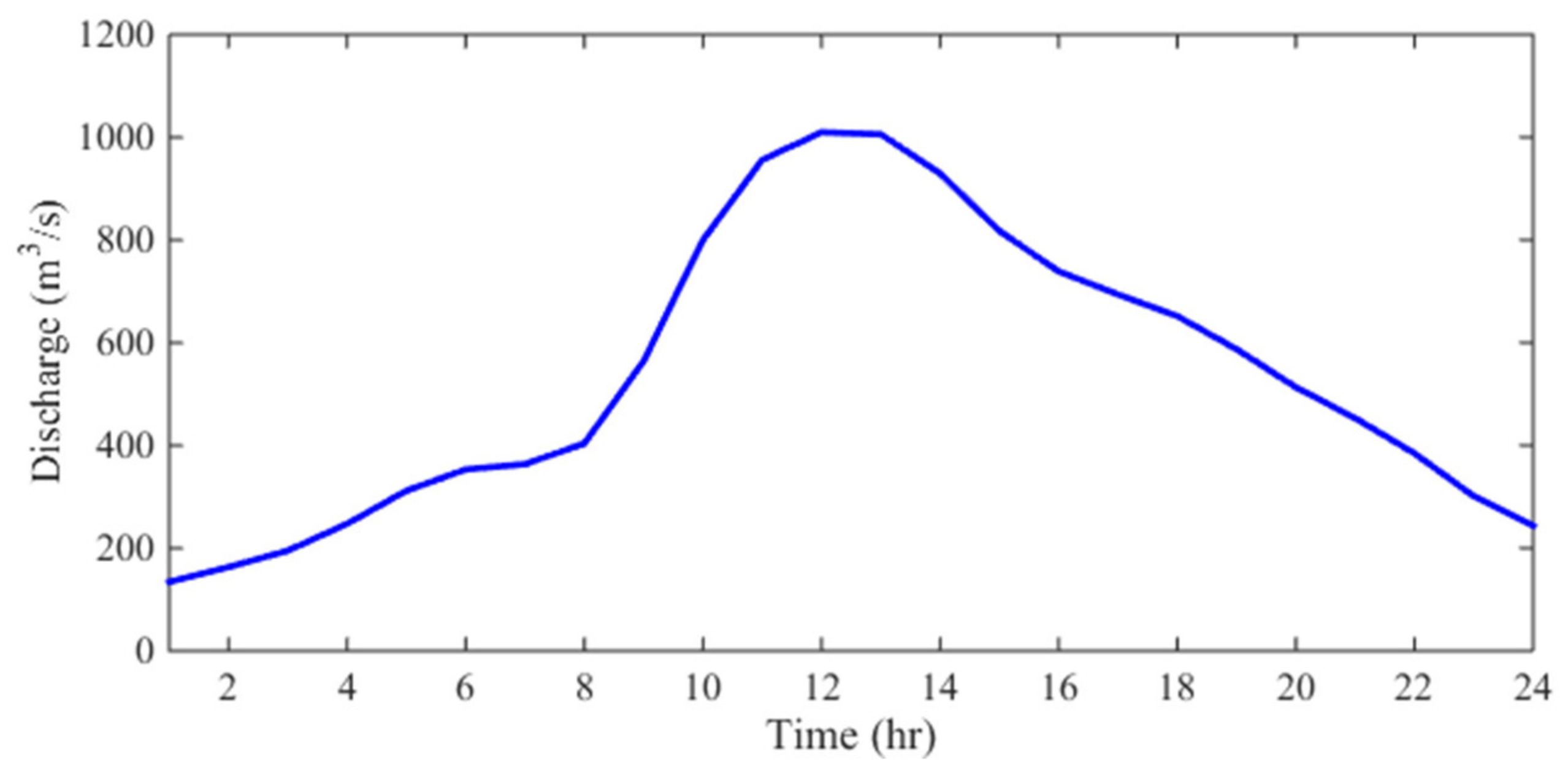
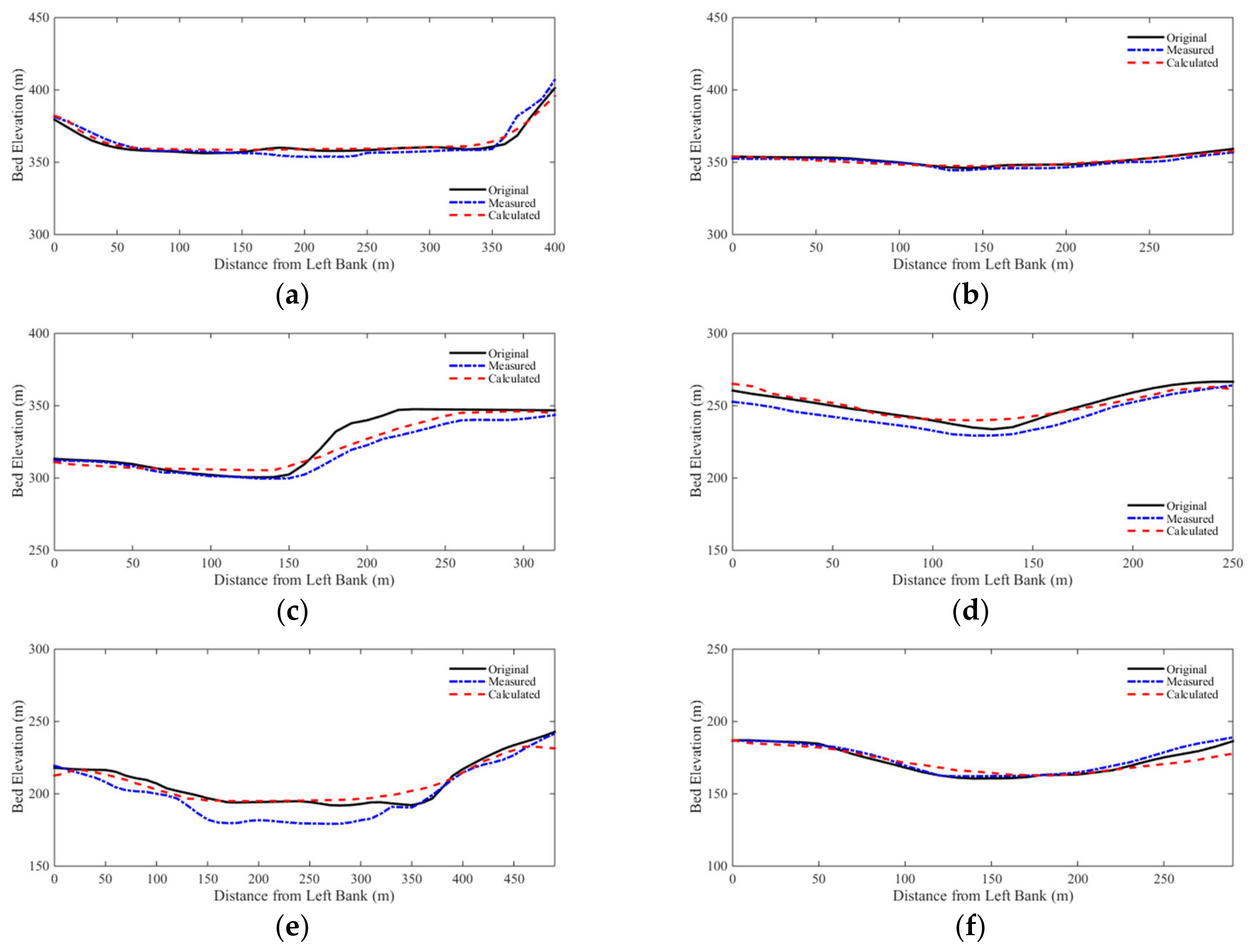
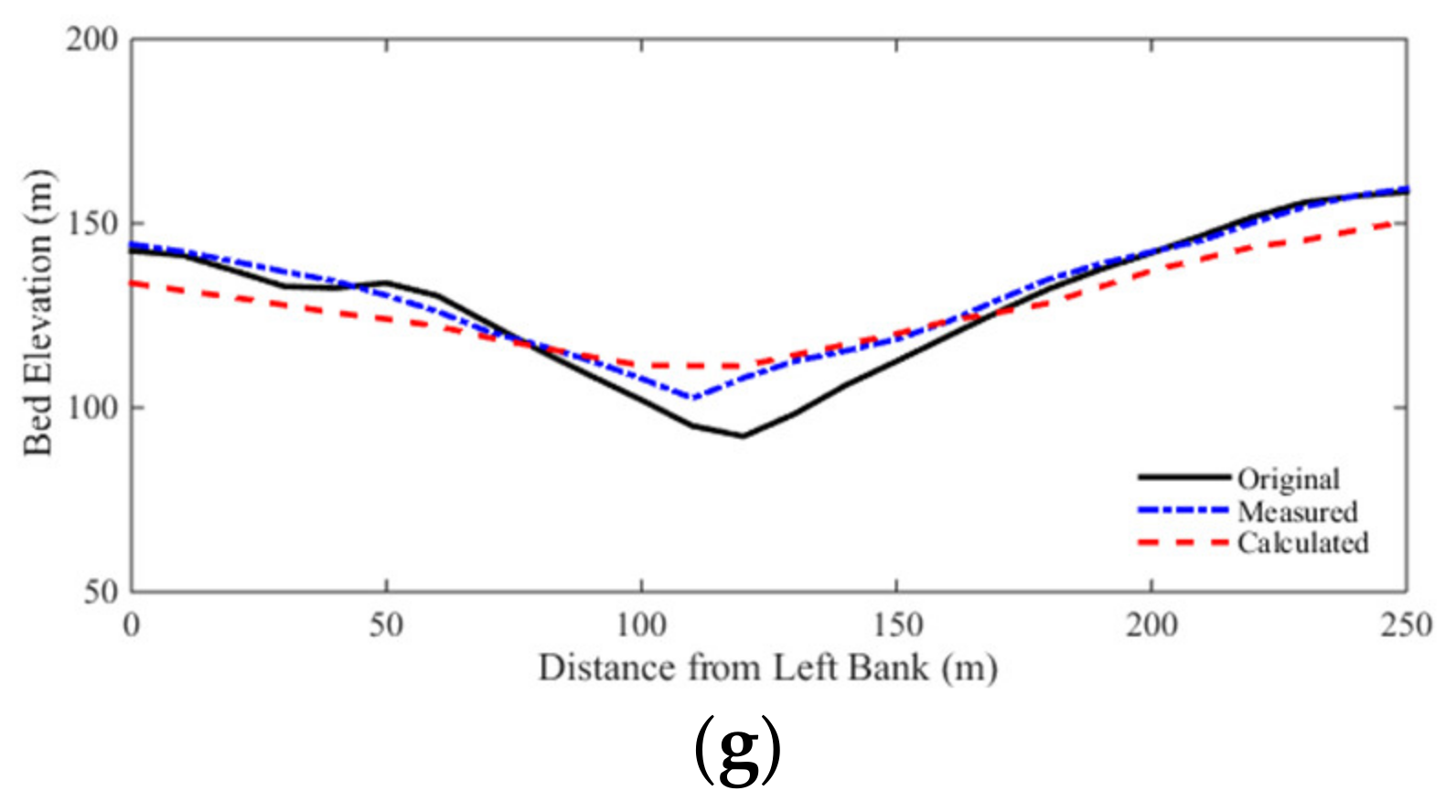
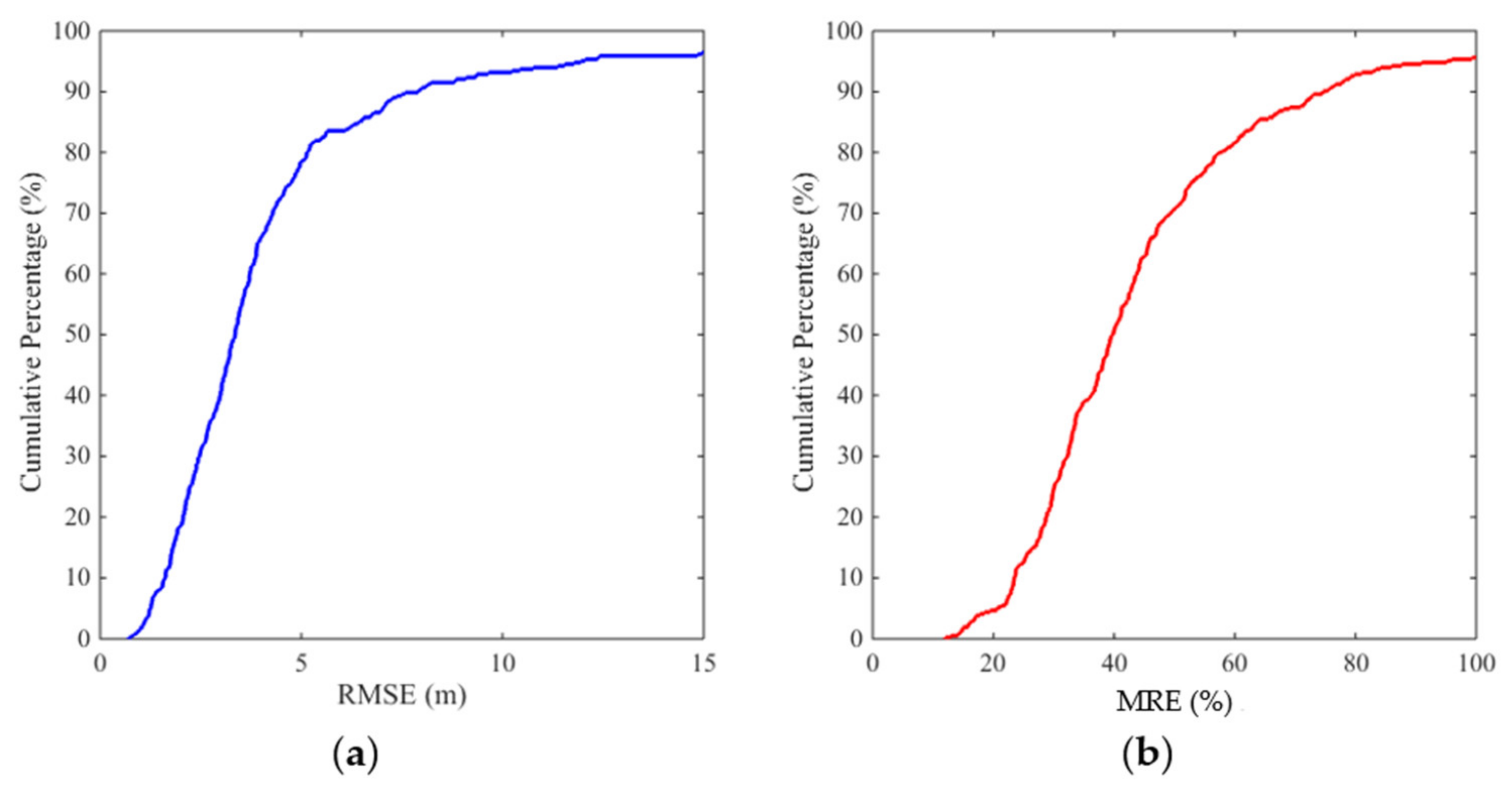
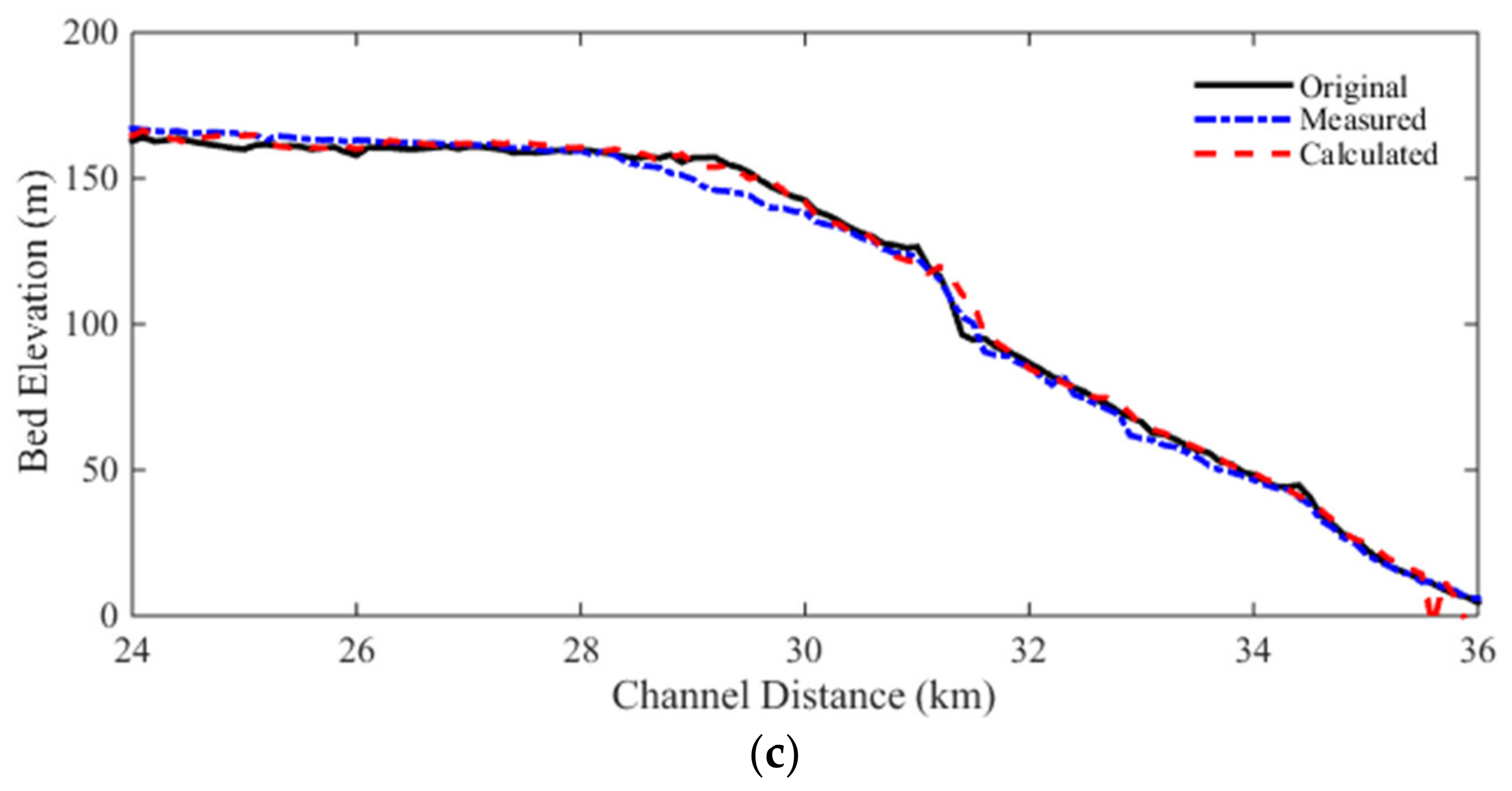
3.4. Case 4: 1996 Lake Ha! Ha! Catastrophic Flood Event
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cao, Z.; Pender, G.; Wallis, S.; Carling, P. Computational Dam-Break Hydraulics over Erodible Sediment Bed. J. Hydraul. Eng. 2004, 130, 689–703. [Google Scholar] [CrossRef]
- Kuiry, S.; Ding, Y.; Wang, S.S.Y. Numerical simulations of morphological changes in barrier islands induced by storm surges and waves using a supercritical flow model. Front. Struct. Civ. Eng. 2014, 8, 57–68. [Google Scholar] [CrossRef]
- Bai, Y.; Duan, J.G. Simulating unsteady flow and sediment transport in vegetated channel network. J. Hydrol. 2014, 515, 90–102. [Google Scholar] [CrossRef]
- Begnudelli, L.; Rosatti, G. Hyperconcentrated 1D Shallow Flows on Fixed Bed with Geometrical Source Term Due to a Bottom Step. J. Sci. Comput. 2011, 48, 319–332. [Google Scholar] [CrossRef]
- Guan, M.; Wright, N.G.; Sleigh, P.A. 2D Process-Based Morphodynamic Model for Flooding by Noncohesive Dyke Breach. J. Hydraul. Eng. 2014, 140, 04014022. [Google Scholar] [CrossRef]
- Leighton, F.Z.; Borthwick, A.G.L.; Taylor, P.H. 1-D numerical modelling of shallow flows with variable horizontal density. Int. J. Numer. Methods Fluids 2009, 62, 1209–1231. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; de Vriend, H.J.; Wang, Z.; Van Maren, D.S. Morphological modeling using a fully coupled, total variation diminishing upwind-biased centered scheme. Water Resour. Res. 2013, 49, 3547–3565. [Google Scholar] [CrossRef] [Green Version]
- Rosatti, G.; Murillo, J.; Fraccarollo, L. Generalized Roe schemes for 1D two-phase, free-surface flows over a mobile bed. J. Comput. Phys. 2008, 227, 10058–10077. [Google Scholar] [CrossRef]
- Wu, W.; Marsooli, R.; He, Z. Depth-Averaged Two-Dimensional Model of Unsteady Flow and Sediment Transport due to Noncohesive Embankment Break/Breaching. J. Hydraul. Eng. 2012, 138, 503–516. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.S. One-dimensional modeling of dam-break flow over movable beds. J. Hydraul. Eng. 2007, 133, 48–58. [Google Scholar] [CrossRef]
- Zhang, S.; Duan, J.G.; Strelkoff, T.S. Grain-scale nonequilibrium sediment-transport model for unsteady flow. J. Hydraul. Eng. 2013, 139, 22–36. [Google Scholar] [CrossRef]
- Zhang, S.; Duan, J.G. 1D finite volume model of unsteady sediment transport model. J. Hydrol. 2011, 405, 57–68. [Google Scholar] [CrossRef]
- Vreugdenhil, C.B. Numerical Methods for Shallow-Water Flow; Kluwer Academic Publishers: Dordrecht, The Netherlands; Boston, MA, USA, 1994. [Google Scholar]
- Fraccarollo, L.; Capart, H. Riemann wave description of erosional dam-break flows. J. Fluid Mech. 2002, 461, 183–228. [Google Scholar] [CrossRef] [Green Version]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction, 3rd ed.; Springer: Dordrecht, The Netherlands; New York, NY, USA, 2009. [Google Scholar]
- Toro, E.F.; Garcia-Navarro, P. Godunov-type methods for free-surface shallow flows: A review. J. Hydraul. Res. 2007, 45, 736–751. [Google Scholar] [CrossRef]
- Brufau, P.; Garcia-Navarro, P.; Ghilardi, P.; Natale, L.; Savi, F. 1D Mathematical modelling of debris flow. J. Hydraul. Res. 2000, 38, 435–446. [Google Scholar] [CrossRef]
- Stein, E.M.; Shakarchi, R. Fourier Analysis: An Introduction; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Castro, M.J.; Pardo Milanés, A.; Parés, C. Well-balanced numerical schemes based on a generalized hydrostatic reconstruction technique. Math. Models Methods Appl. Sci. 2007, 17, 2055–2113. [Google Scholar] [CrossRef]
- Parés, C. Numerical methods for nonconservative hyperbolic systems: A theoretical framework. SIAM J. Numer. Anal. 2006, 44, 300–321. [Google Scholar] [CrossRef]
- Cozzolino, L.; Cimorelli, L.; Covelli, C.; Della Morte, R.; Pianese, D. Novel Numerical Approach for 1D Variable Density Shallow Flows over Uneven Rigid and Erodible Beds. J. Hydraul. Eng. 2014, 140, 254–268. [Google Scholar] [CrossRef]
- Bermudez, A.; Vazquez, M.E. Upwind methods for hyperbolic conservation laws with source terms. Comput. Fluids 1994, 23, 1049–1071. [Google Scholar] [CrossRef]
- Wu, W. Depth-averaged two-dimensional numerical modeling of unsteady flow and nonuniform sediment transport in open channels. J. Hydraul. Eng. 2004, 130, 1013–1024. [Google Scholar] [CrossRef]
- Yu, C.; Duan, J. Two-dimensional depth-averaged finite volume model for unsteady turbulent flow. J. Hydraul. Res. 2012, 50, 599–611. [Google Scholar] [CrossRef]
- Armanini, A.; Di Silvio, G. A one-dimensional model for the transport of a sediment mixture in non-equilibrium conditions. J. Hydraul. Res. 1988, 26, 275–292. [Google Scholar] [CrossRef]
- Abderrezzak, K.E.K.; Paquier, A. One-dimensional numerical modeling of sediment transport and bed deformation in open channels. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Van Emelen, S.; Zech, Y.; Soares-Frazão, S. Impact of sediment transport formulations on breaching modelling. J. Hydraul. Res. 2014, 53, 60–72. [Google Scholar] [CrossRef]
- Cao, Z. Equilibrium Near-Bed Concentration of Suspended Sediment. J. Hydraul. Eng. 1999, 125, 1270–1278. [Google Scholar] [CrossRef]
- LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Greenberg, J.M.; Leroux, A.Y. A Well-Balanced Scheme for the Numerical Processing of Source Terms in Hyperbolic Equations. SIAM J. Numer. Anal. 1996, 33, 1–16. [Google Scholar] [CrossRef]
- Audusse, E.; Bouchut, F.; Bristeau, M.-O.; Klein, R.; Perthame, B. A Fast and Stable Well-Balanced Scheme with Hydrostatic Reconstruction for Shallow Water Flows. SIAM J. Sci. Comput. 2004, 25, 2050–2065. [Google Scholar] [CrossRef] [Green Version]
- Spinewine, B.; Zech, Y. Small-scale laboratory dam-break waves on movable beds. J. Hydraul. Res. 2007, 45 (Suppl. S1), 73–86. [Google Scholar] [CrossRef]
- Soares-Frazão, S.; Canelas, R.; Cao, Z.; Cea, L.; Chaudhry, H.M.; Moran, A.D.; El Kadi, K.; Ferreira, R.; Cadórniga, I.F.; Gonzalez-Ramirez, N.; et al. Dam-break flows over mobile beds: Experiments and benchmark tests for numerical models. J. Hydraul. Res. 2012, 50, 364–375. [Google Scholar] [CrossRef]
- Canelas, R.; Murillo, J.; Ferreira, R.M. Two-dimensional depth-averaged modelling of dam-break flows over mobile beds. J. Hydraul. Res. 2013, 51, 392–407. [Google Scholar] [CrossRef]
- Brooks, G.R.; Lawrence, D.E. The drainage of the Lake Ha! Ha! reservoir and downstream geomorphic impacts along Ha! Ha! River, Saguenay area, Quebec, Canada. Geomorphology 1999, 28, 141–167. [Google Scholar] [CrossRef]
- Capart, H.; Spinewine, B.; Young, D.L.; Zech, Y.; Brooks, G.R.; Leclerc, M.; Secretan, Y. The 1996 Lake Ha! Ha! breakout flood, Québec: Test data for geomorphic flood routing methods. J. Hydraul. Res. 2007, 45 (Suppl. S1), 97–109. [Google Scholar] [CrossRef]
- Abderrezzak, K.E.K.; Paquier, A. Applicability of Sediment Transport Capacity Formulas to Dam-Break Flows over Movable Beds. J. Hydraul. Eng. 2011, 137, 209–221. [Google Scholar] [CrossRef]
- Ferreira, R.M.; Franca, M.J.; Leal, J.G.; Cardoso, A.H. Mathematical modelling of shallow flows: Closure models drawn from grain-scale mechanics of sediment transport and flow hydrodynamics. Can. J. Civ. Eng. 2009, 36, 1605–1621. [Google Scholar] [CrossRef]



| Time (s) | Water Level | Bed Elevation | ||
|---|---|---|---|---|
| RMSE (cm) | MRE (%) | RMSE (cm) | MRE (%) | |
| 0.25 | 1.13 | 3.35 | 0.45 | 23.20 |
| 0.50 | 0.57 | 1.80 | 0.38 | 25.09 |
| 0.75 | 0.78 | 2.79 | 0.39 | 26.47 |
| 1.00 | 0.84 | 3.37 | 0.33 | 22.24 |
| 1.25 | 0.82 | 3.58 | 0.35 | 23.75 |
| 1.50 | 0.87 | 4.83 | 0.32 | 27.35 |
| Average | 0.84 | 3.29 | 0.37 | 24.68 |
| Gauge Number | RMSE (cm) | MRE (%) |
|---|---|---|
| 1 | 1.71 | 15.11 |
| 2 | 2.07 | 12.66 |
| 3 | 2.17 | 12.72 |
| 4 | 1.59 | 13.81 |
| 5 | 1.39 | 18.90 |
| 6 | 1.49 | 20.73 |
| 7 | 1.58 | 21.91 |
| 8 | 1.98 | 21.50 |
| Average | 1.75 | 17.17 |
| Bed Profile (m) | RMSE (cm) | MRE (%) |
|---|---|---|
| 0.20 | 1.24 | 13.03 |
| 0.70 | 1.67 | 32.65 |
| 1.45 | 0.91 | 17.20 |
| Average | 1.27 | 20.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, J.G.; Yu, C.; Ding, Y. Numerical Simulation of Sediment Transport in Unsteady Open Channel Flow. Water 2023, 15, 2576. https://doi.org/10.3390/w15142576
Duan JG, Yu C, Ding Y. Numerical Simulation of Sediment Transport in Unsteady Open Channel Flow. Water. 2023; 15(14):2576. https://doi.org/10.3390/w15142576
Chicago/Turabian StyleDuan, Jennifer G., Chunshui Yu, and Yan Ding. 2023. "Numerical Simulation of Sediment Transport in Unsteady Open Channel Flow" Water 15, no. 14: 2576. https://doi.org/10.3390/w15142576
APA StyleDuan, J. G., Yu, C., & Ding, Y. (2023). Numerical Simulation of Sediment Transport in Unsteady Open Channel Flow. Water, 15(14), 2576. https://doi.org/10.3390/w15142576






