1. Introduction
Water supply systems are an essential part of a vast urban infrastructure system that underpins most economic activity and is used by urban populations to perform basic domestic activities [
1]. A water distribution network is a hydraulic infrastructure that is usually the most costly component of urban infrastructure that delivers water to nodes while maintaining predetermined pressure requirements [
2,
3]. Designing such networks involves choosing optimal combinations of values for decision variables such as pipe sizes, tank shapes and sizes, pump types, and valve locations, while also satisfying several constraints [
4]. Optimal design problems for Water Distribution Systems (WDSs) typically involve selecting the best pipe size, which is challenging due to the problems’ high dimensionality, discreteness, and non-linearity [
5]. To solve these problems, advanced optimization techniques are required due to the complexity of WDSs and their components’ arrangement [
6].
WDS optimization aims to maximize system performance and profitability while minimizing resource consumption and cost, all of which are typically limited [
7]. As constructing these systems is costly, the optimization objective is to find the least expensive network [
8]. The design of water systems is a multi-objective optimization problem (MOPs) that needs to simultaneously optimize a number of objectives in addition to cost such as operational, life cycle, and maintenance costs, system reliability, and water quality [
9]. Optimizing for one objective may result in suboptimal performance for others [
8]. To address this complex problem, engineers have used single-objective optimization models in the past, but multi-objective optimization approaches have become increasingly popular in recent years, providing a way to investigate trade-offs between objectives and make informed decisions.
Optimizing water distribution networks (WDNs) is crucial for their performance and reliability. Network resilience, which refers to the network’s ability to recover from internal or external disturbances, is an important aspect of this optimization [
10]. Incorporating network resilience in the objective function can lead to better results in terms of surplus power and redundancy [
10]. Mechanical or hydraulic failure in WDNs can cause increased head losses and network failure, which is why it is essential to have excess power available for internal dissipation. Simply optimizing for cost can leave the network vulnerable to hydraulic and mechanical failures [
11]. Including reliability in optimization can be computationally intensive, so approximate methods like the resilience index [
12] can be used. The inclusion of network resilience in WDN optimization is critical for maintaining the network’s performance and reliability in both normal and failure conditions [
13].
Various optimization methods are available for water distribution systems and can be categorized into deterministic and stochastic techniques. Deterministic techniques involve linear programming, non-linear programming, and dynamic programming, while stochastic techniques include population-based algorithms and single point-based methods. Metaheuristics, a type of stochastic technique, provides a near-optimal solution in a single run by using principles from nature and involving random components. Genetic algorithms, inspired by mechanisms of biological evolution, have been widely applied in water resources planning and management [
14,
15]. These algorithms are capable of solving nonlinear, nonconvex, multimodal, and discrete problems, expanding their capabilities in handling complex environmental and water resource applications [
15].
Classical search and optimization methods may not be effective in dealing with MOPs due to their inability to find multiple solutions in a single run and the challenges in handling problems with discrete variables and multiple optimal solutions [
9]. Evolutionary algorithms (EAs), particularly MOEAs, are effective for MOPs as they use a population of solutions to find multiple Pareto-optimal solutions in a single run [
16]. Diversity preserving mechanisms can be incorporated into MOEAs to find widely different Pareto-optimal solutions [
9]. EAs are less affected by the shape or continuity of the Pareto front, unlike classical methods [
17]. In water distribution system design, Pareto archived evolutionary strategy (PAES), Strength Pareto evolutionary algorithm (SPEA-2), and non-dominated sorting genetic algorithm II (NSGA-II) [
18] are the most widely used MOEAs that effectively handle multiple objectives and find a set of solutions that are not dominated by others. The use of these MOEAs has greatly improved the efficiency and effectiveness of the water distribution system design process.
The Non-Dominated Sorting Genetic Algorithm (NSGA-II) is a widely used algorithm for solving MOPs with both continuous and discrete variables [
19]. It is considered one of the most representative algorithms in multi-objective optimization [
20] and had been recognized as the EA state-of-the-art in solving WDS-related optimization problems [
21]. NSGA-II is an improved version of the Non-Dominated Sorting Genetic Algorithm (NSGA) that overcomes some of its limitations, such as the absence of elitism and the need to define sharing parameters for diversity preservation [
22]. The design of NSGA-II incorporates an elitist strategy to expand the sample space and improve optimization accuracy, and the crowding distance operator to preserve diversity. NSGA-II is computationally efficient, with an overall complexity of at most O(MN
2), where M is the number of objective functions and N is the population size. The fast non-dominated sorting method used in NSGA-II reduces computational complexity, making it efficient and powerful in exploring the decision space of MOPs. NSGA-II has been widely implemented and applied to various MOPs, demonstrating its effectiveness and reliability.
NSGA-II has been combined with other methods and tools to enhance its effectiveness in solving optimization problems in WDS. The Robust NSGA-II (RNSGA-II) [
23] algorithm was developed based on NSGA II to ensure that the solutions are robust enough and able to sustain longer over multiple generations in the optimization process. The Epsilon-dominance Non-dominated Sorting Genetic Algorithm II (e-NSGA-II) is another optimization algorithm that is based on the original NSGA II that utilizes the e-dominance concept, adaptive population sizing, and self-terminating algorithm to achieve well-spread and well-converged Pareto-optimal solutions. Non-dominated Sorting Genetic Algorithm III (NSGA-III) [
24] is an improved version of NSGA-II using a reference-point-based non-dominated sorting approach. However, NSGA-II is still the most preferred algorithm compared to NSGA-III, and variations of NSGA-II, such as RNSGA-II, e-NSGA-II, and a combination of NSGA-II with other methods, have shown that NSGA-II is still relevant and capable of handling the task [
25].
Wang et al. [
26] applied five state-of-the-art MOEAs to twelve design problems collected from the literature, with minimum time invested in parameterization by using the recommended settings. The study found that the MOEAs were complementary to each other, and that NSGA-II remained a good choice for two-objective optimization of water distribution systems (WDSs) and generally outperformed the other MOEAs in terms of the number of solutions contributed to the best-known Pareto front of each problem. The spread (both extent and uniformity) of its contribution was also comparable, if not better, than other MOEAs. Overall, the paper contributes to the best-known approximations to the true Pareto fronts of a wide range of benchmark problems, and the results are going to be used in this research for comparison of some of the benchmark networks. However, NSGA-II and other MOEAs had limitations with intermediate and large-sized problems, resulting in a limited range of solutions with low diversity. In order to overcome these limitations and achieve better results for multi-objective optimization problems, this study proposes an improved version of NSGA-II. In their work, Cunha et al. [
27] introduced MOSA-GR, a novel multi-objective simulated annealing algorithm equipped with innovative searching mechanisms. MOSA-GR demonstrated superior performance by generating Pareto fronts that surpassed those produced by MOEAs, even when merging their results. In this study, the new searching mechanisms from MOSA-GR will be applied to NSGA-II to develop an improved algorithm for better results and contribute to the advancement of the existing literature on multi-objective optimization algorithms, enabling effective handling of complex real-world problems with enhanced diversity and density of solutions.
2. Materials and Methods
2.1. Problem Definition of the Multi-Objective Problems
The optimization problems in Water Distribution Systems (WDSs) design usually involve two objective functions: minimizing the cost and maximizing the network reliability or robustness. In this context to solve the multi-objective optimization, the objectives defined in model formulation are minimizing the cost while maximizing resilience. The decision variables are diameter, which can be adjusted to obtain an optimal solution that satisfies both objectives. The cost objective function considers the expenditure of pipe components as the total cost of a design solution. The unit cost of a specific pipe diameter for each problem is derived from the paper by [
26] (Equation (1) below).
Resilience in the context of WDS design refers to the ability of the system to continue functioning in the presence of failures or disturbances. The specific definition of resilience may vary depending on the WDS design optimization problem. In this study, the resilience index proposed by [
10] (Equation (2) below) is used as a measure to optimize the reliability of the network. It is recognized that some authors have proposed updates to Todini’s index of resilience and that other indexes have been proposed [
28,
29,
30], however it is used in this paper for the following reasons: (1) it is widely used in the literature on water distribution systems optimization and (2) it enables a comparison with the work of Wang et al. [
26]. The resilience index is defined as the ratio of power dissipated in the network to the maximum power that would be dissipated in order to satisfy the design demand and head requirements at the junction nodes.
The objectives to be optimized to obtain the optimal WDS design solution are presented in mathematical form as Equations (1) and (2), where the cost is minimized while maximizing the resilience index.
where Ir = network resilience; nn = number of demand nodes; C
j, Q
j, H
j, and H
jreq = uniformity, demand, actual head, and minimum head of node j; nr = number of reservoirs; Q
k and H
k = discharge and actual head of reservoir k; npu = number of pumps; P
i = power of pump i; γ = specific weight of water; np
j = number of pipes connected to node j; D
i = diameter of pipe i connected to demand node j.
2.2. Improved NSGA II
The NSGA II algorithm is widely used for solving multi-objective optimization problems. However, the quality of the solutions generated by the algorithm can be improved. Therefore, the main objective of improving the NSGA II algorithm is to enhance the quality of its solutions. This involves increasing the density of solutions, especially in the important regions of the Pareto front, such as the knee area, and improving the diversity of solutions by expanding their range. To achieve this, the improved NSGA II introduces novel improvements in both the diversity and convergence of the algorithm.
One of the main developments of the improved NSGA II algorithm is the implementation of new methods for offspring population generation. Unlike the original NSGA II, which uses all parent population solutions in tournament selection to generate the offspring population, the improved NSGA II focuses on specific solutions among the nondominated solutions found so far to generate new solutions in addition to the original method. By focusing on specific solutions, the improved NSGA II can generate better candidate solutions, ultimately leading to a better quality of solutions in the Pareto front.
The improved NSGA II algorithm introduces different generation methods based on [
27], which is crucial to achieving fast convergence and a high diversity of solutions that are uniformly distributed in the objective space. The different generation methods, including those that target the maximum and minimum regions of the Pareto front and the uncrowded area of the front, are used to increase the range and diversity of solutions. The knee area of the Pareto front is given special attention, as it is a critical region with solutions that exhibit a small improvement in one objective causing a large deterioration in the other.
2.3. Generation Methods
The algorithm generates an offspring population using four main processes (Gs), which are selected in each iteration starting from different starting iterations (ITm) proposed to control the process. Additionally, different probabilities (represented by Ps) are used to select the generation methods. The selection of these probabilities aims to produce new solutions that can perform a global search in the early stages of the process and then include a more localized search towards the end in addition to the global search.
The following are the types of searching methods presented as offspring generation methods:
G1 method: This is the original method used in NSGA II. It involves selecting N (population size) number of parent populations and N offspring populations, evaluating their objective values, and sorting them based on non-dominated sorting and crowd distancing. The parent populations are then randomly paired to create child populations through crossover and mutation.
G2 method: This method saves the new offspring population generated in each iteration to the archive. The archive contains all the populations generated from the start of the iteration. Parent populations are randomly selected from the archive to create new offspring populations through crossover and mutation.
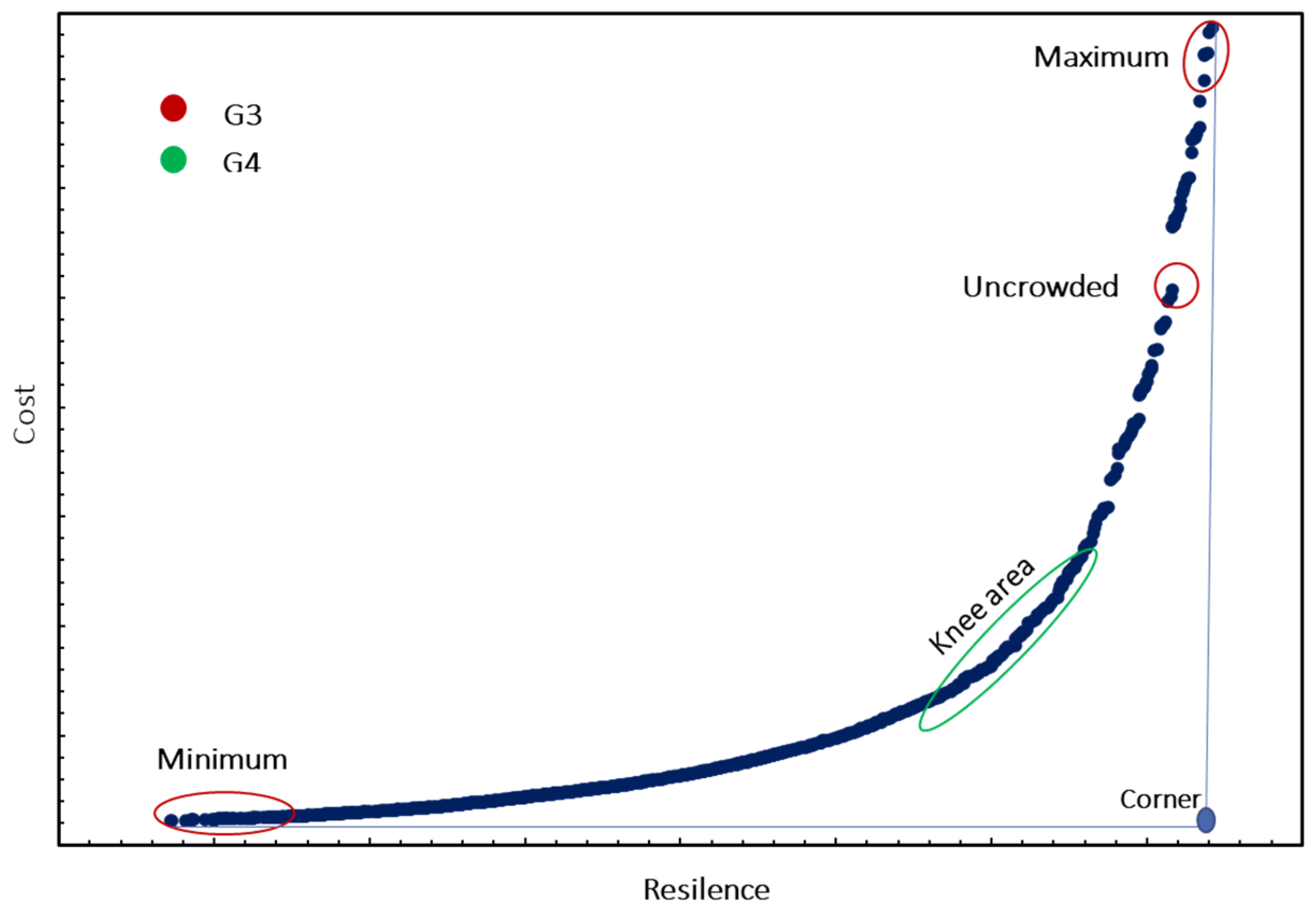
G3 method: This method focuses on specific areas of the Pareto front, such as the extreme and uncrowded areas shown in
Figure 1. At each iteration, a number of points are selected from the required region, and N (population number) offspring populations are generated from these points.
If the selected points are from the maximum region, the offspring population is generated via bound type crossover and weighted average with the maximum possible diameter as in Equation (4), where Rand is a random number between 0 and 1.
On the other hand, if the selected points are from the minimum and uncrowded areas, the offspring population is generated in Equation (5) by randomly assigning a diameter value of the next higher or lower possible diameter value to the selected pipes, where “gene” is the randomly selected pipe.
where Gene = randomly generated number, Parent = selected points, Offspring=generated population from selected points.
- 4.
G4 method: This method generates offspring populations using the knee area of the Pareto front as the parent population. The knee is found by calculating the Euclidean distance of all Pareto front points to the corner, shown in
Figure 1 and selecting points with the least distance. After selecting the parent population, the offspring population is generated using Equation (5).
2.4. Pseudocode
The pseudocode provided in
Figure 2 outlines the steps of the improved NSGA II procedure. The maximum number of iterations is divided into four stages and each stage includes a different combination of generation methods, as shown in
Figure 3. The algorithm starts with the original NSGA II method and includes additional methods one by one into each stage. In the early phases, only the G1 method is used, but as the second stage is initiated, G2 is introduced. In the third stage, G3 becomes available for use, and likewise, G4 is brought into the fold in the fourth stage.
In each iteration, a generation method from the available methods in each stage is picked using a probability decision factor, and that method generates N offspring populations in that iteration. The number of function evaluations each method uses is determined by the probability assigned to each method and the stage’s starting iteration. The four generating processes can be selected according to the starting iteration number (ITm1, ITm2, ITm3, ITm4) and probabilities (P1, P2, P3, P4). These additional parameters (explained below in detail) are used to control the number of function evaluations used by the generation processes and the results they can contribute.
2.5. Parameters
The selection of the four generating processes is based on three additional parameters to the NSGA II algorithm: the starting iteration number (ITm1, ITm2, ITm3, ITm4), probabilities (P1, P2, P3, P4), and the number of selected points as a percentage of population size. These parameters are used to control the number of function evaluations used by the generation processes and the results they can contribute.
ITm1—iteration number where the G1 starts, which is equal to zero.
ITm2—iteration number where the G2 starts.
ITm3—iteration number where the G3 starts.
ITm4—iteration number where the G4 starts.
The ITm parameter represents the iteration number at which the generation methods start and can take values from 0 to 1, where 0 represents the beginning of the iterations and 1 represents the end of the iterations. The starting iteration of a generation method is determined by multiplying ITm by the maximum number of iterations as in Equation (6). For example, the starting iteration of G2 can be calculated as ITm2 multiplied by the maximum number of iterations.
where ITm = a parameter between 0 and 1.
The other parameter is the probability assigned to each method to be selected. In each iteration, a random number between 0 and 1 is generated to determine the probability of selecting a particular generation method.
P2—probability of G2 being selected starting ITm2.
P3—probability of G3 being selected starting ITm3.
P4—probability of G4 being selected starting ITm4.
The probabilities of G2, G3, and G4 are determined by P2, P3, and P4, respectively. The probabilities of these methods are constant from their starting iteration to the maximum number of iterations. The probability of G1, on the other hand, changes throughout the stages. In stage one, G1 is the only method used, and therefore has a probability of 1. In stage two, there are two options: G2 with a probability of P2 and G1 with a probability of (1 − P2). Similarly, in stage three, there are three options: G2 with a probability of P2, G3 with a probability of P3, and G1 with a probability of (1 − P2 − P3). The sum of probabilities for G2, G3, and G4 is less than 1, with G1 taking up the remaining probabilities according to the stage.
As an instance, during stage 3, the selection of a method from G1, G2, and G3 is determined based on specific conditions outlined in Equations (7) through (9). This involves generating a random number between 0 and 1. If this number is less than (1 − P2 − P3) as in Equation (7), G1 is selected. If the random number falls between (1 − P2 − P3) and (1 − P3) as in Equation (8), G2 is chosen. On the other hand, if the random number is greater than (1 − P3) as in Equation (9), G3 is the selected method.
In addition, the number of points selected by each method is a crucial parameter in the improved NSGA II algorithm. G3 and G4 choose the parent population from the search region and generate the offspring population. The number of points to be selected must be determined in advance. The number of selected points is equal to sp multiplied by the population size (N) as in Equation (10), where sp is number of selected points as a percentage of the population size (N).
sp3max—number of selected points in the maximum region as percentage of N.
sp3min—number of selected points in the minimum region as percentage of N.
sp3uc—number of selected points in the uncrowded region as percentage of N.
sp4—number of selected points in the knee area as percentage of N.
G3 selects three types of points based on three additional parameters: P3max, P3min, and P3uc. These parameters control the number of selected points in the maximum region, minimum region, and uncrowded region, respectively.
The pseudocode of generation methods is depicted in
Figure 4, where Rand2 is a second random number between 0 and 1.
The algorithm starts by using G1 in the initial iterations to create the Pareto front and initialize the processes. This generation process can be revisited throughout the entire iteration. Then, G2 is introduced, and it brings back some populations from the archive that were eliminated in the process but may have the potential to find better solutions when combined with the current population. Once a front is established, the algorithm uses G3 and G4 to target specific regions of the front. G4 is executed last because it requires an intensive evaluation, and its characteristics are appropriate for the knee region late in the progression of the front. These strategies help the algorithm converge more quickly to the Pareto optimal front and increase the range of solutions it can find.
In
Figure 5, the generation methods used in the algorithm are illustrated for an example of one run, along with the number of iterations each generation was employed. At the outset, G1 is employed at every iteration, and the line for G1 increases with a slope of 1. When the iteration reaches ITm2 = 500, G2 is added as an option, and the line for G2 begins to increase. The slope of G1 becomes lower at this point since G2 is also in use. The low slope of G2 is related to the probability it is given, which is lower than that of G1 (P1 > P2). At the iteration of ITm3 = 750, G3 is introduced, and the line for G3 starts increasing. The slope of G3 is higher than G2 because it has a higher probability (P3 > P2). Lastly, G4 is included at the last stage when the iteration is at ITm4 = 1250, and the line for G4 begins to increase. The slope of G4 is higher than G2 but lower than G3, indicating that its probability is higher than G2 but lower than G3. As new methods are added, the slope of G1 decreases, and the probability of G1 is a function of the other probabilities (1 − P2 − P3 − P4).
2.6. Case Studies
To test the improved algorithm in this study, five networks of different sizes were used. These networks are taken from the benchmark case studies of [
26] and range from small to intermediate in size.
Table 1 summarizes the benchmark problems, including the number of water sources, decision variables, pipe diameter options, the search space calculated as pipe diameter options to the power of decision variables and the number of function evaluation (NFE) used.
In [
26] different computational budgets are used for the networks based on their size and complexity. To ensure fair comparison, the same computational budget is used for each network in this study. The problems are solved using different population sizes, with 10 runs for each network in three groups, totaling 30 runs for each problem. The results from each run are combined and sorted to obtain the final non-dominated Pareto front. The benchmark problems are of varying complexity, and therefore different computational budgets are required for different cases. This approach helps to ensure that the results are reliable and comparable across different networks and problems.
In the paper of [
26], the Pareto front for each multi-objective optimization problem was obtained by collecting raw data reported by each multi-objective evolutionary algorithm (MOEA) for 30 runs. Duplicates in the dataset of each group, which were obtained using a specific population size, were checked, and removed. The data from different groups were then merged and duplicates were checked and removed once again. The non-dominated sorting procedure was applied to the aggregated dataset to produce the best Pareto front obtained by the current MOEA.
For each problem, the Pareto front obtained by each MOEA was first aggregated, and duplicates in the merged dataset were checked and removed. The non-dominated sorting procedure was then used to generate the best-known Pareto front of the current problem that is presented in [
26] and it will be referred in this study as all evolutionary algorithms (AEAs). Lastly, the contribution from each MOEA to the best-known Pareto front was identified. This process ensured that the AEA was obtained by considering the results from all MOEAs and removing duplicates.
The Best-Known Pareto Front (BKPF) solutions for these problems, which are presented on the Exeter university website “
https://engineering.exeter.ac.uk/research/cws/resources/benchmarks/pareto/ (accessed on 6 July 2023)”, were obtained through a secondary stage of extensive computation on the Pareto front initially obtained by five state-of-the-art MOEAs. For the smaller networks, the true Pareto front was obtained through full enumeration, while for the larger networks, the goal was to approximate the true Pareto fronts.
The improved version of NSGA II is used to generate a Pareto front. The dataset from 10 independent runs with the same population size is collected, and the results are merged to remove any duplicates. Next, the non-dominated sorting method is applied to select the best solutions and form the Pareto front of the group. This process is repeated for each population size to obtain the Pareto front for each group. Finally, the Pareto front for each population size (3 groups) is merged, and any duplicates are removed. The non-dominated sorting method is then applied to the merged solutions to produce the final Pareto front.
3. Results
The proposed methodology was tested on benchmark case studies using the same optimization model and hydraulic simulator to enable fair comparison.
Table 2 presents the results obtained from 30 runs using the improved NSGA II and compares them to the three different results for the five case studies (CS). The first set of solutions, as described in [
26], consists of the results obtained by five state-of-the-art MOEAs within the computational budget. By combining and eliminating duplicates from these results, the values for the AEA column were determined. The second source of solutions is the Best-Known Pareto Front (BKPF) solutions for these problems, which were obtained after extensive calculations on the raw solutions initially obtained by the same five MOEAs as in the AEA.
The last five columns of
Table 2 contain the results obtained by the improved NSGA II algorithm using NFE (number of function evaluations) limitations. The number of solutions obtained by comparing the improved NSGA II solutions with BKPF were recorded, including the number of solutions that are equal to BKPF (ENDS), the number of solutions obtained by the improved NSGA II that are dominated by the BKPF solutions (DS), the number of solutions that dominate BKPF (BNDS), the number of solutions obtained by the improved NSGA II that are nondominated to the BKPF (NDS), and the total number of nondominated solutions obtained by the improved NSGA II (TNDS) for each of the case studies. The aim of these comparisons is to evaluate the effectiveness of the proposed improvement to the NSGA II algorithm in obtaining a good approximation of the true pareto front with the same function evaluations than other state-of-the-art MOEAs.
In the context of evaluating the performance of the proposed improved NSGA II algorithm, it is crucial to consider the benchmark Pareto fronts solution, which serves as a reference for the quality of the results obtained. Therefore, the results obtained by the improved NSGA II will be compared with its predecessor, the original NSGA II, using the same computational budget. This comparison is the primary point of comparison, as it helps determine if the improved NSGA II outperforms the original NSGA II under the same computational budget. If the improved NSGA II can outperform the original NSGA II, it would be a significant improvement.
After comparing the results of the improved NSGA II with the original NSGA II, the algorithm’s performance will be further evaluated by comparing it to AEA and BKPF. AEA and BKPF are both combinations of the five MOEAs, but it is essential to note that the BKPFs are obtained with a much larger computational budget than the number of function evaluations (NFEs) used for the improved NSGA II. By conducting this comprehensive evaluation, it is possible to determine the effectiveness and efficiency of the improved NSGA II algorithm in solving the benchmark problems, considering the quality of the solutions obtained by the five state-of-the-art MOEAs and the extensive computational effort invested in obtaining the BKPFs. This approach helps to provide a more accurate assessment of the effectiveness and efficiency of the improved NSGA II algorithm in solving the benchmark problems.
In the benchmark case studies, the first set of case studies, TLN, the true Pareto solution represents the Pareto front that was obtained by enumerating the entire solution space of the problem. Thus, no better solution can be found for this network. With the proposed improved NSGA II algorithm, all the true Pareto front points were found within the computational budget. On the other hand, the original NSGA II algorithm only finds 77 points out of the 114 Pareto front solutions, even when combining all the five MOEAs, the number of solutions found is still lower than that of the BKPF. With the improvements made to the NSGA II algorithm, all the possible solutions, the true Pareto front solutions, were found. In terms of dominance, the DS (dominated solutions), NDS (nondominated solutions), and BNDS (solutions dominated by BKPF) are all equal to zero because there are no solutions that can dominate the true Pareto front. Furthermore, since all the solutions are found, there are no solutions that are dominated by BKPF.
The performance of the improved NSGA II algorithm was evaluated on two medium-sized networks: HAN and GOY. For the HAN network, the BKPF was found to be 575, and using the improved NSGA II algorithm, a total of 716 (TDNS) solutions were found. Among these 716 solutions, 10 are equal to the BKPF and the non-dominated solutions found by the improved NSGA II algorithm were 664, which is higher than the BKPF. Additionally, 40 solutions that dominate the BKPF were found by the improved NSGA II algorithm, which is higher than the 39 solutions found by the original NSGA II and AEA. For the GOY network, the improved NSGA II algorithm found a total of 341 solutions (TDNS). Among these solutions, 303 were equal to the BKPF and 27 non-dominated solutions compared to the BKPF were found. The number of solutions found by the improved NSGA II algorithm is much higher than the solutions found by the original NSGA II algorithm, which is only 29 solutions, and AEA, which found 67 solutions. The improved NSGA II algorithm was able to find 11 solutions that dominate the BKPF. The improved NSGA II algorithm found solutions lower than the BKPF, but it is important to note that the BKPF was obtained through an extensive computational effort that utilized a combination of five different state-of-the-art multi-objective evolutionary algorithms (MOEAs).
The FOS and PES networks are two intermediate-sized cases with higher solution spaces compared to previous cases. For the FOS network, the algorithm found 532 solutions, which is higher than the 474 solutions found by the BKPF and 91% higher than the 48 solutions found by the original NSGA II and 140 solutions found by the AEA (a combination of the five MOEAs). The solutions that are equal to the BKPF are only three of the solutions found, and only 39 were non-dominated solutions. However, the solutions that dominate the BKPF compromise 490 solutions. This suggests that from the solutions found by the improved NSGA II, there are significantly more solutions that dominate the BKPF.
Another intermediate network is PES with three sources, which increases the difficulty of solving the optimization. The improved NSGA II found 247 solutions, which is higher than the 82 solutions found by the original NSGA II and 215 AEA solutions. We found 100 non-dominated solutions compared to BKPF solutions, and 146 solutions dominated the BKPF. From the solutions found, 59% dominated the BKPF solutions and most of the solutions found are better.
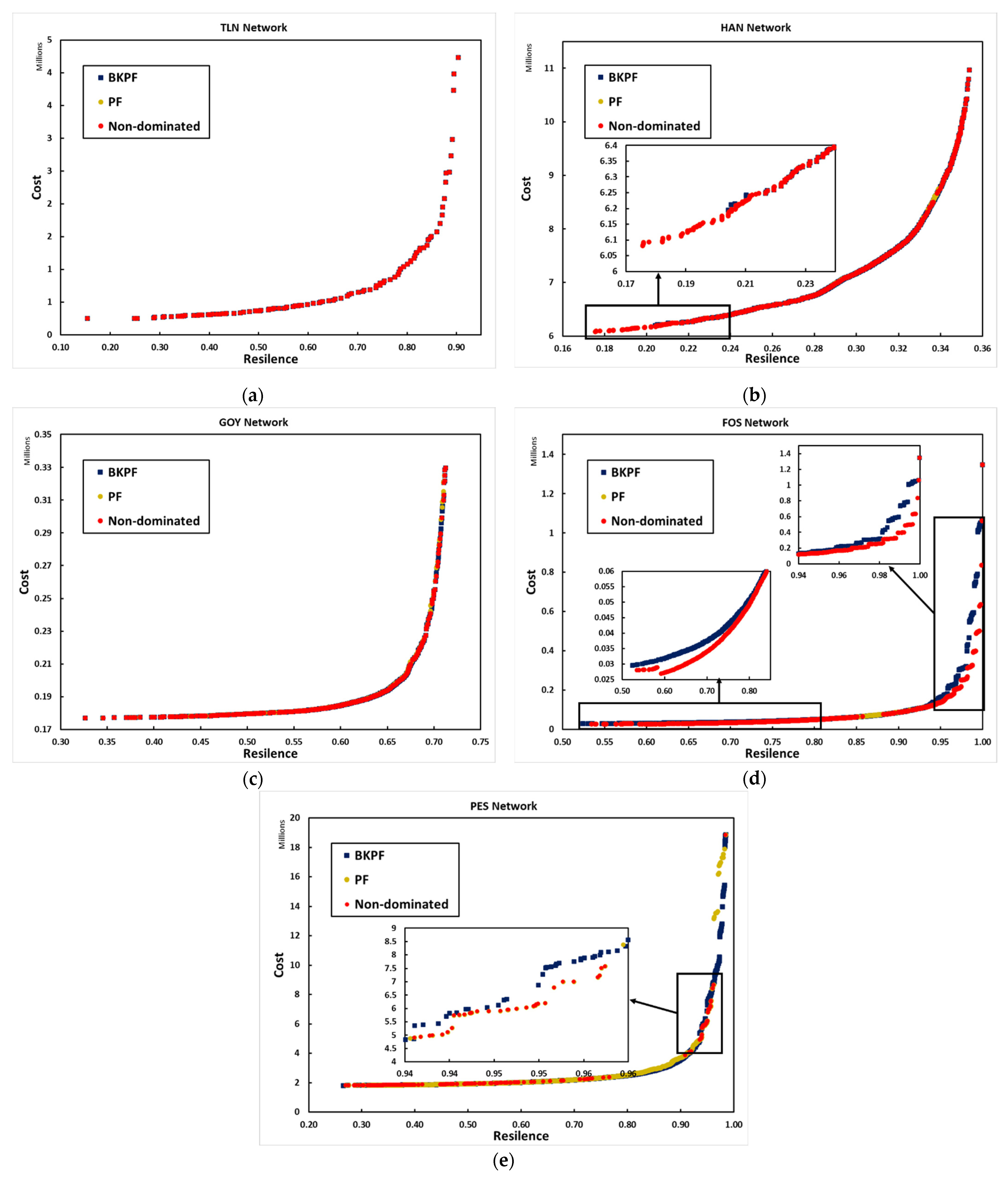
To evaluate the quality of the solutions obtained by the improved NSGA II algorithm, the solutions are compared with the benchmark Pareto fronts (BKPFs). In some cases, parts of the front are zoomed in to highlight the relationship between these two sets of solutions.
The graphs presented below depict the results from the improved NSGA II algorithm with the new methods and the best-known Pareto front. The blue points on the graphs represent the best-known Pareto front of networks presented in [
26]. The yellow points represent the solutions found by the improved NSGA II algorithm with the new methods (PF). The red points indicate the total number of non-dominated solutions compared to the BKPF.
Figure 6a displays the result of the TLN network obtained by utilizing the improved NSGA II algorithm with the new methods and comparing them to the best-known Pareto front. It can be observed that there is a complete overlap between all the true Pareto front points and the solutions obtained by the improved NSGA II algorithm. This is because the improved NSGA II algorithm has successfully found all the true Pareto optimal solutions.
As can be seen in
Figure 6b, for the HAN network the new method has expanded the range of the BKPF and increased the number of solutions. Specifically, the improved NSGA II has discovered more points with minimum resilience and cost, as highlighted in the zoomed-in portion. In the maximum region, the highest possible resilience for HAN has already been achieved, which is 0.3538, and further expansion towards the maximum is not feasible. In the minimum region, 33 additional solutions have been identified. Since more solutions than the BKPF have been uncovered, it indicates that the density of solutions in the remaining part of the Pareto front has been increased.
Figure 6c shows the results of GOY network, illustrating that the improved NSGA II algorithm has successfully generated solutions across the entire range of the pareto front for the GOY network. The improved NSGA II also outperforms the original NSGA II algorithm in terms of solution density, having found a greater number of solutions.
The results obtained from the improved NSGA II for FOS network,
Figure 6d reveal that a considerable number of solutions that dominate the BKPF are found, leading to substantial improvements across most parts of the pareto front. Zooming in on specific parts of the front, it becomes apparent that a significant gap exists between BKPF solutions and the improved NSGA II solutions in the lower resilience region and the knee area, implying that for the same cost better resilience can be achieved. A significant enhancement is observed in the knee area, which is a crucial part of the pareto front. The fourth method (G4) is specifically designed to address this region and generate more solutions. The positive impact of the G4 method can be clearly observed in this network as the solutions have demonstrated significant improvement.
In comparison to the BKPF, the results of the improved NSGA II for PES network in
Figure 6e show that there exist some uncovered sections of the front due to the lower number of solutions found by the improved method. However, it has been observed that the improved NSGA II has found solutions that were not discovered by the original NSGA II. In
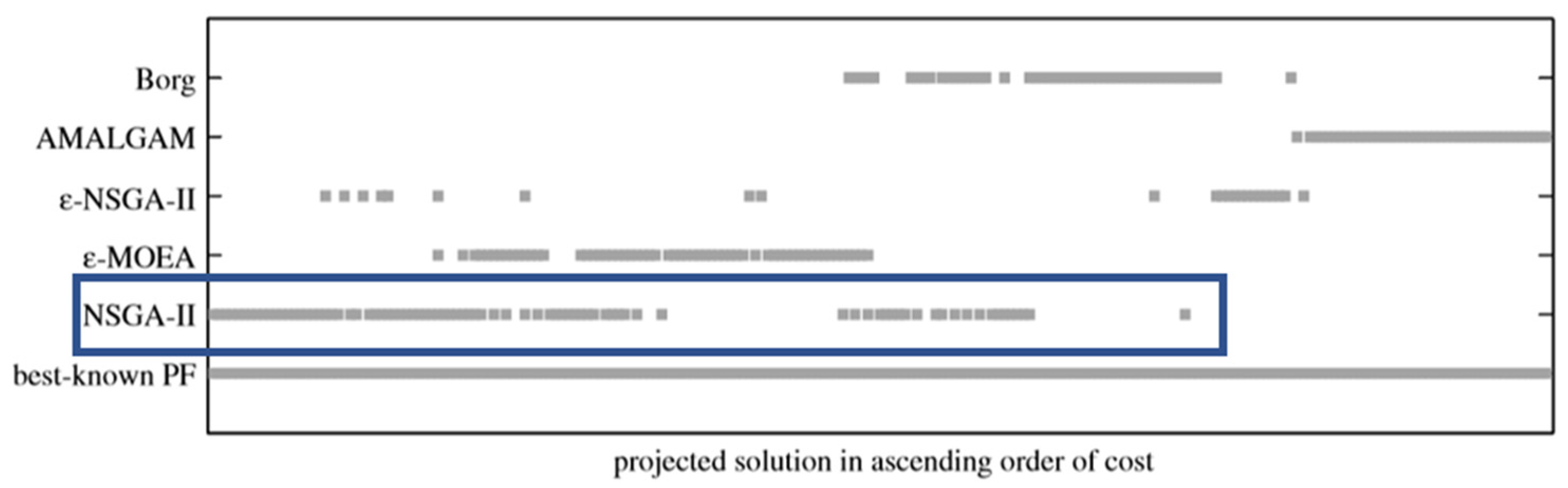
Figure 7 presented from [
26], the contributions of each MOEA to the final result can be seen, and it is evident that the original NSGA II found solutions only in the lower to middle part of the pareto front. On the other hand, the improved NSGA II solution indicates that solutions have been discovered in the maximum region of the front. This is particularly notable in the zoomed-in section, which is located around the knee area, where densely populated solutions are found, and those solutions dominate the BKPF.
4. Discussion
Table 2 presents the results of the improved NSGA II algorithm and compares them in terms of the number of solutions obtained for each of the five case studies. The results demonstrate that the improved NSGA II performs well for all case studies since it has found a large number of total non-dominated solutions. In multi-objective optimization problems, the density and diversity of the solutions across the Pareto front and convergence to the best possible solutions are important factors to consider.
In general, it was observed that the improved NSGA II algorithm discovered a greater number of solutions compared to the original NSGA II for all benchmark networks. Furthermore, the improved NSGA II found more solutions than the combination of five state-of-the-art MOEAs all networks. Even though the BKPF was discovered through extensive computation and the use of multiple MOEAs, the improved NSGA II was able to find more solutions for the TLN, HAN, and FOS networks, which is a significant achievement that demonstrates its effectiveness in solving multi-objective optimization problems. In addition, the improved NSGA II was able to increase the range of the pareto front for HAN and discover a significant number of solutions that dominate the BKPF, especially for intermediate-sized networks, resulting in a better pareto front.
Moreover, the improved NSGA II found solutions in the parts of the pareto front that were not found by the original NSGA II, thereby improving the diversity of solutions that can be discovered. These findings suggest that the improved NSGA II algorithm is a promising approach for solving multi-objective optimization problems and can be applied to a wide range of real-world applications.
It is important to note that although the number of solutions found by the improved NSGA II is lower than that of the BKPF for PES network, many of the solutions found are better than the BKPF solutions. However, a larger computational budget is required for the improved NSGA II algorithm to make a fair and complete comparison with the BKPF in terms of the number of solutions. In summary, the improved NSGA II algorithm shows promising results in solving intermediate-sized problems such as FOS and PES networks, and further improvements can be made by increasing the computational budget.
The results of the improved NSGA II algorithm presented in this study are highly promising and warrant further exploration in the field of multi-objective optimization. Although the algorithm has demonstrated success in solving a two-objective problem, there is room for improvement through further parameter calibration. Future work should focus on fine-tuning the implementation parameters to optimize the algorithm’s performance on all benchmark networks. This can be achieved through extensive testing and experimentation, leading to a more efficient and effective algorithm.
Furthermore, it is recommended that additional tests be conducted on the remaining benchmark networks to further evaluate the algorithm’s capabilities and limitations. These tests will allow researchers to gain a deeper understanding of the algorithm’s performance across a wider range of problem sets. In addition, further research could be conducted to define a new best-known Pareto front through extensive computation.
This study compared the solutions obtained using the improved NSGA II algorithm with the original NSGA II and AEA in terms of the number of solutions and graphical representation. However, for a more comprehensive analysis, it may be useful to evaluate these solutions using additional metrics such as data dispersion. To achieve a better comparison, future research could consider using alternative metrics such as box plots to provide insight into the spread of solutions in the front.
5. Conclusions
This research presents an improved version of the NSGA II algorithm that can effectively tackle multi-objective optimization problems. The NSGA II algorithm is a well-established state-of-the-art approach that has been widely used in the field of multi-objective optimization. The improved NSGA II algorithm employs various generation processes motivated by MOSA-GR to enhance the optimization search. The algorithm is designed to target different regions of the Pareto front to achieve better convergence, diversity, and density. The four generation processes, namely G1, G2, G3, and G4, serve different purposes, such as increasing diversity, searching for specific parts of the Pareto front, and finding solutions in the knee area. By utilizing different generation processes, the algorithm can access parts of the Pareto front that were previously unobtainable using a single generation process.
The improved NSGA II algorithm was tested on a well-known two-objective WDN problem from the literature, and the results were compared with those obtained by the original NSGA II, the combination of five state-of-the-art MOEAs and with the best know pareto front. The comparison demonstrated that the proposed improvement to the NSGA II algorithm was effective in finding more non-dominated solutions and dominating more solutions than the original NSGA II algorithm and other MOEAs in most cases. The algorithm was able to find all true Pareto front solutions for the small case study, widen the range of solutions for the intermediate-sized problem (HAN), and found solutions that dominate the best-known Pareto front, particularly in the knee area of the Pareto front for the intermediate-sized networks.
In conclusion, the proposed modifications to the NSGA II algorithm have the potential to be a significant contribution to the field of multi-objective optimization. The improved NSGA II algorithm is capable of finding solutions that cover all parts of the Pareto front with a single algorithm without increasing the computational effort. The good performance of the improved NSGA II algorithm compared to the original NSGA II algorithm demonstrates the effectiveness of the proposed approach.
In summary, the improved NSGA II algorithm exhibits significant promise in tackling multi-objective optimization problems. Subsequent research endeavors should concentrate on enhancing its implementation and assessing its performance across a broader spectrum of problem sets, while considering larger computational resources.