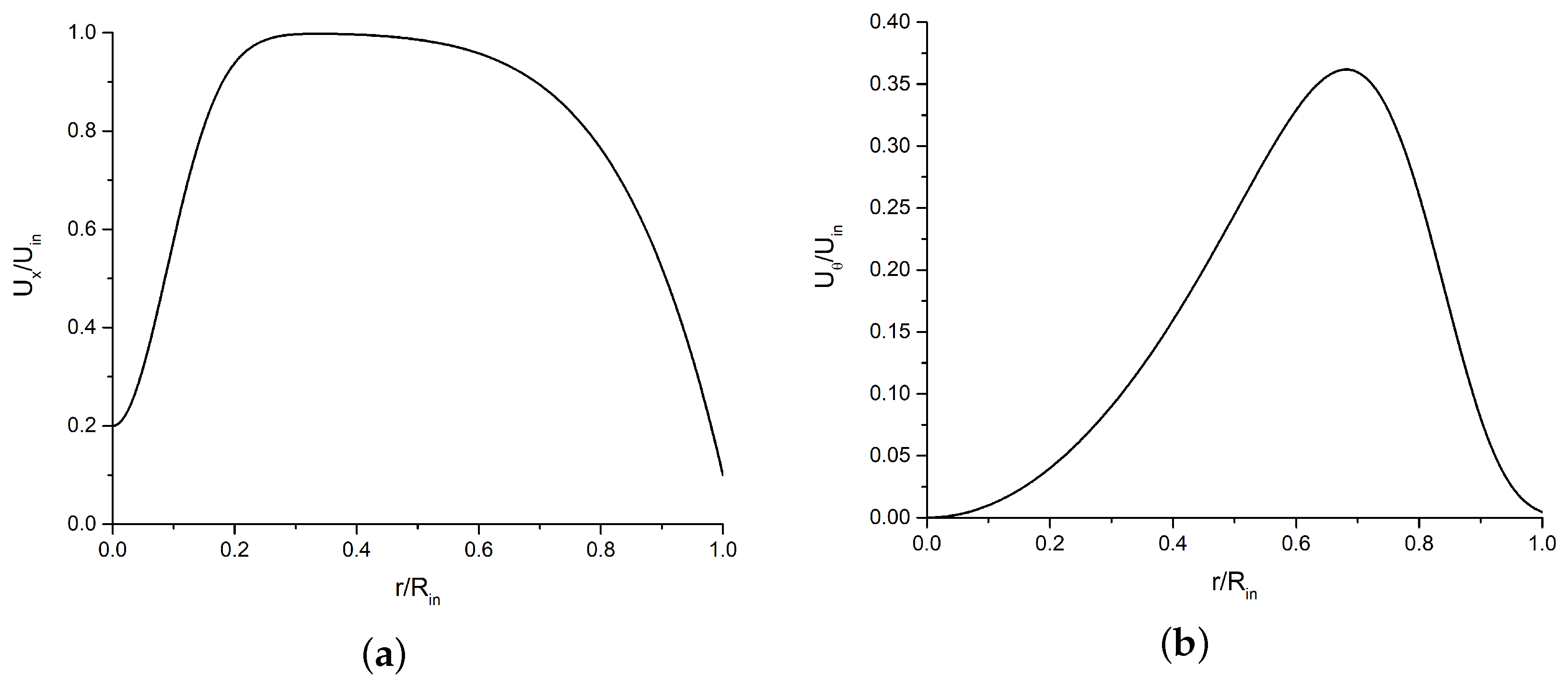Numerical Simulations of Swirling Water Jet Atomization: A Mesh Convergence Study

Abstract

We report on numerical simulations of a swirling water jet flowing out of a nozzle into a still air atmosphere at normal conditions. Primary jet breakup and atomization were studied with an emphasis on the effect of grid resolution on the results. Jet inlet diameter D was set to 0.8 mm, a bulk velocity was set to 7.6 m/s ($Re=6100$, $W{e}_l=650$), and the swirl rate was set to $S=0.3$. The near region of the jet (up to $x/D=16$) was studied. The results were obtained for four different grid resolutions with the smallest cell size of 6 $\mathsf{\mu }$m. It is shown that the use of an adaptive mesh refinement procedure for interface tracking allows us to get to convergent results in terms of both droplets volume and surface area distributions, while the total number of droplets changes with the increased grid refinement level. This phenomenon may be attributed to the formation of small (grid-cell sized) droplets due to numerically-triggered instabilities at the gas-liquid interface.

1. Introduction

Jet atomization is often modeled as a two-stage process, the stages being called primary and secondary breakup. During primary breakup, the liquid exiting the spray nozzle breaks up into droplets due to the instability that develops at the surface of the liquid film. The instability may be due to either shear stress caused by interaction with the surrounding atmosphere (Kelvin-Helmholtz instability) or normal stress (Rayleigh-Taylor instability). If the relative velocity between the drop and the environment is sufficiently high, droplets formed as a result of primary breakup undergo further fragmentation with the formation of even smaller droplets. The breakup of large droplets into smaller ones is called secondary breakup.

Secondary breakup plays an important role in many practical situations such as fuel jet atomization in diesel and gasoline engines. Many of the widespread simplified computational models, for example, TAB [1] model or Kelvin-Helmholtz/Rayleigh-Taylor (KH-RT) [2] atomization model, are developed based on insights gained from secondary breakup studies. Secondary breakup of commonly used liquids, such as water or kerosene, is a useful test case for numerical models.

In recent decades, numerical simulation has become of major importance in the design and development of novel engineering solutions in power generating applications. Currently, Large Eddy Simulations (LES) in combination with turbulent combustion models provide comprehensive information about the working parameters of engines at the R&D stage. However, numerical simulation of primary liquid fuel spray atomization still requires enormous numerical resources and is usually not simulated directly. In this regard, both Euler-Lagrangian and Euler-Euler methods are applicable to regions in which droplets of a known size distribution are injected. This approach is still the most efficient and practical way to model liquid fuel combustion chambers. A significant limitation of this approach is the need to obtain external information on initial droplets size distribution. Such information is available from experimental data, direct numerical simulation (DNS), or analytical/semi-empirical models. In its turn, one should verify such simplified models using experimental data or DNS results.

Primary jet breakup is affected by a large number of different factors that can be described by different dimensionless parameters, for instance, liquid Weber number, dimensionless thickness of the boundary layer inside the nozzle, Kelvin–Helmholtz and Rayleigh–Taylor instabilities wavelength ratio, the ratio of gas and liquid densities, Ohnesorge number [3]. For a high-velocity liquid jet, the list will also include the initial level of turbulence and the intensity of cavitation. Measuring the relative importance of all these parameters in an experimental study of various breakup modes is a difficult task. Numerical simulation of an idealized primary atomization process with strictly determined conditions may help in this regard by allowing to selectively turn on or off different mechanisms involved in the breakup process [4].

In DNS, the goal is to directly resolve the full spectrum of time and length scales in a turbulent flow, thus eliminating the need to model effects on unresolved scales. In a single-phase turbulent flow, the smallest length scale is the Kolmogorov dissipative scale $\eta$. Thus, the numerical resolution of the simulation should draw on this single parameter. In multiphase flows, it is also necessary to introduce an additional length scale associated with the size of the smallest droplets that can stably form in the flow. This usually means that a two-phase flow requires about an order of magnitude more accurate resolution than a single-phase DNS. Fortunately, such a high resolution is only required near the interface.

A number of studies have shown the possibility of modeling atomization through DNS [5,6,7]. However, most of numerical studies use LES formulation with Favre averaging, which may account for the changes in density between phases. This approach neglects subgrid scale effects that arise from the presence of a gas-liquid interface. More precisely, one should refer to this approach as quasi-DNS or underresolved interface DNS combined with LES in single-phase regions. Nevertheless, with dynamical grid refinement at the interface, this approach can provide valuable information about the primary breakup process and the resulting droplet size distribution if it can be shown that the small-scale unresolved interface dynamics do not affect the large-scale dynamics. To test whether this is the case, we should check the convergence of the simulation results with the grid refinement level as the unresolved scales are reduced. De Villiers E. et al. (2004) [8] performed a diesel jet breakup simulation using this quasi-DNS approach. They performed a mesh convergence study and found that droplet size distributions were significantly different, even for large droplets with refined mesh. This indicates that the scales associated with the interface were significantly underresolved. Bianchi et al. (2005, 2007) [9,10] performed a similar diesel spray simulation using a finer mesh. They found that the intensity of turbulence has a strong effect on both the length of the jet before the breakup and the total droplets mass, but has little effect on droplet size distribution. However, a study of the convergence of the results was not performed, which raises doubts about the obtained results. Menard et al. (2007) [11] using the Coupled Level-Set and Volume of Fluid (CLSVOF) method, also studied diesel jet breakup. The authors did not simulate the internal flow zone of the nozzle, but used artificial turbulent velocity oscillations at the inlet of the computational domain generated by the method proposed by [12]. They did not use any subgrid LES models in single-phase regions, thus assuming quasi-DNS regime. However, their grid resolution was probably too coarse for capturing all the flow scales, with a grid-to-Kolmogorov scale ratio of 3. Grid convergence results were not reported. Chesnel et al. (2011) [13] simulated a jet breakup using the LES method and suggested how this method may be improved by using additional models to resolve subgrid scales.

Additional models of jet breakup help to avoid the difficulties associated with underresolution of the liquid-gas interface. In [14], atomization was numerically simulated at high Weber and Reynolds values using the ELSA [15] model (Euler-Lagrange sputtering model). Duret et al. (2013) [5] compared two-phase flow DNS with ELSA model results. This test was carried out for various liquid volume fractions, grid resolution and surface tension coefficients. To verify the validity of the interface density equation used in the ELSA model, the authors collated time-averaging statistics of interface density evolution. The proposed improvements to the ELSA model were compared to the reference DNS for several configurations.

In recent years, increased computing power has made it possible to use the DNS to model both primary and secondary jet breakup. In [16], modeling of diesel jet breakup using DNS and VOF (Volume of Fluid) methods was performed. Piaretti et al. (2020) [7] investigated mesh resolution sensitivity of primary jet breakup simulation. The study showed that during the breakup, droplets with a diameter smaller than the size of the computational grid step are formed. The authors suggest estimating the accuracy of atomization simulation based on the volume fraction of underresolved structures. Torregrosa et al. (2020) [17] performed a DNS of liquid jet spray and proposed a technique for analyzing the turbulence in sprays called a pseudo-fluid method. Feichi et al. (2020) [18] carried out a high resolution numerical simulation of a coaxial atomizer. The team studied the effect of increased pressure in the reactor on the behavior of high-viscosity liquid jets during primary breakup. The results were confirmed by doubly refined simulations. Mukundan et al. (2021) [19] investigated the main atomization characteristics of a liquid jet injected into a transverse gas flow using both DNS and LES approaches. The research demonstrated that the resulting distributions of drops in both cases obey the log-normal law.

Much less attention has been paid to the numerical study of swirling jets primary breakup due to the large number of parameters that affect the flow (bulk velocity, swirl rate, nozzle geometry, and other variables). Among the various nozzle designs, the pressurized swirl nozzle jet is probably the most common. Pressurized swirling atomizers are used in a large variety of industrial applications (powerplant furnaces, jet engines, liquid propellant rocket engines, ramjet and scramjet engines). In particular, two of the above applications, ramjet and scramjet combustion chambers, use swirling fuel jets located at the intersection of air streams. Strict requirements for these high thrust supersonic and hypersonic engines may be satisfied by the swirling injection method due to the large liquid fuel delivery rate and minimal pressure loss.

The vortex atomizer has an additional mechanism (from swirling and centrifugal effects) of liquid sheet breakup and atomization. It converts the total pressure drop into an angular momentum as the fluid travels along a helical path inside the vortex combustion chamber. Due to inertial forces of the swirling motion of the liquid film in a swirl chamber, the conical liquid film, emerging from the injector nozzle, expands radially as it moves downstream and gradually becomes thinner (because the volume of the liquid is conserved). Due to the high fuel flow rate and high relative droplet velocities, droplet collision is expected to be a frequent event immediately after the sheet breaks. Thin hollow conical liquid sheets result in finer spatter and a narrow range of droplet sizes. In [20], the processes of breakup and atomization of a swirling liquid jet injected into a strong crossflow were experimentally studied. The influence of a crossflow on the processes of jet separation, atomization, and spattering were visually studied. The structure and characteristics of the aerosol, including the droplet size spectrum, droplets distribution across the cross section, penetration and breakup length, are measured optically. The interactions between liquid jet and a crossflow and the resulting breakup process are discussed in relation to Weber number and momentum ratio.

In [21], the state of the flow in the outer layer of the liquid was expressed in terms of the Weber number for the liquid cone:

$$W{e}_{lc}=\frac{{\rho }_l{U}_l^2{t}_f}{\sigma }.$$

where Here ${\rho }_l$ is the density of the liquid, $U_l$ is the axial velocity of the liquid, $t_f$ is the thickness of the cone layer, and $\sigma$ is the surface tension. The thickness of the cone layer is expressed by [22]:

$$t_f=3.66{\left(\frac{D_0{m}_l{\mu }_l}{{\rho }_l\Delta P_l}\right)}^{0.25}$$

Thus, although many studies have addressed the process of liquid jet atomization, it is still not clear what resolution the computational grid should have in order to obtain feasible simulation results. The present paper describes a numerical study of the influence of the computational grid resolution on the structure of the swirling liquid jet and the droplets distribution during the jet breakup based on the highly efficient computational code Basilisk. For better interface tracking, the adaptive mesh refinement procedure was applied.

2. Computational Details

Below, we describe governing equations and computational details including the boundary conditions and mesh refinement procedure.

2.1. Governing Equations

We simulate the Navier–Stokes equations in the volume-of-fluid method (VOF) regarding the gas-liquid mixture as a fluid with variable density and viscosity and taking into account the action of the surface tension:

$$\begin{array}{ccc}& & \rho (\frac{\partial u_i}{\partial t}+\frac{\partial u_i{u}_j}{\partial x_j})=\frac{\partial p}{\partial x_i}+\frac{\partial {\sigma }_{ij}}{\partial x_j}+\sigma \kappa {\delta }_s{n}_i,\hfill \end{array}$$

(1)

$$\begin{array}{ccc}& & \frac{\partial u_i}{\partial x_i}=0,\hfill \end{array}$$

(2)

where $\rho$, $u_i$ and $x_i$ represent the density, velocity components and coordinates, respectively; t is the time variable; p is the pressure; $\mu$ is the dynamic viscosity. The viscous stress tensor is defined as ${\sigma }_{ij}=\mu (\partial u_i/\partial x_j+\partial u_j/\partial x_i)$. The Dirac function ${\delta }_s$ is assumed non-zero only at the liquid-gas interface. The surface-tension coefficient, curvature, and normal to the interface are denoted as $\sigma$, $\kappa$, and $n$, respectively.

In the context of the one-fluid formulation for multiphase flows, two different phases are distinguished by the values of characteristic function $c(x,t)$, whose time evolution satisfies the following transport equation:

$$\frac{\partial c}{\partial t}+u_i\frac{\partial c}{\partial x_i}=0.$$

(3)

The physical properties of the fluid depend on the characteristic function:

$$\rho =c{\rho }_l+\left(1-c\right){\rho }_g,$$

(4)

$$\mu =c{\mu }_l+\left(1-c\right){\mu }_g.$$

(5)

Equations are discretized and solved using the open-source continuum dynamics simulation code Basilisk [23,24,25] with a momentum conserving scheme (MCVOF) [26]. The computations were performed using finite-volume discretization with the second order central-difference schemes for space derivatives and the second order implicit time derivative scheme.

2.2. Computational Domain

We analyze the breakup and atomization of a swirling jet injected through a 0.8 mm diameter nozzle into a gas-filled cubical chamber with a 12.8 mm length side. This configuration has a narrow length-scale range and a simple analytical injection velocity profile independent of grid refinement. The problem is solved using the adaptive mesh refinement (AMR) technique with five different maximum grid refinement levels for the same refinement criteria. The properties of the liquid correspond to those of water at normal conditions. Namely, the density ${\rho }_l$ is 1000 kg/m${}^3$, the dynamic viscosity ${\mu }_l$ is $1\times {10}^{-3}$ kg/m · s, and the surface tension $\sigma$ is 0.072 N/m. For the gas phase the density ${\rho }_g$ is 1 kg/m${}^3$ and the dynamic viscosity ${\mu }_g$ is $1\times {10}^{-5}$ kg/m · s.

At the inlet boundary, the profiles of mean longitudinal and tangential velocity components are prescribed with a mean radial velocity of zero. At other boundaries, zero gradient conditions for all velocity components are set. The inner radius of the nozzle $R_{in}$ was 0.4 mm, the max normal velocity $U_{in}$ was 10 m/s. The mean inlet longitudinal and tangential velocity profiles (Figure 1) correspond to the vortex nozzle profiles. The velocity profiles have the following analytical expression:

$$U_x\left(r\right)/U_{in}=1-0.9{\left(\frac{r}{R_{in}}\right)}^6-0.8exp\left[-\frac{r^2}{R_c^2}\right]$$

$$U_{\theta }\left(r\right)/U_{in}=\frac{r^2}{R_{in}^2}exp\left[-{\left(\frac{r}{R_t}\right)}^{N_t}/N_t\right]$$

where $R_c=0.05$ mm, $R_t=0.25$ mm, and $N_t=8$.

The bulk inlet velocity was calculated using the formula:

$$U_{bulk}=\frac{1}{\pi R_{in}^2}{\int }_0^{R_{in}}2\pi rU\left(r\right)dr=0.7625U_{in}$$

In this case, the Reynolds number $Re={\rho }_l{U}_{bulk}2R_{in}/{\mu }_l$ is 6100.

$$W{e}_l=\frac{{\rho }_l{U}_{bulk}^{2}2R_{in}}{\sigma }=650$$

$$W{e}_g=\frac{{\rho }_g{U}_{bulk}^{2}2R_{in}}{\sigma }=0.65$$

$$Oh=\frac{{\mu }_l}{\sqrt{\sigma {\rho }_{l}2R_{in}}}=0.004$$

2.3. Velocity Fluctuations at the Inlet

In contrast to time-evolving turbulence, a simulation of a flow with a prescribed inlet velocity requires turbulent inflow boundary conditions. The results are strongly affected by the prescribed inlet velocity fluctuations. To correctly simulate the growth of instabilities in the near-nozzle region of the jet, inlet fluctuations are essential. In the present paper, inlet velocity fluctuations were modeled according to Klein et al. [12]. Firstly, spatial and temporal characteristic scales of the fluctuations were defined. Then, a three-dimensional array (with dimensions corresponding to two in-plane inlet coordinates $y,z$ and time t) of white-noise random numbers was generated for each velocity component. Next, an exponential low-pass filter was applied on the generated data, taking into account the predefined characteristic scales. The obtained values were used to calculate the velocity fluctuations field after renormalization of the data to comply with the prescribed velocity auto- and cross-correlations [27].

After several time steps of the simulation, their total duration being equal to the time interval between two consecutive layers of the generated array, the array is shifted along the time axis by one layer and a new layer of processed random numbers is added to the array. Thus, by traveling through the array according to the current time in the simulation, and interpolating the array data to the computational mesh, we simulate an inlet velocity fluctuations field.

In present simulations, the maximum amplitude of turbulent fluctuations was set to 5% of the local velocity values. The characteristic timescale of turbulent fluctuations was set to 10 $\mathsf{\mu }$s. The characteristic length of turbulent pulsations was set to $R_{in}/16$ = 25 $\mathsf{\mu }$m.

2.4. Mesh Refinement

The computational mesh in Basilisk is based on cubic cells organized in a multilevel tree structure (octree for 3D cases), where at each level the cell is twice as small as the one at the previous level. The mesh can be adaptively refined using a feature built into the Basilisk code environment [28].

The refinement algorithm is called at each time step, and a particular cell refinement occurs when the value difference of the field variable exceeds the prescribed error margin. If the value difference between adjacent levels is less than $2/3$ of the prescribed error margin, the cell is considered “too fine” and coarsened. During each refinement step, each cubic cell can be subdivided into eight (3D case) equal smaller cells, which can be further subdivided until either the required precision or maximum refinement level is achieved.

The refinement criteria are set for the velocity (approximation error < 0.05 m/s) and liquid volume fraction (approximation error < 0.01) fields. The simulated cases differ in the maximum allowed refinement level (from 8 to 11). For Level 11, the minimum cell size corresponds to dividing the size of the computational domain by $2^{11}$ (6.25 $\mathsf{\mu }$m).

3. Results and Discussion

We carried out simulations of a swirl jet outflow with different resolutions. The initial base mesh (Level 7) had ${128}^3$ cells for all simulations, which corresponds to 100 $\mathsf{\mu }$m cell size. This refinement level was set as the minimum. Meshes were never coarsened below this level.

The actual mean number of cells during simulations was: $2.1\times {10}^6$ for a Level 7 grid; $6\times {10}^6$ for a Level 8 grid; $18\times {10}^6$ for a Level 9 grid; $45\times {10}^6$ for a Level 10 grid; $100\times {10}^6$ for a Level 11 grid.

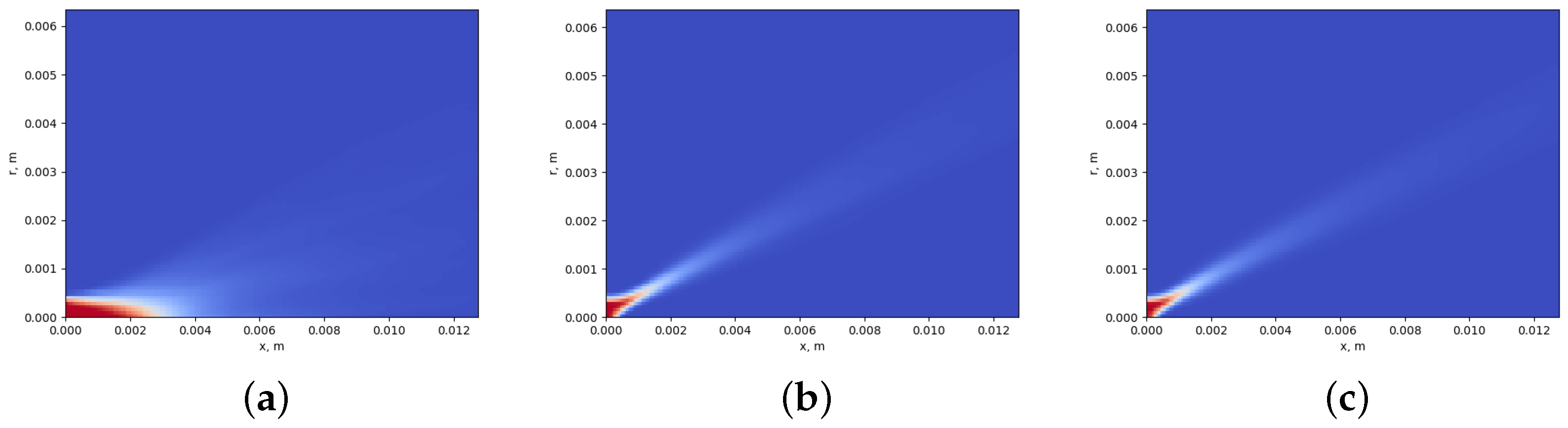
Figure 2 shows an instantaneous view of the jet interface for all resolutions. Each mesh contains a region where interface instability develops. The instability development zone occupies about $1/4$ of the length of the computational domain or eight inlet diameters. When surface instabilities grow above the critical level, the liquid layer breaks into droplets and ligaments. Ligaments are also prone to instabilities, so they rapidly break up into drops of different sizes. At a time of 1.5 ms after the start of the simulation, the first group of drops reaches the right boundary of the computational domain. We suppose that the jet structure is formed at this moment. In this way, the calculation was performed up to a time of 5 ms.

We found that different flow parameters (time-averaged liquid volume fraction and velocity fields, droplet diameters and volume distribution, and interface area) converge at different rates with increasing mesh quality.

3.1. Averaged Fields

The fields of mean liquid volume fraction and velocity have the fastest convergence. To obtain that, we performed averaging in two stages. First, all fields were averaged over 3.5 ms time period in the quasi-stationary flow regime. Then, we carried out averaging over the azimuthal direction. In this way, we obtained two-dimensional averaged fields.

Figure 3 shows the averaged volumetric liquid content fields. For the coarsest mesh with no refinement (Level 7), the cone angle is much smaller than that for the meshes with higher maximum refinement level. This is because for the coarsest grid no recirculation zone appear at the jet axis. However, starting from Level 8 mesh, a recirculation zone appears. The recirculation zone reaches the nozzle, which is usually the cause of some gas entering the nozzle (in this study, the flow inside the nozzle is not simulated, and the boundary condition does not assume a backflow of gas through the inlet). The differences between grids of higher resolution (Levels 9, 10, and 11) are insignificant.

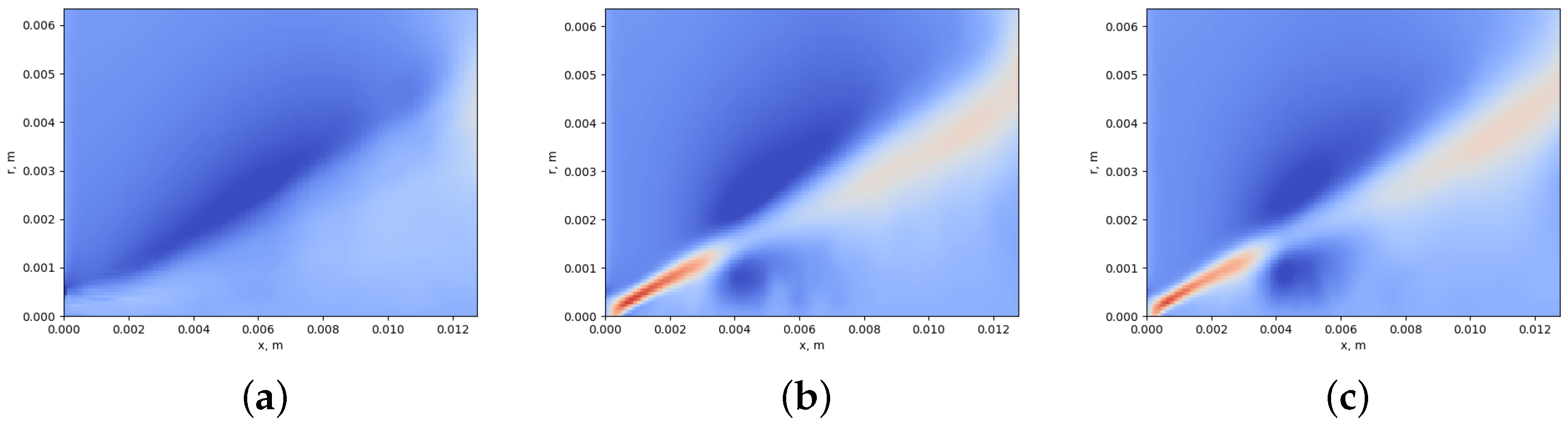
Figure 4 shows the averaged longitudinal velocity fields. The field for the Level 7 mesh differs significantly from the fields with higher maximum refinement levels. The lack of recirculation zone near the nozzle on the coarsest grid also distorts the flow structure far from the nozzle making it more uniform. For fine grids, the liquid jet occurs in the form of a cone with thin walls. Inside the cone, the recirculation zone occupied by the gas phase continues in longitudinal direction up to $x=6$ mm ($x/D_{in}=7.5$). Further downstream, the gas has a slight positive longitudinal velocity due to entrainment from the liquid jet. The maximum value of negative longitudinal velocity in the recirculation zone reaches −5 m/s. When moving away from the nozzle, the jet breaks up into drops, while the longitudinal velocity decays weakly. Figure 4d shows the averaged velocity profile along the axis of symmetry. The differences between Levels 8 and 9 are insignificant.

Figure 5 shows the averaged radial velocity fields. Here, a significant difference between the Level 7 mesh and the other higher refinement level meshes is apparent. The radial velocity component from the coarse grid is several times lower than that on the other meshes. The appearance of a recirculation zone leads to a significant increase in the radial velocity due to focusing of the flow in a thin cone. This leads to an increase in the opening angle of the jet cone. On the fine meshes, the value of the radial velocity reaches 3 m/s for the liquid cone and −1 m/s for the gas inside the recirculation zone. After the breakup of the liquid layer, a sign change in the radial velocity happens, which is associated with the suction of the gas into the central part of the jet. Further downstream, the average radial velocity again raises up and then slowly diffuses.

Figure 6 shows averaged azimuthal velocity fields. Of all velocity components, the azimuthal one decays the fastest; therefore we can say that the rotation of the liquid occurs only in the immediate vicinity of the nozzle until the jet breaks up into ligaments. After the initial breakup of the liquid film, the azimuthal velocity is partially transformed into the radial velocity as the droplets inertia and the loss of interconnection straighten their trajectories and the azimuthal velocity component rapidly decays.

3.2. Instability on the Film Surface

Figure 2 shows that for the coarsest mesh (Level 7), the shape of the jet is qualitatively different from that for the other meshes. The angle of the liquid cone is much smaller, and there are fewer droplets. With the increase of the maximum refinement level of the mesh (Level 8), a significant increase in the angle of the cone is observed. At this resolution, a conical liquid film is visible. Film breakup starts from film perforation and the formation of azimuthally-directed ligaments with their further breakup into droplet chains. It can be seen that perforation of the liquid film occurs with the formation of elongated holes. The perforation of the liquid film may be associated with numerical instability. The latter may happen when the thickness of the liquid film becomes comparable with the size of the computational mesh cell. The visible change in shape of the perforation with an increase of mesh quality (up to Level 10) supports this hypothesis.

With a further increase in the maximum mesh refinement level (Level 11), changes in the visible liquid jet structure are insignificant. At Level 10, the initial jet perforations are mainly round holes of a small diameter (see Figure 7). In this case, a greater number of small drops appear, and the ligaments become shorter and break up into drops earlier. In general, with the increase of resolution, the generated holes become larger, appear further downstream and their number is noticeably reduced. The trend is maintained up to the Level 11 grid.

3.3. Droplets Statistics

The droplets formed as a result of the jet breakup reach the outlet boundary of the computational domain approximately 1.5 ms after the start of the outflow. From this moment, every 10 $\mathsf{\mu }$s the data about the size distribution of droplets are recorded up to a time of 5 ms. Then, the data obtained are averaged over time.

The minimum droplet size can be estimated using the Hinze Scale (HS) [29]. HS is obtained from the balance between the potential energy of the surface tension of the droplets and the kinetic energy of the outflowing jet:

$$HS=\frac{\sigma W{e}_{cr}}{{\rho }_l{U}^2}=12\mathsf{\mu }\mathrm{m}$$

(6)

where $W{e}_{cr}$ is the critical Weber number, for which the balance between fluid deformation due to friction and elastic forces is achieved. Usually, its value is determined close to 10. In the present case, this characteristic scale of the smallest droplets is about 12 $\mathsf{\mu }$m.

In order to estimate the most probable droplet size, the Sauter Mean Diameter (SMD) is usually used. The SMD defines the diameter of a drop that has the same volume to surface area ratio as the ratio of total volume of the liquid phase to its total surface area:

$$SMD=6\frac{\Sigma V_i}{\Sigma A_i}$$

(7)

For the present case parameters, the SMD calculated from the parametrization of Wu et al. [30] is as follows:

$$SMD=2R_{in}\frac{46.4}{W{e}_l^{0.74}}=300\mathsf{\mu }\mathrm{m}$$

(8)

Analyzing the existing data in the literature, we conclude that when modeling the atomization of a jet, one should not focus on the Kolmogorov scale resolution alone, since in many cases it does not govern the atomization process of the jet. The other important parameter is the Hinze scale (HS). In the majority of studies (

Table 1. Calculation parameters.

	Nozzle Diameter, $\mathsf{\mu }$m	${\mathit{Re}}_{\mathit{l}}$	${\mathit{We}}_{\mathit{l}}$	Min Linear Cell Size, $\mathsf{\mu }$m	Kolmogorov Scale, $\mathsf{\mu }$m	Hinze Scale ($\mathit{\sigma }{\mathit{We}}_{\mathit{cr}}/{\mathit{\rho }}_{\mathit{l}}{\mathit{U}}^2$), $\mathsf{\mu }$m	Sauter Mean Diameter, $\mathsf{\mu }$m
Present paper	800	6100	650	6	1.2	12	300
Pairetti et al. [7]	100	5800	11,600	0.37	0.13	0.08	<8
Constante-Amores et al. [31]	4000	1000–10,000	10–1000	26	5.7–26	40–4000	300–4000
Jiao et al. [16]	100	4300–5800	6000–8000	5	0.81	0.1–0.2	15
Torregrosa et al. [17]	90	5037	27,000	2.34	0.5	0.03	<5

), the grid does not resolve the HS. The lack of complete grid convergence shows that physical processes are underresolved. In our study, we show that at a sufficiently fine grid for HS resolution, grid dependence of the results is still observed; however, this dependence is probably not related to physical processes. We attribute this to the numerical errors arising when, with a change in the topology of the interfacial surface, the liquid layer width decreases to zero and the liquid layer breaks.

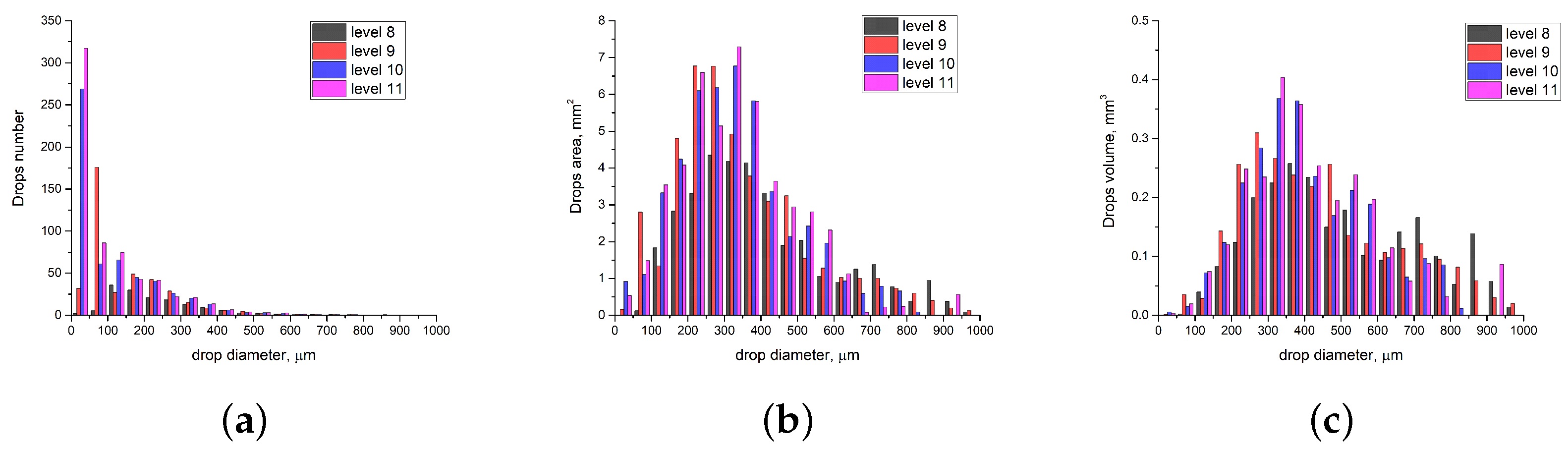
In Figure 8a, you can see a histogram for the the number of droplets with a longitudinal coordinate of more than 8 mm binned by the droplet diameter. In order to exclude the influence of long ligaments and large unstable drops, one needs to consider the droplets that are far from the nozzle, i.e., we assume that the secondary break up of droplets in this region is mostly finished. The diameter bin width for plotting the distribution is 50 $\mathsf{\mu }$m. For a coarse mesh (Level 8), the highest number of droplets lies in the range of 100 to 150 $\mathsf{\mu }$m. Increasing the mesh refinement level (Level 9) shifts the peak to smaller diameters up to the range of 50–100 $\mathsf{\mu }$m. For finer mesh (Level 10, 11), the peak is shifted to the region of smaller diameters (0–50 $\mathsf{\mu }$m). This is likely due to formation of parasitic (numerically based) droplets. Their diameter equals two to three minimum cell sizes. This is consistent with the results reported in the article [7]. Cell size for Levels 8,9,10, and 11 is 48, 24, 12, and 6 $\mathsf{\mu }$m, respectively.

In Figure 8b, you can see a histogram of the droplets accumulated surface area binned with droplet diameter. Despite significant differences in the distribution by the number of droplets for different meshes, the surface area behaves more conservatively than the number of droplets (as the small parasitic droplets have a much lesser effect on the total interface area). A significant increase in the area for droplets of a small diameter (50–100 $\mathsf{\mu }$m) is the case only for Level 9 mesh. For the next level mesh, a monotonous drop in the accumulated area of the droplets is observed with decreasing diameter.

In Figure 8c, you can see shows histograms of accumulated volume of the droplets binned with droplet diameter. Here, the bin width is also 50 $\mathsf{\mu }$m. The histograms obtained for different meshes converge quite well with Levels 10 and 11 being very close to each other. There is a slight difference in distributions for large droplet diameters, which is probably because the statistics for rare events of large droplets formation do not converge completely. The peak of the maximum amplitude illustrated in Figure 8a, which occurs as a result of the formation of parasitic drops, makes an insignificant contribution to the accumulated volume statistics of the droplets. Moreover, as the mesh refinement level increases, the amplitude of this parasitic peak decreases in the accumulated volume statistics, which advocates for the convergence of the results for the maximum considered refinement level (Level 11).

Figure 9 shows the dependence of the time-averaged total area of the liquid-gas interface from the size of the minimal allowed computational cell. This parameter is important in problems with chemical reactions (e.g., combustion of liquid fuels), since it is usually the surface area that limits the reaction progress. The plot shows a trend which is close to linear. The total convergence is not achieved here; however, increasing the refinement level from 10 to 11, with the minimum cell size reduced by two times, only leads to a 6.6% increase in the total surface area.

In the current paper, we do not claim to achieve a complete grid convergence of the results. We show how the grid resolution affects different flow characteristics; in particular, we assume that an important parameter is the area of the interfacial surface. This parameter is the main one for practical applications where the rate of evaporation is crucial. As our results show, the area of the interfacial surface increases with decreasing cell size. However, extrapolating the obtained linear trend, we assume that when the grid cell size tends to zero, the area of the interfacial surface will remain finite and increase only slightly compared with our results. It is not clear whether full grid convergence is possible, since with increasing resolution, the spatial scale of the numerical instability decreases, which leads to the formation of smaller and smaller droplets. It is possible to avoid this by changing the numerical schemes for sampling the interfacial surface.

According to the conventional model, the Laplace pressure at the microscale becomes so large that capillary forces will, whenever possible, form droplets of the smallest possible size. This might be feasible in a very thin conical sheet of the rotating liquid. If such a thin layer of liquid is formed in a numerical simulation, these smallest droplets scale will correlate with the grid cell size. However, the total volume of these small droplets should not be large. In reality, on micron scales, other physical mechanisms come into play, limiting the number of small droplets. One of them is the presence of impurities in the liquid, which, concentrating on the droplet surface, strongly change the physical properties of the interfacial surface on small scales. It leads, in particular, to the fact that the drops begin to behave similar to elastic balls. Another limiting mechanism is the evaporation of small droplets. On the other hand, the physics of the interfacial surface on the micro and nanoscales is currently a rapidly developing area, and so far, even a qualitative understanding of the processes has not been achieved. In this regard, further refinement of the grid is impractical.

4. Conclusions

We numerically investigated a swirling water turbulent jet outflowing into a gas atmosphere using the open-source fluid simulation code Basilisk. The nozzle diameter was 0.8 mm and the inlet Reynolds number was 6100. Analytical longitudinal and azimuthal velocity profiles were specified at the inlet. A distinct feature of the liquid swirling jet is the formation of a liquid cone with thin walls and a recirculation area inside. The presence of such thin walls leads to additional difficulties in the numerical simulation of swirling jets. The averaged spatial distributions of liquid volume fraction, longitudinal, radial, and azimuthal velocities are calculated. Droplet size distributions are also obtained.

Key findings of the work:

• The use of a coarse mesh leads to a significantly erroneous flow structure. The liquid jet does not form a cone, but flows out in the form of a filled swirling jet. An increase in the mesh adaptive refinement level leads to a qualitatively correct flow structure and a formation of a recirculation zone near the nozzle. A further improvement of the mesh quality does not change the mean distribution of flow fields.
• The distribution of the number of drops by size does not seem to converge with an increase in mesh resolution. An increase in the quality of the mesh leads to a shift of the distribution maximum to smaller diameters. When, due to the physics of the process, the value of the computational cell becomes much smaller than the expected mean characteristic size of the droplets, an unphysical peak is observed in the distribution. The droplet diameter corresponding to this peak is close to the value of the minimum calculated cell. The formation of such parasitic drops is associated with a change in a small-scale topology of the jet and a numerical error. At the breakup point, the thickness of the liquid film tends to zero and this raises the numerical errors in the film shape approximation.
• Improving mesh quality leads to the convergence of area and volume distributions, depending on their diameter. Despite the superior number of parasitic droplets, their influence on these parameters is insignificant.