Modeling Spatio-Temporal Dynamics of BMPs Adoption for Stormwater Management in Urban Areas
Abstract
:1. Introduction
2. Study Areas
3. Materials and Methods
3.1. BMP Data Used for Model Development
3.2. Physical and Demographic Factors for BMP Adoption Model
3.3. Potential BMP Adoption Models and Evaluation Metrics
4. Results and Discussion
4.1. Results of BMP Adoption Model Development
4.2. Application of the BMP Adoption Likelihood Model
4.2.1. BMP Adoption Simulation Algorithm
- Step 1
- Based on the initial BMP density setting (e.g., 1 per 1000 housing units), randomly selected N residential parcels for BMP allocation. Set step .
- Step 2
- Calculate the distance of all residential lots to the nearest BMPs. Update the average minimum distance to BMPs for all census tracts.
- Step 3
- Predict the number new BMP adoption for census tract based on the regression model.
- Step 4
- Randomly select residential parcels in census tract for BMP adoption based on possibility as detailed below:
- 4.1.
- For each residential lot, find the maximum distance to the nearest BMP and use the maximum value minus the current distance to the nearest BMP for each residential lot as the weight.
- 4.2.
- Calculate the allocation probability for each residential parcel as weight/sum_of_all_weights
- Step 5
- If the stop criterion is satisfied, terminate the process; else, set , and go to Step 2.
4.2.2. Baseline Simulation Results for BMP Adoption
4.2.3. BMP Adoption Response to Changing Conditions
4.2.4. BMP Adoption and NPS Constituent Control
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- USEPA. National Water Quality Inventory: Report to Congress; US Environmental Protection Agency, Office of Water: Washington, DC, USA, 2017.
- USEPA. Nonpoint-Source Pollution: The Nation’s Largest Water Quality Problem; US Environmental Protection Agency, Office of Water: Washington, DC, USA, 1996.
- Brown, T.C.; Froemke, P. Nationwide assessment of nonpoint source threats to water quality. BioScience 2012, 62, 136–146. [Google Scholar] [CrossRef] [Green Version]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Paris, France, 18–20 September 2000; pp. 849–858. [Google Scholar]
- Dzikiewicz, M. Activities in nonpoint pollution control in rural areas of Poland. Ecol. Eng. 2000, 14, 429–434. [Google Scholar] [CrossRef]
- Hardy, S.D.; Koontz, T.M. Reducing nonpoint source pollution through collaboration: Policies and programs across the US States. Environ. Manag. 2008, 41, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Lian, Q.; Yao, L.; Uddin Ahmad, Z.; Lei, X.; Islam, F.; Zappi, M.E.; Gang, D.D. Nonpoint source pollution. Water Environ. Res. 2019, 91, 1114–1128. [Google Scholar] [CrossRef] [Green Version]
- Baker, L.A. Introduction to nonpoint source pollution in the United States and prospects for wetland use. Ecol. Eng. 1992, 1, 1–26. [Google Scholar] [CrossRef]
- McCoy, N.; Chao, B.; Gang, D.D. Nonpoint source pollution. Water Environ. Res. 2015, 87, 1576–1594. [Google Scholar] [CrossRef]
- Xepapadeas, A. The economics of non-point-source pollution. Annu. Rev. Resour. Econ. 2011, 3, 355–373. [Google Scholar] [CrossRef] [Green Version]
- Xiang, C.; Wang, Y.; Liu, H. A scientometrics review on nonpoint source pollution research. Ecol. Eng. 2017, 99, 400–408. [Google Scholar] [CrossRef]
- Guo, T.; Srivastava, A.; Flanagan, D.C.; Liu, Y.; Engel, B.A.; McIntosh, M.M. Evaluation of Costs and Efficiencies of Urban Low Impact Development (LID) Practices on Stormwater Runoff and Soil Erosion in an Urban Watershed Using the Water Erosion Prediction Project (WEPP) Model. Water 2021, 13, 2076. [Google Scholar] [CrossRef]
- Hsu, D.; Lim, T.C.; Meng, T. Rocky steps towards adaptive management and adaptive governance in implementing green infrastructure at urban scale in Philadelphia. Urban For. Urban Green. 2020, 55, 126791. [Google Scholar] [CrossRef]
- Ice, G. History of innovative best management practice development and its role in addressing water quality limited waterbodies. J. Environ. Eng. 2004, 130, 684–689. [Google Scholar] [CrossRef]
- Zhang, K.; Chui, T.F.M. A comprehensive review of spatial allocation of LID-BMP-GI practices: Strategies and optimization tools. Sci. Total Environ. 2018, 621, 915–929. [Google Scholar] [CrossRef] [PubMed]
- Martin, P. Sustainable Urban Drainage Systems: Design Manual for England and Wales; Ciria: Soria, Spain, 2000. [Google Scholar]
- Fletcher, T.D.; Shuster, W.; Hunt, W.F.; Ashley, R.; Butler, D.; Arthur, S.; Trowsdale, S.; Barraud, S.; Semadeni-Davies, A.; Bertrand-Krajewski, J.-L. SUDS, LID, BMPs, WSUD and more–The evolution and application of terminology surrounding urban drainage. Urban Water J. 2015, 12, 525–542. [Google Scholar] [CrossRef]
- Council, N.R. Urban Stormwater Management in the United States; National Academies Press: Washington, DC, USA, 2009. [Google Scholar]
- Dietz, M.E.; Clausen, J.C. A field evaluation of rain garden flow and pollutant treatment. Water Air Soil Pollut. 2005, 167, 123–138. [Google Scholar] [CrossRef]
- Ahiablame, L.M.; Engel, B.A.; Chaubey, I. Effectiveness of low impact development practices: Literature review and suggestions for future research. Water Air Soil Pollut. 2012, 223, 4253–4273. [Google Scholar] [CrossRef]
- Ahiablame, L.M.; Engel, B.A.; Chaubey, I. Effectiveness of low impact development practices in two urbanized watersheds: Retrofitting with rain barrel/cistern and porous pavement. J. Environ. Manag. 2013, 119, 151–161. [Google Scholar] [CrossRef]
- Benedict, M.A.; McMahon, E.T. Green Infrastructure: Linking Landscapes and Communities; Island Press: Washington, DC, USA, 2006. [Google Scholar]
- Coutts, C.; Hahn, M. Green infrastructure, ecosystem services, and human health. Int. J. Environ. Res. Public Health 2015, 12, 9768–9798. [Google Scholar] [CrossRef] [Green Version]
- López-Ballesteros, A.; Senent-Aparicio, J.; Srinivasan, R.; Pérez-Sánchez, J. Assessing the Impact of Best Management Practices in a Highly Anthropogenic and Ungauged Watershed Using the SWAT Model: A Case Study in the El Beal Watershed (Southeast Spain). Agronomy 2019, 9, 576. [Google Scholar] [CrossRef] [Green Version]
- Mao, X.; Jia, H.; Shaw, L.Y. Assessing the ecological benefits of aggregate LID-BMPs through modelling. Ecol. Model. 2017, 353, 139–149. [Google Scholar] [CrossRef]
- Shafique, M.; Kim, R.; Rafiq, M. Green roof benefits, opportunities and challenges—A review. Renew. Sustain. Energy Rev. 2018, 90, 757–773. [Google Scholar] [CrossRef]
- Tayouga, S.J.; Gagné, S.A. The socio-ecological factors that influence the adoption of green infrastructure. Sustainability 2016, 8, 1277. [Google Scholar] [CrossRef] [Green Version]
- Barnhill, K.; Smardon, R. Gaining ground: Green infrastructure attitudes and perceptions from stakeholders in Syracuse, New York. Environ. Pract. 2012, 14, 6–16. [Google Scholar] [CrossRef]
- Brehm, J.M.; Pasko, D.K.; Eisenhauer, B.W. Identifying key factors in homeowner’s adoption of water quality best management practices. Env. Manag. 2013, 52, 113–122. [Google Scholar] [CrossRef] [PubMed]
- Lim, T.C. An empirical study of spatial-temporal growth patterns of a voluntary residential green infrastructure program. J. Environ. Plan. Manag. 2018, 61, 1363–1382. [Google Scholar] [CrossRef]
- Lim, T.C. Revitalizing Urban Neighborhoods by Adopting Green Infrastructure: The Case of Washington DC; Virginia Tech: Blacksburg, VA, USA, 2018. [Google Scholar]
- Patra, D.; Chanse, V.; Rockler, A.; Wilson, S.; Montas, H.; Shirmohammadi, A.; Leisnham, P.T. Towards attaining green sustainability goals of cities through social transitions: Comparing stakeholders’ knowledge and perceptions between two Chesapeake Bay watersheds, USA. Sustain. Cities Soc. 2021, 75, 103318. [Google Scholar] [CrossRef]
- Maeda, P.K.; Chanse, V.; Rockler, H.; Montas, H.; Shirmohammadi, A.; Wilson, S.; Leisnham, P.T. Linking stormwater best management practices to social factors in two suburban watersheds. PLoS ONE 2018, 13, e0202638. [Google Scholar] [CrossRef] [Green Version]
- Chanse, V.; Mohammed, A.; Wilson, S.; Delamarre, L.; Rockler, A.; Leisnham, P.T.; Shirmohammadi, A.; Montas, H. New approaches to facilitate learning from youth: Exploring the use of Photovoice in identifying local watershed issues. J. Environ. Educ. 2017, 48, 109–120. [Google Scholar] [CrossRef]
- Smith, L.K.M.; Lynes, J.K.; Wolfe, S.E. Community-based social marketing-creating lasting, sustainable, environmental change: Case study of a household stormwater managment program in the resgion of Waterloo, Ontario. Soc. Mark. Q. 2019, 25, 308–326. [Google Scholar] [CrossRef]
- Hazbavi, Z.; Sadeghi, S.H.; Gholamalifard, M.; Davudirad, A.A. Watershed health assessment using the pressure–state–response (PSR) framework. Land Degrad. Dev. 2020, 31, 3–19. [Google Scholar] [CrossRef]
- Hazbavi, Z.; Sadeghi, S.H.R. Watershed health characterization using reliability–resilience–vulnerability conceptual framework based on hydrological responses. Land Degrad. Dev. 2017, 28, 1528–1537. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines; Springer: Berlin/Heidelberg, Germany, 2015; pp. 67–80. [Google Scholar]
- McDonald, G.C. Ridge regression. Wiley Interdiscip. Rev. Comput. Stat. 2009, 1, 93–100. [Google Scholar] [CrossRef]
- Ranstam, J.; Cook, J. LASSO regression. J. Br. Surg. 2018, 105, 1348. [Google Scholar] [CrossRef]
- Segal, M.R. Machine Learning Benchmarks and Random Forest Regression; eScholarship: Oakland, CA, USA, 2004. [Google Scholar]
- Leets, L.; Sprenger, A.; Hartman, R.O.; Jackson, J.H.; Britt, M.; Gulley, A.; Thomas, J.S.; Wijesinghe, S. Promoting tree equity in Washington, DC. Trees For. People 2022, 7, 100209. [Google Scholar] [CrossRef]
- Department of Energy and Environment. RiverSmart Homes. 2021. Available online: https://doee.dc.gov/service/riversmart-homes (accessed on 1 May 2022).
- Wang, Y.; Montas, H.; Leisnham, P.T.; Brubaker, K.; Shirmohammadi, A.; Chanse, V.; Rockler, A. A diagnostic decision support system for BMP selection in a small urban watershed. Water Resour. Manag. 2017, 31, 1649–1664. [Google Scholar] [CrossRef]
- Wilfong, M.; Patra, D.; Pavao-Zuckerman, M.; Leisnham, P.T. Diffusing responsibility, decentralizing infrastructure: Hydrosocial relationships within the shifting stormwater management paradigm. J. Environ. Plan. Manag. 2022, 1–22. [Google Scholar] [CrossRef]
- Wilfong, M.; Paolisso, M.; Patra, D.; Pavao-Zuckerman, M.; Leisnham, P.T. Shifting paradigms in stormwater management–hydrosocial relations and stormwater hydrocitizenship. J. Environ. Policy Plan. 2023, 25, 429–442. [Google Scholar] [CrossRef]
- Baptiste, A.K.; Foley, C.; Smardon, R. Understanding urban neighborhood differences in willingness to implement green infrastructure measures: A case study of Syracuse, NY. Landsc. Urban Plan. 2015, 136, 1–12. [Google Scholar] [CrossRef]
- Brown, H.L.; Bos, D.G.; Walsh, C.J.; Fletcher, T.D.; RossRakesh, S. More than money: How multiple factors influence householder participation in at-source stormwater management. J. Environ. Plan. Manag. 2016, 59, 79–97. [Google Scholar] [CrossRef]
- McPhillips, L.E.; Matsler, A.M. Temporal evolution of green stormwater infrastructure strategies in three US cities. Front. Built Environ. 2018, 4, 26. [Google Scholar] [CrossRef] [Green Version]
- Ando, A.W.; Freitas, L.P. Consumer demand for green stormwater management technology in an urban setting: The case of Chicago rain barrels. Water Resour. Res. 2011, 47, 12. [Google Scholar] [CrossRef]
- Grömping, U. Variable importance assessment in regression: Linear regression versus random forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
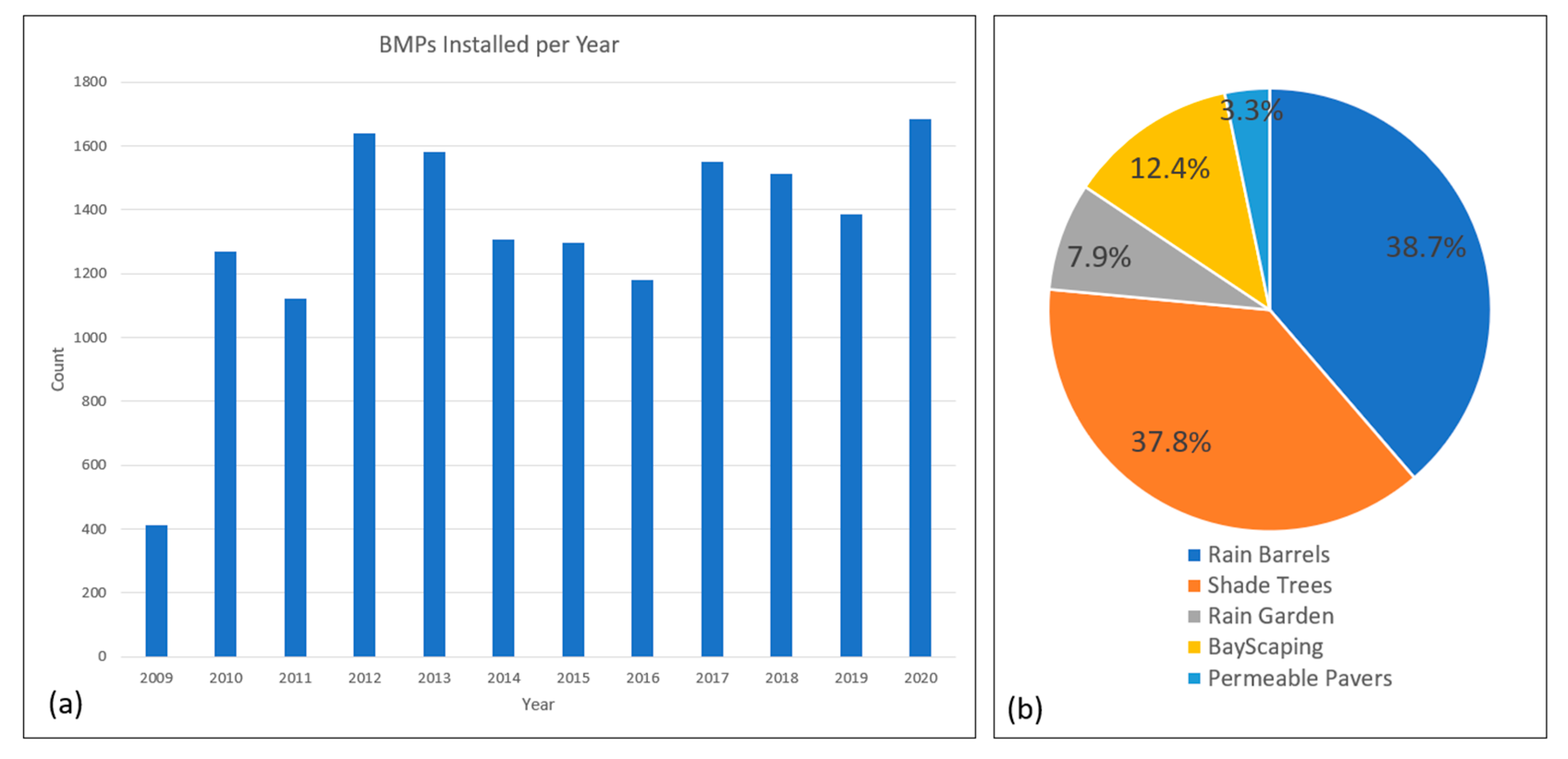

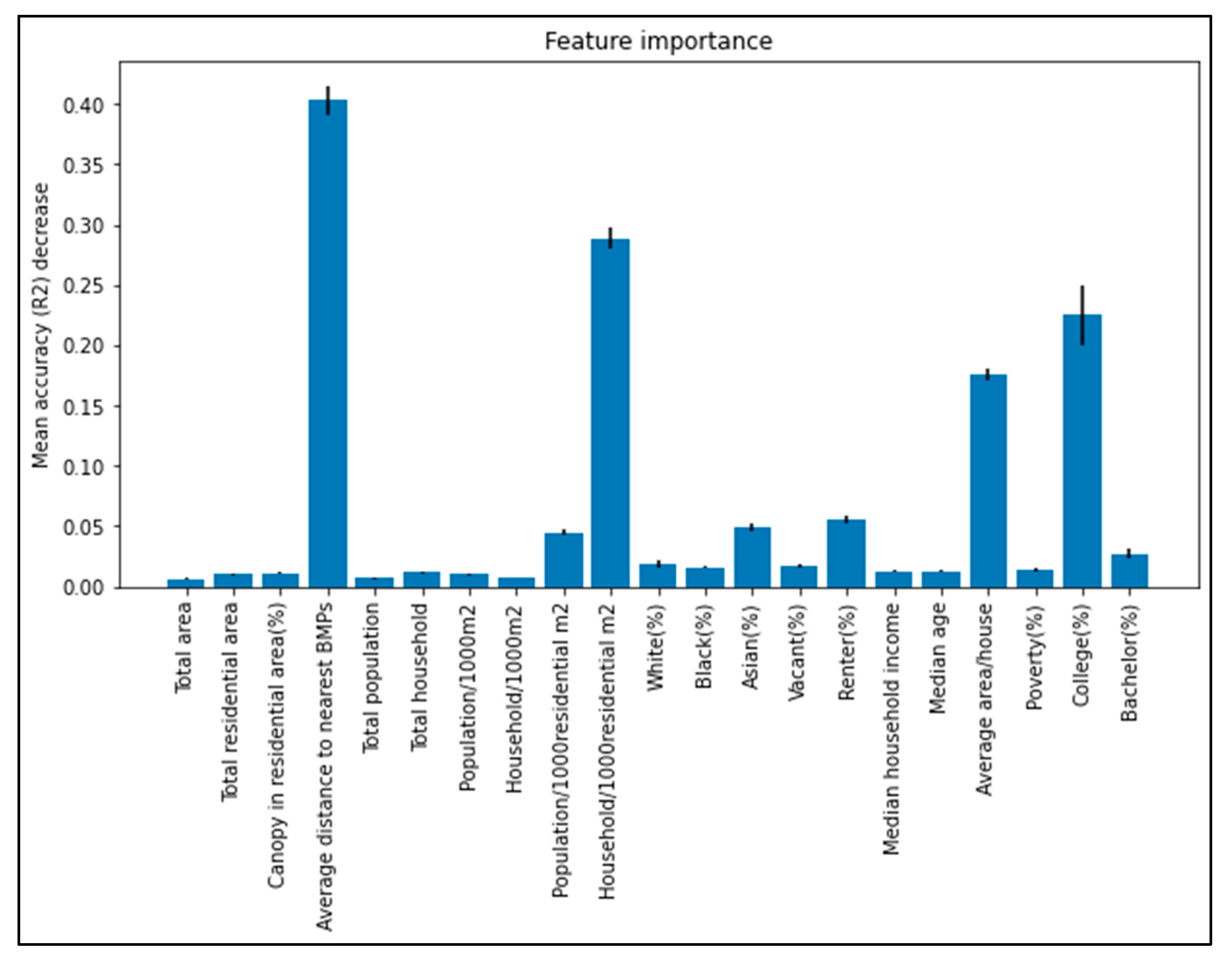

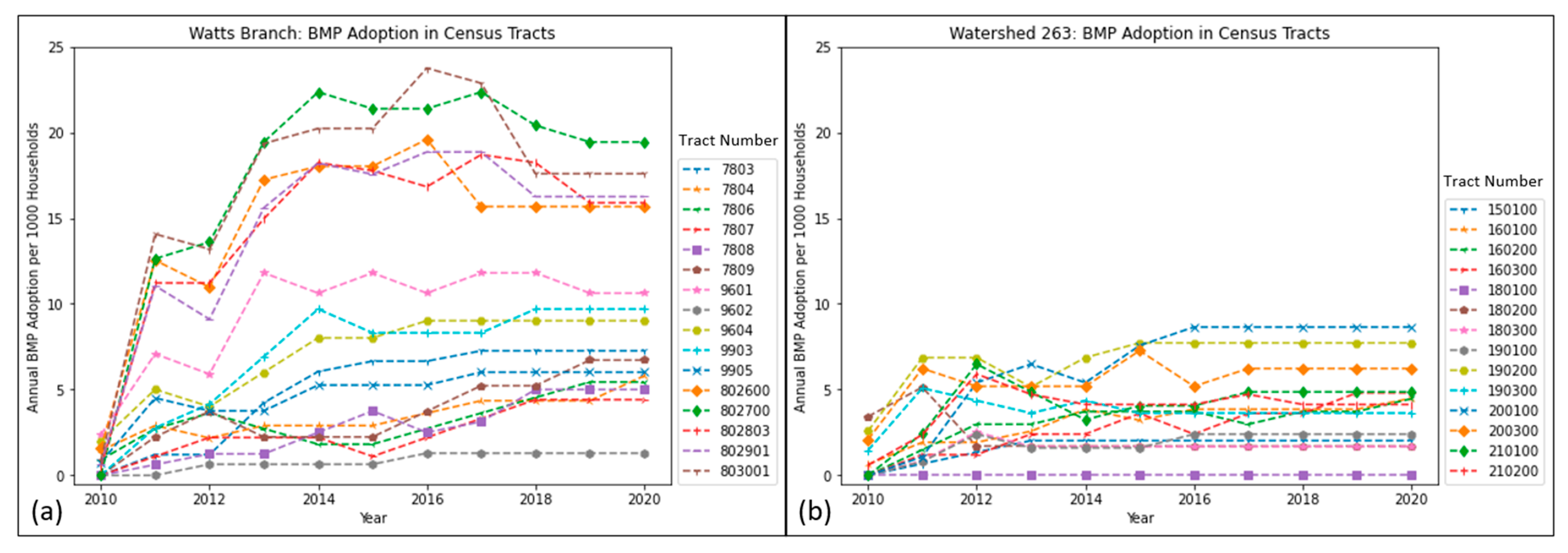


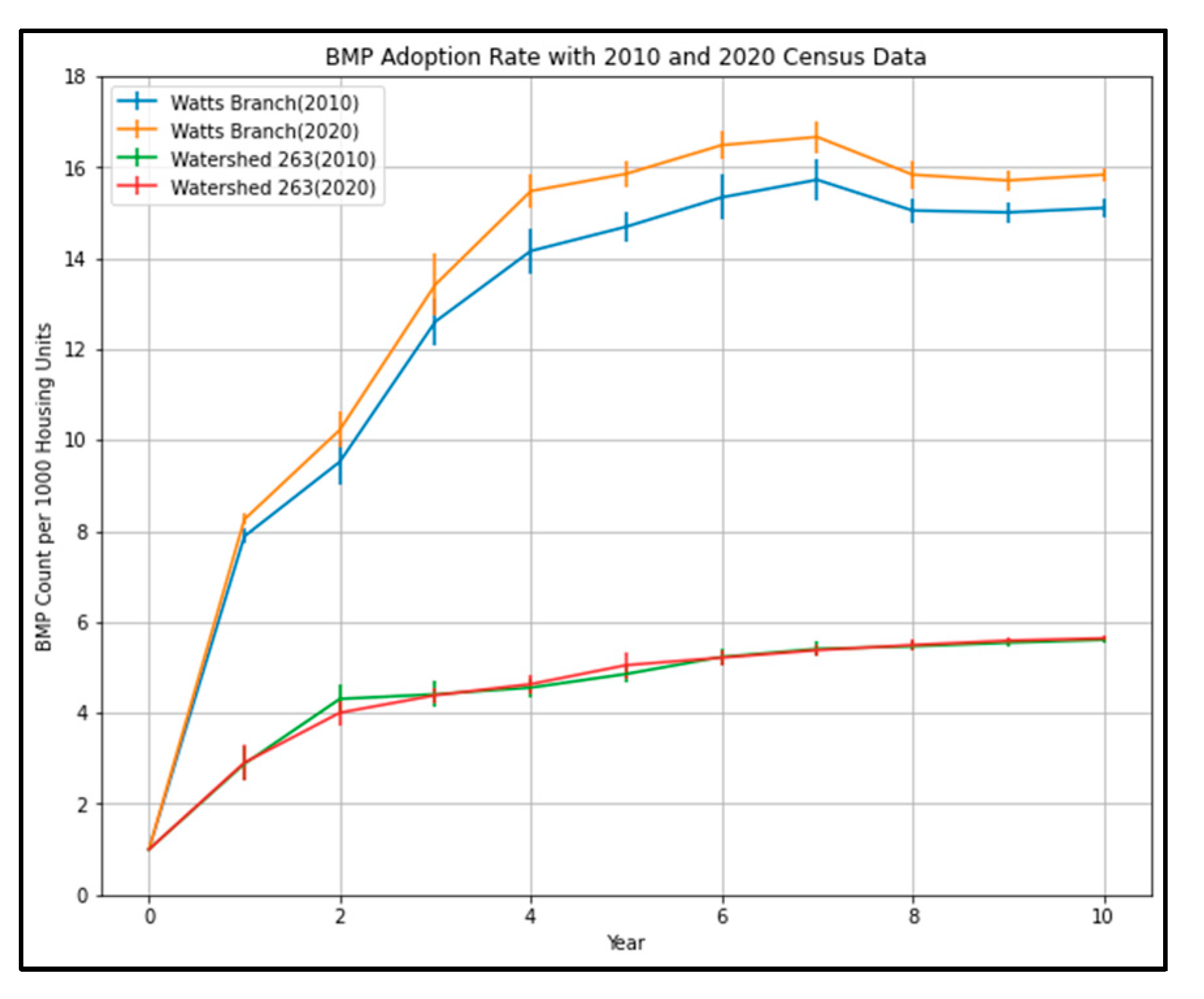
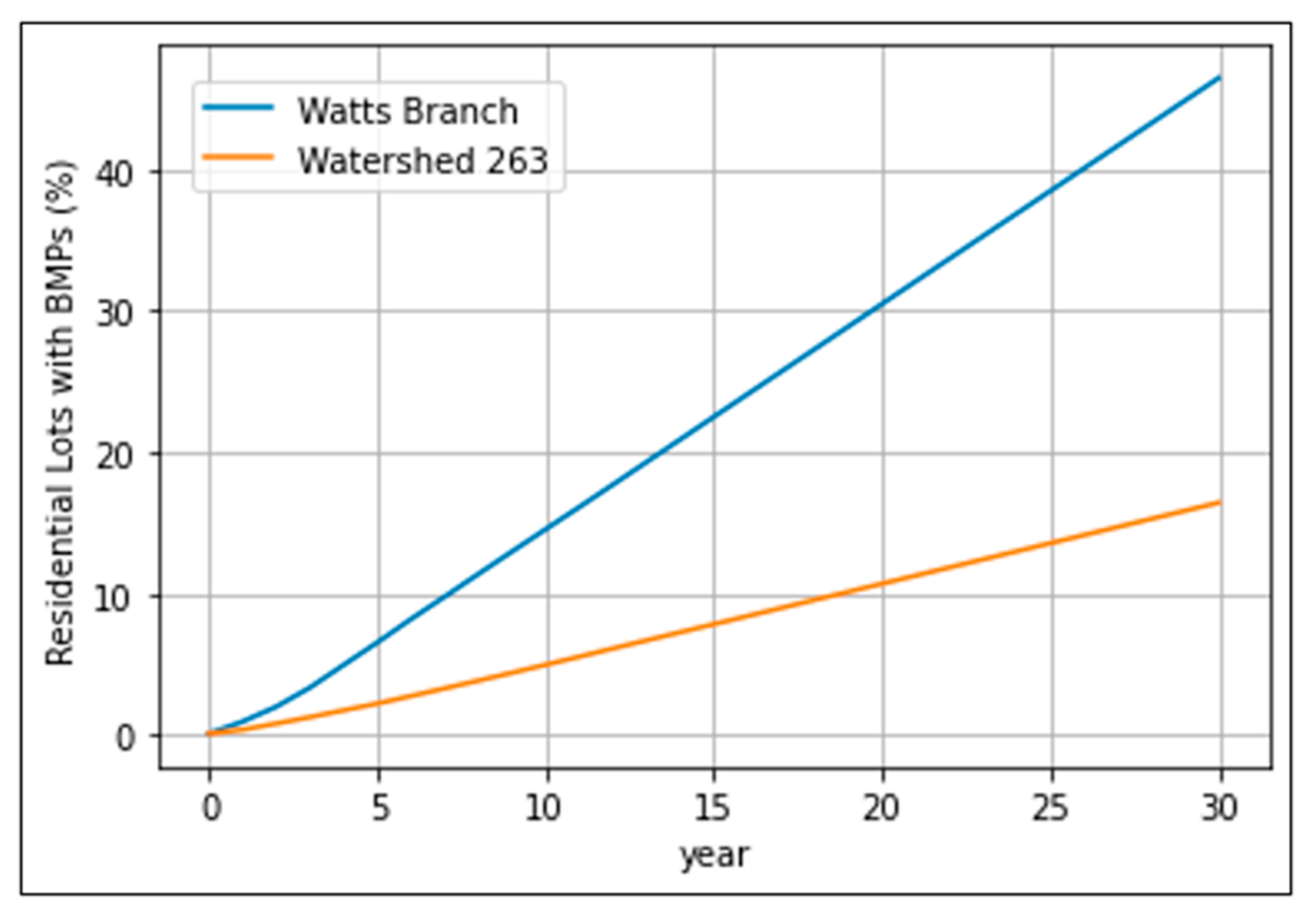

| Watts Branch | Watershed 263 | |||
|---|---|---|---|---|
| 2010 | 2020 | 2010 | 2020 | |
| Physical | ||||
| Total area (km2) | 18.81 | 7.43 | ||
| Residential area (km2) | 6.91 | 1.33 | ||
| Total residential lots | 13,327 | 11,863 | ||
| Demographic | ||||
| Total population | 48,168 | 55,002 | 30,344 | 27,594 |
| Total housing units | 20,536 | 22,021 | 16,668 | 17,054 |
| Vacant rate (%) | 11 | 10 | 30 | 33 |
| Renter rate (%) | 51 | 47 | 67 | 69 |
| Poverty rate (%) | 24 | 21 | 35 | 39 |
| College (%) | 22 | 27 | 16 | 22 |
| Bachelor’s degree (%) | 8 | 13 | 9 | 9 |
| Median household income | USD 37,176 | USD 52,798 | USD 27,125 | USD 32,362 |
| Features | Copayment | Total Costs |
|---|---|---|
| Rain barrels | USD 50 or USD 70 per rain barrel, depending on the types (limit two) | USD 150 per rain barrel |
| Shade trees | USD 0 per shade tree (no limit) | USD 50 per shade tree |
| Rain gardens | USD 100 per 50 sq. ft. (USD 21/m2) (limit two) | USD 86/m2 |
| BayScaping (Native Landscaping) | USD 100 per 120 sq. ft. (USD 8.96/m2) (limit two) | USD 13/m2 |
| Permeable pavers | USD 10/sq. ft. (USD107/m2) for replacing impervious surface with permeable pavers and/or USD 5/sq. ft. (USD 53.82/m2) for removing and replacing impervious surface with vegetation; limit of USD 4000. | USD 128/m2 or USD 60/m2 |
| Mean | Median | Std | Min | Max | |
|---|---|---|---|---|---|
| Physical features | |||||
| Total area (m2) | 988,714 | 601,065 | 1,338,461 | 171,894 | 11,417,542 |
| Total residential area (m2) | 234,567 | 165,268 | 228,058 | 0 | 1,392,595 |
| Percentage of canopy in residential area (%) | 29.44 | 26.96 | 9.16 | 0 | 47.71 |
| Average distance to nearest BMPs (m) | 275 | 154 | 298 | 0 | 2845 |
| Demographic features | |||||
| Total population | 3362 | 3072 | 1301 | 33 | 7436 |
| Total household | 1658 | 1507 | 807 | 2 | 5375 |
| Population/1000 m2 | 6 | 5 | 4 | 0 | 26 |
| Household/1000 m2 | 3 | 3 | 3 | 0 | 17 |
| Population/1000 residential m2 | 34 | 17 | 75 | 0 | 732 |
| Household/1000 residential m2 | 15 | 8 | 25 | 0 | 196 |
| Percentage of White (%) | 34.69 | 25.56 | 32.04 | 0.3 | 90.88 |
| Percentage of Black (%) | 55.4 | 60.24 | 35.38 | 2.15 | 98.35 |
| Percentage of Asian (%) | 3.16 | 2.1 | 3.44 | 0 | 21.27 |
| Vacant rate (%) | 10.15 | 9.29 | 4.79 | 0 | 27.78 |
| Renter rate (%) | 55.2 | 58.24 | 23.24 | 0 | 98.05 |
| Median household income (USD) | 47,433 | 37,400 | 25,810 | 12,202 | 166,298 |
| Median age | 35 | 35 | 7 | 20 | 63 |
| Average area per house (m2) | 172.59 | 124.27 | 234.91 | 0 | 2676.01 |
| Poverty rate (%) | 14.15 | 8.5 | 14.34 | 0 | 58.1 |
| College degree rate (%) | 18.52 | 18.34 | 8.79 | 0 | 42.86 |
| Bachelor’s degree rate (%) | 20 | 20.15 | 11 | 1 | 48.34 |
| BMPs adoptions from 2010 to 2019 | 77 | 41 | 107 | 0 | 619 |
| Coefficient | Standard Error of Coefficient | t | p > |t| | |
|---|---|---|---|---|
| Physical | ||||
| Total area (m2) | −2.26 × 10−6 | 5.29 × 10−7 | −4.266 | 0 |
| Total residential area (m2) | 4.89 × 10−6 | 2.44 × 10−6 | 2.006 | 0.045 |
| Percentage of canopy in residential area | 0.117 | 0.033 | 3.547 | 0 |
| Average distance to nearest BMPs (m) | −0.0037 | 0.001 | −6.054 | 0 |
| Demographic | ||||
| Total population | −0.0004 | 0 | −0.878 | 0.38 |
| Total household | 0.0003 | 0.001 | 0.333 | 0.739 |
| Population/1000 m2 | −0.6524 | 0.223 | −2.921 | 0.004 |
| Household/1000 m2 | 0.438 | 0.362 | 1.21 | 0.227 |
| Population/1000 residential m2 | 0.1788 | 0.069 | 2.605 | 0.009 |
| Household/1000 residential m2 | −0.1433 | 0.093 | −1.532 | 0.126 |
| Percentage of White | −0.0647 | 0.045 | −1.442 | 0.149 |
| Percentage of Black | −0.1077 | 0.037 | −2.903 | 0.004 |
| Percentage of Asian | −0.1403 | 0.101 | −1.387 | 0.166 |
| Vacant rate | −0.0422 | 0.037 | −1.137 | 0.256 |
| Renter rate | −0.1316 | 0.012 | −11.23 | 0 |
| Median household income (USD) | −0.0002 | 1.97 × 10−5 | −9.474 | 0 |
| Median age | 0.0431 | 0.044 | 0.987 | 0.324 |
| Average area per house | 0.0305 | 0.003 | 9.036 | 0 |
| Poverty rate | −0.0264 | 0.018 | −1.483 | 0.138 |
| College degree rate | −0.041 | 0.028 | −1.474 | 0.141 |
| Bachelor’s degree rate | 0.0442 | 0.028 | 1.557 | 0.12 |
| Const | 23.854 | 4.783 | 4.988 | 0 |
| Coefficient | Standard Error of Coefficient | t | p > |t| | |
|---|---|---|---|---|
| Physical | ||||
| Total area (m2) | −1.86 × 10−6 | 3.78 × 10−7 | −4.916 | 0.000 |
| Percentage of canopy in residential area | 0.1376 | 0.029 | 4.785 | 0.000 |
| Average distance to nearest BMPs (m) | −0.0038 | 0.001 | −6.456 | 0.000 |
| Demographic | ||||
| Population/1000 m2 | −0.3351 | 0.056 | −5.982 | 0.000 |
| Population/1000 residential m2 | 0.0643 | 0.012 | 5.269 | 0.000 |
| Percentage of Black | −0.0740 | 0.009 | −7.996 | 0.000 |
| Renter rate | −0.1548 | 0.009 | −17.373 | 0.000 |
| Median household income (USD) | −0.0002 | 1.36 × 10−5 | −14.482 | 0.000 |
| Average area per house | −0.0336 | 0.002 | −14.719 | 0.000 |
| Const | 21.057 | 1.541 | 13.665 | 0.000 |
| Methods | |||
|---|---|---|---|
| Linear regression | 0.51 | −1.88 | 28.09 |
| Linear regression with features (p < 0.05) | 0.52 | −1.22 | 27.50 |
| LASSO regression | 0.52 | −0.62 | 27.84 |
| Ridge regression | 0.51 | −1.87 | 28.09 |
| Support vector regression | 0.13 | −8.05 | 50.68 |
| Random forest regression | 0.67 | −7.24 | 19.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Montas, H.; Shirmohammadi, A.; Leisnham, P.T.; Rockler, A.K. Modeling Spatio-Temporal Dynamics of BMPs Adoption for Stormwater Management in Urban Areas. Water 2023, 15, 2549. https://doi.org/10.3390/w15142549
Zhang Z, Montas H, Shirmohammadi A, Leisnham PT, Rockler AK. Modeling Spatio-Temporal Dynamics of BMPs Adoption for Stormwater Management in Urban Areas. Water. 2023; 15(14):2549. https://doi.org/10.3390/w15142549
Chicago/Turabian StyleZhang, Zeshu, Hubert Montas, Adel Shirmohammadi, Paul T. Leisnham, and Amanda K. Rockler. 2023. "Modeling Spatio-Temporal Dynamics of BMPs Adoption for Stormwater Management in Urban Areas" Water 15, no. 14: 2549. https://doi.org/10.3390/w15142549






