Optimizing Solution in Decision Supporting System for River Basin Management Consisting of a Reservoir System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
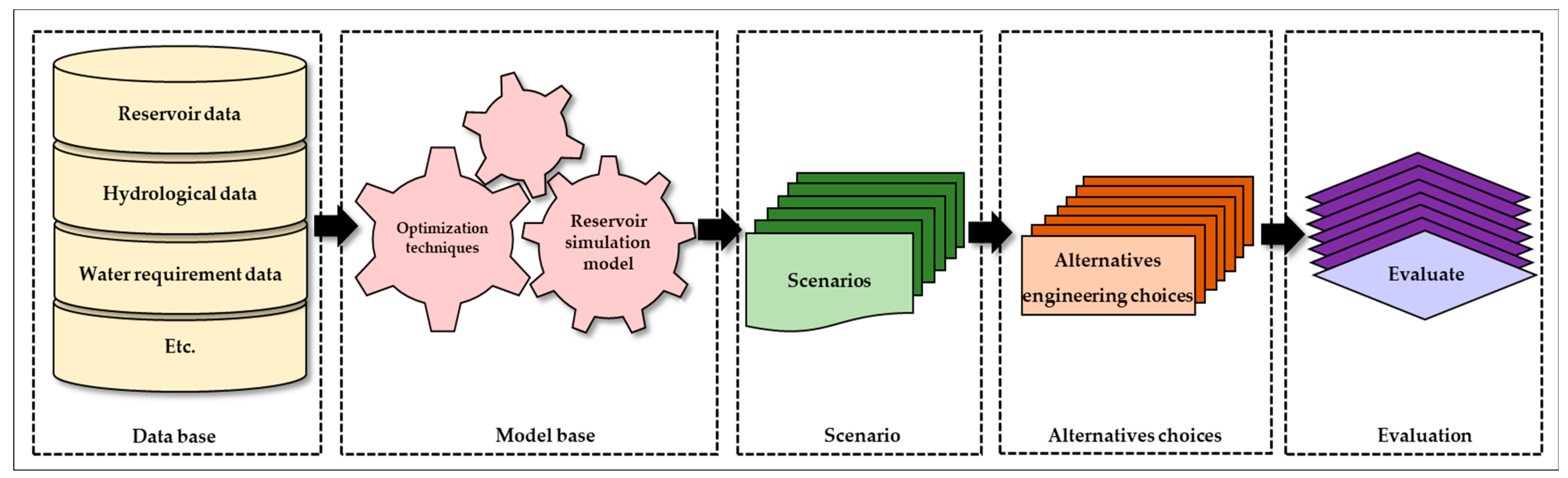
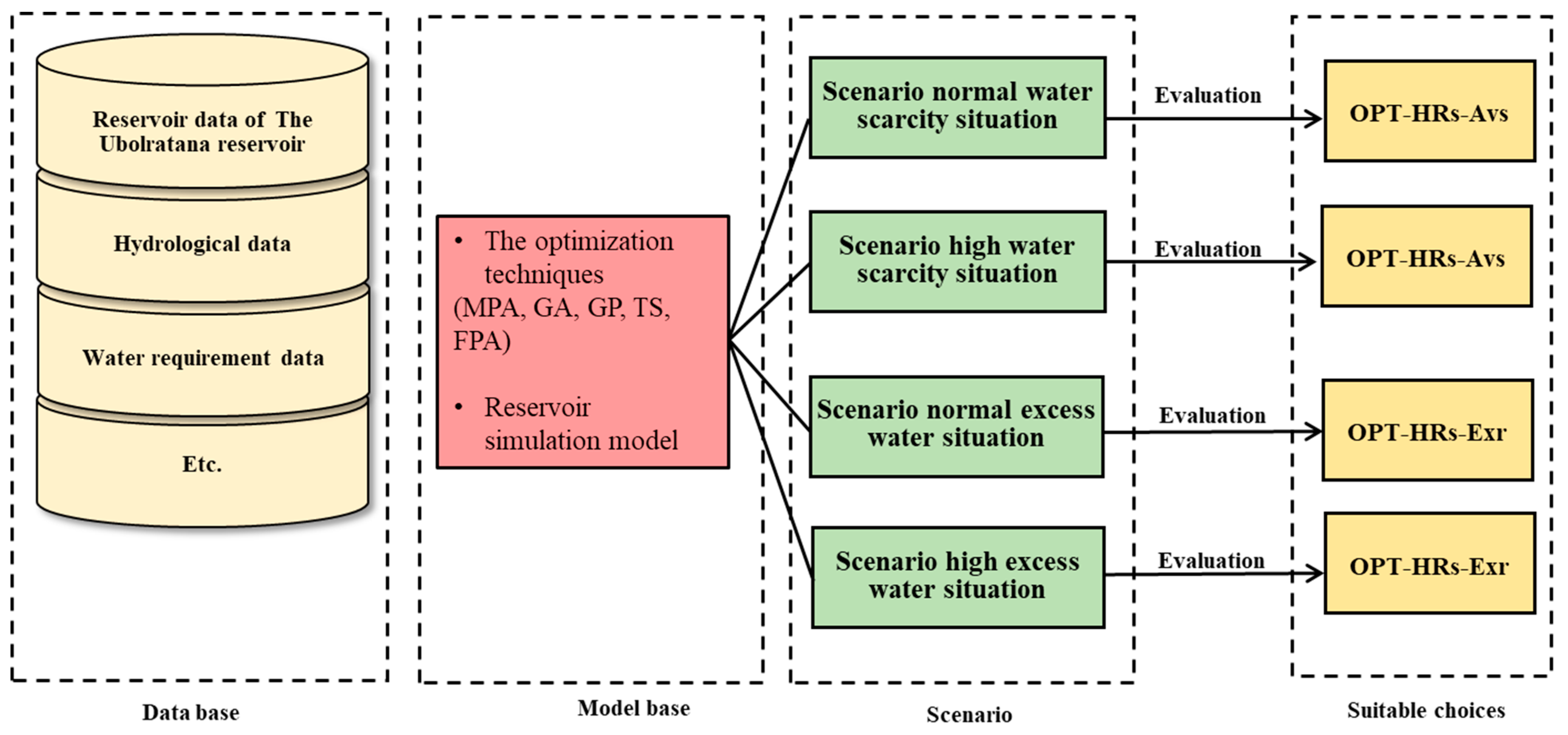
2.2. The Conceptual Model of DSS for a Single Reservoir Operation in a Basin
2.2.1. Data Base
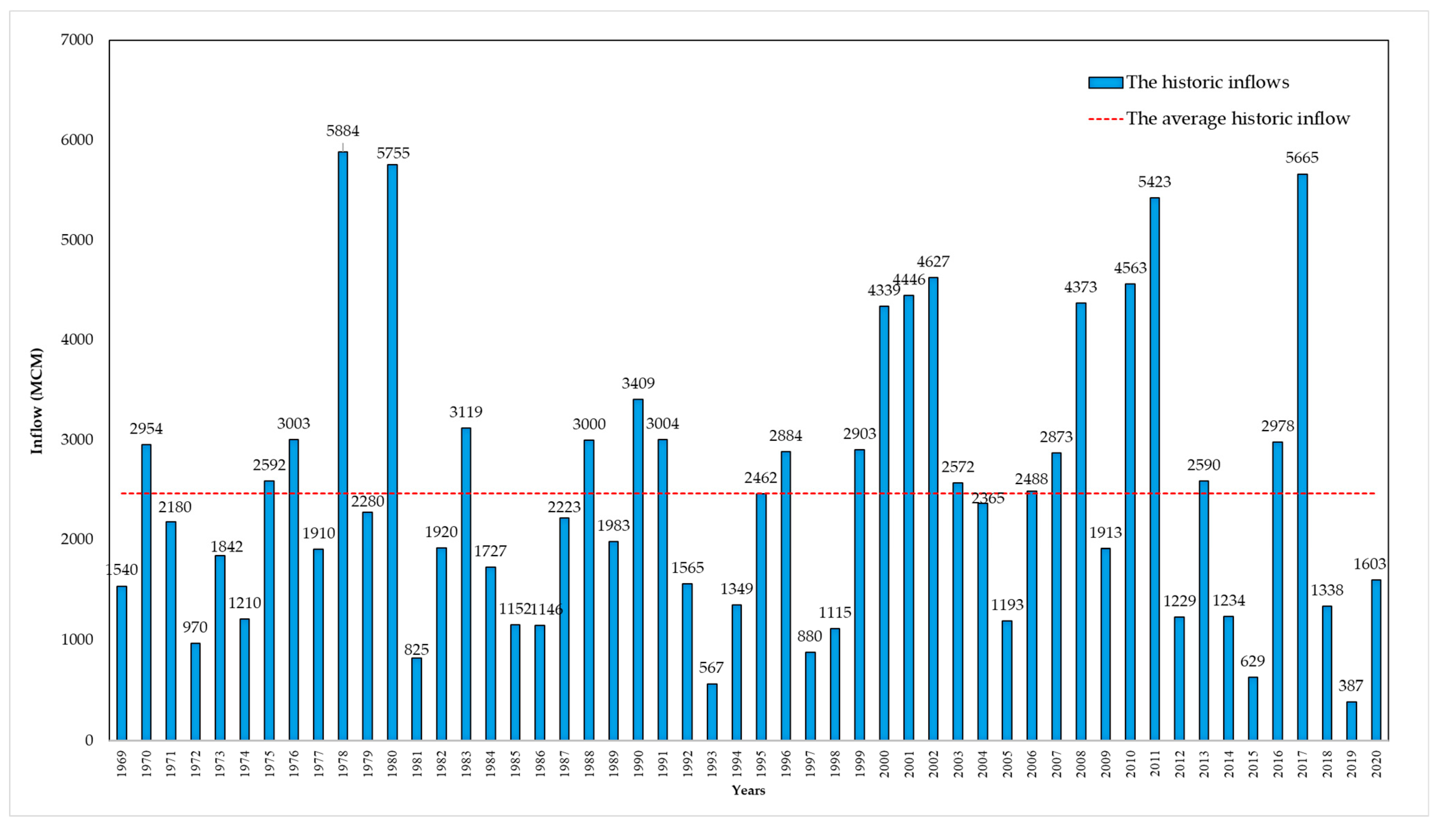
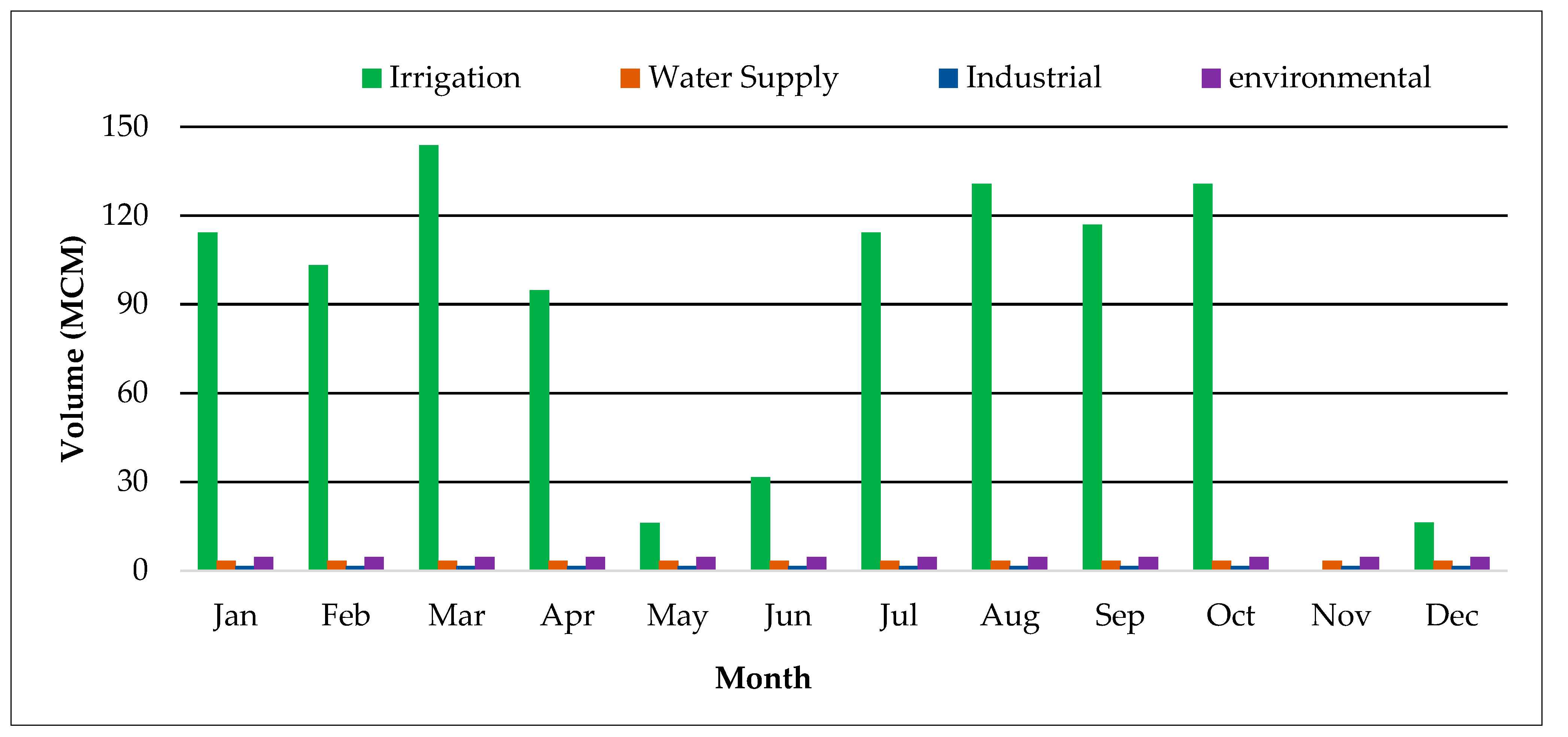
- Inflow data and water demands
- Sediment load assessment at Ubolratana Reservoir
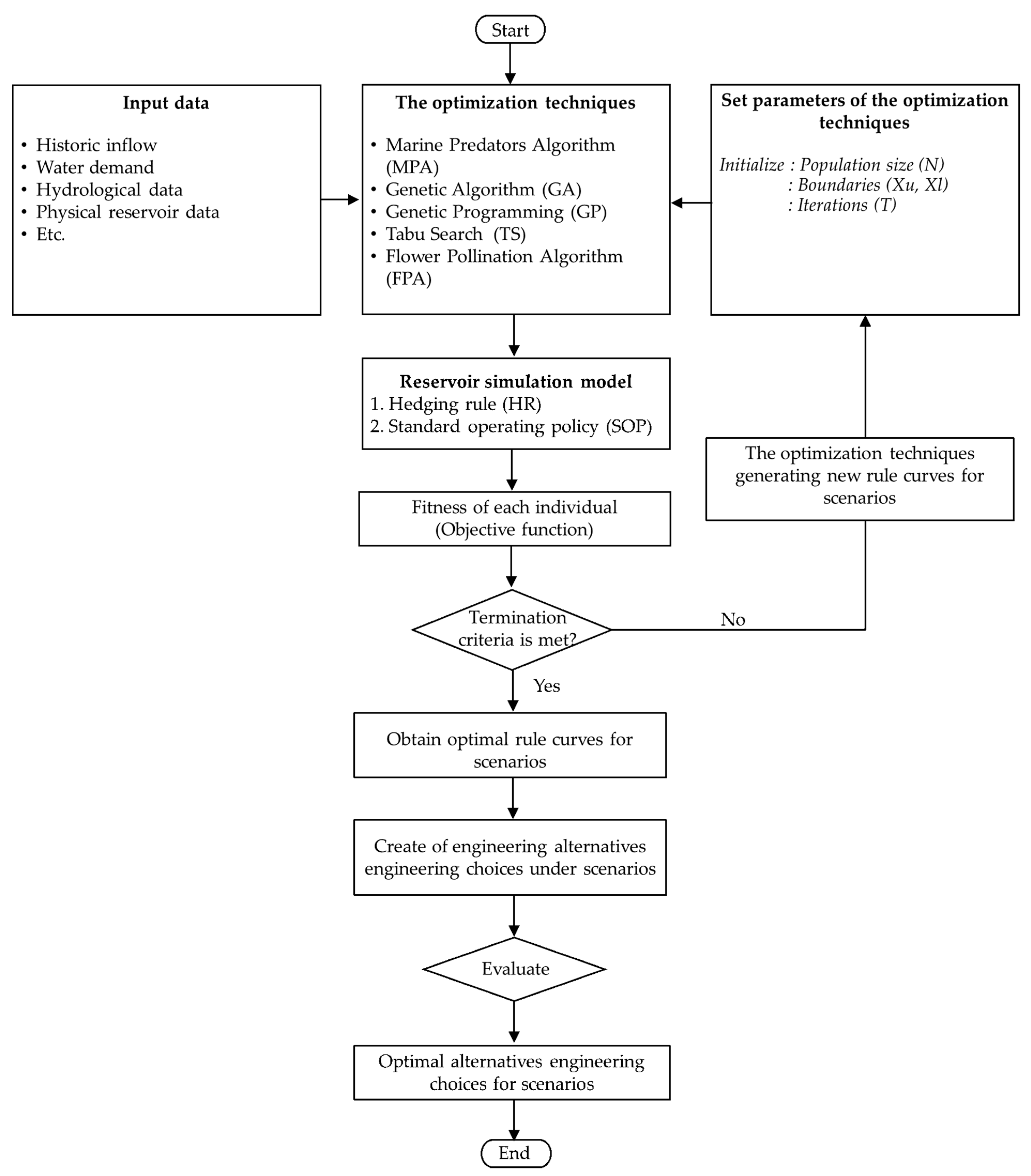
2.2.2. Model Bases
- Reservoir simulation model
- = the available water during a month τ;
- = the stored water at the end of a month τ − 1;
- = the inflow to the reservoir during a month τ;
- = the average value of the evaporation loss during s month τ.

- Optimization techniques
- H(avr) = the minimal average water shortage per year;
- P(avr) = the minimal average excess water per year;
- Shv = the water shortage during the year v (year in which releases are less than the target demand);
- Spv = the excess released water during the year v (year in which releases are more than the target demand);
- n = the whole magnitude of the examined years.
2.2.3. Scenarios to Consider
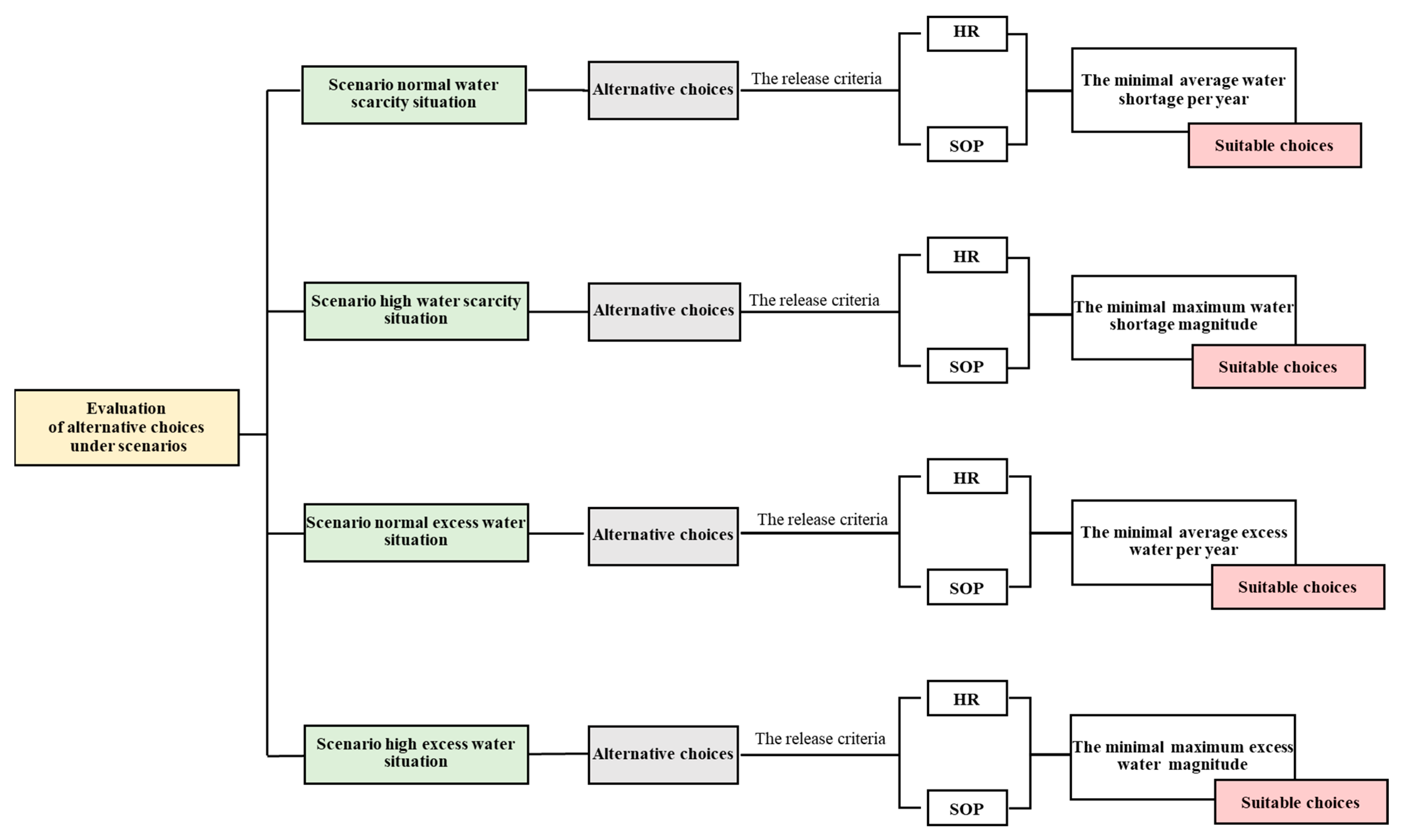
2.2.4. Alternative Evaluation
3. Results and Discussion
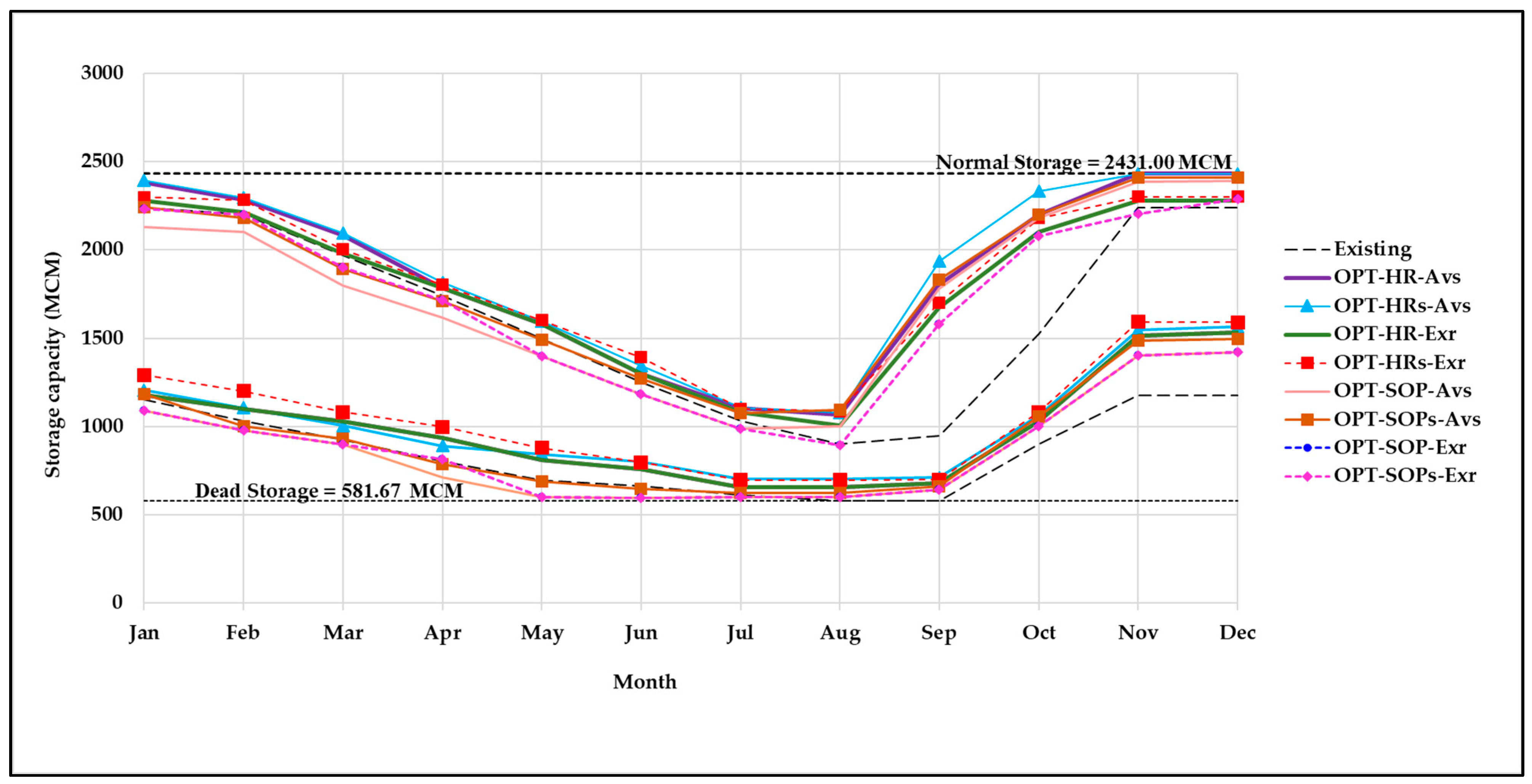
3.1. The Alternative Engineering Choice of Each Scenario
3.2. The Suitable Alternative Engineering Choices
3.2.1. Scenario of Normal Water Scarcity Situation
3.2.2. Scenario of the High Water Shortage Situation
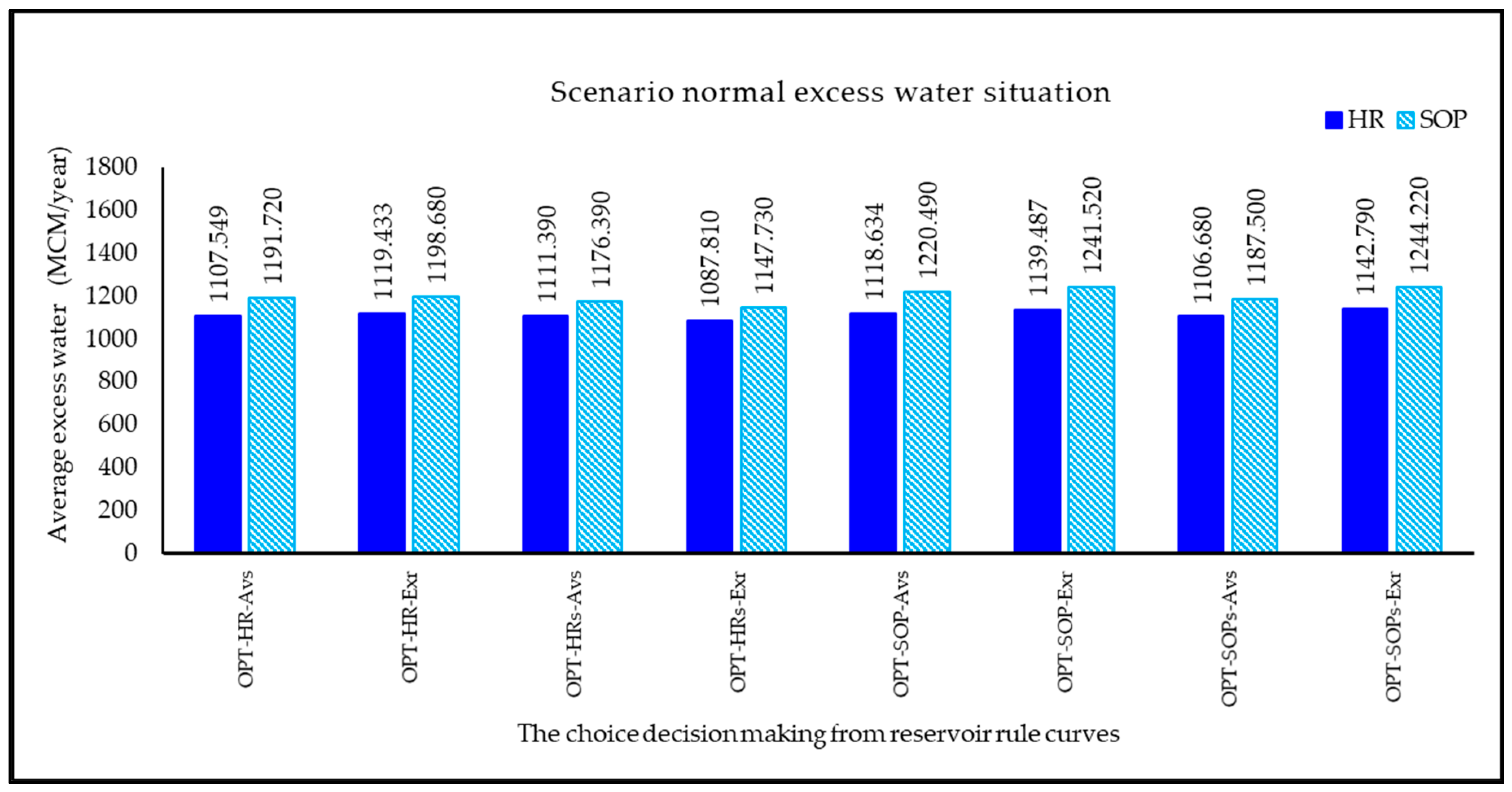
3.2.3. Scenario of Normal Excess Water Situation
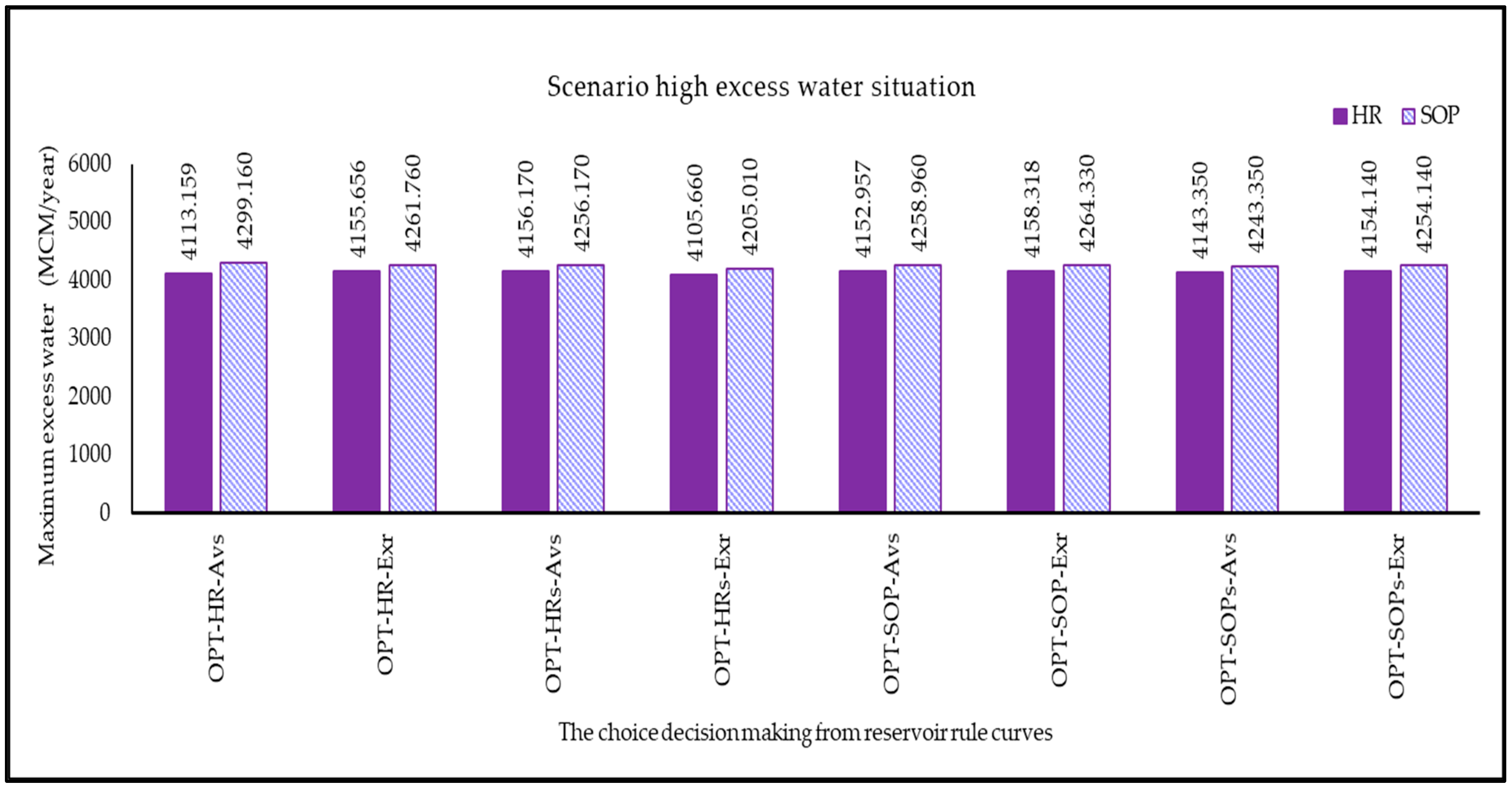
3.2.4. Scenario of High Excess Water Situation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Unnisa, Z.; Govind, A.; Lasserre, B.; Marchetti, M. Water Balance Trends along Climatic Variations in the Mediterranean Basin over the Past Decades. Water 2023, 15, 1889. [Google Scholar] [CrossRef]
- Sambou, M.H.A.; Liersch, S.; Koch, H.; Vissin, E.W.; Albergel, J.; Sane, M.L. Synergies and Trade-Offs in Water Resources Management in the Bafing Watershed under Climate Change. Water 2023, 15, 2067. [Google Scholar] [CrossRef]
- Kangrang, A.; Prasanchum, H.; Hormwichian, H.; Ngamsert, R.; Techarungruengsakul, R.; Phookinghin, N. Improvement of Water Management Project by Correcting Irrigation Water Requirement in Farmer Participation and Optimization. Bulg. J. Agric. Sci. 2019, 25, 852–863. [Google Scholar]
- Li, L.; Yang, Y.; Cui, T.; Li, R.; Zheng, H. Land Use, Climate, and Socioeconomic Factors Determine the Variation in Hydrologic-Related Ecosystem Services in the Ecological Conservation Zone, Beijing, China. Water 2023, 15, 2022. [Google Scholar] [CrossRef]
- Aliyari, H.; Kholghi, M.; Zahedi, S.; Momeni, M. Providing Decision Support System in Groundwater Resources Management for the Purpose of Sustainable Development. J. Water Supply Res. Technol. Aqua 2018, 67, 423–437. [Google Scholar] [CrossRef]
- Amorim, S.; Bezerra, J.M.B.; Marques, S.d.T.M.; Silva, M.M. Multicriteria Decision Support for Selection of Alternatives Directed to Integrated Urban Water Management. Water Resour. Manag. 2020, 34, 4253–4269. [Google Scholar] [CrossRef]
- Shahryar, K.A.; Faisal, H. A Web-Based Decision Support System for Smart Dam Operations Using Weather Forecasts. J. Hydroinform. 2019, 21, 687–707. [Google Scholar]
- Kojiri, T.; Hamaguchi, T.; Ode, M. Assessment of Global Warming Impacts on Water Resources and Ecology of a River Basin in Japan. J. Hydro-Environ. Res. 2008, 1, 164–175. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, S.; Huang, Q.; Wang, H.; Fang, W.; Yang, Y.; Wang, L. Assessing Socioeconomic Drought Based on an Improved Multivariate Standardized Reliability and Resilience Index. J. Hydrol. 2019, 568, 904–918. [Google Scholar] [CrossRef]
- Mehran, A.; Mazdiyasni, O.; AghaKouchak, A. A Hybrid Framework for Assessing Socioeconomic Drought: Linking Climate Variability, Local Resilience, and Demand. J. Geophys. Res. Atmos. 2015, 120, 7520–7533. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S. Incorporating Ecological Requirement into Multipurpose Reservoir Operating Rule Curves for Adaptation to Climate Change. J. Hydrol. 2013, 498, 153–164. [Google Scholar] [CrossRef] [Green Version]
- Zhao, G.; Gao, H.; Naz, B.S.; Kao, S.C.; Voisin, N. Integrating a Reservoir Regulation Scheme into a Spatially Distributed Hydrological Model. Adv. Water Resour. 2016, 98, 16–31. [Google Scholar] [CrossRef] [Green Version]
- Daus, M.; Koberger, K.; Koca, K.; Beckers, F.; Encinas Fernández, J.; Weisbrod, B.; Dietrich, D.; Gerbersdorf, S.U.; Glaser, R.; Haun, S.; et al. Interdisciplinary Reservoir Management—A Tool for Sustainable Water Resources Management. Sustainability 2021, 13, 4498. [Google Scholar] [CrossRef]
- Zhu, Y.; Lin, Z.; Wang, J.; Zhao, Y.; He, F. Impacts of Climate Changes on Water Resources in Yellow River Basin, China. Procedia Eng. 2016, 154, 687–695. [Google Scholar] [CrossRef] [Green Version]
- Mensik, P.; Marton, D. Hybrid Optimization Method for Strategic Control of Water Withdrawal from Water Reservoir with Using Support Vector Machines. Procedia Eng. 2017, 186, 491–498. [Google Scholar] [CrossRef]
- Chaleeraktrakoon, C.; Kangrang, A. Dynamic Programming with the Principle of Progressive Optimality for Searching Rule Curves. Can. J. Civ. Eng. 2007, 34, 170–176. [Google Scholar] [CrossRef]
- Chiamsathit, C.; Adeloye, A.J.; Soundharajan, B.S. Assessing Competing Policies at Ubonratana Reservoir, Thailand. Proc. Inst. Civ. Eng. Water Manag. 2014, 167, 551–560. [Google Scholar] [CrossRef]
- Zhao, T.; Zhao, J. Optimizing Operation of Water Supply Reservoir: The Role of Constraints. Math. Probl. Eng. 2014, 2014, 853186. [Google Scholar] [CrossRef] [Green Version]
- Heydari, M.; Othman, F.; Qaderi, K. Developing Optimal Reservoir Operation for Multiple and Multipurpose Reservoirs Using Mathematical Programming. Math. Probl. Eng. 2015, 2015, 435752. [Google Scholar] [CrossRef] [Green Version]
- Sasireka, K.; Neelakantan, T.R. Optimization of Hedging Rules for Hydropower Reservoir Operation. Sci. Iran. 2017, 24, 2242–2252. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Zhao, J.; Zheng, H. Piecewise-Linear Hedging Rules for Reservoir Operation with Economic and Ecologic Objectives. Water 2018, 10, 865. [Google Scholar] [CrossRef] [Green Version]
- Jamshidi, J.; Shourian, M. Hedging Rules-Based Optimal Reservoir Operation Using Bat Algorithm. Water Resour. Manag. 2019, 33, 4525–4538. [Google Scholar] [CrossRef]
- Men, B.; Wu, Z.; Li, Y.; Liu, H. Reservoir Operation Policy Based on Joint Hedging Rules. Water 2019, 11, 419. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Huang, B.; Yang, Z.; Qiu, J.; Zhao, B.; Cai, Y. Mitigating Drought Conditions under Climate and Land Use Changes by Applying Hedging Rules for the Multi-Reservoir System. Water 2021, 13, 21. [Google Scholar] [CrossRef]
- Pessenlehner, S.; Liedermann, M.; Holzapfel, P.; Skrame, K.; Habersack, H.; Hauer, C. Evaluation of Hydropower Projects in Balkan Rivers Based on Direct Sediment Transport Measurements: Challenges, Limits, and Possible Data Interpretation—Case Study Vjosa River/Albania. River Res. Appl. 2022, 38, 1014–1030. [Google Scholar] [CrossRef]
- Mat Desa, S.; Jamal, M.H.; Mohd, M.S.F.; Samion, M.K.H.; Rahim, N.S.; Muda, R.S.; Sa’ari, R.; Kasiman, E.H.; Mustaffar, M.; Ishak, D.S.M.; et al. Numerical Modelling on Physical Model of Ringlet Reservoir, Cameron Highland, Malaysia: How Flow Conditions Affect the Hydrodynamics. Water 2023, 15, 1883. [Google Scholar] [CrossRef]
- Imanshoar, F.; Jahangirzadeh, A.; Basser, H.; Akib, S.; Kamali, B.; Tabatabaei, M.R.; Kakouei, M. Reservoir Sedimentation Based on Uncertainty Analysis. Abstr. Appl. Anal. 2014, 2014, 367627. [Google Scholar] [CrossRef] [Green Version]
- Viseras, C.; Fernández, J.; García-García, F.; Soria, J.M.; Calvache, M.L.; Jáuregui, P. Dynamics of Sedimentary Environments in the Accelerated Siltation of a Reservoir: The Case of Alhama de Granada, Southern Spain. Environ. Geol. 2009, 56, 1353–1369. [Google Scholar] [CrossRef]
- Weiming, W.; Wang, S.Y.; Yafei, J. Nonuniform Sediment Transport in Alluvial Rivers. J. Hydraul. Res. 2000, 38, 427–434. [Google Scholar]
- Ahmed, K.B.; Sanchez, M. A Study of the Factors and Processes Involved in the Sedimentation of Tarbela Reservoir, Pakistan. Environ. Earth Sci. 2011, 62, 927–933. [Google Scholar] [CrossRef]
- Chao, Y.C.; Hsieh, T.-C.; Chen, C.-W.; Cheng, C.-T.; Li, H.-C.; Yeh, K.-C.; Chen, Y.-M. Impact Assessment of Reservoir Desiltation Measures for Downstream Riverbed Migration in Climate Change: A Case Study in Northern Taiwan. J. Hydro-Environ. Res. 2021, 37, 67–81. [Google Scholar] [CrossRef]
- Iradukunda, P.; Nyadawa, M.O. Impact of Sedimentation on Water Seepage Capacity in Lake Nakuru, Kenya. Appl. Environ. Soil Sci. 2021, 2021, 8889189. [Google Scholar] [CrossRef]
- Jain, S.K.; Goel, M.K.; Agarwal, P.K. Reservoir Operation Studies of Sabarmati System, India. J. Water Resour. Plan. Manag. 1998, 124, 31–37. [Google Scholar] [CrossRef]
- Chaleeraktrakoon, C.; Chinsomboon, Y. Dynamic Rule Curves for Flood Control of a Multipurpose Dam. J. Hydro-Environ. Res. 2015, 9, 133–144. [Google Scholar] [CrossRef]
- Chaleeraktrakoon, C.; Worawiwat, A. Dynamic Rule Curves for Multipurpose Reservoir Operation for Different Floods. J. Water Clim. Chang. 2020, 11, 1001–1008. [Google Scholar] [CrossRef]
- Tayebiyan, A.; Mohammed Ali, T.A.; Ghazali, A.H.; Malek, M.A. Optimization of Exclusive Release Policies for Hydropower Reservoir Operation by Using Genetic Algorithm. Water Resour. Manag. 2016, 30, 1203–1216. [Google Scholar] [CrossRef]
- Ngoc, T.A.; Hiramatsu, K.; Harada, M. Optimizing the Rule Curves of Multi-Use Reservoir Operation Using a Genetic Algorithm with a Penalty Strategy. Paddy Water Environ. 2014, 12, 125–137. [Google Scholar] [CrossRef]
- Ashofteh, P.S.; Bozorg Haddad, O.; Akbari-Alashti, H.; Mariño, M.A. Determination of Irrigation Allocation Policy under Climate Change by Genetic Programming. J. Hydrol. Eng. 2014, 141, 04014059. [Google Scholar] [CrossRef] [Green Version]
- Moeini, R.; Nasiri, K. Hybridizing ANN-NSGA-II Model with Genetic Programming Method for Reservoir Operation Rule Curve Determination (Case Study Zayandehroud Dam Reservoir). Soft Comput. 2021, 25, 14081–14108. [Google Scholar] [CrossRef]
- Thongwan, T.; Kangrang, A.; Prasanchum, H. Multi-Objective Future Rule Curves Using Conditional Tabu Search Algorithm and Conditional Genetic Algorithm for Reservoir Operation. Heliyon 2019, 5, e02401. [Google Scholar] [CrossRef]
- Techarungruengsakul, R.; Kangrang, A. Application of Harris Hawks Optimization with Reservoir Simulation Model Considering Hedging Rule for Network Reservoir System. Sustainability 2022, 14, 4913. [Google Scholar] [CrossRef]
- Kangrang, A.; Techarungruengsakul, R.; Hormwichian, R.; Sriwanpheng, O. Alternative Approach of Wind Driven Optimization for Flood Control Rule Curves. J. Eng. Appl. Sci. 2019, 14, 8026–8033. [Google Scholar] [CrossRef] [Green Version]
- Kangrang, A.; Srikamol, N.; Hormwichia, R.; Prasanchum, H.; Sriwanphen, O. Alternative Approach of Firefly Algorithm for Flood Control Rule Curves. Asian J. Sci. Res. 2019, 12, 431–439. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Saber, S.; Askar, S.S.; Abouhawwash, M. Modified Flower Pollination Algorithm for Global Optimization. Mathematics 2021, 9, 1661. [Google Scholar] [CrossRef]
- Bozorg-Haddad, O.; Azad, M.; Fallah-Mehdipour, E.; Delpasand, M.; Chu, X. Verification of FPA and PSO Algorithms for Rule Curve Extraction and Optimization of Single- and Multi-Reservoir Systems’ Operations Considering Their Specific Purposes. Water Sci. Technol. Water Supply 2021, 21, 166–188. [Google Scholar] [CrossRef]
- Sinthuchai, N.; Kangrang, A. Improvement of Reservoir Rule Curves using Grey Wolf Optimizer. J. Eng. Appl. Sci. 2019, 14, 9847–9856. [Google Scholar] [CrossRef] [Green Version]
- Ngamsert, R.; Kangrang, A. Applying of Marine Predators Algorithm Linked with Reservoir Simulation Model Considering Sedimentation for Reservoir Operation. Adv. Civ. Eng. 2020, 2022, 1631914. [Google Scholar] [CrossRef]
- Bertani, R.; Negulescu, C.; Fuchs, S. A Review of Risk and Vulnerability Assessment Frameworks for Natural Hazards and Their Applicability to Urban Water Systems. Nat. Hazards 2022, 110, 677–699. [Google Scholar]
- Smith, J.A.; Johnson, L.K.; Anderson, R.M. Water Scarcity Impacts on Agricultural Productivity: A Review. Agric. Water Manag. 2022, 267, 107948. [Google Scholar]
- Phumiphan, A.; Kangrang, A. Development of Decision-Making Support Tools for Future Reservoir Management Under Climate and Land Cover Variability: A Case Study. Int. Rev. Civ. Eng. (IRECE) 2021, 12, 271. [Google Scholar] [CrossRef]
- Pagano, A.; Giordano, R.; Vurro, M. A Decision Support System Based on AHP for Ranking Strategies to Manage Emergencies on Drinking Water Supply Systems. Water Resour. Manag. 2021, 35, 613–628. [Google Scholar] [CrossRef]
- Zamani, A.A.; Abbasi, H.R.; Alipour, V.; Peyravi, M.; Shojaei, P.; Goli, A.; Mohammadinia, L. Alternative Water Resources Selection to Supply Drinking Water in Flood Disasters by Multicriteria Decision-Making Techniques (DANP and VIKOR). J. Environ. Public Health 2022, 2022, 5445786. [Google Scholar] [CrossRef] [PubMed]
- Techarungruengsakul, R.; Ngamsert, R.; Thongwan, T.; Hormwichian, R.; Kuntiyawichai, K.; Ashrafi, S.M.; Kangrang, A. Optimal Choices in Decision Supporting System for Network Reservoir Operation. Water 2022, 14, 4090. [Google Scholar] [CrossRef]
- Philin, K. Evaluation Water Indices for Estimation Capacity of Ubolratana Reservoir Using Remote Sensing. Master’s Thesis, Mahasarakham University, Kham Riang, Thailand, 2021; pp. 25–35. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ngamsert, R.; Techarungruengsakul, R.; Kaewplang, S.; Hormwichian, R.; Prasanchum, H.; Sivanpheng, O.; Kangrang, A. Optimizing Solution in Decision Supporting System for River Basin Management Consisting of a Reservoir System. Water 2023, 15, 2510. https://doi.org/10.3390/w15142510
Ngamsert R, Techarungruengsakul R, Kaewplang S, Hormwichian R, Prasanchum H, Sivanpheng O, Kangrang A. Optimizing Solution in Decision Supporting System for River Basin Management Consisting of a Reservoir System. Water. 2023; 15(14):2510. https://doi.org/10.3390/w15142510
Chicago/Turabian StyleNgamsert, Ratsuda, Rapeepat Techarungruengsakul, Siwa Kaewplang, Rattana Hormwichian, Haris Prasanchum, Ounla Sivanpheng, and Anongrit Kangrang. 2023. "Optimizing Solution in Decision Supporting System for River Basin Management Consisting of a Reservoir System" Water 15, no. 14: 2510. https://doi.org/10.3390/w15142510






