1. Introduction
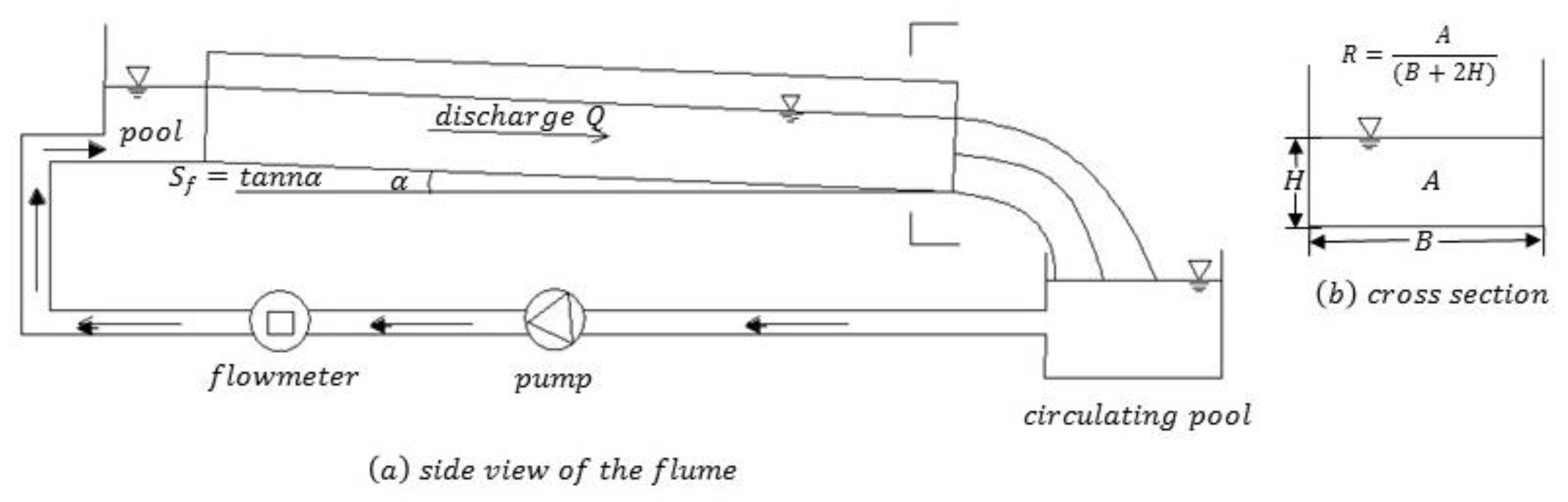
Open-channel flow is widely found in nature and engineering projects. Rivers in nature and water conveyance channels in engineering are typical open channels. In hydraulics, the discharge capacity of constant uniform flow in open channels can be calculated as follows. The variables are shown in
Figure 1.
where
Q is the discharge capacity (m
3/s);
A is the area (m
2);
R is the hydraulic radius (m);
Sf is the energy slope (dimensionless); and
C is the Chezy coefficient (dimensionless).
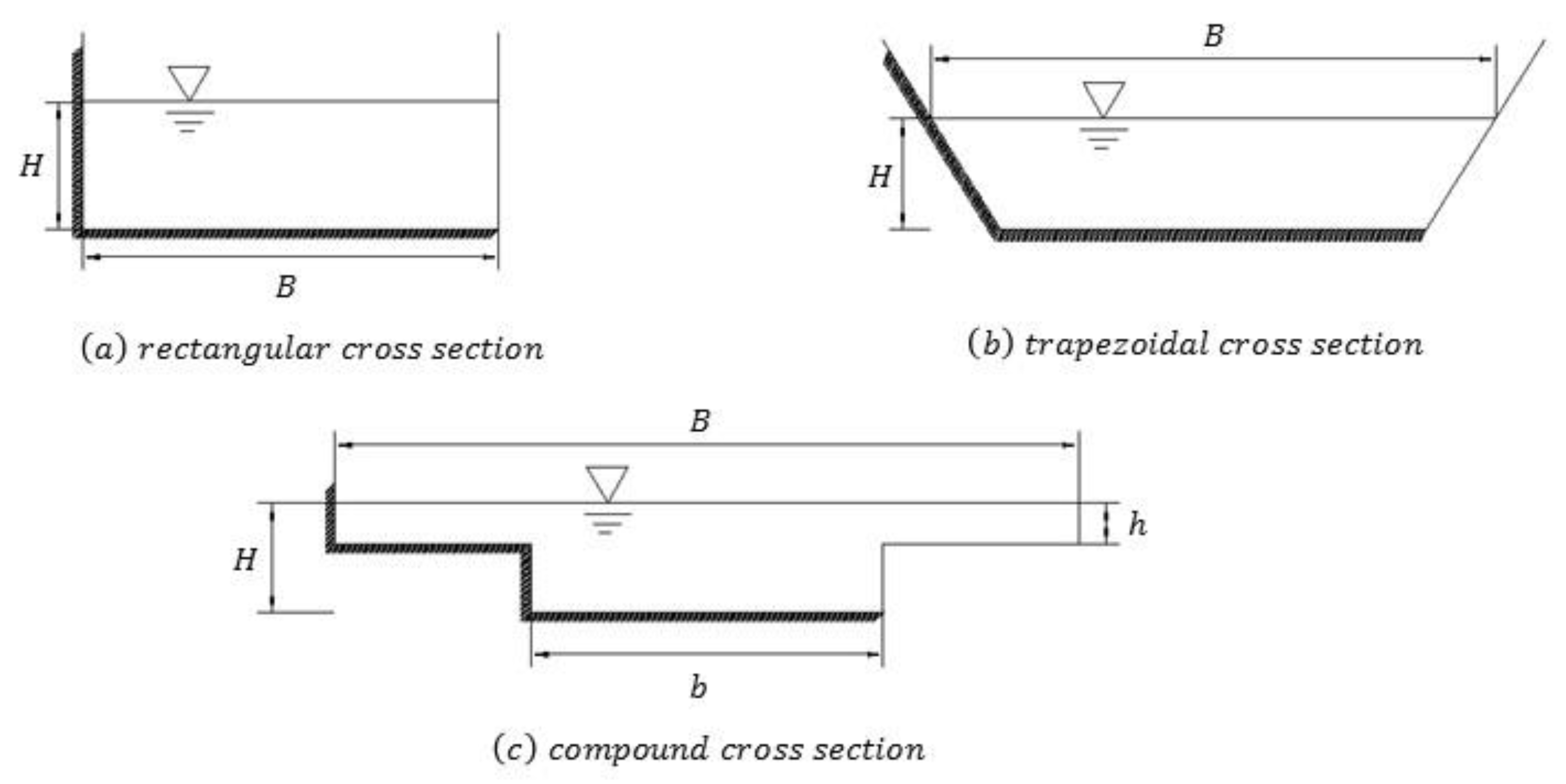
This empirical formula was obtained by Chezy in 1775 based on a large amount of measured data of uniform flow in open channels. The boundary of the artificial channel and the natural channel is varied and there are various cross-sectional shapes in the channels (see
Figure 2). On the basis of the theory of open-channel flow, people generally obtain the expression for the flow capacity of the channel with a certain cross-sectional shape through experiments and numerical simulations. However, in nature and engineering, the cross-sectional shape of an open channel varies. Studying only one type of cross-sectional shape in this manner is feasible; however, extending this to all types of cross-sectional shapes, and for cross-sections with similar shapes, makes the research process challenging and rather cumbersome. At the same time, it is not conducive to the simplicity of engineering calculations. Therefore, it is necessary to find a parameter that can uniformly describe the effect of cross-sectional shape on flow capacity.
As H. Graf [
1] pointed out, at present, no parameter can describe the variability of cross-sectional shapes well. In hydraulics, a semi-empirical model is also used to describe this effect; that is, the effects of all shape factors are expressed as parameters. The hydraulic radius commonly used in hydraulics is not sufficient to reflect the influence of cross-sectional shape on flow capacity. Flow capacity is related to energy loss coefficient
λ. Therefore, the influence of cross-sectional shape on the energy loss coefficient
λ must be considered by multiplying a coefficient
φ in front of hydraulic radius
R. The equation is
where
λ is the coefficient of energy loss (dimensionless);
ks is the rough height (m);
and
are empirical coefficients [
2] related to the discharge and operating conditions (dimensionless);
φ is a coefficient related to the shape, e.g., for a rectangular section,
φ = 0.95, for a trapezoidal section,
φ = 0.80, and for an equilateral triangle section,
φ = 1.25;
R is the hydraulic radius (m); and
,
Red is the Reynolds number with the hydraulic diameter as the characteristic length.
Parameters are used to reflect the effect of cross-sectional shape. However, different researchers have different opinions on which factors these parameters are related to. The following is a review of the literature on this issue. Cantero et al. [
3] showed that the single channel method can be used to estimate discharge capacity. In this method, the equivalent manning coefficient for the entire cross-section,
ne, is related to the wetted perimeter (Chow [
4]; Prinos and Townsend [
5]). Dracos and Hardegger [
6] and French [
7] used a weighted hydraulic radius to estimate flow discharge using the single channel method. For calculating the discharge of symmetrical flood plains, Cantero et al. [
3] provided an expression (Equation (6)) using a flow area
A with a certain weight. This expression is also related to mean flow velocity
U, which is influenced by shape factors such as hydraulic radius, flood plain depth, and wetted perimeter (Wormleaton et al. [
8]). Khatua et al. [
9] provided expressions of two kinds of wetted perimeter coefficients. The expressions contain the power function of the flow area ratio. The expressions used to calculate the flow rate are complicated (see Cantero et al. [
3], Equation (9)). The expressions of the kinetic energy correction coefficient (or Coriolis coefficient)
α and momentum correction coefficient (or Boussinesq coefficient)
β are given by Blalock and Sturm [
10], Field et al. [
11], and Chaudhry and Bhallamudi [
12], respectively. Then, the specific energy function
E, momentum function
S, and flow profile
h = h(x) are calculated. The Froude number of compound open channels was approximated by Blalock and Sturm [
10], and is related to shape parameters such as top width, wetted perimeter, hydraulic radius of the subsection, etc. This is a bulk cross-sectional Froude number, rather than a local Froude number valid for different points in a section. The bulk cross-sectional Froude number can be used to further calculate the water depth and specific energy (Blalock and Sturm [
10]; Blalock and Sturm [
13]; and Costabile and Macchione [
14]).
In addition, it is not clear how the parameter changes in laminar flow or medium and low Reynolds number flow, or high Reynolds number flow. The following is a review of the literature on this issue. There is little data on the connection between Reynolds number and the parameter that can describe the effect of cross-sectional shapes on discharge capacity. Studies mainly focus on the influence of Reynolds number on characteristic variables, such as velocity and depth, etc. Through smooth flume experiments, Johnson and Cowen [
15] found that when the Reynolds number changes from 4950 to 73,800, the velocity index
k changes from 0.82 to 0.93 (
k = Ub/Usurf, where
Ub is the depth-averaged velocity and
Usurf is the local surface velocity), thus affecting the change in average velocity and discharge capacity. Harpold et al. [
16] also observed through experiments that the variation in Reynolds number would affect the variation in the velocity index. The velocity index was set at 0.85 under base flow conditions and 0.93 under high flow conditions. Chen [
17] and Schlichting [
18] found that the logarithmic law of flow velocity is suitable for high Reynolds number flows, while the power law is valid for lower Reynolds number intervals. The coefficients of these functions are generally obtained experimentally.
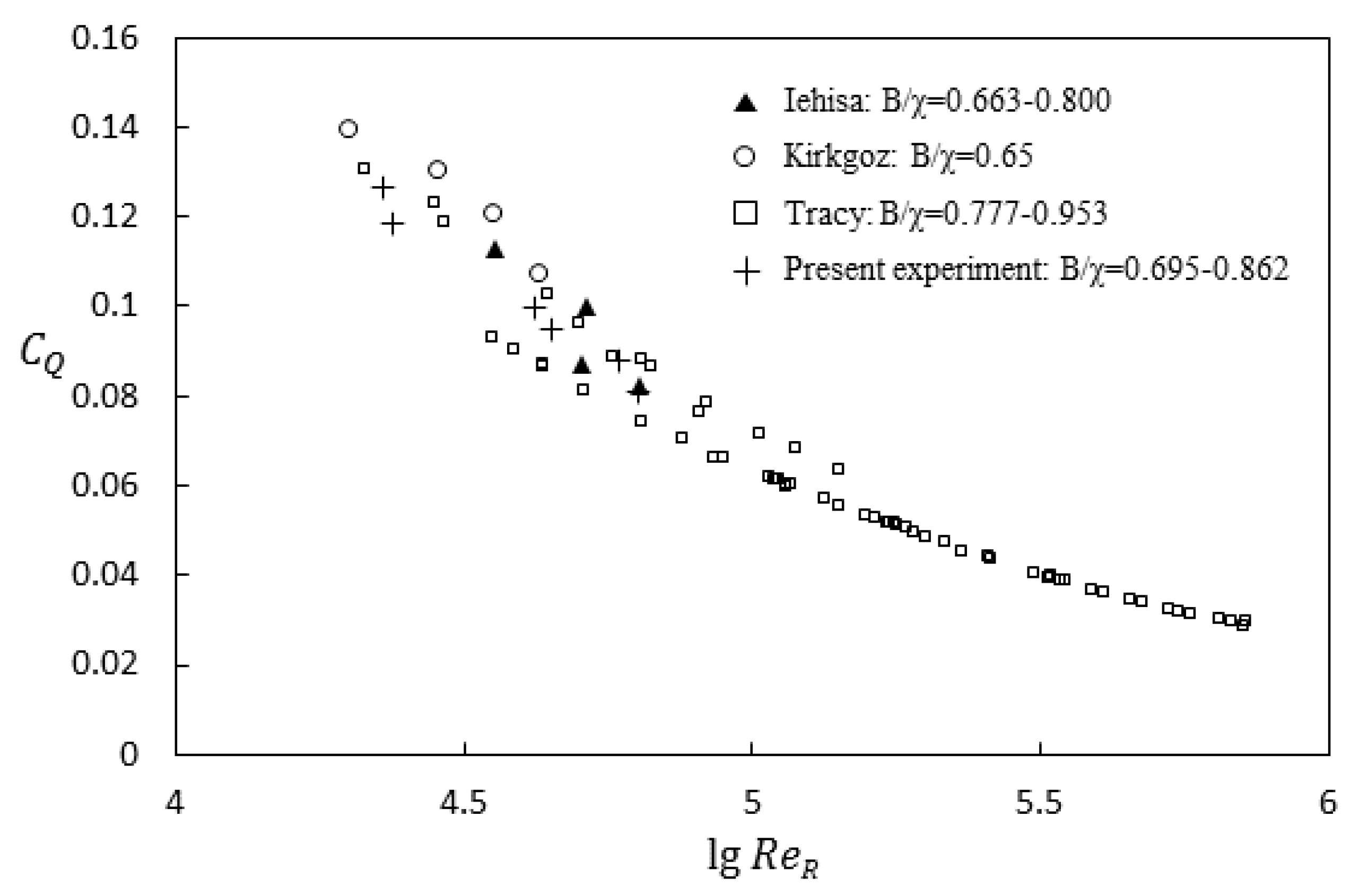
Experimental studies and numerical calculations are important means to investigate the parameter that can describe the effect of cross-sectional shapes on discharge capacity. The following is an introduction of related experimental studies and numerical calculations. Some are directly related to parameters, while others are about characteristic variables, such as the energy loss coefficient,
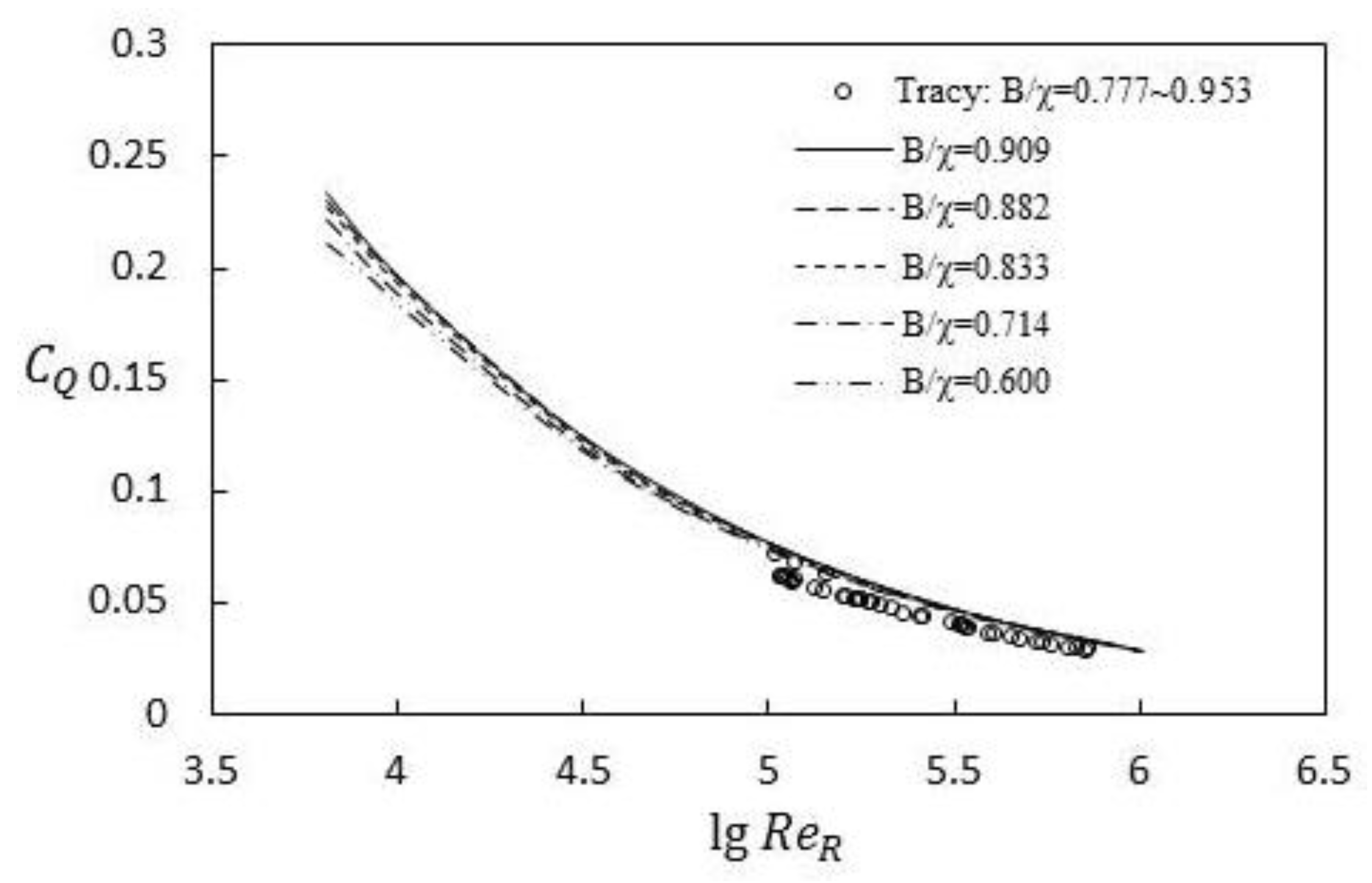
λ, and velocity distribution. For example, Tracy et al. [
19] carried out a series of experiments to study the influence of the side wall of an open channel on velocity distribution and energy loss. Under the same Reynolds number conditions, the energy loss coefficient of rectangular open-channel flow is slightly higher than that of circular channel flow and rectangular open-channel flow with an infinite width-to-depth ratio. Kirkgöz [
20] used a laser Doppler anemometer to measure rectangular open-channel flow with smooth and rough surfaces and analyzed the velocity distribution of cross-sections under different wall conditions. The trapezoidal open-channel flow, compound open-channel flow, and rectangular open-channel flow with different width-depth ratios were studied in a large number of experiments by researchers. Although the results of experimental research and numerical calculations are abundant, no uniform parameter exists to describe the influence of cross-sectional shapes on the discharge capacity of open channels withregular channel boundary conditions.
Recently, we studied the general description of open-channel flow theoretically, in order to acquire the parameter that can describe the effect of cross-sectional shapes on discharge capacity. Based on the theory of movement of viscous liquids, the governing equations of laminar and turbulent motions of homogeneous incompressible viscous liquid in an open channel were directly integrated to construct new integral and differential models, respectively [
21,
22,
23,
24]. As a result, a solid theoretical foundation for a general description of open-channel flow in regular boundary conditions was laid. Then, from the perspective of fluid mechanics, we derived the parameter
CQ, which describes the influence of cross-sectional shape on flow capacity, through backward derivation, generalization, and simplification. The total flow energy equation (one of the governing equations of the integral model) established from the perspective of hydrodynamics solves the following shortcomings in the total flow energy equation in hydraulics: (1) The direct relationship between flow field description in fluid mechanics and total flow description in hydraulics cannot be built. (2) Distinguishing between total flow energy equations in laminar flow conditions and turbulent flow conditions in an open channel is impossible. (3) The effect of viscous dissipation and turbulence on total flow energy loss cannot be calculated directly, so the direct expression of total flow energy loss cannot be given. (4) The pressure on the cross-section must obey the static pressure distribution, but it is difficult to satisfy in the conditions of secondary flow and turbulent flow. This article is based on a new parameter,
CQ, that can describe the effect of cross-sectional shapes on discharge capacity, and the following work was carried out: (1) The general expression of open-channel flow capacity was deduced firstly through theoretical analysis. At the same time, the expression of the flow capacity coefficient
CQ was given. (2) On the basis of the general expression, the direct formula for calculating the coefficient of flow capacity,
CQ, under laminar flow conditions was given. (3) Additionally, on the basis of the general expression, combined with the experiment results of this article and the literature, the variation trend of
CQ under different turbulent flow conditions was obtained. (4) By means of numerical analysis, the variation trends of
CQ in rectangular, trapezoidal, and compound open channels were obtained. (5) In the Discussion section, the variation trends of
CQ in laminar and turbulent zones are shown in the same graph, using the experimental and numerical results. The differences in
CQ in two regions are discussed. (6) The Conclusion section summarizes the variation trend of
CQ in laminar, low and medium Reynolds number turbulent region, and high Reynolds number turbulent region. The research objective of this article was achieved; that is, we identified a flow capacity parameter
CQ to represent the flow discharge capacity. The calculation formula is a direct expression, which is convenient for application in engineering calculations. At the same time, the width-to-wetted perimeter ratio was used to generalize the cross-sectional shape. The variation trend of
CQ with width-to-wetted perimeter ratio and Reynolds number was obtained.
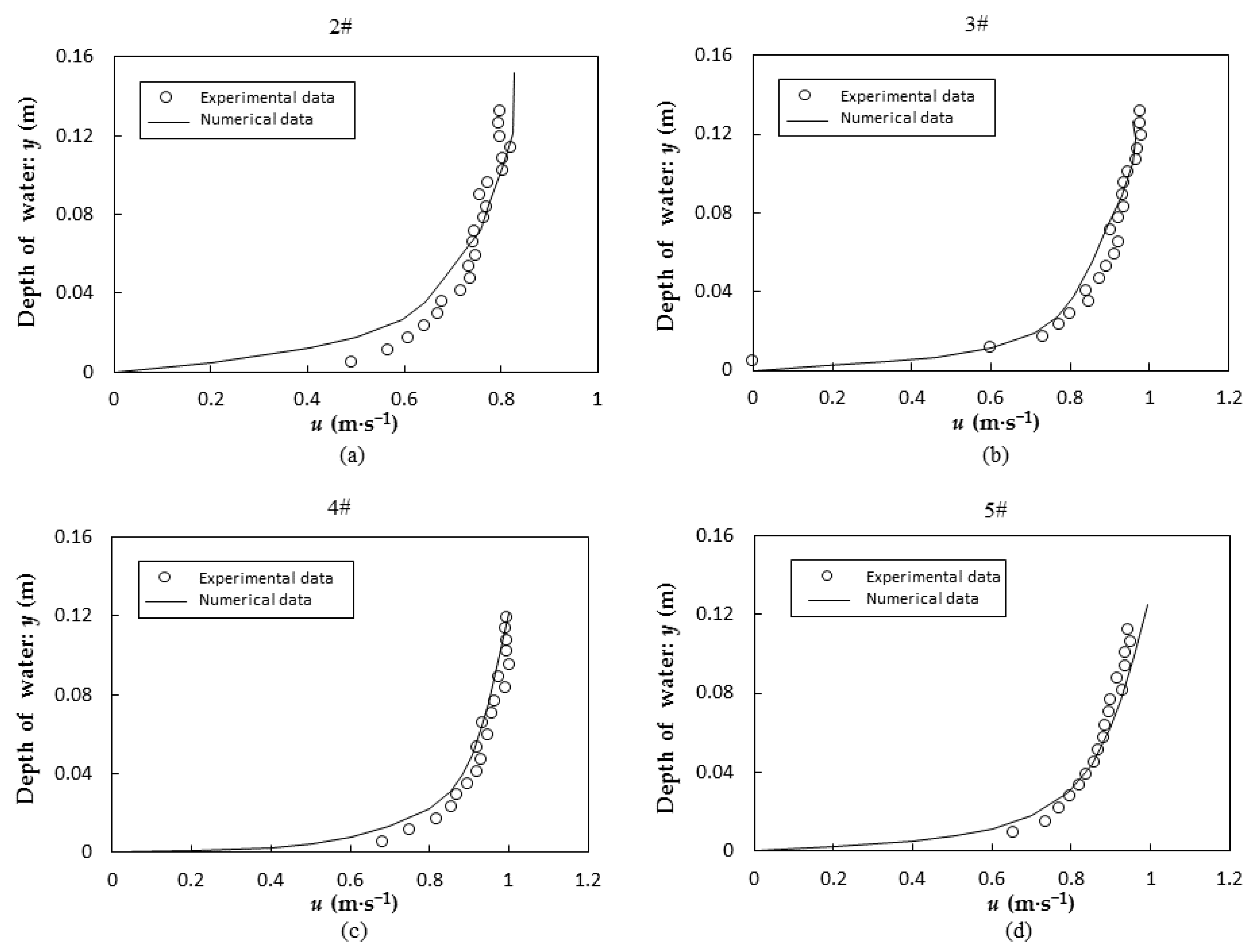
The results of this study can be used to predict the flow capacity of open channels with different cross-sectional shapes, i.e., to estimate the flow discharges of open channels at different water levels. Hydraulics generally describe the flow capacity using the roughness coefficient n and the Chezy coefficient C. However, these are empirical descriptions, not precise expressions of flow capacity. In order to connect the boundary of open channels and flow field, this research was conducted based on coupling the flow field description with the general description. The results of this article can be applied to estimate the discharges at different water levels in open-channel flow with a regular boundary. Natural rivers generally have irregular boundaries. Before using the results of this paper, a generalization of boundary should be conducted first. That is, irregular boundaries are generalized to regular boundaries. Then, the generalized regular boundary can be used to estimate discharge.
4. Discussion
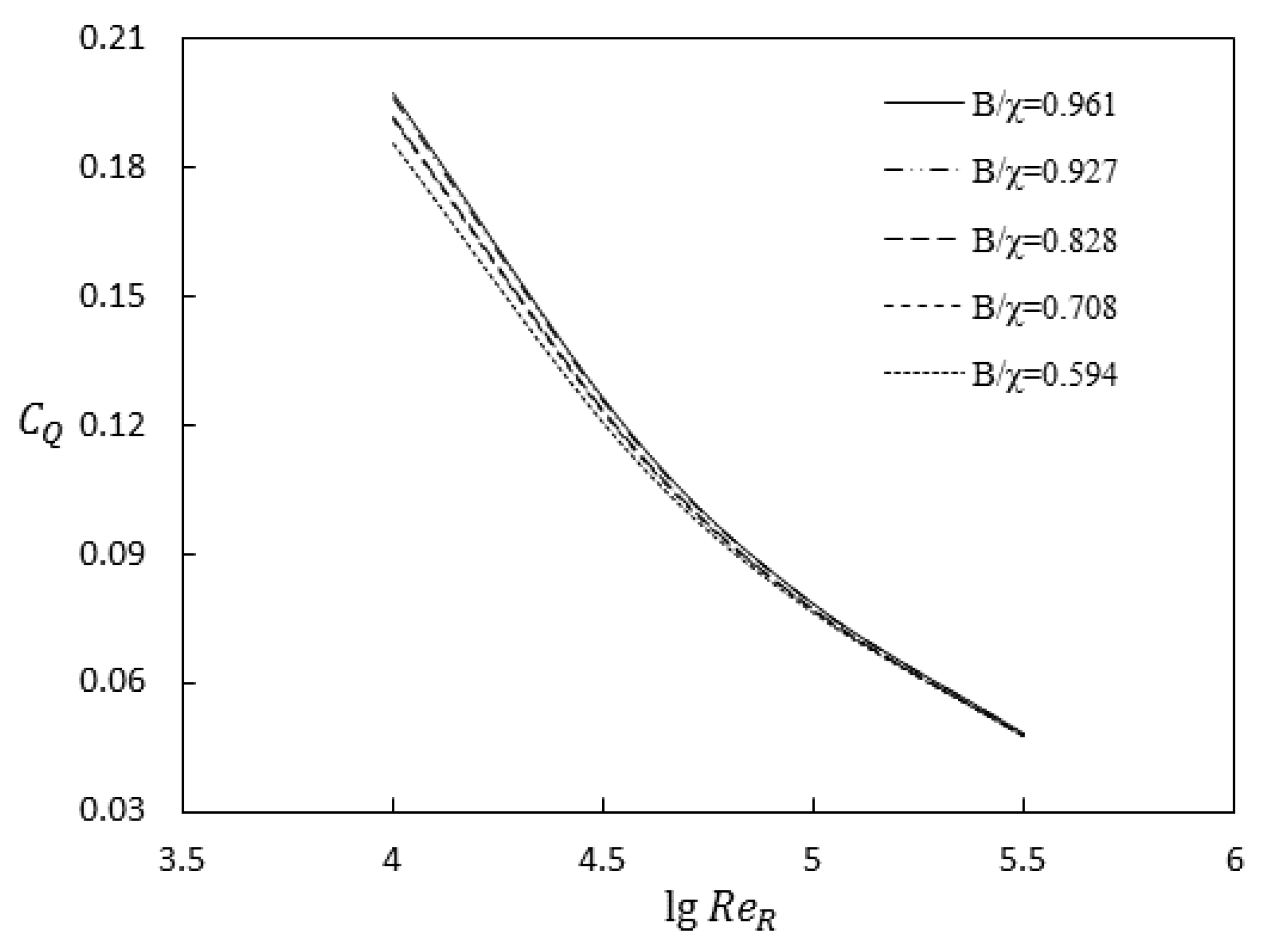
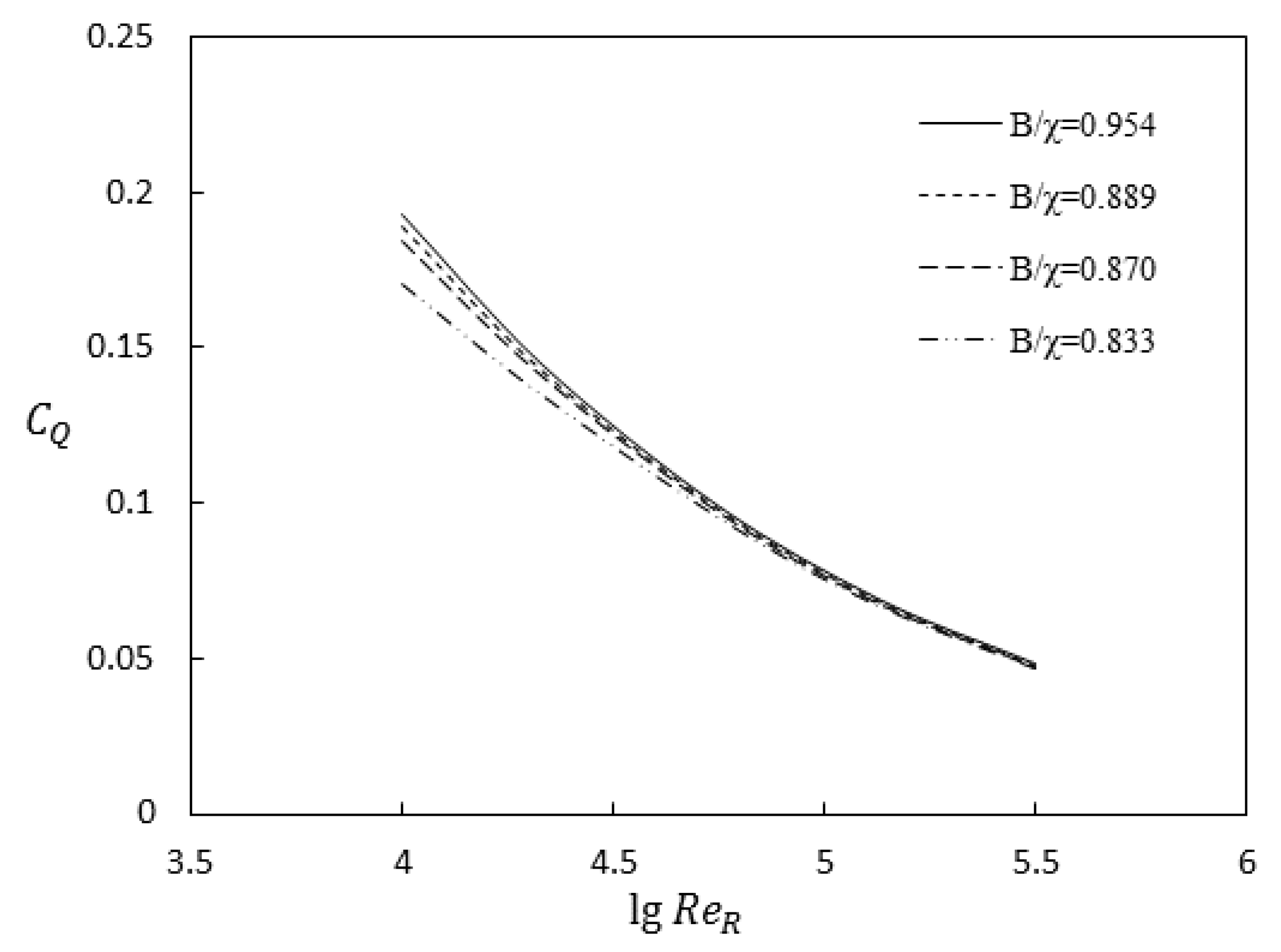
To analyze the variation in the discharge capacity parameter
CQ in conditions with various cross-sectional shapes (rectangular, trapezoidal, and compound), the numerical results and experimental results for turbulent flow and theoretical solutions for laminar flow were combined into the same figure (all for open-channel flow).
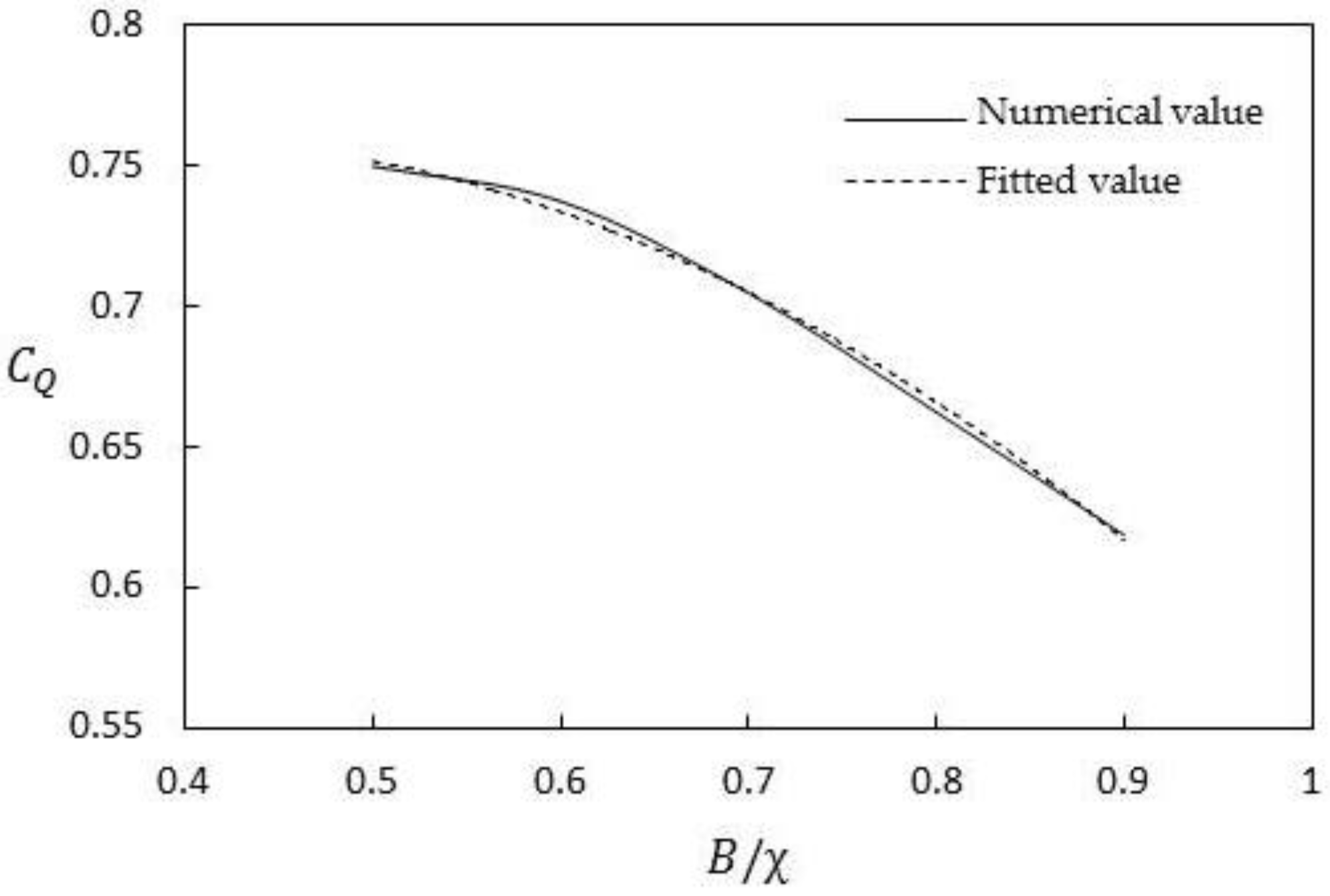
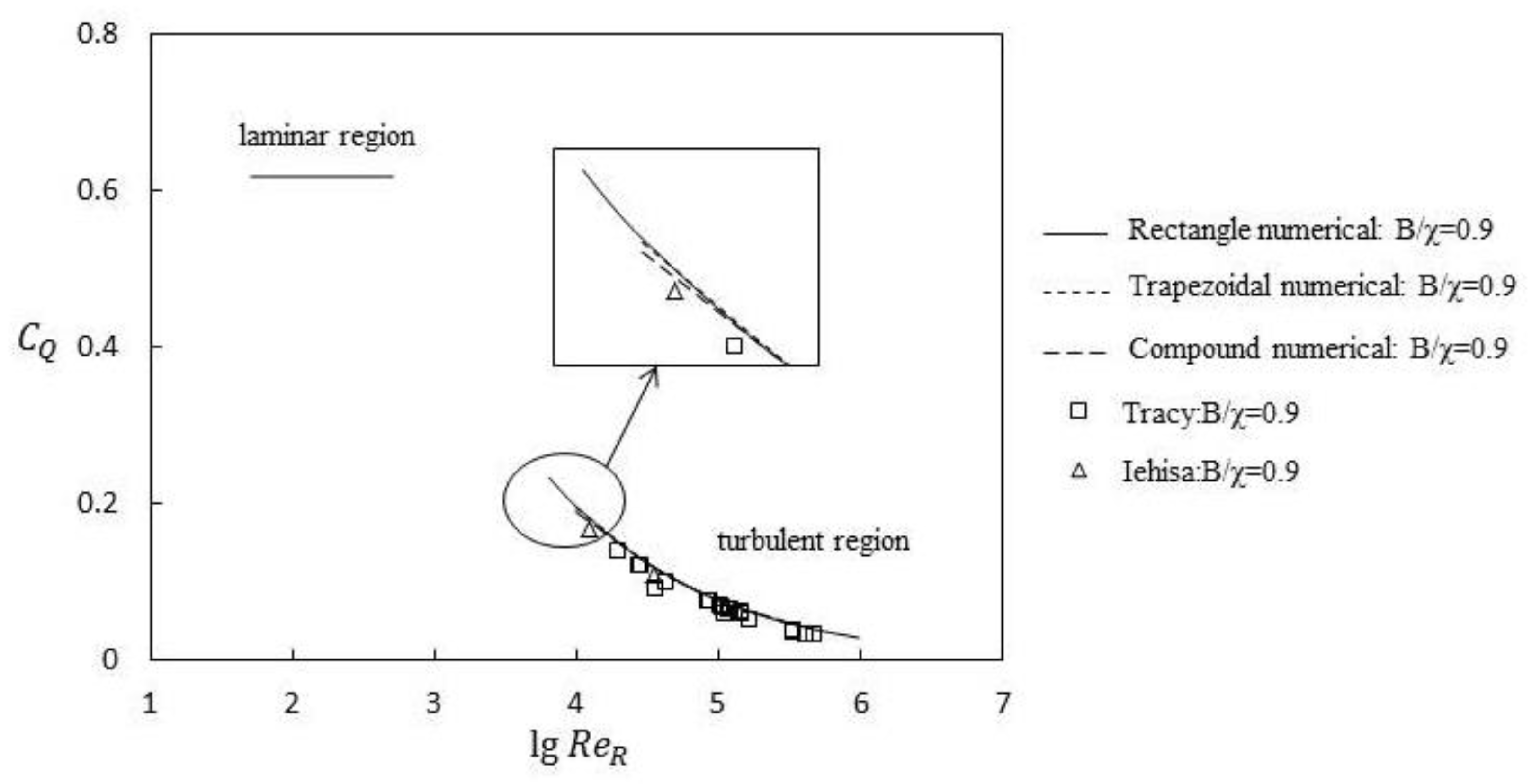
Figure 15 and
Figure 16 show the variation in
CQ with
ReR at a given width-to-wetted perimeter ratio (
B/χ is 0.7 and 0.9, respectively).
Figure 15 and
Figure 16 show the following: (1) For medium and low Reynolds number turbulence with a Reynolds number less than 10
5 with the same
B/χ value, the
CQ of the three types of cross-sectional shapes (namely, rectangular, trapezoidal, and compound) were different from each other. The discharge capacity parameter
CQ varied with the shape of the cross-section, and the mechanism was extremely complex; further study is needed. (2) For turbulent flow with a high Reynolds number greater than 10
5, the numerical values of
CQ in the three cross-sectional conditions were almost the same as the experimental values, and
CQ was no longer dependent on the width-to-wetted perimeter ratio
B/χ. In high Reynolds number turbulent flow conditions, turbulence structures at different scales were fully developed, and the discharge capacity parameter,
CQ, was no longer dependent on the shape of the cross-section. The experimental and numerical results in
Figure 15 and
Figure 16 are mostly consistent. However, the experimental values in
Figure 16 were slightly lower than the numerical results. A possible reason for this is that the actual energy loss was not fully taken into account in the numerical calculations. Therefore, the numerical
CQ values were slightly higher.
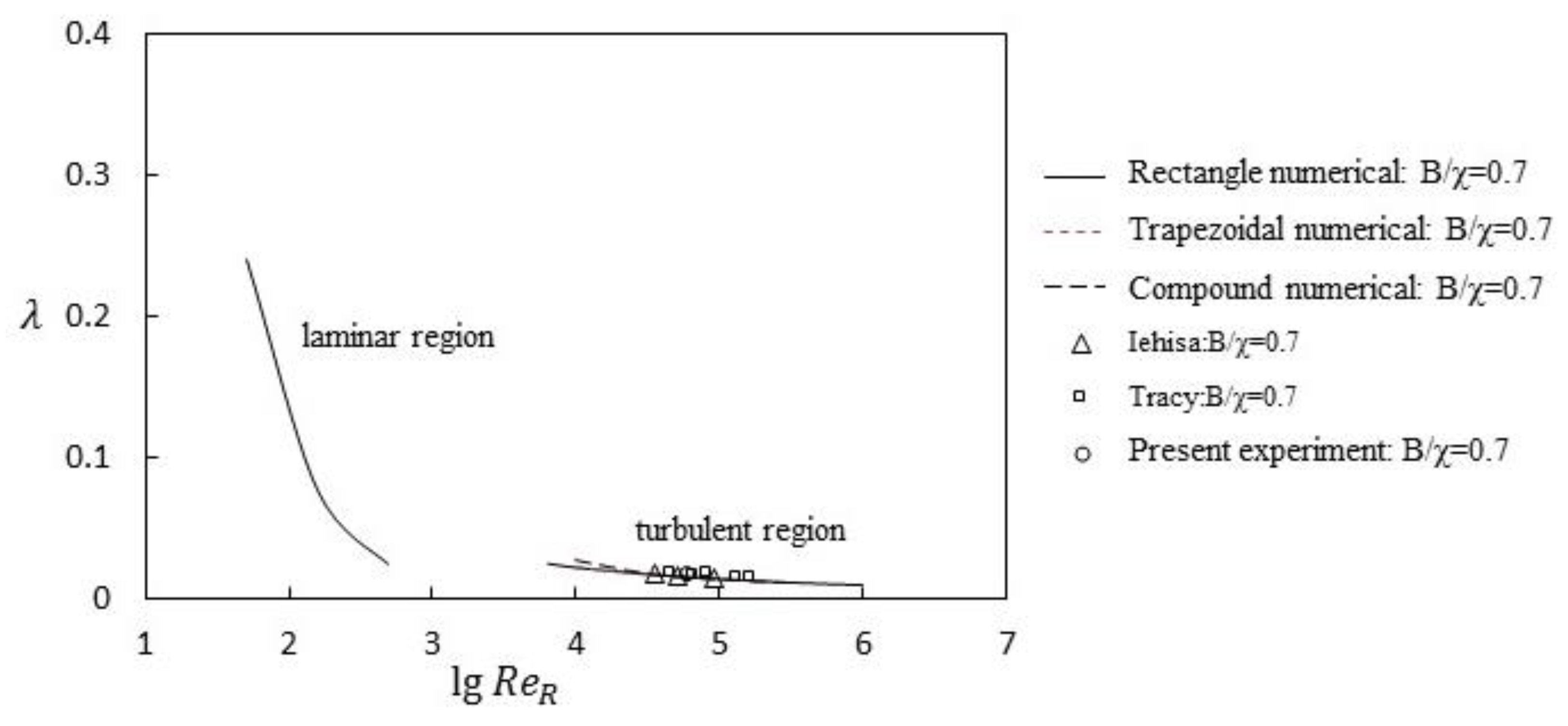
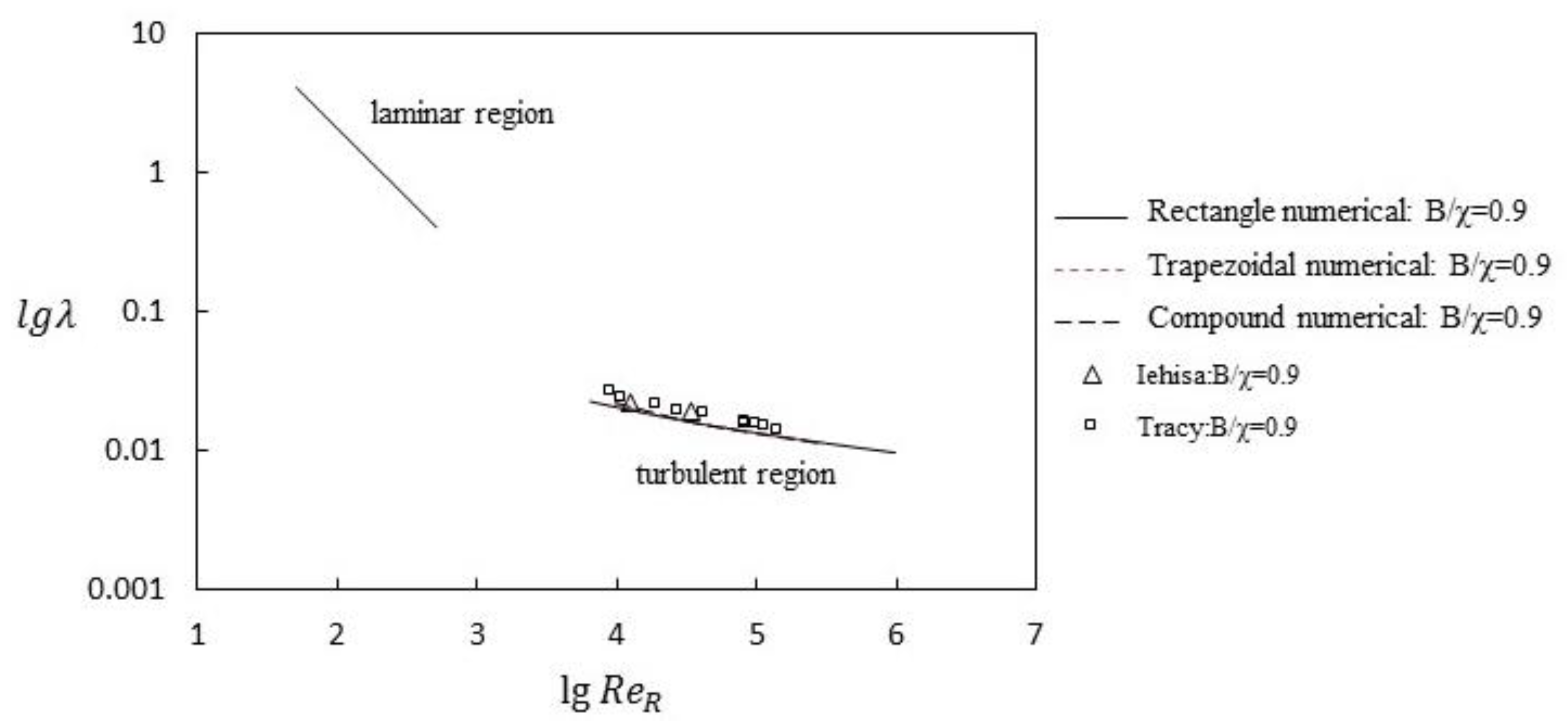
The numerical results and experimental data were used to calculate
λ values in laminar flow and turbulent flow with medium and high Reynolds numbers (
Figure 17 and
Figure 18 for
B/χ = 0.7 and
B/χ = 0.9, respectively). As can be seen in
Figure 17 and
Figure 18,
λ varied greatly in the laminar flow region. This indicates that
λ was obviously affected by the Reynolds number in the laminar flow region. In turbulent regions with medium and high Reynolds numbers, in the experimental data and numerical data and regardless of the shape of the cross-section (rectangle, trapezoidal, or compound shapes,
B/χ = 0.7 or 0.9), the
λ values basically coincided and did not change. The results show that
λ did not depend on the Reynolds number in the middle and high Reynolds number turbulent region. The experimental and numerical results in
Figure 17 and
Figure 18 are mostly consistent. However, the experimental values in
Figure 18 were slightly higher than the numerical results. A possible reason for this is that the actual energy loss was not fully taken into account in the numerical calculations. Therefore, the energy loss values from the numerical calculations were lower.