Large-Eddy Simulation of Compound Channels with Staged Floodplains: Flow Interactions and Turbulent Structures
Abstract
1. Introduction
- The study’s experimental arrangements and flow setup are first described for the three test cases. The mathematical and numerical solution method is then discussed with a computational model setup.
- The validation of the experimental time-averaged primary mean velocity and secondary current are presented for three different depth ratios of multiple staged compound channels.
- Then, the streamwise primary velocity distribution, turbulence statistics and vortical structures to define the mass and momentum exchange are presented.
- The numerical model results and conclusions are made for the new flow configuration with staged floodplains.
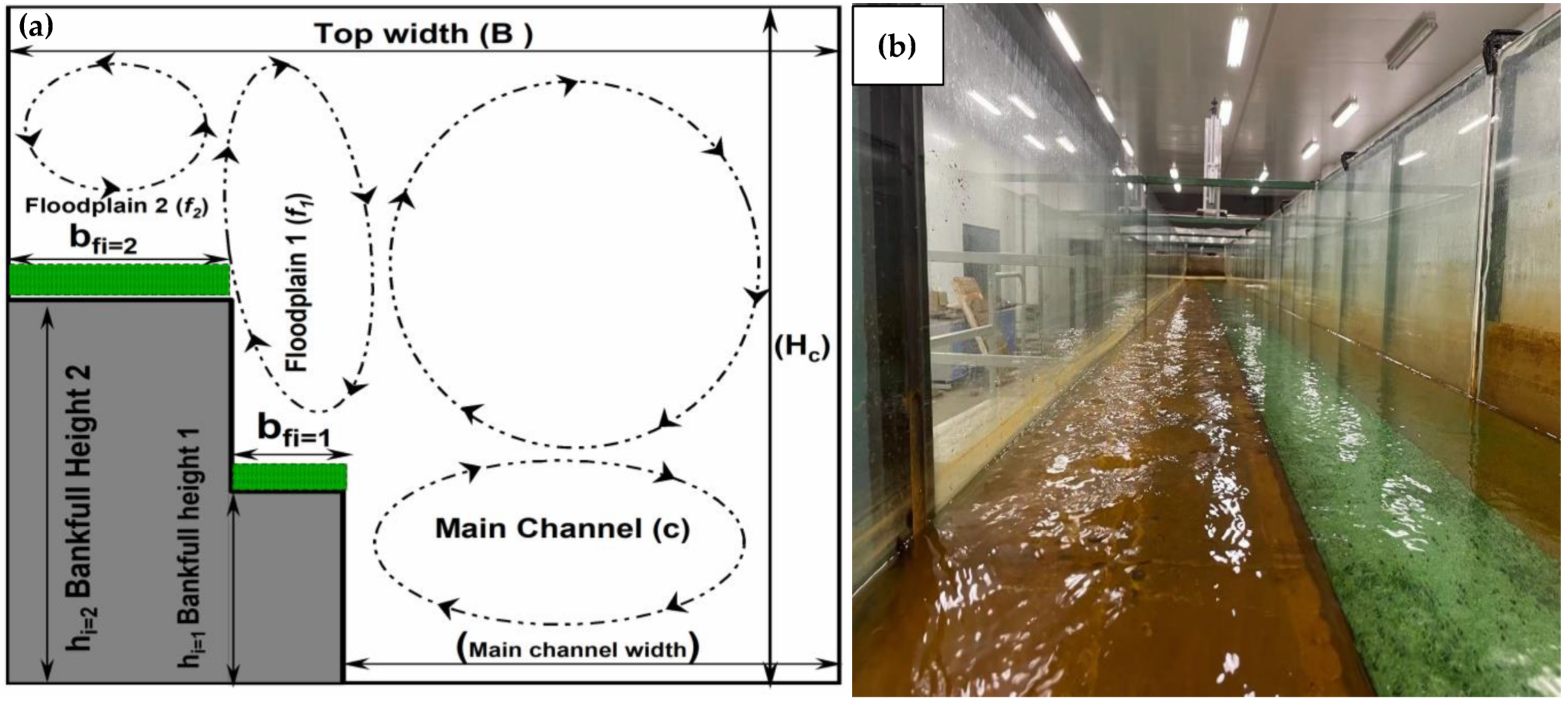
2. Experimental Arrangements
3. Numerical Model
Governing Equations
4. Results and Discussion
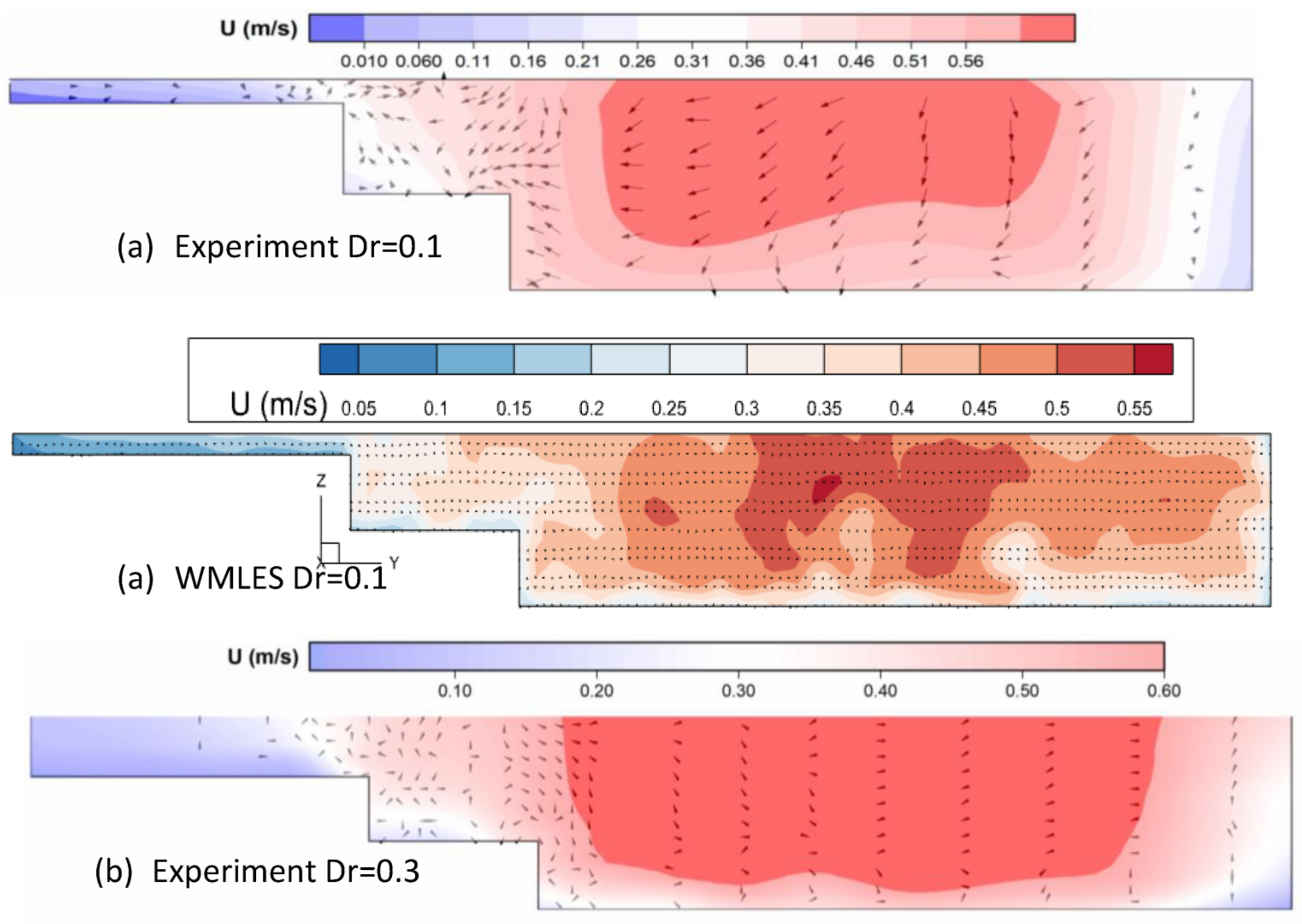
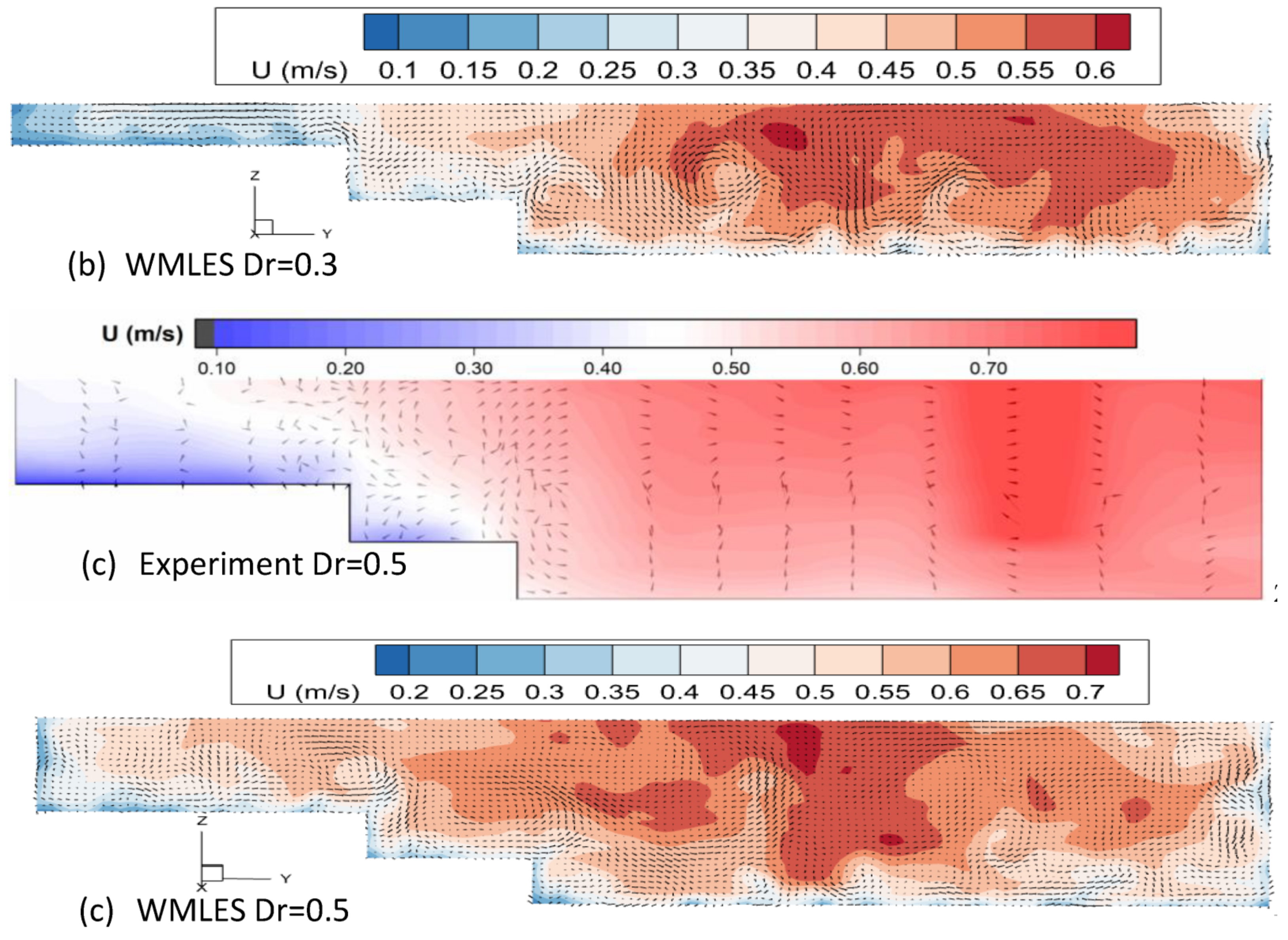
4.1. Distribution of the Mean Streamwise Velocity and Secondary Current
4.2. Distribution of Instantaneous Streamwise Velocity
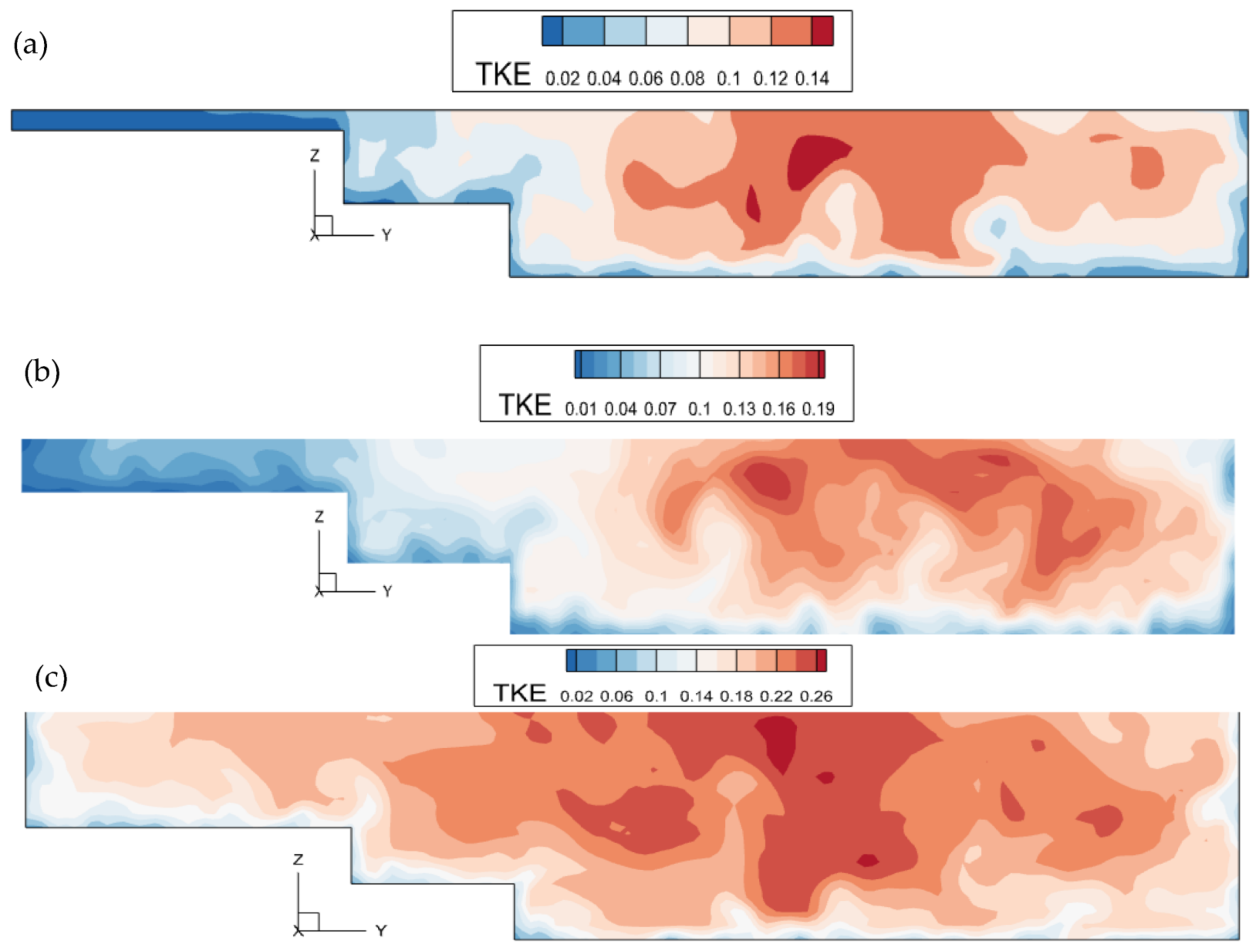
4.3. Distribution of Turbulent Kinetic Energy
4.4. Power Density Spectra (PSD) Using Time Series at Interfaces of Multistage Floodplains
4.5. Vortical Structures
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abril, J.; Knight, D. Stage-discharge prediction for rivers in flood applying a depth-averaged model. J. Hydraul. Res. 2004, 42, 616–629. [Google Scholar] [CrossRef]
- Knight, D. Hydraulic problems in flooding: From data to theory and from theory to practice. In Experimental and Computational Solutions of Hydraulic Problems; Springer: Berlin/Heidelberg, Germany, 2013; pp. 19–52. [Google Scholar]
- Cappato, A.; Baker, E.A.; Reali, A.; Todeschini, S.; Manenti, S. The role of modeling scheme and model input factors uncertainty in the analysis and mitigation of backwater induced urban flood-risk. J. Hydrol. 2022, 614, 128545. [Google Scholar] [CrossRef]
- Knight, D.W.; Shiono, K. Turbulence measurements in a shear layer region of a compound channel. J. Hydraul. Res. 1990, 28, 175–196. [Google Scholar] [CrossRef]
- Peltier, Y. Physical Modelling of Overbank Flows with a Groyne Set on the Floodplain. Ph.D. Thesis, Université Claude Bernard-Lyon I, Lyon, France, 2011. [Google Scholar]
- Atabay, S. Stage-Discharge, Resistance, and Sediment Transport Relationships for Flow in Straight Compound Channels. Doctoral Dissertation, University of Birmingham, Birmingham, UK, 2001. Available online: https://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.427466 (accessed on 14 February 2023).
- Knight, D.W.; Demetriou, J.D. Flood Plain and Main Channel Flow Interaction. J. Hydraul. Eng. 1983, 109, 1073–1092. [Google Scholar] [CrossRef]
- Singh, P.; Tang, X. Interfacial compound section transverse flow variation in symmetric and asymmetric compound open channel flow. In Proceedings of the 9th International Symposium on Environmental Hydraulics, Seoul, Republic of Korea, 18–22 July 2021; pp. 174–175. [Google Scholar]
- Singh, P.; Tang, X.; Rahimi, H.R. Modelling of the apparent shear stress for predicting zonal discharge in rough and smooth asymmetric compound open channels. In River Flow 2020: Proceedings of the 10th Conference on Fluvial Hydraulics, Delft, The Netherlands, 7–10 July 2020; CRC Press/Balkema (Taylor & Francis): Leiden, The Netherlands, 2020; pp. 84–94. [Google Scholar]
- Nicollet, G.; Uan, M. Ecoulements permanents à surface libre en lits composes. La Houille Blanche 1979, 21–30. [Google Scholar] [CrossRef]
- Knight, D.W.; Hamed, M.E. Boundary Shear in Symmetrical Compound Channels. J. Hydraul. Eng. 1984, 110, 1412–1430. [Google Scholar] [CrossRef]
- Tominaga, A.; Nezu, I. Turbulent Structure in Compound Open-Channel Flows. J. Hydraul. Eng. 1991, 117, 21–41. [Google Scholar] [CrossRef]
- Fernandes, J. Compound channel uniform and non-uniform flows with and without vegetation in the floodplain. Ph.D. Thesis, Departamento de Engenharia Civil, Instituto Superior Técnico da Universidade Técnica de Lisboa, Lisboa, Portugal, 2013. [Google Scholar]
- Tang, X.; Knight, D.W. Sediment Transport in River Models with Overbank Flows. J. Hydraul. Eng. 2006, 132, 77–86. [Google Scholar] [CrossRef]
- Pasche, E.; Rouvé, G. Overbank flow with vegetatively roughened flood plains. J. Hydraul. Eng. 1985, 111, 1262–1278. [Google Scholar] [CrossRef]
- Kozioł, A.P. Three-Dimensional Turbulence Intensity in a Compound Channel. J. Hydraul. Eng. 2013, 139, 852–864. [Google Scholar] [CrossRef]
- Dupuis, V.; Proust, S.; Berni, C.; Paquier, A. Mixing layer development in compound channel flows with submerged and emergent rigid vegetation over the floodplains. Exp. Fluids 2017, 58, 1–18. [Google Scholar] [CrossRef]
- Tang, X.; Rahimi, H.R.; Wang, Y.U.; Zhao, Y.U.; Lu, Q.I.; Wei, Z.I.; Singh, P.R. Flow characteristics of open-channel flow with partial two-layered vegetation. In Proceedings of the 38th IAHR World Congress, Panama City, Panama, 1–6 September 2019; pp. 1–6. [Google Scholar]
- Tang, X.; Guan, Y.; Rahimi, H.; Singh, P.; Zhang, Y. Discharge and velocity variation of flows in open channels partially covered with different layered vegetation. E3S Web Conf. 2021, 269, 03001. [Google Scholar] [CrossRef]
- Proust, S.; Fernandes, J.N.; Leal, J.B.; Rivière, N.; Peltier, Y. Mixing layer and coherent structures in compound channel flows: Effects of transverse flow, velocity ratio, and vertical confinement. Water Resour. Res. 2017, 53, 3387–3406. [Google Scholar] [CrossRef]
- Proust, S.; Fernandes, J.N.; Peltier, Y.; Leal, J.B.; Riviere, N.; Cardoso, A.H. Turbulent non-uniform flows in straight compound open-channels. J. Hydraul. Res. 2013, 51, 656–667. [Google Scholar] [CrossRef]
- Naik, B.; Khatua, K.K.; Padhi, E.; Singh, P. Loss of Energy in the Converging Compound Open Channels. Arab. J. Sci. Eng. 2017, 43, 5119–5127. [Google Scholar] [CrossRef]
- Rajaratnam, N.; Ahmadi, R. Hydraulics of channels with floodplains. J. Hydraul. Res. 1981, 19, 43–60. [Google Scholar] [CrossRef]
- Kara, S.; Stoesser, T.; Sturm, T.W. Turbulence statistics in compound channels with deep and shallow overbank flows. J. Hydraul. Res. 2012, 50, 482–493. [Google Scholar] [CrossRef]
- Naot, D.; Nezu, I.; Nakagawa, H. Hydrodynamic Behavior of Compound Rectangular Open Channels. J. Hydraul. Eng. 1993, 119, 390–408. [Google Scholar] [CrossRef]
- Lin, B.; Shiono, K. Numerical modelling of solute transport in compound channel flows. J. Hydraul. Res. 1995, 33, 773–788. [Google Scholar] [CrossRef]
- Sofialidis, D.; Prinos, P. Numerical Study of Momentum Exchange in Compound Open Channel Flow. J. Hydraul. Eng. 1999, 125, 152–165. [Google Scholar] [CrossRef]
- Cokljat, D.; Younis, B.A. Second-Order Closure Study of Open-Channel Flows. J. Hydraul. Eng. 1995, 121, 94–107. [Google Scholar] [CrossRef]
- Kang, H.; Choi, S.-U. Turbulence modeling of compound open-channel flows with and without vegetation on the floodplain using the Reynolds stress model. Adv. Water Resour. 2006, 29, 1650–1664. [Google Scholar] [CrossRef]
- Jing, H.; Li, C.; Guo, Y.; Xu, W. Numerical simulation of turbulent flows in trapezoidal meandering compound open channels. Int. J. Numer. Methods Fluids 2011, 65, 1071–1083. [Google Scholar] [CrossRef]
- Singh, P.K.; Tang, X.; Rahimi, H. A Computational Study of Interaction of Main Channel and Floodplain: Open Channel Flows. J. Appl. Math. Phys. 2020, 08, 2526–2539. [Google Scholar] [CrossRef]
- Wang, W.; Huai, W.-X.; Gao, M. Numerical investigation of flow through vegetated multi-stage compound channel. J. Hydrodyn. 2014, 26, 467–473. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, S.; Huai, W.; Gu, S. General model for stage–discharge prediction in multi-stage compound channels. J. Hydraul. Res. 2018, 57, 517–533. [Google Scholar] [CrossRef]
- Menter, F.; Schutze, J.; Kurbatskii, K.; Lechner, R.; Gritskevich, M.; Garbaruk, A. Scale-Resolving simulation techniques in industrial CFD. In Proceedings of the 6th AIAA Theoretical Fluid Mechanics Conference, Honolulu, HI, USA, 27–30 June 2011; p. 3474. [Google Scholar]
- Thomas, T.; Williams, J. Large eddy simulation of turbulent flow in an asymmetric compound open channel. J. Hydraul. Res. 1995, 33, 27–41. [Google Scholar] [CrossRef]
- Cater, J.E.; Williams, J.J.R. Large eddy simulation of a long asymmetric compound open channel. J. Hydraul. Res. 2008, 46, 445–453. [Google Scholar] [CrossRef]
- Xie, Z.; Lin, B.; Falconer, R.A. Large-eddy simulation of the turbulent structure in compound open-channel flows. Adv. Water Resour. 2012, 53, 66–75. [Google Scholar] [CrossRef]
- Goring, D.G.; Nikora, V.I. Despiking acoustic Doppler velocimeter data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef]
- Nikitin, N.V.; Nicoud, F.; Wasistho, B.; Squires, K.; Spalart, P.R. An approach to wall modeling in large-eddy simulations. Phys. Fluids 2000, 12, 1629–1632. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Zeng, C.; Bai, Y.; Zhou, J.; Qiu, F.; Ding, S.; Hu, Y.; Wang, L. Large Eddy Simulation of Compound Open Channel Flows with Floodplain Vegetation. Water 2022, 14, 3951. [Google Scholar] [CrossRef]
- Ding, S.-W.; Zeng, C.; Zhou, J.; Wang, L.-L.; Chen, C. Impact of depth ratio on flow structure and turbulence characteristics of compound open channel flows. Water Sci. Eng. 2021, 15, 265–272. [Google Scholar] [CrossRef]
- Hussaini, M.Y.; Zang, T.A. Spectral methods in fluid dynamics. Annu. Rev. Fluid 1987, 19, 339–367. [Google Scholar] [CrossRef]
- Hirsch, C. Numerical Computation of Internal and External Flows: The Fundamentals of Computational Fluid Dynamics; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Uijttewaal, W.S.J.; Booij, R. Effects of shallowness on the development of free-surface mixing layers. Phys. Fluids 2000, 12, 392–402. [Google Scholar] [CrossRef]
- Batchelor, G.K. Computation of the Energy Spectrum in Homogeneous Two-Dimensional Turbulence. Phys. Fluids 1969, 12, II-233–II-239. [Google Scholar] [CrossRef]
- Hunt, J.C.; Wray, A.A.; Moin, P. Eddies, streams, and convergence zones in turbulent flows. In Studying Turbulence Using Numerical Simulation Databases, 2. Proceedings of the 1988 Summer Program; NASA: Washington, DC, USA, 1988; p. 19890015184142023. Available online: https://ntrs.nasa.gov/citations/19890015184 (accessed on 14 February 2023).



| 0.1 | 0.0910 | 0.02536 | 1.27 | 9.44 | 0.86 |
| 0.3 | 0.1108 | 0.03542 | 1.46 | 7.40 | 1.36 |
| 0.5 | 0.1617 | 0.06075 | 1.76 | 7.62 | 2.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, P.K.; Tang, X.; Rahimi, H. Large-Eddy Simulation of Compound Channels with Staged Floodplains: Flow Interactions and Turbulent Structures. Water 2023, 15, 983. https://doi.org/10.3390/w15050983
Singh PK, Tang X, Rahimi H. Large-Eddy Simulation of Compound Channels with Staged Floodplains: Flow Interactions and Turbulent Structures. Water. 2023; 15(5):983. https://doi.org/10.3390/w15050983
Chicago/Turabian StyleSingh, Prateek Kumar, Xiaonan Tang, and Hamidreza Rahimi. 2023. "Large-Eddy Simulation of Compound Channels with Staged Floodplains: Flow Interactions and Turbulent Structures" Water 15, no. 5: 983. https://doi.org/10.3390/w15050983
APA StyleSingh, P. K., Tang, X., & Rahimi, H. (2023). Large-Eddy Simulation of Compound Channels with Staged Floodplains: Flow Interactions and Turbulent Structures. Water, 15(5), 983. https://doi.org/10.3390/w15050983






