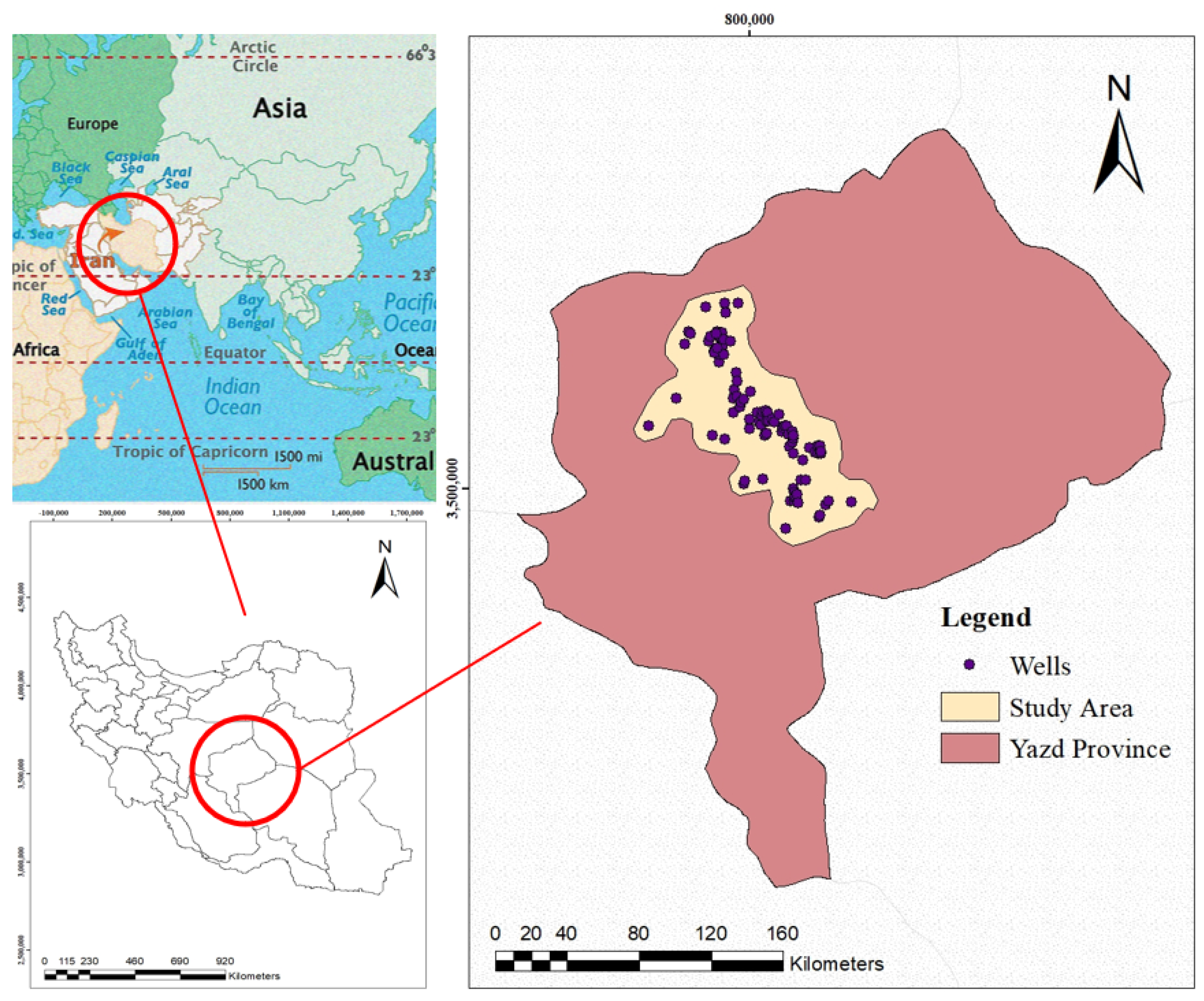
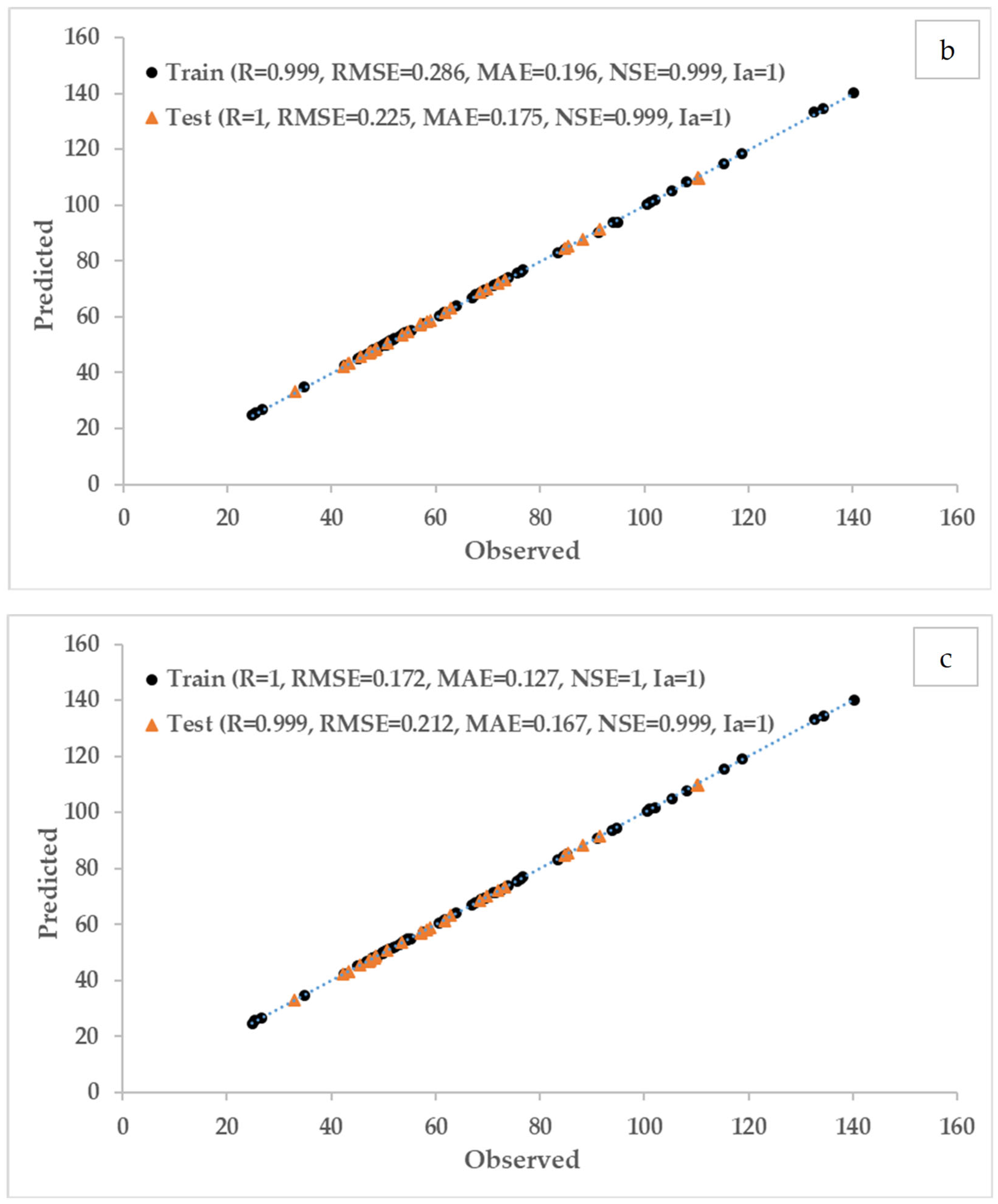
3.1. WQI and FAHP-WQI
The drinking water quality in the study area was evaluated using the WQI index. Moreover, the FAHP-WQI method was used to resolve the inconsistencies in the WQI method.
Figure 2 shows the water quality index within the study area, calculated by means of the Kriging and IDW interpolation methods. As seen in
Figure 2, based on the WQI(WHO) analysis more than 78% of the surface of the Ardakan-Yazd case study area was classified in the excellent or good classes.
As can be observed in
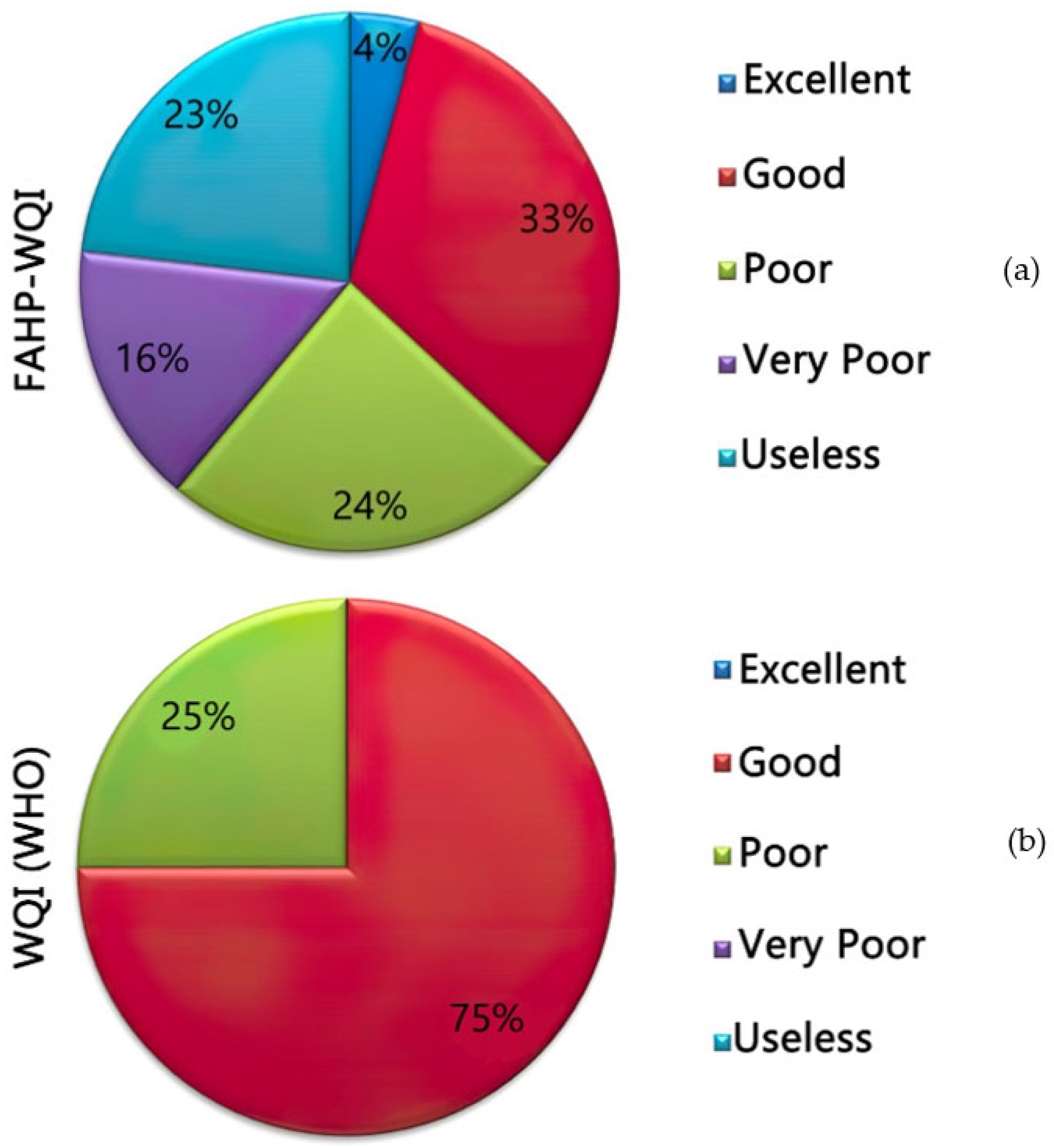
Figure 2, according to the WQI(WHO) analysis 72 wells out of 96 were in a good class regarding water quality, while 23 wells were in a poor class. Furthermore, the southwestern and central regions of the study area had higher-quality drinking water resources compared to the northern and southeastern regions. According to the FAHP-WQI results, 31 water wells out of 96 water wells were in a good class regarding water quality, 23 wells were in the poor class, 22 wells were in the unusable class, and four wells were in the excellent class.
This could be due to the existence of urban areas and the existence of absorptive wells in these parts of the study area. The location of the main wells used for quality assessment in the study area are highlighted in green color. As discussed earlier, the use of the WQI(WHO) method has inconsistencies, but, compared to the FAHP-, more than 60% of the case study areas of Ardakan-Yazd were classified within excellent or good classes. Different interpolation methods used in this study included IDW and ordinary Kriging. The results of classification of the wells under study into five categories of excellent, good, poor, very poor, and unusable, using the WQI(WHO), and FAHP-WQI methods, are presented in
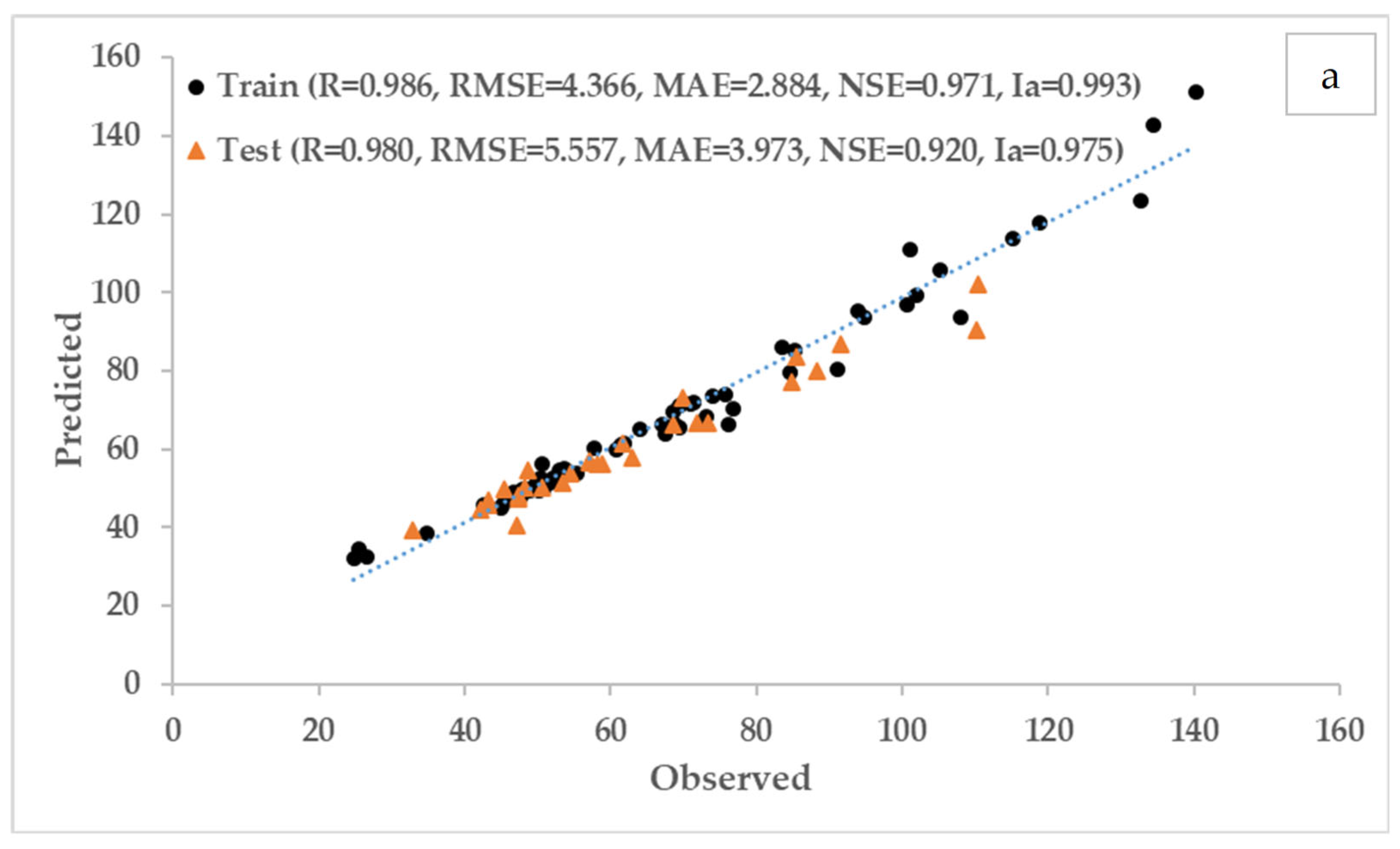
Figure 3. According to the WQI-based rankings, after using the FAHP-WQI model, the results were subject to a lot of changes. Such changes could typically be seen in the vicinity of wells with approximately equal WQI values. When a sample with a lower WQI value had a chemical parameter with a much higher value than other samples with lower WQI degrees, effects, such as those mentioned, became more apparent. Using the Fuzzy Analytic Hierarchy Process method (FAHP), along with WQI, increased the accuracy in weighting parameters and reduced the amount of uncertainty in the water quality calculations.
3.2. Chemical Indicators
To investigate the hydro-geochemistry of groundwaters in the Yazd-Ardakan plain, water samples were collected from 96 agricultural and drinking wells. The samples were collected with the aid of Yazd Agricultural Jihad Management Organization and transferred to the Soil and Water Laboratory of Yazd province for further chemical analysis. the parameters measured in this study included the amounts of calcium (), magnesium (), sodium (), bicarbonate (), sulfate (), chloride (), ec, potassium (), total dissolved solids (tds), total hardness (th), and acidity. Data Quality Assurance and Quality Control (QA/QC) processes were considered throughout the study. Approximately half of the prepared sample volume was specifically and individually checked in the laboratory to ensure QA/QC mechanisms. The accuracy of chemical analysis was confirmed by charge balance errors, and samples were <5% error.
The statistical characteristics of the water of the wells used, along with their standard ranges for the water, are presented in
Table 6. This Table shows that the average of the parameters, pH, HCO
3, Ca, Na, and SO
4, were all located within the normal and standard ranges, but the parameters, EC, TDS, mg, and Ca, were above the allowable standard upper bounds. Despite the average of some samples being in the standard range, the maximum values of all parameters showed that there were areas in the study area that are not suitable for irrigation purposes. The high values of EC and TDS in this plain are due to the existence of salt formations, the amount of water input to the aquifer and the amount of water harvested from it. The electrical conductivity of irrigation water or soil saturation extractives are indicators of the amount of minerals dissolved in the soil environment, and, as such, determine the quality and classification of water and soil in terms of salinity. Therefore, EC must be measured in all studies and research regarding the salinity of water and soil [
50]. The electrical conductivity of groundwater in the region under study was in the range of 375–19,960 μmho/cm, and the average EC value was equal to 4878.21. The total dissolved solid in the study area was also in the range of 240–12,000 mg/L, and the average TDS was equal to 3017.78. As shown in
Figure 4a, the results of constructing a zoning map of the parameters under investigation indicated that, for parameters EC and TDS, the quality of water was not suitable for agriculture in most areas of Yazd-Ardakan plain. In fact, 47.36% of the wells in this plain were in poor condition, according to the EC indicator. Moreover, regarding the parameter TDS, 45.26% of the wells were in poor conditions The salinity in Yazd-Ardakan plain followed a decreasing trend from east to west. There was also a decreasing trend from north to south. The satisfactory water quality in the central and western regions is mainly due to the existence of rocks formed in these regions, because these parts have Eocene-aged rocks of andesite, latite, ignimbrite, and basalt, for which the existing waters are mainly fresh water.
Classification of irrigation water in terms of chloride concentration is necessary due to the special sensitivity of some plants to chloride. Some results showed that a large part (about 38%) of the plain had a concentration higher than the allowable limits. Chloride concentration varies in the range of 0.79 to 208.68 mEq/L and its average for the Yazd-Ardakan plain was equal to 38.39. Chloride had a decreasing trend from east to west and from north to south,
Figure 4b. The probable reasons for rising groundwater Cl concentrations include mixing new waters with higher Cl concentrations, which are mainly of four types: deep liquids, hydrothermal waters, porous water in sea clays, and contaminated surface waters [
51,
52].
The PS indicator reflects the impact of high salt concentrations with respect to chloride and sulfate and increases with the reduction of soil moisture. The water is classified into three classes: good PS (less than 3 mmol/L), average PS (3 to 15 mmol/L) and unusable PS (higher than 15 mmol/L). Using this index, the majority of wells were in the poor range and 41% had no problems in irrigation systems. The decrease in water quality of northern and southern areas with respect to salinity was obvious. Examining the qualitative data from the wells showed that the minimum, maximum and average values were 0.22, 173.99, and 31.81, for sodium, 1.03, 41.82, and 11.88, for magnesium, and 1.2, 46.31, and 10.27 mEq/L for calcium, respectively. This means that 23.15%, 61.05%, and 14.73% of the wells were in poor condition according to these parameters, respectively. The reason for high amounts of magnesium ions and a high percentage of magnesium ions in the water of the wells under investigation is due to reactions to the rocks and geological formations.
Table 6.
Statistical characteristics of well water used, along with their standards [
53].
Table 6.
Statistical characteristics of well water used, along with their standards [
53].
| SO4 | Cl− | Na+ | Mg2+ | Ca2+ | HCO3 | TDS | pH | Ec | Parameter |
|---|
| meq∙L−1 | mg∙L−1 | - | mmoh cm−1 |
|---|
| 45.8 | 208.68 | 173.99 | 41.82 | 46.31 | 10.96 | 12,000 | 8.75 | 19,960 | Maximum |
| 0.42 | 0.79 | 0.22 | 1.03 | 1.2 | 1.52 | 240 | 7 | 375 | Minimum |
| 12.08 | 38.39 | 31.81 | 11.88 | 10.27 | 4.09 | 3017.78 | 7.82 | 4878.21 | Average |
| 10.91 | 45.37 | 37.52 | 10.74 | 9.33 | 1.77 | 2918.01 | 0.31 | 4740.49 | Standard deviation |
| 0–20 | 0–30 | 0–40 | 0–5 | 0–20 | 0–10 | 0–2000 | 6.5–8 | 0–3000 | Standard domain |
Bicarbonate is an important parameter due to the deposition of calcium and magnesium in soil and water, as their deposition increases SAR and intensifies the sodium problem. The amounts of carbonate (CO
3) and bicarbonate (HCO
3) are in equilibrium within ground waters. However, carbonate is released from under the ground immediately after water outflow. Examinations of the data obtained from the wells under study showed that the minimum, maximum and average values were equal to 1.52, 10.96, and 4.09 for bicarbonate, 0.42, 45.8, and 12.08 mEq/L for sulfate, respectively. Equivalence maps of bicarbonate and sulfate values for the Yazd-Ardakan plain were plotted using the ordinary Kriging method and are presented in
Figure 4c.
In the past, water quality was only assessed based on sodium. The truth is that sodium has highly negative effects on soil and plant growth. One way to determine the risk of sodium is to use the sodium absorption ratio. This method was proposed by the American Salinity Laboratory. The minimum, maximum, and average sodium absorption ratios in the Yazd-Ardakan plain were equal to 0.15, 30.9, and 8.37, respectively. Studies suggest that, except for a few cases, waters from other wells had SAR values less than 15, which are within the appropriate range in this regard. This means that 16.9% of the wells were in dire condition in this regard. The values of this index are presented in
Figure 4b, along with the PS index. The calculated total quality index showed that 18.53% of the regions in the Yazd-Ardakan plain had appropriate water quality for irrigation, 65.28% had average water quality, while 18.17% had poor water quality. The SSP ratio, or the percentage of sodium dissolved in water, was calculated using the concentrations of calcium, sodium, and magnesium elements. SSP is an important parameter for investigating salinity risk. High percentages of soluble sodium may prevent plant growth and reduce soil permeability. The maximum, minimum, and average values of the soluble sodium percentage in the Yazd-Ardakan plain were equal to 86.05, 5.05, and 49.08, respectively. The SAR and SSP index zoning map using Kriging interpolation is presented in
Figure 5a. The results showed that 66.31% of the well water had SSP values higher than 40%. The study of spatial changes of this index also showed that its value increased from east to west and from north to south of the plain. The bar diagram of the SSP index and the MAR index of water from wells in the region are presented in
Figure 5. The permissible limit of the MAR parameter for irrigation water is 50% [
54]. Most of the samples under study were above the standard allowable limit of 50% with respect to magnesium absorption ratio. This value reached 60% in some wells, and instances of 80% were also observed in a few wells. The study of zoning of this index, depicted in
Figure 5, showed that the groundwater from the northern areas of the zone had the worst conditions in this regard. Higher magnesium amounts in water not only result in water salinity, but also reduce product yields [
32].
The average Kelley’s ratio for the water of the wells under study was determined to be equal to 1.03. In general, the situation was relatively favorable with respect to this indicator, since Chidambaram et al. [
55] reported that the maximum allowable limit for this component in water is equal to 1. If this ratio became greater than one, it would indicate that the amount of sodium was higher than the two divalent elements of calcium and magnesium, and it would damage soil permeability in the long term. Examining the spatial changes of Kelley’s index in
Figure 5c, the southern areas of the plain were not satisfactory, and the soil permeability had been damaged. The bar diagram of the Kr index, as well as the EC index, along with their allowable limits, are illustrated in
Figure 5.
To investigate the permeability of another index that covers more factors compared to Kelley’s ratio, the permeability index was used. Of course, this index is affected by the long-term use of irrigation water. According to a report by Chidambaram et al. [
55], the appropriate range for the permeability index is from 0.19 to 7.15.
Figure 5c presents the equivalence map of the PI and KR indices throughout the Yazd-Ardakan plain. Examining the spatial variations of PI, the ground waters of this plain had no issues in this regard, but, unlike previous indices, the values for this index were at their highest in the southern and southwestern regions.
Improving groundwater quality, or mitigating the effects of poor water quality, can be complex. In the following, a few suggestions are presented for improving groundwater quality in the study area: (i) implementing Best Management Practices (BMPs). These practices can include reducing the use of fertilizers and pesticides in the agricultural sector and proper waste management; (ii) management of human activities, such as mining, overexploitation of groundwater, and landfilling, which can significantly influence groundwater quality. Proper management and regulation of these activities can help prevent groundwater pollution.