Modified Numerical Method for Improving the Calculation of Rill Detachment Rate
Abstract
:1. Introduction
2. Methods and Data Source
2.1. Rill Erosion Process
2.2. Numerical Method for Calculating Rill Detachment Rate
2.3. Analytical Method for Calculating Rill Detachment Rate
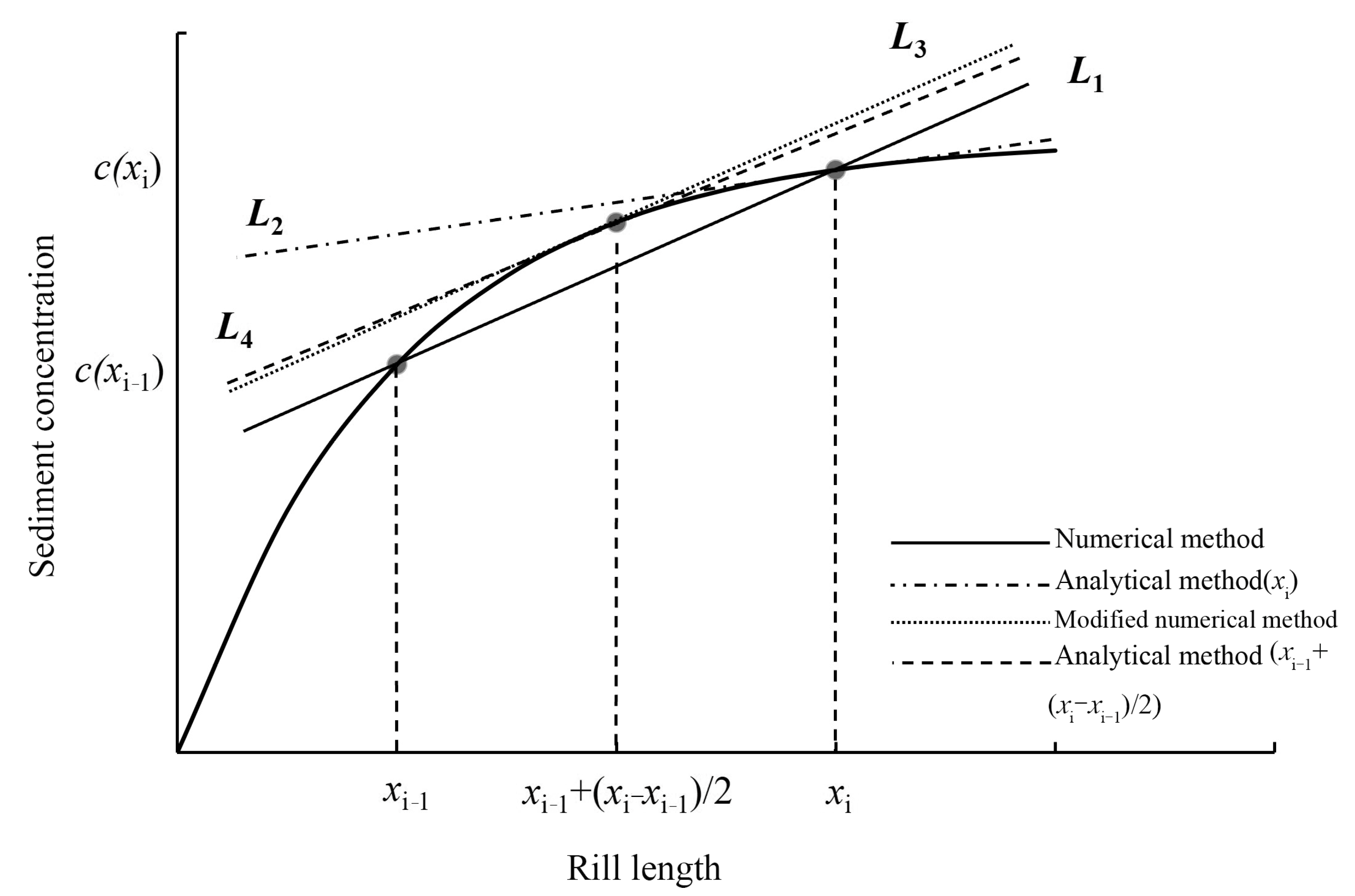
2.4. Principle of Modified Numerical Method
2.5. Basic Dataset
2.6. Statistical Analysis
3. Results
3.1. Comparison of Numerical, Analytical, and Modified Numerical Methods
3.2. Improvement Effect of the Modified Numerical Method
4. Discussion
4.1. Necessity and Application of Modified Numerical Method
4.2. Measurement Strategy for Improving Accuracy of Rill Detachment Rate Calculation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nowak, A.; Schneider, C. Environmental characteristics, agricultural land use, and vulnerability to degradation in Malopolska Province (Poland). Sci. Total Environ. 2017, 590, 620–632. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Coop, M.R.; Zhang, M.; Wang, G. The mechanics of a saturated silty loess and implications for landslides. Eng. Geol. 2018, 236, 29–42. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, A.; Yu, Z.; Yu, J.; Liu, Y.; Zhang, G.; Liu, G.; Wang, P.; Ding, S. Factors contributing to rill erosion of forest roads in a mountainous watershed. J. Environ. Manag. 2023, 326, 116829. [Google Scholar] [CrossRef] [PubMed]
- Du, H.; Dou, S.; Deng, X.; Xue, X.; Wang, T. Assessment of wind and water erosion risk in the watershed of the Ningxia-Inner Mongolia Reach of the Yellow River, China. Ecol. Indic. 2016, 67, 117–131. [Google Scholar] [CrossRef]
- Yimer, F.; Messing, I.; Ledin, S.; Abdelkadir, A. Effects of different land use types on infiltration capacity in a catchment in the highlands of Ethiopia. Soil Use Manag. 2008, 24, 344–349. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, W.; Lei, T.; Li, F.; Li, J. Saturation effect on the distribution of rill detachment rate. Eur. J. Soil Sci. 2021, 72, 2076–2087. [Google Scholar] [CrossRef]
- Chen, X.-Y.; Huang, Y.-H.; Zhao, Y.; Mo, B.; Mi, H.-X. Comparison of loess and purple rill erosions measured with volume replacement method. J. Hydrol. 2015, 530, 476–483. [Google Scholar] [CrossRef]
- Wang, J.F.; Yang, Y.F.; Liu, G.B.; Wang, B.; Zhang, F.B.; Fang, N.F. Investigating the effects of herbaceous root systems on the soil detachment process at the species level. Sci. Total Environ. 2023, 859, 160196. [Google Scholar] [CrossRef]
- Hairsine, P.B.; Rose, C.W. Modeling water erosion due to overland flow using physical principles: 2. Rill flow. Water Resour. Res. 1992, 28, 245–250. [Google Scholar] [CrossRef]
- Morgan, R.P.C.; Qinton, J.N.; Smith, R.E.; Govers, G.; Poesen, J.W.A.; Auerswald, K.; Chisci, G.; Torri, D.; Styczen, M.E. The European soil erosion model (EUROSEM): A dynamic approach for predicting sediment transport from fields and small catchments—Reply. Earth Surf. Process. Landf. 1999, 24, 567–568. [Google Scholar] [CrossRef]
- Nearing, M.A.; Bradford, J.M.; Parker, S.C. Soil detachment by shallow flow at low slopes. Soil Sci. Soc. Am. J. 1991, 55, 339–344. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, N.; Shi, M.; Zhai, Y.; Wu, F. The effects of tillage induced surface roughness, slope and discharge rate on soil detachment by concentrated flow: An experimental study. Hydrol. Process. 2021, 35, e14261. [Google Scholar] [CrossRef]
- Xiao, H.; Liu, G.; Liu, P.; Zheng, F.; Zhang, J.; Hu, F. Response of soil detachment rate to the hydraulic parameters of concentrated flow on steep loessial slopes on the Loess Plateau of China. Hydrol. Process. 2017, 31, 2613–2621. [Google Scholar] [CrossRef]
- Wu, B.; Wang, Z.-l.; Zhang, Q.-W.; Shen, N.; Liu, J. Response of soil detachment rate by raindrop-affected sediment-laden sheet flow to sediment load and hydraulic parameters within a detachment-limited sheet erosion system on steep slopes on Loess Plateau, China. Soil Tillage Res. 2019, 185, 9–16. [Google Scholar] [CrossRef]
- Cao, L.; Zhang, K.; Zhang, W. Detachment of road surface soil by flowing water. Catena 2009, 76, 155–162. [Google Scholar] [CrossRef]
- Rehman, Z.U.; Khalid, U.; Ijaz, N.; Mujtaba, H.; Haider, A.; Farooq, K.; Ijaz, Z. Machine learning-based intelligent modeling of hydraulic conductivity of sandy soils considering a wide range of grain sizes. Eng. Geol. 2022, 311, 106899. [Google Scholar] [CrossRef]
- Ijaz, N.; Ijaz, Z.; Rehman, Z.U. Recycling of paper/wood industry waste for hydromechanical stability of expansive soils: A novel approach. J. Clean. Prod. 2022, 348, 131345. [Google Scholar] [CrossRef]
- Shi, Z.H.; Fang, N.F.; Wu, F.Z.; Wang, L.; Yue, B.J.; Wu, G.L. Soil erosion processes and sediment sorting associated with transport mechanisms on steep slopes. J. Hydrol. 2012, 454, 123–130. [Google Scholar] [CrossRef]
- Li, Z.; Fang, H. Impacts of climate change on water erosion: A review. Earth-Sci. Rev. 2016, 163, 94–117. [Google Scholar] [CrossRef]
- Shen, N.; Wang, Z.; Zhang, F.; Zhou, C. Response of Soil Detachment Rate to Sediment Load and Model Examination: A Key Process Simulation of Rill Erosion on Steep Loessial Hillslopes. Int. J. Environ. Res. Public Health 2023, 20, 2839. [Google Scholar] [CrossRef]
- Zhou, C.; Shen, N.; Zhang, F.; Delang, C.O. Soil detachment by sediment-laden rill flow interpreted using three experimental design methods. Catena 2022, 215, 106332. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, Z.; Liu, J.; Su, X. Effects of root density on soil detachment capacity by overland flow during one growing season. J. Soils Sediments 2022, 22, 1500–1510. [Google Scholar] [CrossRef]
- Ma, J.; Li, Z.; Sun, B.; Ma, B.; Zhang, L. Modeling soil detachment capacity by rill flow under the effect of freeze–thaw and the root system. Nat. Hazards 2022, 112, 207–230. [Google Scholar] [CrossRef]
- Lei, T.W.; Zhang, Q.W.; Zhao, J. Laboratory experiments and computational method of soils detachment rate of sediment loading flow in rills. Trans. Chin. Soc. Agric. Eng. 2001, 17, 24–27. (In Chinese) [Google Scholar]
- Merten, G.H.; Nearing, M.A.; Borges, A.L.O. Effect of sediment load on soil detachment and deposition in rills. Soil Sci. Soc. Am. J. 2001, 65, 861–868. [Google Scholar] [CrossRef]
- Shen, N.; Wang, Z.; Zhang, Q.; Wu, B.; Wang, D.; Zhang, Q.; Liu, J. Quantifying the Contribution of Sediment Load to Soil Detachment Rate by Sediment-Laden Rill Flow. Soil Sci. Soc. Am. J. 2017, 81, 1526–1536. [Google Scholar] [CrossRef]
- Zhang, Q.; Lei, T.; Zhao, J. Estimation of the detachment rate in eroding rills in flume experiments using an REE tracing method. Geoderma 2008, 147, 8–15. [Google Scholar] [CrossRef]
- Chen, X.-Y.; Huang, Y.-H.; Zhao, Y.; Mo, B.; Mi, H.-X.; Huang, C.-H. Analytical method for determining rill detachment rate of purple soil as compared with that of loess soil. J. Hydrol. 2017, 549, 236–243. [Google Scholar] [CrossRef]
- Han, Z.; Chen, X.; Li, Y.; Chen, S.; Gu, X.; Wei, C. Quantifying the rill-detachment process along a saturated soil slope. Soil Tillage Res. 2020, 204, 104726. [Google Scholar] [CrossRef]
- Chen, C.; Lei, T.; Ban, Y. Influence of slope, flow rate, and thawed depth on soil detachment rate in partially thawed black soils. J. Hydrol. 2021, 603, 127009. [Google Scholar] [CrossRef]
- Lei, T.W.; Zhang, Q.W.; Zhao, J.; Xia, W.S.; Pan, Y.H. Soil detachment rates for sediment loaded flow in rills. Am. Soc. Agric. Biol. Eng. 2002, 45, 1897–1903. [Google Scholar] [CrossRef]
- Chen, X.-Y.; Zha, Y.; Mi, H.-X.; Mo, B. Estimating rill erosion process from eroded morphology in flume experiments by volume replacement method. Catena 2016, 136, 135–140. [Google Scholar] [CrossRef]
- Huang, Y.; Li, F.; Wang, W.; Li, J. Rill erosion processes on a constantly saturated slope. Hydrol. Process. 2020, 34, 3955–3965. [Google Scholar] [CrossRef]
- Han, Z.; Chen, X.; Li, Y.; Chen, S.; Gu, X.; Wei, C. Estimating rill erosion and sediment transport processes along a saturated purple soil slope. Can. J. Soil Sci. 2021, 101, 507–516. [Google Scholar] [CrossRef]
- Lane, L.J.; Nearing, M.A. Erosion component. In USDA-Water Erosion Prediction Project: Hillslope Profile Model Documentation; Lafayette, W., Ed.; Soil Erosion Research Laboratory: West Lafayette, IN, USA, 1989. [Google Scholar]
- Nearing, M.A.; Foster, G.R.; Lane, L.J.; Finkner, S.C. A process-based soil erosion model for USDA-water prediction project technology. Am. Soc. Agric, Biol. Eng. 1989, 32, 1587–1593. [Google Scholar] [CrossRef]
- Flanagan, D.C.; Nearing, M.A. USDA Water Erosion Prediction Project Hillslope and Watershed Model Documentation; NSERL Rep. No. 10; Lafayette, W., Ed.; USDAARS National Soil Erosion Research Laboratory: West Lafayette, IN, USA, 1995.
- Foster, G.R.; Meyer, L.D. A closed-form soil erosion equation for upland areas. In Sedimentation Symposium to Honor Professor H. A. Einstein; University of California: Oakland, CA, USA, 1972. [Google Scholar]
- Foster, G.R.; Meyer, L.D. Transport of soil particles by shallow flow. Am. Soc. Agric. Biol. Eng. 1972, 15, 99–102. [Google Scholar] [CrossRef]
- Lei, T.W.; Zhang, Q.W.; Zhao, J.; Nearing, M.A. Tracing sediment dynamics and sources in eroding rills with rare earth elements. Eur. J. Soil Sci. 2006, 57, 287–294. [Google Scholar] [CrossRef]
- Gimenez, R.; Govers, G. Flow detachment by concentrated flow on smooth and irregular beds. Soil Sci. Soc. Am. J. 2002, 66, 1475–1483. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, X.; Li, F.; Zhang, J.; Lei, T.; Li, J.; Chen, P.; Wang, X. Velocity of water flow along saturated loess slopes under erosion effects. J. Hydrol. 2018, 561, 304–311. [Google Scholar] [CrossRef]
- Wang, Y.; Luo, J.; Zheng, Z.; Li, T.; He, S.; Zhang, X.; Wang, Y.; Liu, T. Assessing the contribution of the sediment content and hydraulics parameters to the soil detachment rate using a flume scouring experiment. Catena 2019, 176, 315–323. [Google Scholar] [CrossRef]
- Shen, N.; Wang, Z.; Zhang, Q.; Wu, B.; Liu, J. Modelling the process of soil detachment by rill flow on steep loessial hillslopes. Earth Surf. Process. Landf. 2020, 45, 1240–1247. [Google Scholar] [CrossRef]
- Huang, C.H.; Bradford, J.M.; Laflen, J.M. Evaluation of the detachment-transport coupling concept in the WEEP rill erosion equation. Soil Sci. Soc. Am. J. 1996, 60, 734–739. [Google Scholar] [CrossRef]
- Polyakov, V.O.; Nearing, M.A. Sediment transport in rill flow under deposition and detachment conditions. Catena 2003, 51, 33–43. [Google Scholar] [CrossRef]



| Slope (°) | Flow Rate (L·min−1) | Parameters | Coefficient of Determination (R2) | |
|---|---|---|---|---|
| A (kg·m−3) | B (m−1) | |||
| 5 | 2 | 465.34 | 0.32 | 0.92 |
| 4 | 623.89 | 0.44 | 0.99 | |
| 8 | 696.29 | 0.37 | 0.97 | |
| 10 | 2 | 800.81 | 0.32 | 0.98 |
| 4 | 800.02 | 0.33 | 0.99 | |
| 8 | 767.42 | 0.48 | 0.99 | |
| 15 | 2 | 907.93 | 1.09 | 0.99 |
| 4 | 965.44 | 1.17 | 0.99 | |
| 8 | 929.38 | 0.99 | 0.99 | |
| 20 | 2 | 1027.49 | 1.19 | 0.99 |
| 4 | 1071.35 | 1.08 | 0.99 | |
| 8 | 1054.62 | 1.23 | 0.99 | |
| Slope (°) | Flow Rate (L·min−1) | Rill Detachment Rate (kg·m−2·s−1) | |||
|---|---|---|---|---|---|
| 1 m Rill Length | 2 m Rill Length | 4 m Rill Length | 8 m Rill Length | ||
| 5 | 2 | 0.047 | 0.007 | 0.036 | 0.006 |
| 4 | 0.144 | 0.117 | 0.035 | 0.015 | |
| 8 | 0.363 | 0.148 | 0.066 | 0.049 | |
| 10 | 2 | 0.069 | 0.053 | 0.036 | 0.017 |
| 4 | 0.138 | 0.135 | 0.051 | 0.036 | |
| 8 | 0.413 | 0.198 | 0.121 | 0.045 | |
| 15 | 2 | 0.210 | 0.046 | 0.018 | 0.006 |
| 4 | 0.458 | 0.104 | 0.033 | 0.008 | |
| 8 | 0.783 | 0.279 | 0.082 | 0.006 | |
| 20 | 2 | 0.241 | 0.067 | 0.015 | 0.002 |
| 4 | 0.487 | 0.125 | 0.035 | 0.016 | |
| 8 | 0.994 | 0.294 | 0.033 | 0.026 | |
| Slope (°) | Flow Rate (L·min−1) | Proportional Coefficients | Coefficients of Determination | pr | ps | ||
|---|---|---|---|---|---|---|---|
| h | k | Rr2 | Rs2 | ||||
| 5 | 2 | 1.468 | 1.523 | 0.92 | 0.84 | 0.043 | 0.081 |
| 4 | 1.304 | 1.293 | 0.98 | 0.97 | <0.001 | 0.002 | |
| 8 | 1.305 | 1.360 | 0.94 | 0.90 | 0.006 | 0.014 | |
| 10 | 2 | 1.176 | 1.144 | 0.98 | 0.96 | 0.001 | 0.003 |
| 4 | 1.222 | 1.193 | 0.97 | 0.94 | 0.002 | 0.006 | |
| 8 | 1.293 | 1.295 | 0.98 | 0.97 | 0.001 | 0.001 | |
| 15 | 2 | 1.831 | 1.843 | 0.98 | 0.94 | <0.001 | 0.033 |
| 4 | 1.917 | 1.948 | 0.99 | 0.97 | <0.001 | 0.017 | |
| 8 | 1.714 | 1.719 | 0.99 | 0.99 | <0.001 | 0.003 | |
| 20 | 2 | 1.930 | 1.952 | 0.99 | 0.99 | <0.001 | 0.002 |
| 4 | 1.816 | 1.834 | 0.99 | 0.97 | <0.001 | 0.016 | |
| 8 | 1.970 | 1.952 | 0.99 | 0.99 | <0.001 | 0.004 | |
| Slope (°) | Flow Rate (L·min−1) | Proportional Coefficient | Coefficient of Determination | p |
|---|---|---|---|---|
| m | R2 | |||
| 5 | 2 | 0.930 | 0.68 | 0.054 |
| 4 | 1.028 | 0.97 | 0.001 | |
| 8 | 1.062 | 0.91 | 0.007 | |
| 10 | 2 | 0.988 | 0.99 | <0.001 |
| 4 | 1.016 | 0.96 | 0.002 | |
| 8 | 1.007 | 0.98 | <0.001 | |
| 15 | 2 | 1.062 | 0.98 | <0.001 |
| 4 | 1.068 | 0.99 | <0.001 | |
| 8 | 1.044 | 0.99 | <0.001 | |
| 20 | 2 | 1.064 | 0.99 | <0.001 |
| 4 | 1.057 | 0.99 | <0.001 | |
| 8 | 1.064 | 0.99 | <0.001 |
| Study | Soil Type | Rill Width (m) | Slope | Flow Rate (L·min−1) | Proportional Coefficient | Coefficient of Determination | ph | pm | ||
|---|---|---|---|---|---|---|---|---|---|---|
| h | m | Rh2 | Rm2 | |||||||
| Chen et al. [28] | Purple soil | 0.1 | 10° | 4 | 1.06 | 1.00 | 0.93 | 0.93 | <0.001 | <0.001 |
| 8 | 0.93 | 0.86 | 0.95 | 0.96 | <0.001 | <0.001 | ||||
| 15° | 2 | 1.22 | 1.08 | 0.96 | 0.96 | <0.001 | <0.001 | |||
| 4 | 1.19 | 1.05 | 0.97 | 0.98 | <0.001 | <0.001 | ||||
| 8 | 1.16 | 0.98 | 0.97 | 0.99 | <0.001 | <0.001 | ||||
| 20° | 2 | 1.19 | 1.01 | 0.96 | 0.97 | <0.001 | <0.001 | |||
| 4 | 1.11 | 0.94 | 0.99 | 0.99 | <0.001 | <0.001 | ||||
| 8 | 1.10 | 0.95 | 0.96 | 0.97 | <0.001 | <0.001 | ||||
| 25° | 2 | 1.16 | 1.01 | 0.97 | 0.97 | <0.001 | <0.001 | |||
| 4 | 1.24 | 1.07 | 0.97 | 0.98 | <0.001 | <0.001 | ||||
| 8 | 1.09 | 0.93 | 0.95 | 0.97 | <0.001 | <0.001 | ||||
| Lei et al. [40] | Loess soil | 0.1 | 10° | 4 | 1.00 | 1.00 | 0.95 | 0.95 | <0.001 | <0.001 |
| 8 | 1.03 | 0.99 | 0.91 | 0.91 | <0.001 | <0.001 | ||||
| 12 | 1.00 | 0.99 | 0.99 | 0.99 | <0.001 | <0.001 | ||||
| 15° | 4 | 1.16 | 1.01 | 0.98 | 0.98 | <0.001 | <0.001 | |||
| 8 | 0.99 | 0.99 | 0.96 | 0.96 | <0.001 | <0.001 | ||||
| 12 | 0.99 | 0.98 | 0.97 | 0.97 | <0.001 | <0.001 | ||||
| 20° | 4 | 1.04 | 0.98 | 0.94 | 0.94 | <0.001 | <0.001 | |||
| 8 | 1.03 | 0.98 | 0.89 | 0.9 | <0.001 | <0.001 | ||||
| 12 | 1.04 | 0.99 | 0.97 | 0.97 | <0.001 | <0.001 | ||||
| 25° | 4 | 1.06 | 0.97 | 0.91 | 0.91 | <0.001 | <0.001 | |||
| 8 | 1.06 | 0.99 | 0.95 | 0.95 | <0.001 | <0.001 | ||||
| 12 | 1.06 | 0.99 | 0.96 | 0.96 | <0.001 | <0.001 | ||||
| Zhang et al. [27] | Loess soil | 0.1 | 17.62% | 8 | 1.15 | 1.05 | 0.93 | 0.92 | <0.001 | <0.001 |
| 12 | 1.12 | 1.09 | 0.99 | 0.98 | <0.001 | <0.001 | ||||
| 26.78% | 2 | 1.03 | 0.98 | 0.97 | 0.96 | <0.001 | <0.001 | |||
| 4 | 1.04 | 0.99 | 0.99 | 0.95 | <0.001 | <0.001 | ||||
| 8 | 1.10 | 1.01 | 0.98 | 0.99 | <0.001 | <0.001 | ||||
| 36.38% | 2 | 1.08 | 0.97 | 0.96 | 0.96 | <0.001 | <0.001 | |||
| 4 | 1.06 | 0.94 | 0.96 | 0.97 | <0.001 | <0.001 | ||||
| 8 | 1.12 | 0.99 | 0.99 | 0.99 | <0.001 | <0.001 | ||||
| 46.60% | 2 | 1.19 | 1.02 | 0.98 | 0.98 | <0.001 | <0.001 | |||
| 4 | 1.20 | 1.03 | 0.99 | 0.99 | <0.001 | <0.001 | ||||
| 8 | 1.02 | 0.92 | 0.95 | 0.96 | <0.001 | <0.001 | ||||
| Huang et al. [45] | Russell silt loam | 0.2 | 6.30% | 15.1 | 2.10 | 1.04 | 0.87 | 0.84 | 0.069 | 0.081 |
| 22.7 | 2.40 | 1.05 | 0.99 | 0.88 | 0.066 | 0.061 | ||||
| 30.2 | 1.17 | 0.95 | 0.9 | 0.8 | 0.039 | 0.042 | ||||
| 37.8 | 1.05 | 0.92 | 0.92 | 0.83 | 0.029 | 0.031 | ||||
| Saybrook silt loam | 0.2 | 2.40% | 7.6 | 1.55 | 1.20 | 0.94 | 0.87 | 0.065 | 0.066 | |
| 15.1 | 1.46 | 1.05 | 0.97 | 0.95 | 0.026 | 0.027 | ||||
| 22.7 | 1.01 | 0.94 | 0.99 | 0.99 | <0.001 | <0.001 | ||||
| Polyakov and Nearing [46] | Carmi loam | 0.61 | 7% | 6 | 1.40 | 1.09 | 0.79 | 0.77 | 0.045 | 0.052 |
| 9 | 1.29 | 0.89 | 0.91 | 0.90 | 0.045 | 0.053 | ||||
| Study | Soil Type | Rill Width (m) | Slope | Flow Rate (L·min−1) | Average Absolute Error (kg·m−2·s−1) | |
|---|---|---|---|---|---|---|
| 0–4 m | 4–8 m | |||||
| Huang et al. [6,33] | Loess soil | 0.1 | 5 | 2 | 0.061 | 0.331 |
| 4 | 0.201 | 0.043 | ||||
| 8 | 0.411 | 0.073 | ||||
| 10 | 2 | 0.105 | 0.044 | |||
| 4 | 0.197 | 0.080 | ||||
| 8 | 0.499 | 0.063 | ||||
| 15 | 2 | 0.211 | 0.002 | |||
| 4 | 0.464 | 0.005 | ||||
| 8 | 0.835 | 0.018 | ||||
| 20 | 2 | 0.247 | 0.004 | |||
| 4 | 0.498 | 0.008 | ||||
| 8 | 1.053 | 0.008 | ||||
| Chen et al. [28] | Purple soil | 0.1 | 10° | 4 | 0.055 | 0.017 |
| 8 | 0.125 | 0.061 | ||||
| 15° | 2 | 0.063 | 0.021 | |||
| 4 | 0.147 | 0.044 | ||||
| 8 | 0.382 | 0.066 | ||||
| 20° | 2 | 0.072 | 0.011 | |||
| 4 | 0.168 | 0.023 | ||||
| 8 | 0.368 | 0.074 | ||||
| 25° | 2 | 0.066 | 0.014 | |||
| 4 | 0.196 | 0.038 | ||||
| 8 | 0.349 | 0.048 | ||||
| Lei et al. [40] | loess soil | 0.1 | 10° | 4 | - | - |
| 8 | 0.241 | 0.070 | ||||
| 12 | 0.353 | 0.320 | ||||
| 15° | 4 | 0.228 | 0.073 | |||
| 8 | - | - | ||||
| 12 | 0.416 | 0.507 | ||||
| 20° | 4 | 0.196 | 0.122 | |||
| 8 | 0.343 | 0.099 | ||||
| 12 | 0.555 | 0.067 | ||||
| 25° | 4 | 0.198 | 0.120 | |||
| 8 | 0.375 | 0.113 | ||||
| 12 | 0.583 | 0.095 | ||||
| Zhang et al. [27] | Loess soil | 0.1 | 17.62% | 8 | 0.165 | 0.064 |
| 12 | 0.229 | 0.172 | ||||
| 26.78% | 2 | 0.086 | 0.048 | |||
| 4 | 0.165 | 0.095 | ||||
| 8 | 0.396 | 0.162 | ||||
| 36.38% | 2 | 0.115 | 0.037 | |||
| 4 | - | - | ||||
| 8 | 0.491 | 0.116 | ||||
| 46.60% | 2 | 0.142 | 0.021 | |||
| 4 | 0.276 | 0.041 | ||||
| 8 | 0.477 | 0.112 | ||||
| Huang et al. [45] | Russell silt loam | 0.2 | 6.30% | 15.1 | 0.030 | 0.011 |
| 22.7 | 0.045 | 0.027 | ||||
| 30.2 | 0.058 | 0.030 | ||||
| 37.8 | 0.067 | 0.043 | ||||
| Saybrook silt loam | 0.2 | 2.40% | 7.6 | 0.016 | 0.014 | |
| 15.1 | 0.049 | 0.029 | ||||
| 22.7 | 0.051 | 0.039 | ||||
| Polyakov and Nearing [46] | Carmi loam | 0.61 | 7% | 6 | - | - |
| 9 | 0.005 | 0.002 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Zhao, M.; Wan, D.; Lei, T.; Li, F.; Wang, W. Modified Numerical Method for Improving the Calculation of Rill Detachment Rate. Water 2023, 15, 1875. https://doi.org/10.3390/w15101875
Huang Y, Zhao M, Wan D, Lei T, Li F, Wang W. Modified Numerical Method for Improving the Calculation of Rill Detachment Rate. Water. 2023; 15(10):1875. https://doi.org/10.3390/w15101875
Chicago/Turabian StyleHuang, Yuhan, Mingquan Zhao, Dan Wan, Tingwu Lei, Fahu Li, and Wei Wang. 2023. "Modified Numerical Method for Improving the Calculation of Rill Detachment Rate" Water 15, no. 10: 1875. https://doi.org/10.3390/w15101875




