A New Graph-Based Deep Learning Model to Predict Flooding with Validation on a Case Study on the Humber River
Abstract
:1. Introduction
- Develop a new state-of-the-art model for flooding forecasting, allowing for a more precise and accurate early flooding alert system.
- Verify the addition of spatiotemporal data for improved flooding forecasting results.
- Development of a reliable ML model based on graph theory and DL paradigm.
2. Proposed Model
2.1. Persistence Model
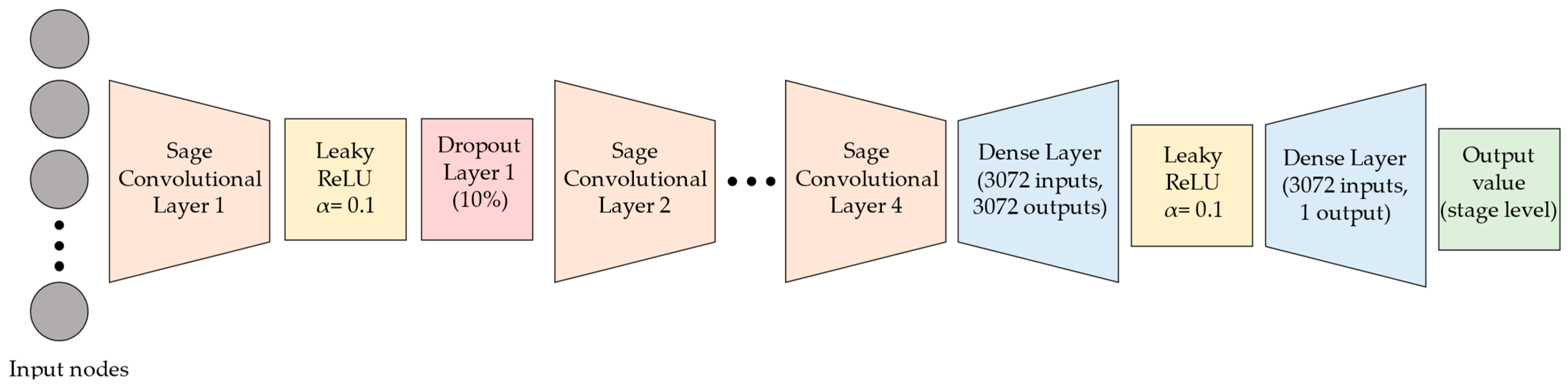
2.2. GNN-SAGE and GNN-ResGated Models
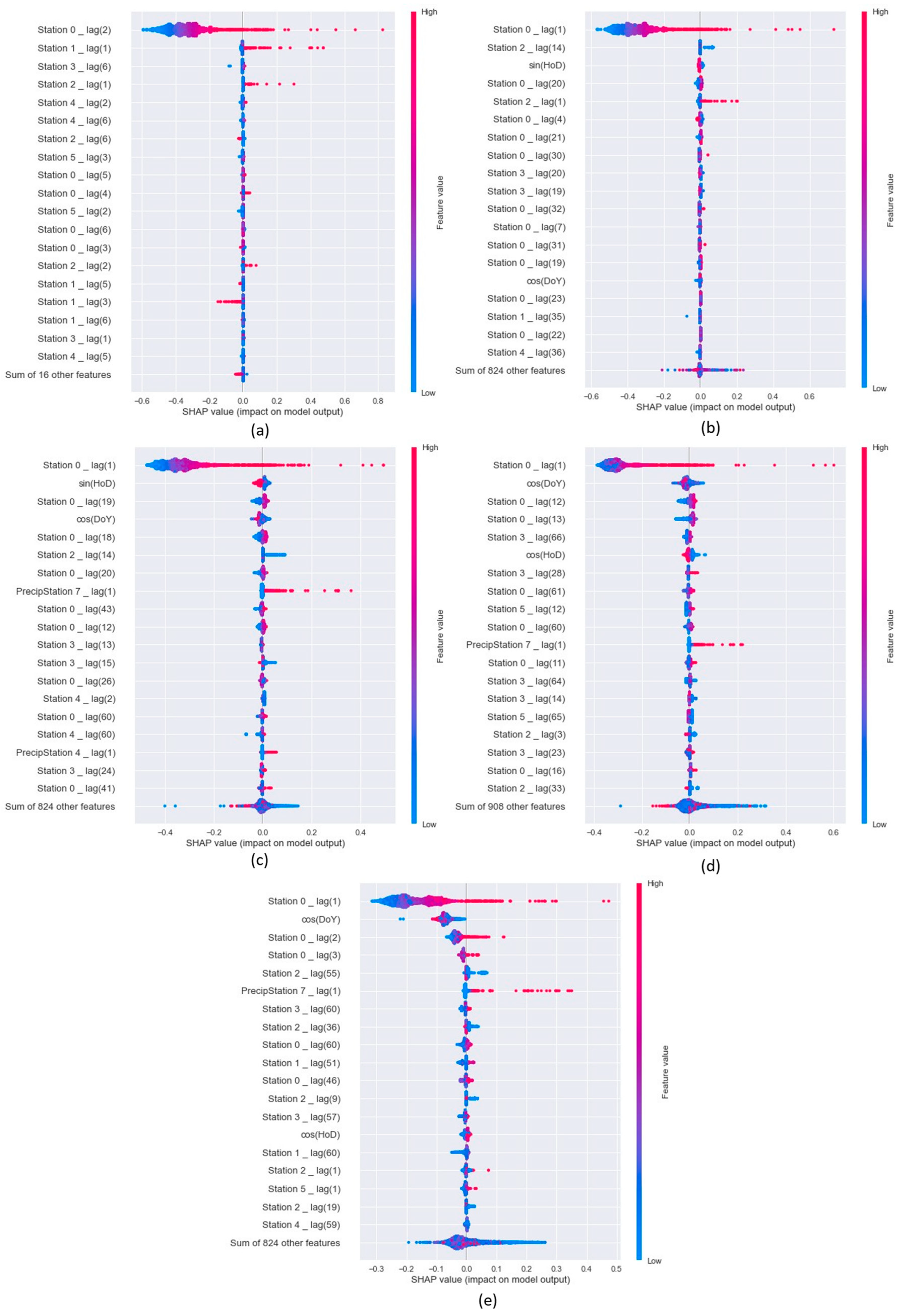
2.3. SHAP Analysis
3. Validation and Analysis of Results
3.1. Humber River Description
3.2. Evaluation Metrics
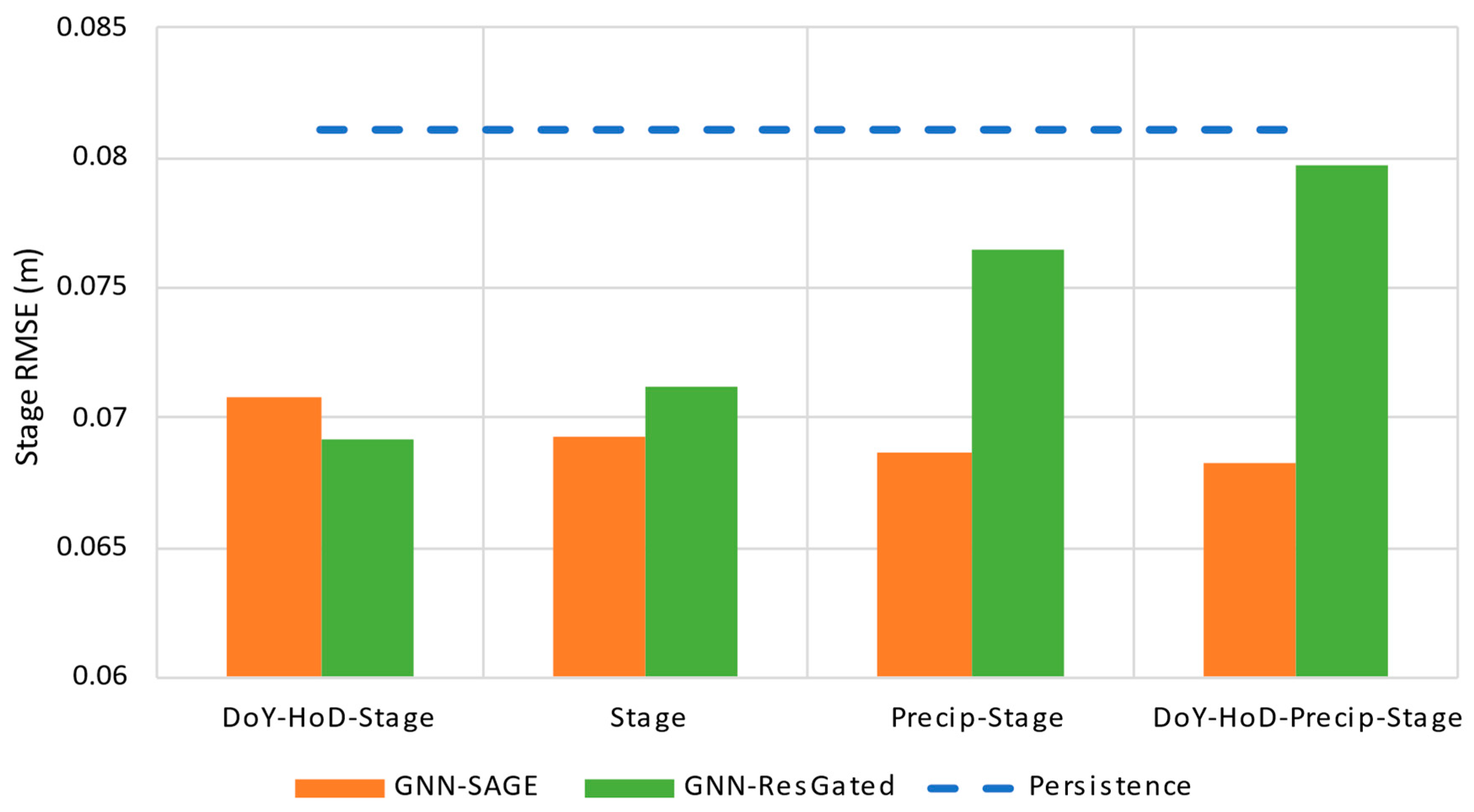
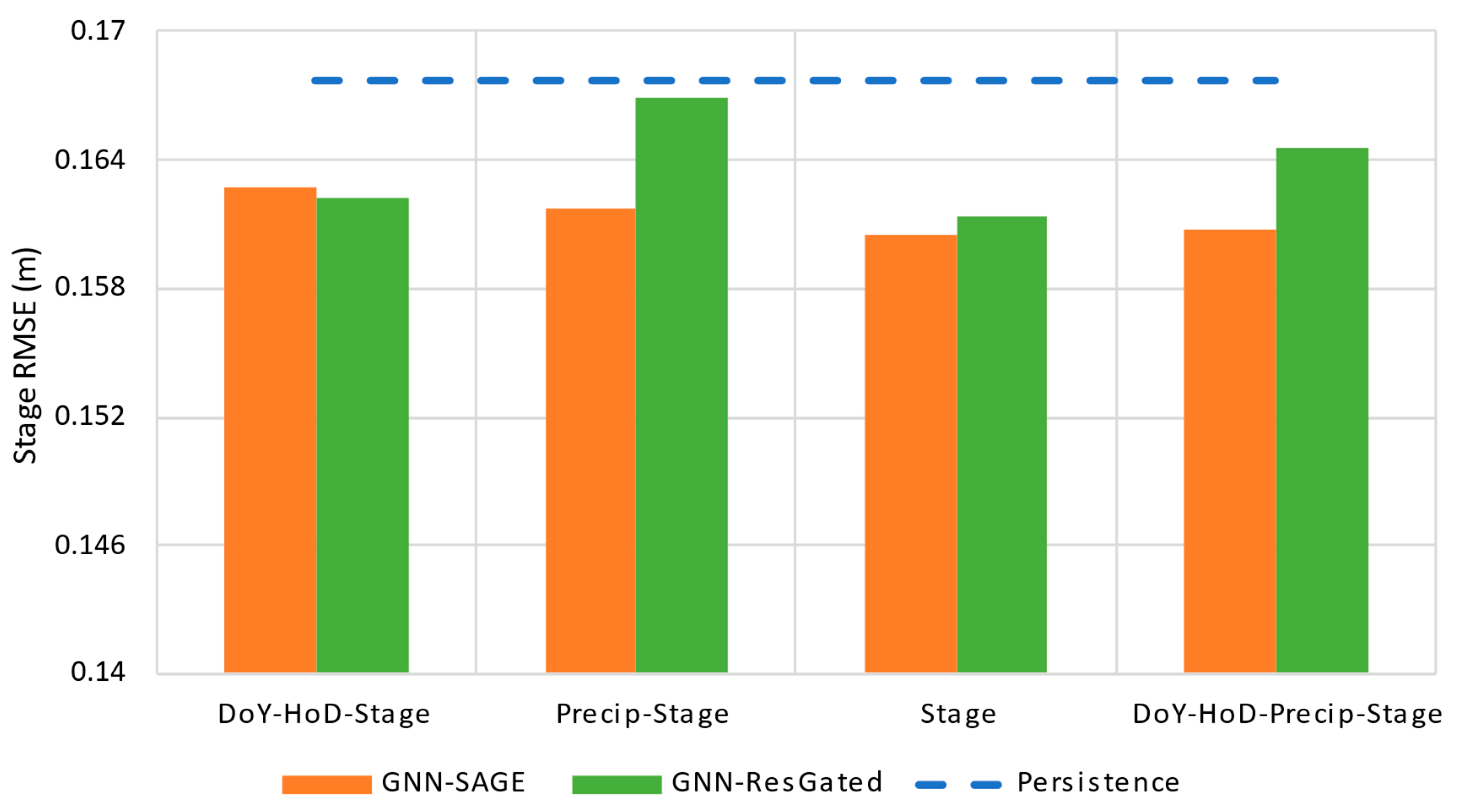
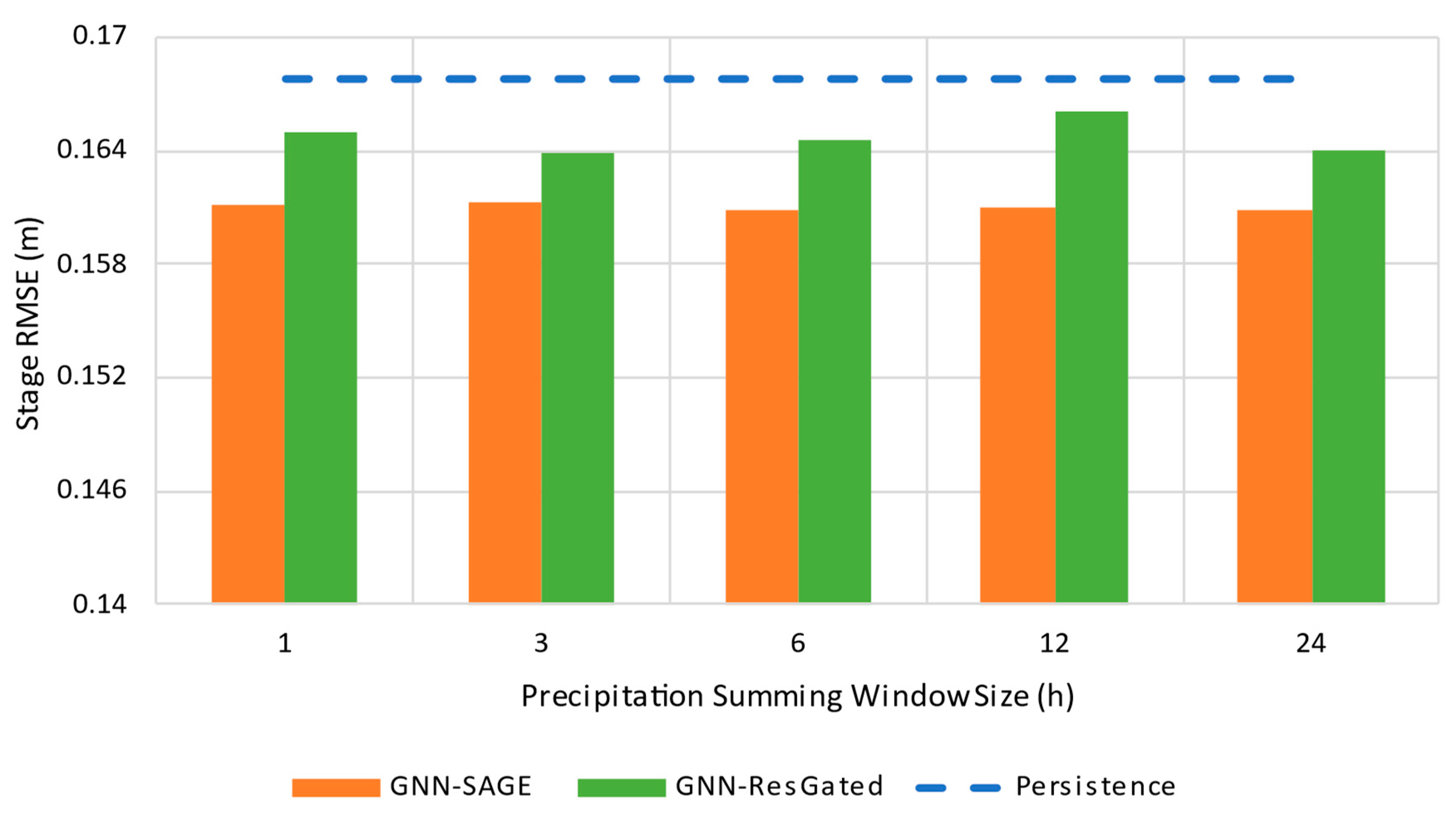
3.3. Dataset Size Evaluation
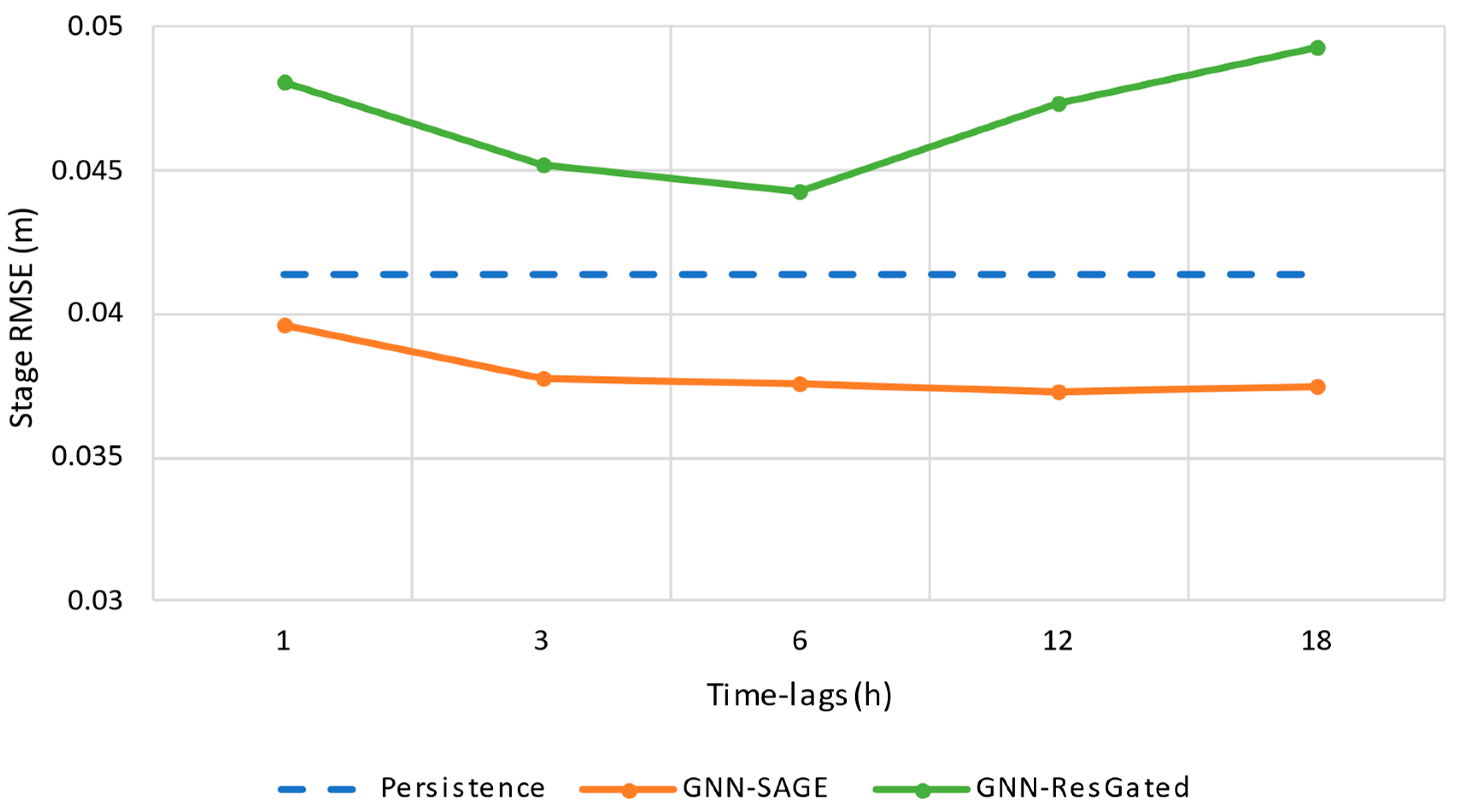
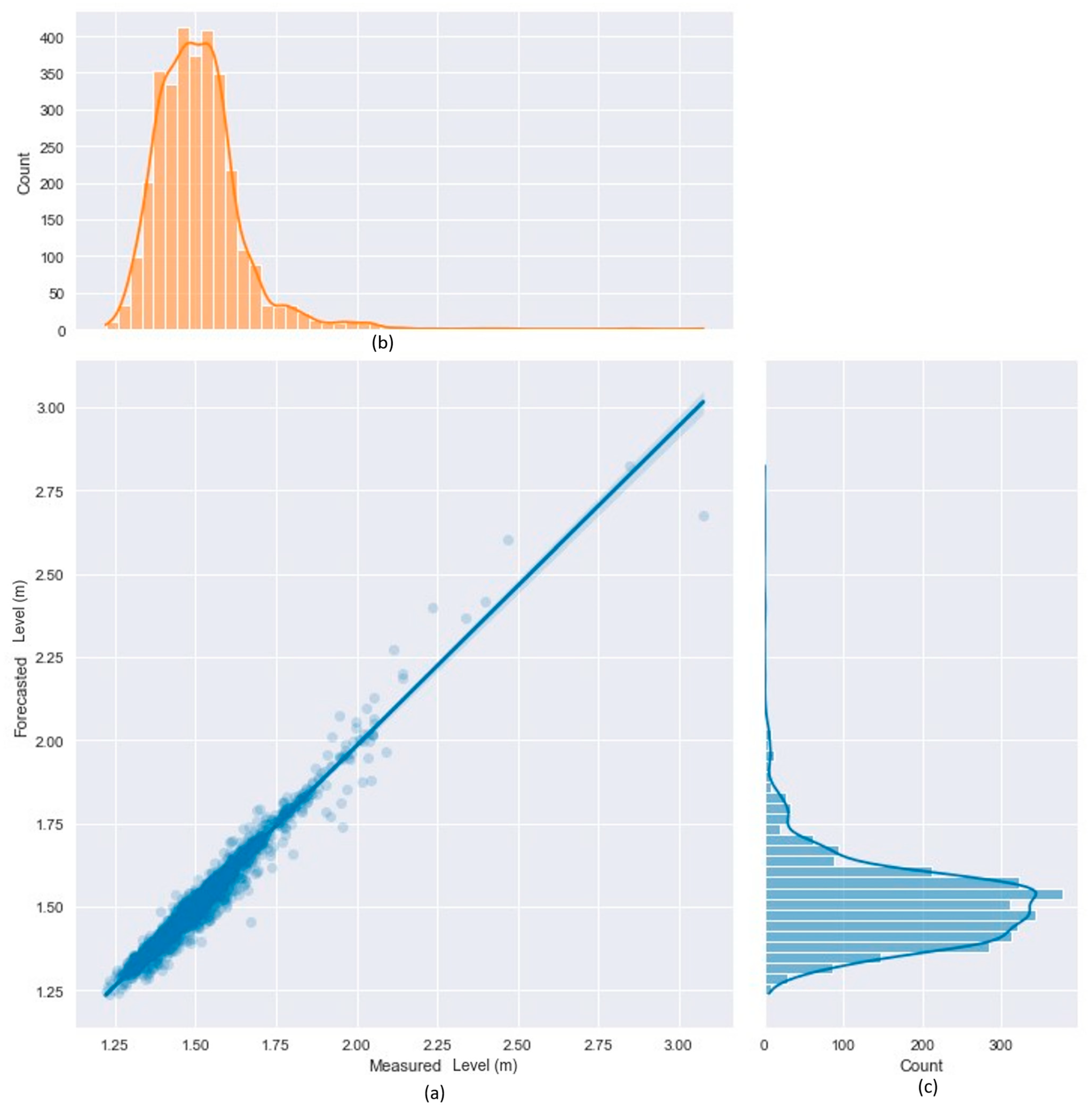
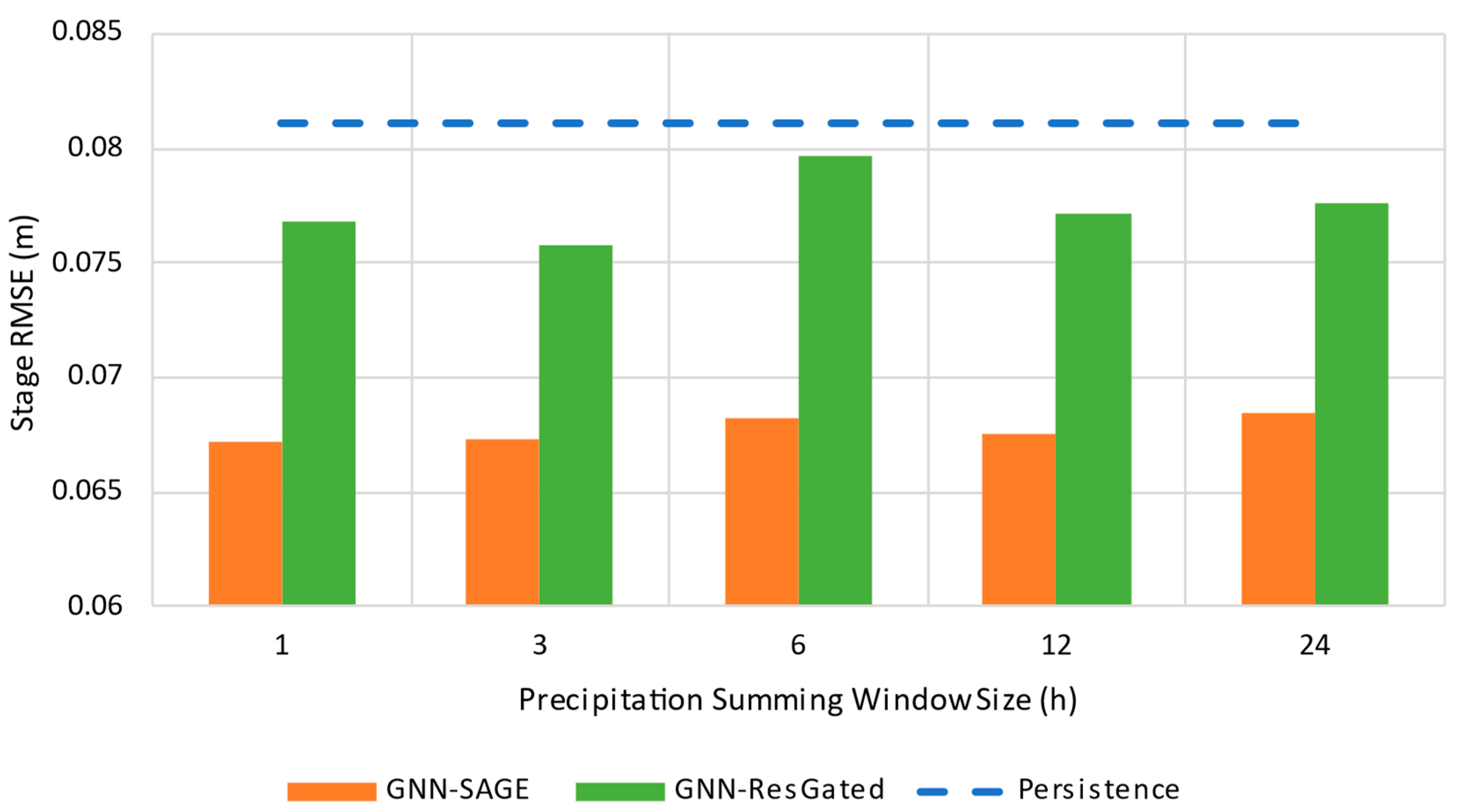
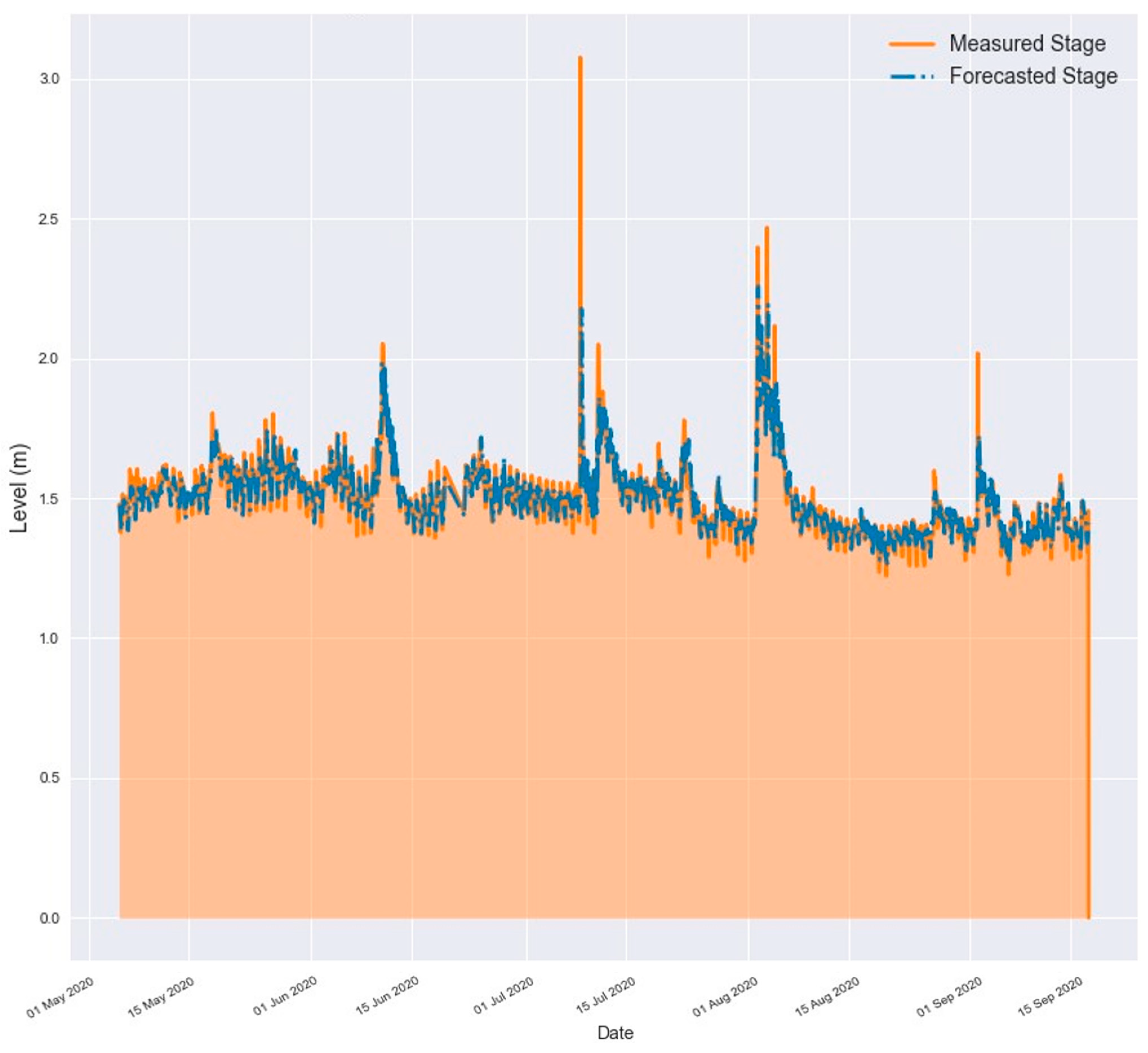
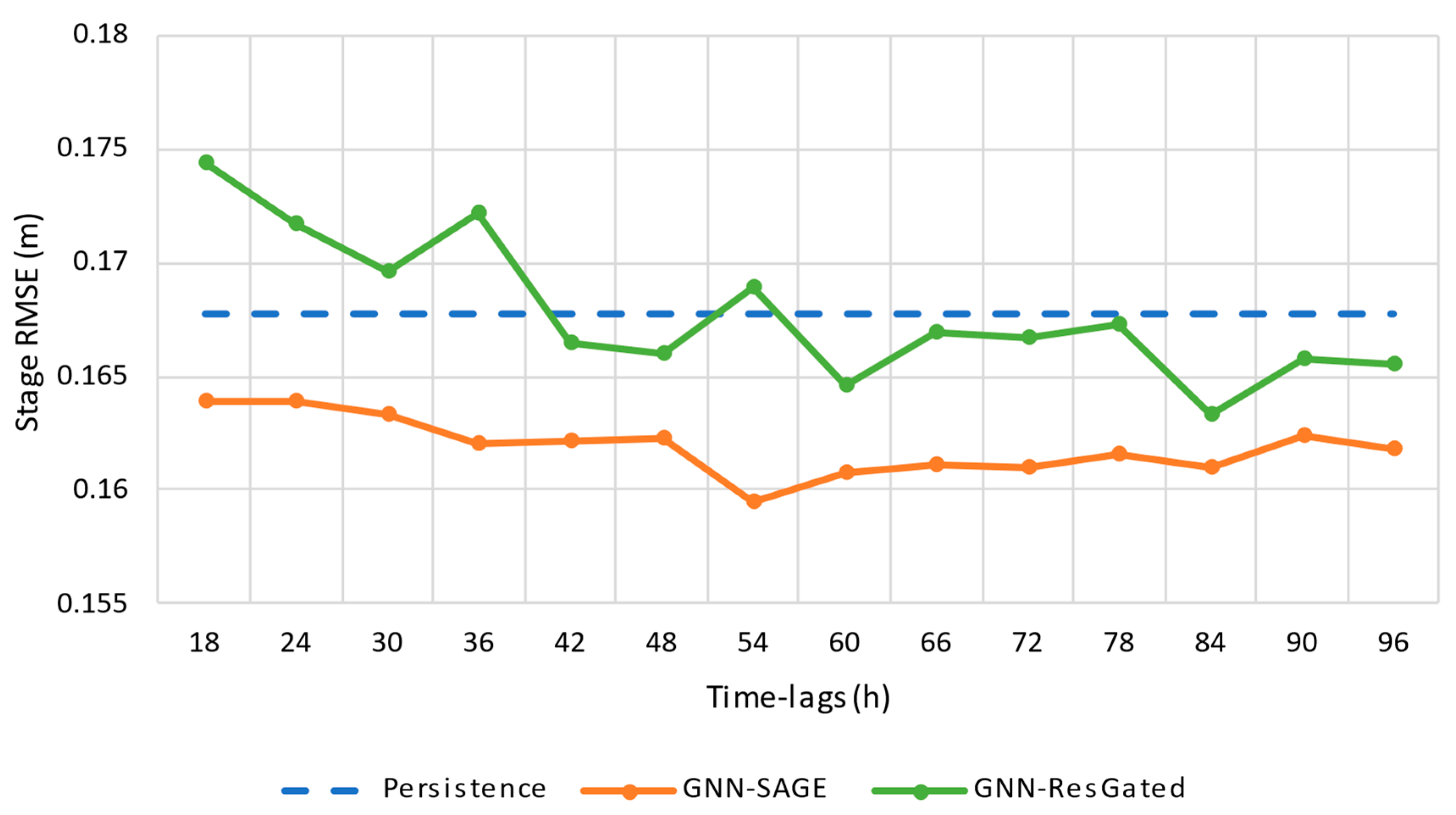
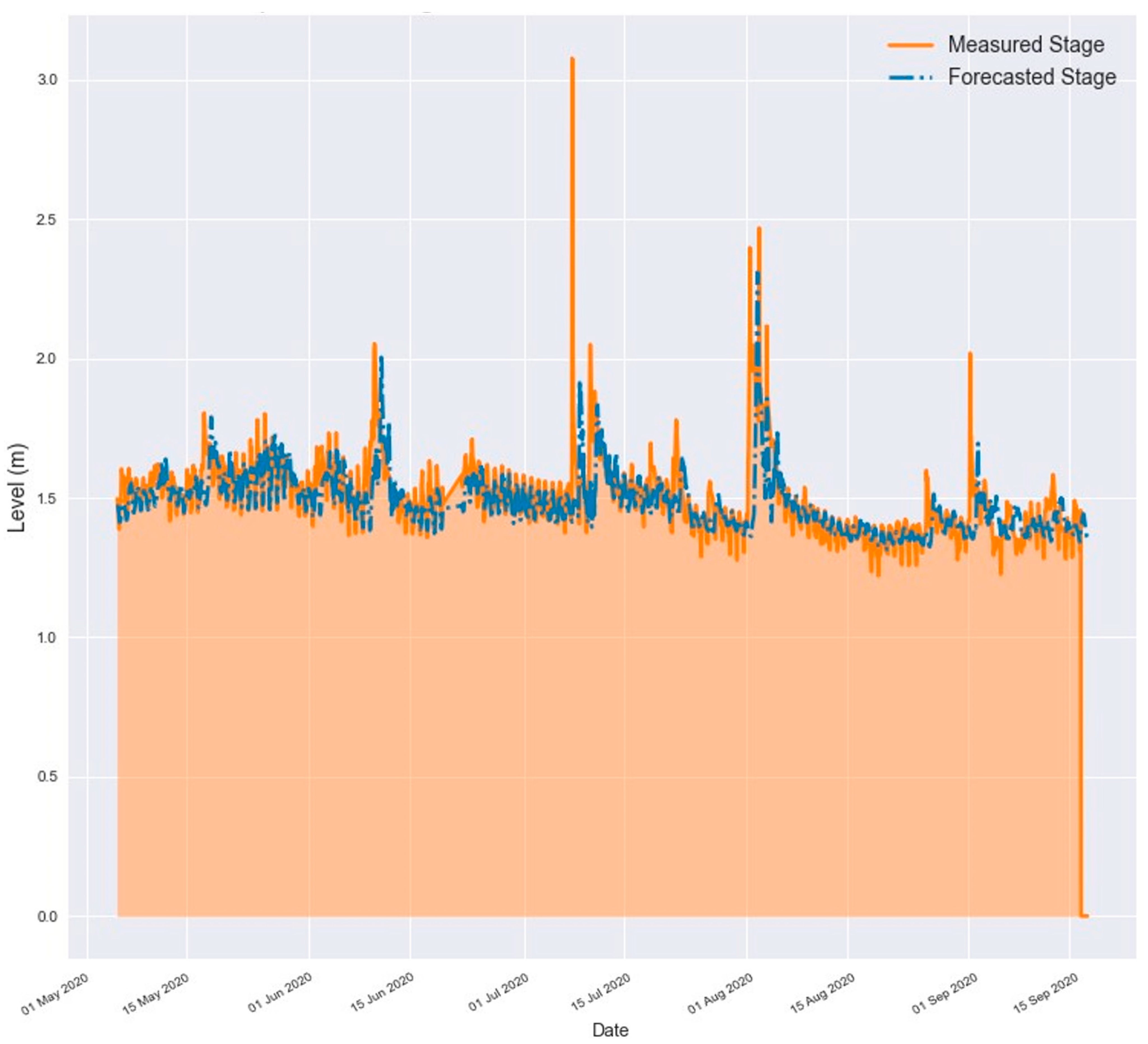
3.4. Results for a 1 h Forecast Horizon
3.5. Results for a 3 h Forecast Horizon
3.6. Results for a 6 h Forecast Horizon
3.7. Results for a 12 h Forecast Horizon
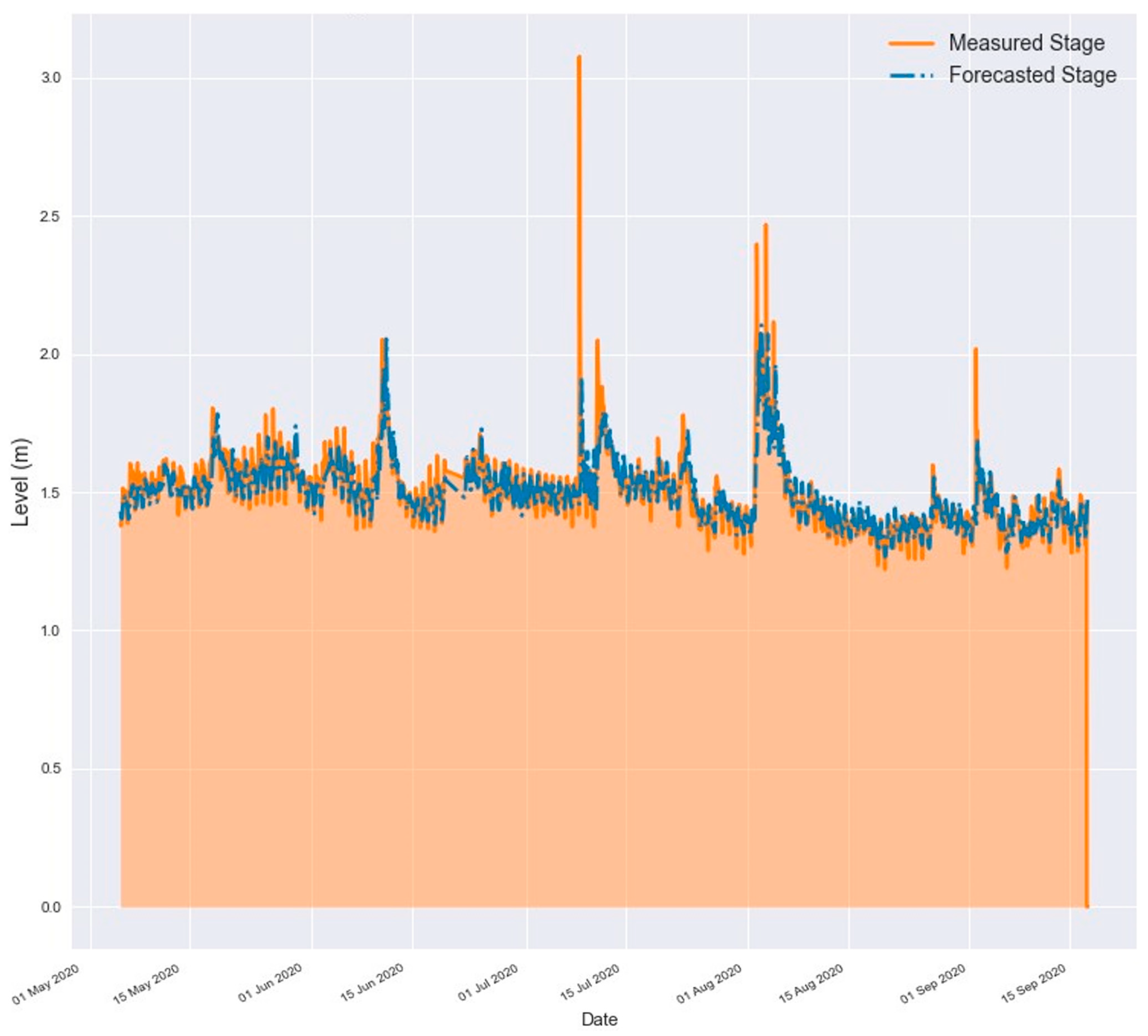
3.8. Results for a 24 h Forecast Horizon
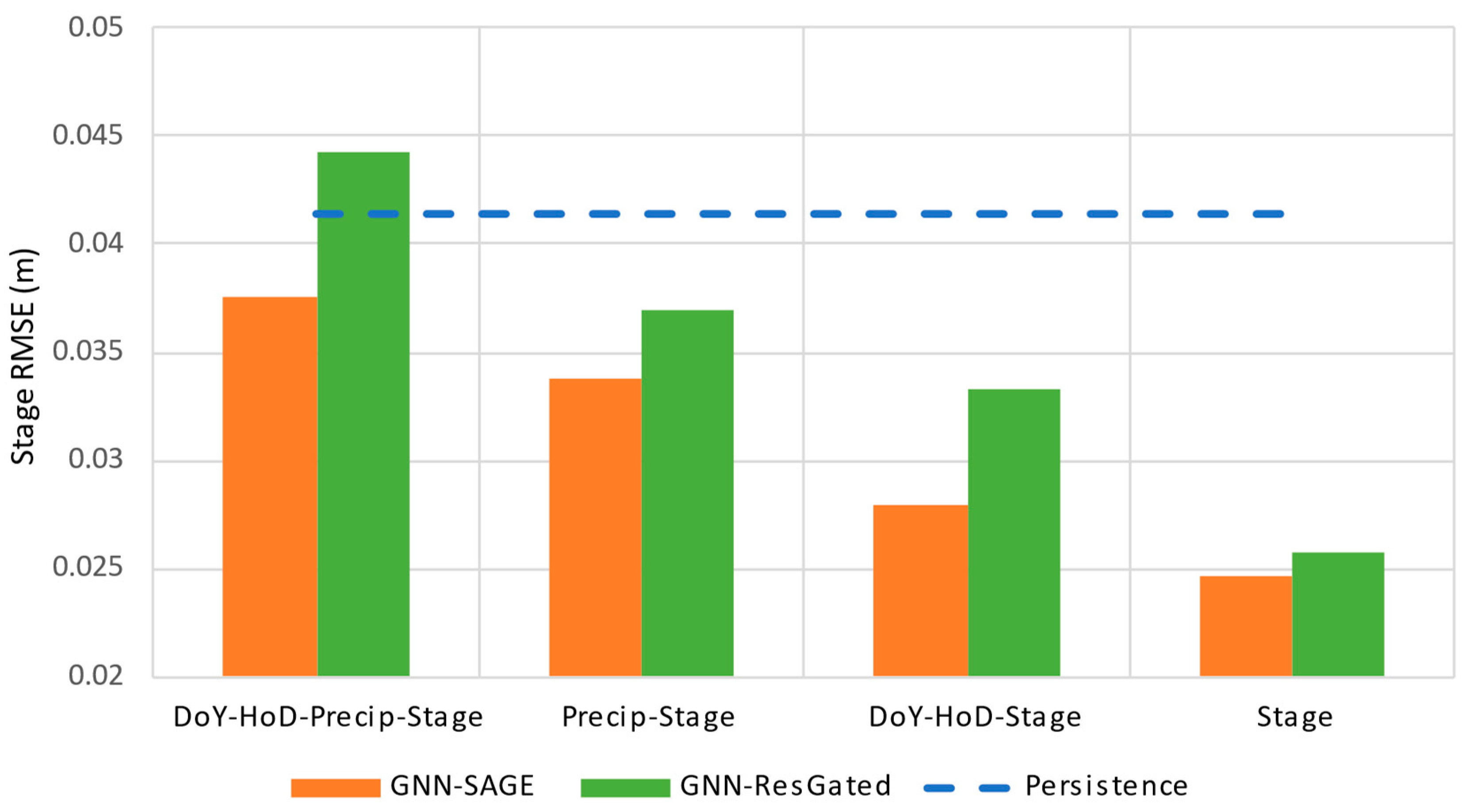
3.9. Results of the SHAP Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bonakdari, H.; Binns, A.D.; Gharabaghi, B. A Comparative Study of Linear Stochastic with Nonlinear Daily River Discharge Forecast Models. Water Resour. Manag. 2020, 34, 3689–3708. [Google Scholar] [CrossRef]
- Taraky, Y.M.; Liu, Y.; Gharabaghi, B.; McBean, E.; Daggupati, P.; Shrestha, N.K. Influence of Headwater Reservoirs on Climate Change Impacts and Flood Frequency in the Kabul River Basin. Can. J. Civ. Eng. 2022, 49, 1300–1309. [Google Scholar] [CrossRef]
- Javadinejad, S. Causes and Consequences of Floods: Flash Floods, Urban Floods, River Floods and Coastal Floods. Resour. Environ. Inf. Eng. 2022, 4, 156–166. [Google Scholar] [CrossRef]
- Sohn, W.; Kim, J.-H.; Li, M.-H.; Brown, R.D.; Jaber, F.H. How Does Increasing Impervious Surfaces Affect Urban Flooding in Response to Climate Variability? Ecol. Indic. 2020, 118, 106774. [Google Scholar] [CrossRef]
- Soltani, K.; Ebtehaj, I.; Amiri, A.; Azari, A.; Gharabaghi, B.; Bonakdari, H. Mapping the Spatial and Temporal Variability of Flood Susceptibility Using Remotely Sensed Normalized Difference Vegetation Index and the Forecasted Changes in the Future. Sci. Total Environ. 2021, 770, 145288. [Google Scholar] [CrossRef] [PubMed]
- Taraky, Y.M.; Liu, Y.; McBean, E.; Daggupati, P.; Gharabaghi, B. Flood Risk Management with Transboundary Conflict and Cooperation Dynamics in the Kabul River Basin. Water 2021, 13, 1513. [Google Scholar] [CrossRef]
- Perdikaris, J.; Gharabaghi, B.; Mcbean, E. A Methodology for Undertaking Vulnerability Assessments of Flood Susceptible Communities. Int. J. Saf. Secur. Eng. 2011, 1, 126–146. [Google Scholar] [CrossRef]
- Munawar, H.S.; Hammad, A.W.A.; Waller, S.T. Remote Sensing Methods for Flood Prediction: A Review. Sensors 2022, 22, 960. [Google Scholar] [CrossRef]
- Oubennaceur, K.; Chokmani, K.; Nastev, M.; Lhissou, R.; El Alem, A. Flood Risk Mapping for Direct Damage to Residential Buildings in Quebec, Canada. Int. J. Disaster Risk Reduct. 2019, 33, 44–54. [Google Scholar] [CrossRef]
- Elkurdy, M.; Binns, A.D.; Bonakdari, H.; Gharabaghi, B.; McBean, E. Early Detection of Riverine Flooding Events Using the Group Method of Data Handling for the Bow River, Alberta, Canada. Int. J. River Basin Manag. 2022, 20, 533–544. [Google Scholar] [CrossRef]
- Serinaldi, F.; Loecker, F.; Kilsby, C.G.; Bast, H. Flood Propagation and Duration in Large River Basins: A Data-Driven Analysis for Reinsurance Purposes. Nat. Hazards 2018, 94, 71–92. [Google Scholar] [CrossRef]
- Jiang, A.Z.; McBean, E.A.; Binns, A.D.; Gharabaghi, B. Guidance on Field Survey Programme Design for Basement Flooding Assessment. Hydrol. Sci. J. 2022, 67, 2524–2533. [Google Scholar] [CrossRef]
- Rentschler, J.; Salhab, M.; Jafino, B.A. Flood Exposure and Poverty in 188 Countries. Nat. Commun. 2022, 13, 3527. [Google Scholar] [CrossRef] [PubMed]
- Piadeh, F.; Behzadian, K.; Alani, A.M. A Critical Review of Real-Time Modelling of Flood Forecasting in Urban Drainage Systems. J. Hydrol. 2022, 607, 127476. [Google Scholar] [CrossRef]
- Rehman, S.; Sahana, M.; Hong, H.; Sajjad, H.; Ahmed, B.B. A Systematic Review on Approaches and Methods Used for Flood Vulnerability Assessment: Framework for Future Research. Nat. Hazards 2019, 96, 975–998. [Google Scholar] [CrossRef]
- Sattar, A.M.A.; Bonakdari, H.; Gharabaghi, B.; Radecki-Pawlik, A. Hydraulic Modeling and Evaluation Equations for the Incipient Motion of Sandbags for Levee Breach Closure Operations. Water 2019, 11, 279. [Google Scholar] [CrossRef]
- Jiang, A.Z.; McBean, E.A.; Binns, A.; Gharabaghi, B. Quantifying Rainfall-Derived Inflow from Private Foundation Drains in Sanitary Sewers: Case Study in London, Ontario, Canada. J. Hydrol. Eng. 2019, 24, 05019023. [Google Scholar] [CrossRef]
- Zahmatkesh, Z.; Kumar Jha, S.; Coulibaly, P.; Stadnyk, T. An Overview of River Flood Forecasting Procedures in Canadian Watersheds. Can. Water Resour. J./Rev. Can. Des Ressour. Hydr. 2019, 44, 213–229. [Google Scholar] [CrossRef]
- Zhang, Y.; Gu, Z.; Thé, J.V.G.; Yang, S.X.; Gharabaghi, B. The Discharge Forecasting of Multiple Monitoring Station for Humber River by Hybrid LSTM Models. Water 2022, 14, 1794. [Google Scholar] [CrossRef]
- Wijayarathne, D.B.; Coulibaly, P. Identification of Hydrological Models for Operational Flood Forecasting in St. John’s, Newfoundland, Canada. J. Hydrol. Reg. Stud. 2020, 27, 100646. [Google Scholar] [CrossRef]
- Kelly, G.; Stodolak, P. Why Insurers Fail; PACICC: Toronto, ON, Canada, 2013. [Google Scholar]
- Pattison-Williams, J.K.; Pomeroy, J.W.; Badiou, P.; Gabor, S. Wetlands, Flood Control and Ecosystem Services in the Smith Creek Drainage Basin: A Case Study in Saskatchewan, Canada. Ecol. Econ. 2018, 147, 36–47. [Google Scholar] [CrossRef]
- Vrban, S.; Wang, Y.; McBean, E.A.; Binns, A.; Gharabaghi, B. Evaluation of Stormwater Infrastructure Design Storms Developed Using Partial Duration and Annual Maximum Series Models. J. Hydrol. Eng. 2018, 23, 04018051. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, Y.; Feng, J.; Zhang, P.; Cheng, Z. Interpretable Spatio-Temporal Attention LSTM Model for Flood Forecasting. Neurocomputing 2020, 403, 348–359. [Google Scholar] [CrossRef]
- Perdikaris, J.; Gharabaghi, B.; Rudra, R. Evaluation of the Simplified Dynamic Wave, Diffusion Wave and the Full Dynamic Wave Flood Routing Models. Earth Sci. Res. 2018, 7, 14. [Google Scholar] [CrossRef]
- Perdikaris, J.; Gharabaghi, B.; Rudra, R. Reference Time of Concentration Estimation for Ungauged Catchments. Earth Sci. Res. 2018, 7, 58. [Google Scholar] [CrossRef]
- Yoon, S.-S. Adaptive Blending Method of Radar-Based and Numerical Weather Prediction QPFs for Urban Flood Forecasting. Remote Sens. 2019, 11, 642. [Google Scholar] [CrossRef]
- Wu, R.-S.; Sin, Y.-Y.; Wang, J.-X.; Lin, Y.-W.; Wu, H.-C.; Sukmara, R.B.; Indawati, L.; Hussain, F. Real-Time Flood Warning System Application. Water 2022, 14, 1866. [Google Scholar] [CrossRef]
- Hussain, F.; Wu, R.-S.; Wang, J.-X. Comparative Study of Very Short-Term Flood Forecasting Using Physics-Based Numerical Model and Data-Driven Prediction Model. Nat. Hazards 2021, 107, 249–284. [Google Scholar] [CrossRef]
- Zahura, F.T.; Goodall, J.L.; Sadler, J.M.; Shen, Y.; Morsy, M.M.; Behl, M. Training Machine Learning Surrogate Models from a High-Fidelity Physics-Based Model: Application for Real-Time Street-Scale Flood Prediction in an Urban Coastal Community. Water Resour. Res. 2020, 56, e2019WR027038. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Kašpar, V.; Zapletal, M.; Samec, P.; Komárek, J.; Bílek, J.; Juráň, S. Unmanned Aerial Systems for Modelling Air Pollution Removal by Urban Greenery. Urban For. Urban Green. 2022, 78, 127757. [Google Scholar] [CrossRef]
- Rocha, P.A.C.; Santos, V.O. Global Horizontal and Direct Normal Solar Irradiance Modeling by the Machine Learning Methods XGBoost and Deep Neural Networks with CNN-LSTM Layers: A Case Study Using the GOES-16 Satellite Imagery. Int. J. Energy Environ. Eng. 2022, 13, 1271–1286. [Google Scholar] [CrossRef]
- Costa Rocha, P.A.; Johnston, S.J.; Oliveira Santos, V.; Aliabadi, A.A.; Thé, J.V.G.; Gharabaghi, B. Deep Neural Network Modeling for CFD Simulations: Benchmarking the Fourier Neural Operator on the Lid-Driven Cavity Case. Appl. Sci. 2023, 13, 3165. [Google Scholar] [CrossRef]
- Parvaze, S.; Khan, J.N.; Kumar, R.; Allaie, S.P. Temporal Flood Forecasting for Trans-Boundary Jhelum River of Greater Himalayas. Theor. Appl. Climatol. 2021, 144, 493–506. [Google Scholar] [CrossRef]
- Puttinaovarat, S.; Horkaew, P. Flood Forecasting System Based on Integrated Big and Crowdsource Data by Using Machine Learning Techniques. IEEE Access 2020, 8, 5885–5905. [Google Scholar] [CrossRef]
- Ivakhnenko, A.G. Heuristic Self-Organization in Problems of Engineering Cybernetics. Automatica 1970, 6, 207–219. [Google Scholar] [CrossRef]
- Ivakhnenko, A.G. Polynomial Theory of Complex Systems. IEEE Trans. Syst. Man Cybern. 1971, SMC-1, 364–378. [Google Scholar] [CrossRef]
- Walton, R.; Binns, A.; Bonakdari, H.; Ebtehaj, I.; Gharabaghi, B. Estimating 2-Year Flood Flows Using the Generalized Structure of the Group Method of Data Handling. J. Hydrol. 2019, 575, 671–689. [Google Scholar] [CrossRef]
- Zaji, A.H.; Bonakdari, H.; Gharabaghi, B. Remote Sensing Satellite Data Preparation for Simulating and Forecasting River Discharge. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3432–3441. [Google Scholar] [CrossRef]
- Zaji, A.H.; Bonakdari, H.; Gharabaghi, B. Applying Upstream Satellite Signals and a 2-D Error Minimization Algorithm to Advance Early Warning and Management of Flood Water Levels and River Discharge. IEEE Trans. Geosci. Remote Sens. 2019, 57, 902–910. [Google Scholar] [CrossRef]
- Bonakdari, H.; Zaji, A.H.; Soltani, K.; Gharabaghi, B. Improving the Accuracy of a Remotely-Sensed Flood Warning System Using a Multi-Objective Pre-Processing Method for Signal Defects Detection and Elimination. Comptes Rendus Géosci. 2020, 352, 73–86. [Google Scholar] [CrossRef]
- Avand, M.; Moradi, H.; Lasboyee, M.R. Using Machine Learning Models, Remote Sensing, and GIS to Investigate the Effects of Changing Climates and Land Uses on Flood Probability. J. Hydrol. 2021, 595, 125663. [Google Scholar] [CrossRef]
- Bonakdari, H.; Zaji, A.H.; Binns, A.D.; Gharabaghi, B. Integrated Markov Chains and Uncertainty Analysis Techniques to More Accurately Forecast Floods Using Satellite Signals. J. Hydrol. 2019, 572, 75–95. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Le, X.H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef]
- Kabir, S.; Patidar, S.; Xia, X.; Liang, Q.; Neal, J.; Pender, G. A Deep Convolutional Neural Network Model for Rapid Prediction of Fluvial Flood Inundation. J. Hydrol. 2020, 590, 125481. [Google Scholar] [CrossRef]
- Marinho, F.P.; Rocha, P.A.C.; Neto, A.R.R.; Bezerra, F.D.V. Short-Term Solar Irradiance Forecasting Using CNN-1D, LSTM, and CNN-LSTM Deep Neural Networks: A Case Study with the Folsom (USA) Dataset. J. Sol. Energy Eng. 2023, 145, 041002. [Google Scholar] [CrossRef]
- Carneiro, T.C.; Rocha, P.A.C.; Carvalho, P.C.M.; Fernández-Ramírez, L.M. Ridge Regression Ensemble of Machine Learning Models Applied to Solar and Wind Forecasting in Brazil and Spain. Appl. Energy 2022, 314, 118936. [Google Scholar] [CrossRef]
- Li, P.; Zhang, J.; Krebs, P. Prediction of Flow Based on a CNN-LSTM Combined Deep Learning Approach. Water 2022, 14, 993. [Google Scholar] [CrossRef]
- Wilson, T.; Tan, P.-N.; Luo, L. A Low Rank Weighted Graph Convolutional Approach to Weather Prediction. In Proceedings of the 2018 IEEE International Conference on Data Mining (ICDM), Singapore, 17–20 November 2018; pp. 627–636. [Google Scholar]
- Zhang, S.; Tong, H.; Xu, J.; Maciejewski, R. Graph Convolutional Networks: A Comprehensive Review. Comput. Soc. Netw. 2019, 6, 11. [Google Scholar] [CrossRef]
- Oliveira Santos, V.; Costa Rocha, P.A.; Scott, J.; Van Griensven Thé, J.; Gharabaghi, B. Spatiotemporal Air Pollution Forecasting in Houston-TX: A Case Study for Ozone Using Deep Graph Neural Networks. Atmosphere 2023, 14, 308. [Google Scholar] [CrossRef]
- Stańczyk, T.; Mehrkanoon, S. Deep Graph Convolutional Networks for Wind Speed Prediction. In Proceedings of the 29th European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Online, 6–8 October 2021; pp. 147–152. [Google Scholar]
- Wu, Q.; Zheng, H.; Guo, X.; Liu, G. Promoting Wind Energy for Sustainable Development by Precise Wind Speed Prediction Based on Graph Neural Networks. Renew. Energy 2022, 199, 977–992. [Google Scholar] [CrossRef]
- Feng, J.; Wang, Z.; Wu, Y.; Xi, Y. Spatial and Temporal Aware Graph Convolutional Network for Flood Forecasting. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–8. [Google Scholar]
- Baïle, R.; Muzy, J.-F. Leveraging Data from Nearby Stations to Improve Short-Term Wind Speed Forecasts. Energy 2023, 263, 125644. [Google Scholar] [CrossRef]
- Baïle, R.; Muzy, J.F.; Poggi, P. Short-Term Forecasting of Surface Layer Wind Speed Using a Continuous Random Cascade Model. Wind. Energy 2011, 14, 719–734. [Google Scholar] [CrossRef]
- Wu, Y.-K.; Hong, J.-S. A Literature Review of Wind Forecasting Technology in the World. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 504–509. [Google Scholar]
- Yang, D.; Kleissl, J.; Gueymard, C.A.; Pedro, H.T.C.; Coimbra, C.F.M. History and Trends in Solar Irradiance and PV Power Forecasting: A Preliminary Assessment and Review Using Text Mining. Sol. Energy 2018, 168, 60–101. [Google Scholar] [CrossRef]
- Hanifi, S.; Liu, X.; Lin, Z.; Lotfian, S. A Critical Review of Wind Power Forecasting Methods—Past, Present and Future. Energies 2020, 13, 3764. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph Neural Networks: A Review of Methods and Applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive Representation Learning on Large Graphs. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef]
- Labonne, M. Hands-On Graph Neural Networks Using Python; Packt Publishing: Birmingham, UK, 2023. [Google Scholar]
- Bresson, X.; Laurent, T. Residual Gated Graph Convnets. arXiv 2017, arXiv:1711.07553. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Marcheggiani, D.; Titov, I. Encoding Sentences with Graph Convolutional Networks for Semantic Role Labeling. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 7–11 September 2017. [Google Scholar]
- Dwivedi, V.P.; Joshi, C.K.; Luu, A.T.; Laurent, T.; Bengio, Y.; Bresson, X. Benchmarking Graph Neural Networks. J. Mach. Learn. Res. 2020, 23, 1–48. [Google Scholar]
- Shafiq, M.; Gu, Z. Deep Residual Learning for Image Recognition: A Survey. Appl. Sci. 2022, 12, 8972. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. [Google Scholar]
- Akbar, S.; Ali, F.; Hayat, M.; Ahmad, A.; Khan, S.; Gul, S. Prediction of Antiviral Peptides Using Transform Evolutionary & SHAP Analysis Based Descriptors by Incorporation with Ensemble Learning Strategy. Chemom. Intell. Lab. Syst. 2022, 230, 104682. [Google Scholar] [CrossRef]
- Abdulalim Alabdullah, A.; Iqbal, M.; Zahid, M.; Khan, K.; Nasir Amin, M.; Jalal, F.E. Prediction of Rapid Chloride Penetration Resistance of Metakaolin Based High Strength Concrete Using Light GBM and XGBoost Models by Incorporating SHAP Analysis. Constr. Build. Mater. 2022, 345, 128296. [Google Scholar] [CrossRef]
- Silva, S.J.; Keller, C.A.; Hardin, J. Using an Explainable Machine Learning Approach to Characterize Earth System Model Errors: Application of SHAP Analysis to Modeling Lightning Flash Occurrence. J. Adv. Model. Earth Syst. 2022, 14, e2021MS002881. [Google Scholar] [CrossRef]
- Bai, R.; Lam, J.C.K.; Li, V.O.K. What Dictates Income in New York City? SHAP Analysis of Income Estimation Based on Socio-Economic and Spatial Information Gaussian Processes (SSIG). Humanit. Soc. Sci. Commun. 2023, 10, 60. [Google Scholar] [CrossRef] [PubMed]
- Rincón, D.; Velandia, J.F.; Tsanis, I.; Khan, U.T. Stochastic Flood Risk Assessment under Climate Change Scenarios for Toronto, Canada Using CAPRA. Water 2022, 14, 227. [Google Scholar] [CrossRef]
- Howell, E.T.; Benoit, N. Nutrient Footprints on the Toronto-Mississauga Waterfront of Lake Ontario. J. Great Lakes Res. 2021, 47, 343–365. [Google Scholar] [CrossRef]
- Rincón, D.; Khan, U.; Armenakis, C. Flood Risk Mapping Using GIS and Multi-Criteria Analysis: A Greater Toronto Area Case Study. Geosciences 2018, 8, 275. [Google Scholar] [CrossRef]
- Weisberg, S. Applied Linear Regression; John Wiley & Sons: Hoboken, NJ, USA, 2005; ISBN 978-0-471-70408-9. [Google Scholar]
- Dazzi, S.; Vacondio, R.; Mignosa, P. Flood Stage Forecasting Using Machine-Learning Methods: A Case Study on the Parma River (Italy). Water 2021, 13, 1612. [Google Scholar] [CrossRef]
- Wang, H.; Hu, Y.; Guo, Y.; Wu, Z.; Yan, D. Urban Flood Forecasting Based on the Coupling of Numerical Weather Model and Stormwater Model: A Case Study of Zhengzhou City. J. Hydrol. Reg. Stud. 2022, 39, 100985. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Chen, S.-T. Real-Time Probabilistic Flood Forecasting Using Multiple Machine Learning Methods. Water 2020, 12, 787. [Google Scholar] [CrossRef]
- Fu, J.-C.; Huang, H.-Y.; Jang, J.-H.; Huang, P.-H. River Stage Forecasting Using Multiple Additive Regression Trees. Water Resour. Manag. 2019, 33, 4491–4507. [Google Scholar] [CrossRef]
- Alexander, A.A.; Thampi, S.G.; NR, C. Development of Hybrid Wavelet-ANN Model for Hourly Flood Stage Forecasting. ISH J. Hydraul. Eng. 2018, 24, 266–274. [Google Scholar] [CrossRef]
- Langridge, M.; Gharabaghi, B.; Bonakdari, H.; Walton, R. Understanding the Dynamic Nature of Catchment Response Time through Machine Learning Analysis. ESS Open Archive 2019. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, D.; Wang, G.; Qiu, J.; Long, K.; Du, Y.; Xie, H.; Wei, Z.; Shangguan, W.; Dai, Y. A Hybrid Deep Learning Algorithm and Its Application to Streamflow Prediction. J. Hydrol. 2021, 601, 126636. [Google Scholar] [CrossRef]
- Ekmekcioğlu, Ö.; Koc, K.; Özger, M.; Işık, Z. Exploring the Additional Value of Class Imbalance Distributions on Interpretable Flash Flood Susceptibility Prediction in the Black Warrior River Basin, Alabama, United States. J. Hydrol. 2022, 610, 127877. [Google Scholar] [CrossRef]
- Aydin, H.E.; Iban, M.C. Predicting and Analyzing Flood Susceptibility Using Boosting-Based Ensemble Machine Learning Algorithms with SHapley Additive ExPlanations. Nat. Hazards 2023, 116, 2957–2991. [Google Scholar] [CrossRef]
- de Amorim Neto, J.P.; Marinho, F.P.; Lima, R.J.P.; Rocha, P.A.C.; Mendonça, S.P.; Bueno, A.V.; da Silva, M.E.V. Thermal Behavior Estimation of a Solar Wall Operated by TiO2 Nanofluids Using Several Machine Learning Models. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 128. [Google Scholar] [CrossRef]








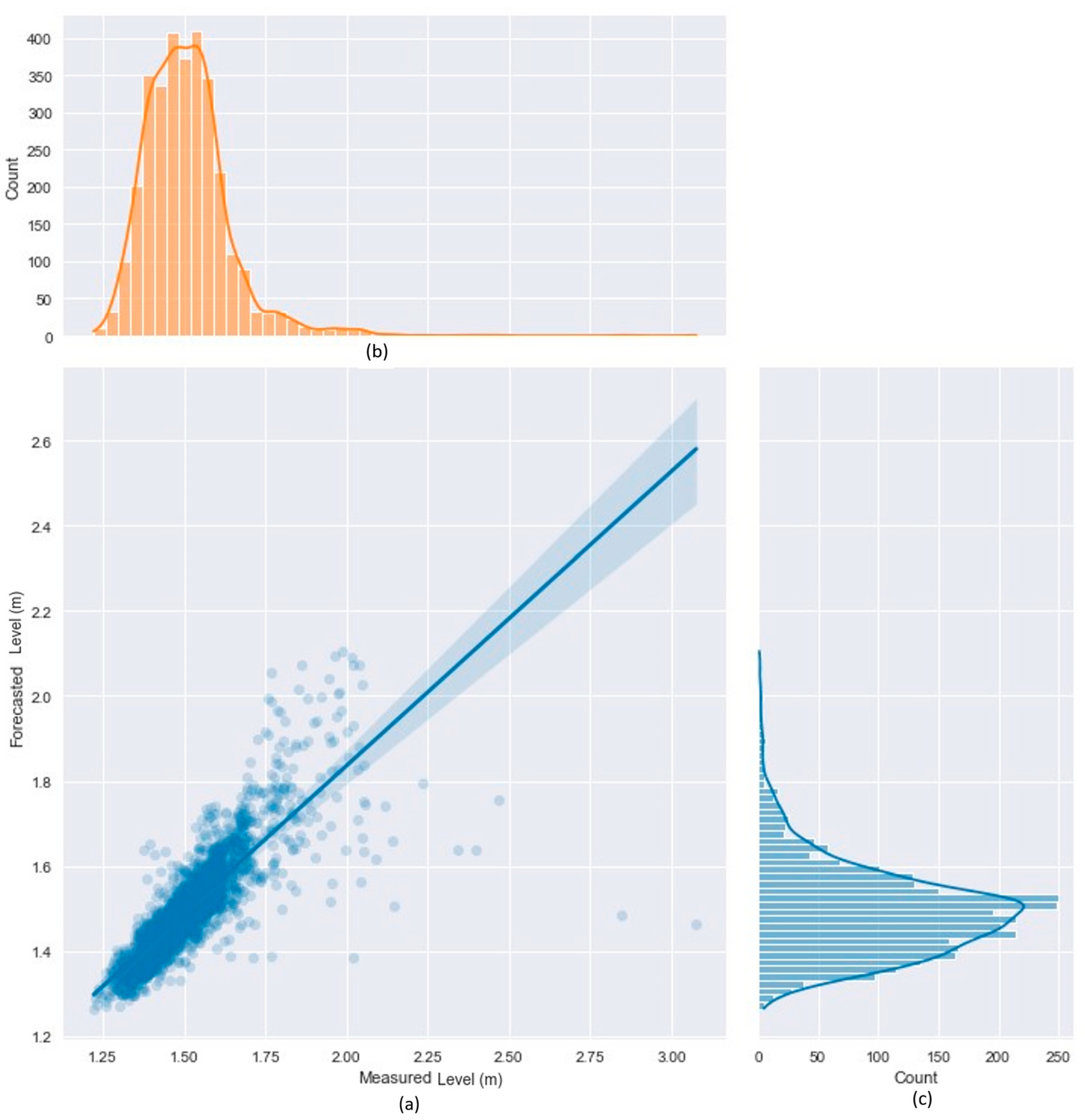

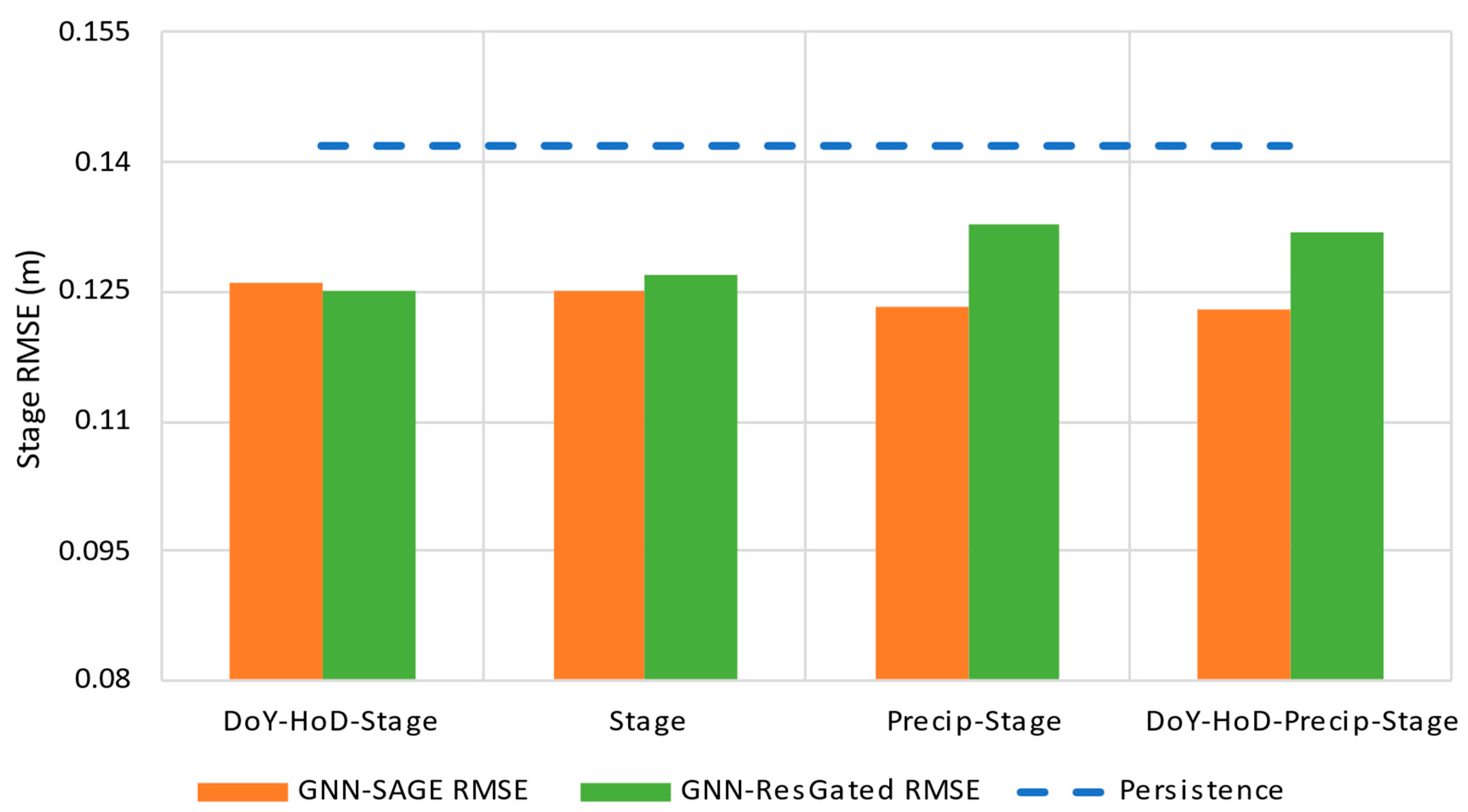
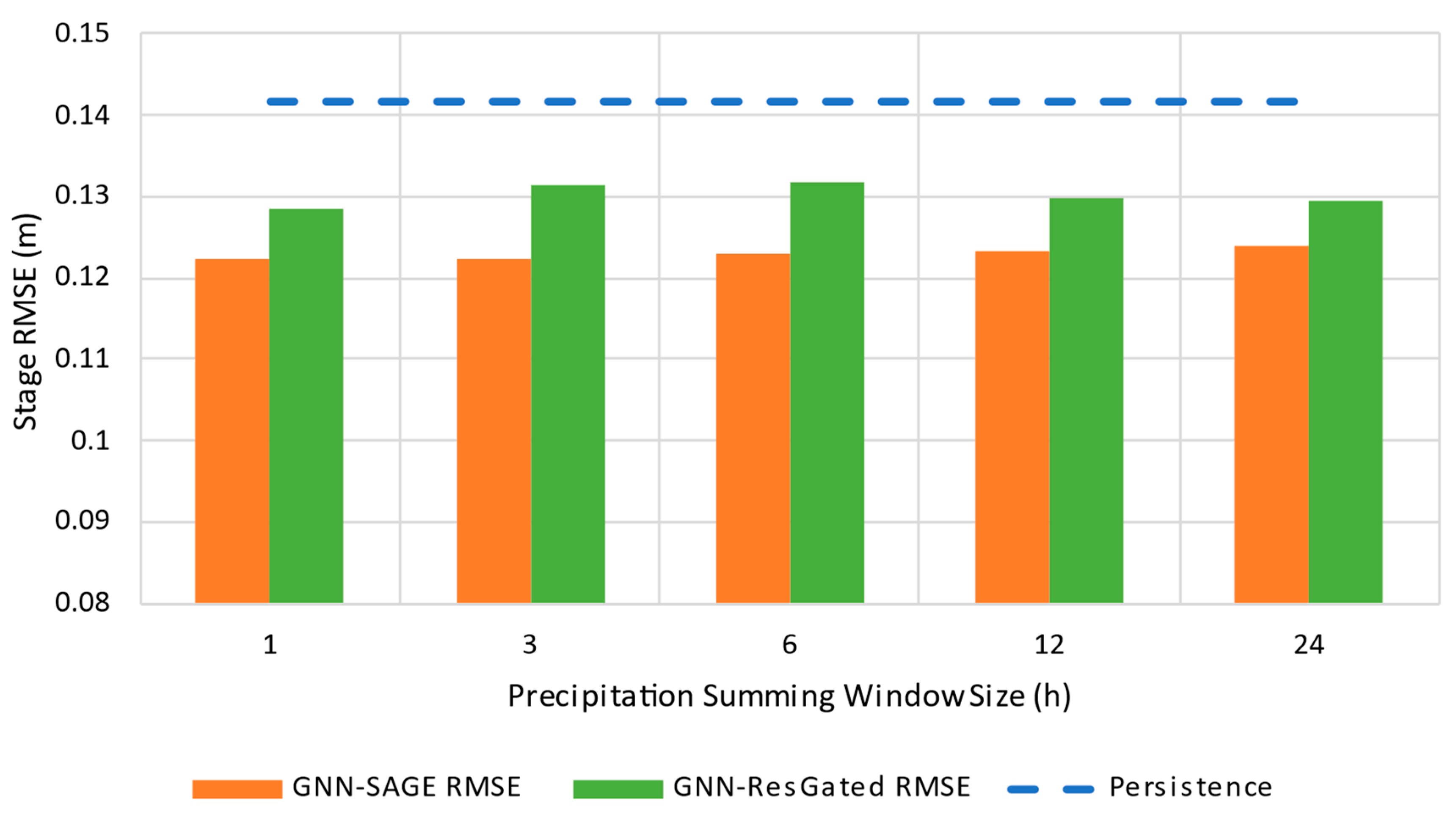
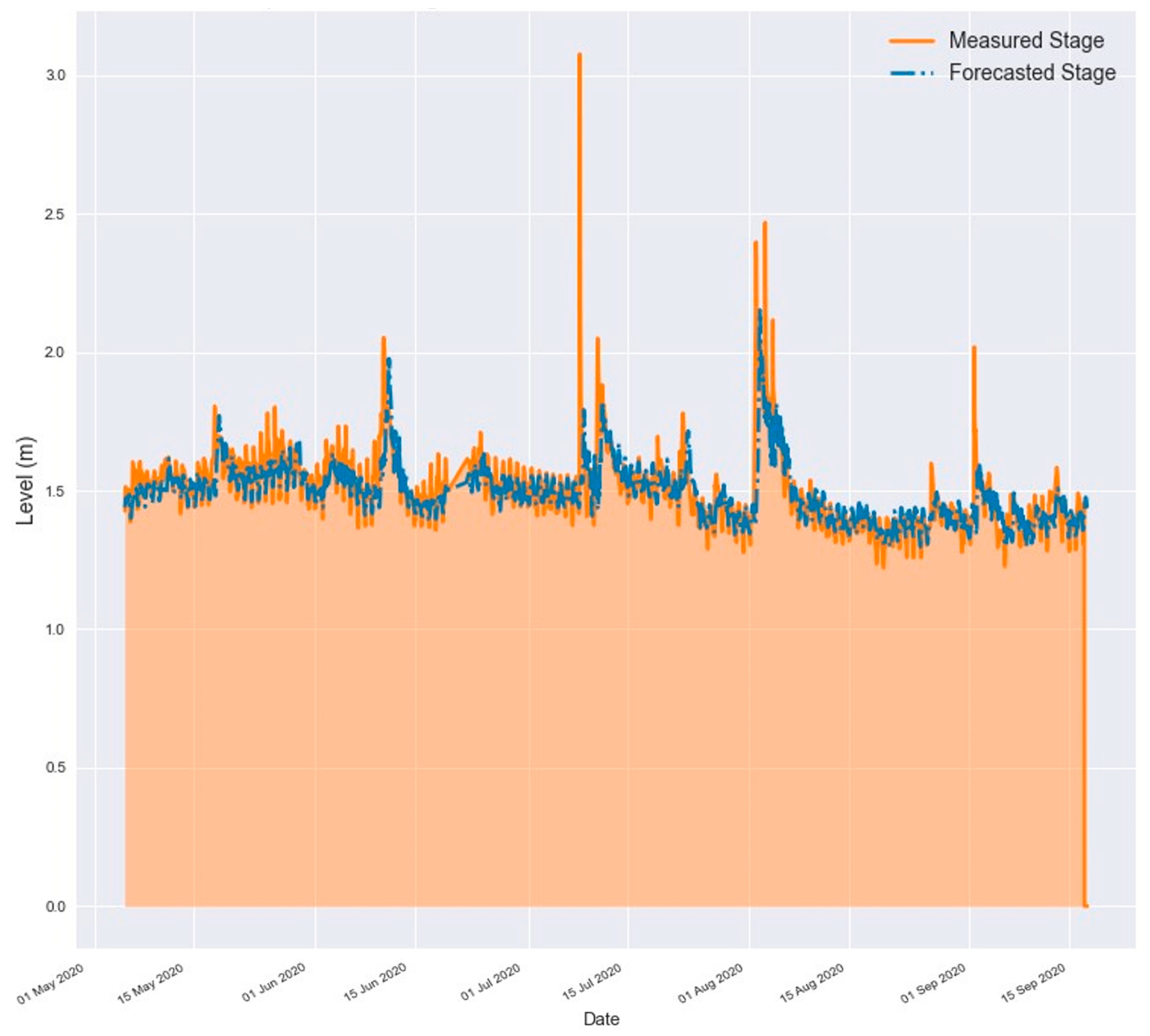

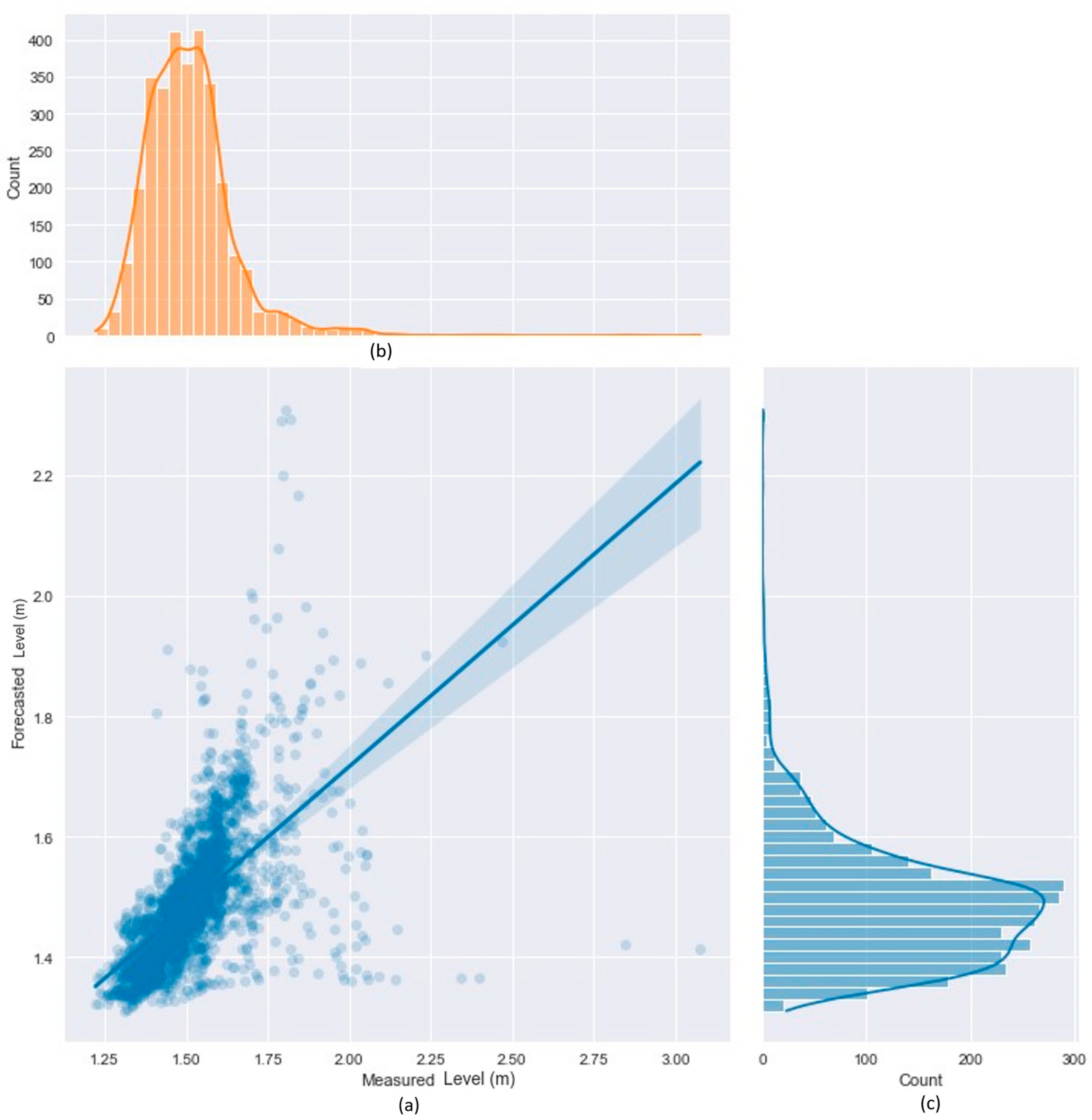
| Metric | 1 h Ahead | 3 h Ahead | 6 h Ahead | 12 h Ahead | 24 h Ahead |
|---|---|---|---|---|---|
| RMSE (m) | 0.02516 | 0.06736 | 0.09200 | 0.12215 | 0.16077 |
| MAE (m) | 0.01592 | 0.0345 | 0.04372 | 0.05514 | 0.07077 |
| MAPE | 1.04% | 2.18% | 2.65% | 3.20% | 3.78% |
| R2 | 96.45% | 75.50% | 59.10% | 40.12% | 22.65% |
| Model | Metric Value | Author |
|---|---|---|
| Spatio-temporal attention LSTM (STA-LSTM) | Error rate 3.96% for 6 h forecasting horizon 3.98% for 12 h forecasting horizon 6.31% for 24 h forecasting horizon | Zhang et al. [19] |
| Quantitative precipitation forecast (QPF) | RMSE 0.09 m for 1 h forecasting horizon | Wu et al. [28] |
| Support vector machine (SVM) | RMSE (MAE) 0.072 m (0.036 m) for 3 h forecasting horizon 0.131 m (0.070 m) for 6 h forecasting horizon | Dazzi et al. [80] |
| Support vector regression (SVR) | RMSE 0.07 m for 1 h forecasting horizon 0.25 m for 3 h forecasting horizon RMSE | Nguyen and Chen [82] |
| Multiple additive regression trees (MART) | 0.14 m for 1 h forecasting horizon 0.29 m for 3 h forecasting horizon | Fu et al. [83] |
| Hybrid wavelet and ANN (WANN) | RMSE (R2) 0.03 m (98%) for 1 h forecasting horizon 0.038 m (97%) for 3 h forecasting horizon 0.12 m (60%) for 6 h forecasting horizon | Alexander et al. [84] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira Santos, V.; Costa Rocha, P.A.; Scott, J.; Thé, J.V.G.; Gharabaghi, B. A New Graph-Based Deep Learning Model to Predict Flooding with Validation on a Case Study on the Humber River. Water 2023, 15, 1827. https://doi.org/10.3390/w15101827
Oliveira Santos V, Costa Rocha PA, Scott J, Thé JVG, Gharabaghi B. A New Graph-Based Deep Learning Model to Predict Flooding with Validation on a Case Study on the Humber River. Water. 2023; 15(10):1827. https://doi.org/10.3390/w15101827
Chicago/Turabian StyleOliveira Santos, Victor, Paulo Alexandre Costa Rocha, John Scott, Jesse Van Griensven Thé, and Bahram Gharabaghi. 2023. "A New Graph-Based Deep Learning Model to Predict Flooding with Validation on a Case Study on the Humber River" Water 15, no. 10: 1827. https://doi.org/10.3390/w15101827






