Sustainable Heat Transfer Management: Modeling of Entropy Generation Minimization and Nusselt Number Development in Internal Flows with Various Shapes of Cross-Sections Using Water and Al2O3/Water Nanofluid
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
2.2. Nanofluid Preparation
3. Governing Equations
3.1. Thermophysical Properties of Nanofluid
3.2. Energy Analysis Equation
3.3. Energy Analysis Equation
4. Uncertainty Analysis
5. Data Collection and Validation
Validation of the Experimental Setup
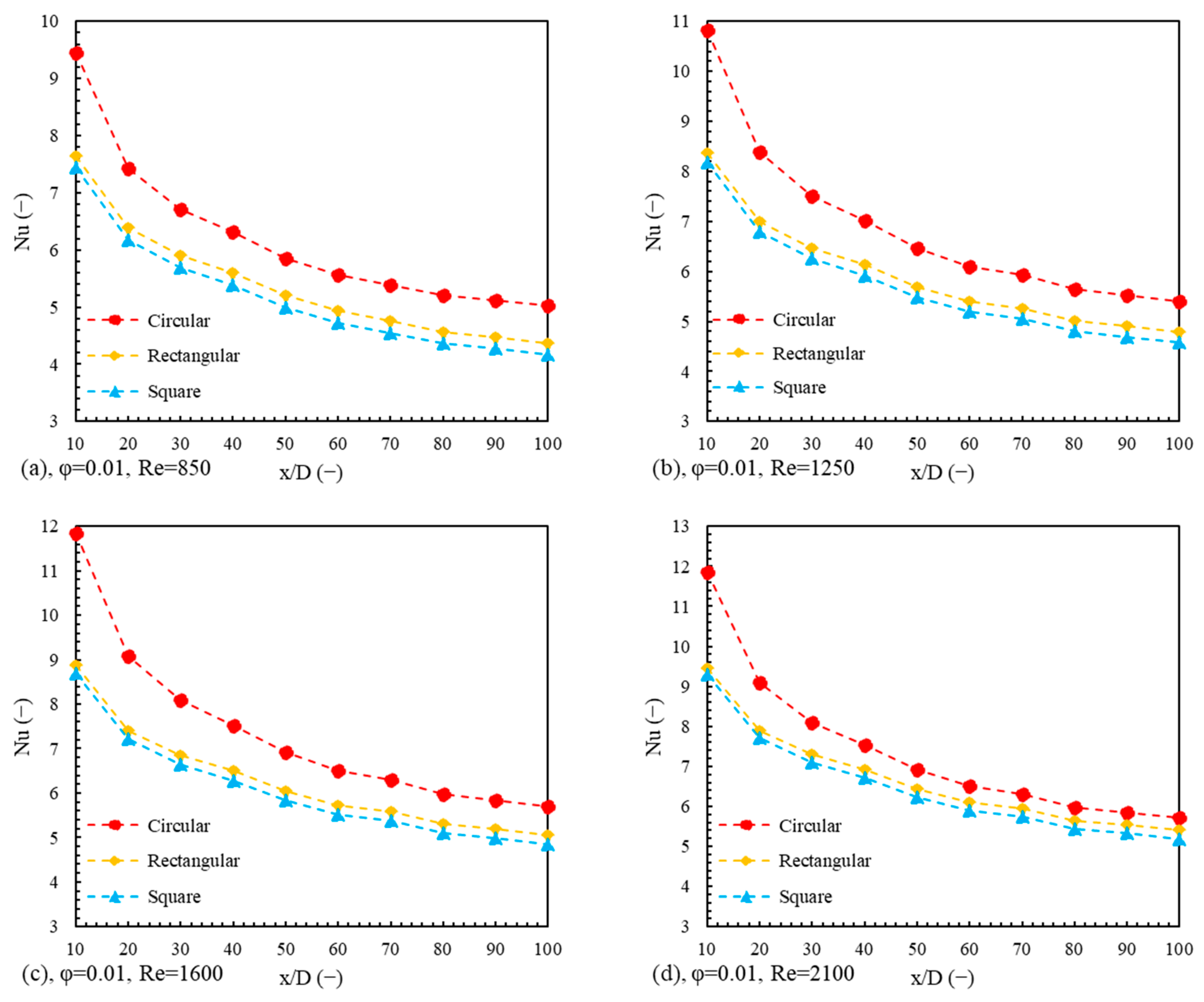
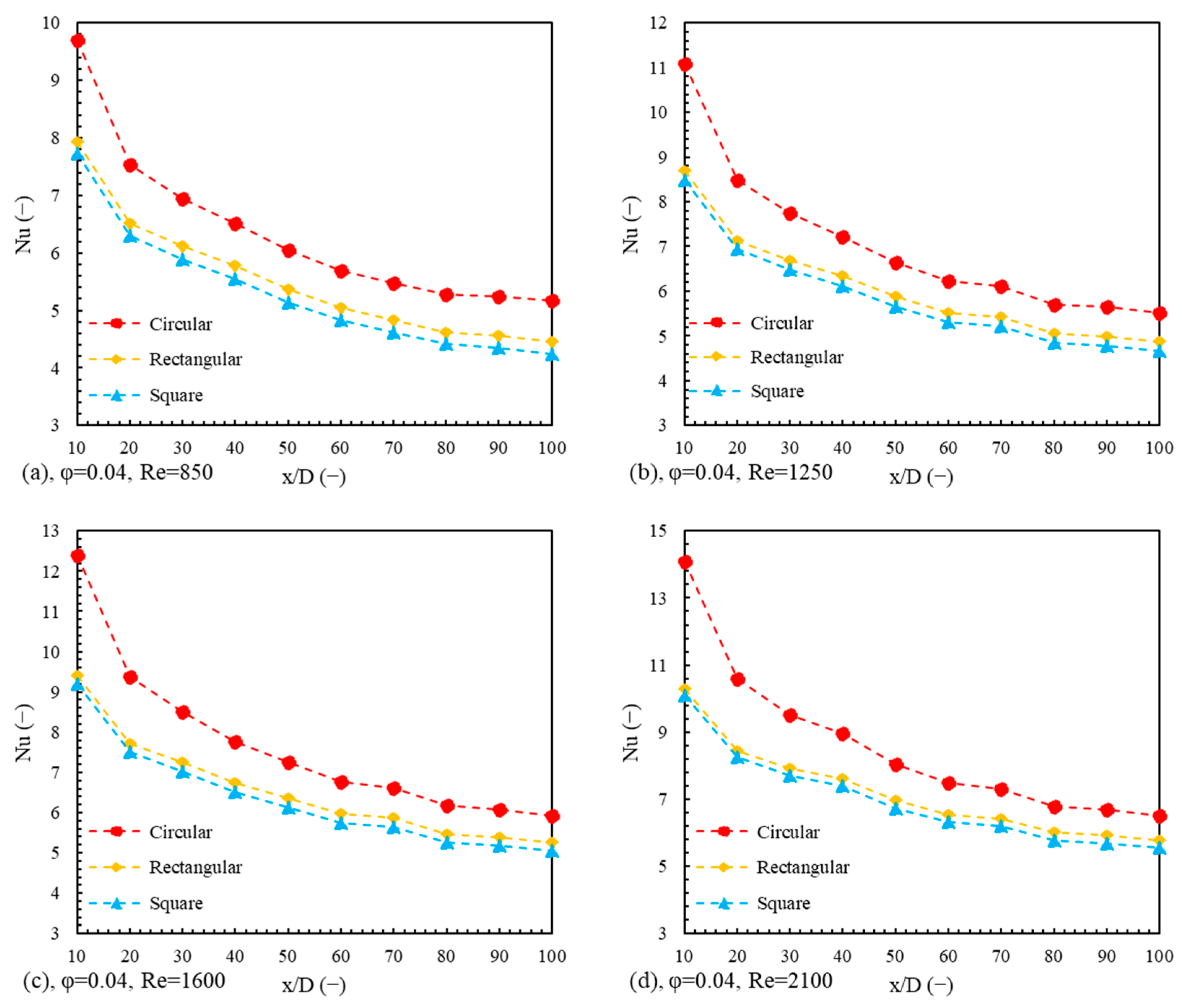
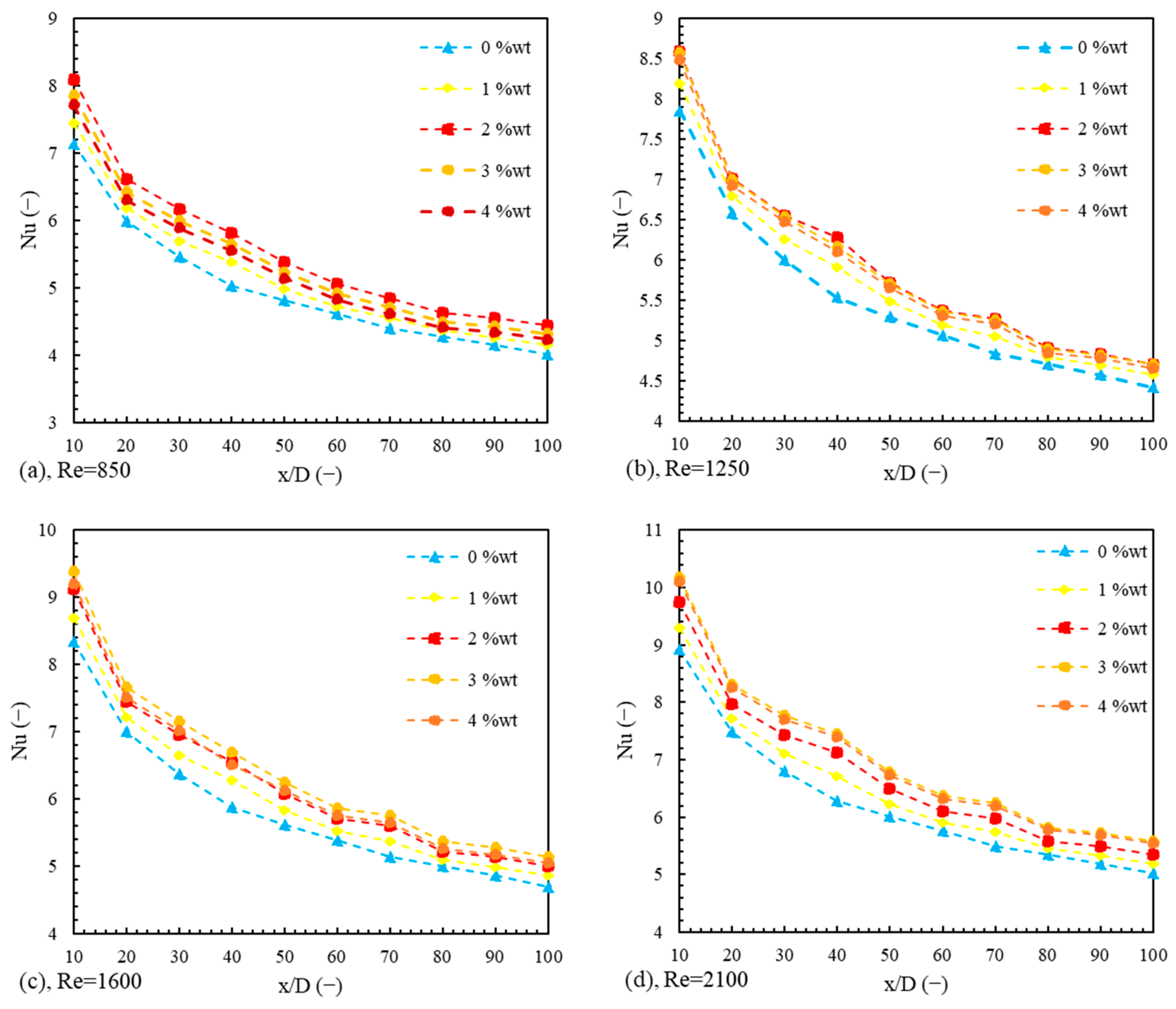
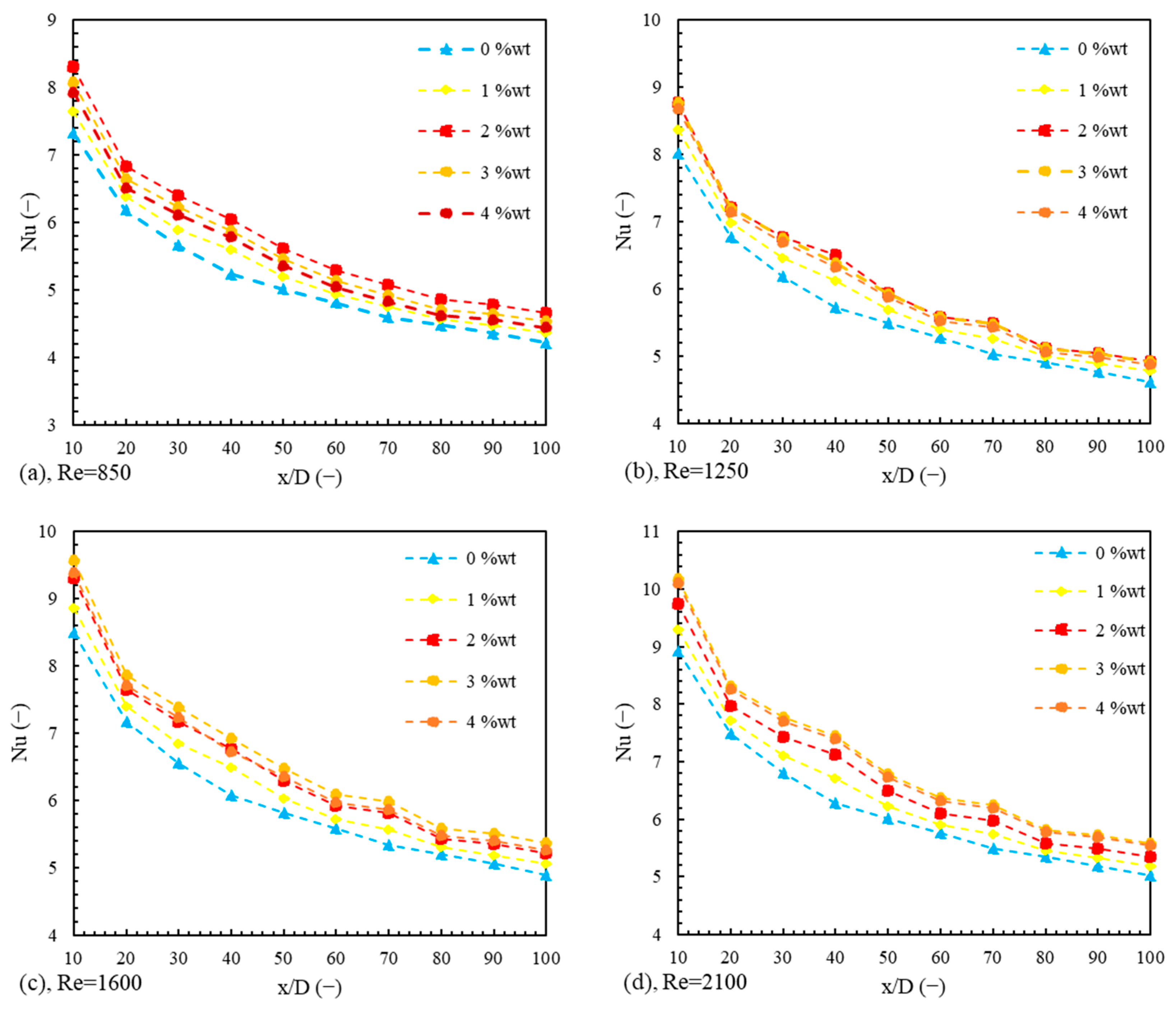
6. Results and Discussion
6.1. Energy Analysis
6.1.1. Circular Cross-Section
6.1.2. Square Cross-Section
6.1.3. Rectangular Cross-Section
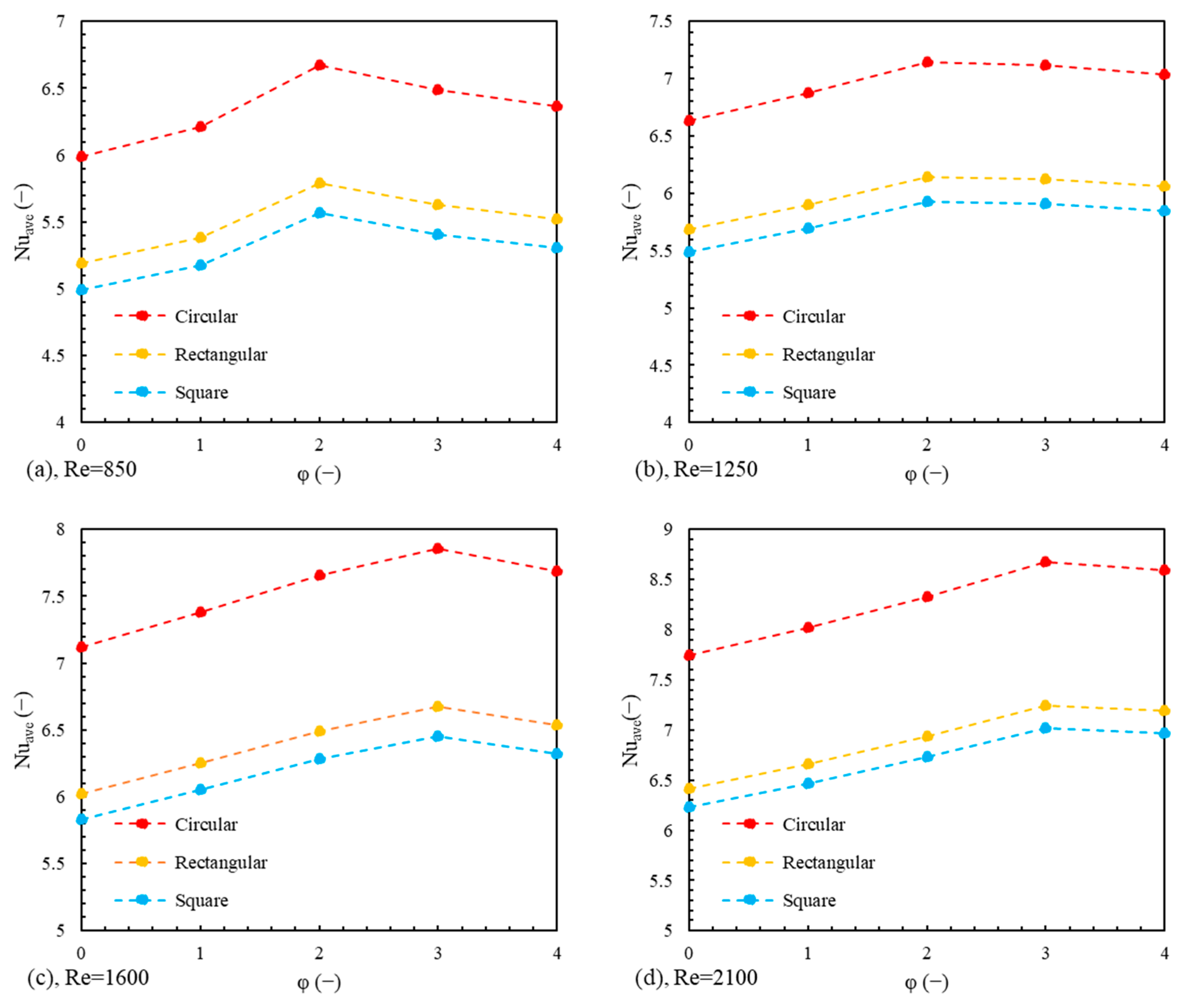
6.1.4. Average Nusselt Number
6.2. Entropy Generation Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| The area of heat transfer () | |
| Specific heat of the fluid () | |
| d & D | Diameter () |
| Friction factor | |
| Gravitational constant () | |
| I | Current (A) |
| Conductivity () | |
| Molar concentration | |
| Mass flux () | |
| Nu | Nusselt number |
| Peripheral () | |
| Heat flux () | |
| Re | Reynolds number |
| Entropy | |
| Temperature () | |
| Velocity () | |
| Voltage (V) | |
| Entrance length (m) | |
| Greek letters | |
| Uncertainty | |
| Viscosity () | |
| Density () | |
| Nanoparticle concentration | |
| Subscripts | |
| Actual | |
| Average | |
| Electrical | |
| Generation | |
| Loss | |
| Total |
References
- Bejan, A. A Study of Entropy Generation in Fundamental Convective Heat Transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef] [Green Version]
- Sahin, A.Z.; Ben-Mansour, R. Entropy generation in laminar fluid flow through a circular pipe. Entropy 2003, 5, 404–416. [Google Scholar] [CrossRef] [Green Version]
- Alimoradi, H.; Eskandari, E.; Pourbagian, M.; Shams, M. A parametric study of subcooled flow boiling of Al2O3/water nanofluid using numerical simulation and artificial neural networks. Nanoscale Microscale Thermophys. Eng. 2022, 26, 129–159. [Google Scholar] [CrossRef]
- Cui, W.; Li, X.; Li, X.; Si, T.; Lu, L.; Ma, T.; Wang, Q. Thermal performance of modified melamine foam/graphene/paraffin wax composite phase change materials for solar-thermal energy conversion and storage. J. Clean. Prod. 2022, 367, 133031. [Google Scholar] [CrossRef]
- Majid, S.; Mohammad, J. Optimal selection of annulus radius ratio to enhance heat transfer with minimum entropy generation in developing laminar forced convection of water-Al2O3 nanofluid flow. J. Cent. South Univ. 2017, 24, 850–1865. [Google Scholar] [CrossRef]
- Zaboli, S.; Alimoradi, H.; Shams, M. Numerical investigation on improvement in pool boiling heat transfer characteristics using different nanofluid concentrations. J. Therm. Anal. Calorim. 2022, 147, 10659–10676. [Google Scholar] [CrossRef]
- Zhong, Q.; Chen, Y.; Zhu, B.; Liao, S.; Shi, K. A temperature field reconstruction method based on acoustic thermometry. Measurement 2022, 200, 111642. [Google Scholar] [CrossRef]
- Roodbari, M.; Alimoradi, H.; Shams, M.; Aghanajafi, C. An experimental investigation of microstructure surface roughness on pool boiling characteristics of TiO2 nanofluid. J. Therm. Anal. Calorim. 2022, 147, 3283–3298. [Google Scholar] [CrossRef]
- Shahsavar, A.; Entezari, S.; Askari, I.B.; Jamei, M.; Karbasi, M.; Shahmohammadi, M. Investigation on two-phase fluid mixture flow, heat transfer and entropy generation of a non-Newtonian water-CMC/CuO nanofluid inside a twisted tube with variable twist pitch: Numerical and evolutionary machine learning simulation. Eng. Anal. Bound. Elem. 2022, 140, 322–337. [Google Scholar] [CrossRef]
- Alimoradi, H.; Soltani, M.; Shahali, P.; Moradi Kashkooli, F.; Larizadeh, R.; Raahemifar, K.; Adibi, M.; Ghasemi, B. Experimental investigation on improvement of wet cooling tower efficiency with diverse packing compaction using ANN-PSO algorithm. Energies 2022, 14, 167. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. A numerical approach on hybrid nanofluid behavior in laminar duct flow with various cross sections. J. Therm. Anal. Calorim. 2020, 140, 2097–2110. [Google Scholar] [CrossRef]
- Alimoradi, H.; Shams, M.; Ashgriz, N.; Bozorgnezhad, A. A novel scheme for simulating the effect of microstructure surface roughness on the heat transfer characteristics of subcooled flow boiling. Case Stud. Therm. Eng. 2021, 24, 100829. [Google Scholar] [CrossRef]
- Dalir, N. Numerical study of entropy generation for forced convection flow and heat transfer of a Jeffrey fluid over a stretching sheet. Alex. Eng. J. 2014, 53, 769–778. [Google Scholar] [CrossRef] [Green Version]
- Biswal, P.; Basak, T. Entropy generation based approach on natural convection in enclosures with concave/convex side walls. Int. J. Heat Mass Transf. 2015, 82, 213–235. [Google Scholar] [CrossRef]
- Nazeryan, M.; Lakzian, E. Detailed entropy generation analysis of a Wells turbine using the variation of the blade thickness. Energy 2018, 143, 385–405. [Google Scholar] [CrossRef]
- Delouei, A.A.; Atashafrooz, M.; Sajjadi, H.; Karimnejad, S. The thermal effects of multi-walled carbon nanotube concentration on an ultrasonic vibrating finned tube heat exchanger. Int. Commun. Heat Mass Transf. 2022, 135, 106098. [Google Scholar] [CrossRef]
- Delouei, A.A.; Sajjadi, H.; Izadi, M.; Mohebbi, R. The simultaneous effects of nanoparticles and ultrasonic vibration on inlet turbulent flow: An experimental study. Appl. Therm. Eng. 2019, 146, 268–277. [Google Scholar] [CrossRef]
- Guo, Z.; Tian, X.; Wu, Z.; Yang, J.; Wang, Q. Heat transfer of granular flow around aligned tube bank in moving bed: Experimental study and theoretical prediction by thermal resistance model. Energy Convers. Manag. 2022, 257, 115435. [Google Scholar] [CrossRef]
- Noghrehabadi, A.; Saffarian, M.R.; Pourrajab, R.; Ghalambaz, M. Entropy analysis for nanofluid flow over a stretching sheet in the presence of heat generation/absorption and partial slip. J. Mech. Sci. Technol. 2013, 27, 927–937. [Google Scholar] [CrossRef]
- Wang, T.; Huang, Z.; Xi, G. Entropy generation for mixed convection in a square cavity containing a rotating circular cylinder using a local radial basis function method. Int. J. Heat Mass Transf. 2017, 106, 1063–1073. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhu, L.; Yu, J.; Li, Y. Optimization of plate-fin heat exchangers by minimizing specific entropy generation rate. Int. J. Heat Mass Transf. 2014, 78, 942–946. [Google Scholar] [CrossRef]
- Falahat, A.; Shabani, M.; Saffarian, M.R. Entropy generation of pseudo-plastic non-Newtonian nanofluids in circular duct under constant wall temperature. J. Mech. Eng. Technol. 2018, 10, 1–10. [Google Scholar]
- Shiravi, A.H.; Shafiee, M.; Firoozzadeh, M.; Bostani, H.; Bozorgmehrian, M. Experimental study on convective heat transfer and entropy generation of carbon black nanofluid turbulent flow in a helical coiled heat exchanger. J. Therm. Anal. Calorim. 2021, 145, 597–607. [Google Scholar] [CrossRef]
- Kadivar, M.; Sharifpur, M.; Meyer, J.P. Convection heat transfer, entropy generation analysis and thermodynamic optimization of nanofluid flow in spiral coil tube. Heat Transf. Eng. 2021, 42, 1573–1589. [Google Scholar] [CrossRef]
- Saffarian, M.R.; Bahoosh, R.; Doranehgard, M.H. Entropy generation in the intake pipe of an internal combustion engine. Eur. Phys. J. Plus 2019, 134, 476. [Google Scholar] [CrossRef]
- Tuncer, A.D.; Sözen, A.; Khanlari, A.; Gürbüz, E.Y.; Variyenli, H.İ. Upgrading the performance of a new shell and helically coiled heat exchanger by using longitudinal fins. Appl. Therm. Eng. 2021, 191, 116876. [Google Scholar] [CrossRef]
- Cui, W.; Si, T.; Li, X.; Li, X.; Lu, L.; Ma, T.; Wang, Q. Heat transfer analysis of phase change material composited with metal foam-fin hybrid structure in inclination container by numerical simulation and artificial neural network. Energy Rep. 2022, 8, 10203–10218. [Google Scholar] [CrossRef]
- Xiong, Q.; Izadi, M.; Shehzad, S.A.; Mohammed, H.A. 3D numerical study of conical and fusiform turbulators for heat transfer improvement in a double-pipe heat exchanger. Int. J. Heat Mass Transf. 2021, 170, 120995. [Google Scholar] [CrossRef]
- Qu, M.; Liang, T.; Hou, J.; Liu, Z.; Yang, E.; Liu, X. Laboratory study and field application of amphiphilic molybdenum disulfide nanosheets for enhanced oil recovery. J. Petroleum Sci. Eng. 2022, 208, 109695. [Google Scholar] [CrossRef]
- Tran, N.; Liaw, J.S.; Wang, C.C. Performance of thermofluidic characteristics of recuperative wavy-plate heat exchangers. Int. J. Heat Mass Transf. 2021, 170, 121027. [Google Scholar] [CrossRef]
- Gasmia, A.; Elboughdirib, N.; Ghernaoutb, D.; Hannachia, A.; Halimb, K.A.; Khanf, M.I. Electrocoagulation process for removing dyes and chemical oxygen demand from wastewater: Operational conditions and economic assessment—A review. Desalination Water Treat. 2022, 271, 74–107. [Google Scholar] [CrossRef]
- Zheng, D.; Yang, J.; Wang, J.; Kabelac, S.; Sundén, B. Analyses of thermal performance and pressure drop in a plate heat exchanger filled with ferrofluids under a magnetic field. Fuel 2021, 293, 120432. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Z. Subset simulation with adaptable intermediate failure probability for robust reliability analysis: An unsupervised learning-based approach. Struct. Multidiscip. Optim. 2022, 65, 1–22. [Google Scholar] [CrossRef]
- Zhao, Y.; Foong, L.K. Predicting Electrical Power Output of Combined Cycle Power Plants Using a Novel Artificial Neural Network Optimized by Electrostatic Discharge Algorithm. Measurement 2022, 198, 111405. [Google Scholar] [CrossRef]
- Al Omari, S.A.B.; Ghazal, A.M.; Elnajjar, E.; Qureshi, Z.A. Vibration-enhanced direct contact heat exchange using gallium as a solid phase change material. Int. Commun. Heat Mass Transf. 2021, 120, 104990. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, H.; Song, C.; Wang, Z. Predicting compressive strength of manufactured-sand concrete using conventional and metaheuristic-tuned artificial neural network. Measurement 2022, 194, 110993. [Google Scholar] [CrossRef]
- Foong, L.K.; Zhao, Y.; Bai, C.; Xu, C. Efficient metaheuristic-retrofitted techniques for concrete slump simulation. Smart Struct. Syst. Int. J. 2021, 27, 745–759. [Google Scholar]
- Shahsavar, A.; Bakhshizadeh, M.A.; Arici, M.; Afrand, M.; Rostami, S. Numerical study of the possibility of improving the hydrothermal performance of an elliptical double-pipe heat exchanger through the simultaneous use of twisted tubes and non-Newtonian nanofluid. J. Therm. Anal. Calorim. 2021, 143, 2825–2840. [Google Scholar] [CrossRef]
- Wu, P.; Liu, A.; Fu, J.; Ye, X.; Zhao, Y. Autonomous surface crack identification of concrete structures based on an improved one-stage object detection algorithm. Eng. Struct. 2022, 272, 114962. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhong, X.; Foong, L.K. Predicting the splitting tensile strength of concrete using an equilibrium optimization model. Steel Compos. Struct. Int. J. 2021, 39, 81–93. [Google Scholar]
- Alimoradi, H.; Zaboli, S.; Shams, M. Numerical simulation of surface vibration effects on improvement of pool boiling heat transfer characteristics of nanofluid. Korean J. Chem. Eng. 2022, 39, 69–85. [Google Scholar] [CrossRef]
- Eskandari, E.; Alimoradi, H.; Pourbagian, M.; Shams, M. Numerical investigation and deep learning-based prediction of heat transfer characteristics and bubble dynamics of subcooled flow boiling in a vertical tube. Korean J. Chem. Eng. 2022, 39, 3227–3245. [Google Scholar] [CrossRef]
- Alimoradi, H.; Shams, M.; Ashgriz, N. Enhancement in the Pool Boiling Heat Transfer of Copper Surface by Applying Electrophoretic Deposited Graphene Oxide Coatings. Int. J. Multiph. Flow 2022, 159, 104350. [Google Scholar] [CrossRef]
- Zhao, Y.; Yan, Q.; Yang, Z.; Yu, X.; Jia, B. A novel artificial bee colony algorithm for structural damage detection. Adv. Civil Eng. 2020, 2020, 3743089. [Google Scholar] [CrossRef] [Green Version]
- Dzyubenko, B.V. Influence of flow twisting on convective heat transfer in banks of twisted tubes. Heat Transf. Res. 2005, 36, 449–460. [Google Scholar] [CrossRef]
- Zhang, X.X.; Wei, G.H.; Sang, Z.F. Experimental research of heat transfer and flow friction properties in twisted tube heat exchanger. Huaxue Gongcheng Chem. Eng. 2007, 35, 17–20. [Google Scholar]
- Qing, D.F.; Duan, X.; Liu, Y.H. Experimental investigation on running characteristics of twisted tube in evaporator. Chem. Eng. 2008, 36, 12–15. [Google Scholar]
- Yu, Y.; Zhu, D.S.; Zeng, L.D.; Zou, J. Experimental investigation on heat transfer enhancement of twisted tube. Chem. Eng. 2015, 39, 18–21. [Google Scholar]
- Samruaisin, P.; Kunlabud, S.; Kunnarak, K.; Chuwattanakul, V.; Eiamsa-Ard, S. Intensification of convective heat transfer and heat exchanger performance by the combined influence of a twisted tube and twisted tape. Case Stud. Therm. Eng. 2019, 14, 100489. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; No. ANL/MSD/CP-84938; CONF-951135-29; Argonne National Lab. ANL: Argonne, IL, USA, 1995. [Google Scholar]
- Zhao, Y.; Joseph, A.J.J.M.; Zhang, Z.; Ma, C.; Gul, D.; Schellenberg, A.; Hu, N. Deterministic snap-through buckling and energy trapping in axially-loaded notched strips for compliant building blocks. Smart Mater. Struct. 2020, 29, 02LT03. [Google Scholar] [CrossRef]
- Alimoradi, H.; Shams, M.; Ashgriz, N. Bubble behavior and nucleation site density in subcooled flow boiling using a novel method for simulating the microstructure of surface roughness. Korean J. Chem. Eng. 2022, 39, 2945–2958. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, H.; Bai, L.; Tang, M.; Chen, H.; Su, D. Fragility analyses of bridge structures using the logarithmic piecewise function-based probabilistic seismic demand model. Sustainability 2021, 13, 7814. [Google Scholar] [CrossRef]
- Bretado-de los Rios, M.S.; Rivera-Solorio, C.I.; Nigam, K.D.P. An overview of sustainability of heat exchangers and solar thermal applications with nanofluids: A review. Renew. Sustain. Energy Rev. 2021, 142, 110855. [Google Scholar] [CrossRef]
- Khoshvaght-Aliabadi, M.; Arani, Z.; Rahimpour, F. Influence of Al2O3–H2O nanofluid on performance of twisted minichannels. Adv. Powder Technol. 2016, 27, 1514–1525. [Google Scholar] [CrossRef]
- Feizabadi, A.; Khoshvaght-Aliabadi, M.; Rahimi, A.B. Numerical investigation on Al2O3/water nanofluid flow through twisted-serpentine tube with empirical validation. Appl. Therm. Eng. 2018, 137, 296–309. [Google Scholar] [CrossRef]
- Omidi, M.; Rabienataj Darzi, A.A.; Farhadi, M. Turbulent heat transfer and fluid flow of alumina nanofluid inside three-lobed twisted tube. J. Therm. Anal. Calorim. 2019, 137, 1451–1462. [Google Scholar] [CrossRef]
- Mahato, S.K.; Rana, S.C.; Barman, R.N.; Goswami, S. Numerical analysis of heat transfer and fluid flow through the twisted square duct (TSD): Nanofluid as working fluid. J. Mech. Sci. Technol. 2019, 33, 5507–5514. [Google Scholar] [CrossRef]
- Zohuri, B.; McDaniel, P. First law of thermodynamics. In Thermodynamics in Nuclear Power Plant Systems; Springer: Cham, Switzerland, 2019; pp. 99–148. [Google Scholar]
- Erguvan, M.; MacPhee, D.W. Second law optimization of heat exchangers in waste heat recovery. Int. J. Energy Res. 2019, 43, 5714–5734. [Google Scholar] [CrossRef]
- Rashidi, S.; Javadi, P.; Esfahani, J.A. Second law of thermodynamics analysis for nanofluid turbulent flow inside a solar heater with the ribbed absorber plate. J. Therm. Anal. Calorim. 2019, 135, 551–563. [Google Scholar] [CrossRef]
- Zhao, Y.; Moayedi, H.; Bahiraei, M.; Foong, L.K. Employing TLBO and SCE for optimal prediction of the compressive strength of concrete. Smart Struct. Syst. 2020, 26, 753–763. [Google Scholar]
- Yan, B.; Ma, C.; Zhao, Y.; Hu, N.; Guo, L. Geometrically Enabled Soft Electroactuators via Laser Cutting. Adv. Eng. Mater. 2015, 21, 1900664. [Google Scholar] [CrossRef]
- Goharkhah, M.; Salarian, A.; Ashjaee, M.; Shahabadi, M. Convective heat transfer characteristics of magnetite nanofluid under the influence of constant and alternating magnetic field. Powder Technol. 2015, 274, 258–267. [Google Scholar] [CrossRef]
- Ratts, E.B.; Raut, A.G. Entropy generation minimization of fully developed internal flow with constant heat flux. J. Heat Transf. 2004, 126, 656–659. [Google Scholar] [CrossRef]
- Hesselgreaves, J.E. Rationalisation of second law analysis of heat exchangers. Int. J. Heat Mass Transf. 2000, 43, 4189–4204. [Google Scholar] [CrossRef]
- Sundar, L.S.; Naik, M.T.; Sharma, K.V.; Singh, M.K.; Reddy, T.C.S. Experimental investigation of forced convection heat transfer and friction factor in a tube with Fe3O4 magnetic nanofluid. Exp. Therm. Fluid Sci. 2012, 37, 65–71. [Google Scholar] [CrossRef]
- Sohn, C.W.; Chen, M.M. Microconvective thermal conductivity in disperse two-phase mixtures as observed in a low velocity Couette flow experiment. J. Heat Transf. 1981, 103, 47–51. [Google Scholar] [CrossRef]
- Shin, S.; Lee, S.H. Thermal conductivity of suspensions in shear flow fields. Int. J. Heat Mass Transf. 2000, 43, 4275–4284. [Google Scholar] [CrossRef]
- Phillips, R.J.; Armstrong, R.C.; Brown, R.A.; Graham, A.L.; Abbott, J.R. A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids A Fluid Dyn. 1992, 4, 30–40. [Google Scholar] [CrossRef]
- Jankowski, T.A. Minimizing entropy generation in internal flows by adjusting the shape of the cross-section. Int. J. Heat Mass Transf. 2009, 52, 3439–3445. [Google Scholar] [CrossRef]
- Kurnia, J.C.; Sasmito, A.P.; Shamim, T.; Mujumdar, A.S. Numerical investigation of heat transfer and entropy generation of laminar flow in helical tubes with various cross sections. Appl. Therm. Eng. 2016, 102, 849–860. [Google Scholar] [CrossRef]









| Cross-Section | 2a | 2b | 2b/2a | Dh |
|---|---|---|---|---|
| Circular | - | - | - | 0.0154 |
| Square | 0.0154 | 0.0154 | 1 | 0.0154 |
| Rectangular | 0.0231 | 0.01155 | 0.5 | 0.0154 |
| 3690 | 880 | 18 | 15 |
| Equipment | Measurement Range | Minimum Measuring Value | The Studied Range in the Present Study | Uncertainty Percentage |
|---|---|---|---|---|
| K-Type thermocouple | 0–120 () | 0.1 | 24.5–38.5 | 0.260 |
| RTD-Pt100 thermocouple | 0–200 () | 0.1 | 25.5–34.5 | 0.290 |
| Voltmeter | 0–100 (V) | 0.01 | 24–48 | 0.021 |
| Ampere meter | 0–10 (A) | 0.001 | 0.85–1.2 | 0.083 |
| Ohmmeter | 0–100 () | 0.001 | 27.4–54.5 | 0.002 |
| Pressure transducer | 0–100 (mbar) | 0.1 | 8.5–45 | 0.222 |
| Flow meter | 0–70 (L/min) | 1 | 10–60 | 1.667 |
| Geometrical dimensions | 1–20 (mm) | 0.1 | 1–20 | 0.500 |
| Physical properties | - | - | - | 0.100 |
| Parameter | Uncertainty Percentage |
|---|---|
| 0.086 | |
| 0.091 | |
| 0.518 | |
| 1.746 | |
| 1.827 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jery, A.E.; Satishkumar, P.; Abdul Jaleel Maktoof, M.; Suplata, M.; Dudic, B.; Spalevic, V. Sustainable Heat Transfer Management: Modeling of Entropy Generation Minimization and Nusselt Number Development in Internal Flows with Various Shapes of Cross-Sections Using Water and Al2O3/Water Nanofluid. Water 2023, 15, 89. https://doi.org/10.3390/w15010089
Jery AE, Satishkumar P, Abdul Jaleel Maktoof M, Suplata M, Dudic B, Spalevic V. Sustainable Heat Transfer Management: Modeling of Entropy Generation Minimization and Nusselt Number Development in Internal Flows with Various Shapes of Cross-Sections Using Water and Al2O3/Water Nanofluid. Water. 2023; 15(1):89. https://doi.org/10.3390/w15010089
Chicago/Turabian StyleJery, Atef El, P. Satishkumar, Mohammed Abdul Jaleel Maktoof, Marian Suplata, Branislav Dudic, and Velibor Spalevic. 2023. "Sustainable Heat Transfer Management: Modeling of Entropy Generation Minimization and Nusselt Number Development in Internal Flows with Various Shapes of Cross-Sections Using Water and Al2O3/Water Nanofluid" Water 15, no. 1: 89. https://doi.org/10.3390/w15010089







