Data Conditioning Modes for the Study of Groundwater Resource Quality Using a Large Physico-Chemical and Bacteriological Database, Occitanie Region, France
Abstract
:1. Introduction
2. Materials and Methods
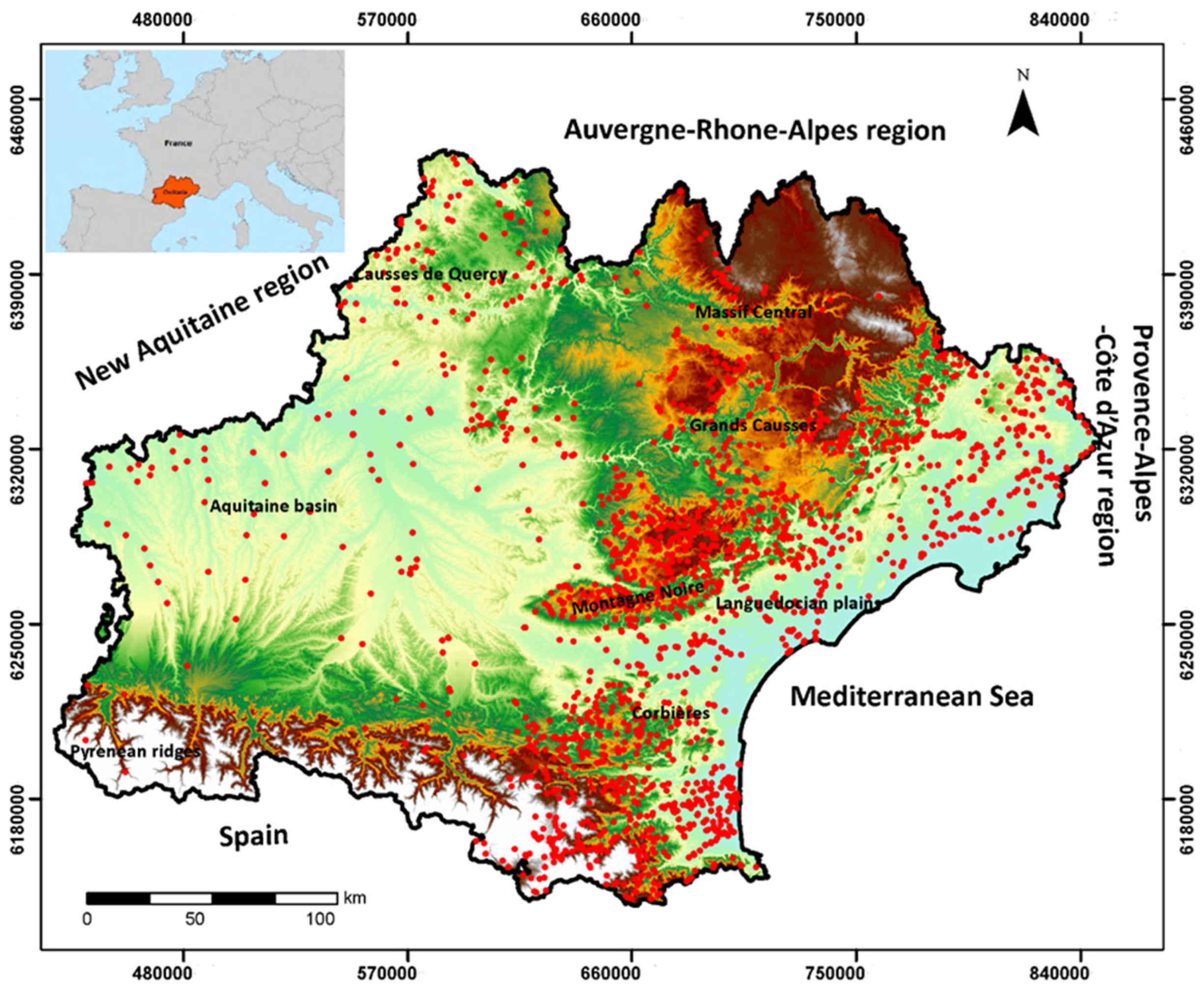
2.1. Study Area
2.2. Database
2.3. Mathematical Tools
3. Results
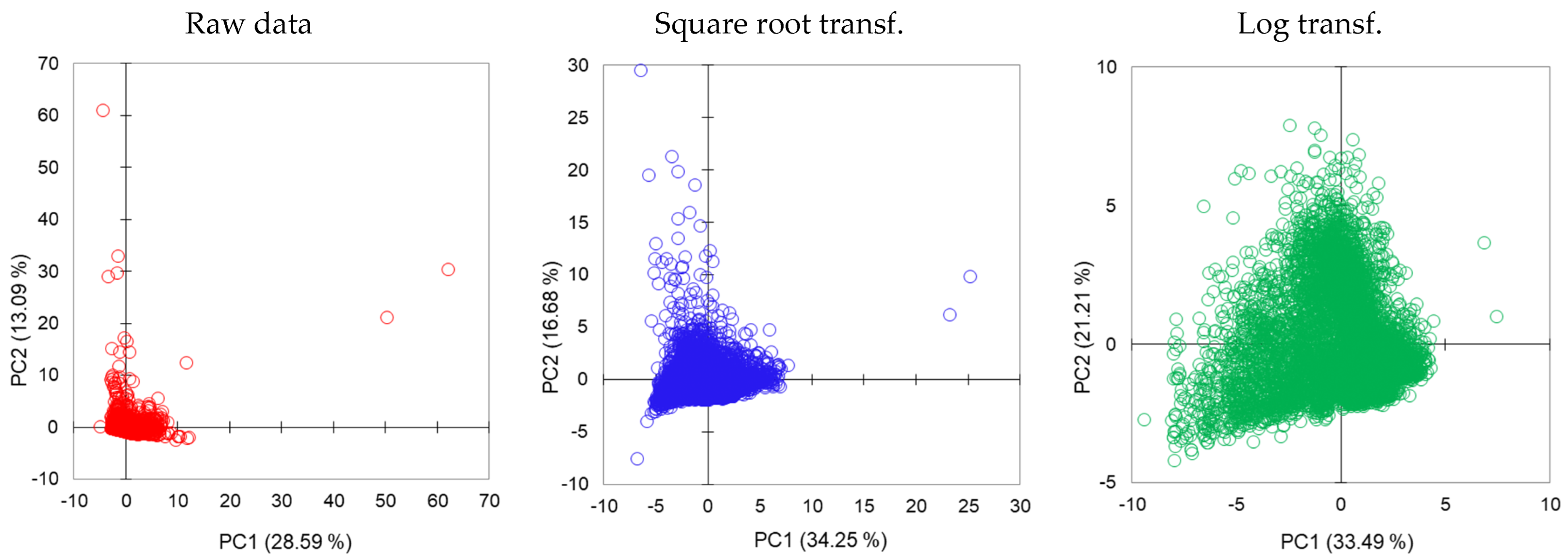
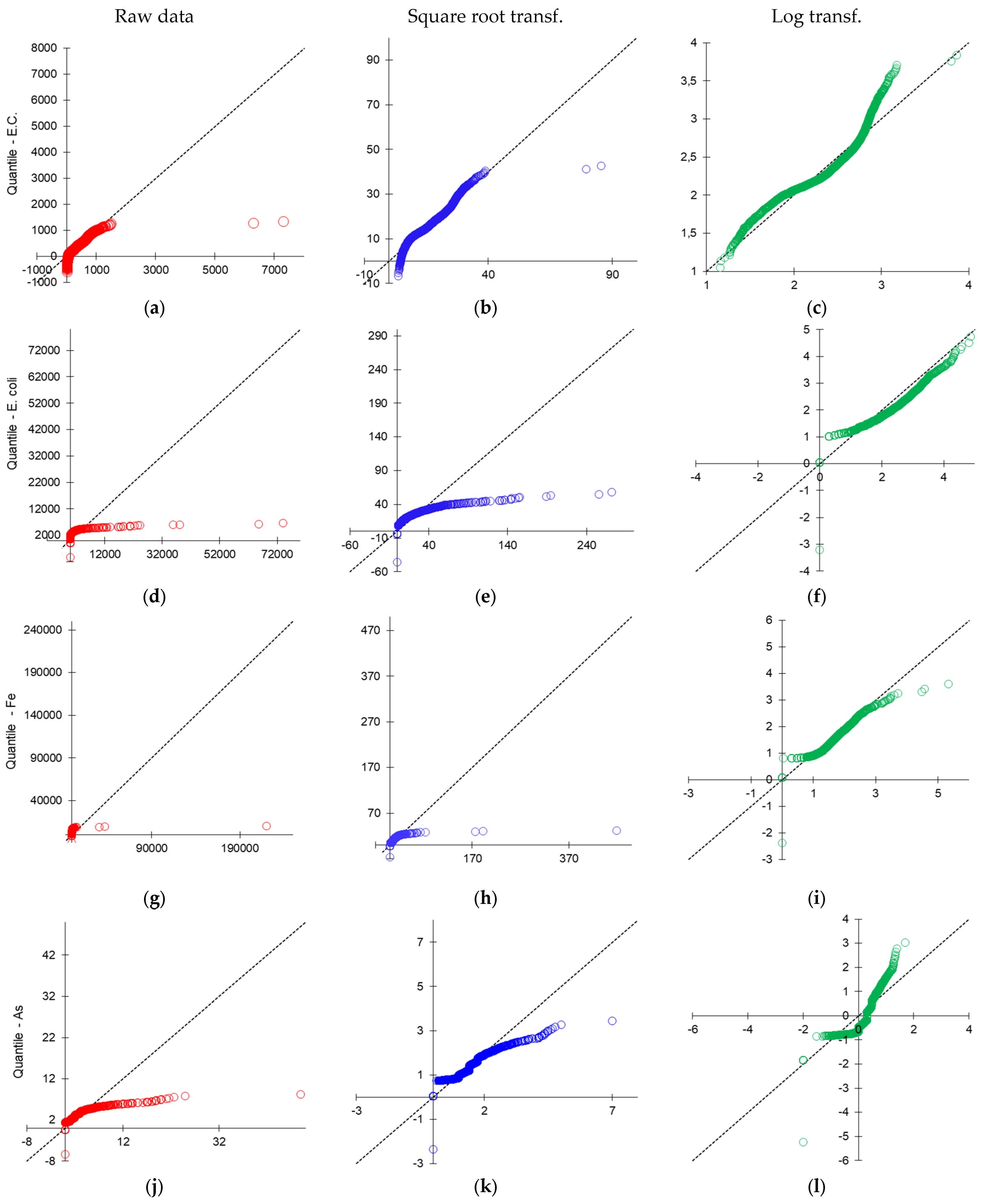
3.1. Extreme and Highly Extreme Values
3.2. Multiple Regression
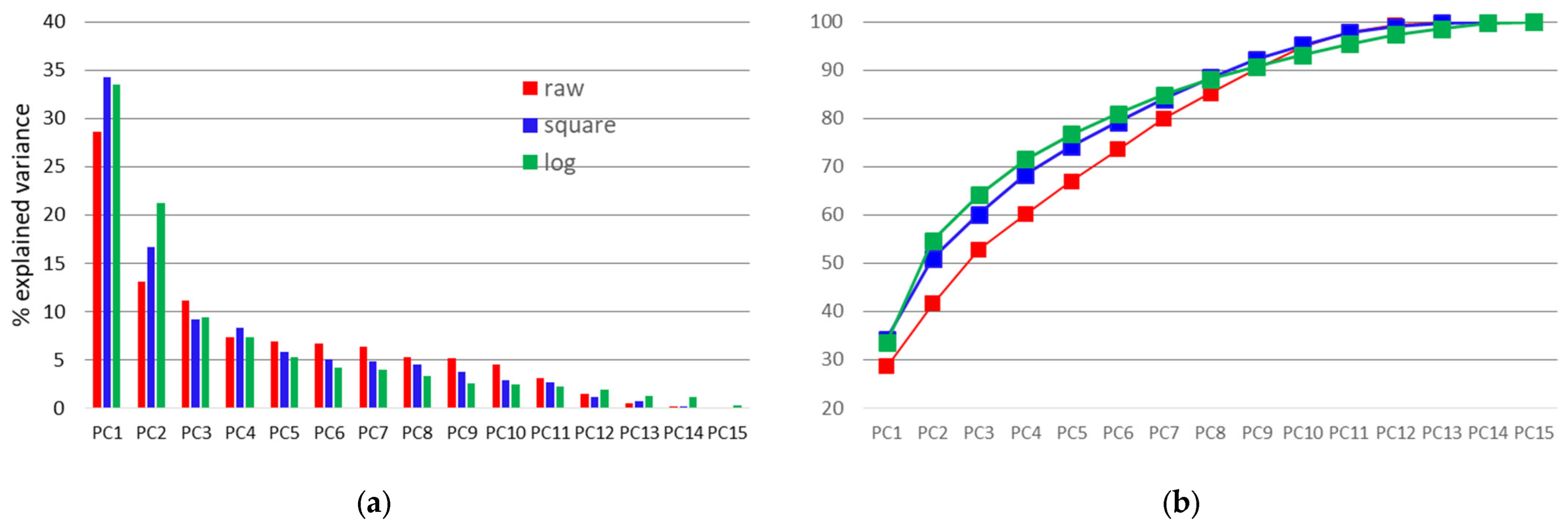
3.3. PCA Using the 3 Data Conditioning Modes
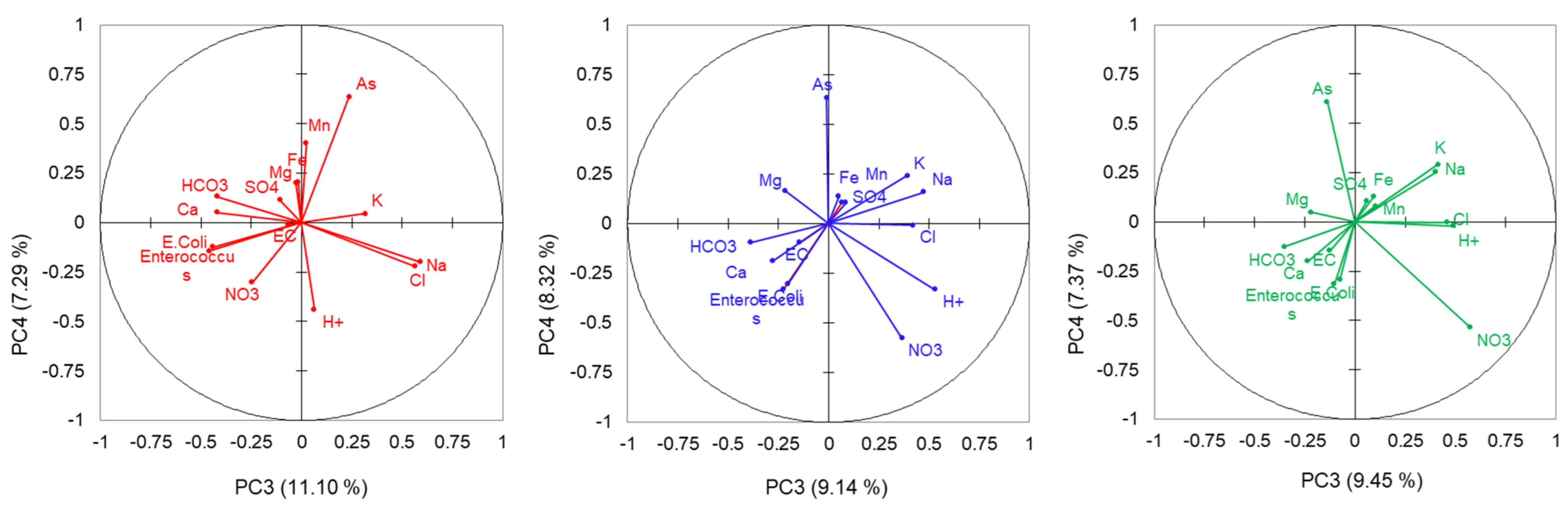
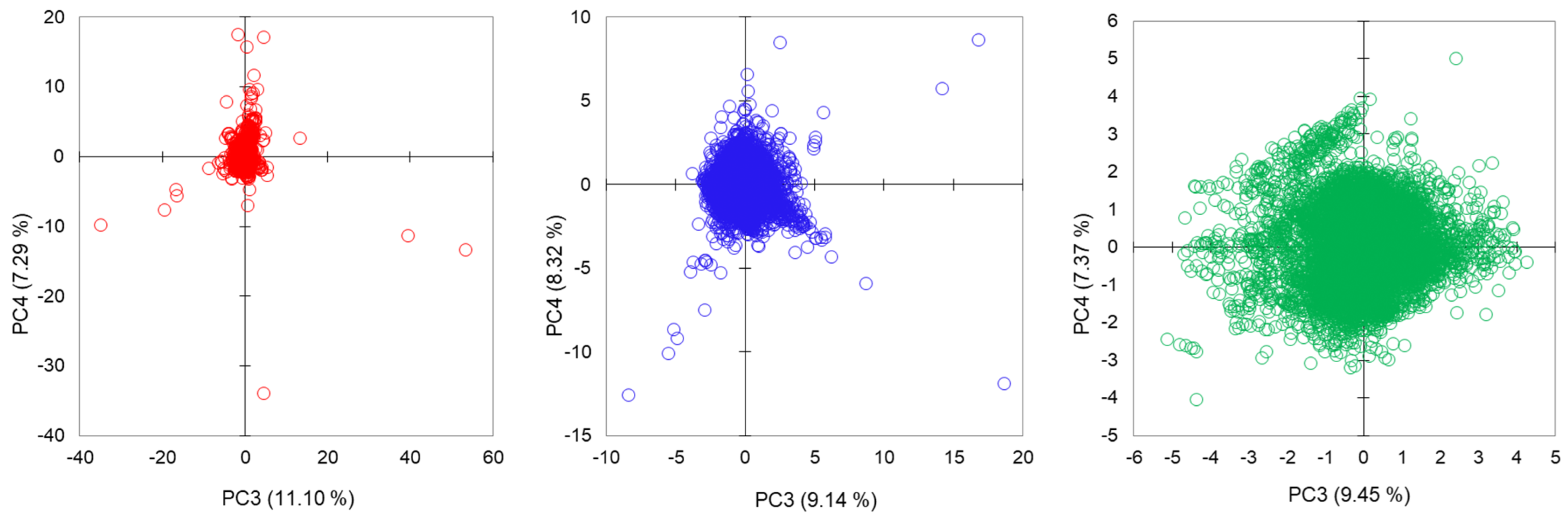
3.3.1. Significance of the First Four Principal Components
3.3.2. Distribution of Water Samples in Factorial Score Plots
3.3.3. Inertia of the Principal Components
3.4. Frequency Distribution
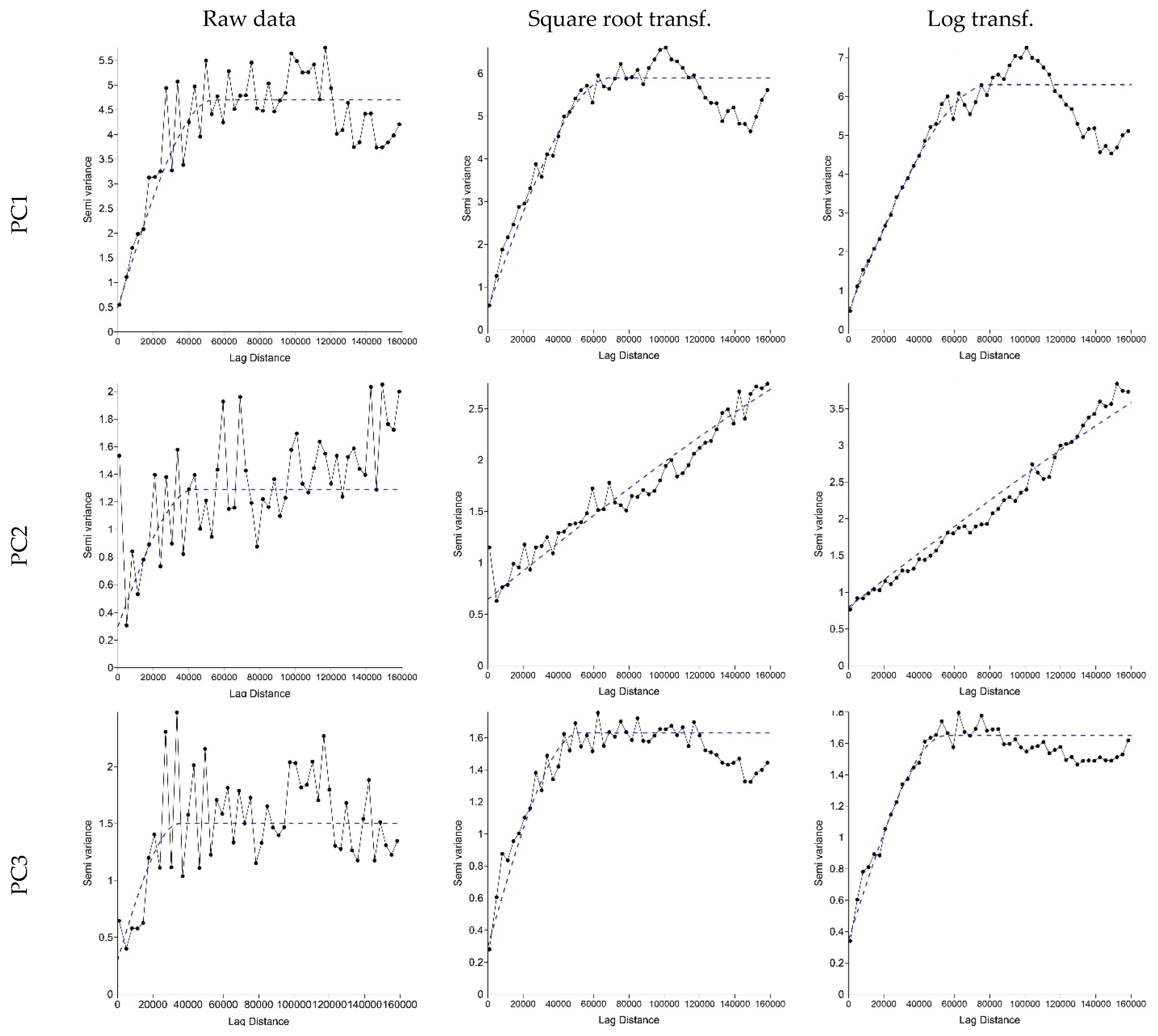
3.5. Variograms and Mapping
4. Discussion
4.1. Need to Work on Transformed Data
4.2. Impact on Process Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Association of Hydrogeologists. Groundwater—More About the Hidden Resource. Available online: https://iah.org/education/general-public/groundwater-hidden-resource (accessed on 27 November 2022).
- Li, P. To Make the Water Safer. Expo. Health 2020, 12, 337–342. [Google Scholar] [CrossRef] [PubMed]
- European Commission. Directive 2000/60/EC of the European Parliament and of the Council of 23 October 2000 establishing a framework for Community action in the field of water policy. Off. J. Eur. Communities 2000, 22, 2000. [Google Scholar]
- European Commission. Directive 2006/118/EC of the European Parliament and of the Council of 12 December 2006 on the protection of groundwater against pollution and deterioration. Off. J. Eur. Union 2006, 372, 19–31. [Google Scholar]
- Martínez Navarrete, C.; Grima Olmedo, J.; Durán Valsero, J.J.; Gómez Gómez, J.D.; Luque Espinar, J.A.; de la Orden Gómez, J.A. Groundwater protection in Mediterranean countries after the European water framework directive. Environ. Geol. 2008, 54, 537–549. [Google Scholar] [CrossRef]
- Danielopol, D.L.; Griebler, C.; Gunatilaka, A.; Notenboom, J. Present state and future prospects for groundwater ecosystems. Environ. Conserv. 2003, 30, 104–130. [Google Scholar] [CrossRef] [Green Version]
- Edmunds, W.M.; Shand, P.; Hart, P.; Ward, R.S. The natural (baseline) quality of groundwater: A UK pilot study. Sci. Total Environ. 2003, 310, 25–35. [Google Scholar] [CrossRef] [Green Version]
- Hinsby, K.; Condesso de Melo, M.T.; Dahl, M. European case studies supporting the derivation of natural background levels and groundwater threshold values for the protection of dependent ecosystems and human health. Sci. Total Environ. 2008, 401, 1–20. [Google Scholar] [CrossRef]
- Masciale, R.; Amalfitano, S.; Frollini, E.; Ghergo, S.; Melita, M.; Parrone, D.; Preziosi, E.; Vurro, M.; Zoppini, A.; Passarella, G. Assessing Natural Background Levels in the Groundwater Bodies of the Apulia Region (Southern Italy). Water 2021, 13, 958. [Google Scholar] [CrossRef]
- Nakić, Z.; Kovač, Z.; Parlov, J.; Perković, D. Ambient Background Values of Selected Chemical Substances in Four Groundwater Bodies in the Pannonian Region of Croatia. Water 2020, 12, 2671. [Google Scholar] [CrossRef]
- Quevauviller, P.; Balabanis, P.; Fragakis, C.; Weydert, M.; Oliver, M.; Kaschl, A.; Arnold, G.; Kroll, A.; Galbiati, L.; Zaldivar, J.M.; et al. Science-policy integration needs in support of the implementation of the EU Water Framework Directive. Environ. Sci. Policy 2005, 8, 203–211. [Google Scholar] [CrossRef]
- Smith, J.W.N.; Bonell, M.; Gibert, J.; McDowell, W.H.; Sudicky, E.A.; Turner, J.V.; Harris, R.C. Groundwater–surface water interactions, nutrient fluxes and ecological response in river corridors: Translating science into effective environmental management. Hydrol. Process. 2008, 22, 151–157. [Google Scholar] [CrossRef]
- Urresti-Estala, B.; Carrasco-Cantos, F.; Vadillo-Pérez, I.; Jiménez-Gavilán, P. Determination of background levels on water quality of groundwater bodies: A methodological proposal applied to a Mediterranean River basin (Guadalhorce River, Málaga, southern Spain). J. Environ. Manag. 2013, 117, 121–130. [Google Scholar] [CrossRef] [PubMed]
- Wendland, F.; Hannappel, S.; Kunkel, R.; Schenk, R.; Voigt, H.J.; Wolter, R. A procedure to define natural groundwater conditions of groundwater bodies in Germany. Water Sci. Technol. 2005, 51, 249–257. [Google Scholar] [CrossRef] [PubMed]
- John, D.E.; Rose, J.B. Review of Factors Affecting Microbial Survival in Groundwater. Environ. Sci. Technol. 2005, 39, 7345–7356. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pachepsky, Y.A.; Shelton, D.R. Escherichia coli and Fecal Coliforms in Freshwater and Estuarine Sediments. Crit. Rev. Environ. Sci. Technol. 2011, 41, 1067–1110. [Google Scholar] [CrossRef]
- Pandey, P.K.; Kass, P.H.; Soupir, M.L.; Biswas, S.; Singh, V.P. Contamination of water resources by pathogenic bacteria. AMB Express 2014, 4, 51. [Google Scholar] [CrossRef] [Green Version]
- Haslauer, C.P.; Heißerer, T.; Bárdossy, A. Including land use information for the spatial estimation of groundwater quality parameters—2. Interpolation methods, results, and comparison. J. Hydrol. 2016, 535, 699–709. [Google Scholar] [CrossRef]
- Haslauer, C.P.; Allmendinger, M.; Gnann, S.; Heisserer, T.; Bárdossy, A. Interpolation of Regional Groundwater Quality Parameters With Categorical and Real-Valued Secondary Information in the State of Baden-Württemberg, Germany. In Proceedings of the AGU Fall Meeting Abstracts, New Orleans, LA, USA, 11–15 December 2017; Volume 2017, p. H53O-07. [Google Scholar]
- Frollini, E.; Preziosi, E.; Calace, N.; Guerra, M.; Guyennon, N.; Marcaccio, M.; Menichetti, S.; Romano, E.; Ghergo, S. Groundwater quality trend and trend reversal assessment in the European Water Framework Directive context: An example with nitrates in Italy. Environ. Sci. Pollut. Res. 2021, 28, 22092–22104. [Google Scholar] [CrossRef]
- Pantaleone, D.V.; Vincenzo, A.; Fulvio, C.; Silvia, F.; Cesaria, M.; Giuseppina, M.; Ilaria, M.; Vincenzo, P.; Rosa, S.A.; Gianpietro, S.; et al. Hydrogeology of continental southern Italy. J. Maps 2018, 14, 230–241. [Google Scholar] [CrossRef] [Green Version]
- El Osta, M.; Masoud, M.; Alqarawy, A.; Elsayed, S.; Gad, M. Groundwater Suitability for Drinking and Irrigation Using Water Quality Indices and Multivariate Modeling in Makkah Al-Mukarramah Province, Saudi Arabia. Water 2022, 14, 483. [Google Scholar] [CrossRef]
- Masoud, M.; El Osta, M.; Alqarawy, A.; Elsayed, S.; Gad, M. Evaluation of groundwater quality for agricultural under different conditions using water quality indices, partial least squares regression models, and GIS approaches. Appl. Water Sci. 2022, 12, 244. [Google Scholar] [CrossRef]
- Webster, R.; Olliver, M.A. Geostatistics for Environmental Scientists, 2nd ed.; Wiley: Chichester, UK, 2007; ISBN 9780470028582. [Google Scholar]
- Tiouiouine, A.; Yameogo, S.; Valles, V.; Barbiero, L.; Dassonville, F.; Moulin, M.; Bouramtane, T.; Bahaj, T.; Morarech, M.; Kacimi, I. Dimension reduction and analysis of a 10-year physicochemical and biological water database applied to water resources intended for human consumption in the provence-alpes-cote d’azur region, France. Water 2020, 12, 525. [Google Scholar] [CrossRef]
- Barbel-Périneau, A.; Barbiero, L.; Danquigny, C.; Emblanch, C.; Mazzilli, N.; Babic, M.; Simler, R.; Valles, V. Karst flow processes explored through analysis of long-term unsaturated-zone discharge hydrochemistry: A 10-year study in Rustrel, France. Hydrogeol. J. 2019, 27, 1711–1723. [Google Scholar] [CrossRef]
- Helena, B.; Pardo, R.; Vega, M.; Barrado, E.; Fernandez, J.M.; Fernandez, L. Temporal evolution of groundwater composition in an alluvial aquifer (Pisuerga River, Spain) by principal component analysis. Water Res. 2000, 34, 807–816. [Google Scholar] [CrossRef]
- Rezende Filho, A.T.; Furian, S.; Victoria, R.L.; Mascré, C.; Valles, V.; Barbiero, L. Hydrochemical variability at the upper paraguay basin and pantanal wetland. Hydrol. Earth Syst. Sci. 2012, 16, 2723–2737. [Google Scholar] [CrossRef] [Green Version]
- Tiouiouine, A.; Jabrane, M.; Kacimi, I.; Morarech, M.; Bouramtane, T.; Bahaj, T.; Yameogo, S.; Rezende-Filho, A.; Dassonville, F.; Moulin, M.; et al. Determining the relevant scale to analyze the quality of regional groundwater resources while combining groundwater bodies, physicochemical and biological databases in southeastern france. Water 2020, 12, 3476. [Google Scholar] [CrossRef]
- Rezende Filho, A.; Valles, V.; Furian, S.; Oliveira, C.M.S.C.; Ouardi, J.; Barbiero, L. Impacts of lithological and anthropogenic factors affecting water chemistry in the Upper Paraguay River Basin. J. Environ. Qual. 2015, 44, 1832–1842. [Google Scholar] [CrossRef]
- Marden, J.I. Positions and QQ Plots. Stat. Sci. 2004, 19, 606–614. [Google Scholar] [CrossRef]
- Steinskog, D.J.; Tjøstheim, D.B.; Kvamstø, N.G. A Cautionary Note on the Use of the Kolmogorov–Smirnov Test for Normality. Mon. Weather Rev. 2007, 135, 1151–1157. [Google Scholar] [CrossRef]
- Bouramtane, T.; Yameogo, S.; Touzani, M.; Tiouiouine, A.; El Janati, M.; Ouardi, J.; Kacimi, I.; Valles, V.; Barbiero, L. Statistical approach of factors controlling drainage network patterns in arid areas. Application to the Eastern Anti Atlas (Morocco). J. African Earth Sci. 2020, 162, 103707. [Google Scholar] [CrossRef]
- O’Hara, R.B.; Kotze, D.J. Do not log-transform count data. Methods Ecol. Evol. 2010, 1, 118–122. [Google Scholar] [CrossRef] [Green Version]
- Feng, C.; Wang, H.; Lu, N.; Chen, T.; He, H.; Lu, Y.; Tu, X.M. Log-transformation and its implications for data analysis. Shanghai Arch. Psychiatry 2014, 26, 105–109. [Google Scholar] [PubMed]




| Data Conditioning | R² |
|---|---|
| Raw data | 0.0597 |
| Chemical profile transformation | 0.0746 |
| Square root transformation | 0.2582 |
| Log-transformation | 0.4943 |
| Raw Data | Explained Variance Square Root Transf. | Log Transf. | |
|---|---|---|---|
| PC1 | 28.59 | 34.25 | 33.49 |
| PC2 | 13.09 | 16.68 | 21.21 |
| PC3 | 11.1 | 9.14 | 9.45 |
| PC4 | 7.29 | 8.32 | 7.37 |
| Sum | 60.07 | 68.39 | 71.52 |
| PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | ||
|---|---|---|---|---|---|---|---|---|
| Raw data | Eigenvalue | 4.29 | 1.96 | 1.67 | 1.09 | 1.03 | 1 | 0.96 |
| Variability (%) | 28.59 | 13.09 | 11.10 | 7.29 | 6.85 | 6.65 | 6.38 | |
| Cumulative % | 28.59 | 41.68 | 52.78 | 60.07 | 66.92 | 73.58 | 79.95 | |
| Squ. root data | Eigenvalue | 5.14 | 2.50 | 1.37 | 1.25 | 0.87 | 0.75 | 0.72 |
| Variability (%) | 34.25 | 16.68 | 9.14 | 8.32 | 5.83 | 5.02 | 4.79 | |
| Cumulative % | 34.25 | 50.94 | 60.07 | 68.39 | 74.22 | 79.24 | 84.03 | |
| Log. data | Eigenvalue | 5.02 | 3.18 | 1.42 | 1.11 | 0.79 | 0.62 | 0.59 |
| Variability (%) | 33.5 | 21.21 | 9.45 | 7.37 | 5.25 | 4.16 | 3.93 | |
| Cumulative % | 33.5 | 54.71 | 64.16 | 71.53 | 76.78 | 80.93 | 84.86 |
| Raw Data | Square Root Transf. | Log Transf. | ||
|---|---|---|---|---|
| PC1 | Nugget | 0.5 | 0.5 | 0.5 |
| Range | 54,000 | 70,000 | 80,000 | |
| Reduced sill | 4.2 | 5.4 | 5.8 | |
| PC2 | Nugget | 0.3 | 0.75 | 0.8 |
| Range | 43,000 | 350,000 | 300,000 | |
| Reduced sill | 1 | 3.2 | 4.9 | |
| PC3 | Nugget | 0.3 | 0.3 | 0.35 |
| Range | 35,000 | 52,000 | 55,000 | |
| Reduced sill | 1.2 | 1.33 | 1.3 | |
| PC4 | Nugget | 0.45 | 0.7 | 0.68 |
| Range | 30,000 | 55,000 | 53,000 | |
| Reduced sill | 0.7 | 0.49 | 0.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jabrane, M.; Touiouine, A.; Bouabdli, A.; Chakiri, S.; Mohsine, I.; Valles, V.; Barbiero, L. Data Conditioning Modes for the Study of Groundwater Resource Quality Using a Large Physico-Chemical and Bacteriological Database, Occitanie Region, France. Water 2023, 15, 84. https://doi.org/10.3390/w15010084
Jabrane M, Touiouine A, Bouabdli A, Chakiri S, Mohsine I, Valles V, Barbiero L. Data Conditioning Modes for the Study of Groundwater Resource Quality Using a Large Physico-Chemical and Bacteriological Database, Occitanie Region, France. Water. 2023; 15(1):84. https://doi.org/10.3390/w15010084
Chicago/Turabian StyleJabrane, Meryem, Abdessamad Touiouine, Abdelhak Bouabdli, Saïd Chakiri, Ismail Mohsine, Vincent Valles, and Laurent Barbiero. 2023. "Data Conditioning Modes for the Study of Groundwater Resource Quality Using a Large Physico-Chemical and Bacteriological Database, Occitanie Region, France" Water 15, no. 1: 84. https://doi.org/10.3390/w15010084
APA StyleJabrane, M., Touiouine, A., Bouabdli, A., Chakiri, S., Mohsine, I., Valles, V., & Barbiero, L. (2023). Data Conditioning Modes for the Study of Groundwater Resource Quality Using a Large Physico-Chemical and Bacteriological Database, Occitanie Region, France. Water, 15(1), 84. https://doi.org/10.3390/w15010084








