Stress Estimation of Concrete Dams in Service Based on Deformation Data Using SIE–APSO–CNN–LSTM
Abstract
:1. Introduction
2. Methodology
- Data configuration. Observations from dam deformation and stress sensors are collected to provide learning data for the estimation model. The supposed failure time of the target stress sensor is considered to be the splitting point between the training and testing periods. The data samples are then configured via the sliding-window approach.
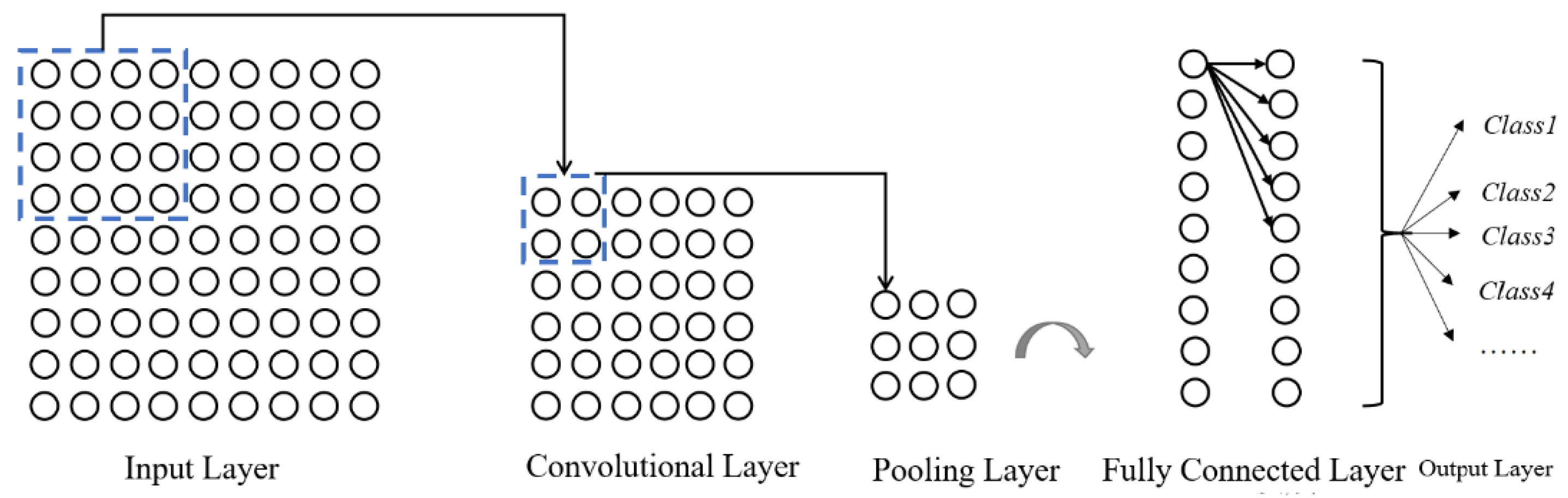
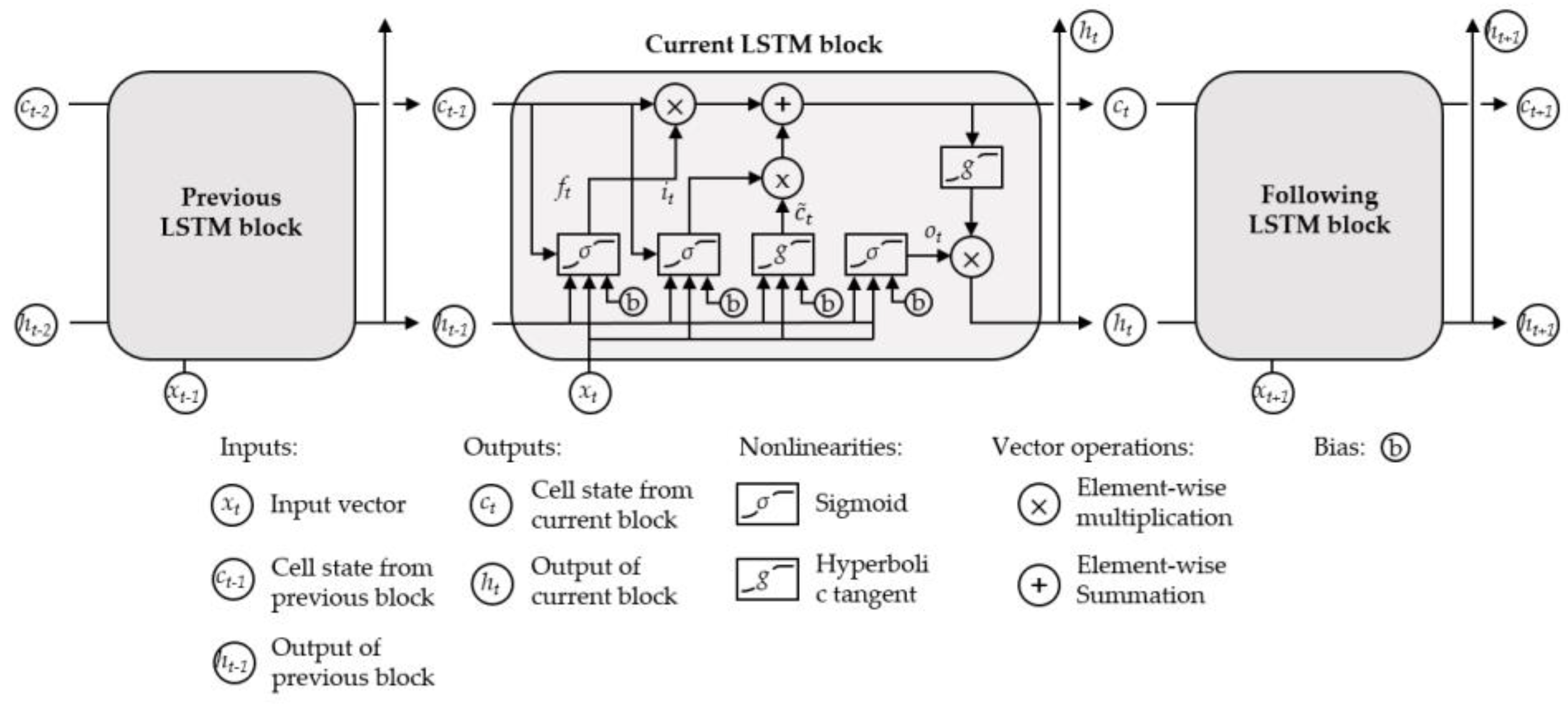
- Model development. Taking the deformation matrix as the model input and extracting the spatial features among different deformation monitoring points via CNN each day produces the output sequence containing the temporal attributes. Take this sequence as the input of the single-layered LSTM to obtain the temporal representation of the sequence. Finally, set a fully connected (FC) layer to get the model output and take it as the value of concrete stress.
- Tuning and training. The training and validation subset are obtained via the time series cross-validation (CV) technique performed on the training data. Subsequently, taking the average accuracy of the validation set of each fold as the fitness function, the hyperparameter tuning of the estimation model is implemented via the proposed SIE–APSO.
- Evaluation. The estimation performance of the trained model is evaluated by feeding it the configured out-of-training data. Furthermore, the root mean square error (RMSE), average absolute percentage error (MAPE), and average relative variance (ARV) are utilized for model evaluation.
2.1. The CNN–LSTM Estimation Model
2.1.1. Convolutional Neural Network
2.1.2. Long Short-Term Memory Network
2.2. Improvement of the Particle Swarm Optimization
- inheritance of its inertia;
- the particle’s cognitive behavior, which represents the thinking of the particle itself;
- the population’s social sharing behavior represents the information sharing and cooperation between particles.
- Reduce the probability of falling into a local optimum. With the preform of iteration, the diversity of particles will continue to decrease, and it is easy to fall into the local optimum. Simulation of particle alienation behavior can reduce the probability of this phenomenon.
- Balance the global and local search capabilities of the algorithm. The particles are uniformly distributed in the early iteration with a larger swarm information entropy. At this stage, the higher alienation rate effectively prevents the particles from moving directly to the current optimal solution, giving it a better global exploration ability. While in the later stage, the particles are gradually concentrated. The decreasing of the alienation rate provides better local development of the particles.
2.3. Time Series Cross-Validation Technique
2.4. Evaluation Metrics
3. Case Study
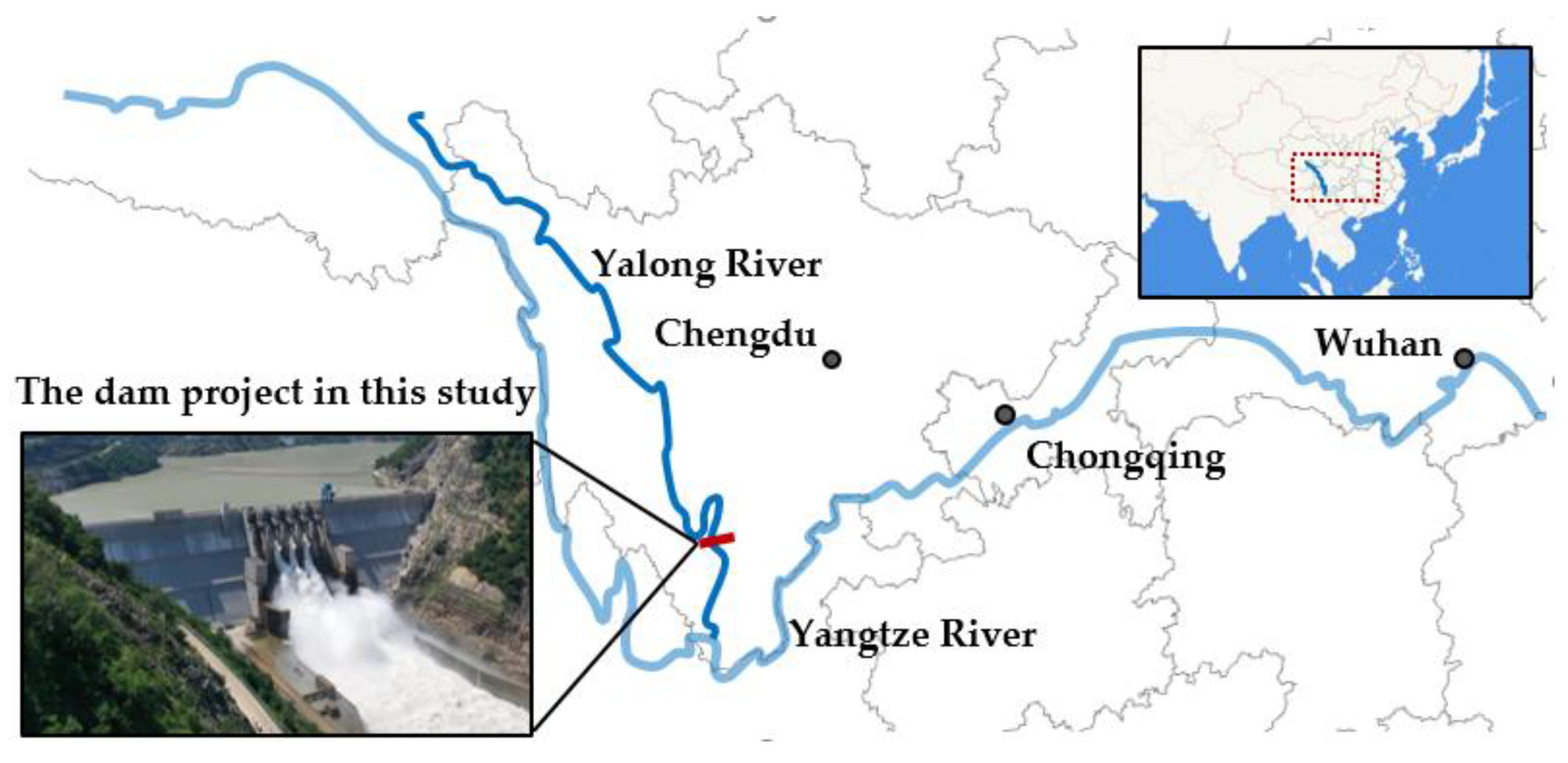
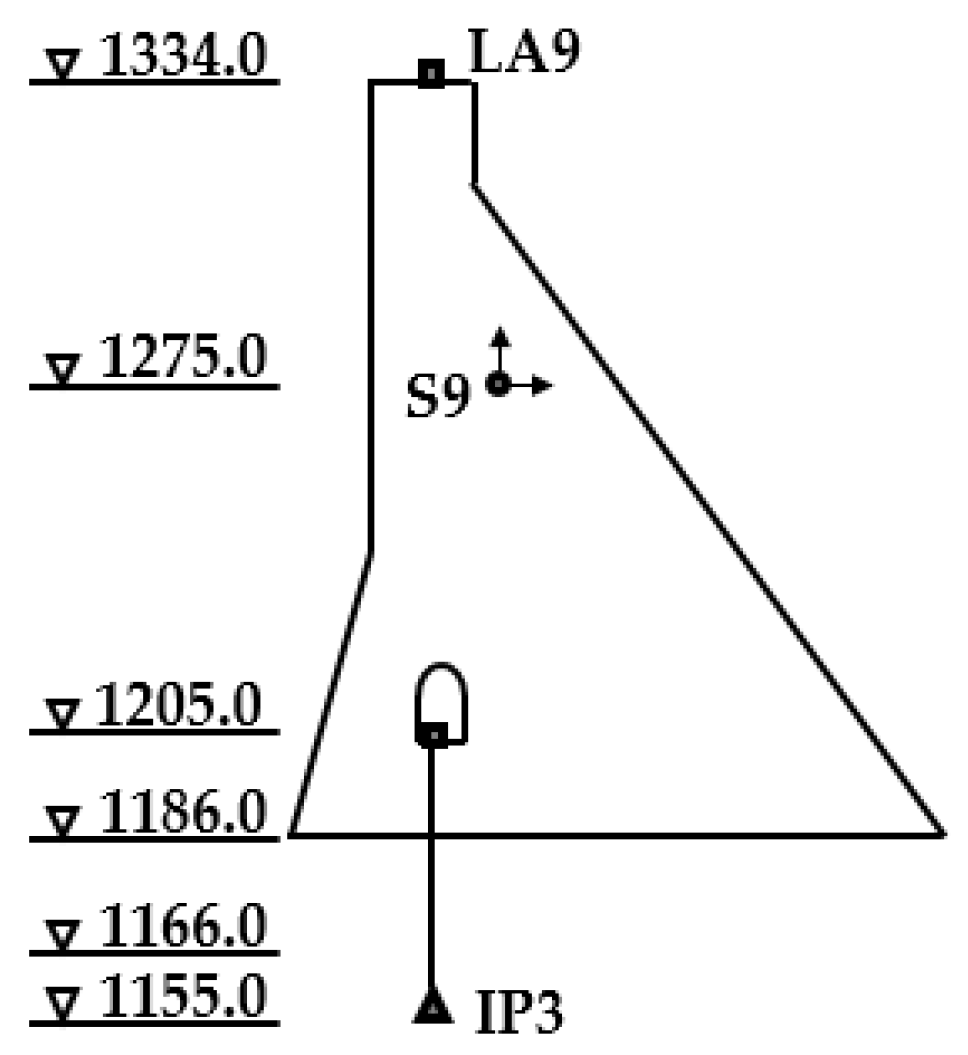
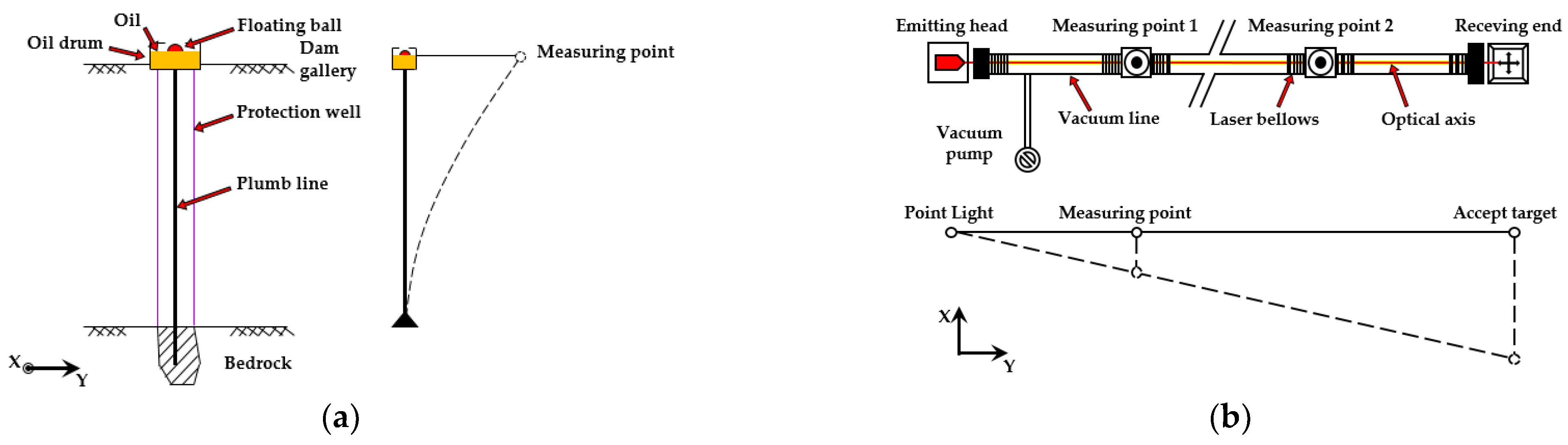
3.1. Project Description
- environment variables;
- horizontal and vertical displacement of the dam;
- the inclination of the dam foundation and dam body;
- the stress and strain of the dam concrete.
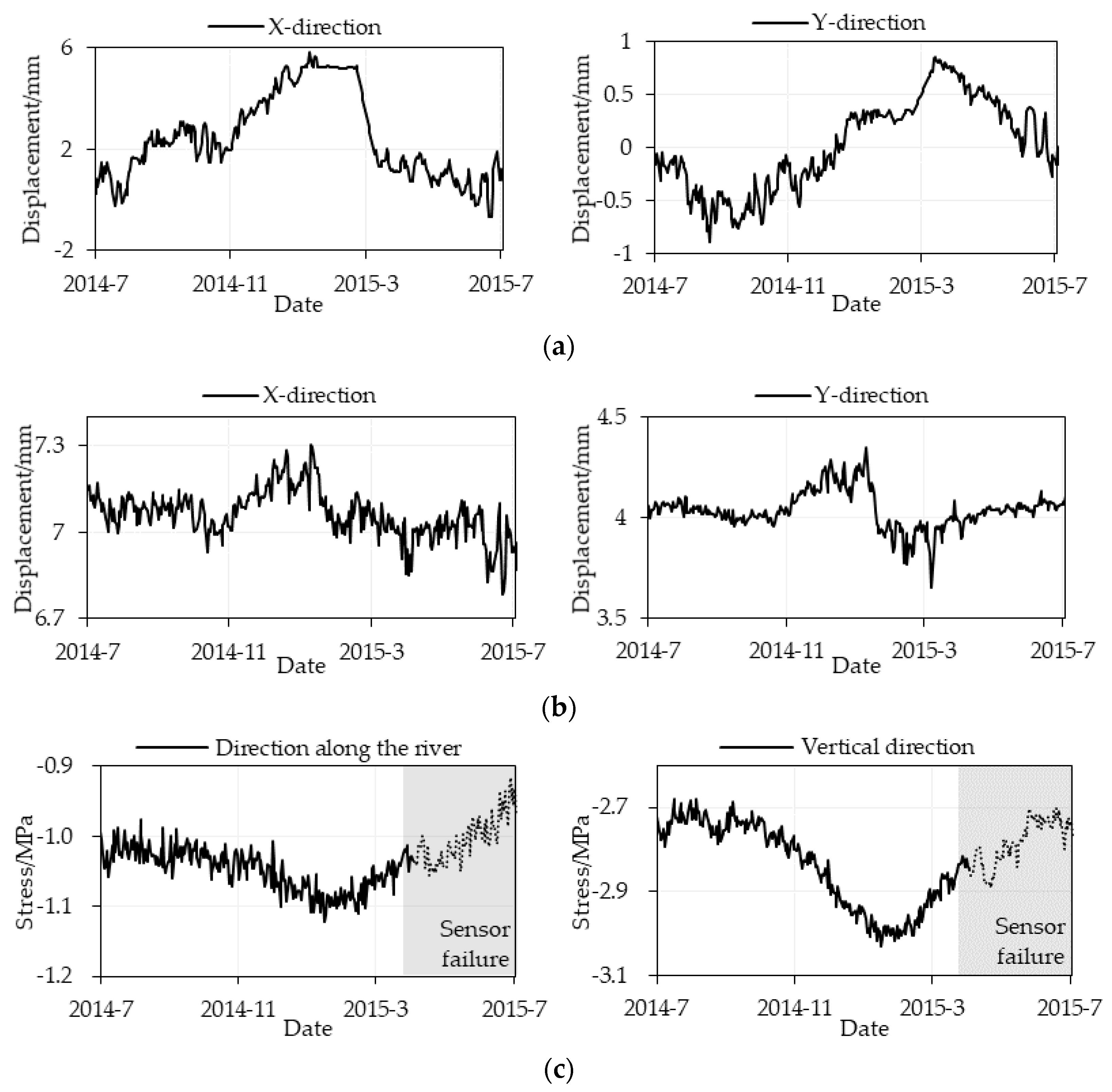
3.2. Data Configuration
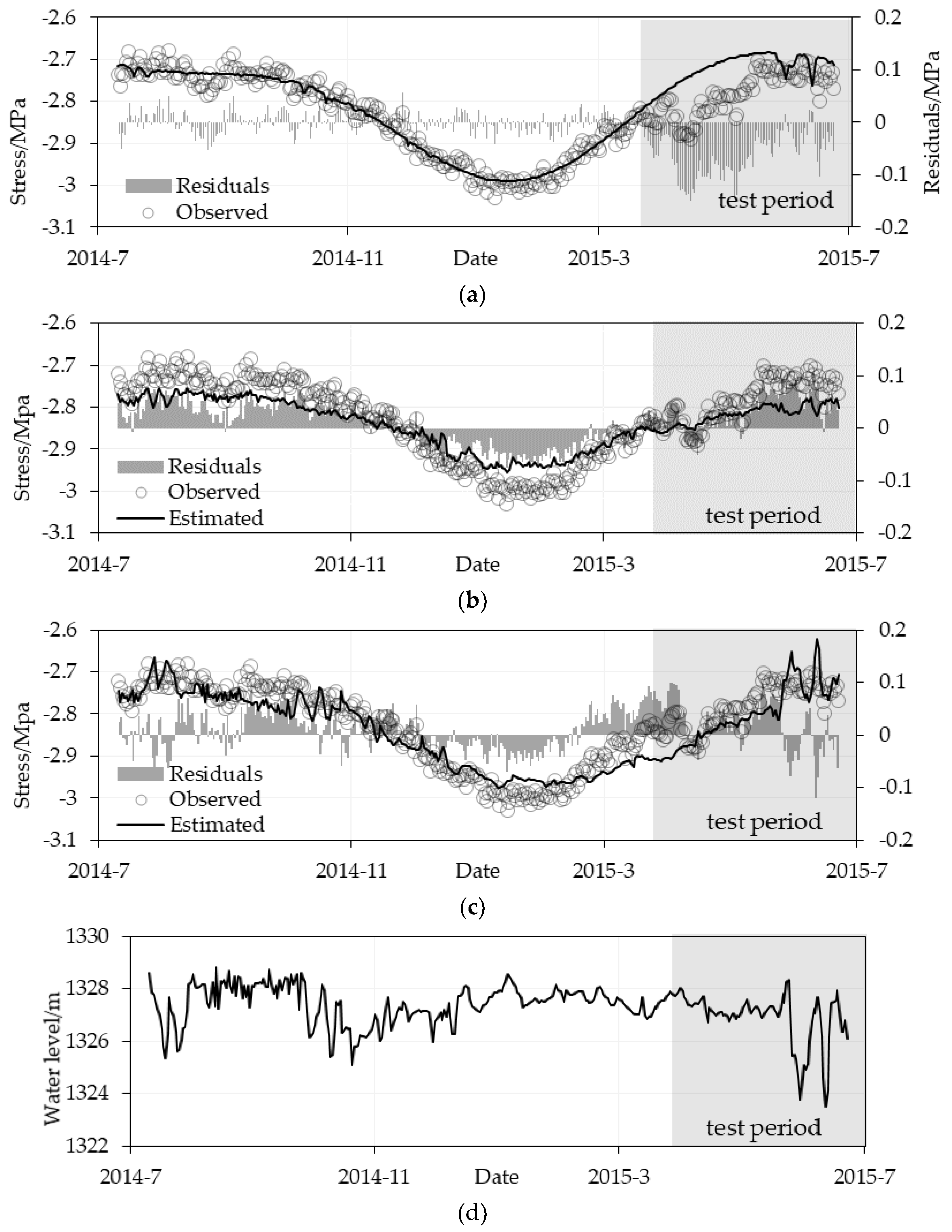
4. Results
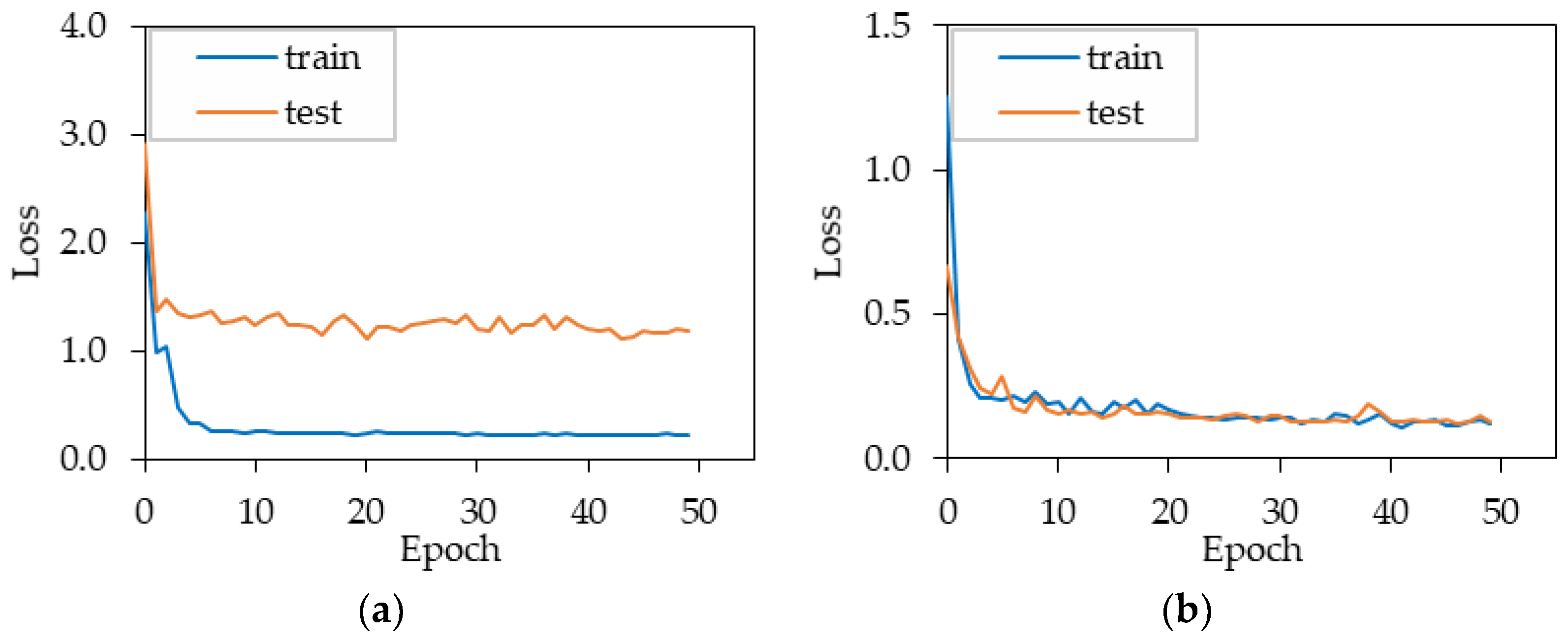
4.1. Hyperparameter Tuning Result of the Model
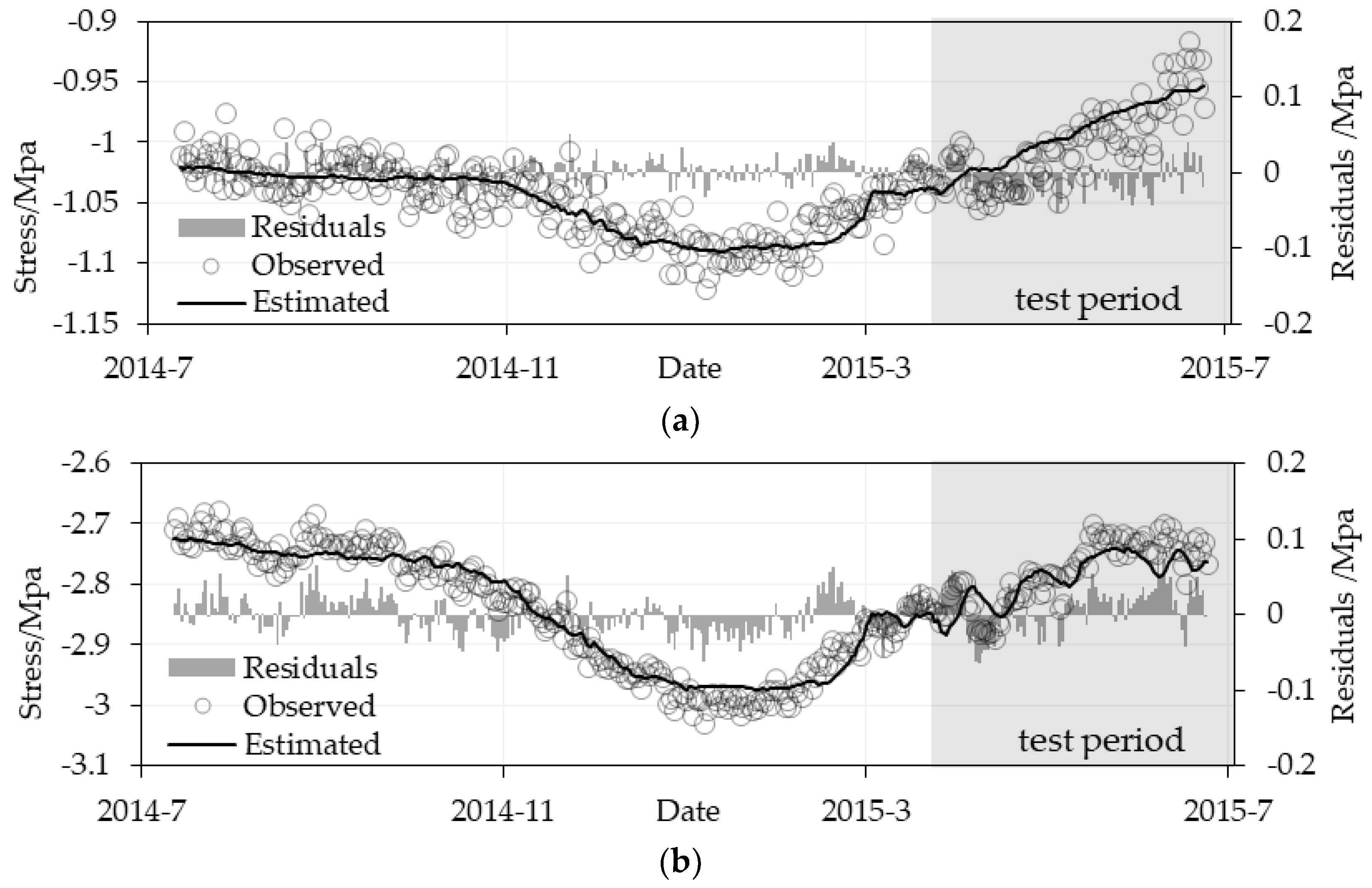
4.2. Estimation Stress Results Evaluation
5. Discussion
5.1. Estimation Performance Comparison
5.2. Evaluation of Tuning Algorithms SIE–APSO
5.3. Effect Analysis of the Input Sample Length
6. Summary and Conclusions
- By comparing three conventional models established with load-stress relationships, this work verified the feasibility of the proposed estimation model based on the data’s spatial–temporal association among the multiple monitoring points of dam deformation and stress.
- The proposed tuning algorithm SIE–APSO, which maintains higher computational accuracy and stability without losing efficiency compared with the standard PSO, is presented and has been tested on the target dataset.
- The estimation method provides reliable data supplements for the strength evaluation of concrete dams under the scenario of sensor failure and data loss, especially dealing with the dam responses under unexperienced conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Layers | Parameters | Domain [Upper Limit, Lower Limit] | Optimization Value |
|---|---|---|---|
| CNN | filter number of each layer | (2, 64) | (13, 19, 10, 9, 16, 15, 17, 14, 15, 12) |
| LSTM | unit number | (2, 32) | 19 |
| dropout rate | (0, 0.5) | 0.335 | |
| MLP | unit number | (2, 32) | 23 |
| Optimizers | algorithms learning rate | - (10-5, 10-1) | Adagrad 0.100 |
| - | batch size | (32, 256) | 165 |
| Layers | Parameters | Domain [Upper Limit, Lower Limit] | Optimization Value |
|---|---|---|---|
| CNN | filter number of each layer | (2, 64) | (27, 35, 21, 12, 24, 33, 26, 31, 20, 23) |
| LSTM | unit number | (2, 32) | 11 |
| dropout rate | (0, 0.5) | 0.187 | |
| MLP | unit number | (2, 32) | 15 |
| Optimizers | algorithms learning rate | - (10-5, 10-1) | Adagrad 0.300 |
| - | batch size | (32, 256) | 76 |
Appendix B
References
- Li, M.-L.; Wang, Z.-M.; Ma, N. A Novel Prediction Model for the Missing Data of Environmental Measurement. J. Sichuan Univ. 2003, 4, 736–739. [Google Scholar]
- Zhang, Z.; Luo, Y. Restoring method for missing data of spatial structural stress monitoring based on correlation. Mech. Syst. Signal Process. 2017, 91, 266–277. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Cheng, L. An interpolation method based on KICA-RVM for missing monitoring data of dam. J. Water Resour. Water Eng. 2017, 28, 197–201. Available online: http://szyysgcxb.alljournals.ac.cn/szyysgcxb/ch/reader/view_abstract.aspx?doi=10.11705/j.issn.1672-643X.2017.01.35 (accessed on 29 November 2022).
- Li, B.; Yang, J.; Hu, D. Dam monitoring data analysis methods: A literature review. Struct. Control Health Monit. 2020, 27, e2501. [Google Scholar] [CrossRef]
- Mata, J.; Tavares de Castro, A.; Sá da Costa, J. Constructing statistical models for arch dam deformation. Struct. Control Health Monit. 2014, 21, 423–437. [Google Scholar] [CrossRef] [Green Version]
- Su, H.; Li, X.; Yang, B.; Wen, Z. Wavelet support vector machine-based prediction model of dam deformation. Mech. Syst. Signal Process. 2018, 110, 412–427. [Google Scholar] [CrossRef]
- Belmokre, A.; Mihoubi, M.K.; Santillán, D. Analysis of Dam Behavior by Statistical Models: Application of the Random Forest Approach. KSCE J. Civ. Eng. 2019, 23, 4800–4811. [Google Scholar] [CrossRef]
- Lin, C.; Li, T.; Chen, S.; Liu, X.; Lin, C.; Liang, S. Gaussian process regression-based forecasting model of dam deformation. Neural Comput. Appl. 2019, 31, 8503–8518. [Google Scholar] [CrossRef]
- Salazar, F.; Toledo, M.; González, J.M.; Oñate, E. Early detection of anomalies in dam performance: A methodology based on boosted regression trees. Struct. Control Health Monit. 2017, 24, e2012. [Google Scholar] [CrossRef]
- Liu, W.; Pan, J.; Ren, Y.; Wu, Z.; Wang, J. Coupling prediction model for long-term displacements of arch dams based on long short-term memory network. Struct. Control Health Monit. 2020, 27, e2548. [Google Scholar] [CrossRef]
- Zhang, J.; Cao, X.; Xie, J.; Kou, P. An Improved Long Short-Term Memory Model for Dam Displacement Prediction. Math. Probl. Eng. 2019, 2019, 6792189. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Zheng, D.-J.; Liu, Y.-T.; Chen, Z.-Y.; Chen, X.-Q. Temporal convolution network-based time frequency domain integrated model of multiple arch dam deformation and quantification of the load impact. Struct. Control Health Monit. 2022, 29, e3090. [Google Scholar] [CrossRef]
- Rawat, W.; Wang, Z. Deep Convolutional Neural Networks for Image Classification: A Comprehensive Review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef]
- Khan, S.; Yairi, T. A review on the application of deep learning in system health management. Mech. Syst. Signal Process. 2018, 107, 241–265. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar] [CrossRef] [Green Version]
- Werbos, P.J. Generalization of backpropagation with application to a recurrent gas market model. Neural Netw. 1988, 1, 339–356. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Zhu, G.; Zhang, L.; Shen, P.; Song, J. Multimodal Gesture Recognition Using 3-D Convolution and Convolutional LSTM. IEEE Access 2017, 5, 4517–4524. [Google Scholar] [CrossRef]
- Yang, Y.; Dong, J.; Sun, X.; Lima, E.; Mu, Q.; Wang, X. A CFCC-LSTM Model for Sea Surface Temperature Prediction. IEEE Geosci. Remote Sens. Lett. 2017, 15, 207–211. [Google Scholar] [CrossRef]
- Zöller, M.-A.; Huber, M.F. Benchmark and Survey of Automated Machine Learning Frameworks. J. Artif. Intell. Res. 2021, 70, 409–472. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Bonyadi, M.R.; Michalewicz, Z. Particle swarm optimization for single objective continuous space problems: A review. Evol. Comput. 2017, 25, 1–54. [Google Scholar] [CrossRef]
- Zhan, Z.-H.; Zhang, J.; Li, Y.; Shi, Y.-H. Orthogonal Learning Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2010, 15, 832–847. [Google Scholar] [CrossRef] [Green Version]
- Gu, J.; Wang, Z.; Kuen, J.; Ma, L.; Shahroudy, A.; Shuai, B.; Liu, T.; Wang, X.; Wang, G.; Cai, J.; et al. Recent advances in convolutional neural networks. Pattern Recognit. 2018, 77, 354–377. [Google Scholar] [CrossRef] [Green Version]
- Cho, K.; Van Merrienboer, B.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. In Proceedings of the Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation (SSST-8), Doha, Qatar, 25 October 2014; pp. 103–111. [Google Scholar] [CrossRef]
- Bratton, D.; Kennedy, J. Defining a Standard for Particle Swarm Optimization. In Proceedings of the 2007 IEEE Swarm Intelligence Symposium, Honolulu, HI, USA, 1–5 April 2007; pp. 120–127. [Google Scholar] [CrossRef]
- Tashman, L.J. Out-of-sample tests of forecasting accuracy: An analysis and review. Int. J. Forecast. 2000, 16, 437–450. [Google Scholar] [CrossRef]
- Bergmeir, C.; Benítez, J.M. On the use of cross-validation for time series predictor evaluation. Inf. Sci. 2012, 191, 192–213. [Google Scholar] [CrossRef]
- Salazar, F.; Toledo, M.A.; Oñate, E.; Morán, R. An empirical comparison of machine learning techniques for dam behaviour modelling. Struct. Saf. 2015, 56, 9–17. [Google Scholar] [CrossRef] [Green Version]
- Smith, L.N.; Topin, N. Deep convolutional neural network design patterns. arXiv 2016, arXiv:1611.00847. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]






| Layers | Parameters | Domain (Upper Limit, Lower Limit) | Optimization Value |
|---|---|---|---|
| CNN | filter number of each layer | (2, 64) | (27, 35, …, 23) |
| LSTM | unit number | (2, 32) | 11 |
| dropout rate | (0, 0.5) | 0.187 | |
| FC | unit number | (2, 32) | 15 |
| Optimizers | algorithms learning rate | - (10−8, 105) | Adagrad 0.300 |
| - | batch size | (32, 256) | 76 |
| Index | RMSE | MAPE | ARV | |||
|---|---|---|---|---|---|---|
| Direction | Training Period | Testing Period | Training Period | Testing Period | Training Period | Testing Period |
| Direction along the river | 0.016 | 0.021 | 1.195% | 1.678% | 0.319 | 0.378 |
| Vertical direction | 0.024 | 0.032 | 0.678% | 0.973% | 0.055 | 0.387 |
| Direction | SIE–APSO | PSO | LDIW–PSO | GSA | GWO |
|---|---|---|---|---|---|
| Direction along the river | 1283.1 | 1074.7 | 1473.2 | 6050.2 | 1887.6 |
| Vertical direction | 1755.4 | 1236.7 | 963.8 | 6738.8 | 2493.7 |
| Average | 1519.2 | 1155.7 | 1218.5 | 6394.5 | 2190.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, L.; Zheng, D.; Wu, X.; Chen, X.; Liu, Y.; Chen, Z.; Jiang, H. Stress Estimation of Concrete Dams in Service Based on Deformation Data Using SIE–APSO–CNN–LSTM. Water 2023, 15, 59. https://doi.org/10.3390/w15010059
Tao L, Zheng D, Wu X, Chen X, Liu Y, Chen Z, Jiang H. Stress Estimation of Concrete Dams in Service Based on Deformation Data Using SIE–APSO–CNN–LSTM. Water. 2023; 15(1):59. https://doi.org/10.3390/w15010059
Chicago/Turabian StyleTao, Liang, Dongjian Zheng, Xin Wu, Xingqiao Chen, Yongtao Liu, Zhuoyan Chen, and Haifeng Jiang. 2023. "Stress Estimation of Concrete Dams in Service Based on Deformation Data Using SIE–APSO–CNN–LSTM" Water 15, no. 1: 59. https://doi.org/10.3390/w15010059
APA StyleTao, L., Zheng, D., Wu, X., Chen, X., Liu, Y., Chen, Z., & Jiang, H. (2023). Stress Estimation of Concrete Dams in Service Based on Deformation Data Using SIE–APSO–CNN–LSTM. Water, 15(1), 59. https://doi.org/10.3390/w15010059







