Investigation on Stall Characteristics of Centrifugal Pump with Guide Vanes
Abstract
:1. Introduction
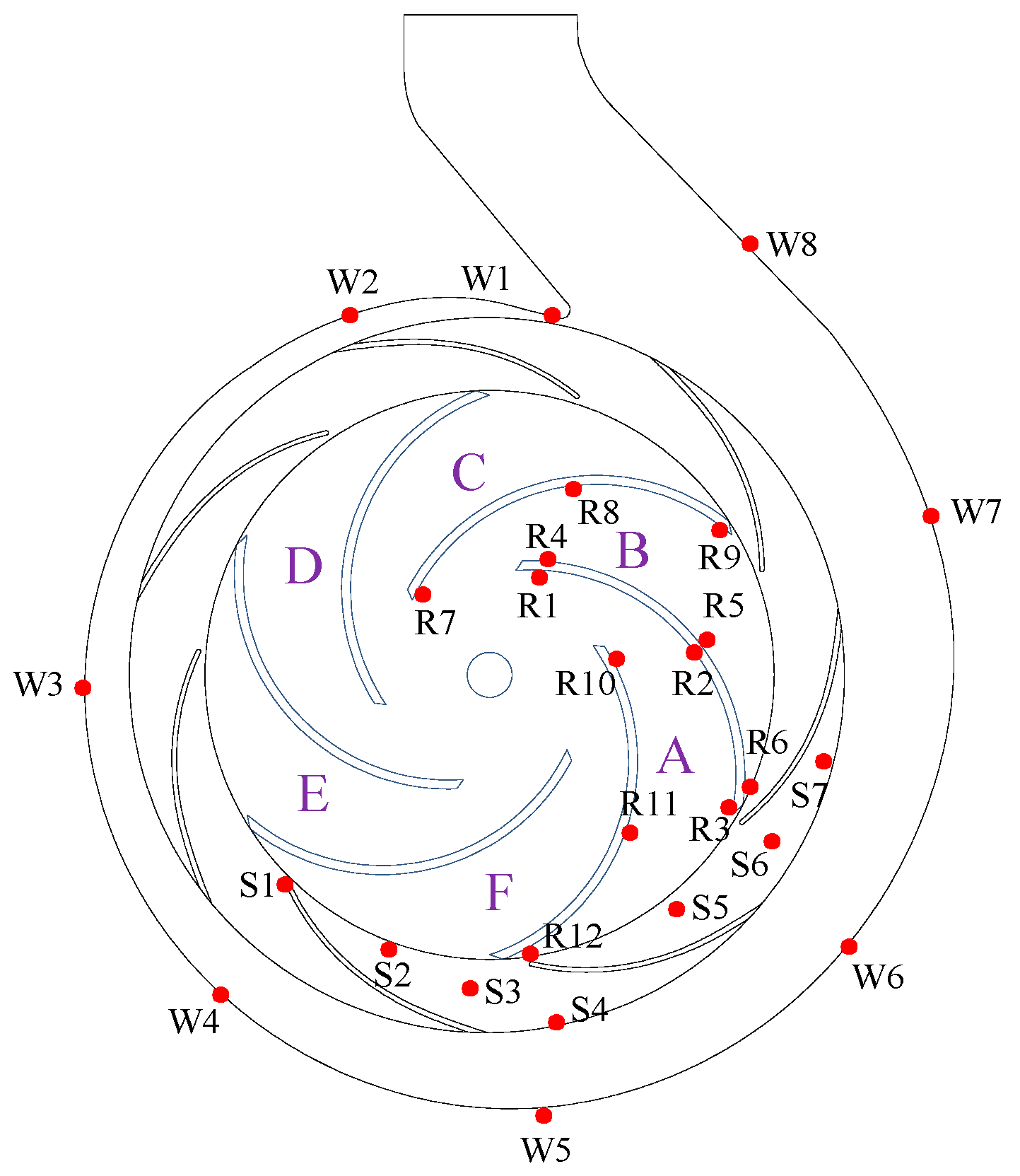
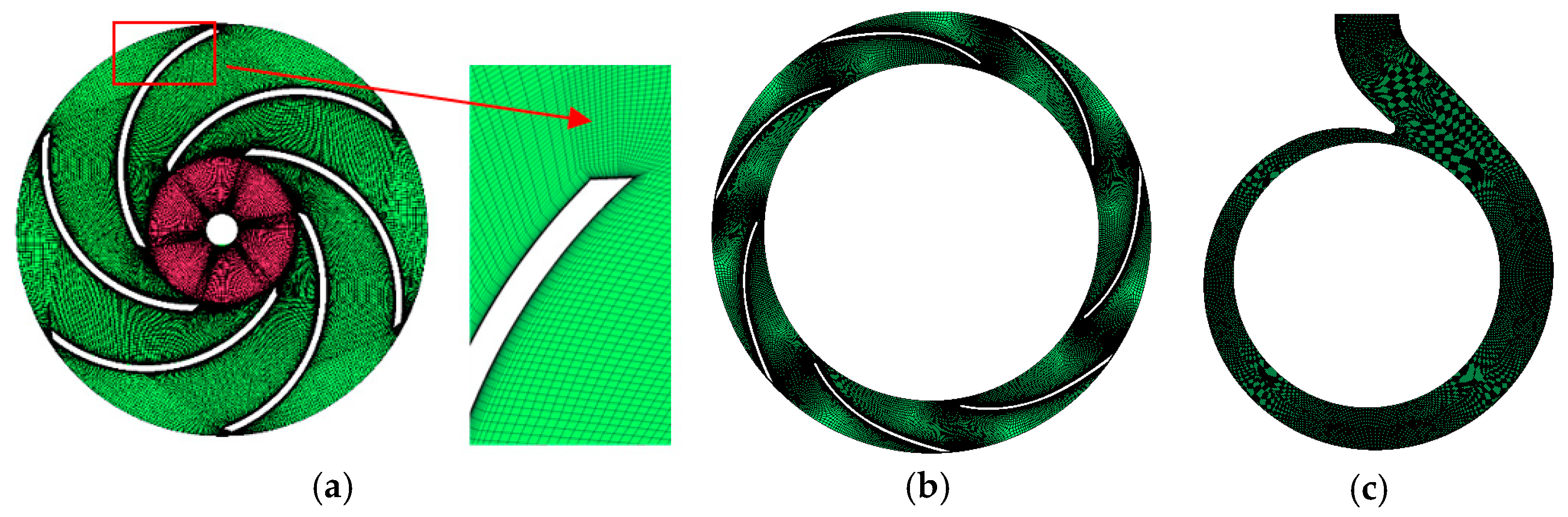
2. Research Object and Numerical Calculation Method
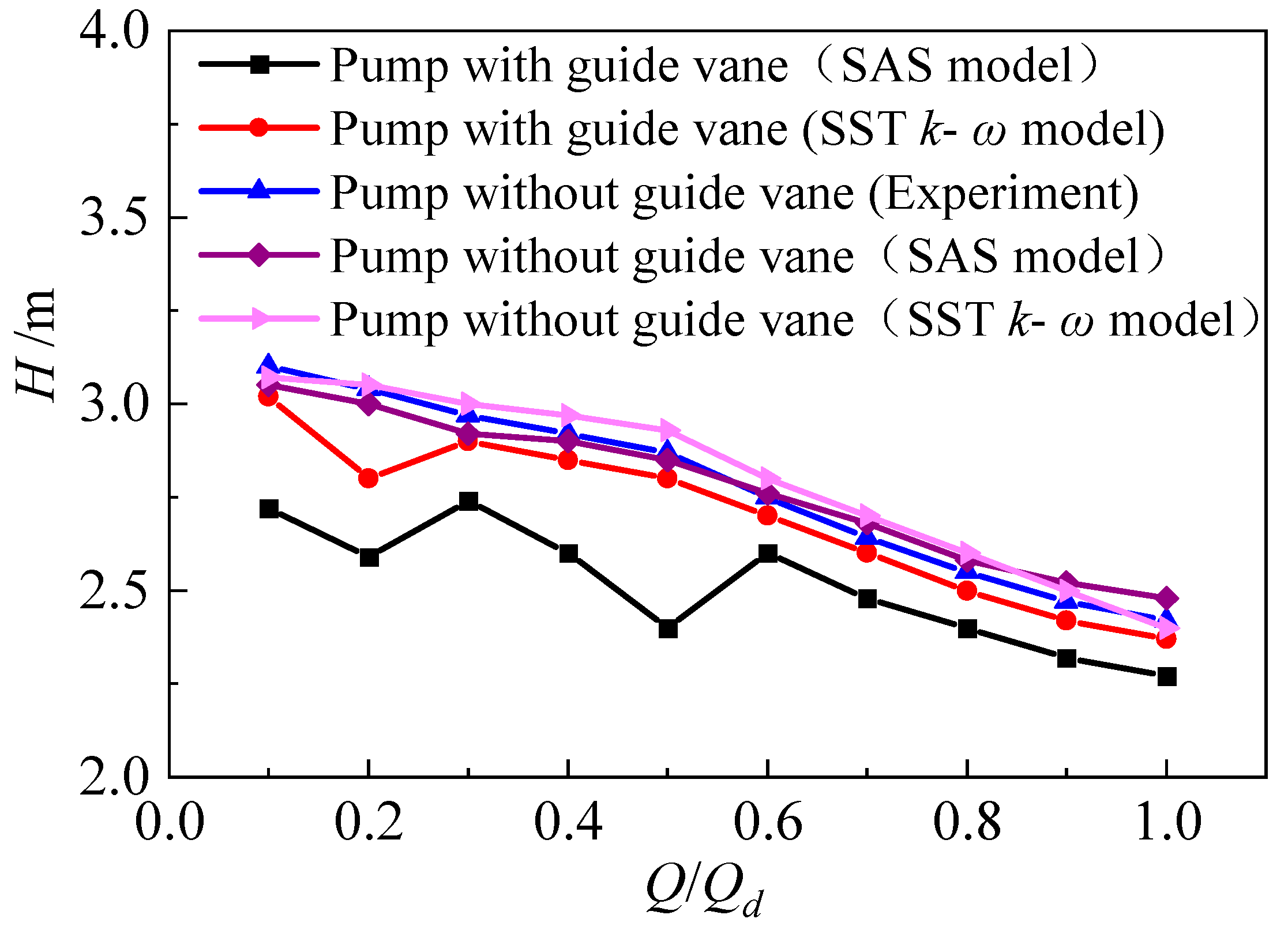
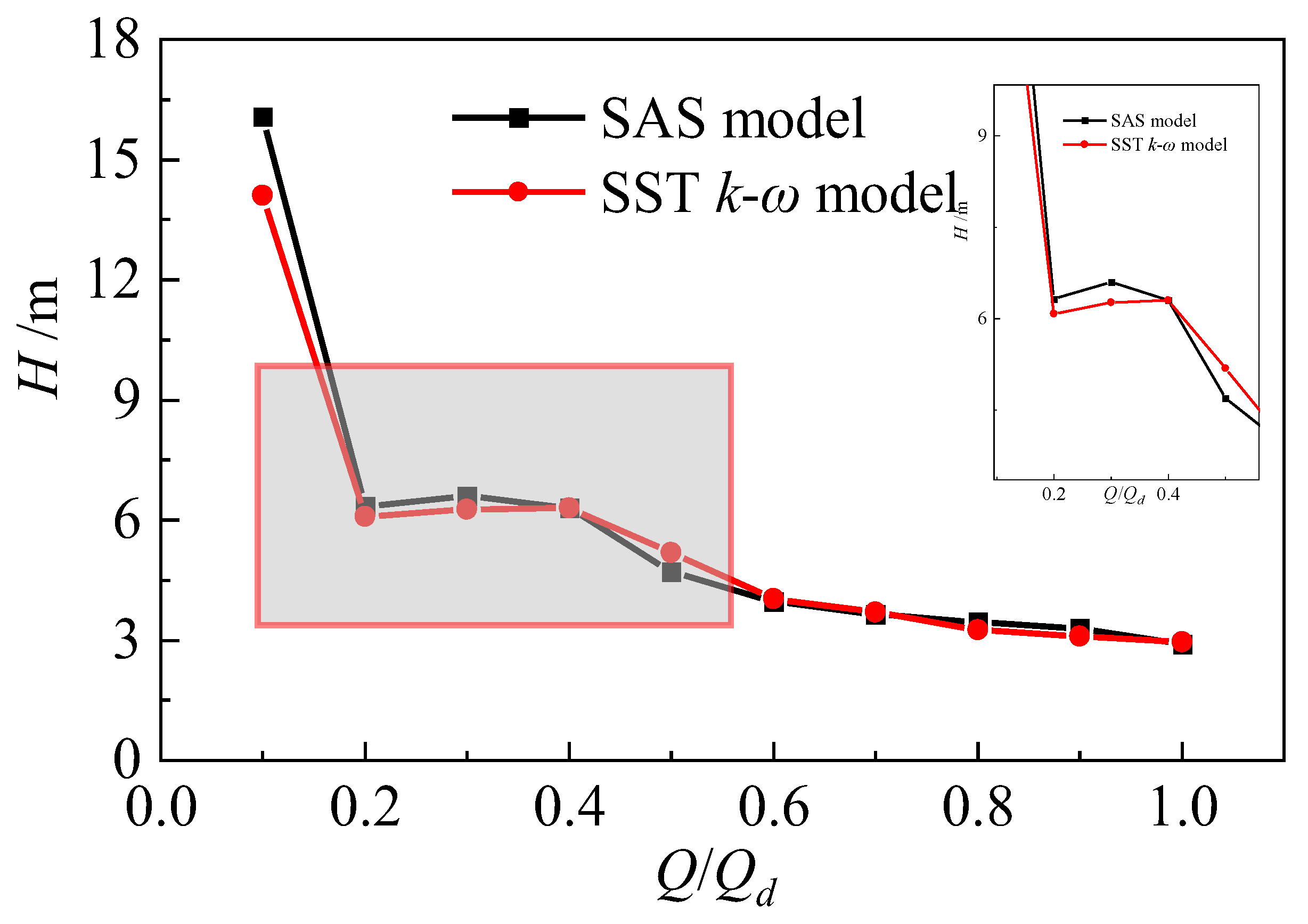
3. Prediction of Centrifugal Pump Performance Curve
4. Characteristic Analysis of Double Humps
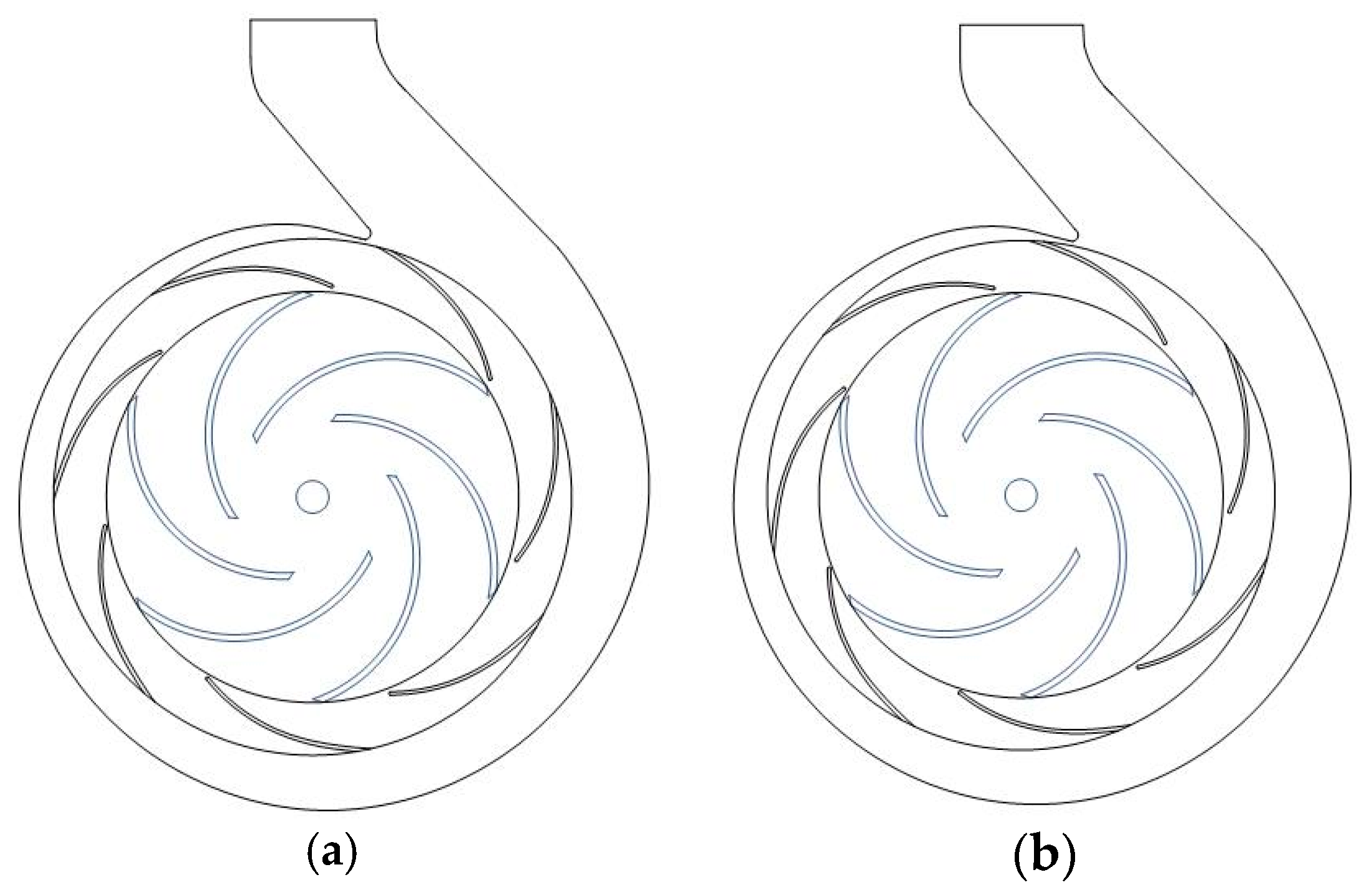
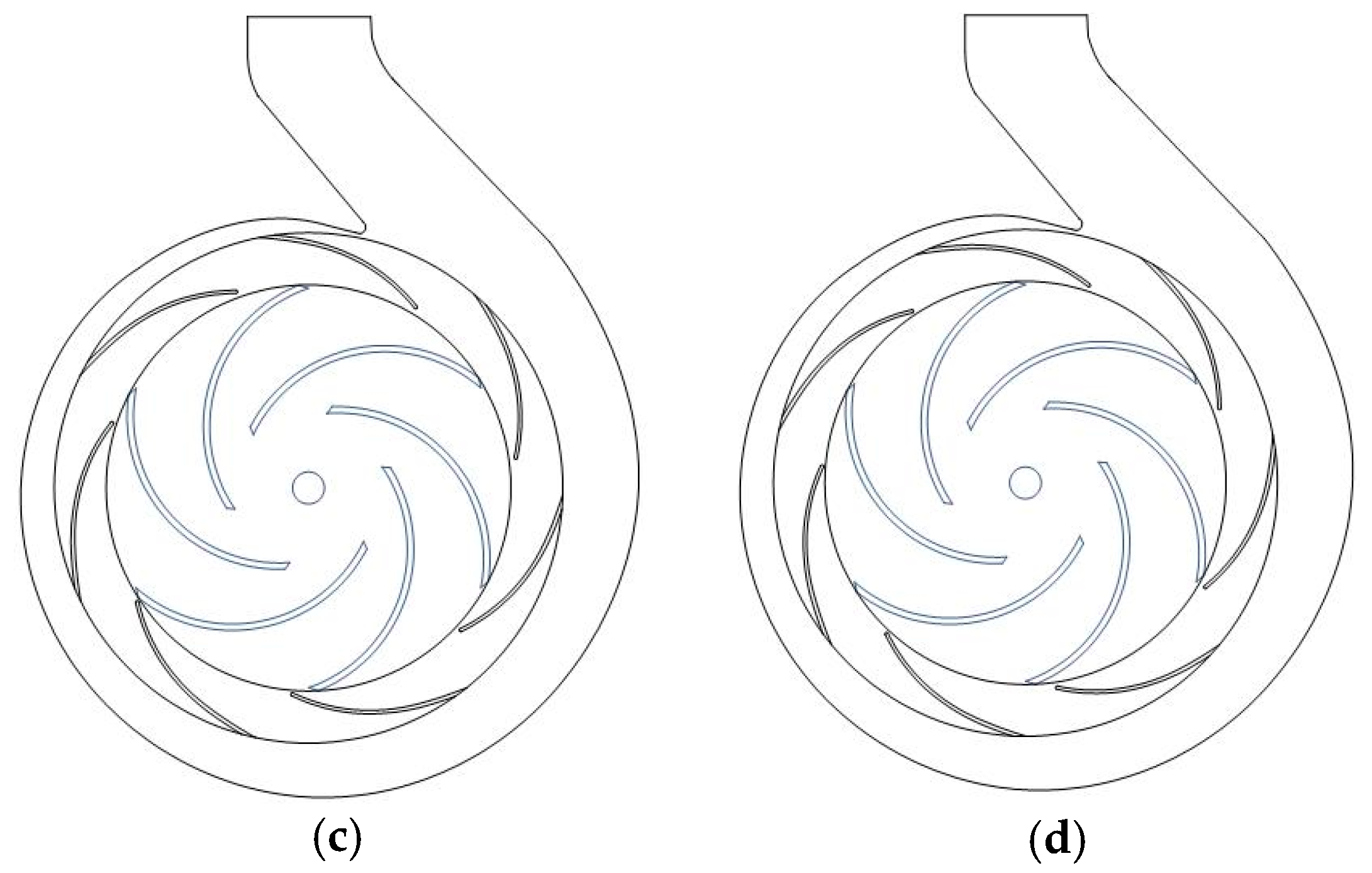
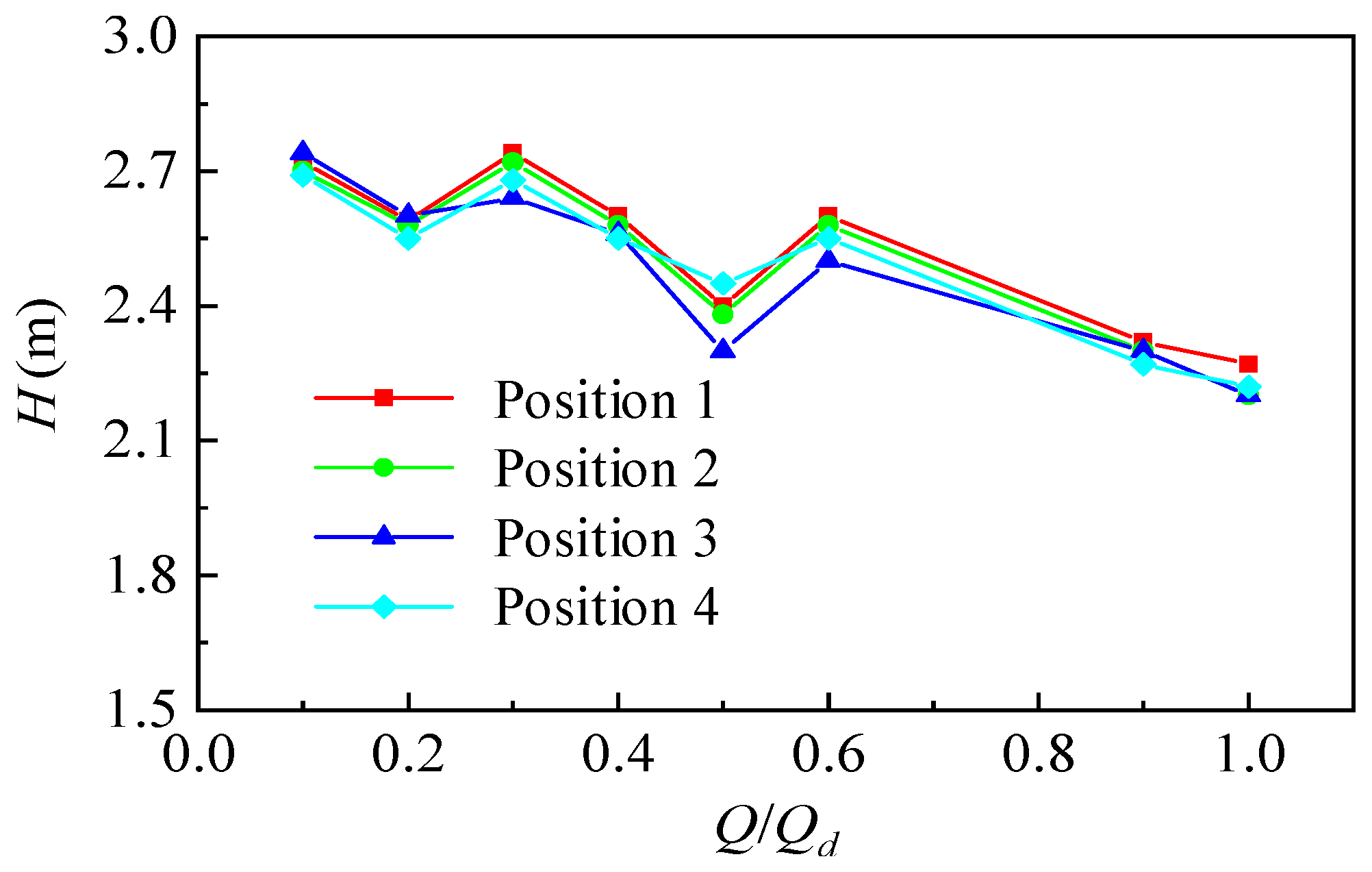
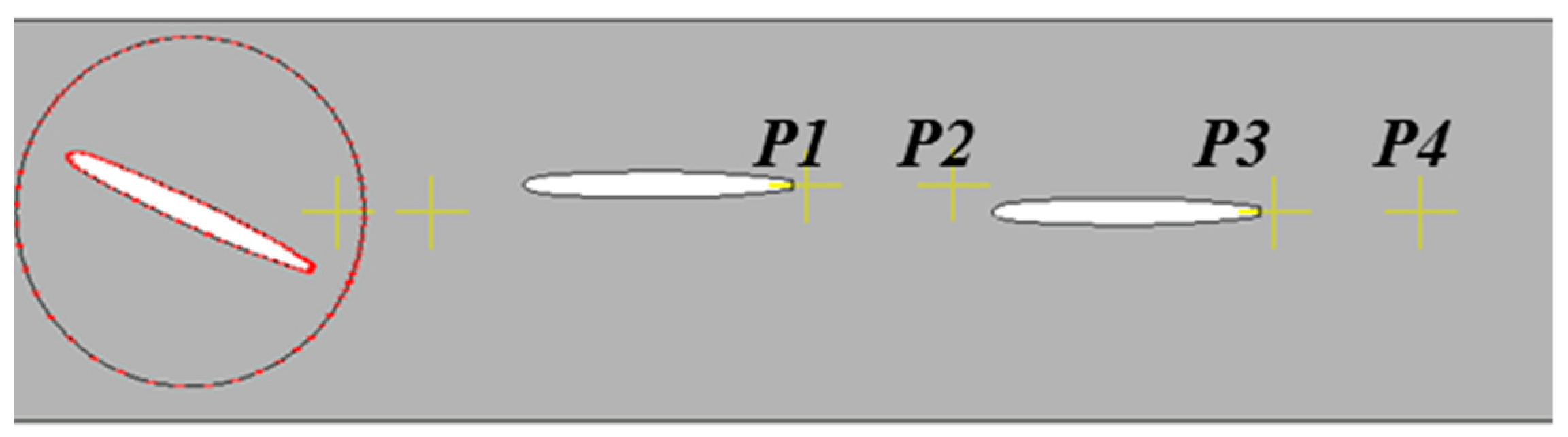
5. Clocking Effect of Guide-Vane Centrifugal Pump under Stall Characteristics
6. Conclusions
- (1)
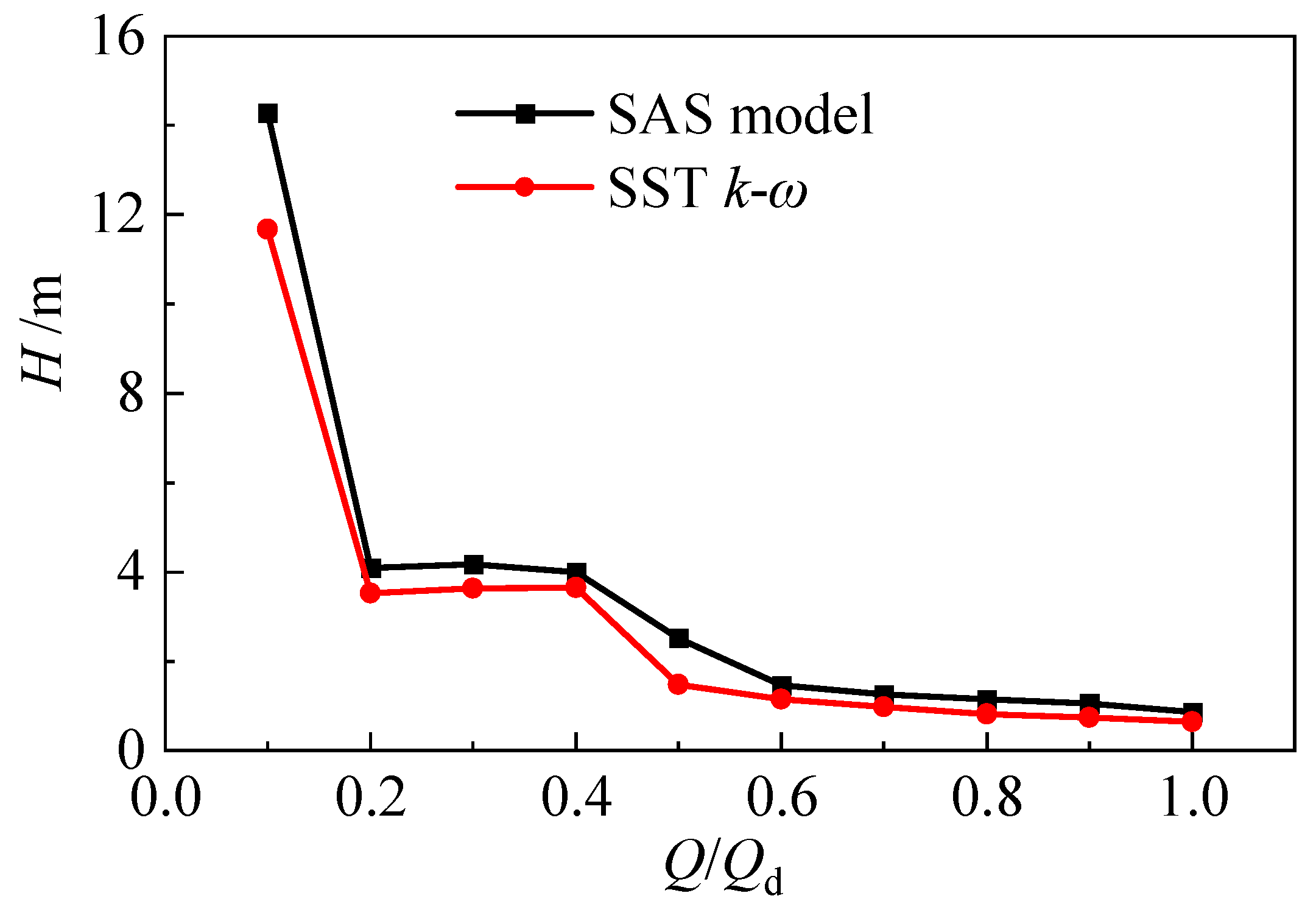
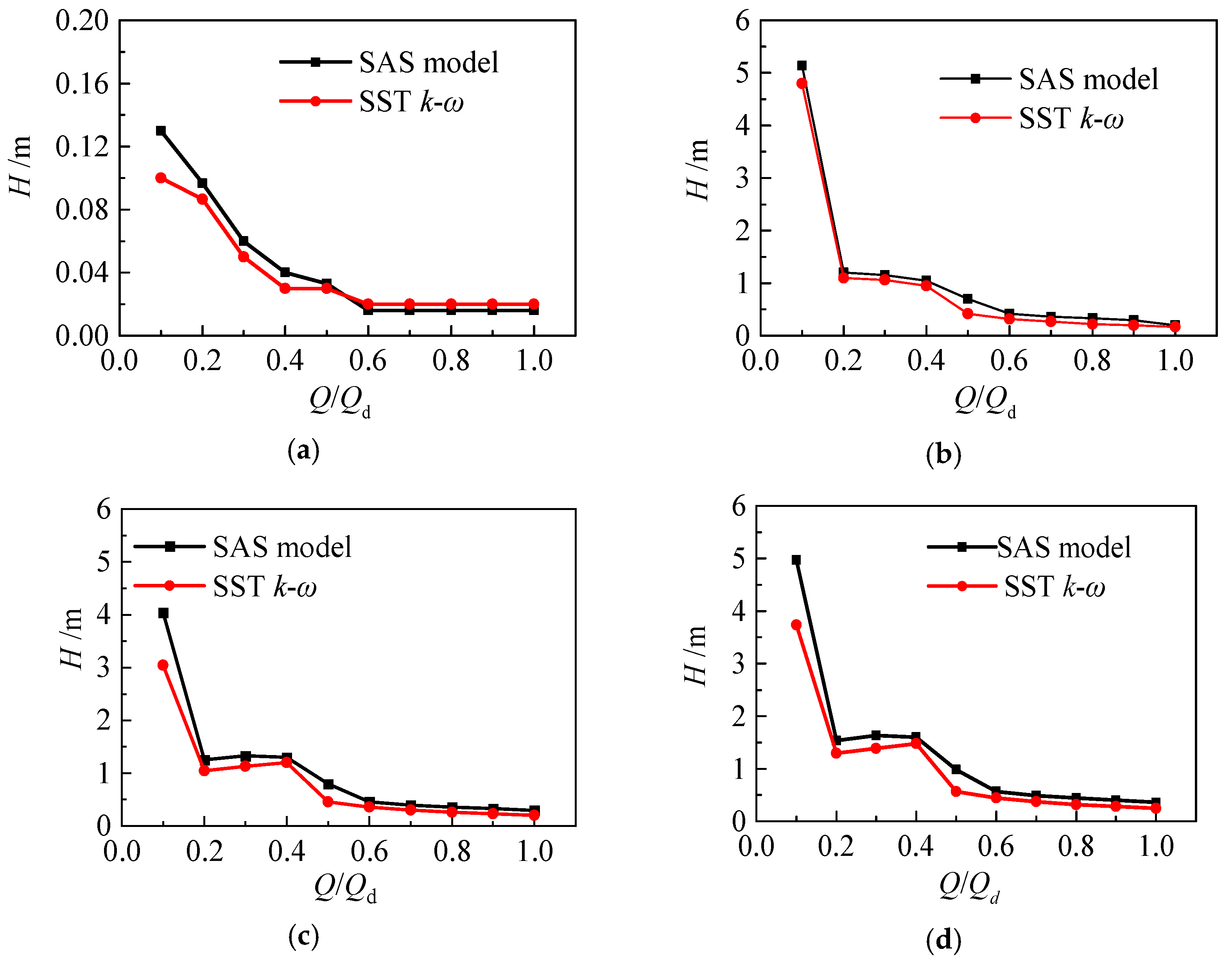
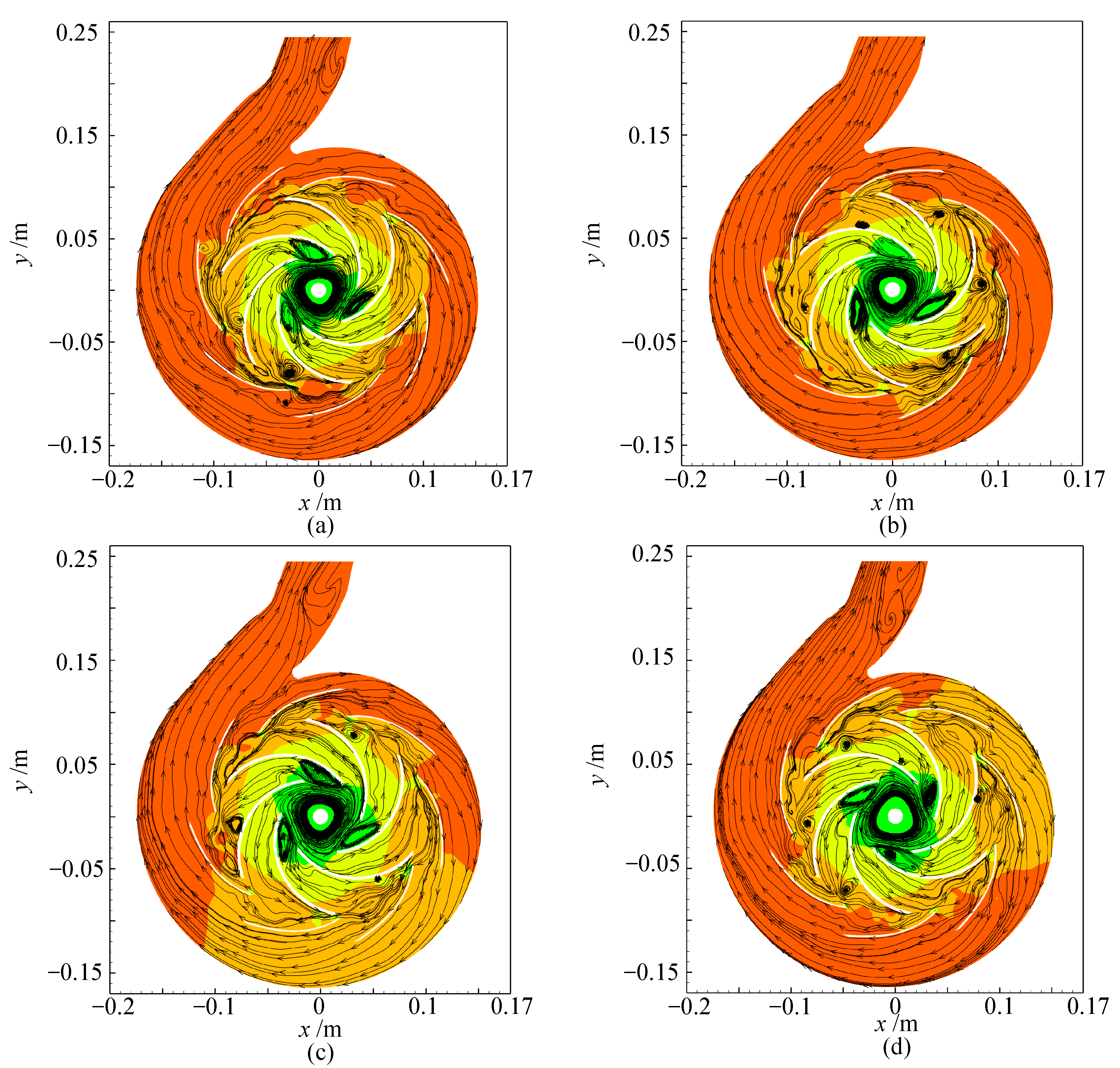
- The double-hump characteristic was found in the head discharge curve by using the SAS model. Comparing the flow field characteristics at different flow rate conditions, it was found that the hump area close to the optimal working condition is caused by hydraulic loss, and the hump area far away from the optimal working condition point is caused by the combined action of Euler head and hydraulic loss. The SAS model can accurately calculate the wall friction loss, thus predicting the double hump phenomenon.
- (2)
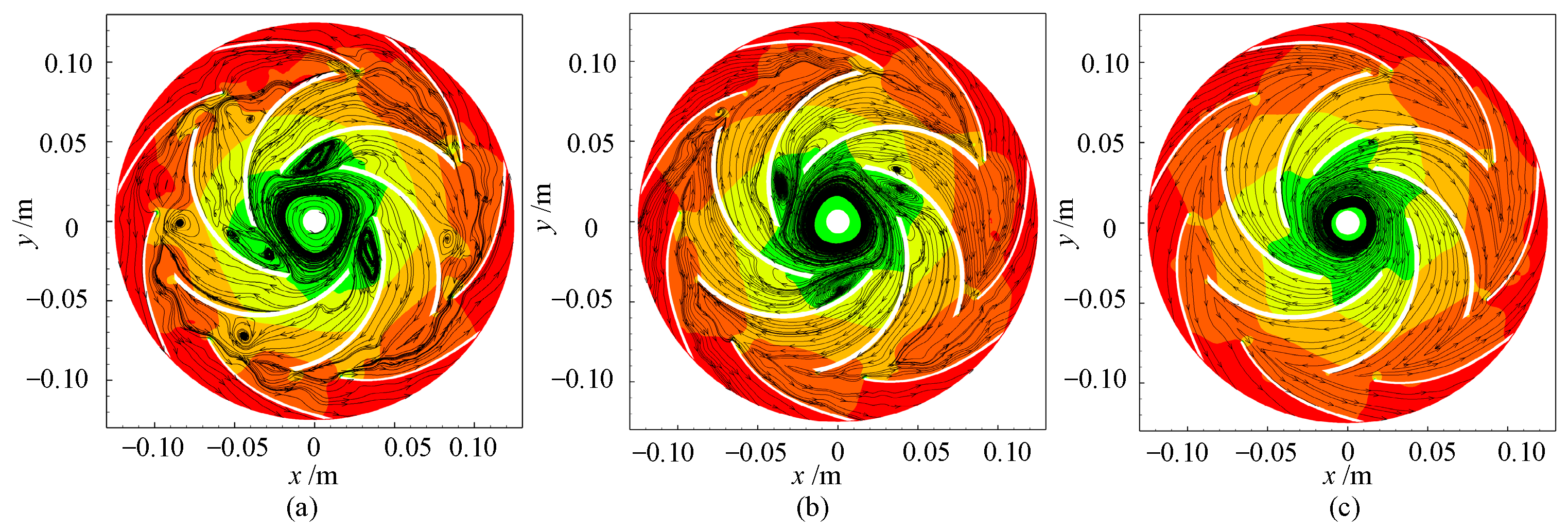
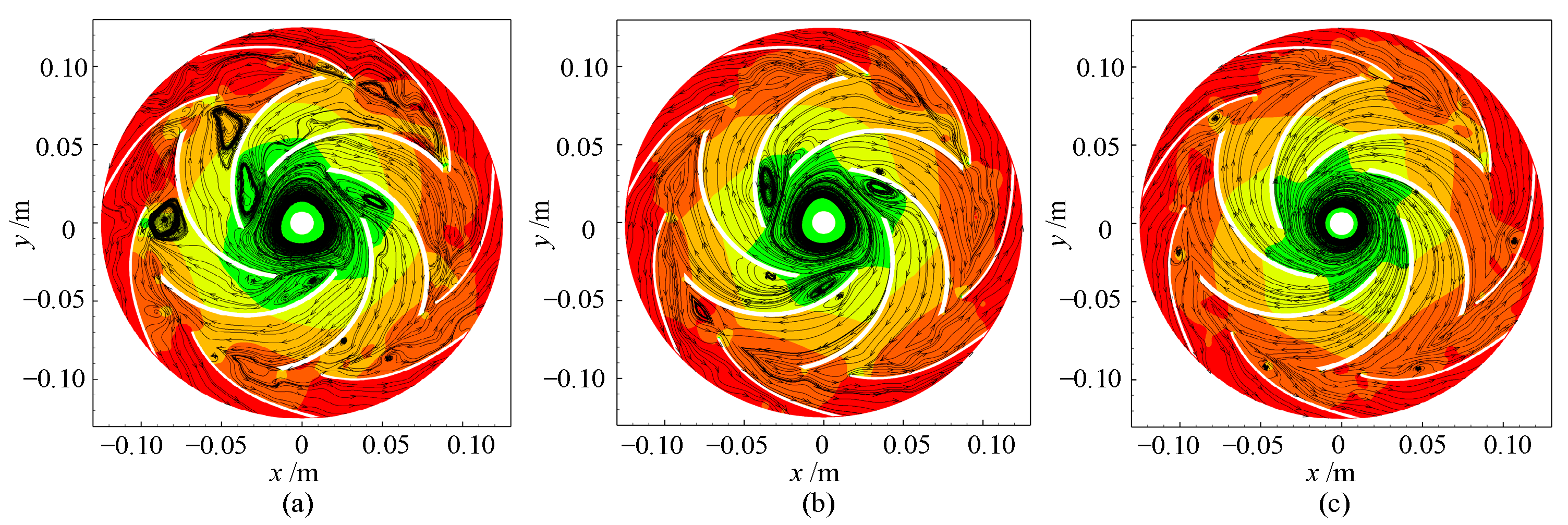
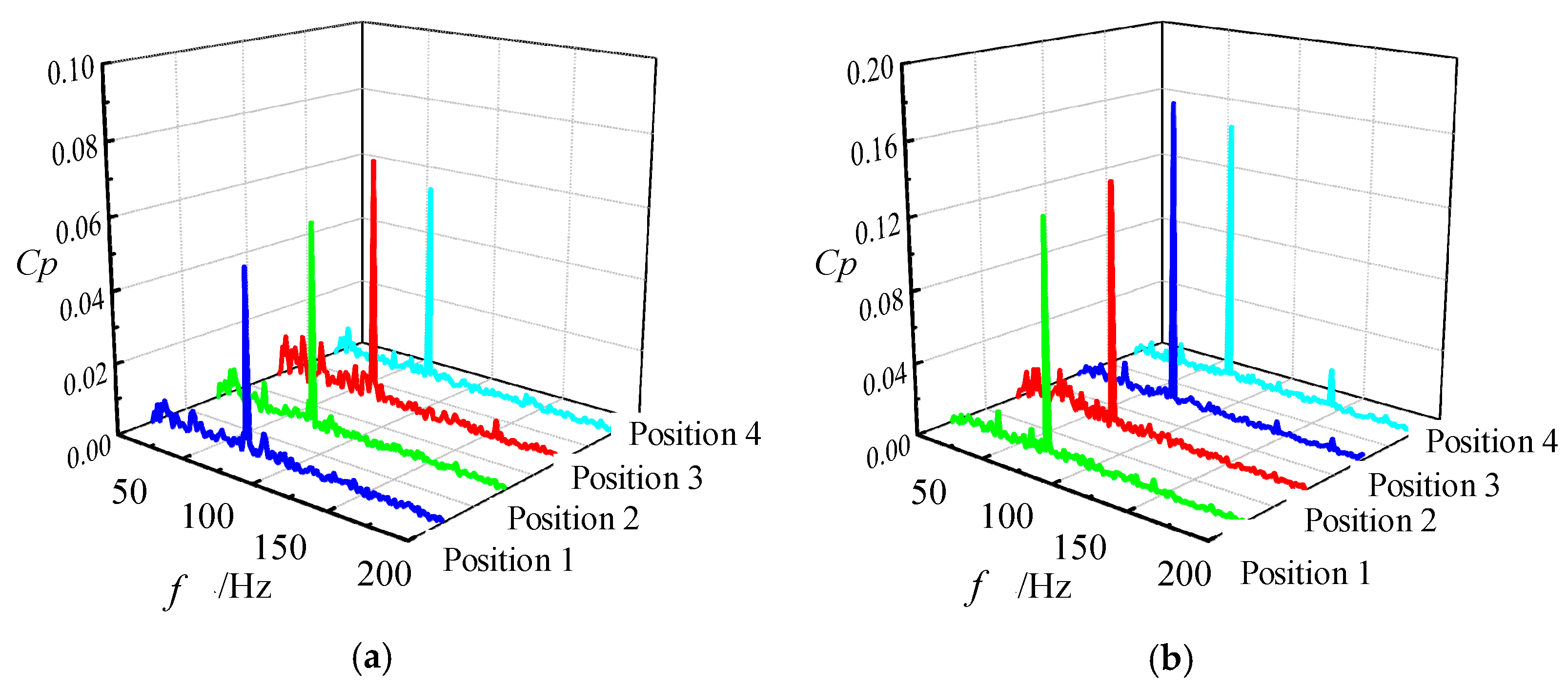
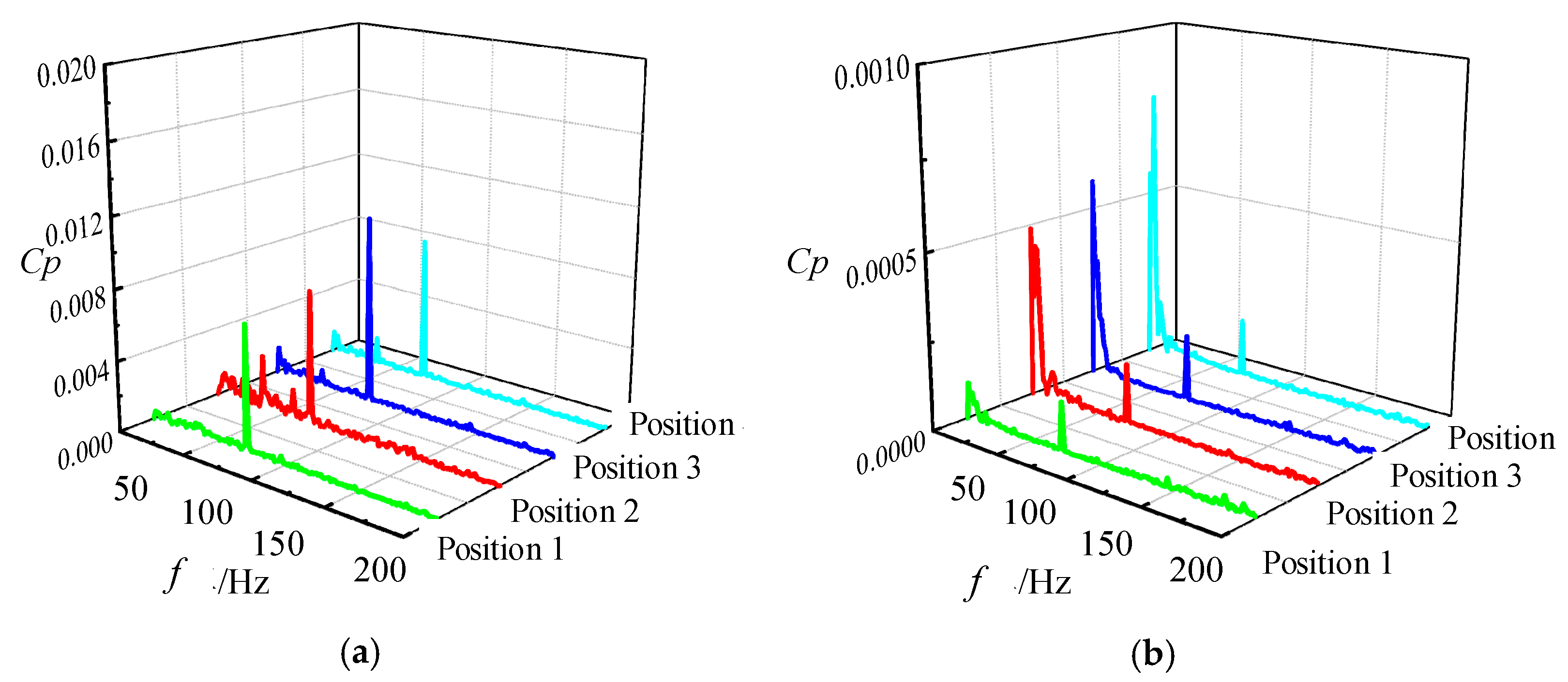
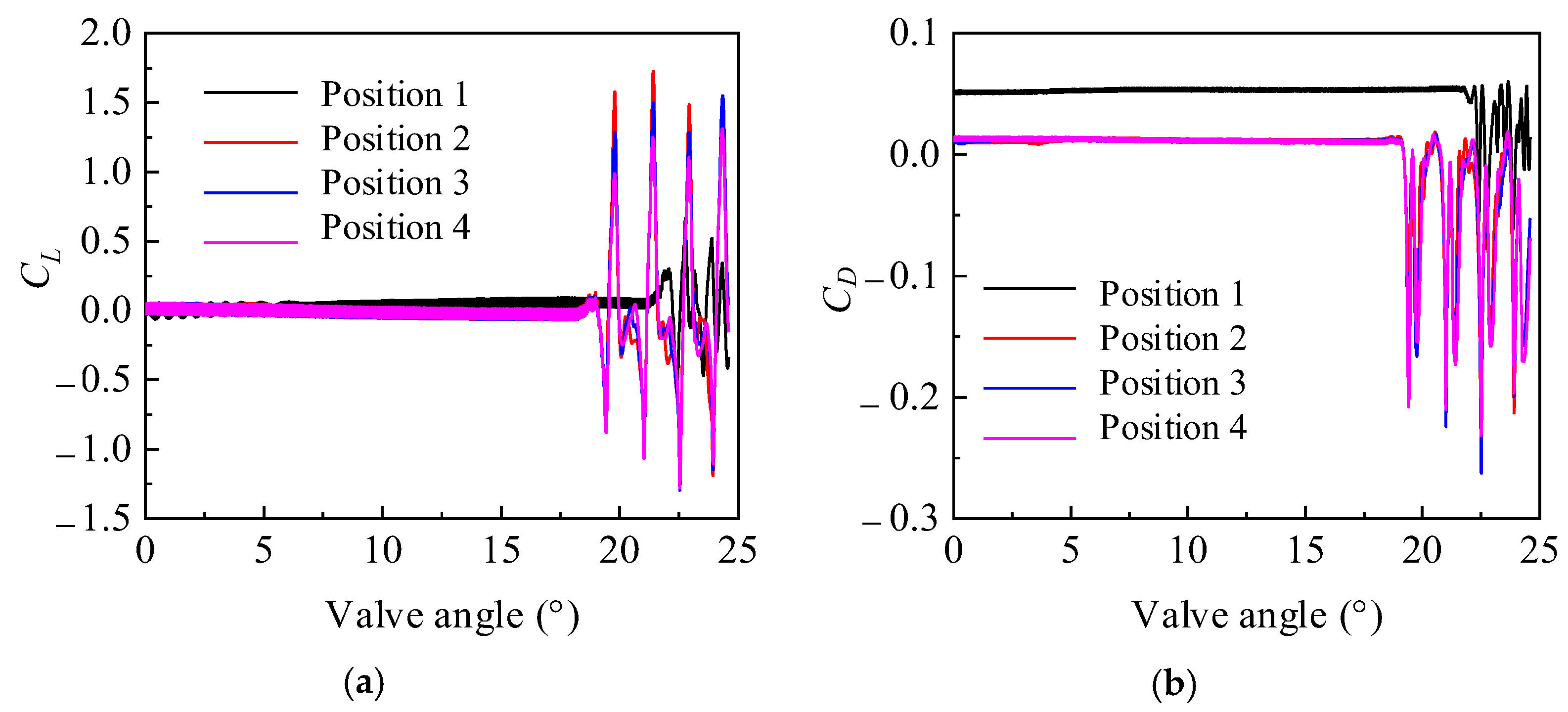
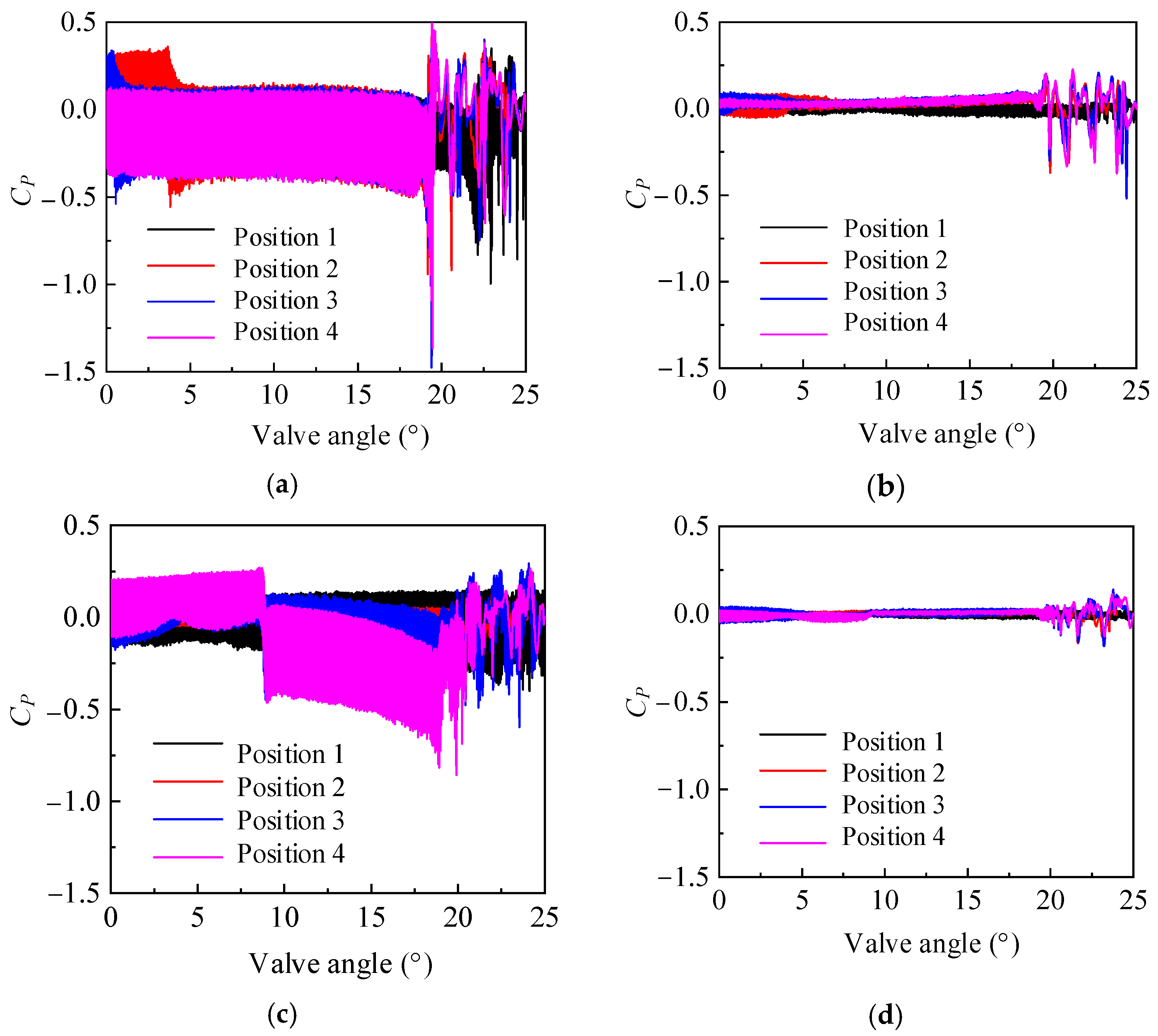
- The pressure fluctuation and head characteristics at different clocking positions under stall conditions were obtained. It was found that when the guide vanes outlet in line with the volute tongue, the flow pattern of the volute and guide vane is good, so the head is high due to small hydraulic loss, and the pressure fluctuation is low.
- (3)
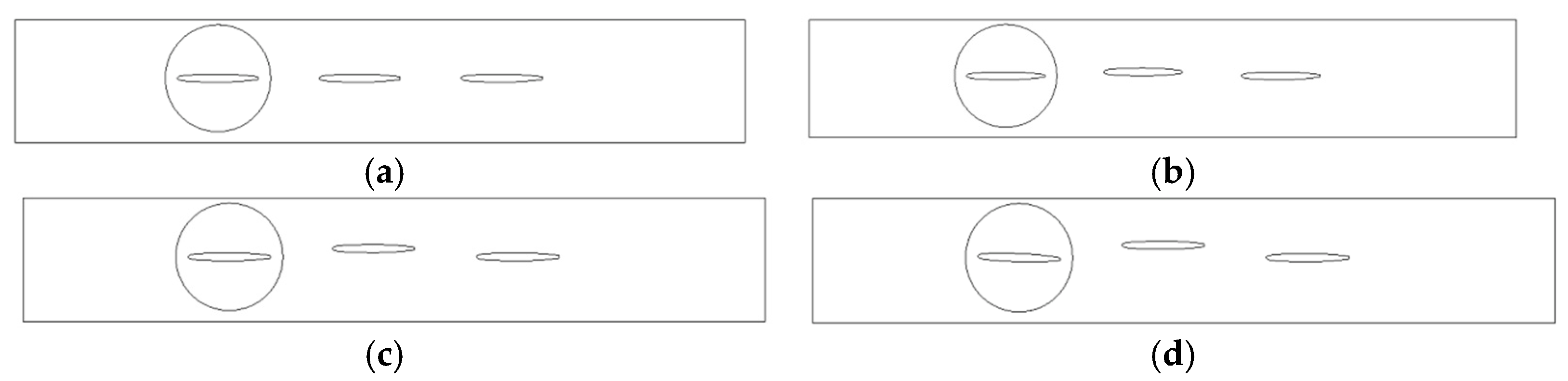
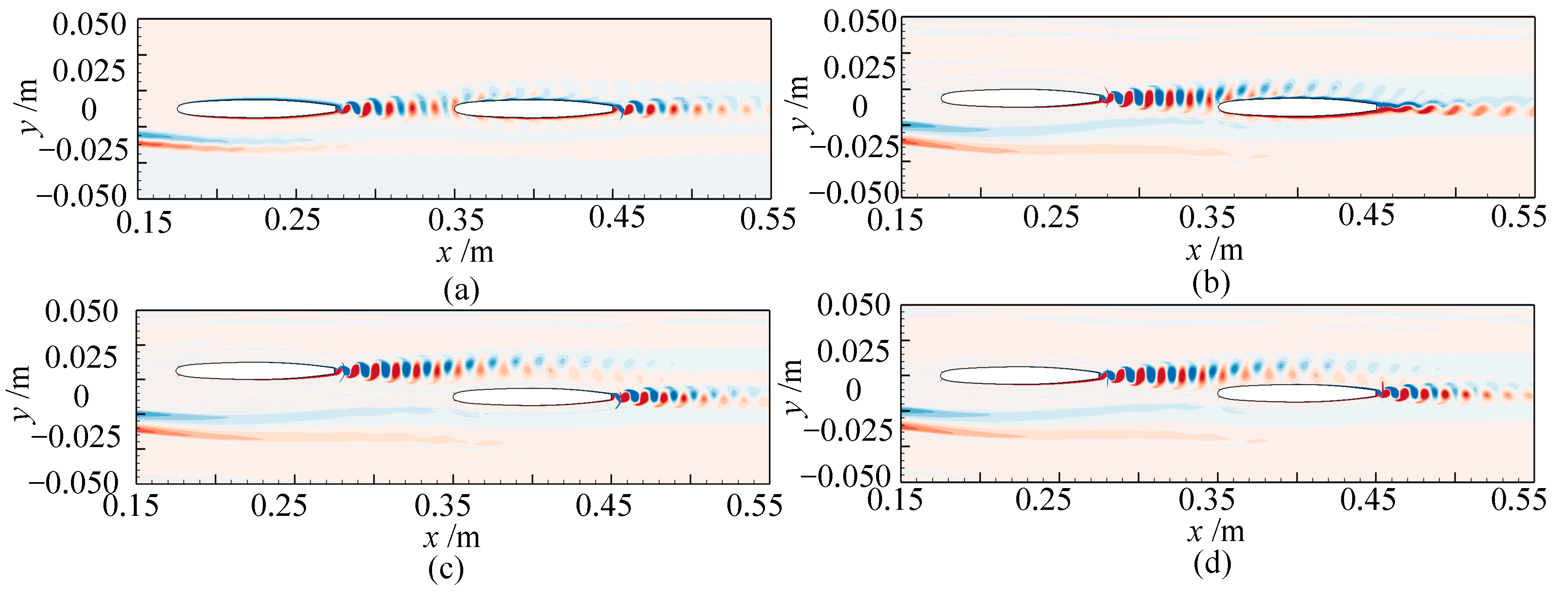
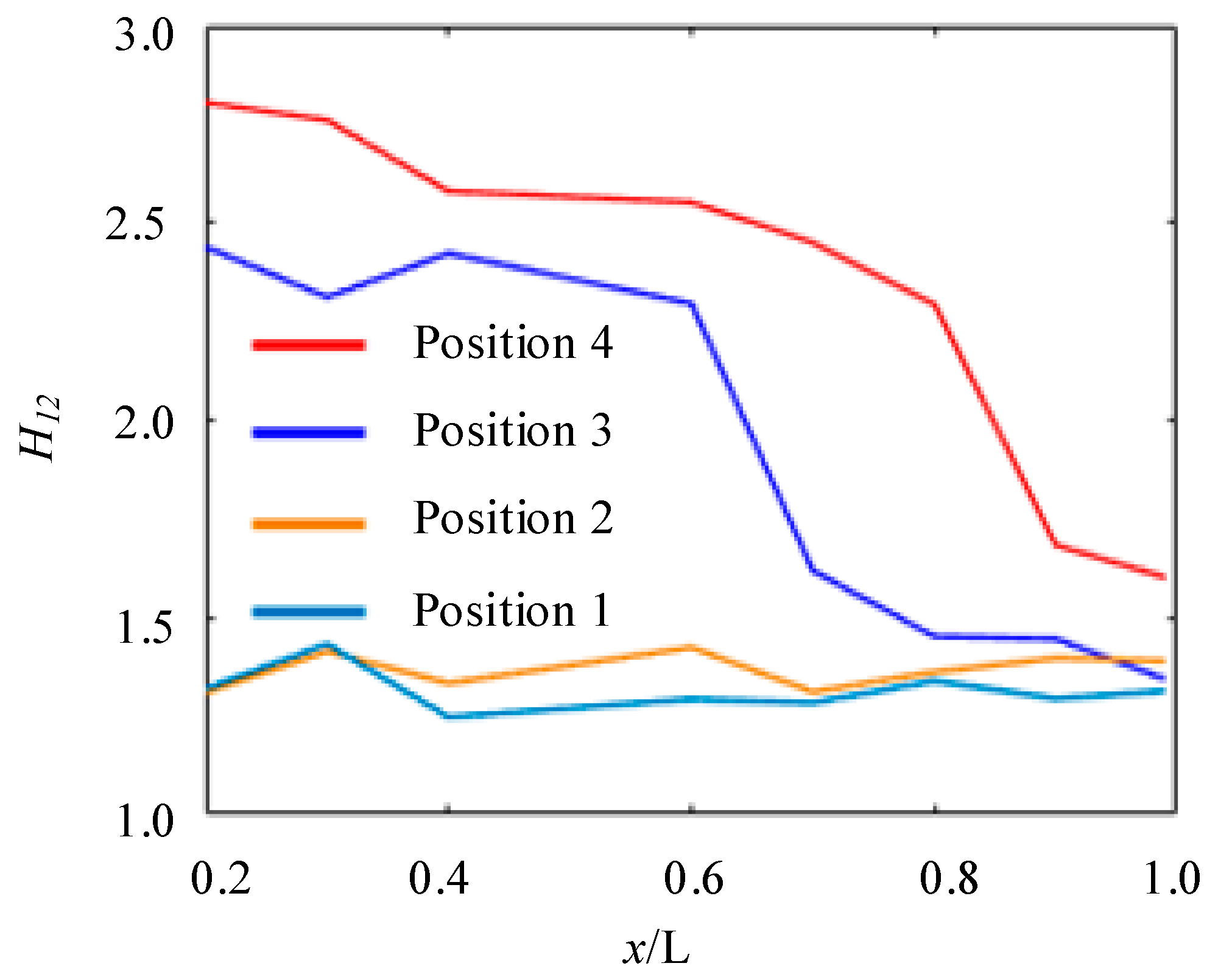
- The mechanism of clocking effect in the centrifugal pump with guide vanes was obtained by simplifying the hydrofoil. Based on the simplified hydrofoil, it can be found that the disturbance of wake to the boundary layer will affect the boundary layer transition and then affect the friction stress of the blade, resulting in the change of flow field pressure amplitude. When the downstream hydrofoil head area is always interfered with by the upstream hydrofoil wake, the wake of the low-energy fluid is mixed with the boundary layer of the same low-energy fluid. At this time, the boundary layer is in a turbulent state to avoid laminar flow separation, causing small vibration of the downstream hydrofoil, so the position where the guide vane’s outlet is in line with the volute tongue is most recommended.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Qd | Design flow | SAS | Scale adaptive simulation |
| Cu | Circumferential component of absolute velocity | LES | Large eddy simulation method |
| U | Circumferential velocity | RANS | Reynolds average method |
| HEnter | Euler head | Cp | Pressure coefficient |
| ΔCu·U | Euler energy | ω | Angular velocity |
References
- Wang, C.; Wang, F.; Li, C.; Chen, W.; Wang, H.; Lu, L. Investigation on energy conversion instability of pump mode in hydro-pneumatic energy storage system. J. Energy Storage 2022, 53, 105079. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, F.; Mou, J. Investigation of rotating stall characteristics in a centrifugal pump impeller at low flow rates. Eng. Comput. 2017, 34, 1989–2000. [Google Scholar] [CrossRef]
- Feng, J.; Ge, Z.; Yang, H.; Zhu, G.; Li, C.; Luo, X. Rotating stall characteristics in the vaned diffuser of a centrifugal pump. Ocean Eng. 2021, 229, 108955. [Google Scholar] [CrossRef]
- Ye, C.L.; Wang, C.Y.; Zi, D.; Tang, Y.; van Esch, B.; Wang, F.J. Improvement of the SST γ-Reθt transition model for flows along a curved hydrofoil. J. Hydrodyn. 2021, 33, 520–533. [Google Scholar] [CrossRef]
- Stenning, A.H.; Kriebel, A.R. Stall propagation in a cascade of airfoils. Trans. Am. Soc. Mech. Eng. 1958, 80, 777–789. [Google Scholar] [CrossRef]
- Emmons, H.W.; Pearson, C.E.; Grant, H.P. Compressor surge and stall propagation. Trans. Am. Soc. Mech. Eng. 1955, 77, 455–467. [Google Scholar] [CrossRef]
- Day, I.J. Stall, surge and 75 years of research. ASME J. Turbomach. 2016, 138, 011001. [Google Scholar] [CrossRef]
- Zhang, N.; Gao, B.; Ni, D.; Liu, X. Coherence analysis to detect unsteady rotating stall phenomenon based on pressure pulsation signals of a centrifugal pump. Mech. Syst. Signal Process. 2021, 148, 107161. [Google Scholar] [CrossRef]
- Huang, X.-B.; Liu, Z.-Q.; Li, Y.-J.; Yang, W.; Guo, Q. Study of the internal characteristics of the stall in a centrifugal pump with a cubic non-linear SGS model. J. Hydrodyn. 2019, 31, 788–799. [Google Scholar] [CrossRef]
- Wang, C.; Wang, F.; Xie, L.; Wang, B.; Yao, Z.; Xiao, R. On the Vortical Characteristics of Horn-Like Vortices in Stator Corner Separation Flow in an Axial Flow Pump. J. Fluids Eng. 2021, 143, 061201. [Google Scholar] [CrossRef]
- Abusorrah, A.M.; Mebarek-Oudina, F.; Ahmadian, A.; Baleanu, D. Modeling of a MED-TVC desalination system by considering the effects of nanoparticles: Energetic and exergetic analysis. J. Therm. Anal. Calorim. 2021, 144, 2675–2687. [Google Scholar] [CrossRef]
- Hassan, M.; Mebarek-Oudina, F.; Faisal, A.; Ghafar, A.; Ismail, A. Thermal energy and mass transport of shear thinning fluid under effects of low to high shear rate viscosity. Int. J. Thermofluids 2022, 15, 100176. [Google Scholar] [CrossRef]
- Wang, C.; Wang, F.; Li, C.; Ye, C.; Yan, T.; Zou, Z. A modified STRUCT model for efficient engineering computations of turbulent flows in hydro-energy machinery. Int. J. Heat Fluid Flow 2020, 85, 108628. [Google Scholar] [CrossRef]
- Posa, A. LES investigation on the dependence of the flow through a centrifugal pump on the diffuser geometry. Int. J. Heat Fluid Flow 2021, 87, 108750. [Google Scholar] [CrossRef]
- Sano, T.; Yoshida, Y.; Tsujimoto, Y.; Nakamura, Y.; Matsushima, T. Numerical Study of Rotating Stall in a Pump Vaned Diffuser. J. Fluids Eng. 2002, 124, 363–370. [Google Scholar] [CrossRef]
- Braun, O. Part Load Flow in Radial Centrifugal Pumps. Ph.D. Thesis, EPFL, Lausanne, Switzerland, 2009. [Google Scholar]
- Lucius, A.; Brenner, G. Unsteady CFD simulations of a pump in part load conditions using scale-adaptive simulation. Int. J. Heat Fluid Flow 2010, 31, 1113–1118. [Google Scholar] [CrossRef]
- Zhang, N.; Jiang, J.; Gao, B.; Liu, X. DDES analysis of unsteady flow evolution and pressure pulsation at off-design condition of a centrifugal pump. Renew. Energy 2020, 153, 193–204. [Google Scholar] [CrossRef]
- Ji, L.; Li, W.; Shi, W.; Tian, F.; Agarwal, R. Effect of blade thickness on rotating stall of mixed-flow pump using entropy generation analysis. Energy 2021, 236, 121381. [Google Scholar] [CrossRef]
- Kan, K.; Zheng, Y.; Chen, Y.; Xie, Z.; Yang, G.; Yang, C. Numerical study on the internal flow characteristics of an axial-flow pump under stall conditions. J. Mech. Sci. Technol. 2018, 32, 4683–4695. [Google Scholar] [CrossRef]
- Krause, N.; Pap, E.R.; The´ venin, D. Influence of the blade geometry on flow instabilities in a radial pump elucidated by time-resolved particle-image velocimetry. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Montreal, Canada, 14–17 May 2007; ASME: New York, NY, USA, 2007; Volume 47950, pp. 1659–1668. [Google Scholar]
- Berten, S.; Dupont, P.; Fabre, L.; Kayal, M.; Avellan, F.; Farhat, M. Experimental investigation of flow instabilities and rotating stall in a high-energy centrifugal pump stage. In Proceedings of the Fluids Engineering Division Summer Meeting, Vali, CO, USA, 2–6 August 2009; Volume 43727, pp. 505–513. [Google Scholar]
- Chudina, M. Noise as an indicator of cavitation in a centrifugal pump. Acoust. Phys. 2003, 49, 463–474. [Google Scholar] [CrossRef]
- Johnson, D.A.; Pedersen, N.; Jacobsen, C.B. Measurements of rotating stall inside a centrifugal pump impeller. In Proceedings of the Fluids Engineering Division Summer Meeting, Houston, TX, USA, 19–23 June 2005; Volume 41987, pp. 1281–1288. [Google Scholar]
- Ye, W.; Huang, R.; Jiang, Z.; Li, X.; Zhu, Z.; Luo, X. Instability analysis under part-load conditions in centrifugal pump. J. Mech. Sci. Technol. 2019, 33, 269–278. [Google Scholar] [CrossRef] [Green Version]
- Ren, X.; Fan, H.; Xie, Z.; Liu, B. Stationary stall phenomenon and pressure fluctuation in a centrifugal pump at partial load condition. Heat Mass Transf. 2019, 55, 2277–2288. [Google Scholar] [CrossRef]
- Takamine, T.; Furukawa, D.; Watanabe, S.; Watanabe, H.; Miyagawa, K. Experimental Analysis of Diffuser Rotating Stallin a Three-Stage Centrifugal Pump. Int. J. Fluid Mach. Syst. 2018, 11, 77–84. [Google Scholar] [CrossRef]
- Liu, X.-D.; Li, Y.-J.; Liu, Z.-Q.; Yang, W.; Tao, R. Dynamic evolution process of rotating stall vortex based on high-frequency PIV system in centrifugal impeller. Ocean Eng. 2022, 259, 111944. [Google Scholar] [CrossRef]
- Pavesi, G.; Cavazzini, G.; Ardizzon, G. Time–frequency characterization of the unsteady phenomena in a centrifugal pump. Int. J. Heat Fluid Flow 2008, 29, 1527–1540. [Google Scholar] [CrossRef]
- Takao, S.; Konno, S.; Ejiri, S.; Miyabe, M. Suppression of Diffuser Rotating Stall in A Centrifugal Pump by Use of Slit Vane. In Proceedings of the Fluids Engineering Division Summer Meeting, Online, 10–12 August 2021; American Society of Mechanical Engineers: New York, NY, USA, 2021; Volume 85291, p. V002T03A007. [Google Scholar]
- Yan, H.; Heng, Y.; Zheng, Y.; Tao, R.; Ye, C. Investigation on Pressure Fluctuation of the Impellers of a Double-Entry Two-Stage Double Suction Centrifugal Pump. Water 2022, 14, 4065. [Google Scholar] [CrossRef]
- Griffini, D.; Insinna, M.; Salvadori, S.; Martelli, F. Clocking Effects of Inlet Nonuniformities in a Fully Cooled High-Pressure Vane: A Conjugate Heat Transfer Analysis. J. Turbomach. 2015, 138, 021006. [Google Scholar] [CrossRef]
- Benigni, H.; Jaberg, H.; Yeung, H.; Salisbury, T.; Berry, O.; Collins, T. Numerical Simulation of Low Specific Speed American Petroleum Institute Pumps in Part-Load Operation and Comparison with Test Rig Results. J. Fluids Eng. 2012, 134, 024501. [Google Scholar] [CrossRef]
- Gu, Y.; Pei, J.; Yuan, S.; Wang, W.; Zhang, F.; Wang, P.; Liu, Y. Clocking effect of vaned diffuser on hydraulic performance of high-power pump by using the numerical flow loss visualization method. Energy 2019, 170, 986–997. [Google Scholar] [CrossRef]
- Wang, W.; Pei, J.; Yuan, S.; Yin, T. Experimental investigation on clocking effect of vaned diffuser on performance characteristics and pressure pulsations in a centrifugal pump. Exp. Therm. Fluid Sci. 2018, 90, 286–298. [Google Scholar] [CrossRef]
- Tan, M.; Lian, Y.; Wu, X.; Liu, H. Numerical investigation of clocking effect of impellers on a multistage pump. Eng. Comput. 2019, 36, 1469–1482. [Google Scholar] [CrossRef]
- Menter, F.R. Improved Two-Equation k-Turbulence Models for Aerodynamic Flows; NASA Technical Memorandum, 103975(1_), 3t; NASA: Washington, DC, USA, 1992.
- Hellsten, A. Some improvements in Menter’s k-omega SST turbulence model. In Proceedings of the 29th AIAA, Fluid Dynamics Conference, Albuquerque, NM, USA, 15–18 June 1998; p. 2554. [Google Scholar]
- Menter, F.R.; Egorov, Y. SAS turbulence modelling of technical flows. In Direct and Large-Eddy Simulation VI; Springer: Dordrecht, The Netherlands, 2006; pp. 687–694. [Google Scholar]
- Pedersen, N. Experimental Investigation of Flow Structures in a Centrifugal Pump Impeller Using Particle Image Velocimetry. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2000. [Google Scholar]
- Li, D.; Song, Y.; Lin, S.; Wang, H.; Qin, Y.; Wei, X. Effect mechanism of cavitation on the hump characteristic of a pump-turbine. Renew. Energy 2020, 167, 369–383. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, H.; Zhou, L.; Liu, Z.; Zeng, Y. Optimization design of the unsmooth bionic structure of a hydrofoil leading edge based on the Grey–Taguchi method. Proc. Inst. Mech. Eng. Part M J. sEng. Marit. Environ. 2022, 14750902221128140. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, C.; An, D.; Huang, W.; Heng, Y.; Zheng, Y. Investigation on Stall Characteristics of Centrifugal Pump with Guide Vanes. Water 2023, 15, 21. https://doi.org/10.3390/w15010021
Ye C, An D, Huang W, Heng Y, Zheng Y. Investigation on Stall Characteristics of Centrifugal Pump with Guide Vanes. Water. 2023; 15(1):21. https://doi.org/10.3390/w15010021
Chicago/Turabian StyleYe, Changliang, Dongsen An, Wanru Huang, Yaguang Heng, and Yuan Zheng. 2023. "Investigation on Stall Characteristics of Centrifugal Pump with Guide Vanes" Water 15, no. 1: 21. https://doi.org/10.3390/w15010021







