Understanding Drainage Dynamics and Irrigation Management in a Semi-Arid Mediterranean Basin
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area Description
2.2. Water Balance
2.2.1. Water Balance Equation
2.2.2. Irrigation and Crop Water Requirements
- Relative Water Irrigation Index (RWII)
- Irrigation Efficiency (IE)
- Water Efficiency (WE):
2.2.3. Remote Sensing for Evapotranspiration
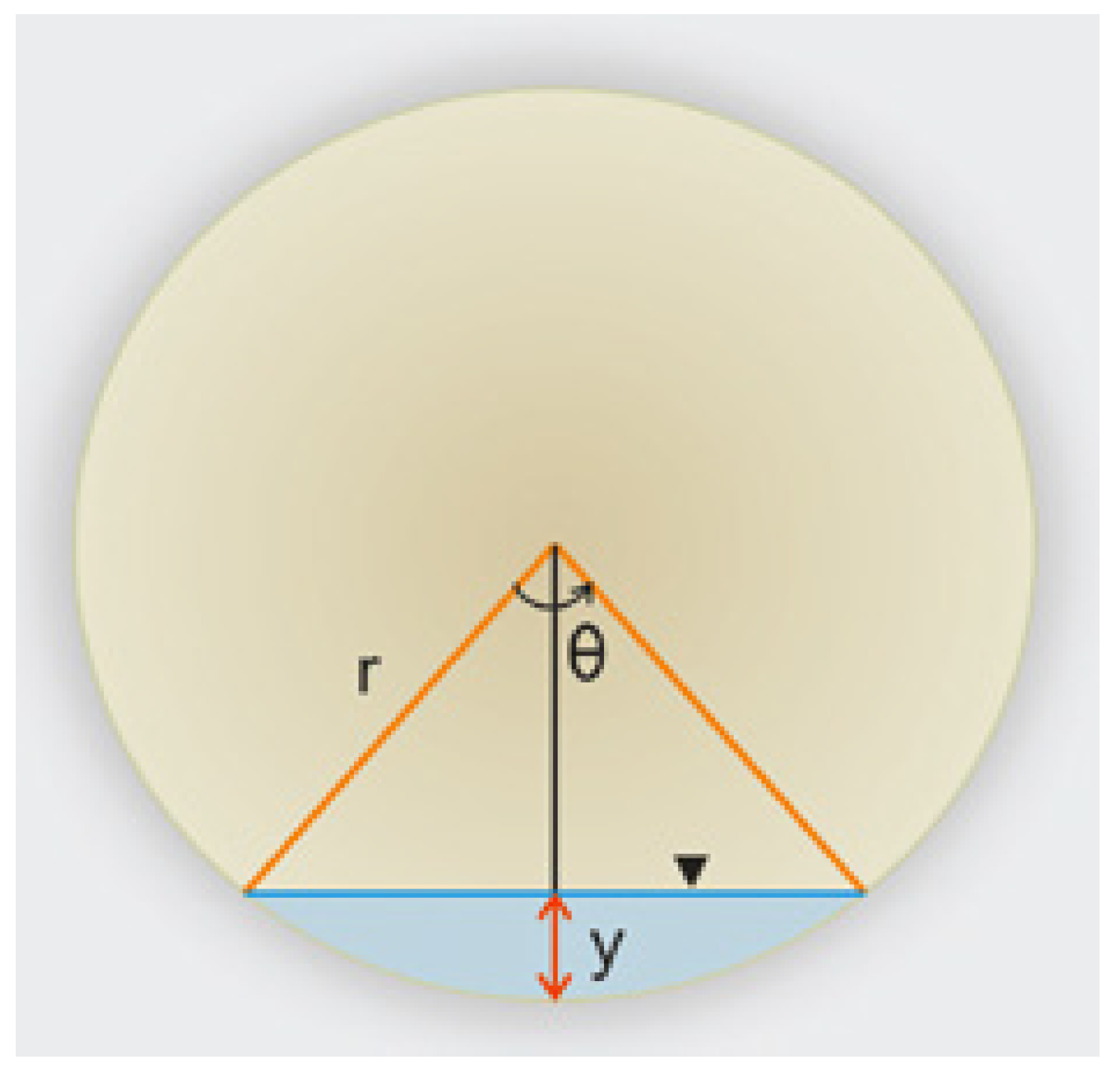
2.2.4. Drainage Water
- Drainage ratio (DR), which corresponds to the leaching fraction, was calculated through Equation (11):
- Rainwater drainage ratio (RWDR)
- Irrigation drainage ratio (IDR)
- HEC-HMS model
- Sub-basin model
- Meteorological model
2.2.5. Statistical Analysis
3. Results
3.1. Amount of Irrigation Water Applied
3.2. Estimated Crop Water Irrigation Requirements
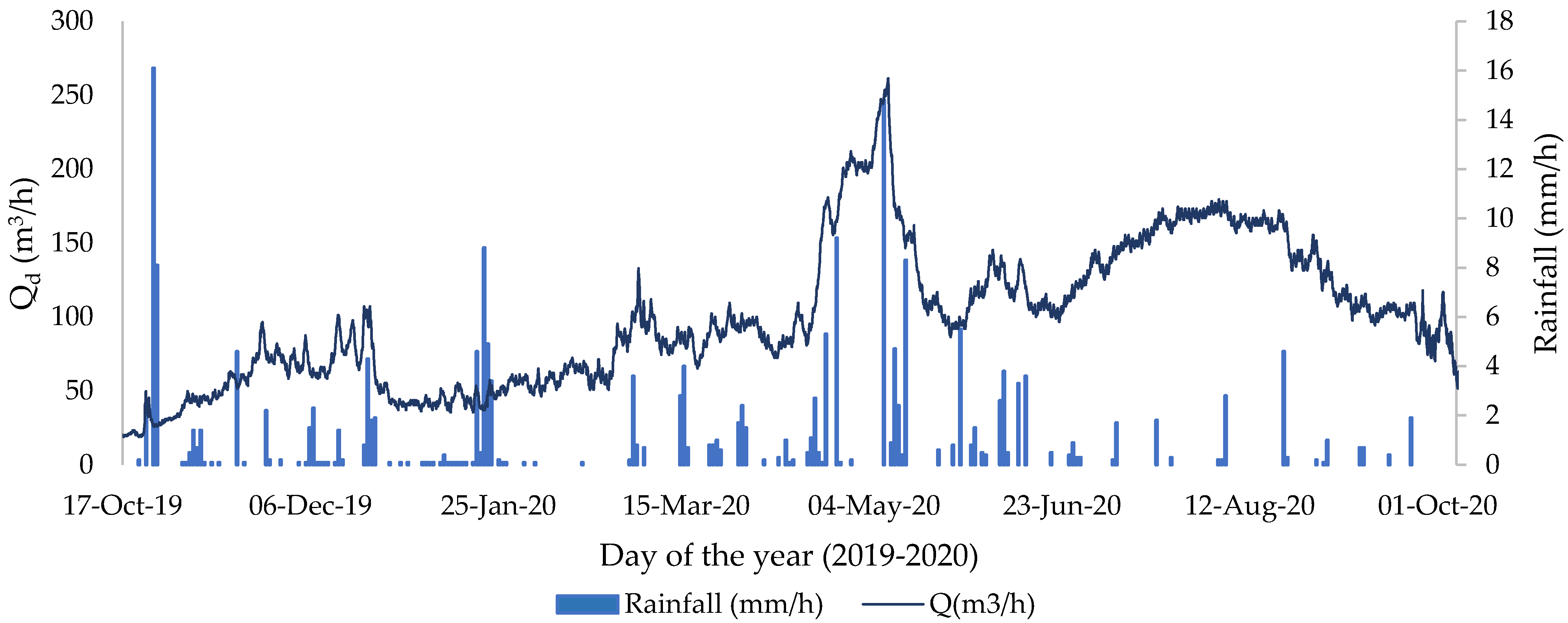
3.3. Drainage Water
HEC-HMS Model
3.4. Actual Evapotranspiration (ETa)
3.5. Water Balance at the Sub-Basin Level
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Organisation for Economic Co-Operation and Development OECD Environmental Outlook to 2050: The Consequences of Inaction—Key Facts and Figures—OECD. Available online: https://www.oecd.org/env/indicators-modelling-outlooks/oecdenvironmentaloutlookto2050theconsequencesofinaction-keyfactsandfigures.htm (accessed on 3 October 2022).
- Confederación Hidrográfica del Ebro, Ministerio para la Transición Ecológica. Usos del Agua—Portal CHEbro. Available online: https://www.chebro.es/en-GB/usos-del-agua (accessed on 3 October 2022).
- Philip, J.R. Plant Water Relations: Some Physical Aspects. Annu. Rev. Plant Physiol. 1966, 17, 245–268. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; Volume 5. [Google Scholar] [CrossRef] [Green Version]
- Brouwer, M.; Heibloem, C. Irrigation Water Needs. In Irrigation Water Management: Training Manual no. 3; Food and Agriculture Organization of the United Nations: Rome, Italy, 1986. [Google Scholar]
- Van Aart, R.; Bos, M.G.; Braun, H.M.H.; Lenselink, K.J.; Ritzema, H.P. Drainage Principles and Applications, 3rd ed.; Ritzema, H.P., Ed.; International Institute for Land Reclamation and Improvement: Wageningen, The Netherland, 2006; Volume 16, ISBN 9070754339. [Google Scholar]
- Blann, K.L.; Anderson, J.L.; Sands, G.R.; Vondracek, B. Effects of agricultural drainage on aquatic ecosystems: A review. Crit. Rev. Environ. Sci. Technol. 2009, 39, 909–1001. [Google Scholar] [CrossRef]
- Merchán, D.; Sanz, L.; Alfaro, A.; Pérez, I.; Goñi, M.; Solsona, F.; Hernández-García, I.; Pérez, C.; Casalí, J. Irrigation implementation promotes increases in salinity and nitrate concentration in the lower reaches of the Cidacos River (Navarre, Spain). Sci. Total Environ. 2020, 706, 135701. [Google Scholar] [CrossRef] [PubMed]
- Spaling, H.; Smit, B. A conceptual model of cumulative environmental effects of agricultural land drainage. Agric. Ecosyst. Environ. 1995, 53, 99–108. [Google Scholar] [CrossRef]
- Dougherty, T.C.; Hall, A. Environmental Impact Assessment of Irrigation and Drainage Projects; Food and Agriculture Organization of the United Nations: Rome, Italy, 1995; Volume 53. [Google Scholar]
- Doorenbos, J.; Pruitt, W.O. Guidelines for Predicting Crop Water Requirements; Food and Agriculture Organization of the United Nations: Rome, Italy, 1977; Volume 24. [Google Scholar]
- Tanji, K.K.; Program, H.; Kielen, N.C. Agricultural Drainage Water Management in Arid and Semi-Arid Areas; Food and Agriculture Organization of the United Nations: Rome, Italy, 2002; Volume 61. [Google Scholar]
- Barros, R.; Isidoro, D.; Aragüés, R. Three study decades on irrigation performance and salt concentrations and loads in the irrigation return flows of La Violada irrigation district (Spain). Agric. Ecosyst. Environ. 2012, 151, 44–52. [Google Scholar] [CrossRef] [Green Version]
- Barros, R.; Isidoro, D.; Aragüés, R. Long-term water balances in La Violada Irrigation District (Spain): II. Analysis of irrigation performance. Agric. Water Manag. 2011, 98, 1569–1576. [Google Scholar] [CrossRef] [Green Version]
- Schulz, S.; Becker, R.; Richard-Cerda, J.C.; Usman, M.; aus der Beek, T.; Merz, R.; Schüth, C. Estimating water balance components in irrigated agriculture using a combined approach of soil moisture and energy balance monitoring, and numerical modelling. Hydrol. Process. 2021, 35, e14077. [Google Scholar] [CrossRef]
- Tedeschi, A.; Beltrán, A.; Aragüés, R. Irrigation management and hydrosalinity balance in a semi-arid area of the middle Ebro river basin (Spain). Agric. Water Manag. 2001, 49, 31–50. [Google Scholar] [CrossRef]
- Gonçalves, J.M.; Ferreira, S.; Nunes, M.; Eugénio, R.; Amador, P.; Filipe, O.; Duarte, I.M.; Teixeira, M.; Vasconcelos, T.; Oliveira, F.; et al. Developing Irrigation Management at District Scale Based on Water Monitoring: Study on Lis Valley, Portugal. AgriEngineering 2020, 2, 78–95. [Google Scholar] [CrossRef]
- García-Garizábal, I.; Causapé, J.; Abrahao, R. Nitrate contamination and its relationship with flood irrigation management. J. Hydrol. 2012, 442–443, 15–22. [Google Scholar] [CrossRef]
- Abrahao, R.; Causapé, J.; García-Garizábal, I.; Merchán, D. Implementing irrigation: Salt and nitrate exported from the Lerma basin (Spain). Agric. Water Manag. 2011, 102, 105–112. [Google Scholar] [CrossRef]
- Andrés, R.; Cuchí, J.A. Salt and nitrate exports from the sprinkler-irrigated Malfarás creek watershed (Ebro river valley, Spain) during 2010. Environ. Earth Sci. 2014, 72, 2667–2682. [Google Scholar] [CrossRef]
- Sanderson, R. Introduction to Remote Sensing. 1991; Available online: https://www.researchgate.net/publication/349988121_Introduction_to_Remote_Sensing (accessed on 15 November 2020).
- Chuvieco, E. Fundamentals of Satellite Remote Sensing: An Environmental Approach, 3rd ed.; CRC press: Boca Raton, FL, USA, 2020. [Google Scholar] [CrossRef]
- Senay, G.B.; Leake, S.; Nagler, P.L.; Artan, G.; Dickinson, J.; Cordova, J.T.; Glenn, E.P. Estimating basin scale evapotranspiration (ET) by water balance and remote sensing methods. Hydrol. Process. 2011, 25, 4037–4049. [Google Scholar] [CrossRef]
- Fuzzo, D.F.S.; Carlson, T.N.; Kourgialas, N.N.; Petropoulos, G.P. Coupling remote sensing with a water balance model for soybean yield predictions over large areas. Earth Sci. Informatics 2019, 13, 345–359. [Google Scholar] [CrossRef]
- Garrido-Rubio, J.; González-Piqueras, J.; Campos, I.; Osann, A.; González-Gómez, L.; Calera, A. Remote sensing–based soil water balance for irrigation water accounting at plot and water user association management scale. Agric. Water Manag. 2020, 238. [Google Scholar] [CrossRef]
- Courault, D.; Seguin, B.; Olioso, A. Review on estimation of evapotranspiration from remote sensing data: From empirical to numerical modeling approaches. Irrig. Drain. Syst. 2005, 19, 223–249. [Google Scholar] [CrossRef]
- Liou, Y.A.; Kar, S.K. Evapotranspiration Estimation with Remote Sensing and Various Surface Energy Balance Algorithms—A Review. Energies 2014, 7, 2821–2849. [Google Scholar] [CrossRef] [Green Version]
- Merlin, O.; Chirouze, J.; Olioso, A.; Jarlan, L.; Chehbouni, G.; Boulet, G. An image-based four-source surface energy balance model to estimate crop evapotranspiration from solar reflectance/thermal emission data (SEB-4S). Agric. For. Meteorol. 2014, 184, 188–203. [Google Scholar] [CrossRef]
- Jofre-Cekalovic, C.; Nieto, H.; Girona, J.; Pamies-Sans, M.; Bellvert, J. Accounting for Almond Crop Water Use under Different Irrigation Regimes with a Two-Source Energy Balance Model and Copernicus-Based Inputs. Remote Sens. 2022, 14, 2106. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Jones, S.B.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, Proximal, and Satellite Remote Sensing of Soil Moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar] [CrossRef] [Green Version]
- Hssaine, B.A.; Chehbouni, A.; Er-Raki, S.; Khabba, S.; Ezzahar, J.; Ouaadi, N.; Ojha, N.; Rivalland, V.; Merlin, O. On the Utility of High-Resolution Soil Moisture Data for Better Constraining Thermal-Based Energy Balance over Three Semi-Arid Agricultural Areas. Remote Sens. 2021, 13, 727. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Melton, F.; Johnson, L.; Wang, T.; López-Urrea, R.; Cancela, J.J.; Allen, R.G. Prediction of crop coefficients from fraction of ground cover and height. Background and validation using ground and remote sensing data. Agric. Water Manag. 2020, 241, 106197. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Kustas, W.P. Upscaling of evapotranspiration fluxes from instantaneous to daytime scales for thermal remote sensing applications. Hydrol. Earth Syst. Sci. 2014, 18, 1885–1894. [Google Scholar] [CrossRef] [Green Version]
- Villar Mir, J.M.; Pascual, M.; Rufat, J.; Villar, P. El impacto del riego en la calidad del agua de drenaje en una nueva zona regable. Ing. Agua 2015, 19, 241–253. [Google Scholar] [CrossRef] [Green Version]
- Gil, C.; Santos, J.A.; Esnaola, J.M. Mapa geológico y Memoria de la Hoja no 359 (Balaguer). In Mapa Geológico de España Escala 1:50.000; Instituto Tecnologico Geomeinero de Espa: Madrid, Spain, 1998. [Google Scholar]
- Mensua, S.; Fernández, S.M.; Ibáñez, M.J.I.M.; Marcellán, M.J.I.; Yetano, M.; Ruiz, M.Y. Sector Central de la Depresión del Ebro, Mapa de Terrazas Fluviales y Glacis, 1st ed.; Universidad de Zaragoza, Departamento de Geografía: Zaragoza, Spain, 1977. [Google Scholar]
- Ascaso, E.; Boixadera, J.; Olarieta, J.R. Detailed Soil Survey Map of Catalonia of the Irrigated Area by Algerri-Balaguer Canal (La Noguera) (1:25,000); Departament d’Agricultura, Alimentació i Acció Rural, Generalitat de Catalunya: Barcelona, Spain, 1991. [Google Scholar]
- Institut Cartogràfic i Geològic de Catalunya. Balaguer 359-2-1 (64–27) Soil Map 1:25.000. Available online: https://www.icgc.cat/Administracio-i-empresa/Descarregues/Cartografia-geologica-i-geotematica/Cartografia-de-sols/GT-IV.-Mapa-de-sols-1-25.000 (accessed on 15 November 2020).
- Soil Survey Staff. Keys to Soil Taxonomy, 12th ed.; USDA-Natural Resources Conservation Service: Washington, DC, USA, 2014; ISBN 0926487221. [Google Scholar]
- Griffiths, E. Classification of land for irrigation in New Zealand. New Zeal. Soil Bur. Sci. Rep. 1975, 22, 66. [Google Scholar]
- Ayers, R.S.; Wescot, D.W. Water Quality for agriculture; Food and Agriculture Organization of the United Nations: Rome, Italy, 1985; Volume 29. [Google Scholar]
- European Comission. WAD | World Atlas of Desertification. Available online: https://wad.jrc.ec.europa.eu/patternsaridity (accessed on 13 October 2022).
- Departament d’Acció Climàtica, Alimentació i Agenda Rural. Dades agrometeorològiques. Available online: https://ruralcat.gencat.cat/agrometeo.estacions (accessed on 24 January 2022).
- Wang, L.; Liu, H. An efficient method for identifying and filling surface depressions in digital elevation models for hydrologic analysis and modelling. Int. J. Geogr. Inf. Sci. 2006, 20, 193–213. [Google Scholar] [CrossRef]
- Institut Cartogràfic i Geològic de Catalunya. Digital Elevation Model 2 × 2. Available online: https://www.icgc.cat/ca/Descarregues/Elevacions/Model-d-elevacions-del-terreny-de-2x2-m (accessed on 20 January 2021).
- Departament d’Acció Climàtica, Alimentació i Agenda Rural. DUN-SIGPAC CROP MAP. Available online: http://agricultura.gencat.cat/ca/serveis/cartografia-sig/aplicatius-tematics-geoinformacio/sigpac/mapa-cultius/ (accessed on 1 November 2021).
- Ministry of Agriculture Fisheries and Food. Sistema de Información Geográfica de Parcelas Agrícolas (SIGPAC). Available online: https://www.mapa.gob.es/es/agricultura/temas/sistema-de-informacion-geografica-de-parcelas-agricolas-sigpac-/default.aspx (accessed on 3 November 2022).
- Kumar, R.; Kumar, M.; Farooq, Z.; Dadhich, S.M. Evaluation of models and approaches for effective rainfall in irrigated agriculture—An overview. J. Soil Water Conserv. 2017, 16, 32–36. [Google Scholar] [CrossRef]
- Martin, D.L.; Stegman, E.C.; Fereres, E. Irrigation Scheduling Principles. In Management of Farm Irrigation Systems; Glenn, J.H., Terry, A.H., Kenneth, H.S., Eds.; ASAE Monograph: St. Joseph, MI, USA, 1990. [Google Scholar]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Guzinski, R.; Nieto, H.; Sandholt, I.; Karamitilios, G. Modelling high-resolution actual evapotranspiration through Sentinel-2 and Sentinel-3 data fusion. Remote Sens. 2020, 12, 1433. [Google Scholar] [CrossRef]
- Bellvert, J.; Jofre-Ĉekalović, C.; Pelechá, A.; Mata, M.; Nieto, H. Feasibility of using the two-source energy balance model (TSEB) with Sentinel-2 and Sentinel-3 images to analyze the spatio-temporal variability of vine water status in a vineyard. Remote Sens. 2020, 12, 2299. [Google Scholar] [CrossRef]
- Priestley, C.H.B.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol. 1999, 94, 13–29. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F. Sentinel2 ToolBox Level2 Products S2ToolBox Level 2 products: LAI, FAPAR, FCOVER Version 1.1; INRA-CSE: Avignon, France, 2016. [Google Scholar]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Gao, F.; Kustas, W.P.; Anderson, M.C. A Data Mining Approach for Sharpening Thermal Satellite Imagery over Land. Remote Sens. 2012, 4, 3287–3319. [Google Scholar] [CrossRef] [Green Version]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied hydrology. J. Hydrol. 1968, 6, 224–225. [Google Scholar] [CrossRef]
- Feldman, A. Hydrologic Modeling System HEC-HMS Technical Reference Manual; U.S. Army Corps of Engineers: Washington, DC, USA, 2000. [Google Scholar]
- Schaffenberg, W. Hydrologic Modeling System HEC-HMS, User Manual: Version 4.0; U.S. Army Corps of Engineers, Hydrologic Engineering Center HEC: Davis, CA, USA, 2013. [Google Scholar]
- U.S. Army Corps of Engineers. Hydrologic Modeling System (HEC-HMS) Application Guide: Version 4.0; Institute for Water Resources, Hydrologic Engineering Center: Davis, CA, USA, 2015. [Google Scholar]
- Cabrera-balarezo, J.J.; Timbe-castro, L.M.; Crespo-sánchez, P.J. Evaluation of the HEC-HMS model for the hydrological simulation of a paramo basin • Evaluación del modelo HEC-HMS para la simulación hidrológica de una cuenca de páramo. DYNA 2019, 86, 338–344. [Google Scholar]
- Duque-Sarango, P.; Patiño, D.M.; López, X.E. Evaluación del Sistema de Modelamiento Hidrológico HEC-HMS para la Simulación Hidrológica de una Microcuenca Andina Tropical. Inf. Tecnol. 2019, 30, 351–362. [Google Scholar] [CrossRef] [Green Version]
- Belayneh, A.; Sintayehu, G.; Gedam, K.; Muluken, T. Evaluation of satellite precipitation products using HEC-HMS model. Model. Earth Syst. Environ. 2020, 6, 2015–2032. [Google Scholar] [CrossRef]
- Bhuiyan, H.A.K.M.; McNairn, H.; Powers, J.; Merzouki, A. Application of HEC-HMS in a cold region watershed and use of RADARSAT-2 soil moisture in initializing the model. Hydrology 2017, 4, 9. [Google Scholar] [CrossRef]
- Rauf, A.-U.; Ghumman, A.R. Impact assessment of rainfall-runoffsimulations on the flow duration curve of the Upper Indus river-a comparison of data-driven and hydrologic models. Water 2018, 10, 876. [Google Scholar] [CrossRef] [Green Version]
- Ministerio de Fomento. Boletín Oficial del Estado; Ministerio de Fomento: Madrid, Spain, 2016; Volume 60, pp. 18882–19023. [Google Scholar]
- USDA. Urban Hydrology for Small Watersheds; USDA: Washington, DC, USA, 1986. [Google Scholar]
- Pereira, L.S.; Paredes, P.; López-Urrea, R.; Hunsaker, D.J.; Mota, M.; Mohammadi Shad, Z. Standard single and basal crop coefficients for vegetable crops, an update of FAO56 crop water requirements approach. Agric. Water Manag. 2021, 243, 106196. [Google Scholar] [CrossRef]
- Cavero, J.; Beltrán, A.; Aragüés, R. Nitrate Exported in Drainage Waters of Two Sprinkler-Irrigated Watersheds. J. Environ. Qual. 2003, 32, 916–926. [Google Scholar] [CrossRef]
- Abrahao, R.; Causapé, J.; García-Garizábal, I.; Merchán, D. Implementing irrigation: Water balances and irrigation quality in the Lerma basin (Spain). Agric. Water Manag. 2011, 102, 97–104. [Google Scholar] [CrossRef]
- Pascolini-Campbell, M.A.; Reager, J.T.; Fisher, J.B. GRACE-based Mass Conservation as a Validation Target for Basin-Scale Evapotranspiration in the Contiguous United States. Water Resour. Res. 2020, 56, e2019WR026594. [Google Scholar] [CrossRef]
- Liu, Y.; Racah, E.; Correa, J.; Khosrowshahi, A.; Lavers, D.; Kunkel, K.; Wehner, M.; Collins, W. Application of Deep Convolutional Neural Networks for Detecting Extreme Weather in Climate Datasets. arXiv 2016, arXiv:1605.01156. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Smith, M.; Raes, D.; Wright, J.L. FAO-56 Dual Crop Coefficient Method for Estimating Evaporation from Soil and Application Extensions. J. Irrig. Drain. Eng. 2005, 131, 2–13. [Google Scholar] [CrossRef] [Green Version]
- García-Garizábal, I.; Valenzuela, J.C.; Abrahão, R. Evolution of the efficiency and agro-environmental impact of a traditional irrigation land in the middle Ebro Valley (2001–2007). Spanish J. Agric. Res. 2009, 7, 465–473. [Google Scholar] [CrossRef]

| Type of Soil Series | USDA Soil Taxonomy | Depth (m) | Hydraulic Conductivity (m/Day) | Infiltration Velocity (m/Day) | Subjacent Material |
|---|---|---|---|---|---|
| Bellcaire | Typic Calcixerepts | 0.8–1.2 | 0.12–1.6 | 0.12–1.6 | Lutite |
| Bellvís | Petrocalcic Calcixerepts | 0.4–0.8 | 1.6–3.1 | 0.5–3.1 | Lutite |
| Comelles | Typic Xerofluvents | >1.20 | 0.5–1.6 | 0.1–0.5 | Lutite |
| Cava | Xeric Petrocalcids | 0.2–0.4 | 3.1–6 | 3.1–6 | Cemented Gravel |
| Seana | Xeric Petrocalcids | 0.4–0.6 | 3.1–6 | 3.1–6 | Cemented Gravel |
| Crop Type | Land Use (ha) | % Land Use | Crop Cycle(s) |
|---|---|---|---|
| Maize | 172 | 41.1 | April-October |
| Alfalfa | 95 | 22.7 | Permanent |
| Barley | 73 | 17.4 | January-June |
| Wheat + Maize | 30 | 7.1 | January-October |
| Olive trees | 22 | 5.3 | Permanent |
| Barley + Maize | 14 | 3.3 | January-October |
| Peas + Maize | 8 | 1.9 | February-October |
| Soybeans | 2 | 0.5 | May-September |
| Grapevine | 2 | 0.5 | Permanent |
| Total | 419 | 100 |
| Crop | Sowing Time (month) | L ini | L dev | L mid | L lat | L total | Kcini | Kcmid | Kclat |
|---|---|---|---|---|---|---|---|---|---|
| Maize (FAO 700) | May | 30 | 45 | 45 | 30 | 150 | 0.3 | 1.2 | 0.6 |
| Maize * (FAO 300) | June | 20 | 30 | 30 | 20 | 100 | 0.3 | 1.2 | 0.6 |
| Alfalfa | March | 30 | 30 | 60 | 60 | 180 | 0.4 | 0.95 | 0.9 |
| Barley | January | 30 | 40 | 40 | 30 | 140 | 0.3 | 1.15 | 0.25 |
| Wheat | January | 30 | 40 | 40 | 30 | 140 | 0.7 | 1.15 | 0.3 |
| Peas | February | 30 | 30 | 30 | 30 | 120 | 0.5 | 1.15 | 0.3 |
| Soybeans | May | 20 | 30 | 30 | 25 | 105 | 0.4 | 1.15 | 0.5 |
| Olive Tree | - | 20 | 60 | 90 | 60 | 230 | 0.65 | 0.7 | 0.7 |
| Grapevine | - | 20 | 50 | 75 | 60 | 205 | 0.3 | 0.7 | 0.45 |
| Sub-Basin Model | |||
|---|---|---|---|
| Parameter Method | Method Used | Values | |
| Discretization model | No discretization | - | - |
| Canopy method | Simple canopy | Initial storage (%) | 33 |
| Max storage (mm) | 40 | ||
| Evapotranspiration | Only in dry periods | ||
| Uptake method | Simple | ||
| Surface method | None | - | - |
| Loss method | SCS curve number | Ia (mm) | 14 |
| CN | 79 | ||
| Transform method | Clark unit hydrograph | Method | Standard |
| Time of concentration (h) | 3.12 | ||
| Storage coefficient (h) | 5.8 | ||
| Time-Area method | Default | ||
| Baseflow method | Monthly constant | Monthly value (m3/s) | 0.005 |
| Crop | Average Irrigation (m3/ha) | Standard Deviation (m3/ha) | Total Water Applied (m3) | Number of Fields (n) |
|---|---|---|---|---|
| Maize | 7574 A | 2294 | 1,287,119 | 13 |
| Alfalfa | 6598 A | 1600 | 660,288 | 3 |
| Barley | 2371 B | 1143 | 219,100 | 5 |
| Wheat + Maize | 6438 A | 143 | 191,815 | 3 |
| Olive | 2320 B | 3327 | 54,266 | 8 |
| Barley + Maize | 7879 A | 851 | 105,652 | 4 |
| Peas + Maize | 5105 A,B | 292 | 40,176 | 2 |
| Soybeans | 6067 A,B | 0 | 13,832 | 1 |
| Grapevine | 680 B | 0 | 1531 | 1 |
| Crop | ETc ini (mm) | ETc mid (mm) | ETc lat (mm) | ETc (mm) | NIR (mm) | GIR (mm) |
|---|---|---|---|---|---|---|
| Alfalfa | 26 | 352 | 293 | 672 | 556 | 654 |
| Maize (FAO 700) | 41 | 571 | 31 | 643 | 591 | 696 |
| Maize (FAO 300) | 45 | 391 | 62 | 499 | 484 | 569 |
| Barley | 5 | 224 | 34 | 264 | 109 | 129 |
| Wheat | 13 | 245 | 41 | 298 | 144 | 169 |
| Peas | 22 | 174 | 41 | 236 | 134 | 158 |
| Olive Tree | 43 | 488 | 36 | 567 | 332 | 391 |
| Soybeans | 54 | 324 | 76 | 454 | 403 | 474 |
| Grapevine | 20 | 260 | 147 | 426 | 191 | 225 |
| Crop | Land Use (ha) | GIR (m3/ha) | I (m3/ha) | GIR (m3) | RWII (%) |
|---|---|---|---|---|---|
| Maize | 172 | 6958 | 7574 | 1,196,756 | −8.9 |
| Alfalfa | 95 | 6544 | 6598 | 621,669 | −0.8 |
| Barley | 73 | 1285 | 2371 | 93,826 | −84.5 |
| Wheat + Maize | 30 | 7388 | 6438 | 221,644 | 12.9 |
| Olive | 22 | 3910 | 2320 | 86,023 | 40.7 |
| Barley + Maize | 14 | 6980 | 7879 | 101,128 | −12.9 |
| Peas + Maize | 8 | 7277 | 5105 | 58,215 | 29.8 |
| Soybeans | 2 | 4737 | 6067 | 9473 | −28.1 |
| Grapevine | 2 | 2251 | 680 | 4503 | 69.8 |
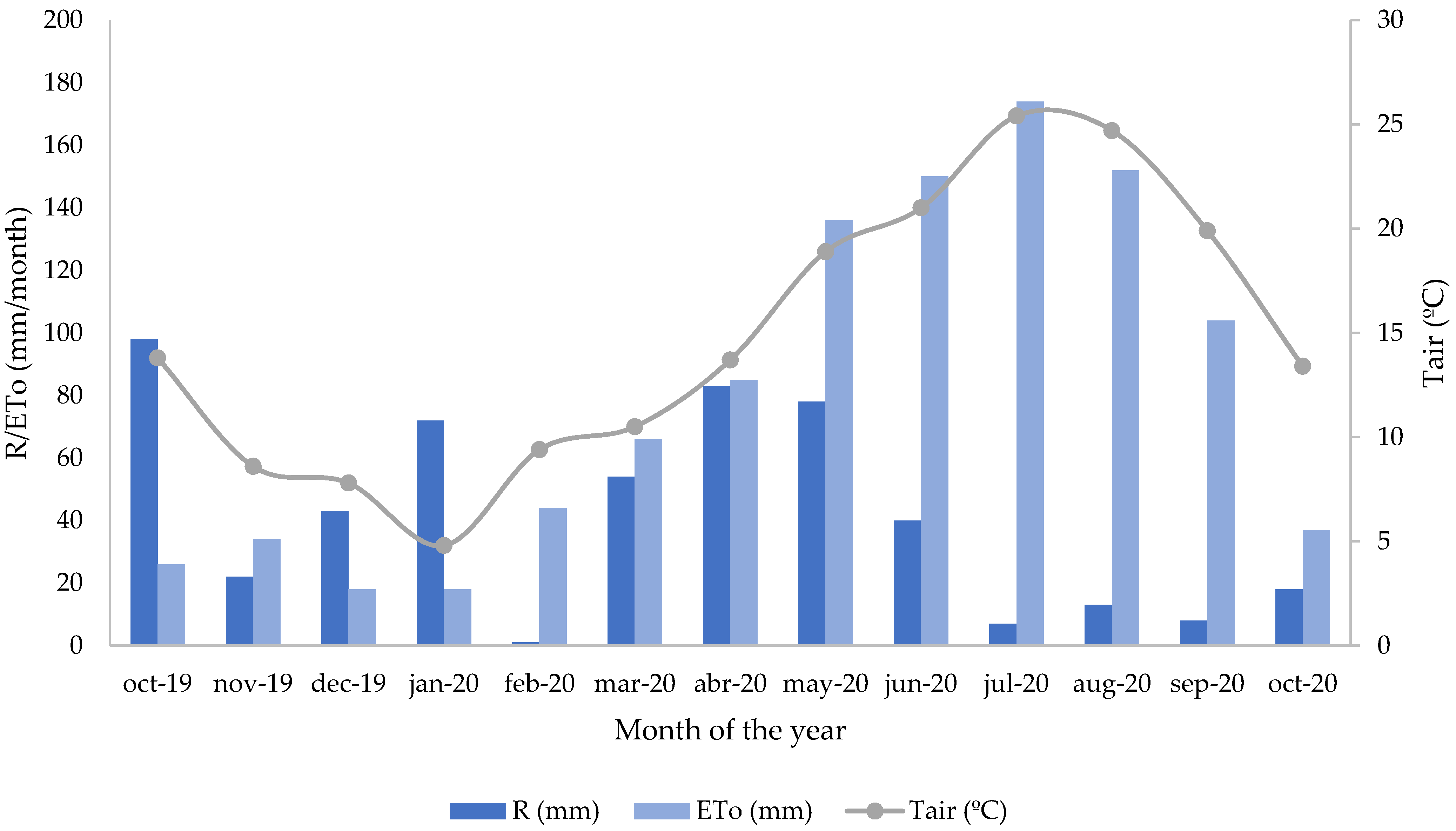
| Year | Month | y (mm) | V (m/s) | Qd (m3/s) | Qd (m3/day) | Qd (mm/day) | Qm (m3/month) | R (mm) |
|---|---|---|---|---|---|---|---|---|
| 2019 | October | 77 | 0.44 | 0.007 | 628 | 0.148 | 9422 | 98 |
| November | 115 | 0.56 | 0.016 | 1391 | 0.327 | 41,716 | 21 | |
| December | 124 | 0.58 | 0.019 | 1617 | 0.380 | 50,112 | 42 | |
| 2020 | January | 103 | 0.52 | 0.013 | 1109 | 0.261 | 34,367 | 72 |
| February | 122 | 0.57 | 0.018 | 1541 | 0.363 | 44,695 | 1 | |
| March | 146 | 0.63 | 0.025 | 2153 | 0.507 | 66,745 | 54 | |
| April | 176 | 0.68 | 0.035 | 3030 | 0.713 | 90,886 | 83 | |
| May | 194 | 0.71 | 0.041 | 3538 | 0.832 | 109,674 | 78 | |
| June | 170 | 0.68 | 0.033 | 2832 | 0.666 | 84,951 | 40 | |
| July | 200 | 0.73 | 0.043 | 3732 | 0.878 | 115,695 | 7 | |
| August | 201 | 0.73 | 0.044 | 3777 | 0.889 | 117,079 | 13 | |
| September | 158 | 0.66 | 0.029 | 2502 | 0.589 | 75,052 | 8 | |
| October | 118 | 0.56 | 0.017 | 1466 | 0.345 | 21,849 | 18 |
| Year | Month | ETo | ETc FAO 56 | ETa TSEB |
|---|---|---|---|---|
| 2019 | October | 64 | 39 | |
| November | 34 | 43 | ||
| December | 18 | 41 | ||
| 2020 | January | 18 | 4 | 46 |
| February | 44 | 13 | 58 | |
| March | 66 | 30 | 94 | |
| April | 85 | 50 | 114 | |
| May | 136 | 65 | 154 | |
| June | 150 | 115 | 106 | |
| July | 174 | 183 | 133 | |
| August | 152 | 159 | 161 | |
| September | 104 | 83 | 117 | |
| October | 65 | 37 | ||
| Total | 1110 | 702 | 1144 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altés, V.; Bellvert, J.; Pascual, M.; Villar, J.M. Understanding Drainage Dynamics and Irrigation Management in a Semi-Arid Mediterranean Basin. Water 2023, 15, 16. https://doi.org/10.3390/w15010016
Altés V, Bellvert J, Pascual M, Villar JM. Understanding Drainage Dynamics and Irrigation Management in a Semi-Arid Mediterranean Basin. Water. 2023; 15(1):16. https://doi.org/10.3390/w15010016
Chicago/Turabian StyleAltés, Víctor, Joaquim Bellvert, Miquel Pascual, and Josep Maria Villar. 2023. "Understanding Drainage Dynamics and Irrigation Management in a Semi-Arid Mediterranean Basin" Water 15, no. 1: 16. https://doi.org/10.3390/w15010016
APA StyleAltés, V., Bellvert, J., Pascual, M., & Villar, J. M. (2023). Understanding Drainage Dynamics and Irrigation Management in a Semi-Arid Mediterranean Basin. Water, 15(1), 16. https://doi.org/10.3390/w15010016







